No CrossRef data available.
Article contents
Embeddings of non-simply-connected 4-manifolds in 7-space. II. On the smooth classification
Published online by Cambridge University Press: 22 January 2021
Abstract
We work in the smooth category. Let 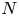 $N$ be a closed connected orientable 4-manifold with torsion free
$N$ be a closed connected orientable 4-manifold with torsion free 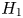 $H_1$, where
$H_1$, where 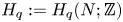 $H_q := H_q(N; {\mathbb Z} )$. Our main result is a readily calculable classification of embeddings
$H_q := H_q(N; {\mathbb Z} )$. Our main result is a readily calculable classification of embeddings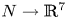 $N \to {\mathbb R}^7$up to isotopy, with an indeterminacy. Such a classification was only known before for
$N \to {\mathbb R}^7$up to isotopy, with an indeterminacy. Such a classification was only known before for 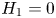 $H_1=0$ by our earlier work from 2008. Our classification is complete when
$H_1=0$ by our earlier work from 2008. Our classification is complete when 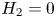 $H_2=0$ or when the signature of
$H_2=0$ or when the signature of  $N$ is divisible neither by 64 nor by 9.
$N$ is divisible neither by 64 nor by 9.
The group of knots 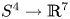 $S^4\to {\mathbb R}^7$ acts on the set of embeddings
$S^4\to {\mathbb R}^7$ acts on the set of embeddings 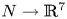 $N\to {\mathbb R}^7$ up to isotopy by embedded connected sum. In Part I we classified the quotient of this action. The main novelty of this paper is the description of this action for
$N\to {\mathbb R}^7$ up to isotopy by embedded connected sum. In Part I we classified the quotient of this action. The main novelty of this paper is the description of this action for  $H_1 \ne 0$, with an indeterminacy.
$H_1 \ne 0$, with an indeterminacy.
Besides the invariants of Part I, detecting the action of knots involves a refinement of the Kreck invariant from our work of 2008.
For  $N=S^1\times S^3$ we give a geometrically defined 1–1 correspondence between the set of isotopy classes of embeddings and a certain explicitly defined quotient of the set
$N=S^1\times S^3$ we give a geometrically defined 1–1 correspondence between the set of isotopy classes of embeddings and a certain explicitly defined quotient of the set 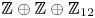 ${\mathbb Z} \oplus {\mathbb Z} \oplus {\mathbb Z} _{12}$.
${\mathbb Z} \oplus {\mathbb Z} \oplus {\mathbb Z} _{12}$.
MSC classification
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 152 , Issue 1 , February 2022 , pp. 163 - 181
- Copyright
- Copyright © The Author(s), 2021. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh



