Hostname: page-component-6bf8c574d5-xtvcr Total loading time: 0 Render date: 2025-02-22T11:48:59.845Z Has data issue: false hasContentIssue false
  • English
  • Français

Baer semigroup coordinatisations of distributive lattices

Published online by Cambridge University Press:  14 November 2011

T. S. Blyth
T. S. Blyth
Affiliation:
Mathematical Institute, University of St Andrews
Get access Rights & Permissions [Opens in a new window]

Synopsis

In a previous publication we investigated certain idempotent residuated mappings and showed how these could be used to provide a solution to the problem of finding a Baer semigroup coordinatisation of bounded modular lattices. Here we use essentially the same idempotents to provide a coordinatisation of bounded distributive lattices. Specifically, we prove that a bounded lattice L is distributive if and only if it can be coordinatised by a Baer semigroup S such that if eS, fS, gS ∈ R(S) with eS ∩ fS = eS ∩ gS then there are idempotents ē, 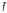, 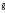∈ S such that ēS = eS, 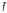S = fS, 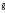S = gS and ē commutes with both 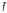and .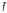

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 85 , Issue 3-4 , 1980 , pp. 307 - 312
Copyright
Copyright © Royal Society of Edinburgh 1980

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Blyth, T. S.. Baer semigroup coordinatisations of modular lattices. Proc. Roy. Soc. Edinburgh Sect. A, 81 (1978), 49–56.CrossRefGoogle Scholar
2Blyth, T. S. and Janowitz, M. F.. Residuation Theory (Oxford: Pergamon, 1972).Google Scholar