Hostname: page-component-6dbcb7884d-lhnfz Total loading time: 0 Render date: 2025-02-14T07:53:16.211Z Has data issue: false hasContentIssue false
  • English
  • Français

Some results for semi-stable radial solutions of k-Hessian equations with weight on ℝn

Part of: Elliptic equations and systems Partial differential equations

Published online by Cambridge University Press:  15 November 2022

Miguel Angel Navarro Open the ORCID record for Miguel Angel Navarro [Opens in a new window]  and
Justino Sánchez Open the ORCID record for Justino Sánchez [Opens in a new window]
Miguel Angel Navarro
Affiliation:
Departamento de Matemáticas, Universidade da Coruña, Campus de Esteiro, Rúa Mendizábal s/n, 15403 Ferrol, A Coruña, Spain (miguel.navarro.burgos@gmail.com)
Justino Sánchez
Affiliation:
Departamento de Matemáticas, Universidad de La Serena, Avenida Cisternas 1200, La Serena, Chile (jsanchez@userena.cl)
Get access Rights & Permissions [Opens in a new window]

Abstract

We devote this paper to study semi-stable nonconstant radial solutions of $S_k(D^2u)=w(\left \vert x \right \vert )g(u)$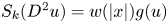 on the Euclidean space $\mathbb {R}^n$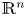. We establish pointwise estimates and necessary conditions for the existence of such solutions (not necessarily bounded) for this equation. For bounded solutions we estimate their asymptotic behaviour at infinity. All the estimates are given in terms of the spatial dimension $n$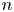, the values of $k$ 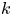and the behaviour at infinity of the growth rate function of $w$.

Keywords

k-Hessian operatorsemi-stable solutionsweight functions

MSC classification

Primary: 35B35: Stability
Secondary: 35J60: Nonlinear elliptic equations
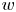Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 153 , Issue 5 , October 2023 , pp. 1751 - 1776
Check for updates
Copyright
Copyright © The Author(s), 2022. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Caffarelli, L., Nirenberg, L. and Spruck, J.. The dirichlet problem for nonlinear second-order elliptic equations. III. Functions of the eigenvalues of the Hessian. Acta Math. 155 (1985), 261–301.CrossRefGoogle Scholar
Castorina, D., Esposito, P. and Sciunzi, B.. Low dimensional instability for semilinear and quasilinear problems in $\Bbb R^N$. Commun. Pure Appl. Anal. 8 (2009), 1779–1793.CrossRefGoogle Scholar
Clément, Ph., Manásevich, R. and Mitidieri, E.. Some existence and non-existence results for a homogeneous quasilinear problem. Asymptot. Anal. 17 (1998), 13–29.Google Scholar
Farina, A. and Navarro, M. A.. Some liouville-type results for stable solutions involving the mean curvature operator : the radial case. Discrete Contin. Dyn. Syst. 40 (2020), 1233–1256.CrossRefGoogle Scholar
Fazly, M.. Effect of weights on stable solutions of a quasilinear elliptic equation. Can. Appl. Math. Q. 20 (2012), 435–464.Google Scholar
Lei, Y.. Critical conditions and finite energy solutions of several nonlinear elliptic PDEs in $R^n$. J. Differ. Equ. 258 (2015), 4033–4061.CrossRefGoogle Scholar
Navarro, M. A. and Sánchez, J.. A characterization of semistable radial solutions of $k$-Hessian equations. J. Math. Anal. Appl. 497 (2021), 124902.CrossRefGoogle Scholar
Navarro, M. A. and Villegas, S.. Semi-stable radial solutions of $p$-Laplace equations in $\Bbb {R}^N$. Nonlinear Anal. 149 (2017), 111–116.CrossRefGoogle Scholar
Villegas, S.. Asymptotic behavior of stable radial solutions of semilinear elliptic equations in $\mathbb {R}^N$. J. Math. Pures Appl. (9) 88 (2007), 241–250.CrossRefGoogle Scholar
Wang, Y. and Lei, Y.. On critical exponents of a $k$-Hessian equation in the whole space. Proc. Roy. Soc. Edinburgh Sect. A 149 (2019), 1555–1575.CrossRefGoogle Scholar