We consider the problem −Δu = c0K(x)upε, u > 0 in Ω, u = 0 on δΩ, where Ω is a smooth, bounded domain in ℝN, N ≥ 3, c0 = N(N − 2), pε = (N + 2)/(N − 2) − ε and K is a smooth, positive function on 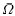. We prove that least-energy solutions of the above problem are non-degenerate for small ε > 0 under some assumptions on the coefficient function K. This is a generalization of the recent result by Grossi for K ≡ 1, and needs precise estimates and a new argument.