Hostname: page-component-6bf8c574d5-qdpjg Total loading time: 0 Render date: 2025-02-14T10:35:46.315Z Has data issue: false hasContentIssue false
  • English
  • Français

Strongly Jordan property and free actions of non-abelian free groups

Part of: Surfaces and higher-dimensional varieties Automorphic functions Complex spaces with a group of automorphisms

Published online by Cambridge University Press:  11 August 2022

Jin Hong Kim
Jin Hong Kim*
Affiliation:
Department of Mathematics Education, Chosun University, 309 Pilmun-daero, Dong-gu, Gwangju, 61452, Republic of Korea (jinhkim11@gmail.com)
Get access Rights & Permissions [Opens in a new window]

Abstract

Let $X$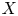 be a connected complex manifold and let $Z$ 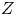be a compact complex subspace of $X$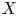. Assume that ${\rm Aut}(Z)$ 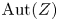is strongly Jordan. In this paper, we show that the automorphism group ${\rm Aut}(X,\, Z)$ 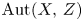of all biholomorphisms of $X$ preserving $Z$ is strongly Jordan. A similar result has been proved by Meng et al. for a compact Kähler submanifold $Z$ of $X$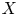 instead of a compact complex subspace $Z$ 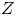of $X$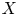. In addition, we also show some rigidity result for free actions of large groups on complex manifolds.

Keywords

Jordan propertystrongly JordanJordan constantsautomorphism groupsbirational automorphism groupsFujiki's classfinite bounded subgroupsfree actionsnon-abelian free groupscomplex torus

MSC classification

Primary: 14J50: Automorphisms of surfaces and higher-dimensional varieties
Secondary: 32M05: Complex Lie groups, automorphism groups acting on complex spaces
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 65 , Issue 3 , August 2022 , pp. 736 - 746
Check for updates
Copyright
Copyright © The Author(s), 2022. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Cantat, S., Paris-Romaskevich, O. and Xie, J., Free actions of large groups on complex threefolds, Bull. London Math. Soc., to appear; arXiv:2002.00494v1.Google Scholar
Curtis, C. W. and Reiner, I., Representation theory of finite groups and associative algebras, Pure and Applied Mathematics, Vol. XI (Interscience Publishers, New-York, 1962).Google Scholar
Demailly, J. P. and Păun, M., Numerical characterization of the Kähler cone of a compact Kähler manifold, Ann. Math. 159 (2004), 1247–1274.CrossRefGoogle Scholar
Fujiki, A., On automorphism groups of compact Kähler manifolds, Invent. Math. 44 (1978), 225–258.CrossRefGoogle Scholar
Kim, J. H., Jordan property and automorphism groups of normal compact Kähler varieties, Commun. Contemp. Math. 20(3) (2018), 1750024.CrossRefGoogle Scholar
Lieberman, D. I., Compactness of the Chow scheme: applications to automorphisms and deformations of Kähler manifolds, Fonctions de plusieurs variables complexes III, 140–186, Lect. Notes in Math. Vol. 670 (Springer, Berlin, 1978).Google Scholar
Meng, S. and Zhang, D.-Q., Jordan property for non-linear algebraic groups and projective varieties, Amer. J. Math. 140 (2018), 1133–1145.CrossRefGoogle Scholar
Meng, S., Perroni, F. and Zhang, D.-Q., Jordan property for automorphism groups of compact spaces in Fujiki's class $\mathcal {C}$, J. Topology 15(2) (2022), 806–814.CrossRefGoogle Scholar
Popov, V. L., On the Makar-Limanov, Derksen invariants, and finite automorphism groups of algebraic varieties, Affine Algebraic Geometry, 289–311, CRM Proc. Lecture Notes, Vol. 54 (Amer. Math. Soc., Providence, RI, 2011).CrossRefGoogle Scholar
Popov, V. L., The Jordan property for Lie groups and automorphism groups of complex spaces, Math. Notes 103 (2018), 811–819.CrossRefGoogle Scholar
Prokhorov, Y. and Shramov, C., Jordan property for groups of birational selfmaps, Compo. Math. 150 (2014), 2054–2072.CrossRefGoogle Scholar
Serre, J. P., Bounds for the orders of the finite subgroups of $G(k)$, Group Representation Theory, EPFL Press, Lausanne, 405–450, 2007.Google Scholar
Tosatti, V., Nakamaye's theorem on complex manifolds, Algebraic Geometry: Salt lake City 2015, 633–655, Proc. Sympos. Pure Math. Vol. 97 (Amer. Math. Soc., Providence, RI, 2018).CrossRefGoogle Scholar
Zarhin, Y. G., Theta groups and products of abelian and rational varieties, Proc. Edinb. Math. Soc. 57 (2014), 299–304.CrossRefGoogle Scholar
Zarhin, Y. G., Jordan groups and elliptic ruled surfaces, Transform. Groups 20 (2015), 557–572.CrossRefGoogle Scholar
Zhang, D.-Q., Dynamics of automorphisms on projective complex manifolds, J. Diff. Geom. 82 (2009), 691–722.Google Scholar