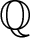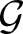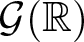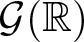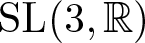1. Introduction
The notion of strongly dense was introduced by Breuillard, Green, Guralnick and Tao in [Reference Breuillard, Green, Guralnick and Tao3]. A subgroup Γ of a semi-simple 
$\mathbb{Q}$ algebraic group 
$\mathcal{G}$ is called strongly dense if every pair of non-commuting elements generate a Zariski dense subgroup. In particular, this says that every subgroup of Γ is abelian or Zariski dense. Amongst other things, Breuillard et al. [Reference Breuillard, Green, Guralnick and Tao3] prove that there exist strongly dense free subgroups in 
$\mathcal{G}(\mathbb{R})$ and, in [Reference Breuillard, Green, Guralnick and Tao3, Problem 1], state (which is slightly adapted here for convenience):
It remains a challenging problem to determine whether or not a Zariski dense subgroup of 
$\mathcal{G}(\mathbb{R})$ always contains a strongly dense free subgroup.
It is this we address here for certain subgroups of 
$\textrm{SL}(3,\mathbb{R})$. To state our results, we need to recall some of the notions of higher Teichmüller theory. While much of what we describe here applies more generally, (we draw attention to [Reference Alessandrini, Lee and Schaffhauser1] and [Reference Labourie7]) we focus almost exclusively on the cocompact Fuchsian group 
$ \Delta(p,q,r) $ which is such that 
$\Sigma(p,q,r)=\textbf{ H}^2/\Delta(p,q,r)$ has underlying surface being a two-sphere and there are three cone points of orders p, q and r where 
$1/p + 1/q + 1/r \lt 1$. These are the so-called (hyperbolic) triangle groups. The hyperbolic structure gives a discrete faithful representation 
$\rho_\infty: \Delta(p,q,r) \longrightarrow \textrm{PSL}(2,\mathbb{R})\cong \textrm{SO}_0(2,1)$ (the subgroup of 
$\textrm{SO}(2,1)$ preserving the upper sheet of the hyperboloid 
$x^2+y^2-z^2=-1$) which in this case is unique up to conjugacy. We may compose this representation with the three-dimensional representation 
$\tau_3: \textrm{SO}(2,1)\longrightarrow \textrm{SL}(3,\mathbb{R})$ to obtain the point 
$\tau_3\rho_\infty \in \textrm{Hom}( \Delta(p,q,r), \textrm{SL}(3,\mathbb{R}))$. As usual it is technically advantageous to work with characters and we define 
$X^{\mbox{Hit}}( \Delta(p,q,r), \textrm{SL}(3,\mathbb{R}))$ to be the component of the character variety of 
$X(\Delta(p,q,r), \textrm{SL}(3,\mathbb{R}))$ which contains the character of the representation 
$\tau_3\rho_\infty$. This is the so-called Hitchin component (for n = 3). Henceforth, for a representation ρ we denote its character by χρ.
This situation was analysed (in fact for general Fuchsian groups) in [Reference Goldman6] and [Reference Choi and Goldman5] where it is shown that the characters on the Hitchin component correspond to convex real projective structures on the underlying two-orbifold. In particular, with the additional hypothesis that none of 
$p,q,r$ is 2, there are interesting projective deformations and 
$X^{\mbox{Hit}}( \Delta(p,q,r), \textrm{SL}(3,\mathbb{R}))$ is an open two-disc and all the characters correspond to discrete and faithful representations of 
$\Delta(p,q,r)$. The rigidity of the hyperbolic structure on 
$\Sigma(p,q,r)$ implies that exactly one point of the Hitchin component corresponds to a representation into 
$\textrm{SO}(2,1)$, we call this the Fuchsian point (or character).
It is not difficult to see that every non-Fuchsian character χρ on the Hitchin component gives a representation whose image is Zariski dense in 
$\textrm{SL}(3,\mathbb{R})$. In this paper, we examine the question of when characters on the Hitchin component have associated representations that have strongly dense image.
It is an important fact, that follows from [Reference Goldman6] in this case (see also [Reference Alessandrini, Lee and Schaffhauser1] and [Reference Labourie7]) for the more general cases) that if 
$\gamma\in \Delta(p,q,r)$ is an element of infinite order and 
$\chi_\rho\in X^{\mbox{Hit}}( \Delta(p,q,r), \textrm{SL}(3,\mathbb{R}))$ then the three eigenvalues of 
$\rho(\gamma)$ are real, distinct and positive. At the Fuchsian point, one of these eigenvalues is 1 and motivated by this, given 
$\gamma\in \Delta(p,q,r)$ and some 
$\chi_\rho\in X^{\mbox{Hit}}(\Gamma, \textrm{SL}(3,\mathbb{R}))$ we say γ is Fuchsian at χρ if 
$\rho(\gamma)$ has a 1-eigenvalue.
Finding representations with strongly dense image in this setting is a somewhat delicate matter as a result of the following pair of simple observations.
Proposition 1.1. (i) Let Δ be a hyperbolic two-orbifold group with a cone point of even order, which in the case that Δ is a triangle group should be different from 2. Then there are elements of infinite order in Δ that are Fuchsian at all 
$\chi_{\rho}\in X^{{\textit{Hit}}}(\Delta, \textrm{SL}(3,\mathbb{R}))$.
(ii) There is a line of characters in 
$X^{{\textit{Hit}}}(\Delta(3,4,4), \textrm{SL}(3,\mathbb{R}))$ for which the associated representations do not have strongly dense image.
The proof of (i) is rather easy hyperbolic geometry: Given an element of order two, τ say, its action on the circle at infinity is free, so one can find a hyperbolic element γ whose fixed points are disjoint from the τ images. Now it follows from the classification of elements of SO(2,1) that (possibly after taking powers) the commutator of γ and 
$\tau{\cdot}\gamma{\cdot}\tau$ is a non-trivial hyperbolic. This commutator is conjugated to its inverse by τ, forcing an eigenvalue = 1.
The hypothesis ≠ 2 is simply to ensure that the Hitchin component is positive dimensional in the triangle group case. Of course, this is a rather general argument: for example, it can be used to show that any non-arithmetic surface which is a regular cover of a minimal orbifold containing torsion of even order and different from 2 in the triangle group case will have such an element.
For (ii), we require the more detailed understanding of 
$X^{\mbox{Hit}}( \Delta(3,4,4), \textrm{SL}(3,\mathbb{R}))$ that was developed in [Reference Long, Reid, Breuillard and Oh8, Theorem 2.3] building on the methods of [Reference Long, Reid and Thistlethwaite9]. Very briefly, what is shown in [Reference Long, Reid, Breuillard and Oh8] is that for 
$\chi_\rho\in X^{\mbox{Hit}}(\Delta(3,4,4), \textrm{SL}(3,\mathbb{R}))$ the representation ρ could be parametrized by variables u and v which are constrained by a certain discriminant polynomial being positive. In what follows, we use the notation 
$\rho_{(u,v)}$ to describe this association.
In this notation, it can be shown that along the line u = v, the infinite index subgroup of 
$\Delta(3,4,4)$ given by 
$ \lt a, b.a.b \gt \cong \mathbb{Z}/3 \ast \mathbb{Z}$ of 
$\Delta(3,4,4)$ preserves a quadratic form of signature 
$(2,1)$. Hence, none of the associated representations 
$\rho_{(u,u)}$ have strongly dense image.
A more subtle family of examples is offered in § 4.
Nonetheless, the principal result of this paper is the following, which to the authors’ knowledge is the first new family of examples to appear in print since the original work of [Reference Breuillard, Green, Guralnick and Tao3].
Theorem 1.2. Away from possibly countably many real subvarieties of codimension one, the representations on 
$X^{{\textit{Hit}}}( \Delta(3,4,4), \textrm{SL}(3,\mathbb{R}))$ have strongly dense image.
Thus in a very strong sense, almost all representations on 
$X^{\mbox{Hit}}(\Delta(3,4,4), \textrm{SL}(3,\mathbb{R}))$ have strongly dense image and by restricting such a representation to a torsion free subgroup of finite index yields representations of surface groups with strongly dense image.
In the context of [Reference Breuillard, Green, Guralnick and Tao3, Problem 1], we also have the following corollary.
Corollary 1.3. Under the hypothesis of Theorem 1.2, the image representations contain a strongly dense free subgroup.
Here is a sketch of the proof of Theorem 1.2. Using the parameterization of representations of 
$\Delta(3,4,4)$ described above, we first pass to a one-dimensional subfamily of representations ρs (the hyperbolic structure occurs at s = 0), whose characters all lie on the Hitchin component for s real. It is very slightly cleaner technically (and represents no loss) to work with the commutator subgroup of 
$\Delta(3,4,4)$ which has index 4 and is the fundamental group of the orbifold 
$S^2(3,3,3,3)$.
Fix a non-elementary subgroup 
$G \subset \pi_1(S^2(3,3,3,3))$, one may as well assume that G is free. We note that given any 
$\chi_\rho\in X^{\mbox{Hit}}(\Delta(3,4,4), \textrm{SL}(3,\mathbb{R}))$, certain Zariski closures for 
$\rho(G)$ can be ruled out for rather simple reasons. For example, at the purely group theoretic level, the Zariski closure cannot be a soluble (or nilpotent or abelian) algebraic subgroup since it contains 
$\rho(G)$, a free subgroup. There are also more subtle constraints which follow from the geometric fact that 
$\chi_\rho\in X^{\mbox{Hit}}(\Delta(3,4,4), \textrm{SL}(3,\mathbb{R}))$ correspond to a convex real projective structure on the orbifold. This guarantees that the Zariski closure of 
$\rho(G)$ cannot generically be 
$\textrm{SL}(2, \mathbb{R}) \times \mathbb{R}$ (see § 3).
In this way, we see that the only case of real interest is ruling out that the Zariski closure of 
$\rho(G)$ is 
$\textrm{SO}(2,1)$ and to this end the main claim is:
Theorem 1.4. Suppose that G is a non-elementary free subgroup of 
$\pi_1(S^2(3,3,3,3))$.
Then there is a real value s 0 so that 
$\rho_{s_0}(G)$ does not preserve any non-degenerate real quadratic form.
Theorem 1.2 follows quite easily from here and this is the utility of Theorem 1.4. Here is a sketch: It is not difficult to show using Theorem 1.4 that this implies that there is a 
$\gamma \in G$ for which 
$\rho_{s_0}(\gamma)$ is not Fuchsian and using the (u, v)-parameterization of 
$X^{\mbox{Hit}}(\Delta(3,4,4), \textrm{SL}(3,\mathbb{R}))$ described above, we deduce (see § 3 for details) that 
$\rho_{(u,v)}(\gamma)$ cannot be Fuchsian on the entire variety 
$X^{\mbox{Hit}}(\Delta(3,4,4), \textrm{SL}(3,\mathbb{R}))$. The condition that 
$\rho_{(u,v)}(\gamma)$ is Fuchsian is a polynomial condition on u and v which does not vanish identically and so away from that subvariety G cannot be Fuchsian. There are countably many finitely generated non-elementary subgroups contained in 
$\pi_1(S^2(3,3,3,3))$ and this proves the result.
Added in Proof:
Whilst the original version of this paper was being refereed, email discussions with Maxime Wolff resulted in the paper [Reference Long, Reid and Wolff10] which proves a more general version of the main result proved here; namely, it is shown that generically Hitchin representations in 
$\textrm{SL}(n,\mathbb{R})$ have strongly dense image. The proof of this result uses the irreducibility of the variety 
$\textrm{Hom}(\pi_1(\Sigma_g), \textrm{SL}(n,\mathbb{C}))$ for 
$g\geq 2$, residual freeness of 
$\pi_1(\Sigma_g)$ and the work of [Reference Breuillard, Green, Guralnick and Tao3]. However, it seems worthwhile to continue to keep this paper in its original form since the method is very different, in particular it is not dependent on the results of [Reference Breuillard, Green, Guralnick and Tao3].
We also point out that a follow-up paper to [Reference Breuillard, Green, Guralnick and Tao3] has now appeared [Reference Breuillard, Guralnick and Larsen4], and this latter paper also constructs strongly dense representations of surface groups in various settings.
2. Proof of Theorem 1.4
As outlined in § 1, the proof of Theorem 1.4 is accomplished by using a geometric understanding of a one-dimensional subfamily of representations which arise by specializing the parameters u and v.
If we present the group 
$\Delta(3,4,4)$ as
\begin{equation*}\Delta(3,4,4) = \lt a, b \mid a^3=b^4 = (ab)^4 = 1 \gt \end{equation*}then
\begin{equation*} \rho_s(a) = \left(
\begin{array}{ccc}
1 & 0 & 0 \\
\frac{1}{2} \left(s^2+s+4\right) & -\frac{2 s}{s^2+s+6} & \frac{\left(s^2+3\right) \left(s^2+12\right)}{\left(s^2+s+6\right)^2} \\
-\frac{\left(s^2+4\right) \left(s^2+s+6\right)}{2 \left(s^2+12\right)} & -1 & \frac{-s^2+s-6}{s^2+s+6} \\
\end{array}
\right)
\end{equation*}and
\begin{equation*}\rho_s(b) =\left(
\begin{array}{ccc}
\frac{-s^2+s-6}{s^2+s+6} & \frac{2 \left(s^2+4\right) \left(s^2+9\right)}{\left(s^2+s+6\right)^2} & -\frac{4 \left(s^2+9\right) \left(s^2+12\right)}{\left(s^2+s+6\right)^3} \\
0 & 1 & 0 \\
\frac{\left(s^2+4\right) \left(s^2+s+6\right)}{2 \left(s^2+12\right)} & -\frac{s^4+s^3+13 s^2+8 s+36}{s^2+12} & \frac{s^2-s+6}{s^2+s+6} \\
\end{array}
\right)
\end{equation*} determines a homomorphism. Using the parameterization of [Reference Long, Reid, Breuillard and Oh8], it follows that for every real s, 
$\chi_{\rho_s}$ lies on the Hitchin component with the Fuchsian point occurring at s = 0 and one can show (for example, using the method described in [Reference Ballas and Long2]) that all the traces are polynomials in s. In fact, for every integral s, this representation can be conjugated into 
$\textrm{SL}(3,\mathbb{Z})$ but we make no use of this fact.
For reasons that will soon be apparent we restrict attention to the commutator subgroup of 
$ \Delta(3,4,4)$, this has index 4 and corresponds geometrically to a 
$S^2(3,3,3,3)$ which four-fold covers 
$ \Sigma(3,4,4)$.
For our purposes, the crucial fact about ρs is that at the non-real specialization 
$s = 3i$ the representation is reducible, with the yz plane being an invariant subspace V. Denote this representation by 
$(\rho_{3i}|_V)$.
It is an easy computation that the image of 
$(\rho_{3i}|_V)$ is unitary with respect to the Hermitian form of signature 
$(1,1)$
\begin{equation*}\left(
\begin{array}{cc}
1 & -\frac{1}{2}-\frac{i}{2} \\
-\frac{1}{2}+\frac{i}{2} & -1 \\
\end{array}
\right)\end{equation*} so that 
$(\rho_{3i}|_V)$ is a 
$\textrm{U}(1,1)$ representation of 
$ \Delta(3,4,4)$ and we will show inter alia that it is discrete and faithful.
If we pass to the commutator subgroup 
$(\rho_{3i}|_V)(\pi_1(S^2(3,3,3,3)))$, this group of matrices now lies in 
$\textrm{SU}(1,1)$ and acts on the three-dimensional vector space 
$\textrm{Sym}(3)$ of symmetric complex 
$2 \times 2$ matrices where X acts as 
$\sigma \longrightarrow X^{T}{\cdot}\sigma{\cdot}X$. Our first claim towards the proof of Theorem 1.4 is the following:
Theorem 2.1. With G as in 1.4, there is no non-zero symmetric form left invariant by 
$(\rho_{3i}|_V)(G)$.
Proof. We begin with some computational preliminaries (a file with details of these computations has been placed at [11]).
A simple covering space argument shows easily that 
$\pi_1(S^2(3,3,3,3))$ is generated by four elements of order three 
$x_t = b^t.a.b^{-t}$, 
$0 \leq t \leq 3$ satisfying 
$x_0x_1x_2x_3 = I$ and one can compute that the action on the three-dimensional complex vector space 
$\textrm{Sym}(3)$ can be conjugated to the real representation
\begin{equation*} \xi(x_0) = \left(
\begin{array}{ccc}
1 & 5 & 6 \\
0 & 1 & 3 \\
0 & -1 & -2 \\
\end{array}
\right), \quad
\xi(x_1) = \left(
\begin{array}{ccc}
-1 & 0 & -1 \\
3 & 1 & 6 \\
1 & 0 & 0 \\
\end{array}
\right),
\quad \xi(x_2) =
\left(
\begin{array}{ccc}
1 & 1 & 0 \\
-3 & -2 & 0 \\
9 & 4 & 1 \\
\end{array}
\right)\end{equation*} (with the image 
$\xi(x_3)$ being defined by the relation 
$\xi(x_0x_1x_2x_3) = I$).
It is also a routine computation that these matrices lie in 
$\textrm{SO}(J)$ for the quadratic form J of signature 
$(2,1)$ shown below
\begin{equation*}J=\left(
\begin{array}{ccc}
1 & 3 & 5 \\
3 & 1 & 3 \\
5 & 3 & 1 \\
\end{array}
\right).\end{equation*} Finally, one can show that the transposes of these matrices are conjugate to the matrices coming from ρ 0 on this subgroup so the representation ξ is a discrete faithful representation corresponding to a hyperbolic structure on 
$S^2(3,3,3,3)$ in some 
$\textrm{SO}(2,1)$.
With these preliminaries in hand, we argue as follows. Given 
$\gamma \in G$ the symmetric forms 
$(\rho_{3i}|_V)(\gamma)$ leaves invariant correspond precisely to the 1-eigenspace in the three-dimensional representation ξ. Since we have identified that action with a hyperbolic structure, we can think of the invariant form as corresponding to the space-like vector for the 
$\xi(\gamma)$ action. For our purpose, the way to understand the space-like vector is the following.
Working in the projective model of hyperbolic space, there is an invariant ellipse corresponding to the light-like vectors of J. This ellipse has two fixed points on it coming from rays which are the eigenvectors of the 
$\xi(\gamma)$ action and the space-like vector is the intersection of the two tangent lines to the ellipse at those fixed points.
The group G is non-elementary and so contains a free group of rank two, say this is generated by γ 1 and γ 2. If these elements leave invariant some non-zero symmetric form, the above formalism implies that 
$\xi(\gamma_1)$ and 
$\xi(\gamma_2)$ have a common invariant space-like vector which is therefore the invariant space-like vector for every element of the image 
$\xi(G)$. However, this is easily seen to be impossible. For example, 
$\xi( \lt \gamma_1, \gamma_2 \gt )$ is a Schottky group and so its limit set is a Cantor set. Choose elements h 1 and h 2 in this subgroup so that their attracting (respectively repelling) fixed points are extremely close on the ellipse. The tangent line description now shows that their space-like vectors cannot be the same. 
$\sqcup\!\!\!\!\sqcap$
Lemma 2.2. In the notation of Theorem 1.4, suppose that at 
$s=s_0$ the image group 
$\rho_{s_0}(G)$ leaves invariant some non-degenerate real quadratic form 
$\Sigma(s_0)$.
Then 
$\Sigma(s_0)$ is unique up to real scaling.
Proof. Suppose that 
$\Sigma'$ is another invariant form for 
$\rho_{s_0}(G)$. This form is assumed non-zero; however, we allow that it might be degenerate.
One easily sees that the matrix 
$\Sigma(s_0)^{-1}{\cdot}\Sigma'$ centralizes the whole group 
$\rho_{s_0}(G)$. However, 
$\chi_{\rho_0}$ lies on the Hitchin component and it is known [Reference Labourie7] that every infinite order element can be diagonalized with distinct real eigenvalues. It follows that 
$\Sigma(s_0)^{-1}{\cdot}\Sigma'$ is 
$\textrm{GL}(3,\mathbb{R})$-conjugate to a diagonal matrix. If this matrix is not just a homothety, then pick one of the non-zero eigenvalues λ ≠ 0 and we see that 
$\textrm{ker}(\Sigma(s_0)^{-1}{\cdot}\Sigma' - \lambda{\cdot}I)$ is a non-trivial invariant subspace for 
$\rho_{s_0}(G)$. But it is known [Reference Labourie7] that all the representations associated with characters on the Hitchin component are irreducible. It follows that 
$\Sigma' = \lambda \Sigma(s_0)$.
Proof of Theorem 1.4.
Suppose to the contrary that for every real value of s the image group 
$\rho_{s}(G)$ leaves invariant some (generically) non-degenerate real quadratic form 
$\Sigma(s)$. Without much loss of generality we may write 
$G = \lt \gamma_1, \gamma_2 \gt $, and by Lemma 2.2, this form is the unique solution up to scaling to the family of homogeneous linear equations
\begin{equation*}
\rho_s(\gamma_1)^T{\cdot}\Sigma(s){\cdot}\rho_s(\gamma_1) = \Sigma(s) \hspace{0.5in} \rho_s(\gamma_2)^T{\cdot}\Sigma(s){\cdot}\rho_s(\gamma_2) = \Sigma(s).
\end{equation*} Therefore, the entries of 
$\Sigma(s)$ can be regarded as rational functions and by scaling, polynomials in s with integer coefficients. By further scaling if needed, we may suppose there is no polynomial dividing every entry of 
$\Sigma(s)$.
Consider the value 
$s=3i$; since 
$ \Sigma(3i)$ is symmetric and invariant, the analysis performed in 2.1 for the invariant subspace V at this value shows that 
$ \Sigma(3i)$ must have the shape
\begin{equation*} \Sigma(3i) = \left(
\begin{array}{ccc}
p_1 & q_1 & q_2 \\
q_1 & 0 & 0 \\
q_2 & 0 & 0 \\
\end{array}
\right).\end{equation*} However, a matrix in the image of 
$\rho_{3i}$ has the shape
\begin{equation*}\left(
\begin{array}{ccc}
1 & 0 & 0 \\
v_1 & a_1 & a_2\\
v_2 & a_3 & a_4 \\
\end{array}
\right)
\end{equation*} and one computes that the condition that the symmetric matrix 
$ \Sigma(3i) $ is preserved by such a form is exactly that
\begin{equation*}\left(
\begin{array}{cc}
a_1 & a_3 \\
a_2 &a_4 \\
\end{array}
\right){\cdot}\left(\begin{array}{c}q_1\\ q_2\end{array}\right) = \left(\begin{array}{c}q_1\\ q_2\end{array}\right).
\end{equation*} However, this implies that 
$q_1=q_2=0$ since we have identified the matrix 
$$
\begin{pmatrix}
a_1 & a_2 \\
a_3 &a_4 \\
\end{pmatrix}
$$ with a matrix in the 
$\textrm{SU}(1,1)$ image of G, so any such matrix has two real eigenvalues λ > 1 and 
$1/\lambda$, in particular, there is no eigenvector corresponding to an eigenvalue = 1. It follows then that the only possibility is
\begin{equation*} \Sigma(3i) = \left(
\begin{array}{ccc}
p_1 & 0 & 0 \\
0 & 0 & 0 \\
0 & 0 & 0 \\
\end{array}
\right).\end{equation*} If the complex number 
$p_1=0$, this is a contradiction, since it implies that all the entries of 
$\Sigma(s)$ were divisible by 
$(9+s^2)$ and we had assumed the matrix scaled so the entries had no common polynomial factor. So we may assume that this is not the case.
In fact, this form is left invariant by the image of 
$\rho_{3i}$ so we must argue further. To this end, we recall the notion of a contragradient representation, defined by 
$cg_s(\gamma) = (\rho_s(\gamma)^{-1})^T$. Easily, ρs preserves a generically non-degenerate invariant form 
$\Sigma(s)$ if and only if 
$cg_s(\gamma)$ preserves the generically non-degenerate invariant form 
$cg(\Sigma(s))$, where 
$cg(\Sigma(s))$ is 
$\Sigma(s)^{-1}$ up to scaling and removing common factors. Notice that while 
$cg_{3i}$ continues to be reducible, the invariant subspace is now a one-dimensional subspace 
$ \lt \bf v \gt $ so the two-dimensional information comes by projecting onto the space 
$\mathbb{C}^3/ \lt \textbf{v} \gt $.
Our information on the form to this point shows that we have
\begin{equation*} \Sigma(s) =
\left(
\begin{array}{ccc}
a(s) & b(s) \left(s^2+9\right) & c(s) \left(s^2+9\right) \\
b(s) \left(s^2+9\right) & e(s) \left(s^2+9\right) & f(s) \left(s^2+9\right) \\
c(s) \left(s^2+9\right) & f(s) \left(s^2+9\right) & k(s) \left(s^2+9\right) \\
\end{array}
\right)
\end{equation*} where 
$a(3i) \neq 0$. One finds that after inverting and multiplying by 
$\det(\Sigma(s))$, the entries have a common factor of 
$(9+s^2)$, removing this factor and setting 
$s=3i$ we see
\begin{equation*} cg(\Sigma(3i))=\left(
\begin{array}{ccc}
0 & 0 & 0 \\
0 & a(3i) k(3i) & -a(3i) f(3i) \\
0 & -a(3i) f(3i) & a(3i) e(3i) \\
\end{array}
\right).
\end{equation*} Now matrices in the contragradient representation of 
$\rho_{3i}$ have the shape
\begin{equation*}\left(
\begin{array}{ccc}
1 & v_1 & v_2 \\
0 & a_1 & a_2\\
0 & a_3 & a_4 \\
\end{array}
\right)
\end{equation*} and one checks that the condition such a matrix preserves the form 
$cg(\Sigma(3i))$ is exactly that the projected representation matrix 
$$\begin{pmatrix}
a_1 & a_2 \\
a_3 &a_4 \\
\end{pmatrix}
$$ preserves 
$$\begin{pmatrix}
k(3i) & -f(3i) \\
- f(3i) & e(3i) \\
\end{pmatrix}
$$ (we have divided by 
$a(3i)=p_1$ which we know is not zero) and we may use an analogous 
$2 \times 2$ analysis as before on the projected representation to deduce that this is in fact the zero form. However, this yields the same contradiction – we assumed that the entries of 
$cg(\Sigma(s))$ have no polynomial in common so cannot ever be simultaneously be zeroed by any complex specialization. This contradiction completes the proof of Theorem 1.4.
Remark. Notice that the question of which real values s for which 
$\rho_s(G)$ can preserve a non-degenerate real quadratic form amounts solving a family of polynomial equations, in this case with a single real variable s. Thus the existence of s 0 for which there is no such form implies that there can only be finitely many real values of s for which 
$\rho_s(G)$ can preserve a form.
3. Proof of 1.2
We are given a free subgroup 
$G = \lt \gamma_1, \gamma_2 \gt \subset \Delta(3,4,4)$; we first show that we can find at least one representation from the family ρs for which the Zariski closure of 
$\rho(G)$ (which we denote by H) is 
$\textrm{SL}(3,\mathbb{R})$. As noted in the introduction, for trivial algebraic reasons, for any value of s, H can never be soluble or nilpotent.
We may also argue from geometric considerations that we may assume that H is irreducible for small s. For notice that at the hyperbolic structure 
$\rho_0(\gamma_1)$ and 
$\rho_0(\gamma_2)$ do not have any eigenvectors in common. This follows for the eigenvectors corresponding to eigenvalues ≠ 1 by simple hyperbolic considerations applied to the non-elementary subgroup G and for the space-like vectors, this is the same argument as used in the proof of Theorem 2.1. Moreover, since ρ 0 is a 
$\textrm{SO}(2,1)$ representation it is conjugate to its contragradient and therefore the same conclusion holds. It therefore follows that for all small s, 
$\rho_s(\gamma_1)$ and 
$\rho_s(\gamma_2)$ (and their contragradients) do not have any eigenvectors in common. The Zariski closure of any such 
$\rho_s(G)$ therefore cannot be reducible since if it were, either H or its contragradient would have a one-dimensional invariant subspace and therefore a common invariant subspace for 
$\rho_s(\gamma_1)$ and 
$\rho_s(\gamma_2)$. This consideration rules out the Zariski closure being 
$\textrm{SL}(2, \mathbb{R}) \times \mathbb{R}$ for small s, for example.
A similar argument applied to the eigenvalues of 
$\rho_s(G)$ shows that we can rule out the case that H is compact for small s.
We are reduced to showing that there is some representation ρs whose Zariski closure is not 
$\textrm{SO}(2,1)$. To this end, we observe that if the representation 
$\rho_s(G)$ has all elements being Fuchsian, then, for any s, every element in 
$\rho_s(G)$ has an eigenvalue = 1. This can be expressed by the algebraic condition 
$\det(\rho_s(\gamma)-I)=0$ for all 
$\gamma\in G$. It follows that for any real specialization 
$s=s_0$ near zero exhibits 
$\rho_{s_0}(G)$ as a subgroup of the real algebraic group 
$\textrm{SL}(3,\mathbb{R})$ obtained by adding the polynomial equations 
$\det(\rho_s(\gamma)-I)=0$ for all 
$\gamma\in G$. This is the algebraic group 
$\textrm{SO}(2,1)$ since we know that H is not compact. Theorem 1.4 and the remark which follows it shows that there are real specializations for which this does not happen and we conclude that for any G, 
$\rho_s(G)$ contains non-Fuchsian elements.
The characteristic polynomial of any non-Fuchsian element of 
$\rho_s(G)$ has the shape
\begin{equation*}Q^3 - f(s)Q^2 + g(s)Q - 1\end{equation*} where f(s) and g(s) are traces and therefore polynomials which are different since the element is generically non-Fuchsian. The condition on s that this be a Fuchsian element is that it be a root of the non-zero polynomial 
$f(s) -g(s)$. This implies that the set of s for which 
$\rho_s(G)$ is Fuchsian is contained in the zero set of a collection of real (integral!) polynomials and is therefore finite. Thus for any G, there is a small real s for which the Zariski closure of 
$\rho_s(G)$ is 
$\textrm{SL}(3,\mathbb{R})$.
This analysis now carries over to all of 
$X^{\mbox{Hit}}(\Delta(3,4,4), \textrm{SL}(3,\mathbb{R}))$: If 
$\gamma \in G$ is non-Fuchsian for 
$\rho_s(G)$ then it must be non-Fuchsian for a general point and although the analogous condition 
$f(u,v) = g(u,v)$ (in terms of the parameters u and v introduced previously) involves the square root of a radical, a straightforward computation shows that we can manipulate it to be an integral polynomial condition 
$F_\gamma(u,v) = 0$. This cannot vanish on the whole variety since we have found infinitely many points where γ is not Fuchsian so 
$F_\gamma(u,v)$ defines a proper one-dimensional subvariety: away from this variety G cannot preserve any non-degenerate quadratic form. Since we have argued that every such non-elementary G contains a non-Fuchsian element of this sort, the union of those countably many codimension one varieties proves Theorem 1.2.
4. A non-strongly dense construction
The ideas set forth here can also be used to construct examples which demonstrates how subtle a phenomenon strong density is in the setting of this paper.
In the notation established above, consider the element of order two 
$\tau = b{\cdot}b$. As we observed in § 1, the elements 
$g_i = \tau{\cdot}x_i{\cdot}\tau{\cdot}x_i^{-1}$ are Fuchsian for any choice of xi. If the whole group 
$ \lt g_1, g_2 \gt $ is to be Fuchsian then all the elements are, and the shortest element not guaranteed to be conjugated to its inverse by τ is 
$c = g_1{\cdot}g_2{\cdot}g_1^{-1}{\cdot}g_2^{-1}$. This gives an obstruction. For example taking 
$x_1= a{\cdot}b^{-1}$ and 
$x_2= a{\cdot}b{\cdot}a^{-1}{\cdot}b^{-1}$, one computes that the characteristic polynomial P(Q) of c evaluated at Q = 1 is
\begin{align*}
& -s \left(s^2+9\right) \left(s^2-s+8\right) \left(s^2+s+8\right) \left(s^2+2 s+5\right) \left(s^3+9 s+2\right)\\ &\quad \times\left(s^4-2 s^3+14 s^2-16 s+40\right).
\end{align*} The root s = 0 is forced since the whole group lives inside 
$\textrm{SO}(2,1)$ at that value. We see that there is one other real root arising from a solution of 
$ \left(s^3+9 s+2\right)=0$ and one can check that 
$ \lt g_1, g_2 \gt $ is indeed Fuchsian at this value, so that representation is not strongly dense. The elements x 1 and x 2 are close to being arbitrary so this gives a rich family of non-strongly dense examples.
Acknowledgements
The authors thank both the anonymous referees for their wonderfully detailed reading of the paper and their helpful suggestions. We are also indebted E. Breuillard for correspondence concerning strongly dense subgroups and to S. Ballas for his careful reading of an early version.
