Hostname: page-component-6bf8c574d5-t27h7 Total loading time: 0 Render date: 2025-02-15T17:48:44.100Z Has data issue: false hasContentIssue false
  • English
  • Français

Stability in pro-homotopy theory

Published online by Cambridge University Press:  20 January 2009

R. M. Seymour
R. M. Seymour
Affiliation:
Department of MathematicsUniversity CollegeGower StreetLondon WC1E 6BT
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

If 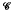is a category, an object of pro- 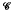is stable if it is isomorphic in pro- 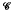to an object of 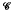. A local condition on such a pro-object, called strong-movability, is defined, and it is shown in various contexts that this condition is equivalent to stability. Also considered, in the case 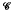is a suitable model category, is the stability problem in the homotopy category Ho(pro-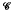), where pro- 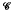has the induced closed model category structure defined by Edwards and Hastings [6].

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 33 , Issue 3 , October 1990 , pp. 419 - 441
Copyright
Copyright © Edinburgh Mathematical Society 1990

References

REFERENCES

1.Artin, M. and Mazur, B., Étale Homotopy, (Lecture Notes in Math., 100, Springer-Verlag, Berlin-Heidelberg-New York, 1969).CrossRefGoogle Scholar
2.Borsuk, K., A note on the theory of shape of compacta, Fund. Math. 67 (1970), 265–278.CrossRefGoogle Scholar
3.Dydak, J., On the Whitehead Theorem in pro-homotopy and on a question of Mardešić, Bull. Acad. Polon. Sci. Sér. Sci. Math. Astron. Phys. 23 (1975), 775–779.Google Scholar
4.Edwards, D. A. and Geoghegan, R., The stability problem in shape and pro-homotopy, Trans. Amer. Math. Soc. 214 (1975), 261–277.CrossRefGoogle Scholar
5.Edwards, D. A. and Geoghegan, R., Stability theorems in shape and pro-homotopy, Trans. Amer. Math. Soc. 222 (1976), 389–403.CrossRefGoogle Scholar
6.Edwards, D. A. and Hastings, H. M., Čech and Steenrod Homotopy Theories with Applications to Geometric Topology (Lecture Notes in Math. 542, Springer-Verlag, Berlin-Heidelberg-New York, 1976).CrossRefGoogle Scholar
7.Mardešič, S., Strongly Movable Compacts and Shape Retracts (Proc. Intern. Symp. on Top. and its Appl., Budva, 1972, Savez Društava Mat. Fiz. Astron., Beograd, 1973), 163–166.Google Scholar
8.Mardešič, S. and Segal, J., Shape Theory: the Inverse System Approach (North-Holland, Amsterdam-New York, 1982).Google Scholar
9.Porter, T., Stability results for topological spaces, Math. Z. 140 (1974), 1–21.CrossRefGoogle Scholar
10.Quillen, D., Homotopical Algebra (Lecture Notes in Math. 43, Springer-Verlag, Berlin-Heidelberg-New York, 1967).CrossRefGoogle Scholar
11.Seymour, R. M., Whitehead Theorems in pro-homotopy theory, J. London Math. Soc. 32(2) (1985), 337–356.CrossRefGoogle Scholar