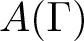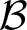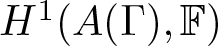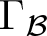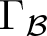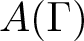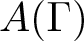1. Introduction
This paper forms part of a program to study the relationship between the algebraic structure of right-angled Artin groups and the combinatorial structure of graphs, and specifically how one can extract combinatorial properties of a graph Γ from an abstract group G which is isomorphic to 
$A(\Gamma)$. The methods of this paper investigate the interplay between group theory, linear algebra, algebraic topology, combinatorics and commutative algebra which arise in the study of graphs and right-angled Artin groups. The reader is directed to [Reference Koberda30] for background and commentary.
Translational tools between combinatorial properties and algebraic properties are interesting from a purely theoretical point of view, and they also arise in applied contexts such as group based cryptography (cf. [Reference Flores, Kahrobaei and Koberda16], for instance). Computational tractability motivates the present work to a high degree.
Good characterizations of many combinatorial properties of graphs via the algebraic structure of right-angled Artin groups have been obtained by various authors, for instance, being a non-trivial join [Reference Servatius35], being disconnected [Reference Brady and Meier3], containing a square [Reference Kambites25, Reference Kim and Koberda27], being a co-graph [Reference Kim and Koberda27, Reference Kim and Koberda28], being a finite tree or complete bipartite graph [Reference Hermiller and Šunić24], admitting a non-trivial automorphism [Reference Flores, Kahrobaei and Koberda16], being k-colourable [Reference Flores, Kahrobaei and Koberda17], fitting in a sequence of expanders [Reference Flores, Kahrobaei and Koberda19], admitting a Hamiltonian path or cycle [Reference Flores, Kahrobaei and Koberda18] and being (outer)planar [Reference Gheorghiu20]. In this paper, we present a new perspective on characterizing (outer)planarity of the underlying graph, through the cohomology of the right-angled Artin group, which makes use of the properties of the Colin de Verdière invariant [Reference de Verdière11] and permits to describe other graph properties in terms of groups, as for example being a linear forest or being linklessly embeddable in 
$\mathbb{R}^3$. Moreover, our method also characterizes when the complement of the graph has some of these properties. The key and more difficult point of our argument is Theorem 1.1, which establishes a certain embedding of graphs.
Let us now give a more precise setup. Let Γ be a finite simplicial graph. That is, Γ is undirected, and its geometric realization is a one-dimensional simplicial complex. Such graphs are also sometimes called simple. This paper focusses on the problem of extracting combinatorial information about Γ from the associated right-angled Artin group
\begin{align*}
A(\Gamma)=\langle V(\Gamma)\mid [v,w]=1,\, \{v,w\}\in E(\Gamma)\rangle.
\end{align*} Let 
$\mathbb{F}$ be an arbitrary field. We consider the cohomology ring 
$H^*(A(\Gamma),\mathbb{F})$. It is well-known that 
$H^*(A(\Gamma),\mathbb{F})$ can be recovered from an arbitrary presentation of 
$A(\Gamma)$, see 
$\S$ 2.5. Moreover, 
$A(\Gamma)$ is 1-formal, meaning that 
$H^*(A(\Gamma),\mathbb{F})$, and in particular the restriction of the cup product to the first degree, completely determines Γ. The fact that the right-angled Artin group determines the underlying graph up to isomorphism is obtained as the main result of [Reference Droms14], and a related rigidity result was established by [Reference Sabalka34]. An alternative proof that the cohomology ring of a right-angled Artin group determines the underlying graph is given as Theorem 6.4 in [Reference Koberda29], cf. Theorem 15.2.6 of [Reference Koberda30].
1.1. The cohomology basis graph and the defining graph
We will be interested in effective ways of reconstructing Γ from 
$A(\Gamma)$, especially through 
$H^*(A(\Gamma),\mathbb{F})$. For this, let 
$\mathcal B$ be an arbitrary basis of 
$H^1(A(\Gamma),\mathbb{F})$. The cohomology basis graph associated with 
$\Gamma_{\mathcal{B}}$ is the graph whose vertices are elements of 
$\mathcal{B}$, and whose edge relation is given by having a non-trivial cup product.
The main result of this paper is the following. We give an algebraic topology–combinatorics version, though there are many other equivalent formulations, see 
$\S$ 3.2. Here and in what follows, we do not require subgraphs to be full.
Theorem 1.1.
Let Γ be a finite simplicial graph and let 
$\mathcal{B}$ be an arbitrary basis for 
$H^1(A(\Gamma),\mathbb{F})$. Then Γ is a subgraph of 
$\Gamma_{\mathcal{B}}$.
The importance of this result for us is two-fold: first, it is the cornerstone on which almost all results in the present paper are based and permits the use of minor-monotonicity of the Colin de Verdière invariant to provide group-theoretic characterizations of many graph properties, cf. Theorem 1.5. Second, it has equivalent formulations in other contexts (such as in commutative algebra), wherein the corresponding results were previously unknown.
In the course of the proof, we develop a novel perspective on the computation of the determinant of an invertible matrix. This method greatly generalizes the approach used in [Reference Flores, Kahrobaei and Koberda18] and highlights the role of certain graphs that arise naturally from the structure of the minors of the matrix, cf. 
$\S$ 3. This is where the main difficulty in establishing Theorem 1.1 lies: the main result implicitly finds a bijection between the vertices of Γ and the basis 
$\mathcal{B}$ which has good algebraic properties, though in general no canonical bijection exists.
Since it is easy to see that Γ and 
$\Gamma_{\mathcal{B}}$ have the same number of vertices, Theorem 1.1 says that Γ can be obtained from 
$\Gamma_{\mathcal{B}}$ by deleting edges:
Corollary 1.2. For a finite simplicial graph Γ, we have that 
$\Gamma\cong\Gamma_{\mathcal{B}}$ for any basis 
$\mathcal{B}$ of 
$H^1(A(\Gamma),\mathbb{F})$ which minimizes the number of edges in 
$\Gamma_{\mathcal{B}}$.
From Corollary 1.2, one can give an a priori bound on the complexity of reconstructing Γ from 
$H^*(A(\Gamma),\mathbb{F})$, since one can apply the corollary to a field with two elements, over which there are only finitely many bases.
Recall that to every finite graph Γ, we may associate the Colin de Verdière invariant 
$\mu(\Gamma)$, which is a natural number that characterizes disconnected graphs, forests, outerplanar graphs, planar graphs and many other classes of graphs. The reader may find the definition and basic properties of 
$\mu(\Gamma)$ in 
$\S$ 2.3.
Theorem 1.3.
For a finite simplicial graph Γ and natural number k, we have that 
$\mu(\Gamma)\leq k$ if and only if there exists a basis 
$\mathcal{B}$ of 
$H^1(A(\Gamma),\mathbb{F})$ such that 
$\mu(\Gamma_{\mathcal{B}})\leq k$.
From the computability of the cohomology ring (cf. 
$\S$ 2.5), we have the following consequence:
Corollary 1.4. From an arbitrary finitely presented group 
$G=\langle S\mid R\rangle$ such that 
$G\cong A(\Gamma)$ for some finite simplicial graph Γ, the value of 
$\mu(\Gamma)$ is computable from 
$\langle S\mid R\rangle$.
Recall that a graph is planar if its geometric realization can be embedded in the plane, and outerplanar if it can be embedded in the plane in such a way that every vertex is adjacent to the unbounded component of the complement. Moreover, a graph is linklessly embeddable in 
$\mathbb{R}^3$ if there is an embedding of the graph in 
$\mathbb{R}^3$ such that no pair of cycles are linked after being embedded; observe that this property can be thought of as a three-dimensional analogue of planarity.
Obtaining the following consequence was another motivation for carrying out the present work.
Theorem 1.5.
Let P be a property of graphs that is characterized by excluding a class of forbidden subgraphs. A finite simplicial graph Γ has property P if and only if there exists a basis 
$\mathcal{B}$ of 
$H^1(A(\Gamma),\mathbb{F})$ such that 
$\Gamma_{\mathcal{B}}$ has property P.
Moreover, let P one of the following graph properties:
• Emptiness (having no edges).
• Being a linear forest (union of disjoint paths).
• Planarity.
• Outerplanarity.
• Linkless embeddability.
Then a finite simplicial graph Γ has property P if and only if there exists a basis 
$\mathcal{B}$ of 
$H^1(A(\Gamma),\mathbb{F})$ such that 
$\Gamma_{\mathcal{B}}$ has property P.
One must be careful in generalizing Theorem 1.5 to forbidden minors, since the cohomology basis graph does not behave well under taking minors of Γ, see 
$\S$ 5. Theorem 1.5 behaves well for properties which are monotone with respect to taking minors, such as having Colin de Verdière invariant bounded by a fixed integer, see [Reference Chartrand, Geller and Hedetniemi10] for a discussion of graphs characterized by forbidden subgraphs.
Analogous characterizations of some of the properties enumerated in Theorem 1.5 for the complement of a given graph are also possible, see Proposition 3.6.
As was mentioned already, the formulation of the previous theorem makes no reference to any distinguished set of generators of the group 
$A(\Gamma)$. Moreover, information about graph properties can be effectively obtained out of any presentation of the associated right-angled Artin group, via the basis cohomology graph associated to that presentation and using 
$\mathbb{F}_2$-coefficients (see Example 4.3 and the discussion at the end of 
$\S$ 2.5). This last observation contrasts with the recent results of Gheorghiu in [Reference Gheorghiu20], at least from the computational point of view. Indeed, Gheorghiu finds an intrinsic characterization of right-angled Artin groups on planar graphs for instance, but it is not clear whether his methods are effective. In this vein, we note that Theorem 1.5 also furnishes a linear algebraic characterization of planarity of finite simple graphs, in the spirit of Maclane (cf. [Reference O’Neil33]).
The full extent of information which can be gleaned from the cohomology basis graph is not yet clear.
Question 1.6.
Let Γ and 
$A(\Gamma)$ be as above.
(1) What is the effect of different fields on the structure of the cohomology basis graph? Note that depending on the characteristic, different edges may appear or be deleted.
(2) What further data about the defining graph can be extracted from the cohomology basis graph? For instance, how can the cycles of Γ be read off?
(3) If one considers all possible bases for the cohomology of
$A(\Gamma)$, one obtains a partially ordered set under inclusion of subgraphs. Which subgraphs between Γ and the complete graph on the vertices of Γ occur? To what extent does the answer depend on Γ?
The paper is structured as follows: in 
$\S$ 2, we provide background about right-angled Artin groups and the Colin de Verdière invariant, as well as different aspects of the cohomology of right-angled Artin groups that are relevant to our analysis. Section 3 contains the proofs of the main results. In 
$\S$ 4, we describe some specific examples which illustrate the difficulties in establishing the main result. We conclude with 
$\S$ 5, where we investigate the relationship between the minors of the defining graph and of the cohomology basis graphs in more detail.
2. Background
2.1. Notation and terminology
We follow generally accepted conventions and notation for graphs, see [Reference Diestel13], for instance. Of particular interest will be graph minors. A graph Λ is an elementary minor of Γ if Λ is obtained from Γ by deleting a vertex, deleting an edge or contracting an edge. We say that Λ is a minor of Γ if there is a sequence 
$\{\Gamma_0,\ldots,\Gamma_n\}$ of graphs such that
\begin{align*}
\Gamma=\Gamma_0,\quad \Gamma_n=\Lambda,\quad \Gamma_{i+1}\text{ is an elementary minor of }\Gamma_i\text{ for all }i.
\end{align*} We will adopt some slightly non-standard linear algebra terminology. For a matrix A, we will write entries 
$a_i^j$, where i indicates the row and j indicates the column. We will write 
$\{a_1,\ldots,a_n\}$ for the rows of a matrix. A minor of A is simply a (possibly empty) square submatrix of A obtained by deleting some (possibly empty) collection of rows and columns of A. The dimension of such a minor is just the number of rows or columns in the minor.
We will write Sn for the symmetric group on n letters and σ for an arbitrary element of Sn.
2.2. Cohomology of right-angled Artin groups
We recall some basic facts about the structure of the cohomology algebra of a right-angled Artin group 
$A(\Gamma)$. The result recorded here is easy and well-known and follows from standard methods in geometric topology together with the fact that the Salvetti complex associated with Γ is a classifying space for 
$A(\Gamma)$. More details can be found in [Reference Flores, Kahrobaei and Koberda19, Reference Koberda30], for instance.
Let 
$V(\Gamma)=\{v_1,\ldots,v_n\}$ and 
$E(\Gamma)=\{e_1,\ldots,e_m\}$ be the vertices and edges of Γ and write 
$\smile$ for the cup product pairing on 
$H^*(A(\Gamma),\mathbb{F})$.
Lemma 2.1. Let Γ be a finite simplicial graph. Then there are bases 
$\{v_1^*,\ldots,v_n^*\}$ for 
$H^1(A(\Gamma),\mathbb{F})$ and 
$\{e_1^*,\ldots,e_m^*\}$ for 
$H^2(A(\Gamma),\mathbb{F})$ such that:
(1) We have
$v_i^*\smile v_j^*= 0$ if and only if $\{v_i,v_j\}\notin E(\Gamma)$;(2) We have
$v_i^*\smile v_j^*=\pm e_k^*$ whenever $\{v_i,v_j\}=e_k\in E(\Gamma)$.
Let
\begin{align*}
w_i=\sum_{j=1}^n a_i^j v_j^*
\end{align*} for 
$i=1,2$, and for coefficients 
$a_i^j$ in a field. From Lemma 2.1, we observe that 
$w_1\smile w_2\neq 0$ if and only if there is a pair of indices j and k such that 
$v_j^*\smile v_k^*\neq 0$ and the matrix
\begin{align*}
\begin{pmatrix}a_1^j&a_1^k\\ a_2^j&a_2^k\end{pmatrix}
\end{align*}is non-singular. This fact will be used implicitly throughout the rest of this paper.
2.3. The Colin de Verdière invariant
The Colin de Verdière invariant of a graph is an invariant arising from spectral graph theory, which gives a vast generalization of classical planarity criteria for graphs. General references on the Colin de Verdière invariant are [Reference de Verdière11] and [Reference van der Holst, Lovász and Schrijver36]. We give a brief summary of the definition and main properties of this invariant for the convenience of the reader, which can be found in the aforementioned references.
We represent a finite simple connected graph Γ by its vertex set 
$V=\{1,\ldots,n\}$ and its edge set E. We consider symmetric real n × n matrices M such that the following three conditions hold:
• For all distinct indices
$1\leq i,j\leq n$, we have $M_i^j \lt 0$ if $\{i,j\}\in E$ and $M_i^j=0$ otherwise;• M has exactly one negative eigenvalue of multiplicity one;
• There is no non-zero symmetric real n × n matrix X such that MX = 0 and such that
$X_i^j=0$ whenever i = j or $M_i^j\neq 0$.
The Colin de Verdière invariant 
$\mu(\Gamma)$ is the largest corank of any M satisfying these conditions. Here, for a symmetric matrix m × m of rank r, the corank is equal to m − r.
Although the original definition of the invariant assumes the graph to be connected, it is easy to extend the definition to disconnected non-empty graphs by taking the maximum of the value of the invariant on the components; for empty graphs, the invariant is defined to be zero, see [Reference Kotlov, Lovász and Vempala31].
The following result illustrates the power of this invariant:
Theorem 2.2.
Let Γ be a finite simple graph such that 
$\mu(\Gamma)\leq k$. Then:
• k = 0 if and only if Γ has no edges.
• k = 1 if and only if Γ is a union of disjoint paths.
• k = 2 if and only if Γ is outerplanar.
• k = 3 if and only if Γ is planar.
• k = 4 if and only if Γ is linklessly embeddable in
$\mathbb{R}^3$.
It is also possible to describe the planarity properties of the complement of the graph in terms of this invariant. Recall that two vertices in a graph are twins if they have the same set of neighbours.
Theorem 2.3.
Let Γ be a finite simple graph of n vertices with no twin vertices, and such that 
$\mu(\Gamma)\geq n-k$. Then:
• k = 5 if and only if the complement of Γ is planar.
• k = 4 if and only if the complement of Γ is outerplanar.
The previous result can be refined further. For example, the ‘only if’ implications are true without assuming any conditions on the vertices. Moreover, there are also (weaker) characterizations of the complement being a linear forest or linklessly embeddable in 
$\mathbb{R}^3$, also using the Colin de Verdière invariant, see [Reference Kotlov, Lovász and Vempala31].
2.4. Right-angled Artin groups and formality
As was noted already, the isomorphism type of 
$A(\Gamma)$ determines the isomorphism type of the defining graph Γ. In [Reference Koberda29], a proof was given that passed through the cohomology rings of right-angled Artin groups, cf. [Reference Koberda30]. That is, the cohomology of the right-angled Artin group up to dimension 2, together with the cup product pairing, determines the isomorphism type of the underlying graph Γ. This fact fits into a much broader theory of formality, in particular, 1-formality. This is a phenomenon closely related to the de Rham fundamental group, quadratic presentability of the Mal’cev algebra and the minimal 1-model, see [Reference Amorós, Burger, Corlette, Kotschick and Toledo2]. For general Artin groups, 1-formality is a consequence of the work of Kapovich and Millson [Reference Kapovich and Millson26]. Categorical perspectives on right-angled Artin groups and their defining graphs are investigated by Grossack [Reference Grossack22].
2.5. Effectiveness, automaticity and computation
For a general finitely presented group, one can algorithmically recover the cohomology ring structure in degree 1 (i.e. products of elements in degree 1), using a standard five-term exact sequence from group cohomology (arising from the Lyndon–Hochschild–Serre spectral sequence, cf. [Reference Brown6]). Explicitly, if G is a finitely generated group and H is its abelianization, then one can compute the kernel of the cup product map
\begin{align*}
\bigwedge^2 H\longrightarrow H^2(G)
\end{align*} via the lower central series. In particular, it can be decided which products in 
$\bigwedge^2$ are trivial or not. Thus, from any generating set for the first cohomology of a right-angled Artin group, one can recover the structure of the associated cohomology basis graph without appealing to the duals of Artin generators. If we consider coefficients in 
$\mathbb{F}_2$ and generating sets whose cardinality is the rank of the group, this method and Corollary 1.2 provide an effective way of reconstructing Γ from the data of 
$H^*(A(\Gamma),\mathbb{F})$, and assuming all queries take a unit amount of time, one can construct a naive algorithm to compute Γ whose complexity is 
$O(e^{|V(\Gamma)|^2})$. The complexity of recovering Γ from an arbitrary finite presentation of 
$A(\Gamma)$ is a somewhat different matter.
We remark that, in general, computing the second cohomology of a finitely presented group is difficult. Indeed, one can bootstrap the unsolvability of the word problem in general finitely presented groups to prove that it is generally undecidable whether or not 
$H^2(G,\mathbb{Z})=0$, cf. [Reference Gordon21].
For a right-angled Artin group, these pathologies do not occur. Indeed, right-angled Artin groups are biautomatic, cf. [Reference Brieskorn and Saito5, Reference Charney7–Reference Charney9, Reference Deligne12]. The exact definition of this property is irrelevant for our purposes, and we direct the reader to the seminal text [Reference Epstein, Cannon, Holt, Levy, Paterson and Thurston15].
The property of automatic or biautomatic does not depend on the underlying presentation, though passing between different automatic structures can be mysterious. For a finitely presented group which is known to be biautomatic, practically finding a biautomatic structure is not always clear. From a given biautomatic structure on a group G, it is a theorem of Bridson–Reeves [Reference Bridson and Reeves4] that there is an algorithm to construct a finite dimensional approximation to a classifying space for G (i.e. a finite dimensional skeleton of BG). Thus, for an arbitrary finitely presented group which is abstractly isomorphic to a right-angled Artin group, there is an algorithm which computes all of 
$H^*(G,\mathbb{Z})$.
Observe that any presentation of a right-angled Artin group defines a basis for the cohomology, and then the arguments above allow us to directly compute the cohomology basis graph. Any bound on the Colin de Verdière invariant for this graph immediately gives the same bound for the defining graph. In particular, we obtain a planarity test for the defining graph whose input is any presentation of the right-angled Artin group, see Example 4.3.
3. Γ-null-connectedness and the proof of the main results
The ideas we use to establish the main result expand and generalize the constructions developed by the first three authors in [Reference Flores, Kahrobaei and Koberda18], which in turn are partially inspired by classical expansions of the determinant relying on the computation of 
$2\times 2$ minors, such as Laplace expansion, the Dodgson condensation formula and the Sylvester formula [Reference Abeles1].
3.1. Null-connectedness
For the remainder of this section, we fix a finite simple graph Γ, with vertices 
$\{1,\ldots,n\}$, as well as 
$A\in\mathrm{M}_n(\mathbb{F})$. The indices in the labelling of columns of A will be identified with the vertices of Γ.
Recall that we write row vectors of A as 
$a_r=(a_r^1,\ldots,a_r^n)$. We say two rows ar and as of A are Γ-null-connected if the minor
\begin{align*}
\begin{pmatrix}
a_r^i&a_r^j\\
a_s^i&a_s^j
\end{pmatrix}
\end{align*} is singular whenever 
$\{i,j\}$ is an edge of Γ.
A submatrix M of A will be called a Γ-1-block if the following conditions are satisfied.
(1) M has at least two rows and two columns.
(2) All entries of M are non-zero.
(3) The indices of the columns occurring in M span a connected subgraph of Γ.
(4) The rows of A which meet M span a connected graph with the Γ-null-connectedness adjacency relation.
(5) M is maximal with respect to these conditions, in the sense that there is no submatrix N of A which properly contains M and which satisfies the previous conditions.
A Γ-1-minor is a minor of A with at least two rows, which is contained in a Γ-1-block.
Lemma 3.1. Let M be a Γ-1-block in A. Then the row space of M is one-dimensional.
Proof. Clearly the row space of M is at least one-dimensional. Let 
$\{i,j\}$ be indices of columns in M that span an edge of Γ, and let a 1 and a 2 be null-connected rows of A. We have that the matrix
\begin{align*}
\begin{pmatrix}a_1^i&a_1^j\\ a_2^i&a_2^j\end{pmatrix}
\end{align*} is singular and has only non-zero entries, whereby it follows that the vector 
$(a_2^i,a_2^j)$ is a non-zero scalar multiple 
$\lambda_{i,j}$ of 
$(a_1^i,a_1^j)$. By definition, the indices of the columns meeting M span a connected subgraph 
$\Lambda\subset\Gamma$. For every edge of Λ spanned by vertices 
$\{s,t\}$, we obtain a non-zero scalar 
$\lambda_{s,t}$ relating 
$(a_2^s,a_2^t)$ and 
$(a_1^s,a_1^t)$. Moreover, if two edges of Λ share a vertex then the two corresponding scalars must coincide. It follows by induction on the diameter of the subgraph Λ and from the fact that all entries in M are non-zero that the scalars 
$\lambda_{s,t}$ depend only on a 1 and a 2 and not on the indices s and t of the columns. It follows that the two rows a 1 and a 2 of M are scalar multiples of each other. Since the rows of M span a connected graph under the null-connectivity relation, we see that any two rows of M are scalar multiples of each other, the desired conclusion.
The following property of Γ-1-blocks is crucial for canonical sorting of summands making up the determinant. Again, a similar statement and proof are found as Lemma 2.10 in [Reference Flores, Kahrobaei and Koberda18].
Lemma 3.2. Let M 1 and M 2 be two distinct Γ-1-blocks of A. Then M 1 and M 2 are disjoint as submatrices of A.
Proof. Let 
$I\subset \{1,\ldots,n\}$ be the set of columns meeting M 1 and 
$J\subset\{1,\ldots,n\}$ be the set of columns meeting M 2, and let 
$\{\ell_1,\ldots,\ell_s\}$ be the indices of the rows in M 2. Write 
$\Lambda_I$ and 
$\Lambda_J$ for the corresponding connected subgraphs of Γ. Suppose 
$a_{\ell_1}^{k}$ is an entry appearing in both M 1 and M 2. We will show that in this case 
$M_1=M_2$.
By definition, for all 
$i\in I$, we have that 
$a_{\ell_1}^i$ is a non-zero entry of M 1, and that 
$a_{\ell_m}^k$ is a non-zero entry of M 2. By Lemma 3.1, the row spaces of both M 1 and M 2 are one-dimensional. We have 
$k\in I\cap J$ and 
$a_{\ell_1}$ is a row meeting both M 1 and M 2.
If 
$a_{\ell_m}$ is another row meeting M 2 then 
$a_{\ell_1}$ and 
$a_{\ell_m}$ lie in the same Γ-null-connected component of the rows of A. Suppose first that they are actually Γ-null-connected. Then we have that the matrix
\begin{align*}
\begin{pmatrix}a_{\ell_1}^{k}&a_{\ell_1}^i\\ a_{\ell_m}^k &a_{\ell_m}^i\end{pmatrix}
\end{align*} is necessarily singular and consists of all non-zero entries since 
$a_{\ell_m}^k\neq 0$. By the same argument as in Lemma 3.1 (using the connectivity of 
$\Lambda_I$), the rows 
$a_{\ell_1}^I$ and 
$a_{\ell_m}^I$, consisting of entries in the columns indexed by I, are non-zero scalar multiples of each other. Since the rows of M 2 span a connected graph under the Γ-null-connectivity relation, we obtain that 
$a_{\ell_1}^I$ and 
$a_{\ell_m}^I$ are non-zero scalar multiples of each other for all 
$1\leq m\leq s$. By the maximality condition on M 2 and the connectivity of 
$\Lambda_I$ and 
$\Lambda_J$, we have that 
$I\subseteq J$. By symmetry, I = J. By the maximality conditions on M 1 and M 2, we obtain that 
$M_1=M_2$, the desired conclusion.
Lemma 3.2 allows us to canonically partition the entries of a matrix into three different types:
(1) Non-zero entries that lie in a Γ-1-block.
(2) Non-zero entries that do not lie in a Γ-1-block.
(3) Zero entries.
Next, we need to generalize to this context the notion of Γ-1-track defined in [Reference Flores, Kahrobaei and Koberda18]. By definition, this is a sequence 
$\{A_1,\ldots,A_k\}$ of minors of A with the following properties.
(1) For each i, the minor Ai is either a
$1\times 1$ submatrix or a Γ-1-minor.(2) Each column of A meets exactly one Ai.
(3) For i ≠ j, it is not the case that Ai and Aj belong to a common Γ-1-minor.
Two Γ-1-tracks are said to be different if they consist of different sets of submatrices of A.
The preceding definitions serve to sort the summands that make up the determinant of the matrix A, the latter of which is simply viewed as a signed combination of products of matrix entries. We write 
$\mathfrak a=(a_{\sigma(1)}^1,\ldots,a_{\sigma(n)}^n)$ for an arbitrary string of non-zero entries of A. Such a string belongs to a Γ-1-track 
$\{A_1,\ldots,A_k\}$ if for all i there exists a j such that 
$a_{\sigma(i)}^i$ is an entry of Aj.
Lemma 3.3. Let 
$\mathfrak a=(a_{\sigma(1)}^1,\ldots,a_{\sigma(n)}^n)$ be a string of non-zero entries of A. Then 
$\mathfrak a$ belongs to a unique Γ-1-track in A.
Proof. For B a Γ-1-block, we let 
$\{b_1,\ldots,b_s\}$ be the (possibly empty) set of entries of 
$\mathfrak a$ which lie in B. Each row and each column of A contain exactly one entry of 
$\mathfrak a$, and so 
$\{b_1,\ldots,b_s\}$ defines a Γ-1-minor AB in B of dimension exactly s. By construction, for distinct Γ-1-blocks B 1 and B 2, the Γ-1-minors 
$A_{B_1}$ and 
$A_{B_2}$ are disjoint. The remaining entries of 
$\mathfrak a$, say 
$\{c_1,\ldots,c_t\}$, are 
$1\times 1$ non-zero matrices that belong to no Γ-1-block. Thus, the Γ-1-track associated with 
$\mathfrak a$ is
\begin{align*}
\{A_B\}_{B\in\mathcal B}\cup \{c_1,\ldots,c_t\},
\end{align*} where 
$\mathcal B$ ranges over all Γ-1-blocks of A. The disjointness of distinct Γ-1-blocks guarantees that this is actually a Γ-1-track.
It is clear that this Γ-1-track in A is unique. Indeed, the constituents 
$\{c_1,\ldots,c_t\}$ and 
$\{A_B\}_{B\in\mathcal B}$ are canonically defined and hence unique.
Recall the Leibniz formula for the determinant of an n × n matrix, namely
\begin{align*}
\det A=\sum_{\sigma\in S_n} \mathrm{sgn}(\sigma)\prod_{i=1}^n a_{\sigma(i)}^i.
\end{align*} For a given Γ-1-track 
$\mathcal{T}$ of A, we write 
$(\det A)_{\mathcal{T}}$ for the restriction of the sum defining the determinant to permutations σ such that 
$\mathfrak a=(a_{\sigma(1)}^1,\ldots,a_{\sigma(n)}^n)$ belongs to 
$\mathcal{T}$.
Lemma 3.4. Let 
$\mathcal{T}$ be a Γ-1-track of A. Suppose 
$\mathcal{T}$ contains a minor of dimension at least two. Then
\begin{align*}
(\det A)_{\mathcal{T}}=0.
\end{align*}Proof. Let M be such a minor. Without loss of generality, M consists of the top left k × k minor of A, and we may identify Sk with the group of permutations of the rows of M, and we extend these permutations by the identity. If 
$\mathfrak a$ belongs to 
$\mathcal{T}$ and 
$\tau\in S_k$, then so does the string 
$\mathfrak a^{\tau}$, which is obtained by applying τ to the row indices of 
$\mathfrak a$. Since the signature of a permutation is a homomorphism, we have that the contribution of 
$\mathfrak a^{\tau}$ to 
$(\det A)_{\mathcal{T}}$ differs from that of 
$\mathfrak a$ by 
$\mathrm{sgn} (\tau)$. Since the row space of a Γ-1-block is one-dimensional, we have that the product of entries of 
$\mathfrak a$ and 
$\mathfrak a^{\tau}$ are equal. It is now immediate that 
$(\det A)_{\mathcal{T}}=0$, since exactly half the permutations in Sk have signature 1 and half have signature −1.
In the case of 
$\mathbb{F}_2$, Lemma 3.4 could be proved by simply noting that if 
$\mathcal{T}$ contains a minor of dimension at least two then an even number of distinct strings 
$\mathfrak a$ belongs to 
$\mathcal{T}$.
Corollary 3.5. Suppose A is invertible. Then there exists a reordering of the rows of A such that for all edges 
$\{i,j\}$ of Γ, we have that ai and aj are not Γ-null-connected.
Proof. We suppose the contrary and argue that 
$\det A=0$. Let 
$\mathfrak a=(a_{\sigma(1)}^1,\ldots,a_{\sigma(n)}^n)$ be a string of non-zero entries of A. By assumption, there is an edge 
$\{i,j\}$ of Γ which witnesses the fact that σ fails to be a suitable reordering. By reordering the rows by σ −1, we may assume 
$\mathfrak a=(a_1^1,\ldots,a_n^n)$. We have that the matrix
\begin{align*}
M=\begin{pmatrix}a_i^i&a_j^i\\ a_i^j&a_j^j\end{pmatrix}
\end{align*} is singular, because these rows must be Γ-null-connected. Since the matrix M has non-zero diagonal entries and is singular, it must lie inside of a Γ-1-block of A. It follows that the unique Γ-1-track 
$\mathcal{T}$ to which 
$\mathfrak a$ belongs contains a Γ-1-minor of dimension at least two, and so 
$(\det A)_{\mathcal{T}}=0$. The choice of 
$\mathfrak a$ was arbitrary, and so each such string belongs to a Γ-1-track 
$\mathcal{T}$ such that 
$(\det A)_{\mathcal{T}}=0$. Now, the uniqueness of the track to which 
$\mathfrak a$ belongs implies that 
$\det A$ is the sum of 
$(\det A)_{\mathcal{T}}$, where 
$\mathcal{T}$ varies over all possible Γ-1-tracks. The desired result now follows.
Proof of Theorem 1.1.
We fix notation and write 
$\{v^*_1,\ldots,v^*_n\}$ for the standard basis for 
$H^1(A(\Gamma),\mathbb{F})$, and we let 
$A\in \mathrm{GL}_n(\mathbb{F})$ be arbitrary. We let 
$\mathcal{B}=\{w_1,\ldots,w_n\}$ be the result of applying A, viewed as a change of basis, so that
\begin{align*}
w_i=\sum_{j=1}^n a_i^j v_j^*.
\end{align*} We let σ be a reordering of the rows of A as guaranteed by Corollary 3.5, and we relabel the vectors 
$\{w_1,\ldots,w_n\}$ according to σ. Computing 
$w_i\smile w_j$, we see that this cup product is zero if and only if the rows ai and aj of A are Γ-null-connected. It follows that the cohomology basis graph 
$\Gamma_{\mathcal{B}}$ contains Γ as a subgraph, as desired.
Observe that Corollary 1.2 is immediate from Theorem 1.1, as for an inclusion of graphs 
$\Gamma^{\prime}\subseteq\Gamma$ with the same number of vertices, equality in the number of edges implies isomorphism. Theorem 1.3 is a consequence of Theorem 1.1 and the minor-monotonicity of the Colin de Verdière invariant. As right-angled groups are biautomatic, Corollary 1.4 follows. Finally, Theorem 1.5 is implied in turn by Theorem 1.3, together with the properties of the invariant discussed in 
$\S$ 2.3.
We conclude by stating a property concerning complements, which is analogous to Theorem 1.5:
Proposition 3.6. Let Γ be a finite simple graph with no twin vertices. Then the complement of Γ is planar (respectively outerplanar) if and only if for every basis 
$\mathcal{B}$ of 
$H^1(A(\Gamma),\mathbb{F})$, the complement of the cohomology basis graph 
$\Gamma_{\mathcal{B}}$ is planar (respectively outerplanar).
Proof. We prove the case of planarity; the argument for outerplanarity is analogous. By Theorem 2.3, the complement of Γ is planar if and only if 
$\mu(\Gamma)\geq n-5$, where 
$n=|V(\Gamma)|$. By the minor monotonicity of µ, we see that 
$\mu(\Gamma_{\mathcal{B}})\geq n-5$ for every cohomology basis graph 
$\Gamma_{\mathcal{B}}$. By Theorem 2.3, the complement of every such 
$\Gamma_{\mathcal{B}}$ is planar. The other implication is immediate.
3.2. A reformulation in terms of edge ideals
There are equivalent reformulations of the main Theorem 1.1 in other contexts, which to our knowledge were also open questions; this was communicated to the authors by Van Tuyl [Reference Van Tuyl38]. Here we discuss a perspective from commutative algebra and in the next section from graph theory.
One fruitful context for investigating the interplay between combinatorics of graphs and commutative algebra is through clutters and monomial ideals, and especially edge ideals, which are in turn related to the theory of polyhedral products and Stanley–Reisner rings; the reader is directed to [Reference Hà and Van Tuyl23, Reference Morey and Villarreal32] for background.
We consider 
$k=\mathbb{F}_2$, the field with two elements, and a polynomial ring 
$R=k[x_1,\ldots,x_n]$. We let 
$I\subset R$ be an ideal generated by square-free monomials of degree 2, and we let 
$\Gamma_I$ be the graph having I as its edge ideal. A matrix 
$A\in\mathrm{GL}_n(k)$ determines a linear change of variables 
$x_i\mapsto w_i$ that preserves degrees of polynomials. We let I ʹ be the complement of I, which is to say that I ʹ is generated by all degree 2 monomials that do not lie in I, and we let 
$\overline R=R/I^\prime$.
One can now consider the ideal 
$J\subset k[w_1,\ldots,w_n]$ generated by products 
$w_iw_j$, with i ≠ j, and its image 
$\overline J\subset\overline R$. We write 
$\Gamma_J$ for the graph with vertices 
$\{w_1,\ldots,w_n\}$, and with an edge whenever the monomial 
$w_iw_j$ survives in 
$\overline J$. These graphs have been extensively studied in the literature, see, for example, [Reference Van Tuyl37] and references therein.
The following result can easily be seen to follow from Theorem 1.1:
Corollary 3.7. The graph 
$\Gamma_I$ is a subgraph of 
$\Gamma_J$.
Conversely, observe that every finite simple graph can be represented by 
$\Gamma_I$ for some edge ideal. Moreover, every change of basis can be effected by an invertible matrix. Thus, if 
$\Gamma_I$ is always a subgraph of 
$\Gamma_J$ as above, then Theorem 1.1 holds over a field of characteristic 2.
3.3. A reformulation in classical graph theory
Let 
$A\in \mathrm{GL}_n(\mathbb{F}_2)$, and let Γ be a fixed graph on n vertices 
$\{v_1,\ldots,v_n\}$. We now define a new finite simple graph with vertex set 
$\{e_1,\ldots,e_n,w_1,\ldots,w_n\}$. The edge relation is given as follows:
(1) We place an edge between ei and ej precisely when there is an edge between vi and vj.
(2) We place an edge between wi and ej precisely when the entry
$a_i^j$ of A is non-zero.(3) For i ≠ j, we place a new edge between wi and wj if and only if there exist indices k and
$\ell$ such that the following conditions hold:(a) There is an edge between vk and
$v_{\ell}$.(b) There is a path of length 3 between wi and wj that contains the edge between ek and
$e_{\ell}$ induced by the previous condition and the two edges arising from (2) above, and there is no path of length two in the subgraph induced by $\{w_i,w_j,e_k,e_{\ell}\}$.
We write 
$\Gamma^{\prime}$ for the graph spanned by 
$\{w_1,\ldots,w_n\}$, and let 
$\mathcal B$ be the basis for 
$H^1(A(\Gamma),\mathbb{F}_2)$ induced by the rows of A; by construction, we may naturally identify elements of 
$\mathcal B$ with 
$\{w_1,\ldots,w_n\}$. It is straightforward to see that wi and wj are adjacent in 
$\Gamma^{\prime}$ if and only if wi and wj are adjacent in 
$\Gamma_{\mathcal B}$: indeed, this can be seen from explicitly writing out the cup product in terms of the basis of 
$H^1(A(\Gamma),\mathbb{F}_2)$ coming from the vertices of Γ, cf. 
$\S$ 2.2. Thus, Theorem 1.1 is equivalent to:
Corollary 3.8. The graph Γ is a subgraph of 
$\Gamma^{\prime}$.
4. Some examples
In this section, we describe explicit examples that we find illustrative for understanding the difficulties that arise in attempts to prove the main result directly.
One of the basic issues that makes finding a proof of Theorem 1.1 non-trivial is the ‘global’ nature of the assertion it makes. The result says that from an arbitrary basis for 
$H^1(A(\Gamma),\mathbb{F})$, one can find an assignment between these arbitrary basis vectors and vectors in the standard basis which respects the cup product structure. Experiments suggest and careful consideration shows that there is no canonical way to realize such a bijection, and this is the reason that inductive strategies do not seem to work; even if one assumes the existence of such a bijection for a proper subgraph, extending by even one vertex seems technically impossible. These issues already appear in the following simple example:
Example 4.1. Consider the defining graph Γ with vertices 
$\{v_1,v_2,v_3,v_4\}$ and edges
\begin{align*}
\{v_1,v_2\}, \{v_1,v_3\},\{v_1,v_4\},
\end{align*} and the basis 
$\mathcal B=\{w_1,w_2,w_3,w_4\}$ for the first cohomology of 
$A(\Gamma)$ given by the change of basis matrix
\begin{align*}
A=\begin{pmatrix}1&0&0&0\\ 0&1&0&1\\0&1&0&0\\ 0&0&1&0 \end{pmatrix}.
\end{align*} Now, the associated cohomology basis graph 
$\Gamma_{\mathcal{B}}$ has edges
\begin{align*}
\{w_1,w_2\}, \{w_1,w_3\}, \{w_1,w_4\},
\end{align*} which is isomorphic to Γ. Hence, the natural assignment 
$v_i\mapsto w_i$ induces an isomorphism of graphs, and in particular an inclusion 
$\Gamma\subseteq\Gamma_{\mathcal{B}}$.
Now, we add the edge 
$\{v_2,v_4\}$ to the defining graph, obtaining a new graph Λ, and we retain the basis 
$\mathcal B$. The cohomology basis graph 
$\Lambda_{\mathcal{B}}$ has edges
\begin{align*}
\{w_1,w_2\}, \{w_1,w_3\}, \{w_1,w_4\}, \{w_2,w_3\},
\end{align*} and the previous assignment 
$v_i\mapsto w_i$ do not extend to the new graphs. Of course, Theorem 1.1 ensures that there exists another suitable assignment for the new graphs, for instance one sending v 3 to w 4 and v 4 to w 3, but this is an ad hoc modification that is difficult to make canonical.
In searching for a formula defining a canonical bijection between the vertices of the graph and the arbitrary basis vectors, one encounters many reasonable-sounding linear algebraic claims which end up being false. One might hope, for example, that if 
$A\in\mathrm{GL}_n(\mathbb{F}_2)$ then there is a reordering of the rows of A so that all the principal minors are non-singular; one might hope for this to be the case for just the two-dimensional principal minors, and it is not difficult to see how this claim would imply Theorem 1.1. A counterexample to the claim is given by the following:
Example 4.2. Consider the invertible matrix
\begin{align*}
A=\begin{pmatrix}1&1&0&0\\ 1&1&1&1\\0&0&1&0\\ 0&1&1&1 \end{pmatrix}.
\end{align*}Then, a straightforward analysis shows that in every reordering of the rows there is at least one 2-dimensional principal minor which is singular.
One further example that we give in this section concerns the practicality of the planarity test described at the end of 
$\S$ 2.5.
Example 4.3. Consider the group
\begin{align*}
G=\langle x_1,x_2,x_3,x_4,x_5 | x_1x_2x_5x_4=x_2x_5x_4x_1, x_3x_2x_5x_4=x_2x_5x_4x_3, x_4x_5=x_5x_4\rangle.
\end{align*}This groups is abstractly isomorphic to a right-angled Artin group on a graph with five vertices. If we consider the dual generators
\begin{align*}
\{x^*_1,x^*_2,x^*_3,x^*_4,x^*_5\}
\end{align*} in 
$H^1(G;\mathbb{F}_2)$, it is not hard to check using the arguments of 
$\S$ 2.5 that the only non-trivial products of two of these elements are 
$x_2^*x_i^*$ for every i ≠ 2 and 
$x_4^*x_5^*$. Hence, the cohomology graph is a star with one additional edge, which is planar. Thus, the defining graph is also planar, by Theorem 1.3.
5. Graph minors and the cohomology basis graph
In this last section, we investigate the behaviour of the cohomology graph 
$\Gamma_{\mathcal{B}}$ under taking minors of Γ. This is particularly relevant in light of Wagner’s theorem (i.e. a graph is planar if and only if it does not admit K 5 or 
$K_{3,3}$ as a minor), though we will show that the cohomology basis graph and graph minors do not interact in a sufficiently nice way to make this a viable approach to characterizing planarity. Thus, we have another justification for Theorem 1.1 being the ‘correct’ approach to understanding planarity through cohomological means.
Notice that if Λ is an elementary minor of Γ obtained by deleting an edge or vertex then there is a natural inclusion of Λ into Γ. If Λ is an elementary minor under contracting an edge with vertices v 1 and v 2, then Λ is equipped with a special vertex which we can formally and suggestively label 
$v_1+v_2$.
Let 
$\mathcal{B}$ be an arbitrary basis for 
$H^1(A(\Gamma),\mathbb{F})$. We begin by writing the elements of 
$\mathcal{B}$ in terms of the cohomology classes that are dual to vertices of Γ, i.e. 
$\{v^*_1,\ldots,v^*_n\}$. If Λ is an elementary minor of Γ, then there is a natural way to obtain a basis 
$\mathcal{B}^\prime$ for 
$H^1(A(\Lambda),\mathbb{F})$. Then, we have the following moves:
(1) If Λ is obtained from Γ by deleting an edge of Γ then
$\mathcal{B}^\prime=\mathcal{B}$;(2) If Λ is obtained from Γ by deleting the vertex corresponding to the cohomology class
$v^*_i$, then the vectors of $\mathcal{B}^\prime$ are simply the vectors of $\mathcal{B}$ with every occurrence of $v^*_i$ deleted and any repeats or trivial vectors discarded and, if necessary, one further vector discarded to ensure that $\mathcal{B}^\prime$ is linearly independent;(3) If Λ is obtained from Γ by contracting the edge connecting vertices corresponding to
$v^*_i$ and $v^*_j$, then the vectors of $\mathcal{B}^\prime$ are vectors of $\mathcal{B}$ with $v^*_i$ and $v^*_j$ replaced by $v^*_i+v^*_j$, and with any repeats or trivial vectors discarded and, if necessary, one further vector discarded to ensure that $\mathcal{B}^\prime$ is linearly independent.
To fix terminology, if 
$\mathcal{B}$ is an arbitrary basis for 
$H^1(A(\Gamma),\mathbb{F})$, we will call a basis 
$\mathcal{B}^\prime$ for 
$H^1(A(\Lambda),\mathbb{F})$ obtained by one of the previous three moves an elementary minor basis.
We first make some remarks about the naturality of the transformation from 
$\mathcal{B}$ to 
$\mathcal{B}^\prime$. For edge deletions, there is little to say. If Λ is obtained from Γ by deleting an edge between vertices v 1 and v 2, then there is a natural homomorphism 
$\phi\colon: A(\Lambda)\to A(\Gamma)$ which is defined by simply declaring that v 1 and v 2 commute with each other. In this case, we get a natural map
\begin{align*}
\phi^*\colon H^1(A(\Gamma),\mathbb{F})\to H^1(A(\Lambda),\mathbb{F}),
\end{align*} and 
$\phi^*(\mathcal{B})=\mathcal{B}^\prime$.
The case of vertex deletion is similar, using the fact that the inclusion 
$\Lambda\to\Gamma$ induces a map 
$\psi\colon A(\Lambda)\to A(\Gamma)$, and consequently a map
\begin{align*}
\psi^*\colon H^1(A(\Gamma),\mathbb{F})\to H^1(A(\Lambda),\mathbb{F}).
\end{align*} We then consider 
$\psi^*(\mathcal{B})$, which contains a basis of 
$H^1(A(\Lambda),\mathbb{F})$, and so we discard a vector if necessary to obtain 
$\mathcal{B}^\prime$.
Though 
$\mathcal{B}^\prime$ is obtained from 
$\mathcal{B}$ in a reasonably natural way, there is still a matter of the choice of which vector to discard. Proposition 5.1 shows that the choice made is absorbed by a choice of minor on the cohomology basis graph side.
The case of edge contraction is slightly different, since there is a natural map
\begin{align*}
\chi\colon A(\Gamma)\to A(\Lambda),
\end{align*} though not the other way. Let v 1 and v 2 be two adjacent vertices of Γ that are identified in Λ, wherein we call the resulting vertex v 0. Write 
$\{v_1^*,v_2^*,v_0^*\}$ for the corresponding dual cohomology classes. Under the natural induced map 
$H^1(A(\Lambda),\mathbb{F})\to H^1(A(\Gamma),\mathbb{F})$, the cohomology class 
$v_0^*$ is sent to the cohomology class 
$v_1^*+v_2^*$. Thus, 
$H^1(A(\Lambda),\mathbb{F})$ is canonically isomorphic to a subspace of 
$H^1(A(\Gamma),\mathbb{F})$ with the identification 
$v_0^*\mapsto v_1^*+v_2^*$. We let
\begin{align*}
\varphi\colon H^1(A(\Gamma),\mathbb{F})\to H^1(A(\Gamma),\mathbb{F})
\end{align*} be the endomorphism which is the identity on all generators dual to vertices other than v 1 and v 2, and otherwise 
$v_1^*,v_2^*\mapsto v_1^*+v_2^*$. Finally, we let
\begin{align*}
\chi_*\colon H^1(\varphi(A(\Gamma),\mathbb{F}))\to H^1(A(\Lambda),\mathbb{F})
\end{align*} be the map that is the identity on all generators dual to vertices other than v 1 and v 2, which sends 
$v_1^*+v_2^*\mapsto v_0^*$. Then, 
$\chi_*\circ \varphi(\mathcal{B})$ contains a basis for 
$H^1(A(\Lambda),\mathbb{F})$, and so we discard a vector if necessary to obtain 
$\mathcal{B}^\prime$.
Proposition 5.1. Let Γ be a graph, let Λ an elementary minor of Γ obtained by either edge deletion or vertex deletion, let 
$\mathcal{B}$ be an arbitrary basis for 
$H^1(A(\Gamma),\mathbb{F})$ and let 
$\mathcal{B}^\prime$ be an elementary minor basis for 
$H^1(A(\Lambda),\mathbb{F})$. Then the graph 
$\Gamma_{\mathcal{B}^\prime}$ is a minor of the graph 
$\Gamma_{\mathcal{B}}$.
Proof. We verify the claim for the two moves that we allow.
Edge deletion. In this case, 
$\mathcal{B}=\mathcal{B}^\prime$. Suppose 
$b_1,b_2\in\mathcal{B}$ are adjacent to each other in 
$\Gamma_{\mathcal{B}}$, and write these basis vectors as a sum of cohomology classes dual to the vertices of Γ. Abusing notation slightly, there is an edge 
$\{v_1,v_2\}$ of Γ such that v 1 but not v 2 occurs in the expression of b 1, and v 2 but not v 1 occurs in the expression of b 2. If the edge 
$\{v_1,v_2\}$ persists in Λ then b 1 and b 2 remain adjacent in 
$\Gamma_{\mathcal{B}^\prime}$. If the edge 
$\{v_1,v_2\}$ does not persist in Λ, then b 1 and b 2 may or may not remain adjacent in 
$\Gamma_{\mathcal{B}^\prime}$, contingent on the existence of another edge of Γ that witnesses the continued adjacency of b 1 and b 2.
If b 1 and b 2 are non-adjacent in 
$\Gamma_{\mathcal{B}}$, then we wish to argue that these vertices remain non-adjacent in 
$\Gamma_{\mathcal{B}^\prime}$. Let 
$\{v_1,v_2\}$ denote an arbitrary edge of Γ. Necessarily, one of the following three possibilities holds, up to relabelling vertices or basis elements:
(1) Neither v 1 nor v 2 occurs in the expressions for b 1 and b 2;
(2) Both v 1 and v 2 occur in both expressions for b 1 and b 2;
(3) The class v 1 occurs in the expression for b 1 but v 2 does not occur in the expression for b 2.
Now, there is a pair of vertices 
$\{v_i,v_j\}$ which span an edge of Γ but such that 
$v_i^*\smile v_j^*=0$ in 
$H^1(A(\Lambda))$, with no other cup products between dual vertex basis vectors being changed. It follows immediately then that pairs of non-adjacent vertices in 
$\Gamma_{\mathcal{B}}$ remain non-adjacent in 
$\Gamma_{\mathcal{B}^\prime}$.
Vertex deletion. Retaining notation from above, let 
$\psi^*(\mathcal{B})\subset H^1(A(\Lambda))$ be the image of 
$\mathcal{B}$ under the map induced by the inclusion 
$\Lambda\to\Gamma$, and let 
$b_1,b_2\in\mathcal{B}$. For 
$i\in\{1,2\}$, writing 
$\psi^*(b_i)$ and bi in terms of the vertex duals, we simply have that a summand v is deleted from 
$\psi^*(b_i)$ if it occurs in bi. If 
$\psi^*(b_1)=\psi^*(b_2)$ then we will begin by deleting one of them (which is vertex deletion in 
$\Gamma_{\mathcal{B}}$) and then proceed by applying 
$\psi^*$, which will then yield 
$\mathcal{B}^\prime$ without any further deletions.
Suppose that b 1 and b 2 are adjacent in 
$\Gamma_{\mathcal{B}}$, and that this adjacency is witnessed only by edges in Γ that are incident to v. Then after deleting v from Γ, all these edges are severed, in which case 
$\psi^*(b_1)\smile \psi^*(b_2)=0$. If the adjacency is witnessed by an edge that is not incident to v, then 
$\psi^*(b_1)\smile \psi^*(b_2)\neq 0$.
Suppose that b 1 and b 2 are non-adjacent in 
$\Gamma_{\mathcal{B}}$. Then for an arbitrary edge 
$\{v_1,v_2\}$ of Γ, we have the three possibilities as in the case of edge deletion. It is straightforward to check that the three possibilities persist after applying 
$\psi^*$, in which case 
$\psi^*(b_1)\smile \psi^*(b_2)=0$.
Let 
$\Gamma_{\psi^*}$ be the graph obtained by taking vertices to be elements 
$\psi^*(\mathcal{B})$ and adjacency to be given by non-vanishing cup product. Then the preceding argument shows that 
$\Gamma_{\psi^*}$ is a minor of 
$\Gamma_{\mathcal{B}}$. The basis 
$\mathcal{B}^\prime$ is obtained by (possibly) deleting an element of 
$\psi^*(\mathcal{B})$, in which case we see that 
$\Gamma_{\mathcal{B}^\prime}$ is a minor of 
$\Gamma_{\psi^*}$, as desired.
It is not generally true that if Λ is obtained from Γ by edge contraction then 
$\Gamma_{\mathcal{B}^\prime}$ is a minor of 
$\Gamma_{\mathcal{B}}$. Consider for instance the dumbbell graph Γ from Figure 1. It has 
$n + m + 1$ edges.
Figure 1. The dumbbell graph Γ.
For compactness of notation, we will conflate names of vertices and corresponding dual cohomology classes and cease writing asterisk superscripts. To simplify notation further, we will write sums of cohomology classes multiplicatively. Let
\begin{align*}
\mathcal{B}=\{b_1,\ldots,b_m,a_1b_1,v_1a_1,\ldots,v_1a_n,
v_2a_1\}.
\end{align*} It is straightforward to verify that this is indeed a basis for 
$H^1(A(\Gamma),\mathbb{F})$. The edges of 
$\Gamma_{\mathcal{B}}$ are of the following form:
(1)
$\{b_i,v_2a_1\}$ for $1\leq i\leq m$;(2)
$\{v_2a_1,v_1a_j\}$ for $1\leq j\leq n$;(3)
$\{v_2a_1,a_1b_1\}$;(4)
$\{v_1a_i,v_1a_j\}$ for i ≠ j;(5)
$\{a_1b_1,v_1a_j\}$ for $1\leq j\leq n$.
We check easily that 
$\Gamma_{\mathcal{B}}$ has
\begin{align*}
\frac{n^2}{2}+\frac{3n}{2}+m+1
\end{align*} total edges. Now to compute 
$\mathcal{B}^\prime$ and 
$\Gamma_{\mathcal{B}^\prime}$, we introduce the symbol z for 
$v_1+v_2$. Each occurrence of v 1 and v 2 is replaced by z. The vertices 
$v_2a_1$ and 
$v_1a_1$ become identical, and so we delete one of them. Then we have
\begin{align*}
\mathcal{B}^\prime=\{b_1,\ldots,b_m,a_1b_1,za_1,\ldots,za_n\}.
\end{align*} The edges of 
$\Gamma_{\mathcal{B}^\prime}$ are of the following form:
(1)
$\{b_i,za_j\}$ for $1\leq i\leq m$ and $1\leq j\leq n$;(2)
$\{za_i,za_j\}$ for i ≠ j;(3)
$\{a_1b_1,za_j\}$ for $1\leq j\leq n$.
We check easily that 
$\Gamma_{\mathcal{B}^\prime}$ has
\begin{align*}
\frac{n^2}{2}+mn+\frac{n}{2}
\end{align*} total edges. Thus, the difference between the total number of edges of 
$\Gamma_{\mathcal{B}^\prime}$ and 
$\Gamma_{\mathcal{B}}$ is 
$(m-1)(n-1)-2$. Evidently, this difference can be made positive by choosing the parameters n and m suitably. Now, if 
$\Gamma_{\mathcal{B}^\prime}$ were a minor of 
$\Gamma_{\mathcal{B}}$ then 
$\Gamma_{\mathcal{B}^\prime}$ would have fewer edges than 
$\Gamma_{\mathcal{B}}$, which is a contradiction.
Acknowledgements
We thank Y. Antolín, O. Cárdenas, M. Casals-Ruiz, M. Chudnovsky, J. Gálvez, M. Gheorghiu, P. Giménez, J. González-Meneses, C. Johnson, A. Márquez, J. Martínez, S. Morey, F. Muro, C. Valencia and A. Viruel for helpful comments. We are in particular very grateful to K. Li, M. Tsatsomeros and A. van Tuyl for their interest in our work. The authors are grateful to an anonymous referee who provided numerous helpful comments which greatly improved the paper.
Funding Statement
Ramón Flores is supported by FEDER-MEC grant PID2020-117971GB-C21 of the Spanish Ministery of Science. Thomas Koberda is partially supported by NSF Grant DMS-2002596. Delaram Kahrobaei is supported in part by an, ONR grant, 62909-24-1-2002. Corentin Le Coz is supported by the FWO and the F.R.S.–FNRS under the Excellence of Science (EOS) program (project ID 40007542).
