Published online by Cambridge University Press: 23 May 2016
An invertible polynomial in n variables is a quasi-homogeneous polynomial consisting of n monomials so that the weights of the variables and the quasi-degree are well defined. In the framework of the construction of mirror symmetric orbifold Landau–Ginzburg models, Berglund, Hübsch and Henningson considered a pair (f, G) consisting of an invertible polynomial f and an abelian group G of its symmetries together with a dual pair 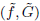 . Here we study the reduced orbifold zeta functions of dual pairs (f, G) and
. Here we study the reduced orbifold zeta functions of dual pairs (f, G) and 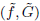 and show that they either coincide or are inverse to each other depending on the number n of variables.
and show that they either coincide or are inverse to each other depending on the number n of variables.