No CrossRef data available.
Article contents
On the Quantitative Metric Theory of Continued Fractions in Positive Characteristic
Part of:
Measure-theoretic ergodic theory
Probabilistic theory: distribution modulo $1$; metric theory of algorithms
Published online by Cambridge University Press: 07 February 2018
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
Let 𝔽q be the finite field of q elements. An analogue of the regular continued fraction expansion for an element α in the field of formal Laurent series over 𝔽q is given uniquely by
where 
$$\alpha = A_0(\alpha ) + \displaystyle{1 \over {A_1(\alpha ) + \displaystyle{1 \over {A_2(\alpha ) + \ddots }}}},$$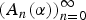
$(A_{n}(\alpha))_{n=0}^{\infty}$ is a sequence of polynomials with coefficients in 𝔽q such that deg(An(α)) ⩾ 1 for all n ⩾ 1. In this paper, we provide quantitative versions of metrical results regarding averages of partial quotients. A sample result we prove is that, given any ϵ > 0, we have
for almost everywhere α with respect to Haar measure.
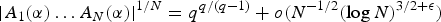$$\vert A_1(\alpha ) \ldots A_N(\alpha )\vert ^{1/N} = q^{q/(q - 1)} + o(N^{ - 1/2}(\log N)^{3/2 + {\rm \epsilon }})$$
MSC classification
- Type
- Research Article
- Information
- Proceedings of the Edinburgh Mathematical Society , Volume 61 , Issue 1 , February 2018 , pp. 283 - 293
- Creative Commons
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.- Copyright
- Copyright © Edinburgh Mathematical Society 2018
References
1.
Berthé, V. and Nakada, H., On continued fraction expansions in positive characteristic: equivalence relations and some metric properties, Expo. Math.
18(4) (2000), 257–284.Google Scholar
2.
de Vroedt, C., Metrical problems concerning continued fractions, Compos. Math.
16 (1964), 191–195.Google Scholar
3.
Gál, I. S. and Koksma, J. F., Sur l'ordre de grandeur des fonctions sommables, Indag. Math.
12 (1950), 638–653.Google Scholar
4.
Houndonougbo, V., Développement en fractions continues et répartititon modulo 1 dans un corps de séries formelles Thése de troisiéme cycle
, Université de Bordeaux I, 1979.Google Scholar
5.
Iosifescu, M. and Kraaikamp, C., Metrical theory of continued fractions, in Mathematics and its applications, Volume 547, pp. 225–232 (Kluwer Academic Publishers, Dordrecht, 2002).CrossRefGoogle Scholar
6.
Khinchin, A. Ya., Continued fractions (Dover Publications, Mineola, NY, Russian edition, 1997). With a preface by Gnedenko, B. V., Reprint of the 1964 translation.Google Scholar
7.
Lertchoosakul, P. and Nair, R., On the metric theory of continued fractions in positive characteristic, Mathematika
60(2) (2014), 307–320.CrossRefGoogle Scholar
8.
Niederreiter, H., The probabilistic theory of linear complexity, In Advances in cryptology – Eurocrypt 88, Davos 88, Lecture Notes in Computer Science, Volume 330, pp. 195–197 (Springer, Berlin
1988).Google Scholar
9.
Schmidt, W. M., On continued fractions and Diophantine approximation in power series fields, Acta Arith.
95(2) (2000), 139–166.Google Scholar
10.
Sprindžuk, V. G., Mahler's problem in metric number theory. Translated from the Russian by Volkmann, B.. Translations of Mathematical Monographs, Volume 25, p. 99 (American Mathematical Society, Providence, RI, 1969).Google Scholar
You have
Access
Open access