Hostname: page-component-6bf8c574d5-xtvcr Total loading time: 0 Render date: 2025-02-21T21:33:11.268Z Has data issue: false hasContentIssue false
  • English
  • Français

Distinguishedness of weighted Fréchet spaces of continuous functions

Published online by Cambridge University Press:  20 January 2009

Françoise Bastin
Françoise Bastin
Affiliation:
Université de LiègeInstitut de MathématiqueAvenue des Tilleuls, 154000 Liege, Belgium
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper, we prove that if 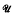is an increasing sequence of strictly positive and continuous functions on a locally compact Hausdorff space X such that 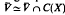then the Fréchet space C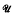(X) is distinguished if and only if it satisfies Heinrich's density condition, or equivalently, if and only if the sequence 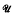satisfies condition (H) (cf. e.g.‵[1] for the introduction of (H)). As a consequence, the bidual λ∞(A) of the distinguished Köthe echelon space λ0(A) is distinguished if and only if the space λ1(A) is distinguished. This gives counterexamples to a problem of Grothendieck in the context of Köthe echelon spaces.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 35 , Issue 2 , June 1992 , pp. 271 - 283
Copyright
Copyright © Edinburgh Mathematical Society 1992

References

REFERENCES

1.Bastin, F., Weighted spaces of continuous functions, Bull. Soc. Roy. Sci. Liege 1 (1990), 1–81.Google Scholar
2.Bierstedt, K.-D. and Bonet, J., Stefan Heinrich's density condtion for Fréchet spaces and the characterization of the distinguished Köthe echelon spaces, Math. Nachr. 135 (1988), 149–180.CrossRefGoogle Scholar
3.Bierstedt, K.-D. and Meise, R., Distinguished echelon spaces and the projective description of the weighted inductive limits of type C(X), in Aspects of Mathematics and its Applications (Elsevier Science Publ. B.V. North-Holland Math. Library, 1986).Google Scholar
4.Bierstedt, K.-D., Meise, R. and Summers, W. Köthe sets and Köthe sequence space, in Functional Analysis. Holomorphy and Approximation Theory (North-Holland Math. Studies 71, 1982), 27–91.Google Scholar
5.Bonet, J., Dierolf, S. and Fernandez, C., The bidual of a distinguished Fréchet space need not be distinguished (1990), preprint.CrossRefGoogle Scholar
6.Vogt, D., Distinguished Kothe spaces, Math. Z. 202 (1989), 143–146.CrossRefGoogle Scholar