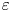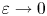Hostname: page-component-745bb68f8f-b6zl4 Total loading time: 0 Render date: 2025-02-05T14:33:24.257Z Has data issue: false hasContentIssue false
  • English
  • Français

Dirichlet vs Neumann

Part of: Partial differential equations

Published online by Cambridge University Press:  22 November 2022

Eduard Marušić-Paloka
Eduard Marušić-Paloka*
Affiliation:
Department of mathematics, Faculty of Science and Mathematics, University of Zagreb, Bijenička 30, 10000 Zagreb, Croatia (emarusic@math.hr)
Rights & Permissions [Opens in a new window]

Abstract

We study the asymptotic behaviour of the periodically mixed Zaremba problem. We cover the part of the boundary by a chess board with a small period (square size) $\varepsilon$ and impose the Dirichlet condition on black and the Neumann condition on white squares. As $\varepsilon \to 0$, we get the effective boundary condition which is always of the Dirichlet type. The Dirichlet data on the boundary, however, depend on the ratio between the magnitudes of the two boundary values.

Keywords

periodic boundary conditionhomogenizationboundary layerLaplace equationthe Zaremba problem

MSC classification

Primary: 35B27: Homogenization; equations in media with periodic structure 35B25: Singular perturbations 35B40: Asymptotic behavior of solutions
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 65 , Issue 4 , November 2022 , pp. 1063 - 1074
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society

1. Introduction

Suppose that a part of the boundary, denoted $\Gamma$, of the domain $\Omega \subset \mathbf {R}^{3}$ is covered by a fine chess board with square size $\varepsilon$. On each black square, we impose the Dirichlet boundary condition

\[ u^{\varepsilon} = g_\varepsilon \]

and on each white square the Neumann condition

\[ \frac{\partial u^{\varepsilon}}{\partial\mathbf{n}} =h. \]

As $\varepsilon \to 0$ the squares become smaller and smaller but, at the same time, their number becomes larger and larger. At the end, the black and white squares merge and we get some homogeneous grey area.

The question is: what happens with the boundary condition? Which one prevails? Do we get Dirichlet, Neumann or something else?

We call the boundary condition satisfied by the limit the effective boundary condition, as it should be effectively applied in situations when $\varepsilon$ is small. So, what is the effective boundary condition?

The periodic function, as its period tends to zero, tends (weakly) to its mean value. As the original (microscopic) boundary condition is equally spread mix of Dirichlet and Neumann condition, at first glance, one would expect some average between the Neumann and Dirichlet condition. Disappointingly, the first answer is much simpler. The effective boundary condition is always the Dirichlet condition

\[ u=G\text{ on }\Gamma. \]

On the bright side, the value of the effective Dirichlet datum $G$ is not so obvious and depends on the ratio between the magnitudes of $g_\varepsilon$ and $h$.

As expected (taking int account [Reference Filo and Luckhaus3]), if the Dirichlet datum $g_\varepsilon$ and the Neumann datum $h$ have the same magnitude, then only $g_\varepsilon$ remains in the picture and $h$ disappears. Thus the effective Dirichlet value $G$ is derived from $g_\varepsilon$ only, and does not depend on $h$. If $g_\varepsilon$ is weaker (for example, in the sense of $L^{2}$ norm) then there is a critical ratio when they both appear in the limit Dirichlet condition. Beyond that critical ratio, the Neumann datum $h$ becomes dominant and the Dirichlet datum $g_\varepsilon$ disappears from the limit.

Boundary value problems with the periodic structure on the micro-level have been studied, using the method of homogenization, for more then 50 years (see e.g. [Reference Bensoussan, Lions and Papanicolau1]). In particular, effective boundary conditions with periodic geometry are not new subjects (see e.g. [Reference Filo2–Reference Jäger and Mikelić5] or [Reference Marušić-Paloka8]). Problems similar to ours have been studied in [Reference Filo and Luckhaus3], in case of heat-conduction equation in two dimensions (see also [Reference Filo2]). The main difference is that the Dirichlet condition in those papers is homogeneous, corresponding to our situation with $g_\varepsilon =0$. Thus, the limit satisfies the homogeneous Dirichlet condition. An asymptotic expansion was found and the second-order corrector contains the trace of the Neumann boundary condition. The idea was generalized in paper [Reference Filo and Luckhaus4] to n dimension and almost-periodic boundary condition, but still with zero Dirichlet datum $g=0$.

The novelty and the most important feature here is that the Dirichlet value $g_\varepsilon$ is not zero and depends on $\varepsilon$ in the way that $g_\varepsilon = \varepsilon ^{\beta } g$. Also, we use a different approach based on the very-weak formulation of the problem, weak convergence and the boundary-layer-type test function.

Further analysis, with higher-order asymptotics, can be found in [Reference Marušić-Paloka and Pažanin11]. Application of similar ideas, to the viscous fluid flow was done in [Reference Marušić-Paloka and Pažanin10, Reference Marušić-Paloka and Pažanin12].

Figure 1. Domain $\Omega$ with alternating Neumann and Dirichlet conditions on $\Gamma$.

1.1. The geometry

Let $\Omega \subset \mathbf {R}^{3}$ be a smooth bounded domain. We assume, for simplicity, that the boundary $\partial \Omega$ has a flat part

\[ \Sigma = \lbrace \mathbf{x}= (x_1 ,x_2 ,x_3) \in \mathbf{R}^{3}:\mathbf{x}' = (x_1 ,x_2) \subset \omega,\quad x_3=0\rbrace \subset \partial\Omega. \]

Let $\Gamma \subset \subset \Sigma$ be compactly embedded in $\Sigma$, with smooth boundary $\partial \Gamma$. We cover $\Gamma$ with chessboard. The square size (and period) is denoted $\varepsilon$.

As we said before, on each black square, we impose the Dirichlet boundary condition and on each white square the Neumann condition.

More precisely, we denote by $\mathcal {Y}=\langle 0,\,1\rangle ^{2}$ the unit square consisting of four squares of equal size

\[ {\mathcal{Y}}_{11} = \left\langle 0,\frac{1}{2}\right\rangle^{2},{\mathcal{Y}}_{21} = \left\langle \frac{1}{2} , 1\right\rangle \times \left\langle 0,\frac{1}{2}\right\rangle ,{\mathcal{Y}}_{12} = \left\langle 0, \frac{1}{2} \right\rangle \times \left\langle \frac{1}{2} , 1\right\rangle,{\mathcal{Y}}_{22} = \left\langle \frac{1}{2} , 1\right\rangle^{2}. \]

Now ${\mathcal {Y}}_{11}$ and ${\mathcal {Y}}_{22}$ are black squares, while ${\mathcal {Y}}_{12}$ and ${\mathcal {Y}}_{21}$ are white ones.

Thus, we define

(1)\begin{align} \gamma^{D}& ={\mathcal{Y}}_{11}\cup {\mathcal{Y}}_{22}-\text{the Dirichlet (black) squares} \end{align}
(2)\begin{align} \gamma^{N}& = {\mathcal{Y}}_{12} \cup {\mathcal{Y}}_{21}-\text{the Neumann (white) squares} \end{align}

Let

(3)\begin{align} & \Gamma_\varepsilon^{D} = \left(\bigcup_{\mathbf{i}\in \mathbf{Z}^{2}}\varepsilon (\mathbf{i} + \gamma^{D})\right)\cap \Gamma -\text{the Dirichlet (black) boundary} \end{align}
(4)\begin{align} & \Gamma_\varepsilon^{N} = \left(\bigcup_{\mathbf{i}\in \mathbf{Z}^{2}}\varepsilon (\mathbf{i} + \gamma^{N})\right) \cap \Gamma -\text{the Neumann (white) boundary}. \end{align}

Clearly, $\Gamma _\varepsilon ^{N} \cup \Gamma _\varepsilon ^{D} = \Gamma$ and $\Gamma _\varepsilon ^{N} \cap \Gamma _\varepsilon ^{D} = \emptyset$.

2. The problem

For simplicity, our model problem is the Laplace equation. In order to focus on the mixed boundary condition, we take the zero right-hand side. On the rest of the boundary we assume the homogeneous boundary condition. That is by no means essential, any other boundary condition will do.

(5)\begin{equation} \left\lbrace \begin{array}{@{}l} \Delta u^{\varepsilon} = 0 \text{ in }\Omega \\ u^{\varepsilon} =\varepsilon^{\beta} g \text{ on } \Gamma_\varepsilon^{D} \text{ - Dirichlet part}\\ \displaystyle\dfrac{\partial u^{\varepsilon}}{\partial \mathbf{n}} = h\text{ on } \Gamma_\varepsilon^{N}\text{ - Neumann part}\\ u^{\varepsilon} =0 \text{ on }\partial\Omega\backslash \Gamma. \end{array}\right.\end{equation}

To take into account the magnitude of those two conditions, we have placed $\varepsilon ^{\beta }$ in front of the Dirichlet condition. As the problem is linear it makes no sense to put some power of $\varepsilon$ in front of both boundary values, so we have picked the Dirichlet one, but it would be the same if we have picked the Neumann one.

The standard weak formulation approach demands to assume that $g\in H^{\frac {1}{2}} (\Gamma _\varepsilon ^{D} )$ and $h\in L^{2} (\Gamma _\varepsilon ^{N})$. It gives the existence of the weak solution in $H^{1} (\Omega )$ (see for instance [Reference Rjasanow and Steinbach14] or [Reference Savaré16]). It is an easy exercise. However, there is a regularity issue with the solution since the standard Elliptic regularity does not apply [Reference Savaré16].

We do not use the usual weak formulation of the problem, but the very-weak one:

Find ${u^{\varepsilon }} \in L^{2} ({\Omega })$, such that for all

(6)\begin{align} & \phi \in H =\left\lbrace \psi \in H^{1} ({\Omega} );\Delta { \psi} \in L^{2} (\Omega),\ \psi =0\text{ on } \Gamma\backslash\Gamma_\varepsilon^{N}\;\;\mbox{and}\;\;\frac{\partial \psi}{\partial\textbf{n}} =0\text{ on } \Gamma_\varepsilon^{N} \right\rbrace\nonumber\\ & \displaystyle\int_{\Omega} {u^{\varepsilon}} \Delta \phi = \varepsilon^{\beta} \left\langle g\; \biggl|\;\displaystyle\frac{\partial \phi}{\partial \mathbf{n}} \right\rangle_{\Gamma_\varepsilon^{D}}- \int_{\Gamma_\varepsilon^{N}} h \;\phi, \end{align}

where $\left \langle \;\cdot \; \bigl |\;\cdot \; \right \rangle _{\Gamma _\varepsilon ^{D}}$ stands for duality between $H^{-1/2} (\Gamma _\varepsilon ^{D})$ and $H^{1/2} (\Gamma _\varepsilon ^{D})$. We notice here that $\phi \in H^{1} (\Omega )$ is insufficient to define the trace of the normal derivative on the boundary, but if (in addition) $\Delta \phi \in L^{2} (\Omega )$, then the trace $\frac {\partial \phi }{\partial \mathbf {n}}$ is defined but in the weaker sense, and belongs to $H^{-1/2} (\Gamma )$, the dual of the standard trace space $H^{1/2} (\Gamma )$ . The reader can consult, for instance [Reference Tartar17]. For the very-weak formulation of the elliptic problems, see for instance, [Reference Lions and Magenes6] and for the generalization to the Navier-Stokes system [Reference Marušić-Paloka7].

Usually, the very-weak formulation is used due to the lack of regularity. We use it here to facilitate the asymptotic analysis on the boundary. Indeed, the advantage of this formulation is that (unlike in the weak formulation) the Dirichlet boundary condition here appears explicitly in the formulation (see e.g. [Reference Marušić-Paloka9]).

As described above, our goal is to study the asymptotic behaviour of the solution as $\varepsilon \to 0$. It turns out that the effective condition is always of the Dirichlet type. The effective Dirichlet value on the boundary depends on $\beta$.

For $\beta < 1$ it equals $g$. For $\beta =1$, it is a linear combination of $g$ and $h$, while for $\beta >1$, it is proportional to $h$.

3. Asymptotic analysis

3.1. A priori estimates

Proposition 1 Suppose that $g\in H^{\frac {1}{2}}_{00} (\Gamma )$ and $h\in L^{2} (\Gamma )$. Let $u^{\varepsilon }$ be the solution to the problem (5). Then, there exists a constant $C>0,$ independent from $\varepsilon,$ such that

(7)\begin{align} & \left|u^{\varepsilon}\right|_{H^{1} (\Omega)} \leq C (\varepsilon^{\beta} \left| g\right|_{H^{\frac{1}{2}} (\Gamma)} + \left| h\right|_{L^{2} (\Gamma)} ) \end{align}
(8)\begin{align} & \left|u^{\varepsilon}\right|_{L^{2} (\Omega)} \leq C (\varepsilon^{\beta} \left| g\right|_{H^{\frac{1}{2}} (\Gamma)} + \varepsilon \left| h\right|_{L^{2} (\Gamma)} ). \end{align}

Proof. The $H^{1} (\Omega )$ estimate is straightforward but not optimal. The $L^{2} (\Omega )$ estimate is sharp and we give the proof in detail. The idea is to take the test function as the solution to the transposed problem

(9)\begin{align} & -\Delta \phi = u^{\varepsilon}\text{ in }\Omega \nonumber\\ & \phi =0\text{ on }\Gamma_\varepsilon^{D}, \displaystyle\frac{\partial \phi}{\partial \mathbf{n}} = 0\text{ on }\Gamma_\varepsilon^{N}\\ & \phi =0\text{ on }\partial\Omega\backslash \Gamma. \nonumber \end{align}

It has a unique weak solution $\phi \in H^{1} (\Omega )$ such that

(10)\begin{equation} \left|\phi\right|_{H^{1} (\Omega)} \leq C \left|u^{\varepsilon} \right|_{L^{2} (\Omega)}.\end{equation}

Furthermore, it is easy to see that

(11)\begin{equation} \left|\phi\right|_{H^{{-}1/2} (\Gamma)} \leq C \left|u^{\varepsilon} \right|_{L^{2} (\Omega)}.\end{equation}

However, since that is a mixed problem, there is a regularity issue with such a test function (see e.g. [Reference Savaré16] or [Reference Tartar17]).

We recall that $\phi \in H^{1} (\Omega )$ and $\Delta \phi =-u^{\varepsilon } \in H^{1} (\Omega )$. Thus, the traces of those two functions on $\Gamma$ are well defined and (denoting $\phi$ and its trace on $\Gamma$ $\phi \bigl |_\Gamma$ by the same symbol)

\[ \phi \in H^{\frac{1}{2}} (\Gamma),\quad\Delta \phi \in H^{\frac{1}{2}} (\Gamma). \]

Let $\kappa \in C^{1} (\overline {\Omega })$ be such that $\kappa \geq 0$ on $\Sigma$ and $\kappa =1$ on $\Gamma$, while $\kappa =0$ on $\partial \Omega \backslash \Sigma$. We start with

\[ \int_{\Gamma} \left|\nabla_{x'} \phi\right|^{2}\leq \int_{\Sigma }\kappa \left|\nabla_{x'} \phi\right|^{2} \]

with

\[ \nabla_{x'} \phi = \bigg(\frac{\partial\phi}{\partial x_1} , \frac{\partial\phi}{\partial x_2}\bigg). \]

On the other hand

\begin{align*} & \displaystyle\int_{\Sigma }\kappa \left|\nabla \phi\right|^{2}= \int_{\Omega}\displaystyle\frac{\partial}{\partial x_3} (\kappa \left|\nabla \phi\right|^{2}) = \int_{\Omega} \frac{\partial \kappa}{\partial x_3} \,\left| \nabla \phi \right|^{2} + 2\int_{\Omega} \kappa \nabla\phi\,\nabla \bigg(\frac{\partial\phi}{\partial x_3}\bigg)\\ & \quad=\displaystyle\int_{\Omega} \displaystyle\frac{\partial \kappa}{\partial x_3} \,\left| \nabla \phi \right|^{2} -2\int_{\Omega} \kappa\, \frac{\partial \phi}{\partial x_3}\;\Delta\phi - 2 \int_{\Omega} \nabla\kappa\;\nabla\phi\,\frac{\partial\phi}{\partial x_3} + \int_{\Sigma }\kappa \bigg(\frac{\partial \phi}{\partial x_3}\bigg)^{2}\\ & \quad\leq \int_{\Sigma }\kappa \bigg(\frac{\partial \phi}{\partial x_3}\bigg)^{2} + C \left|\phi\right|_{H^{1} (\Omega)} (\left|\Delta \phi\right|_{L^{2} (\Omega)}+\left|\phi\right|_{H^{1} (\Omega)} )\\ & \quad\leq \int_{\Sigma }\kappa \bigg(\frac{\partial \phi}{\partial x_3}\bigg)^{2} + C \left| u^{\varepsilon}\right|_{L^{2} (\Omega)}^{2}. \end{align*}

Since

\[ \left|\nabla \phi\right|^{2} = \left|\nabla_{x'} \phi\right|^{2} +\bigg(\frac{\partial \phi}{\partial x_3}\bigg)^{2} \]

we get

\[ \int_{\Gamma} \left|\nabla_{x'} \phi\right|^{2}\leq \int_{\Sigma }\kappa \left|\nabla_{x'} \phi\right|^{2} \leq C \left| u^{\varepsilon}\right|_{L^{2} (\Omega)}^{2}, \]

so that $\nabla _{x'} \phi \in L^{2} (\Gamma )$ i.e. $\phi \in H^{1} (\Gamma )$. Furthermore, $\phi =0$ on $\Gamma _\varepsilon ^{D}$. The Poincaré inequality on perforated domain $\Gamma$ (see e.g. [Reference Sanchez-Palencia15]) implies that

(12)\begin{equation} \left|\phi\right|_{L^{2} (\Gamma_\varepsilon^{N})} \leq C\ \varepsilon \left|\nabla \phi \right|_{L^{2} (\Gamma)}\leq C\varepsilon \left|u^{\varepsilon} \right|_{L^{2} (\Omega)}.\end{equation}

Using $\phi$ as the test function in (5), and applying (12), gives

(13)\begin{align} \displaystyle\displaystyle\int_\Omega \left| u^{\varepsilon}\right|^{2} & ={-}\int_\Omega u^{\varepsilon} \Delta\phi =\int_{\Omega}\nabla u^{\varepsilon} \nabla\phi -\varepsilon^{\beta} \int_{\Gamma_\varepsilon^{D}} g\; \displaystyle\frac{\partial \phi}{\partial \mathbf{n}}\\ & ={-}\varepsilon^{\beta} \displaystyle\int_{\Gamma_\varepsilon^{D}} g\; \displaystyle\frac{\partial \phi}{\partial \mathbf{n}} + \int_{\Gamma_\varepsilon^{N}} h\;\phi\leq \varepsilon^{\beta} \left| \frac{\partial\phi}{\partial\mathbf{n}}\right|_{H^{{-}1/2} (\Gamma_\varepsilon^{D})} \left| g\right|_{H^{1/2} (\Gamma)}\nonumber\\ & \quad+ \left| \phi\right|_{L^{2} (\Gamma_\varepsilon^{N})} \left| h\right|_{L^{2} (\Gamma)} \leq C ( \varepsilon^{\beta} \left| g\right|_{H^{1/2} (\Gamma)} + \varepsilon \left| h\right|_{L^{2} (\Gamma)} ) \left|u^{\varepsilon} \right|_{L^{2} (\Omega)}. \nonumber \end{align}

3.2. Convergence

In case $\beta \leq 0$, the convergence and its proof are simple. Although the technique that we will apply in case $\beta >0$ works here, we prefer to start with a simpler version.

Proposition 2 Suppose that $g\in H^{\frac{1}{2}}_{00} (\Gamma )$ and $h\in L^{2} (\Gamma )$. Let $u^{\varepsilon }$ be the solution to the problem (5). If $\beta \leq 0$ then

(14)\begin{equation} \displaystyle\frac{u^{\varepsilon}}{\varepsilon^{\beta}} \rightharpoonup v\text{ weakly in }H^{1} (\Omega),\end{equation}

where $v\in H^{1} (\Omega )$ is the unique solution to the Dirichlet problem

(15)\begin{equation} \Delta v =0\text{ in }\Omega,\quad v=g\text{ on }\Gamma,\ v=0\text{ on }\partial\Omega\backslash\Gamma.\end{equation}

Proof. Due to the estimate (7) the sequence $\frac {u^{\varepsilon }}{\varepsilon ^{\beta }}$ is bounded in $H^{1} (\Omega )$ Therefore, it has a subsequence converging to some $v\in H^{1} (\Omega )$, weakly in $H^{1} (\Omega )$, strongly in $L^{2} (\Omega )$, and (due to the compactness of the trace operator $tr : H^{1} (\Omega ) \to L^{2} (\Gamma)$), the trace of $\frac {u^{\varepsilon }}{\varepsilon ^{\beta }}$ converges to the trace of $v$ strongly in $L^{2} (\Gamma )$. Let the test function be $\psi \in H^{2} (\Omega ) \cap H^{1}_0 (\Omega )$. Starting from the very-weak formulation of the problem

(16)\begin{equation} \displaystyle\int_{\Omega} {u^{\varepsilon}} \Delta \psi = \varepsilon^{\beta} \int_{\Gamma_\varepsilon^{D}} g\;\displaystyle\frac{\partial \psi}{\partial \mathbf{n}},\end{equation}

and using

(17)\begin{align} & \varepsilon^{-\beta} \displaystyle\int_{\Omega} {u^{\varepsilon}} \Delta \psi \to \int_{\Omega} v \Delta \psi \end{align}
(18)\begin{align} & \displaystyle\int_{\Gamma_\varepsilon^{D}} g\; \displaystyle\frac{\partial \psi}{\partial \mathbf{n}} \to \left| \gamma^{D} \right| \int_{\Gamma} g\;\frac{\partial \psi}{\partial \mathbf{n}} \end{align}
(19)\begin{align} & \int_{\Gamma_\varepsilon^{N}} \frac{u^{\varepsilon}}{\varepsilon^{\beta}}\; \frac{\partial \psi}{\partial \mathbf{n}} \to \left| \gamma^{N} \right| \int_{\Gamma} v\;\frac{\partial \psi}{\partial \mathbf{n}}. \end{align}

We now have

(20)\begin{equation} \displaystyle\int_{\Omega} v \Delta \psi = \left| \gamma^{D}\right|\int_{\Gamma} g\;\displaystyle\frac{\partial \psi}{\partial \mathbf{n}} + \left| \gamma^{N}\right|\int_{\Gamma} v\;\frac{\partial \psi}{\partial \mathbf{n}}.\end{equation}

That is exactly the very-weak formulation of the problem

(21)\begin{equation} \Delta v =0\text{ in }\Omega,\quad v= \left|\gamma^{D}\right|g + \left|\gamma^{N}\right| v\text{ on }\Gamma,\ v=0\text{ on }\partial\Omega\backslash\Gamma.\end{equation}

Since $\left |\gamma ^{D}\right | + \left |\gamma ^{N}\right | =1$ that is equivalent to (15). The Dirichlet problem (15) has a unique solution $v\in H^{1} (\Omega )$ so that the whole sequence ${u^{\varepsilon }}$ converges to $v$ and not only the subsequence.

For other values of $\beta$, we have the following theorem:

Theorem 1 Suppose that $g\in H^{\frac {1}{2}}_{00} (\Gamma )$ and $h\in L^{2} (\Gamma )$. Let $u^{\varepsilon }$ be the solution to the problem (5). Then:

  • • For $\beta < 1$

    \[ \frac{u^{\varepsilon}}{\varepsilon^{\beta}} \rightharpoonup v\text{ weakly in }L^{2} (\Omega), \]
    where $v\in H^{1} (\Omega )$ is the unique weak solution of the problem
    (22)\begin{equation} \Delta v =0 \text{ in }\Omega,\quad v=0\text{ on }\partial\Omega\backslash\Gamma, v=g\text{ on }\Gamma.\end{equation}

  • • For $\beta =1$

    \[ \frac{u^{\varepsilon}}{\varepsilon} \rightharpoonup v\text{ weakly in }L^{2} (\Omega), \]
    where $v \in L^{2} (\Omega )$ is the unique very-weak solution of the problem
    (23)\begin{equation} \Delta v =0 \text{ in }\Omega,\quad v=0\text{ on }\partial\Omega\backslash\Gamma,\ v=g + \overline{M}\,h\text{ on }\Gamma,\end{equation}
    and $\overline {M} >0$ is defined from the auxiliary boundary-layer problem (26) with (31).

  • • For ${\beta > 1 }$

    \[ \frac{u^{\varepsilon}}{\varepsilon} \rightharpoonup v\text{ weakly in }L^{2} (\Omega), \]
    where $v\in L^{2} (\Omega )$ is the unique very-weak solution of the problem
    (24)\begin{equation} \Delta v =0 \text{ in }\Omega,\quad v=0\text{ on }\partial\Omega\backslash\Gamma,\ v=\overline{M}\,h\text{ on }\Gamma.\end{equation}

If $h\in H^{\frac {1}{2}}_{00} (\Gamma )$ then the solution $v\in H^{1} (\Omega )$ is weak in all cases.

Proof. Let $\alpha = \min \lbrace \beta,\, 1 \rbrace$.

The estimate (8) implies that there exist a subsequence of $u^{\varepsilon }$, denoted by the same symbol, and a function $v\in L^{2} (\Omega )$ such that

(25)\begin{equation} \displaystyle\frac{1}{\varepsilon^{\alpha}}\;u^{\varepsilon} \rightharpoonup v\text{ weakly in }L^{2} (\Omega).\end{equation}

Our goal is to identify that limit. We have no convergence for the gradient nor for the trace on the boundary. Thus the only tool we have is the good choice of the test function. As in the previous case, we start with $\psi \in H^{2} (\Omega ) \cap H_0^{1} (\Omega )$.

Then we need the boundary-layer corrector defined from the problem posed in an infinite strip

\[ Z=Y\times \,\langle -\infty , 0 \rangle. \]

We denote the fast variable by $\mathbf {y} = \frac {\mathbf {x}}{\varepsilon }$ and then $M$ is the solution to the problem

(26)\begin{equation} \left\lbrace \begin{array}{@{}l} \Delta_y M= 0\text{ in }Z\\ M =0\text{ on }\gamma^{D}, \displaystyle\dfrac{\partial M}{\partial y_3} ={-}1\text{ on }\gamma^{N}\\ M,\text{ is } 1 - \text{ periodic in }\mathbf{y}' = (y_1 , y_2)\\ \nabla_y M \in L^{2} (Z). \end{array}\right.\end{equation}

That auxiliary boundary-layer-type problem has a unique solution

\begin{align*} M\in D^{1} (Z)& =\lbrace K \in H^{1}_{loc} (Z); \nabla_y K \in L^{2} (Z),\quad K=0\text{ on }\gamma^{D}, \\ & K\text{ is }1 - \text{periodic in } \mathbf{y}' \rbrace, \end{align*}

endowed with the norm

\[ \left| K \right|_{D^{1} (Z)} = \left| \nabla K \right|_{L^{2} (Z)}. \]

The existence proof is an easy exercise, as it is a linear elliptic equation. The variational form of the problem reads

\[ \int_Z \nabla_y M\nabla_y K ={-}\int_{\gamma^{N}} K,\quad\forall\ K\in D^{1} (Z). \]

Furthermore, there exists a constant $M_\infty$ such that $M$ exponentially stabilizes to $M_\infty$ far from the upper boundary $y_3=0$. More precisely

\[ e^{\lambda \left|y_3\right|}\; (M(y) - M_\infty )\;\in L^{2} (Z). \]

The details (up to a slight modification due to the mixed boundary condition) can be found in [Reference Jäger and Mikelić5] or [Reference Marušić-Paloka and Starčević13].

Integrating Equation (26) with respect to $\mathbf {y}'$, we get

\[ \frac{d^{2}}{dy_3^{2}} \int_{0}^{1} \int_{0}^{1} M(y_1 , y_2 , y_3)\,{\rm d}y_1\,{\rm d}y_2 =0\ \Rightarrow\ \int_{0}^{1} \int_{0}^{1} M(y_1 , y_2 , y_3)\,{\rm d}y_1\,{\rm d}y_2 = C_0 y_3 + C_1. \]

As $\nabla _y M$ decays at infinity, we conclude that $C_0 =0$ so that, for any $y_3 \leq 0$,

(27)\begin{equation} \displaystyle\int_{0}^{1} \int_{0}^{1} M(y_1 , y_2 , y_3)\,{\rm d}y_1\,{\rm d}y_2 =C_1 \;,\;\int_{0}^{1} \int_{0}^{1} \displaystyle\frac{\partial M}{\partial y_3}(y_1 , y_2 , y_3)\,{\rm d}y_1\,{\rm d}y_2 =0.\end{equation}

We now construct the test function. Let $\psi$ be a smooth function, such that $\psi =0$ on $\Gamma$ and let

\[ \psi_\varepsilon (\mathbf{x}) = \psi (\mathbf{x}) + \varepsilon \,M(\mathbf{y})\,\frac{\partial \psi}{\partial x_3} (\mathbf{x}' ,0). \]

What is important for us is that on the boundary, we have

(28)\begin{equation} \psi_\varepsilon =0 \text{ on }\Gamma_\varepsilon^{D}\end{equation}

and

(29)\begin{equation} \displaystyle\frac{\partial \psi_\varepsilon }{\partial x_3} (\mathbf{x}' ,0 )=\frac{\partial \psi}{\partial x_3} (\mathbf{x}' ,0 )+ \frac{\partial M}{\partial y_3}(\mathbf{y}' ,0 )\frac{\partial \psi }{\partial x_3} (\mathbf{x}' ,0 ) = 0 \text{ on }\Gamma_\varepsilon^{N}.\end{equation}

Furthermore

\begin{align*} \Delta \psi_\varepsilon & = \Delta \psi +\displaystyle\frac{1}{\varepsilon} \Delta_y M\;\frac{\partial\psi}{\partial x_3} (\mathbf{x}' ,0) + \displaystyle\sum_{i=1}^{2} \frac{\partial M}{\partial y_i} \frac{\partial^{2} \psi}{\partial x_i\partial x_3} + \varepsilon M\Delta_{x'} \frac{\partial \psi}{\partial x_i} (\mathbf{x}' ,0)\\ & =\Delta \psi + \displaystyle\sum_{i=1}^{2} \displaystyle\frac{\partial M}{\partial y_i} \frac{\partial^{2} \psi}{\partial x_i\partial x_3} + O(\varepsilon). \end{align*}

We notice that

\[ \left| \sum_{i=1}^{2} \frac{\partial M}{\partial y_i} \frac{\partial^{2} \psi}{\partial x_i\partial x_3} \right|_{L^{2} (\Omega)} \leq C \sqrt{\varepsilon} \]

due to the fact that $\nabla _y M \in L^{2} (Z)$.

Then we use $\psi _\varepsilon$ as the test function in the very-weak formulation (6)

(30)\begin{equation} \displaystyle\int_{\Omega} \displaystyle\frac{{u^{\varepsilon}}}{\varepsilon^{\alpha}} \Delta \psi_\varepsilon = \varepsilon^{\beta - \alpha} \int_{\Gamma_\varepsilon^{D}} g\;\frac{\partial \psi_\varepsilon}{\partial \mathbf{n}} +\varepsilon^{- \alpha} \int_{\Gamma_\varepsilon^{N}} h\,\psi_\varepsilon .\end{equation}

Obviously

\begin{align*} & \varepsilon^{-\alpha} \displaystyle\int_{\Omega} {u^{\varepsilon}} \Delta \psi_\varepsilon \to \int_{\Omega} v \Delta \psi\\ & \quad\int_{\Gamma_\varepsilon^{D}} g\; \displaystyle\frac{\partial \psi_\varepsilon}{\partial \mathbf{n}} =\int_{\Gamma_\varepsilon^{D}} g\bigg(\frac{\partial \psi_\varepsilon}{\partial \mathbf{n}} + \frac{\partial M}{\partial y_3}\,\frac{\partial\psi}{\partial x_3}\bigg)\\ & \quad\to \left(\left| \gamma^{D} \right| + \overline{\frac{\partial M}{\partial y_3}}\right) \int_{\Gamma} g \frac{\partial \psi}{\partial x_3} \\ & \quad\varepsilon^{{-}1} \int_{\Gamma^{N}_\varepsilon} h\,\psi_\varepsilon = \int_{\Gamma_\varepsilon^{N}} h (\mathbf{x}')\,M\bigg(\frac{\mathbf{x}'}{\varepsilon} , 0\bigg)\,\frac{\partial \psi}{\partial x_3} (\mathbf{x}' ,0)\\ & \quad\to \overline{M}\;\int_{\Gamma} h (\mathbf{x}') \frac{\partial \psi}{\partial x_3} (\mathbf{x}' ,0) \end{align*}

with

(31)\begin{equation} \overline{M} = \displaystyle\int_{\gamma^{N}} M(\mathbf{y}' ,0)\;d\mathbf{y}' = C_1\end{equation}

($C_1$ defined in (27)) and

\[ \overline{\frac{\partial M}{\partial y_3}} = \int_{\gamma^{D}} \frac{\partial M}{\partial y_3}(\mathbf{y}' ,0)\;d\mathbf{y}'. \]

Due to (27), we know that

\begin{align*} 0& =\displaystyle\int_{\gamma} \displaystyle\frac{\partial M}{\partial y_3}(\mathbf{y}' ,0)\;d\mathbf{y}' = \int_{\gamma^{D}} \frac{\partial M}{\partial y_3}(\mathbf{y}' ,0)\;d\mathbf{y}' +\int_{\gamma^{N}} \frac{\partial M}{\partial y_3}(\mathbf{y}' ,0)\;d\mathbf{y}'\\ & = \displaystyle\int_{\gamma^{D}} \displaystyle\frac{\partial M}{\partial y_3}(\mathbf{y}' ,0)\;d\mathbf{y}' -\left| \gamma^{N}\right|\;\;. \end{align*}

so that

\[ \overline{\frac{\partial M}{\partial y_3}} = \left| \gamma^{N}\right| \]

and

\[ \left| \gamma^{D} \right| + \overline{\frac{\partial M}{\partial y_3}} = \left| \gamma^{D} \right| + \left| \gamma^{N} \right| =1. \]

Thus, we finally obtain the limit problem in the very-weak form, depending on whether $\beta$ is larger, smaller or equal to $1$.

Furthermore, using $M$ as the test function in (26) gives

(32)\begin{equation} \displaystyle\int_{Z} \left|\nabla M \right|^{2} = \int_{\gamma^{N}} M = \overline{M}.\end{equation}

For $\beta < 1$, we get

(33)\begin{equation} \displaystyle\int_{\Omega} v \Delta \psi = \int_{\Gamma} g\displaystyle\frac{\partial \psi}{\partial x_3}.\end{equation}

For $\beta = 1$

(34)\begin{equation} \displaystyle\int_{\Omega} v \Delta \psi = \int_{\Gamma} g\;\displaystyle\frac{\partial \psi}{\partial x_3} +\overline{M} \int_{\Gamma} h\;\frac{\partial \psi}{\partial x_3},\end{equation}

where $\overline {M} >0$ (see (32)) is defined from the auxiliary boundary-layer problem (26) with (31).

Finally, for $\beta >1$

(35)\begin{equation} \displaystyle\int_{\Omega} v \Delta \psi = \overline{M} \int_{\Gamma} h\;\displaystyle\frac{\partial \psi}{\partial x_3}.\end{equation}

So, in all three cases, we get the Dirichlet problem for the Laplace equation

\[ \Delta v=0\text{ in }\Omega \]

and the Dirichlet condition

\[ v=0\text{ on }\partial\Omega\backslash \Gamma. \]

The difference is in the Dirichlet condition on $\Gamma$ that equals

\[ v=\left\lbrace \begin{array}{@{}l@{}} g\text{ for }\beta<1\\ g+ \overline{M}\, h\text{ for }\beta=1\\ \overline{M}\, h\text{ for }\beta>1\ \end{array} \right\rbrace\text{ on }\Gamma. \]

Remark 1 We could summarize all cases by saying that the effective boundary condition asymptotically has the form

\[ u=\varepsilon^{\beta} g + \varepsilon\ \overline{M}\ h\text{ on }\Gamma. \]

In case $g=0$, studied by Filo and Luckhaus in [Reference Filo and Luckhaus3] and [Reference Filo and Luckhaus4], we get

\[ u=\varepsilon \,\overline{M} h. \]

More precisely, the limit of $u^{\varepsilon }$ is trivial

\[ u^{\varepsilon} \to 0\text{ in }L^{2} (\Omega) \]

but

\[ \frac{u^{\varepsilon}}{\varepsilon} \rightharpoonup v\text{ weakly in }L^{2} (\Omega), \]

where $v$ is the solution to the problem (24). This does not correspond to the result of Filo and Luckhaus because they have a non-zero right-hand side and initial condition leading to the non-trivial limit of $u^{\varepsilon }$.

Remark 2 We have assumed the chess-board structure to simplify the presentation. In fact, the same result can be obtained for any other periodic distribution of the Dirichlet and the Neumann condition. We could take the unit cell ${\mathcal {Y}}=\langle 0 ,\,1 \rangle ^{2}$, then pick an open subset $\gamma ^{D}\subset {\mathcal {Y}}$ with smooth boundary and $\gamma ^{N}= {\mathcal {Y}}\backslash \overline {\gamma ^{D}}$. Then follow the same steps and get the same result.

Acknowledgements

This work has been supported by the grant HRZZ 2735 of the Croatian Science Foundation.

References

Bensoussan, A., Lions, J. L. and Papanicolau, G., Asymptotic analysis for periodic structures (North Holland, 1978).Google Scholar
Filo, J., A note on asymptotic expansion for periodic boundary condition, Arch Math. 34 (1998), 83–92.Google Scholar
Filo, J. and Luckhaus, S., Asymptotic expansion for a periodic boundary condition, J. Differ. Eq. 120 (1995), 133–173.CrossRefGoogle Scholar
Filo, J. and Luckhaus, S., Homogenization of a boundary condition for the heat equation, J. Eur. Math. Soc. 2 (2000), 217–258.CrossRefGoogle Scholar
Jäger, W. and Mikelić, A., On the roughness-induced effective boundary conditions for a viscous flow, J. Differ. Equ. 170 (2001), 96–122.CrossRefGoogle Scholar
Lions, J.l. and Magenes, E., Non-homogeneous boundary value problems and applications, Volume 1 (Springer, 1972).Google Scholar
Marušić-Paloka, E., Solvability of the Navier-Stokes system with $L^{2}$ boundary data, Appl. Math. Optim. 41 (2000), 365–375.CrossRefGoogle Scholar
Marušić-Paloka, E., Averaging the Navier's law on rapidly oscillating boundary, J. Math. Anal. Appl. 259 (2001), 685–701.CrossRefGoogle Scholar
Marušić-Paloka, E., Application of very weak formulation on homogenization of boundary value problems in porous media, Czech. Math. J. 71 (2021), 975–989.Google Scholar
Marušić-Paloka, E. and Pažanin, I., Rigorous justification of the effective boundary condition on a porous wall via homogenization, Z. Angew. Math. Phys. 72 (2021), 146.CrossRefGoogle Scholar
Marušić-Paloka, E. and Pažanin, I., Homogenization of a mixed boundary condition, Appl. Anal. 101 (2022), 4113–4125.CrossRefGoogle Scholar
Marušić-Paloka, E. and Pažanin, I., The effective boundary condition on a porous wall, Int. J. Eng. Sci. 173 (2022), 103638.CrossRefGoogle Scholar
Marušić-Paloka, E. and Starčević, M., High-order approximations for an incompressible viscous flow on a rough boundary, Appl. Anal.(0003–6811) 94 (2015), 1305–1333.CrossRefGoogle Scholar
Rjasanow, S. and Steinbach, O., The fast solution of boundary integral equations (Springer, 2007).Google Scholar
Sanchez-Palencia, E., Non-homogeneous media and vibration theory, Lecture Notes in Physics, Volume 127 (Springer, 1980).Google Scholar
Savaré, G., Regularity and perturbation results for mixed second order elliptic problems, Commun. Partial Differ. Eq. 22 (1997), 869–899.CrossRefGoogle Scholar
Tartar, L., An introduction to Sobolev spaces and interpolation spaces (Springer, 2007).Google Scholar
Figure 0

Figure 1. Domain $\Omega$ with alternating Neumann and Dirichlet conditions on $\Gamma$.