For a state $\omega$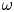 on a C$^{*}$-algebra $A$, we characterize all states $\rho$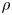 in the weak* closure of the set of all states of the form $\omega \circ \varphi$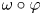, where $\varphi$ is a map on $A$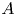 of the form $\varphi (x)=\sum \nolimits _{i=1}^{n}a_i^{*}xa_i,$ 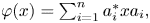$\sum \nolimits _{i=1}^{n}a_i^{*}a_i=1$ ($a_i\in A$, $n\in \mathbb {N}$). These are precisely the states $\rho$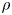 that satisfy $\|\rho |J\|\leq \|\omega |J\|$ 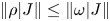for each ideal $J$ of $A$. The corresponding question for normal states on a von Neumann algebra $\mathcal {R}$ (with the weak* closure replaced by the norm closure) is also considered. All normal states of the form $\omega \circ \psi$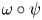, where $\psi$ is a quantum channel on $\mathcal {R}$ (that is, a map of the form $\psi (x)=\sum \nolimits _ja_j^{*}xa_j$, where $a_j\in \mathcal {R}$ are such that the sum $\sum \nolimits _ja_j^{*}a_j$ converge to $1$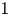 in the weak operator topology) are characterized. A variant of this topic for hermitian functionals instead of states is investigated. Maximally mixed states are shown to vanish on the strong radical of a C$^{*}$-algebra and for properly infinite von Neumann algebras the converse also holds.