Signature theory plays an important part in the field of reliability. In this paper, the ordered multi-state system signature and its related properties are discussed based on a life-test of independent and non-identical coherent or mixed systems with independent and identical binary-state components. Dynamic properties of these systems are considered through a new notion called dynamic multi-state system signature, and then related comparisons are made based on system lifetimes and costs. Finally, the theoretical results established are illustrated with some specific examples to demonstrate the use of dynamic ordered multi-state system signature in evaluating used multi-state coherent or mixed systems.

Almost stochastic dominance has been receiving a great amount of attention in the financial and economic literatures. In this paper, we characterize the properties of almost first-order stochastic dominance (AFSD) via distorted expectations and investigate the conditions under which AFSD is preserved under a distortion transform. The main results are also applied to establish stochastic comparisons of order statistics and receiver operating characteristic curves via AFSD.

We consider a collection of statistically identical two-state continuous time Markov chains (channels). A controller continuously selects a channel with the view of maximizing infinite horizon average reward. A switching cost is paid upon channel changes. We consider two cases: full observation (all channels observed simultaneously) and partial observation (only the current channel observed). We analyze the difference in performance between these cases for various policies. For the partial observation case with two channels or an infinite number of channels, we explicitly characterize an optimal threshold for two sensible policies which we name “call-gapping” and “cool-off.” Our results present a qualitative view on the interaction of the number of channels, the available information, and the switching costs.

For a bivariate random vector $(X, Y)$, suppose $X$ is some interesting loss variable and $Y$ is a benchmark variable. This paper proposes a new variability measure called the joint tail-Gini functional, which considers not only the tail event of benchmark variable $Y$, but also the tail information of $X$ itself. It can be viewed as a class of tail Gini-type variability measures, which also include the recently proposed tail-Gini functional. It is a challenging and interesting task to measure the tail variability of $X$ under some extreme scenarios of the variables by extending the Gini's methodology, and the two tail variability measures can serve such a purpose. We study the asymptotic behaviors of these tail Gini-type variability measures, including tail-Gini and joint tail-Gini functionals. The paper conducts this study under both tail dependent and tail independent cases, which are modeled by copulas with so-called tail order property. Some examples are also shown to illuminate our results. In particular, a generalization of the joint tail-Gini functional is considered to provide a more flexible version.

This paper examines the preservation of several aging classes of lifetime distributions in the formation of coherent and mixed systems with independent and identically distributed (i.i.d.) or identically distributed (i.d.) component lifetimes. The increasing mean inactivity time class and the decreasing mean time to failure class are developed for the lifetime of systems with possibly dependent and i.d. component lifetimes. The increasing likelihood ratio property is also discussed for the lifetime of a coherent system with i.i.d. component lifetimes. We present sufficient conditions satisfied by the signature of a coherent system with i.i.d. components with exponential distribution, under which the decreasing mean remaining lifetime, the increasing mean inactivity time, and the decreasing mean time to failure are all satisfied by the lifetime of the system. Illustrative examples are presented to support the established results.

In the usual shock models, the shocks arrive from a single source. Bozbulut and Eryilmaz [(2020). Generalized extreme shock models and their applications. Communications in Statistics – Simulation and Computation 49(1): 110–120] introduced two types of extreme shock models when the shocks arrive from one of $m\geq 1$ possible sources. In Model 1, the shocks arrive from different sources over time. In Model 2, initially, the shocks randomly come from one of $m$ sources, and shocks continue to arrive from the same source. In this paper, we prove that the lifetime of Model 1 is less than Model 2 in the usual stochastic ordering. We further show that if the inter-arrival times of shocks have increasing failure rate distributions, then the usual stochastic ordering can be generalized to the hazard rate ordering. We study the stochastic behavior of the lifetime of Model 2 with respect to the severity of shocks using the notion of majorization. We apply the new stochastic ordering results to show that the age replacement policy under Model 1 is more costly than Model 2.

We consider the problem of group testing (pooled testing), first introduced by Dorfman. For nonadaptive testing strategies, we refer to a nondefective item as “intruding” if it only appears in positive tests. Such items cause misclassification errors in the well-known COMP algorithm and can make other algorithms produce an error. It is therefore of interest to understand the distribution of the number of intruding items. We show that, under Bernoulli matrix designs, this distribution is well approximated in a variety of senses by a negative binomial distribution, allowing us to understand the performance of the two-stage conservative group testing algorithm of Aldridge.

As the queue becomes exhausted, different maintenance tasks can be performed according to the fatigue load and wear degree of the service equipment. At the same time, considering the customer's sensitivity to time delay, the service facility will not completely remain inactive during the maintenance period. To describe this objectively existing phenomenon arising in the waiting line system, we consider a hyper-exponential working vacation queue with a batch renewal arrival process. Through the calculation of the well-structured roots of the associated characteristic equation, the shift operator method in the theory of difference equations and the supplementary variable technique for stochastic modeling plays a central role in the queue-length distribution analysis. Comparison with other ways to analyze queueing models, the advantage of our approach is that we can avoid deriving the complex transition probability matrix of the queue-length process embedded at input points. The feasibility of this approach is verified by extensive numerical examples.

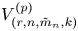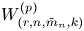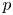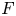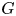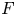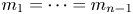Let $V_{(r,n,\tilde {m}_n,k)}^{(p)}$ and $W_{(r,n,\tilde {m}_n,k)}^{(p)}$ be the $p$-spacings of generalized order statistics based on absolutely continuous distribution functions $F$ and $G$, respectively. Imposing some conditions on $F$ and $G$ and assuming that $m_1=\cdots =m_{n-1}$, Hu and Zhuang (2006. Stochastic orderings between p-spacings of generalized order statistics from two samples. Probability in the Engineering and Informational Sciences 20: 475) established $V_{(r,n,\tilde {m}_n,k)}^{(p)} \leq _{{\rm hr}} W_{(r,n,\tilde {m}_n,k)}^{(p)}$ for 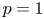$p=1$ and left the case 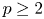$p\geq 2$ as an open problem. In this article, we not only resolve it but also give the result for unequal $m_i$'s. It is worth mentioning that this problem has not been proved even for ordinary order statistics so far.

Zhu and He [(2018). A new closed-form formula for pricing European options under a skew Brownian motion. The European Journal of Finance 24(12): 1063–1074] provided an innovative closed-form solution by replacing the standard Brownian motion in the Black–Scholes framework using a particular skew Brownian motion. Their formula involves numerically integrating the product of the Guassian density and corresponding distribution function. Being different from their pricing formula, we derive a much simpler formula that only involves the Gaussian distribution function and Owen's $T$ function.

This paper is devoted to the study of the asset allocation problem for a DC pension plan with minimum guarantee constraint in a hidden Markov regime-switching economy. Suppose that four types of assets are available in the financial market: a risk-free asset, a zero-coupon bond, an inflation-indexed bond and a stock. The expected return rate of the stock depends on unobservable economic states, and the change of states is described by a hidden Markov chain. In addition, the CIR process is used to describe the evolution of the nominal interest rate. The contribution rate is also assumed to be stochastic. The goal of investment management is to minimize the convex risk measure of the terminal wealth in excess of the minimum guarantee constraint. First, we transform the partially observable optimization problem into the one with complete information using the Wonham filtering technique and deal with the minimum guarantee constraint by constructing auxiliary processes. Furthermore, we derive the optimal investment strategy by the BSDE approach. Finally, some numerical results are presented to illustrate the impacts of some important parameters on investment behaviors.

One way to model telecommunication networks are static Boolean models. However, dynamics such as node mobility have a significant impact on the performance evaluation of such networks. Consider a Boolean model in $\mathbb {R}^d$ and a random direction movement scheme. Given a fixed time horizon $T>0$, we model these movements via cylinders in $\mathbb {R}^d \times [0,T]$. In this work, we derive central limit theorems for functionals of the union of these cylinders. The volume and the number of isolated cylinders and the Euler characteristic of the random set are considered and give an answer to the achievable throughput, the availability of nodes, and the topological structure of the network.