2. LITERATURE REVIEW

The large number of publications on modeling TCP behavior is a statement both about the difficulty of constructing a robust model of such complex behavior and the importance of TCP congestion control to the Internet. It is impossible for space reasons to comment on all of these models, but we do review the most prominent examples from several approaches used. All of the models described here consider the dynamic behavior of a single TCP connection as it would respond to loss events as indicators of link congestion. At a high level, the models are distinguished by three characteristics: the model of loss events (independent versus correlated), the aspects of TCP mechanisms assumed to have negligible influence on the results and not considered in the model, and whether the analysis computes expected values (e.g., the TCP window size or throughput) or produces a probability distribution of window sizes. An excellent discussion of many important issues in TCP model construction and validation can be found in [11].

The important distinctions between our model and the ones reviewed below are that it avoids certain common simplifying assumptions (e.g., an unbounded window size or loss rates independent of window size) and it gives the probability distribution of window sizes.

2.1. Models with Independent Losses

An early derivation of a simple stochastic model of steady-state TCP behavior in its congestion-avoidance mode is presented in [32] and explained in more detail in Section 3. This model produced the well-known result that the mean TCP window size is

, where p is the probability that an arbitrary segment will be independently dropped in the network and C is a constant term that reflects details of the TCP acknowledgment algorithm (C = 1.22 if every segment is acknowledged and C = 0.87 if at least every other segment is acknowledged). Given this mean window size estimate, throughput is bounded by

, where MSS is the maximum segment size and RTT is the mean round-trip time of the connection. This model is often called the “periodic-drop” model because the underlying analysis assumes that a constantly sending TCP source emits 1/p segments between segment drops. An even earlier model derivation that is closely related can be found in [17,20].

The form of the model is to compute the mean window size based on its evolution as a series of discrete segment-by-segment events. The model only captures TCP window adjustments associated with TCP's congestion-avoidance phase and only for segment drops that can be recovered without a time-out by reacting to three duplicate acknowledgments. Key elements of TCP behavior not considered in this model are the effects of time-out periods (in which throughput is zero), the TCP connection-establishment latency, the time TCP spends in its slow-start mode (also explained in Section 3), either following connection establishment or after a loss recovered by time-out, multiple losses in a single window of segments (that typically results in a time-out unless selective acknowledgment (SACK) is used), throughput limits imposed by the size of the receiver's advertised window, and delayed acknowledgments. Because these elements are not considered, the duration (latency) of the connection cannot be derived for a given size of data transfer.

References [27,28] present an analysis of the mean throughput of a TCP connection that was developed concurrently with (and apparently independently of) [32,37]. Two cases are modeled. The first is one in which losses are not random but instead caused when the connection's window grows to a point that causes a segment to be lost because the capacity of the buffer at the bottleneck link is exceeded (assuming only the one connection is using the link). This analysis considers both slow-start and congestion-avoidance phases. The second case considers both losses from overflow at the bottleneck buffer and random losses (from other causes), where the loss events are independent with fixed per-segment probability. Only congestion-avoidance with fast retransmission (no recovery with time-outs) is considered in this analysis. In both cases, connection establishment, receiver window limits, time-out intervals (zero throughput), and delayed acknowledgments are not modeled. Reference [29] extends the analysis in [27,28] to include asymmetric delays and congestion-induced loss on the “forward” (data) and “reverse” (acknowledgment) paths.

Reference [1] builds on the model and analysis from [27] to include loss models for i.i.d. losses and also a two-state (loss, no loss) first-order Markov model for the per-segment error process to include effects of correlated loss. The model also accounts for the effects of loss recovery by time-outs (including exponential back-off of the interval timer). Otherwise, it has the same assumptions and limitations as [27]. Reference [2] gives an earlier version of this model that considers only i.i.d. losses.

Reference [26] describes a Markov renewal-reward process model assuming independent segment losses. The model takes into account the explicit details of several versions of TCP (Tahoe, Reno, NewReno) along with factors such as time-out values and their granularity, receiver window size, and the number of duplicate acknowledgments used to infer loss. The detailed evolution of the window size for each TCP version is examined to determine the probability that multiple losses can be recovered without a time-out and the probability of recovery by time-outs. Reference [49] presents a modeling approach similar to [26] but using a two-state (loss, no loss) first-order Markov model for the per-segment error process to include effects of correlated loss.

References [38,39] cover the most widely cited and influential of the early TCP models. The new considerations in this model account for the effects of error recovery by retransmission after a time-out (given a mean time-out duration), the limits imposed by the maximum receiver's window (assumed to be constant at the value advertised at connection establishment), and the number of segments covered by an acknowledgment. The model of segment loss defines a probability, p, that a segment is lost given that no preceding segment from the window is lost (i.e., the probability that a given segment becomes the first loss within a window). Loss in one window is assumed independent of loss in any other window. To approximate the effects of correlated losses, if one segment from a window is lost, all following segments are considered lost also. Two assumptions also made explicit are that RTT and window size are independent [i.e., window size does not influence queuing delays (or that RTT consists only of propagation delays)], and that the time to transmit all segments in a window is less than the RTT.

Construction of the model in [39] proceeds from a detailed segment-by-segment analysis for the evolution of the TCP window as a stochastic process (Markov regenerative process with rewards). The result is an expression for the long-term expected value of throughput in segments/unit time, B, expressed as E(Y)/E(A), where Y is the number of segments sent in intervals of time, A, between loss events of different types using the mean RTT as a measure of time. The model equation includes a term that expresses the

relationship between mean window size and loss rate (e.g., the models of [32,37] are special cases of this model). They note also that for larger values of p, TCP window behavior is better approximated by C/p than by

. The validity of this model is established with extensive empirical measurements of TCP connection throughputs along with the loss rates experienced.

In [22], the model of [39] is revised and extended. The primary motivation was to express the loss model in terms of independent random loss (Bernoulli) model with intensity, p, which can be determined from conventional router-maintained counters. Using this model, the authors derive an expression for the probability that i segments will be lost from window of size W given independent losses, replacing the assumption that all segments following the first loss in a window are also lost (an approximation to correlated loss). From this, they also derive a new estimate of the probability of a time-out. A further refinement is to model the fact that the window size following loss events depends on the number of losses occurring in a window of size W, replacing the assumption in [39] that the window is reduced to W/2. Other than these two refinements, the model has the same assumptions and limitations as [39].

Reference [13] significantly extends the model in [38] to consider the effects of TCP connection establishment (including the possibility of segment loss), throughput during the initial slow-start phase (but not slow start following a time-out for a loss event), and the timing effects of delayed acknowledgments. Because the model is an extension of [38], the same assumptions and parameters are used. Another novel aspect of this model is that it is expressed in terms of expected values for connection latency given a size of data transfer (from which a throughput rate over the entire latency interval can also be calculated). Note that this allows the model to be accurate for transfers of any size, including those that are quite short (never encounter a loss or leave slow start). This model is validated through comparison with network simulator (NS) simulations and live Internet measurements.

The models presented in [44,45] are based on the same assumptions and some of the analysis and equations (such as approximations for correlated losses) from [13,38]. Their analysis and model differs from those earlier models because it is based on determining how many segments from an N-segment transfer are transmitted in each of the slow-start phases (both the initial one and following a loss event indicated by time-out) or in the congestion-avoidance phase as a function of the number of loss events. The approach in their analysis is somewhat similar to [26], in which the detailed evolution of the window size is examined to determine if multiple losses can be recovered without a time-out. They also develop a more refined model of the slow-start phase that accounts for effects of the delayed-acknowledgment timer. In [45], the analysis is refined to include specific details that reflect differences among TCP Tahoe, Reno, and SACK algorithms. They claim this model is more accurate for estimating total latency (and throughput) than [13] for short transfers but found little difference for transfers of more than 10,000 bytes. Results of empirical measurements (both new measurements and those in [39]) are presented to support this claim.

Reference [47] presents a generalization of the model in [39] to include two additional parameters, α and β, where α is the rate of increase in the window (measured in segments) when there is no loss in an RTT and β is the fraction of the current window that exists following a loss. In all other aspects, their model is identical to [39] and requires the same assumptions and has the same limitations related to elements of behavior not reflected in the model.

Reference [34] presents a model of steady-state TCP throughput. The new result is a model of window size behavior as a Poisson–Counter-driven stochastic differential equation where the loss events are treated as a Poisson stream of arrivals with rate λ at the source (instead of modeling segments as being sent out but lost with a given fixed probability) and the window size is approximated as a fluid (with continuous changes). Like [39], the model accounts for time-outs, receiver window size, and number of segments covered by an acknowledgment (but not connection establishment, initial slow start, and delays in returning acknowledgments). The result is an expression for the expected values of TCP window size and throughput as functions of the arrival rates of time-outs and duplicate-acknowledgment loss events, RTT, the mean time-out delay, and the maximum window size. There is no

term in this model, but it was shown that the model includes those such as [32] as a special case. The model was also shown to produce results comparable to or better than [39] when compared to the same empirical measurements.

Stochastic differential equation models for TCP throughput have also been considered in [25]. The authors consider a network with multiple resources and users. The throughput rate for the rth user increases additively in the absence of loss signals and decreases multiplicatively at a rate proportional to the stream of feedback signals received from the various resources. The stream of feedback signals is modeled either via a Poisson process (with a stochastic rate function) or a diffusion process. The rate of the Poisson process (or the governing parameters in the diffusion), for a given resource, depends on the load on the resource. In that respect, the model is quite similar to the model studied in the current article; however, the authors do not take into account the finiteness of the receiver window size or time-outs. Furthermore, they do not obtain the asymptotic distribution of the window size or throughput rate.

Reference [36] used simulations to explore the implications of some assumptions common to a number of the analytical models (loss model, no lost acknowledgments, etc.). The authors examined the distribution of latencies for transfers of a given number of segments, N, and found that the shape of the distribution function was largely invariant for difference scenarios but was shifted or scaled by linear transformations. They suggested that this indicates that analytic models can be extended to compute distributions of latencies, not just first and second moments.

2.2. Models with Correlated Losses

The emphasis in [3] is on improving the realism of the loss models. In particular, the expressions derived include a term for the correlation function of the interloss times in addition to the usual parameters for the loss rate, RTT, number of segments per acknowledgment, the maximum receiver window, the mean time-out, and the window increase/decrease rates resulting from losses indicated by duplicate acknowledgments or time-outs. Loss processes can then be varied in the models by specifying the correlation function of interloss times. In terms of the elements of TCP behavior represented, this model is equivalent to [34,38]. It is also shown that for i.i.d. random losses, the

result is a special case. An extensive set of empirical measurement is used to show that a variety of loss models are necessary to capture the effects found on real Internet paths and that the proposed model produces good results for different patterns of loss actually observed. Other aspects of their work on TCP performance with correlated losses can be found in [4,5].

Reference [8] uses a two-state (loss, no loss) first-order Markov model for the per-segment error process to include effects of correlated loss. Five versions of TCP algorithms (from Tahoe to SACK) are modeled during steady-state data transfers. The TCP elements not considered are the initial connection-establishment phase and exponential back-off of the time-out value for multiple consecutive losses. The detailed analysis considers the number of segments sent as a “train” during each interval during the evolution of the TCP window (in both slow-start and congestion-avoidance phases) between loss-recovery events and produces an expression for the expected value of throughput.

2.3. Models with a Distribution of Window Sizes

The computation of the stationary distribution of the window size has not received as much attention in the literature as the expected window size. The early model in [37] (apparently never published) is the first use of a fluid approximation to the discrete TCP window-evolution process. It assumes that segment losses are independent events with probability p. In addition to the use of a fluid approximation, the other novel contribution is to give the stationary distribution function (actually the complementary c.d.f.) for the window size process. The mean of the window-evolution process is derived from this distribution with the final result being

with a slightly different value of C = 1.31. The same elements of TCP behavior not considered in [32] are also not considered in this model.

Reference [33] presents a generalization of the model from [37] to consider segment loss probability that varies as a nondecreasing function of the TCP window size instead of being a constant probability. The effects of delayed acknowledgments are also modeled, but, otherwise, this model omits all the same elements of TCP behavior as [32,37], especially the limits imposed by the receiver's window and the impact of time-outs. As in [37], the result is expressed in terms of computing the cumulative distribution function of the TCP window size in number of TCP segments. No throughput results are given, but they can presumably be computed from the distribution of window sizes given round-trip times. The results of computing window sizes with the model are shown to compare favorably with results from NS simulations.

The models described in [14,15] are closely related to [35,37] and mostly consider only those aspects of TCP behavior modeled in [32]. Specifically, they consider only idealized TCP steady-state behavior in the congestion-avoidance mode with independent segment losses of constant probability and no time-outs. They do, however, model the effects of the limitations imposed by the receiver's window, and the increase/decrease ratios are parameterized as in [47]. The major contribution of these works is to provide convergence results for the distribution of window sizes (and throughput) for small loss probabilities (p → 0). A subset of the limit results for certain special cases is given in [14].

In [15,33], the authors show that a time and space scaled version of the window-size process converges in distribution to a Markov process, which can then be analyzed by the standard methods to obtain the limiting distribution. The general nature of the loss function in [33] forces them to write the limiting distribution as an infinite sum of increasing dimensional multiple integrals, which can be evaluated numerically. The analysis in [15] is closer to our analysis. They derive the limiting distribution as an infinite sum of hypoexponential probability density functions (p.d.f.'s), whereas we get finite sums of simpler functions. Their approach seems to hide the interesting features of the limiting distribution, such as the atom at zero, and discontinuities in the p.d.f., that we have illustrated in this article.

Our model is described in more detail in Section 3. It takes into account recovery from packet losses with both fast recovery and time-outs, boundary behavior at zero and maximum window size, and slow start after time-outs. As far as we know, ours is the first model that accounts for all these aspects of TCP and also provides a distribution of window sizes.

3. TCP DYNAMICS

We consider a single application instance sending data over the Internet using one TCP connection. We briefly describe the features of TCP that are relevant to the models developed here. TCP implements window-based protocols that control the rate at which segments are transmitted by the sender to the receiver. For each connection, TCP maintains two variables: congestion window size and receiver window size. Both are specified in bytes, but because we assume that all segments have mean size B, we assume that the window sizes are in number of segments of size B. The minimum of the two window sizes is called the effective TCP window size, or just window size.

Let W_C(t) be the congestion window size (in number of segments) at time t, let W_R(t) be the receiver's window size at time t, and let RTT be the mean round-trip time (in seconds) for the TCP connection. The receiver's window size is the number of segments the receiver has space for and is typically a fixed quantity K. It rarely changes, due to the high speed at which the receiver's buffer can be emptied as compared to the speed at which the segments are received. Similarly, the round-trip time and the segment sizes may vary over the duration of the connection, but we will use their mean values in the analysis and define B as the mean segment size and RTT as the mean round-trip time over the connection duration. The TCP window size is given by

The TCP congestion control has two phases: slow start and congestion-avoidance. In the congestion-avoidance phases, TCP behaves roughly as follows. At time t, the sender transmits W(t) number of segments back to back. As soon as the receiver receives a segment, an acknowledgment for that segment is sent back to the sender. (We ignore the batching of acknowledgments that is done by some TCP versions.) Thus, by time t + RTT, the sender receives W(t) acknowledgments, if there are no problems in transmission and delivery of the segments.

If the segment is error-free and is in the correct sequence, the receiver sends an acknowledgment for the highest sequence number received correctly. If a segment has unrecoverable errors or is out of sequence, the receiver continues to send the highest sequence number received correctly in its acknowledgment (sends a duplicate acknowledgment). A loss is indicated if the sender receives three duplicate acknowledgments or if the time-out period for a segment expires without an acknowledgment for its sequence number.

The congestion window W_C(t) changes dynamically at every instant an acknowledgment is received. In the absence of any loss indications, the window size increases by one every round-trip time. If an acknowledgment is received that is a third duplicate acknowledgment (indicating a segment loss), the window is reduced to (1 − α)W(t) + 1 (typically α = 0.5), and the TCP protocol continues in the congestion-avoidance phase. This operation is called fast recovery. We use (1 − α)W(t) + 1 in place of the customary (1 − α)W(t) for two reasons: TCP's congestion window is never reduced below one segment and increasing the window slightly is an approximation to account for the segments sent during fast recovery before the window is reduced to its final value. If a time-out occurs, the window size is reduced to one. After time-out, the TCP protocol switches to the slow-start phase and rapidly increases the window size to one plus (1 − α) fraction of the prevailing window size just before the time-out occurred. Again, there are many variations of TCP; we will analyze this one. Note that the response to a segment loss is determined by W(t), not W_C(t).

We will study the dynamics of the window size process {W(t), t ≥ 0} in two steps. In the next section, we assume that there are no time-outs and develop the probabilistic analysis of the window size process in steady state. In Section 4, we extend this analysis to include the time-outs.

4. TCP MODEL WITH NO TIME-OUTS

As a first step toward the analysis of the complete TCP dynamics, we begin with the assumption that there are no time-outs. Thus, once the TCP gets out of the slow-start phase, it stays in the congestion-avoidance phase forever. Assume that each returning acknowledgment indicates a segment loss with probability

, independent of anything else. Let X(t) be the number of acknowledgments received during (t, t + RTT) that indicate segment losses. With the assumption of independence, we see that X(t) is a binomial

random variable. We assume that

is sufficiently small so that we can ignore the possibility that X(t) ≥ 2, and, thus, X(t) can be taken to be a Bernoulli random variable with

Thus, in effect, we assume that there is at most one segment loss per RTT. Now, as long as 0 < W_C(t) < K, we have W(t) = W_C(t), and the dynamics of the TCP protocol can be approximated as

Rearranging, we get

Hence, we get

where

Now, we approximate the distribution of X(t) by that of N(t + RTT) − N(t), where {N(t), t ≥ 0} is a Poisson process with a time-varying stochastic rate function pW(t), where

. Thus, Eq. (4.2) can be written as

The above equation can be thought of as the finite-difference version of the following stochastic differential equation for {W(t), t ≥ 0}:

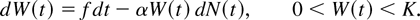
Next, we modify the above equation to account for the boundary behavior at W(t) = K. Once W(t) reaches K, W_C(t) may keep changing, but W(t) stays at K until a segment loss occurs. We incorporate this condition by modifying the stochastic differential equation (4.3) as follows:

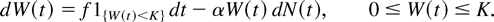
The above stochastic differential implies that the W process increases continuously at a constant rate f as long as it is less than K and there are no events in the N process. When it hits the upper limit K, it stays at K. When an event occurs in the N process, the W process jumps down by a factor 1 − α. Figure 1 shows a typical sample path of the W process.

Sample paths of W and WC processes in the absence of time-outs.

5. LIMITING BEHAVIOR OF W WITH NO TIME-OUTS

In this section, we study the limiting behavior of the TCP window size, assuming that it evolves as described in the previous section; that is, we obtain the limiting distribution of the solution to Eq. (4.4) as t → ∞. Let

be the limiting distribution of the W(·) process. The sample path of the W process shows that the limiting distribution of W has a probability mass v_K at x = K and a probability density u(x) (defined as the left derivative of F) over x ∈ [0, K). Thus,

The following theorem gives v_K and u(·).

Theorem 5.1: The density u(x), 0 < x < K, is given by

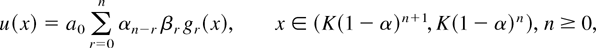
where a₀ is a normalizing constant,

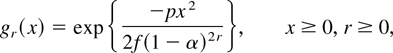
and the constants {α_i} and {β_i} are

for r > 0. The probability mass v_K is given by

Finally, the normalizing constant a₀ is chosen so that

Proof: Because W is an irreducible Markov process on [0, K] , it has a stationary distribution F. Let W(0) have distribution F. Then, W(t) has distribution F for all t ≥ 0. Then, for 0 < x < K,

Thus, we have that

Taking the limit as h → 0, we have that

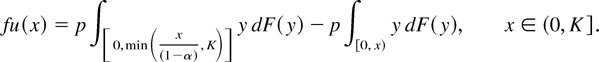
In particular, we have that

which yields Eq. (5.5).

Consider now the case when x ∈ I₀ ≡ (K(1 − α), K). Then, from (5.6), it follows that

Differentiating, we have that

and solving the above equation, we get

where a₀ is some constant. Thus, we have shown (5.1) for the case n = 0. We will prove (5.1) for a general n via induction. Now, suppose that (5.1) holds for n = 0,1,…, j. We begin by observing that from (5.6), it follows that for x ∈ [0, K(1 − α)),

Thus, from the induction hypothesis, it follows that for x ∈ (K(1 − α)^j+2, K(1 − α)^j+1),

We can solve the above differential equation to get

where a_j+1 is some constant.

In order to determine a_j+1, we now consider the cases j = 0 and j ≥ 1 separately.

Case 1: j = 0: In this case, we have from (5.6) that

Using this observation, the induction hypothesis, and (5.8), we now have that

Thus, solving for a₁, we get

Case 2: j ≥ 1: Next, note that from (5.6), it follows that u(·) is continuous on (0, K(1 − α)); thus, if j ≥ 1, then u(K(1 − α)^j+1+) = u(K(1 − α)^j+1−). Using this observation, (5.8), and the induction hypothesis, we have that

Solving for a_j+1 and rearranging the terms, we now have that

Substituting the above observations in (5.8), we have (5.1) for the case n = j + 1. This proves the result. █

The typical form of the limiting distribution is shown by the upper graph in Figure 2. Note that u(·) has a jump discontinuity at x = K(1 − α) and its derivative has a jump discontinuity at x = K(1 − α)². The lower graph shows u^T, the limiting density of the window size in the presence of time-outs, which is studied in the next section.

Typical graph of the density u and uT of the window size.

6. TCP MODEL WITH TIME-OUTS

The above analysis does not account for the response of TCP for lost segments that will be detected by time-outs. Typically, such events are accompanied by intervals of zero throughput for a random amount of time. The reason is that the sender at some point reaches the limit of its current effective window, but the lost segment's time-out interval (which depends on an estimated RTT and thus behaves like a random variable) has not occurred to initiate recovery and start sending again. We make the assumption that a fixed fraction c of the events in the N process are time-outs, and the remaining 1 − c fraction of the events are fast-recovery events. We assume that the effective window size jumps down to zero in the event of a time-out and it stays zero for an exponential duration with mean 1/μ, the expected duration of the time-out interval. We assume that after this zero window-size interval, the window size jumps instantaneously to (1 − α)W⁻, where W⁻ is the window size when the time-out occurred. In other words, we approximate the rapid exponential increase in the window size during the slow-start phase by an instantaneous jump at the end of the time-out period. The window size then begins to evolve according to Eq. (4.4) until the next loss event is encountered. We denote the window-size process in the presence of time-outs by {W^T(t), t ≥ 0}, to distinguish it from the window size process {W(t), t ≥ 0} without the time-outs. Figure 3 shows the sample paths of W^T(t) and W_C(t) and their relation to each other, taking into account the fast recovery, the time-out events and the boundary behavior at K and zero. It is clear the sample paths of the W^T process can be thought of as the sample paths of the W process, where periods of zero window size are inserted after a fraction c of the downward jumps in the W process in a completely random fashion. This observation implies that there is a very close relation between the limiting c.d.f. of the W process and that of the W^T process. This relation is made clear in Theorem 6.1.

Sample paths of WC(t) and W(t) in the presence of time-outs.

The sample path of the W^T process shows that the limiting distribution of W^T has a probability mass v₀^T at x = 0 and v_K^T at x = K, and a probability density u^T(x), 0 < x < K. Let

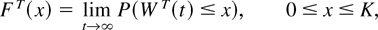
be the limiting distribution of the W^T(·) process.

Theorem 6.1 gives v₀^T, v_K^T, and u^T(·) in terms of the quantities v_K and u(·) of Theorem 5.1 and

Theorem 6.1: We have

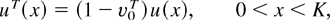
Proof: Let

Since the window size is zero when the time-out is in progress, we see that

Also,

where F(x) is from Theorem 5.1.

It is clear that v₀^T is the fraction of the time the W^T process is in the time-out period. Hence, conditioning on whether the time-out is in progress or not, we get

Equations (6.2) and (6.3) immediately follow from this. We thus need to derive Eq. (6.1) to complete the proof. Note that the rate at which the W^T process leaves state 0 in steady state is v₀^T μ. The rate at which it enters state 0 is given by

Equating these two, we get Eq. (6.1). This completes the proof. █

Figure 2 shows the typical shape of the density function u^T. It also shows the two probability masses v₀^T and v_K^T. The fact that u^T(0) = 0 is the result of our approximation of the exponential growth of window size in the slow-start phase by an instantaneous jump. In the next section, we validate the analytical results of this section by simulation using NS. As expected, we find that the empirical p.d.f. of the window size near zero is indeed not zero. An extension of the analytical technique to better account for the slow-start growth is complicated, but it is under consideration.

7. VALIDATION BY SIMULATION

To evaluate the effectiveness of this model at representing TCP behavior, we compared the results from the analytic model with the results from simulations using the NS simulator [12]. This simulator is widely used in networking research and has a very detailed model of TCP error recovery and congestion-control mechanisms. It has been subjected to careful validations and is regarded as a standard tool for TCP research. The simulated environment we chose for evaluating the model emphasizes the role of link-level congestion as the dominant factor that causes segment losses. For our experiments, we constructed a model of an enterprise or campus network having a single wide-area link to an upstream Internet service provider (ISP). The high-level view of the simulations is that a single, continuous TCP flow sending at the maximum rate it can achieve shares a bottleneck link with a large number of TCP flows used for Web-like traffic. The motivation for choosing Web-like traffic to share the link was the assumption that this traffic would exhibit highly variable and bursty demands on the link (specifically, a self-similar segment arrival process). The empirical data used to generate our Web traffic [16] had heavy-tailed distributions for both “think” (OFF) times and response size (ON) times, which would lead to self-similar traffic from the aggregation of sources [46]. This segment arrival process entering the fixed capacity queue in the router serving the congested link provides a realistic simulation of the loss processes found in the Internet when router buffers overflow. Thus, the simulation does not assume a particular loss model (independent, correlated, etc.), but, instead, the loss process is a direct result of running the simulation with different levels of load from self-similar Web traffic.

We study the dynamics of the single continuously sending TCP flow when it shares this congested link with many other TCP flows carrying Web-like traffic. The simulated Web clients (browsers) are all located on the enterprise or campus network and all of their requests are satisfied by Web servers located somewhere on the Internet beyond the ISP link. The traffic model that drives the simulation is based on a contemporary model of Web browsing reported in [16]. This model is an application-level description of the critical elements that characterize how HTTP/1.0 protocol is used. It is based on empirical data and is intended for use in generating synthetic Web workloads. Because response sizes are much larger than requests in this traffic model, the load on the network link that carries traffic from the servers to the browsers will be much greater than on the link carrying traffic in the opposite direction that is basically uncongested. The continuously sending TCP flow also sends its segments along the congested path carrying Web traffic from servers to clients.

The load generated by the Web-like flows at the bottleneck link was varied in different runs of the simulation from 40% to 98% of a link capacity that was fixed at 10,000,000 bits per second. The continuous TCP flow attempted to send at the maximum rate it could sustain, given the competing load from the Web traffic on the shared link. For example, at a 40% load for Web traffic, the continuous flow was able to send at a rate equivalent to nearly 60% of the link capacity. Note that because the continuous TCP flow can use all of link bandwidth the web traffic is not using, the link is congested in all cases. As the load from the Web traffic is increased, the continuously sending TCP flow will experience greater segment loss and lower throughput.

The version of TCP simulated is TCP Reno and the delayed-acknowledgments option was turned off. The continuous TCP flow had a maximum receiver's window size of 45 segments of 1460 bytes. The buffer size in the router was 60 of these maximum size segments.

Each simulation was run for 60 min of simulated time and data from the first 10 min was discarded to eliminate transient start-up effects. Scripts for running the NS simulations which also show various parameter settings can be found in [50]. In each simulation run, we recorded for the continuous TCP flow, the number of segments transmitted, the number of three-duplicate-acknowledgment loss events, the number of time-out loss events, the mean round-trip time, the mean throughput, and the effective size of the TCP window sampled every 10 ms. The frequencies of loss events experienced by the continuous TCP flow in the simulations were used as loss probabilities in the analytic TCP model for a comparison of results. The mean round-trip time (including transmission, propagation, and queuing delays) for the continuous TCP flow in the simulations was used as the mean RTT in the analytic model. The estimates of p, c, and RTT (in milliseconds) are given in Table 1 for the seven different load conditions. They are also shown in Figures 5 and 6. Figure 5 shows the values of p1 = p(1 − c) and p2 = pc; Figure 6 shows the plot of the mean RTT (in milliseconds) for the seven runs.

Estimates of p, c, and RTT for the Seven Runs

In the NS simulation of TCP, the effective size of the TCP window is not reset to its minimum size (one segment) until the end of a time-out period, whereas the analytic model considers the effective window to be minimum (zero segments) for a random interval during the time-out period. The TCP window sizes sampled at 10-ms intervals during the simulations were adjusted to match this definition by setting the sample value to zero if the sample was taken during a time-out period. If the sample was not taken during a time-out period, the sample value was recorded without change.