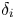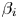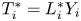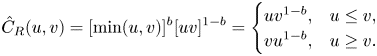1. Introduction
To cover risk, an insurance company charges an amount periodically from the insured person, known as premium. The premium can be paid monthly, bi-monthly, quarterly or annually. There are various types of insurance (covering health, life, car, home and other valuables) that one can purchase from an insurer. In insurance analysis, the calculation of the premium for a policy is a problem of vital interest. For determining the premium amount, insurance companies use credit scores and history. In addition, the smallest claim amounts play an important role in determining premium, as they provide useful information in this regard. Furthermore, in actuarial science, an interesting problem is to reveal preferences over the random future gains or losses. Stochastic orders are highly useful for this purpose. For example, let us consider two random risk values 
$R_{1}$ and 
$R_{2}$. A risk analyst would prefer 
$R_{1}$ over 
$R_{2}$ if 
$R_{1}$ is smaller than 
$R_{2}$ in the sense of usual stochastic order (see Definition 2.1(a)). Moreover, in the analysis of risk, hazard rate has a nice interpretation; given that no default has occurred till now, the hazard rate represents the instantaneous default probability on payment. Thus, a bond with a smaller hazard rate would be preferable. Apart from these applications, stochastic comparison results also have found applications in various other fields such as operations research, reliability theory and survival analysis; see Müller and Stoyan [Reference Müller and Stoyan16], Shaked and Shanthikumar [Reference Shaked and Shanthikumar21] and Li and Li [Reference Li and Li12].
In an insurance period, for 
$i\in \mathbb {I}_{n}$, let 
$X_{i}$ represent the total amount of random severity of a policy holder that can be demanded from an insurer. Associated with 
$X_{i}$, let 
$L_{i}$ be a Bernoulli random variable, such that
$$L_i= \left\{\begin{array}{ll} 1, & \textrm{if the }i\textrm{th insured person makes random claim }X_{i}\textrm{,}\\ 0, & \textrm{otherwise}, \end{array} \right.$$where 
$i\in \mathbb {I}_{n}$. Then, the quantity 
$T_{i}=L_{i}X_{i}$ represents the random claim amount corresponding to the 
$i$th insured person in a portfolio of risks. In various contexts, extreme claim amounts are of interest; in particular, the comparison of claim amounts in the sense of stochastic orders is an interesting problem and has received great attention from several researchers. Barmalzan and Payandeh Najafabadi [Reference Barmalzan and Payandeh Najafabadi3] considered Weibull distribution for comparing smallest claim amounts according to convex transform and right spread orders under the assumption that the claim amounts are independently distributed. Next, Barmalzan et al. [Reference Barmalzan, Payandeh Najafabadi and Balakrishnan4] developed some results with respect to the likelihood ratio and dispersive orders in a similar setting. Barmalzan et al. [Reference Barmalzan, Payandeh Najafabadi and Balakrishnan5] considered a general family of distributions to obtain different stochastic comparison results between the extreme claim amounts. Zhang et al. [Reference Zhang, Cai and Zhao23] developed several sufficient conditions for comparing extreme claim amounts according to different stochastic orderings. Recently, Nadeb et al. [Reference Nadeb, Torabi and Dolati18] developed stochastic comparison results among the smallest as well as largest claim amounts when the random claim amounts follow independent transmuted-
$G$ models. Das et al. [Reference Das, Kayal and Balakrishnan8] investigated ordering results between the smallest claim amounts for independent exponentiated location-scale models. Thus, it may be noted that most of the above-mentioned works are for independent claim amounts. This is primarily due to the complicated form of expressions in the case of dependent variables. But, the assumption of independent claims is not always reasonable from a practical point of view. In several situations, the behavior of insured risks is similar. For instance, in group life insurance, the remaining lifetimes of life partners can be shown to have a certain degree of positive dependence. For this reason, there has been some recent interest in the comparison of extreme claim amounts of two heterogeneous portfolios of risks with dependent claims. For modeling the dependence structure of the random variables, the notion of copulas turns out to be useful (see [Reference Nelsen20]). In this regard, Balakrishnan et al. [Reference Balakrishnan, Zhang and Zhao1] considered two sets of dependent heterogeneous portfolios and established ordering results between the largest claim amounts. Nadeb et al. [Reference Nadeb, Torabi and Dolati17] and Nadeb et al. [Reference Nadeb, Torabi and Dolati19] developed stochastic ordering results between the smallest claim amounts as well as the largest claim amounts from two sets of interdependent heterogeneous portfolios. Torrado and Navarro [Reference Torrado and Navarro22] investigated distribution-free comparisons between the extreme claim amounts according to several stochastic orderings when the risks have a fixed dependence structure. More recently, Barmalzan et al. [Reference Barmalzan, Akrami and Balakrishnan2] addressed stochastic comparisons of extreme claim amounts with location-scale claim severities.
The aim of this work is to develop different ordering results between the smallest claim amounts based on the usual stochastic and hazard rate orders when claim severities are dependent and have heterogeneous exponentiated location-scale distributions. Let 
$F$ and 
$f$ denote the baseline cumulative distribution function and the probability density function, respectively. Then, a nonnegative absolutely continuous random variable 
$X$ is said to follow an exponentiated location-scale model if the cumulative distribution function of 
$X$ is given by
\begin{equation} F_X(x)=F^{\alpha}\left(\frac{x-\lambda}{\theta}\right),\quad x>\lambda>0,\ \alpha,~\theta>0. \end{equation} In (1.1), 
$\alpha$, 
$\lambda$ and 
$\theta$ are, respectively, the shape, location and scale parameters. Note that when 
$\lambda =0$ and 
$\alpha =1$, (1.1) becomes a scale model. Furthermore, (1.1) reduces to the proportional reversed hazard rate and location models when 
$\lambda =0$, 
$\theta =1$ and 
$\alpha =1$, 
$\theta =1$, respectively. Usually, an insurer faces a claim from an insured person after a gap of time from the date of enrollment of a purchased policy. Thus, location parameter plays an important role in modeling insurance-related data. The location parameter is termed the threshold parameter in engineering applications; see, for example, Castillo et al. [Reference Castillo, Hadi, Balakrishnan and Sarabia6]. Furthermore, in finance, the data are often skewed and to fit such a dataset, a statistical model with skewness (shape) parameter is required. The general exponentiated location-scale model serves this purpose very well due to its great flexibility. Das et al. [Reference Das, Kayal and Choudhuri9], Das and Kayal [Reference Das and Kayal7] and Das et al. [Reference Das, Kayal and Balakrishnan8] considered (1.1) to obtain different stochastic ordering results.
Next, let 
$\{X_{1},\ldots ,X_{n}\}$ be a set of interdependent nonnegative random variables such that 
$X_{i}\sim F^{\alpha _{i}}({(x-\lambda _{i})}/{\theta _{i}})$, for 
$i\in \mathbb {I}_{n}=\{1,\ldots ,n\}.$ Furthermore, let 
$\{L_1,\ldots ,L_n\}$ be independent Bernoulli random variables, independently of 
$X_{i}$'s, such that 
$E(L_{i})=p_{i}$, for 
$i\in \mathbb {I}_{n}$. Thus, the portfolio of risks is the set 
$\{T_{1},\ldots ,T_{n}\}$, where 
$T_{i}=L_{i}X_{i}$, for 
$i\in \mathbb {I}_{n}$. The quantity 
$T_{1:n}=\min \{T_{1},\ldots ,T_{n}\}$ then corresponds to the smallest claim amount in the portfolio of risks 
$\{T_{1},\ldots ,T_{n}\}$. Analogously, another portfolio of risks is the set 
$\{T_{1}^{*},\ldots ,T_{n}^{*}\}$, where 
$T^{*}_{i}=L_{i}^{*}Y_{i}$, for 
$i\in \mathbb {I}_{n}$. For this portfolio, the smallest claim amount is denoted by 
$T_{1:n}^{*}=\min \{T_{1}^{*},\ldots ,T_{n}^{*}\}$. In this paper, stochastic comparisons between the smallest claim amounts 
$T_{1:n}$ and 
$T_{1:n}^{*}$ with respect to the usual stochastic and hazard rate orders are discussed under some conditions involving the concept of vector majorization and related orders. The study first carries out the required stochastic ordering when the dependence structure is modeled by an Archimedean survival copula and then by a general survival copula. It is worth mentioning that throughout the paper, the expression Archimedean survival copula means that the survival copula of the random vector is Archimedean type.
The rest of this article proceeds as follows. Some key definitions and lemmas are presented first in Section 2. Section 3 consists of two subsections: In Subsection 3.1, different sufficient conditions are presented for the comparison of two smallest claim amounts according to the usual stochastic and hazard rate orders. The claim sizes are taken to be dependent, and the dependence structure is modeled by Archimedean survival copula with different generators; Subsection 3.2 provides conditions under which two smallest claim amounts are comparable with respect to the usual stochastic order when the dependence structure of the claim sizes is modeled by a general survival copula.
2. Preliminaries and some useful lemmas
Throughout the article, random variables are considered to be nonnegative absolutely continuous. The term increasing is used to mean nondecreasing and similarly decreasing is used to mean nonincreasing. For any differentiable function 
$g$, we denote 
$g'(x)={dg(x)}/{dx}$. This section describes briefly some stochastic orderings, majorizations and some lemmas, which are essential for establishing the main results in the subsequent sections. Let 
$U$ and 
$V$ be two nonnegative absolutely continuous random variables. Suppose 
$f_{U}(\cdot )$ and 
$f_{V}(\cdot )$, 
$F_{U}(\cdot )$ and 
$F_{V}(\cdot )$, 
$\bar {F}_{U}(\cdot )$ and 
$\bar {F}_{V}(\cdot )$, 
$r_U(\cdot )=f_U(\cdot )/\bar {F}_U(\cdot )$ and 
$r_V(\cdot )=f_V(\cdot )/\bar {F}_V(\cdot )$, 
$\tilde {r}_U(\cdot )=f_U(\cdot )/F_U(\cdot )$ and 
$\tilde {r}_V(\cdot )=f_V(\cdot )/F_V(\cdot )$ are the corresponding probability density functions, cumulative distribution functions, survival functions, hazard rate functions and reversed hazard rate functions of 
$U$ and 
$V$, respectively.
Definition 2.1 ([Reference Shaked and Shanthikumar21])
Let 
$U$ and 
$V$ be two nonnegative absolutely continuous random variables. Then, 
$U$ is said to be smaller than 
$V$ in the sense of
(a) the usual stochastic order (written as
$U\le _{\textrm {st}}V$) if $\bar {F}_{U}(x) \le \bar {F}_{V}(x)$, for all $x\in \mathbb {R}^{+}$;(b) the hazard rate order (written as
$U\le _{hr}V$) if $\bar {F}_{V}(x)/\bar {F}_{U}(x)$ is increasing in $x>0$, or equivalently, $r_U(x)\geq r_V(x)$, for all $x\in \mathbb {R}^{+}$.
One can refer to Shaked and Shanthikumar [Reference Shaked and Shanthikumar21] for an extensive discussion on several stochastic orderings and their applications. The concept of majorization is one of the effective tools for establishing various inequalities. Let 
$\boldsymbol {l}=(l_{1},\ldots ,l_{n})$ and 
$\boldsymbol {m}=(m_{1},\ldots ,m_{n})$ be two 
$n$-dimensional vectors. Furthermore, let 
$l_{1:n}\le \cdots \le l_{n:n}$ and 
$m_{1:n}\le \cdots \le m_{n:n}$ denote the increasing arrangements of the components of 
$\boldsymbol {l}$ and 
$\boldsymbol {m}$, respectively.
Definition 2.2 ([Reference Marshall, Olkin and Arnold14])
A vector 
$\boldsymbol {l}$ is said to be
(a) weakly supermajorized by vector
$\boldsymbol {m}$ (written as $\boldsymbol {l}\preceq ^{w}\boldsymbol {m}$) if $\sum _{k=1}^{j}l_{k:n}\ge \sum _{k=1}^{j}m_{k:n},$ for $j\in \mathbb {I}_{n}$;(b) weakly submajorized by vector
$\boldsymbol {m}$ (written as $\boldsymbol {l}\preceq _{w}\boldsymbol {m}$) if $\sum _{k=i}^{n}l_{k:n}\le \sum _{k=i}^{n}m_{k:n}$, for $i\in \mathbb {I}_{n}$;(c) majorized by vector
$\boldsymbol {m}$ (written as $\boldsymbol {l}\preceq ^{m}\boldsymbol {m}$) if $\sum _{k=1}^{n}l_{k}=\sum _{k=1}^{n}m_{k}$ and $\sum _{k=1}^{j}l_{k:n}\ge \sum _{k=1}^{j}m_{k:n},$ for $j\in \mathbb {I}_{n-1}$.
It can be verified that 
$\boldsymbol {l}\preceq ^{m}\boldsymbol {m}$ implies both 
$\boldsymbol {l}\preceq ^{w}\boldsymbol {m}$ and 
$\boldsymbol {l}\preceq _{w}\boldsymbol {m}$. Also, it is known that the hazard rate order implies the usual stochastic order. Majorization is useful for comparing two 
$n$-dimensional real-valued vectors 
$\boldsymbol {l}$ and 
$\boldsymbol {m}$ in terms of dispersion of their components. Specifically, the order 
$\boldsymbol {l}\preceq ^{m}\boldsymbol {m}$ reveals that 
$l_i$'s are more dispersed than 
$m_i$'s, for a fixed sum. For a detailed discussion on majorization-type orders and their applications, one may refer to Marshall et al. [Reference Marshall, Olkin and Arnold14]. Next, the definitions of Schur-convex and Schur-concave functions are provided.
Definition 2.3 ([Reference Marshall, Olkin and Arnold14, Def. A.1])
For all 
$\boldsymbol {l},\boldsymbol {m}\in \mathbb {D}\subseteq \mathbb {R},$ let 
$\Psi :\mathbb {D}\rightarrow \mathbb {R}$ be a function satisfying 
$\boldsymbol {l}\preceq ^{m} \boldsymbol {m}\Rightarrow \Psi (\boldsymbol {l})\leq (\geq ) \Psi (\boldsymbol {m})$. Then, 
$\Psi$ is said to be Schur-convex (Schur-concave) on 
$\mathbb {D}$.
The following lemmas will play an important role in establishing results in the subsequent sections.
Lemma 2.1 ([Reference Marshall, Olkin and Arnold14, Thm. A.4])
For any open interval 
$I\subseteq \mathbb {R},$ let 
$\chi$ be a real-valued continuously differentiable function on 
$I^{n}$. Then, 
$\chi$ is said to be Schur-convex 
$[\text {Schur-concave}]$ on 
$I^{n}$ if and only if 
$\chi$ is symmetric on 
$I^{n}$, and for all 
$i\neq j$ and 
$\boldsymbol {z}\in I^{n},$
$$(z_i-z_j)\left(\frac{\partial\chi(\boldsymbol{z})}{\partial z_i}-\frac{\partial\chi(\boldsymbol{z})}{\partial z_j}\right)\geq[{\leq} ]0,$$where the partial derivative of 
$\chi (\boldsymbol {z})$ is represented by 
${\partial \chi (\boldsymbol {z})}/{\partial z_i},$ the derivative with respect to its 
$i$th argument.
Lemma 2.2 ([Reference Marshall, Olkin and Arnold14, Prop. 3.B.2])
Suppose there exists a function 
$\xi :\mathbb {R}^{n}\rightarrow \mathbb {R}$ such that 
$\xi$ is decreasing and Schur-convex. Then, 
$\xi (\boldsymbol {x})=\xi (g(x_1),\ldots ,g(x_n))$ is also decreasing and Schur-convex, where 
$g$ is an increasing concave function.
The concept of copula helps reduce the complexity when one has to deal with dependent variables. Suppose 
$\boldsymbol {X}=(X_{1},\ldots ,X_{n})$ is a random vector. Let 
$L$ and 
$\bar {L}$ be the joint distribution and survival functions of 
$\boldsymbol {X}$, respectively. Furthermore, for 
$i\in \mathbb {I}_{n},$ let 
$F_{X_{i}}$'s and 
$\bar {F}_{X_{i}}$'s represent the marginal distribution and reliability functions of 
$X_{i}$'s, respectively. Now, if there exist 
$C:[0,1]^{n}\rightarrow [0,1]$ and 
$\hat C:[0,1]^{n}\rightarrow [0,1]$ such that
\begin{equation} L(x_1,\ldots,x_n)=C(F_{X_{1}},\ldots,F_{X_{n}}) \end{equation}and
\begin{equation} \bar{L}(x_1,\ldots,x_n)=\hat{C}(\bar{F}_{X_{1}},\ldots,\bar{F}_{X_{n}}), \end{equation}then 
$C$ and 
$\hat C$ are called copula and survival copula of 
$\boldsymbol {X}$, respectively. The following definition is useful in introducing Archimedean copula.
Definition 2.4 ([Reference McNeil and Nešlehová15, Def. 2.3])
Let 
$f$ be a real-valued function in 
$(a,b)$, where 
$a,b \in \overline {\mathbb {R}}$ (closure of 
$\mathbb {R}$). Then, the function 
$f$ is said to be 
$d$-monotone, where 
$d \ge 2$, if the following properties hold:
(i) the derivative of
$f$ exists up to $d - 2$ order and satisfies $(-1)^{i}{f}^{i}(x)\geq 0$, $i=0,1,\ldots ,d-2$;(ii)
$(-1)^{d-2}{f}^{d-2}$ is nonincreasing convex in $(a,b)$.
Suppose there exists a nonincreasing continuous function 
$\psi :[0,\infty )\rightarrow [0,1]$ such that 
$\psi$ satisfies 
$d$-monotone property with 
$\psi (0)=1$ and 
$\psi (\infty )=0$. Furthermore, suppose 
$\phi ={\psi }^{-1}$ represents the pseudo-inverse. Then, a copula 
$C_{\psi }$ is said to be an Archimedean copula if it is of the form
\begin{equation} C_{\psi}(v_1,\ldots,v_n)=\psi({\phi(v_1)},\ldots,\phi(v_n))\quad \text{for all } v_i\in[0,1],\ i\in\mathbb{I}_{n}. \end{equation}For a comprehensive discussion on copula and Archimedean copula, see Nelsen [Reference Nelsen20] and McNeil and Nešlehová [Reference McNeil and Nešlehová15]. The following lemmas will be used extensively in proving the main results in the subsequent sections.
Lemma 2.3 ([Reference Li and Fang13])
For two 
$n$-dimensional Archimedean copulas 
$C_{\psi _1}$ and 
$C_{\psi _2}$, if 
$\phi _2\circ \psi _1$ satisfies super-additive property, then 
$C_{\psi _1}(\boldsymbol {v})\leq C_{\psi _2}(\boldsymbol {v})$ for all 
$\boldsymbol {v}\in [0,1]^{n},$ where 
$\boldsymbol {v}=(v_{1},\ldots ,v_{n})$.
The following definition and lemmas are associated with the concept of Schur-concavity of an Archimedean copula.
Definition 2.5 ([Reference Nelsen20, Def. 2.2.5])
For a copula 
$C$, consider a function 
$\delta _C:[0,1]\rightarrow [0,1]$ such that 
$\delta _C(x)=C(x,\ldots ,x)$. Then, 
$\delta _C$ is said to be the main diagonal section of 
$C$.
Lemma 2.4 ([Reference Dolati and Dehgan Nezhad10, Prop. 4.11])
Every Achimedean copula is Schur-concave.
Lemma 2.5 ([Reference Nelsen20, Def. 5.7.1])
Let 
$\hat {C}_R$ be a survival copula. Then, 
$\hat {C}_R$ is said to be positively upper orthant dependent (PUOD) if 
$\hat {C}_R(\boldsymbol {a})\geq \prod _{i=1}^{n}a_i$ for all 
$\boldsymbol {a}\in [0,1]^{n},$ where 
$\boldsymbol {a}=(a_1,\ldots ,a_n)$.
Lemma 2.6 ([Reference Nelsen20, Def. 2.8.1])
Consider two survival copulas 
$\hat {C}_R$ and 
$\hat {C}^{*}_R$, such that 
$\forall \boldsymbol {a}\in [0,1]^{n},$ 
$\hat {C}_R(\boldsymbol {a})\leq \hat {C}^{*}_R(\boldsymbol {a})$. Then, 
$\hat {C}_R$ is said to be less than 
$\hat {C}^{*}_R$, written as 
$\hat {C}_R\prec \hat {C}^{*}_R$.
Lemma 2.7 ([Reference Nelsen20, p. 11])
Let 
$W(z_1,\ldots ,z_n)=\max \{\sum _{i=1}^{n}z_i-n+1,0\}$ and 
$M(z_1,\ldots ,z_n)=\min \{z_1,\ldots ,z_n\}$. Then, for all copulas 
$C$ and for all 
$\boldsymbol {z}\in [0,1]^{n}$, we have
$$W(z_1,\ldots,z_n)\leq C(\boldsymbol{z})\leq M(z_1,\ldots,z_n),$$where 
$W(z_1,\ldots ,z_n)$ and 
$M(z_1,\ldots ,z_n)$ represent the Fréchet–Hoeffding lower and upper bounds, respectively.
Lemma 2.8 Let 
$\varphi :(0,\infty )\times (0,\infty )\times (0,\infty )\rightarrow (0,1)$ be a function such that 
$\varphi (\alpha ,\lambda ,\theta )=1-[F({(x-\lambda )}/{\theta })]^{\alpha },$ where 
$x>\lambda >0$, 
$\theta >0$, 
$\alpha >0$. Then, the following properties hold:
(i)
$\varphi$ is increasing and concave in $\lambda$, if $\alpha \geq 1$ and $F'=f$ is increasing;(ii)
$\varphi$ is increasing and concave in $\alpha$, for all $\lambda$ and $\theta$;(iii)
$\varphi$ is increasing and concave in $\theta$, for all $\lambda$ and $\alpha$, if $x^{2}\tilde {r}(x)$ is increasing.
Proof. The first- and second-order partial derivatives of 
$\varphi$ with respect to 
$\lambda$, 
$\theta$ and 
$\alpha$ are as follows:
\begin{equation} \frac{\partial\varphi(\alpha,\lambda,\theta)}{\partial\lambda}= \frac{\alpha}{\theta}f\left(\frac{x-\lambda}{\theta}\right)F^{\alpha-1} \left(\frac{x-\lambda}{\theta}\right) \end{equation}and
\begin{align} \frac{\partial^{2}\varphi(\alpha,\lambda,\theta)}{\partial\lambda^{2}}& = \frac{\alpha(1-\alpha)}{\theta^{2}}[f\left(\frac{x-\lambda}{\theta}\right)]^{2}F^{\alpha-2} \left(\frac{x-\lambda}{\theta}\right)\nonumber\\ & \quad -\frac{\alpha}{\theta^{2}}f'\left(\frac{x-\lambda}{\theta}\right)F^{\alpha-1} \left(\frac{x-\lambda}{\theta}\right), \end{align}
\begin{align} \frac{\partial\varphi(\alpha,\lambda,\theta)}{\partial\theta}& = \frac{\alpha}{x-\lambda}F^{\alpha}\left(\frac{x-\lambda}{\theta}\right) \left[\left(\frac{x-\lambda}{\theta}\right)^{2}\tilde{r}\left(\frac{x-\lambda}{\theta}\right)\right] \end{align}and
\begin{align} \frac{\partial^{2}\varphi(\alpha,\lambda,\theta)}{\partial\theta^{2}} & =\frac{-\alpha^{2}}{\theta^{2}(x-\lambda)}F^{\alpha-1}\left(\frac{x-\lambda}{\theta}\right)f \left(\frac{x-\lambda}{\theta}\right)\left[\left(\frac{x-\lambda}{\theta}\right)^{2}\tilde{r} \left(\frac{x-\lambda}{\theta}\right)\right]\nonumber\\ & \quad -\left(\frac{1}{\theta^{2}}\right)\frac{\alpha F^{\alpha}\left(\frac{x-\lambda}{\theta}\right)}{x-\lambda} \left[\left(\frac{x-\lambda}{\theta}\right)^{2}\tilde{r}\left(\frac{x-\lambda}{\theta}\right)\right]', \end{align}and
\begin{equation} \frac{\partial\varphi(\alpha,\lambda,\theta)}{\partial\alpha}={-}\log \left[F\left(\frac{x-\lambda}{\theta}\right)\right]F^{\alpha}\left(\frac{x-\lambda}{\theta}\right) \end{equation}and
\begin{equation} \frac{\partial^{2}\varphi(\alpha,\lambda,\theta)}{\partial\alpha^{2}}={-}\left[\log \left[F\left(\frac{x-\lambda}{\theta}\right)\right]\right]^{2}F^{\alpha} \left(\frac{x-\lambda}{\theta}\right), \end{equation}respectively. From the above expressions, we can easily show the desired results under the assumptions made.
The following notations will be used throughout this article:
Notation 2.1 (i) 
$\mathcal {D}^{+}_{n}=\{(z_1,\ldots ,z_n):z_{1}\geq z_{2}\geq \cdots \geq z_{n}>0\}$; (ii) 
$\mathcal {E}^{+}_{n}=\{(z_1,\ldots ,z_n):0< z_{1}\leq z_{2}\leq \cdots \leq z_{n}\};$ (iii) 
$\boldsymbol {1}_n=\{1,\ldots ,1\};$ 
$(iv)~\mathbb {I}_n=\{1,\ldots ,n\}$.
3. Ordering results
Throughout this section, we assume 
$\{X_1,\ldots ,X_n\}$ and 
$\{Y_1,\ldots ,Y_n\}$ are pairs of heterogeneous interdependent random samples. For 
$i\in \mathbb {I}_n$, assume that 
$X_i\sim F^{\alpha _{i}}({(x-\lambda _{i})}/{\theta _{i}})$ and 
$Y_i\sim G^{\beta _{i}}({(x-\mu _{i})}/{\delta _{i}})$. Here, 
$F(\cdot )$ and 
$G(\cdot )$ are known as the baseline cumulative distribution functions with respective probability density functions 
$f(\cdot )$ and 
$g(\cdot )$, hazard rate functions 
$r_X(\cdot )$ and 
$r_Y(\cdot ),$ and reversed hazard rate functions 
$\tilde {r}_X(\cdot )$ and 
$\tilde {r}_Y(\cdot )$. Furthermore, let 
$\{L_{1},\ldots ,L_{n}\}$ and 
$\{L_{1}^{*},\ldots ,L_{n}^{*}\}$ be two sets of independent Bernoulli random variables, independently of 
$X_{i}$'s and 
$Y_{i}$'s, with 
$E(L_{i})=p_{i}$ and 
$E(L_{i}^{*})=p_{i}^{*}$, for 
$i\in \mathbb {I}_n$. Let 
$T_i=L_iX_i$ and 
$T^{*}_{i}=L^{*}_{i}Y_{i},$ for 
$i\in \mathbb {I}_n$, be the claim amounts in the two portfolios of risks.
3.1. Based on an Archimedean survival copula
In this subsection, we develop different majorization-based ordering results between the smallest claim amounts in terms of the usual stochastic and hazard rate orders. Throughout this subsection, the smallest claim amounts are assumed to come from two heterogeneous portfolios with dependent claim sizes. For 
$i\in \mathbb {I}_{n},$ let the survival copulas associated with the claim sizes 
$X_{i}$'s and 
$Y_{i}$'s be Archimedean with the generators 
$\psi _1$ and 
$\psi _2$, respectively. Denote 
$\phi _{1}=\psi ^{-1}_{1}$ and 
$\phi _{2}=\psi ^{-1}_{2}$. Bold letters are used to denote vectors with 
$n$ components, unless otherwise stated. For example, 
$\boldsymbol {\lambda }=(\lambda _1,\ldots ,\lambda _n),$ 
$\boldsymbol {\alpha }=(\alpha _1,\ldots ,\alpha _n),$ 
$\boldsymbol {\theta }=(\theta _1,\ldots ,\theta _n),$ 
$\Psi (\boldsymbol {p})=(\Psi (p_1),\ldots ,\Psi (p_n))$ and 
$\Psi (\boldsymbol {p}^{*})=(\Psi (p_1^{*}),\ldots ,\Psi (p_n^{*}))$. In the following theorem, it is assumed that the random claims of two portfolios have exponentiated location-scale models with common location, scale and shape parameter vectors. It is then shown that the usual stochastic order between the smallest claim amounts holds under weakly supermajorization order between 
$\Psi (\boldsymbol {p})$ and 
$\Psi (\boldsymbol {p}^{*})$ and the usual stochastic order between 
$X$ and 
$Y$.
Theorem 3.1 Suppose 
$\{X_{1},\ldots ,X_{n}\}$ 
$[\{Y_{1},\ldots ,Y_{n}\}]$ is a set of nonnegative interdependent random variables such that for 
$i\in \mathbb {I}_n,$ 
$X_{i}\sim F^{\alpha _{i}}({(x-\lambda _{i})}/{\theta _{i}})$ 
$[Y_{i}\sim G^{\alpha _{i}}({(x-\lambda _{i})}/{\theta _{i}})]$ having an Archimedean survival copula with generator 
$\psi _1\ [\psi _2],$ where 
$F\ [G]$ is the baseline distribution function. Also, consider 
$\{L_{1},\ldots ,L_{n}\}$ 
$[\{L_{1}^{*},\ldots ,L_{n}^{*}\}]$ to be a set of independent Bernoulli random variables, independently of 
$X_{i}$'s [
$Y_{i}$'s], with 
$E(L_{i})=p_{i}$ 
$[E(L_{i}^{*})=p_{i}^{*}]$, for 
$i\in \mathbb {I}_n$. Furthermore, assume 
$\Psi :(0,1)\rightarrow (0,\infty )$ is a differentiable function, such that 
$\Psi (v)$ is increasing convex. If 
$\phi _2\circ \psi _1$ is super-additive, 
$\boldsymbol {\lambda }$, 
$\boldsymbol {\theta }$, 
$\boldsymbol {\alpha }$, 
$\Psi (\boldsymbol {p})$, 
$\Psi (\boldsymbol {p}^{*})\in \mathcal {D}^{+}_{n}$ (or 
$\mathcal {E}^{+}_{n}$) and 
$X\leq _{\textrm {st}}Y$, then
$${\Psi(\boldsymbol p)}\succeq^{w}{\Psi(\boldsymbol {p}^{*})}\Rightarrow T_{1:n}\leq_{\textrm{st}}T^{*}_{1:n}.$$Proof. The reliability functions of 
$T_{1:n}$ and 
$T^{*}_{1:n}$ are given by
$$\bar{F}_{T_{1:n}}(x)=\prod_{i=1}^{n}\Psi^{{-}1}(v_i)\left[\psi_1\sum_{i=1}^{n}\phi_1 \left\{1-\left[F\left(\frac{x-\lambda_i}{\theta_i}\right)\right]^{\alpha_i}\right\}\right]$$and
$$\bar{F}_{T^{*}_{1:n}}(x)=\prod_{i=1}^{n}\Psi^{{-}1}(v^{*}_i)\left[\psi_2\sum_{i=1}^{n}\phi_2 \left\{1-\left[G\left(\frac{x-\lambda_i}{\theta_i}\right)\right]^{\alpha_i}\right\}\right],$$respectively, where 
$x\geq \max _{i}\{\lambda _i\}$, 
$v_i=\Psi (p_i)$ and 
$v^{*}_i=\Psi (p^{*}_i),$ for 
$i\in \mathbb {I}_n$. Now, by Lemma 2.3, we have
\begin{align*} & \prod_{i=1}^{n}\Psi^{{-}1}(v_i)\left[\psi_1\sum_{i=1}^{n}\phi_1\left\{1-\left[F\left(\frac{x-\lambda_i}{\theta_i}\right)\right]^{\alpha_i}\right\}\right]\\ & \quad \leq \prod_{i=1}^{n}\Psi^{{-}1}(v_i)\left[\psi_2\sum_{i=1}^{n}\phi_2\left\{1-\left[F\left(\frac{x-\lambda_i}{\theta_i}\right)\right]^{\alpha_i}\right\}\right]. \end{align*} Furthermore, using the decreasing behavior of 
$\phi _2(\cdot )$ and 
$\psi _2(\cdot )$ and 
$X\leq _{\textrm {st}}Y,$ we see that
\begin{align*} & \prod_{i=1}^{n}\Psi^{{-}1}(v_i)\left[\psi_2\sum_{i=1}^{n}\phi_2\left\{1-\left[F\left(\frac{x-\lambda_i}{\theta_i}\right)\right]^{\alpha_i}\right\}\right]\\ & \quad \leq \prod_{i=1}^{n}\Psi^{{-}1}(v_i)\left[\psi_2\sum_{i=1}^{n}\phi_2\left\{1-\left[G\left(\frac{x-\lambda_i}{\theta_i}\right)\right]^{\alpha_i}\right\}\right]. \end{align*}Therefore, to obtain the required result, it is sufficient to show that
\begin{align*} & \prod_{i=1}^{n}\Psi^{{-}1}(v_i)\left[\psi_2\sum_{i=1}^{n}\phi_2\left\{1-\left[G\left(\frac{x-\lambda_i}{\theta_i}\right)\right]^{\alpha_i}\right\}\right]\\ & \quad \leq \prod_{i=1}^{n}\Psi^{{-}1}(v^{*}_i)\left[\psi_2\sum_{i=1}^{n}\phi_2\left\{1-\left[G\left(\frac{x-\lambda_i}{\theta_i}\right)\right]^{\alpha_i}\right\}\right]. \end{align*}For this purpose, let us denote
$$D(x)=\prod_{i=1}^{n}\Psi^{{-}1}(v_i)\left[\psi_2\sum_{i=1}^{n}\phi_2\left\{1-\left[G\left(\frac{x-\lambda_i}{\theta_i}\right)\right]^{\alpha_i}\right\}\right].$$ Its derivative with respect to 
$v_i$ is given by
\begin{align} \frac{\partial D(x)}{\partial v_i}=\frac{1}{\Psi^{{-}1}(v_i)}\frac{\partial \Psi^{{-}1}(v_i)}{\partial v_i}D(x). \end{align} Let 
$\boldsymbol {v}\in \mathcal {D}^{+}_{n}~(\mathcal {E}^{+}_{n})$. Then, increasing and convexity properties of 
$\Psi (\cdot )$ ensure that 
$\Psi ^{-1}(\cdot )$ is increasing concave. Therefore, 
${1}/{(\Psi ^{-1}(v_i))}\leq (\geq ) {1}/{(\Psi ^{-1}(v_j))}$ and 
${(\partial \Psi ^{-1}(v_i))}/{\partial v_i}\leq (\geq ){(\partial \Psi ^{-1}(v_j))}/{\partial v_j}$. Thus, from Lemma 3.1 (Lemma 3.3) of [Reference Kundu, Chowdhury, Nanda and Hazra11], we have 
$D(x)$ to be nondecreasing and Schur-concave in 
$\boldsymbol {v}\in \mathcal {D}^{+}_{n}~(\mathcal {E}^{+}_{n})$. Now, from Theorem A.8 of [Reference Marshall, Olkin and Arnold14], the rest of the proof follows.
It should be noted that the condition on transform function in Theorem 3.1 is quite general and can be easily verified for many well-known functions. For example, one can consider (i) 
$\Psi (v)=e^{v}$, 
$v\in (0,1)$ and (ii) 
$\Psi (v)=v$, 
$v\in (0,1)$. Clearly, these functions are increasing convex.
Remark 3.1 For various subfamilies of Archimedean survival copulas, an interpretation of the super-additive property of 
$\phi _2\circ \psi _1$ is that Kendall's 
$\tau$ of the 
$2$-dimensional copula with generator 
$\psi _2$ is larger than that of the copula with generator 
$\psi _1$ and consequently, is more positive dependent.
Using this Remark, from Theorem 3.1, we can conclude that for a portfolio of risks with heterogeneous interdependent claims following the exponentiated location-scale model, the less positive dependence and more heterogeneity in the parametric functions 
$(\Psi (p_1),\ldots ,\Psi (p_{n}))$ in the sense of weak supermajorization order lead to a stochastically smaller minimum claim amount.
Remark 3.2 It should be noted that when the baseline distribution functions of the two portfolios of risks are the same in Theorem 3.1, that is, 
$F=G$, then the condition of the usual stochastic order on 
$X$ and 
$Y$ may be relaxed to get a similar finding.
The following theorem states that 
$T_{1:n}$ is dominated by 
$T^{*}_{1:n}$ in terms of the usual stochastic order when there is less positive dependence and more heterogeneity in the shape parameters in terms of weak supermajorization order. Let us denote 
$X_{1:n}=\min \{X_{1},\ldots ,X_{n}\}$. Similarly, let 
$Y_{1:n}$ denote the minimum of 
$\{Y_{1},\ldots ,Y_{n}\}$.
Theorem 3.2 Suppose 
$\{X_{1},\ldots ,X_{n}\}$ 
$[\{Y_{1},\ldots ,Y_{n}\}]$ is a set of interdependent random variables such that, for 
$i\in \mathbb {I}_n,$ 
$X_{i}\sim F^{\alpha _{i}}({(x-\lambda _{i})}/{\theta _{i}})$ 
$[Y_{i}\sim G^{\beta _{i}}({(x-\lambda _{i})}/{\theta _{i}})]$ having an Archimedean survival copula with generator 
$\psi _1\ [\psi _2],$ where 
$F\ [G]$ is the baseline distribution function. Furthermore, let 
$\{L_{1},\ldots ,L_{n}\}$ 
$[\{L_{1}^{*},\ldots ,L_{n}^{*}\}]$ be a collection of independent Bernoulli random variables, independently of 
$X_{i}$'s [
$Y_{i}$'s], with 
$E(L_{i})=p_{i}$ 
$[E(L_{i}^{*})=p_{i}^{*}]$, for 
$i\in \mathbb {I}_n$. Moreover, let 
$\boldsymbol {\lambda }$, 
$\boldsymbol {\theta }$, 
$\boldsymbol {\alpha }$, 
$\boldsymbol {\beta }\in \mathcal {D}^{+}_{n}\ (\mathcal {E}^{+}_{n})$ and 
$\prod _{i=1}^{n}p_{i}\leq \prod _{i=1}^{n}p^{*}_{i}$. If 
$\psi '_{1}/\psi _1$ or 
$\psi '_{2}/\psi _2$ is increasing, 
$\phi _2\circ \psi _1$ is super-additive and 
$X\leq _{\textrm {st}}Y$, then
$${{\boldsymbol\alpha}}\succeq^{w}{{\boldsymbol\beta}}\Rightarrow T_{1:n}\leq_{\textrm{st}}T^{*}_{1:n}.$$Proof. Under the assumptions made and using Theorem 3.5 of Das and Kayal [Reference Das and Kayal7], we have 
${{\boldsymbol \alpha }}\succeq ^{w}{{\boldsymbol \beta }}\Rightarrow X_{1:n}\leq _{\textrm {st}}Y_{1:n}$, that is, 
$\bar {F}_{X_{1:n}}(x)\leq \bar {F}_{Y_{1:n}}(x)$. Now, upon combining this inequality with 
$\prod _{i=1}^{n}p_{i}\leq \prod _{i=1}^{n}p^{*}_{i}$, the required result follows. This completes the proof of the theorem.
The following example provides an illustration of the result in Theorem 3.2.
Example 3.1 Let 
$F(x)=[1-e^{-x^{5}}]^{2}$, 
$x>0,$ and 
$G(x)=1-\exp (1-x^{2})$, 
$x\geq 1$. It is not difficult to see that 
$X\leq _{\textrm {st}}Y$. Furthermore, let 
$\psi _1(x)={(1+b_1x)^{-{1}/{b_1}}}$ and 
$\psi _2(x)={(1+b_2x)^{-{1}/{b_2}}}$, where 
$b_1,~b_2,~x>0$. These are the generators of Clayton survival copula. Consider the three-dimensional vectors 
$\boldsymbol {\lambda }=\boldsymbol {\mu }=(0.3,1,1.5)$, 
$\boldsymbol {\alpha }=(0.5,0.9,1),$ 
$\boldsymbol {\theta }=\boldsymbol {\delta }=(2.5,3,4)$, 
$\boldsymbol {\beta }=(0.6,1,2)$, 
$\boldsymbol {p}=(0.1,0.2,0.3)$ and 
$\boldsymbol {p}^{*}=(0.6,0.7,0.8)$. For 
$b_2=9$ and 
$b_1=7,$ it can be verified that 
$\phi _2\circ \psi _1(x)$ is convex in 
$x$. Again, 
$\psi _1(x)$ and 
$\psi _2(x)$ are log-convex. Clearly, 
$\boldsymbol {\lambda }$, 
$\boldsymbol {\theta }$, 
$\boldsymbol {\alpha }$, 
$\boldsymbol {\beta }\in \mathcal {E}^{+}_{3}$ and 
${\boldsymbol \alpha }\succeq ^{w}{\boldsymbol \beta }$. Thus, all the conditions of Theorem 3.2 are satisfied. As can be seen in Figure 1(a), the difference between the reliability functions of 
$T_{1:3}$ and 
$T^{*}_{1:3}$ takes all negative values, supporting the result that 
$T_{1:3}\le _{\textrm {st}}T_{1:3}^{*}$.
FIGURE 1. (a) Graph of 
$[\bar {F}_{T_{1:3}}(x)-\bar {F}_{T^{*}_{1:3}}(x)]$ in Example 3.1. (b) Graph of 
$\bar {F}_{T_{1:3}}(x)-\bar {F}_{T^{*}_{1:3}}(x)$ in Counterexample 3.1.
We next present a counterexample to show that if some of the conditions in Theorem 3.2 are violated, then the established usual stochastic order between the smallest claim amounts will not hold.
Counterexample 3.1 Let 
$F(x)=1-e^{-x}$ and 
$G(x)=e^{-{1}/{x}},$ for 
$x>0,$ be the baseline distribution functions. Consider the generators of Gumbel–Barnett survival copula as 
$\psi _1(x)=e^{\frac {1}{0.5}(1-e^{x})}$ and 
$\psi _2(x)=e^{\frac {1}{0.3}(1-e^{x})},$ for 
$x>0$. Let us consider the three-dimensional vectors 
$\boldsymbol {\lambda }=\boldsymbol {\mu }=(0.3,2,2.5)$, 
$\boldsymbol {\beta }=(2.5,2.6,3)$, 
$\boldsymbol {\alpha }=(1.5,2.3,2.5)$, 
$\boldsymbol {\theta }=\boldsymbol {\delta }=(4.5,5,6)$, 
$\boldsymbol {p}=(0.91,0.92,0.93)$ and 
$\boldsymbol {p}^{*}=(0.71,0.72,0.73)$. Note that all the conditions of Theorem 3.2 are satisfied except 
$\prod _{i=1}^{n}p_{i}\leq \prod _{i=1}^{n}p^{*}_{i}$ and 
$\psi '_{1}/\psi _1$ or 
$\psi '_{2}/\psi _2$ is increasing. The plot of the difference between the reliability functions of 
$T_{1:3}$ and 
$T^{*}_{1:3}$ is presented for this case in Figure 1(b). This confirms that the reliability functions of 
$T_{1:3}$ and 
$T^{*}_{1:3}$ intersect each other, indicating that the result in Theorem 3.2 does not hold.
By using an approach similar to the one used in Theorem 3.2, the following theorem can be established by using Theorem 3.6 of Das and Kayal [Reference Das and Kayal7]. So, the proof is omitted here for conciseness.
Theorem 3.3 Suppose 
$\{X_{1},\ldots ,X_{n}\}$ 
$[\{Y_{1},\ldots ,Y_{n}\}]$ is a set interdependent random variables such that, for 
$i\in \mathbb {I}_n,$ 
$X_{i}\sim F^{\alpha _{i}}({(x-\lambda _{i})}/{\theta _{i}})$ 
$[Y_{i}\sim G^{\alpha _{i}}({(x-\mu _{i})}/{\theta _{i}})]$ having an Archimedean survival copula with generator 
$\psi _1\ [\psi _2],$ where 
$F~[G]$ is the baseline distribution function. Furthermore, let 
$\{L_{1},\ldots ,L_{n}\}$ 
$[\{L_{1}^{*},\ldots ,L_{n}^{*}\}]$ be a set of independent Bernoulli random variables, independently of 
$X_{i}$'s [
$Y_{i}$'s], with 
$E(L_{i})=p_{i}$ 
$[E(L_{i}^{*})=p_{i}^{*}]$, for 
$i\in \mathbb {I}_n$. Moreover, let 
$\boldsymbol {\lambda },\ \boldsymbol {\theta },\ \boldsymbol {\alpha }~(\geq \boldsymbol {1}_n),\ \boldsymbol {\mu }\in \mathcal {D}^{+}_{n}\ (\mathcal {E}^{+}_{n})$, 
$\prod _{i=1}^{n}p_{i}\leq \prod _{i=1}^{n}p^{*}_{i}$ and 
$r_X(x)$ or 
$r_Y(x)$ be increasing. Then,
$${\boldsymbol\lambda}\succeq^{w}{\boldsymbol\mu}\Rightarrow T_{1:n}\leq_{\textrm{st}}T^{*}_{1:n},$$provided 
$\psi '_{1}/\psi _1$ or 
$\psi '_{2}/\psi _2$ is increasing, 
$\phi _2\circ \psi _1$ is super-additive and 
$X\leq _{\textrm {st}}Y$.
It can be established that for 
$c\ge ({1}/{n})\sum _{i=1}^{n}c_{i}$, 
$(c_1,\ldots ,c_n)\succeq ^{w}(c,\ldots ,c)$ holds. Thus, the following corollary follows immediately from Theorems 3.1–3.3.
Corollary 3.1 In addition to the assumptions as in
(i) Theorem 3.1, let
$p_{1}^{*}=\cdots =p_{n}^{*}=p^{*}$. Then, $\Psi (p^{*})\ge ({1}/{n})\sum _{i=1}^{n}\Psi (p_i)\Rightarrow T_{1:n}\le _{\textrm {st}}T_{1:n}^{*}$;(ii) Theorem 3.2, let
$\beta _{1}=\cdots =\beta _{n}=\beta$. Then, $\beta \ge ({1}/{n}) \sum _{i=1}^{n}\alpha _i\Rightarrow T_{1:n}\le _{\textrm {st}}T_{1:n}^{*}$;(iii) Theorem 3.3, let
$\mu _{1}=\cdots =\mu _{n}=\mu$. Then, $\mu \ge ({1}/{n})\sum _{i=1}^{n}\lambda _i\Rightarrow T_{1:n}\le _{\textrm {st}}T_{1:n}^{*}$.
The following counterexample demonstrates that the result in Theorem 3.3 does not hold if some conditions are not satisfied.
Counterexample 3.2 The baseline distribution functions are 
$F(x)=1-e^{-x}$ and 
$G(x)=e^{-{1}/{x}}$, for 
$x>0$. Let 
$\psi _1(x)=e^{\frac {1}{0.7}(1-e^{x})}$ and 
$\psi _2(x)=e^{\frac {1}{0.5}(1-e^{x})},$ 
$x>0,$ be the generators of the Gumbel–Barnett survival copula. Consider the three-dimensional vectors 
$\boldsymbol {\lambda }=(0.3,2,2.5)$, 
$\boldsymbol {\mu }=(0.5,2.5,5)$, 
$\boldsymbol {\alpha }=\boldsymbol {\beta }=(1.5,2.3,2.5),$ 
$\boldsymbol {\theta }=\boldsymbol {\delta }=(4.5,5,6)$, 
$\boldsymbol {p}=(0.91,0.92,0.93)$ and 
$\boldsymbol {p}^{*}=(0.1,0.2,0.3)$. It is then easy to check that all the conditions of Theorem 3.3 are satisfied, except 
$\prod _{i=1}^{n}p_{i}\leq \prod _{i=1}^{n}p^{*}_{i}$, 
$\psi '_{1}/\psi _1$ or 
$\psi '_{2}/\psi _2$ is increasing and 
$r_Y(x)$ is increasing. Figure 2(a) represents the plot of the difference between the reliability functions of 
$T_{1:3}$ and 
$T^{*}_{1:3}$, which crosses the horizontal axis. So, this shows that the result in Theorem 3.3 does not hold.
FIGURE 2. (a) Graph of 
$\bar {F}_{T_{1:3}}(x)-\bar {F}_{T^{*}_{1:3}}(x)$ in Counterexample 3.2. (b) Graph of 
$\bar {F}_{T^{*}_{1:3}}(x)/\bar {F}_{T_{1:3}}(x)$ in Example 3.2.
Under some conditions, the following theorem presents the usual stochastic order between the smallest claim amounts associated with two interdependent heterogeneous portfolios of risks. The proof of the theorem follows by using Theorem 3.7 of Das and Kayal [Reference Das and Kayal7] and the assumptions made, and so it is not presented here for the sake of brevity.
Theorem 3.4 Let 
$\{X_{1},\ldots ,X_{n}\}$ 
$[\{Y_{1},\ldots ,Y_{n}\}]$ be a set of nonnegative interdependent random variables such that, for 
$i\in \mathbb {I}_n,$ 
$X_{i}\sim F^{\alpha _{i}}({(x-\lambda _{i})}/{\theta _{i}})$ 
$[Y_{i}\sim G^{\alpha _{i}}({(x-\lambda _{i})}/{\delta _{i}})]$ having an Archimedean survival copula with generator 
$\psi _1\ [\psi _2],$ where 
$F\ [G]$ is the baseline distribution function. Furthermore, let 
$\{L_{1},\ldots ,L_{n}\}$ 
$[\{L_{1}^{*},\ldots ,L_{n}^{*}\}]$ be a collection of independent Bernoulli random variables, independently of 
$X_{i}$'s [
$Y_{i}$'s], with 
$E(L_{i})=p_{i}$ 
$[E(L_{i}^{*})=p_{i}^{*}]$, for 
$i\in \mathbb {I}_n$. Moreover, let 
$\boldsymbol {\lambda }$, 
$\boldsymbol {\theta }$, 
$\boldsymbol {\alpha }\ (\geq \boldsymbol {1}_n)$, 
$\boldsymbol {\delta }\in \mathcal {D}^{+}_{n}\ (\mathcal {E}^{+}_{n})$, 
$\prod _{i=1}^{n}p_{i}\leq \prod _{i=1}^{n}p^{*}_{i}$ and 
$r_X(x)$ or 
$r_Y(x)$ be increasing in 
$x$. If 
$\psi '_{1}/\psi _1$ or 
$\psi '_{2}/\psi _2$ is increasing, 
$\phi _2\circ \psi _1$ is super-additive and 
$X\leq _{\textrm {st}}Y$, then
$$\left(\frac{1}{\theta_1},\ldots,\frac{1}{\theta_n}\right)\succeq_{w}\left(\frac{1}{\delta_1},\ldots,\frac{1}{\delta_n}\right)\Rightarrow T_{1:n}\leq_{\textrm{st}}T^{*}_{1:n}.$$ According to Theorem 3.4, for a heterogeneous portfolio of risks with 
$n$ dependent claims having exponentiated location-scale distributions, the less positive dependence and the more heterogeneous, the reciprocal of the scale parameters are in the sense of weak submajorization order, the stochastically smaller claim amount will be achieved. Furthermore, since 
$(c_1,\ldots ,c_n)\succeq _{w}(c,\ldots ,c)$ holds, for 
$c\le ({1}/{n})\sum _{i=1}^{n}c_i$, the following corollary follows readily from Theorem 3.4.
Corollary 3.2 In addition to the conditions of Theorem 3.4, let 
$\delta _1=\cdots =\delta _n=\delta$. Then, 
$1/\delta \le ({1}/{n})\sum _{i=1}^{n} ({1}/{\theta _i})\Rightarrow T_{1:n}\leq _{\textrm {st}}T^{*}_{1:n}$.
Remark 3.3 It needs to be mentioned that when the baseline distribution functions of the two portfolios of risks are different but generators are the same in Theorem 3.4, that is, 
$\psi _1=\psi _2$, then the condition ‘
$\psi '_{1}/\psi _1$ or 
$\psi '_{2}/\psi _2$ is increasing’ and ‘ 
$\phi _2\circ \psi _1$ is super-additive’ may be relaxed to get an analogous result.
The following remark demonstrates that there are many copulas for which 
$\phi _2\circ \psi _1$ is super-additive and 
$\psi _1$ or 
$\psi _2$ is log-convex.
Remark 3.4
(i) For the independence survival copula with generators
$\psi _1(x)=\psi _2(x)=e^{-x}$, $x>0,$ it can be shown that $\psi _1$ and $\psi _2$ are log-convex. Moreover, $\phi _2\circ \psi _1(x)=x$ satisfies the super-additive property;(ii) Consider the Clayton survival copula with generators
$\psi _1(x)=(a_1x+1)^{-1/a_1}$ and $\psi _2(x)=(b_1x+1)^{-1/b_1},$ where $x>0,~a_1,~b_1\geq 0$. We can verify that $\psi _1$ and $\psi _2$ are both log-convex. Also, $\phi _2\circ \psi _1(x)=[(a_1x+1)^{b_1/a_1}-1]/b_1$ is convex, for $b_1\geq a_1\geq 0$. Hence, $\phi _2\circ \psi _1$ is super-additive;(iii) Consider the Ali-Mikhail-Haq survival copula with generators
$\psi _1(x)={(1-a)}/{(e^{x}-a)}$ and $\psi _2(x)={(1-b)}/{(e^{x}-b)},$ where $a,~b\in [0,1)$, $x>0$. It is clear that both $\psi _1$ and $\psi _2$ are log-convex. Also, $\phi _2\circ \psi _1(x)=\log [({(1-b)(e^{x}-a)}/{(1-a)})+b]$ is convex, for $0\leq a< b<1$. Hence, $\phi _2\circ \psi _1(x)$ is super-additive;(iv) Consider the Gumbel–Hougaard survival copula with generators
$\psi _1(x)=e^{-x^{1/a_1}}$ and $\psi _2(x)=e^{-x^{1/a_2}},~x>0,~a_1,~a_2\in [1,\infty )$. Here, $\psi _1$ and $\psi _2$ are both log-convex. Furthermore, for $a_1\leq a_2,$ $\phi _2\circ \psi _1(x)=x^{a_2/a_1}$ satisfies the super-additive property.
Next, under some new sufficient conditions, we strengthen the established results from the usual stochastic order to the hazard rate order. We now assume that the random claims share a common dependence structure. Under this assumption, the result below provides sufficient conditions under which the hazard rate order between the smallest claim amounts arising from two dependent and heterogeneous portfolios of risks holds.
Theorem 3.5 Let 
$\{X_{1},\ldots ,X_{n}\}$ 
$[\{Y_{1},\ldots ,Y_{n}\}]$ be a collection of nonnegative interdependent random variables such that, for 
$i\in \mathbb {I}_n,$ 
$X_{i}\sim F({(x-\lambda _{i})}/{\theta _{i}})$ 
$[Y_{i}\sim F({(x-\lambda _{i})}/{\delta _{i}})]$ having an Archimedean survival copula with a common generator 
$\psi$, where 
$F$ is the baseline distribution function. Furthermore, let 
$\{L_{1},\ldots ,L_{n}\}$ 
$[\{L_{1}^{*},\ldots ,L_{n}^{*}\}]$ be a set of independent Bernoulli random variables, independently of 
$X_{i}$'s [
$Y_{i}$'s], with 
$E(L_{i})=p_{i}$ 
$[E(L_{i}^{*})=p_{i}^{*}]$, for 
$i\in \mathbb {I}_n$. Moreover, let 
$\boldsymbol {\lambda }$, 
$\boldsymbol {\theta }$, 
$\boldsymbol {\delta }\in \mathcal {D}^{+}_{n}~(\mathcal {E}^{+}_{n})$. Then,
$$(-\log\theta_1,\ldots,-\log\theta_n)\succeq_{w}(-\log{\delta_1},\ldots,-\log\delta_n)\Rightarrow T_{1:n}\leq_{hr}T^{*}_{1:n},$$provided the following conditions hold:
(i)
$w\tilde {r}_X(w)$ is increasing convex, and $r_X(w)$ is increasing;(ii)
$({\psi (u)}/{\psi '(u)})[{(1-\psi (u))}/{\psi '(u)}]'$ and ${\psi (u)}/{\psi '(u)}$ are increasing;(iii)
${(1-\psi (u))}/{\psi '(u)}$ is decreasing;(iv)
$\prod _{i=1}^{n}p^{*}_i\geq \prod _{i=1}^{n}p_i$.
Proof. To prove the desired result, we need to show that
$$\frac{\bar{F}_{T^{*}_{1:n}}(x)}{\bar{F}_{T_{1:n}}(x)}= \frac{\prod_{i=1}^{n}p^{*}_i}{\prod_{i=1}^{n}p_i}\times\frac{\bar{F}_{Y_{1:n}}(x)}{\bar{F}_{X_{1:n}}(x)}$$is increasing in 
$x$, which is equivalent to showing that 
$X_{1:n}\leq _{hr} Y_{1:n}$. The hazard rate function of 
$X_{1:n}$ is given by
\begin{align} \vartheta(\boldsymbol{b})& \overset{\textrm{def}}{=}r_{X_{1:n}}(x)=\frac{\psi'(\sum_{k=1}^{n}\phi(\bar{F}({x-\lambda_k})e^{b_k}))}{\psi(\sum_{k=1}^{n}\phi(\bar{F}({x-\lambda_k}){e^{b_k}}))}\nonumber\\ & \quad \times \sum_{k=1}^{n}\left[\{{e^{b_k}\tilde{r}_X({(x-\lambda_k)}{e^{b_k}})}\} \left\{\frac{1-\psi(\phi(\bar{F}(({x-\lambda_k}){e^{b_k}})))}{\psi'(\phi(\bar{F}(({x-\lambda_k}){ e^{b_k}})))}\right\}\right], \end{align}where 
$b_i=-\log {\theta _i}$, for 
$i\in \mathbb {I}_n$ and 
$\boldsymbol {b}=(b_1,\ldots ,b_n)$. Differentiating (3.2) partially with respect to 
$b_i,$ for 
$i\in \mathbb {I}_n,$ we obtain
\begin{align} \frac{\partial \vartheta({\boldsymbol b})}{\partial b_i}& ={-}t_i \tilde{r}_X(t_i)\frac{1-\psi(\upsilon_i)}{\psi'(\upsilon_i)}\left[\frac{d}{dz}\left[\frac{\psi'(z)}{\psi(z)}\right]\right] \sum_{k=1}^{n}\left[\frac{{t_k}\tilde{r}_X(t_k)}{x-\lambda_k}\left[\frac{1-\psi(\upsilon_k)}{\psi'(\upsilon_k)}\right]\right]\nonumber\\ & \quad +\left[\frac{\psi'(z)}{\psi(z)}\right]\left[{e^{b_i}}\frac{d}{dt_i}[t_i \tilde{r}_X(t_i)]\left[\frac{1-\psi(\upsilon_i)}{\psi'(\upsilon_i)}\right]\right]\nonumber\\ & \quad -{e^{b_i}}r(t_{i})[t_{i} \tilde{r}_X(t_{i})]\frac{\psi'(z)}{\psi(z)}\left[\left[\frac{{\psi}(v)}{{\psi}'(v)}\right] {\frac{d}{dv}\left[\frac{1-{\psi}(v)}{{\psi}'(v)}\right]}\right]_{v=\upsilon_{i}}, \end{align}where 
$z=\sum _{i=1}^{n}\upsilon _i$, 
$\upsilon _i=\phi (\bar F(({x-\lambda _i})e^{b_i}))$ and 
$t_i=({x-\lambda _i})e^{b_i}$. Then, to establish the required result, it is enough to show that 
$\vartheta ({\boldsymbol b})$ is increasing in 
$b_i,$ for 
$i\in \mathbb {I}_n,$ and Schur-convex in 
$\boldsymbol {b}\in \mathcal {E}^{+}_{n}~(\mathcal {D}^{+}_{n})$ (see Theorem A.8 of [Reference Marshall, Olkin and Arnold14]). Based on the assumed conditions, it is not difficult to show that 
$\vartheta ({\boldsymbol b})$ is increasing in 
$b_i,$ for 
$i\in \mathbb {I}_n$. Now, the Schur-convexity of 
$\vartheta ({\boldsymbol b})$ can be verified as follows. For 
$1\leq i\leq j \leq n,$ 
$\lambda _i\geq (\leq )\lambda _j$, 
$\theta _i\geq (\leq )\theta _j,$ and so 
$t_i\leq (\geq )t_j$ and 
$\upsilon _i\leq (\geq )\upsilon _j$. By using the fact that 
$w\tilde {r}_X(w)$ is increasing convex, the following two inequalities hold:
\begin{equation} \begin{aligned} & [w \tilde{r}_X(w)]_{w=t_i}\leq({\geq})[w \tilde{r}_X(w)]_{w=t_j}\\ \text{and}\quad & {e^{b_i}}\frac{d}{d w}[w \tilde{r}_X(w)]_{w=t_i}\leq({\geq}){e^{b_j}}\frac{d}{d w}[w \tilde{r}_X(w)]_{w=t_j}. \end{aligned} \end{equation} Observing the behavior of 
${(1-\psi )}/{\psi '}$, we can write
\begin{equation} \left[\frac{1-\psi(u)}{{\psi}'(u)}\right]_{u=\upsilon_i}\geq({\leq}) \left[\frac{1-\psi(u)}{{\psi}'(u)}\right]_{u=\upsilon_j}. \end{equation} Furthermore, it has been assumed that 
$({\psi (u)}/{\psi '(u)})({d}/{du})[{(1-\psi (u))}/{\psi '(u)}]$ is increasing. So,
\begin{equation} \left(\frac{\psi(u)}{\psi'(u)}\frac{d}{du}\left[\frac{1-\psi(u)}{\psi'(u)}\right]\right)_{u=\upsilon_i}\leq({\geq}) \left(\frac{\psi(u)}{\psi'(u)}\frac{d}{du}\left[\frac{1-\psi(u)}{\psi'(u)}\right]\right)_{u=\upsilon_j}. \end{equation} Again, the increasing property of 
$r_X(w)$ provides
\begin{equation} e^{b_i}[r_X(w)]_{w=t_i}\leq({\geq})e^{b_j}[r_X(w)]_{w=t_j}. \end{equation} Finally, upon using (3.4)–(3.7), for 
$1\leq i\leq j \leq n$, the following inequality can be obtained:
$$\frac{\partial \vartheta({\boldsymbol b})}{\partial b_i}-\frac{\partial \vartheta({\boldsymbol b})}{\partial b_j}\leq({\geq}) 0, \text{ for each } b_i\in\mathcal{E}^{+}_{n}~(\mathcal{D}^{+}_{n}).$$ Now, applying Lemma 3.3 (Lemma 3.1) of [Reference Kundu, Chowdhury, Nanda and Hazra11], we have 
$\vartheta ({\boldsymbol b})$ to be Schur-convex in 
$\boldsymbol {b}\in \mathcal {E}^{+}_{n}~(\mathcal {D}^{+}_{n})$. This completes the proof of the theorem.
The following example provides a demonstration of Theorem 3.5.
Example 3.2 Suppose 
$F(x)=G(x)=[{x}/{1000}]^{2}$, 
$0< x\leq 1000$. Clearly, 
$r_X(x)$ is increasing, and 
$x\tilde {r}_X(x)$ is increasing convex. Let 
$\psi (x)=e^{\frac {1}{0.99}(1-e^{x})}$, 
$x>0,$ be the generator of the Gumbel–Barnett survival copula. Set the three-dimensional vectors 
$\boldsymbol {\lambda }=\boldsymbol {\mu }=(0.6,1.1,2)$, 
$\boldsymbol {\theta }=(e^{5},e^{7},e^{9})$, 
$\boldsymbol {\delta }=(e^{6},e^{8},e^{10})$, 
$\boldsymbol {p}=(0.11,0.21,0.31)$ and 
$\boldsymbol {p}^{*}=(0.62,0.70,0.82)$. Furthermore, we can check that 
$\psi$ satisfies Conditions (ii) and (iii) in Theorem 3.5. Moreover, 
$\boldsymbol {\lambda }$, 
$\boldsymbol {\theta }$, 
$\boldsymbol {\delta }\in \mathcal {E}^{+}_{3}$ and 
$(-\log {\theta }_{1},-\log {\theta }_{2},-\log {\theta }_{3})\succeq _{w}(-\log {\delta }_{1},-\log {\delta }_{2},-\log {\delta }_{3})$. Figure 2(b) displays the plot of the ratio of the survival functions of 
$T^{*}_{1:3}(x)$ and 
$T_{1:3}(x),$ as a function of 
$x$, which shows it is increasing with respect to 
$x,$ providing a validation of the result in Theorem 3.5.
Now, we provide a counterexample to show that if some of the conditions in Theorem 3.5 are violated, then the established hazard rate order between the smallest claim amounts will not hold.
Counterexample 3.3 Let 
$F(x)=e^{-x^{-0.2}},$ for 
$x>0,$ be the baseline distribution function. Consider the generator of Gumbel–Hougaard survival copula 
$\psi (x)=e^{-x^{{1}/{2}}},$ for 
$x>0$. Let us consider the three-dimensional vectors 
$\boldsymbol {\lambda }=\boldsymbol {\mu }=(0.6,5,0.2)$, 
$\boldsymbol {\beta }=\boldsymbol {\alpha }=(1,1,1)$, 
$\boldsymbol {\theta }=(e^{0.5},e^{4},e^{0.9})$, 
$\boldsymbol {\delta }=(e^{6},e^{0.8},e^{10})$, 
$\boldsymbol {p}=(0.11,0.31,0.41)$ and 
$\boldsymbol {p}^{*}=(0.72,0.80,0.82)$. Note that all the conditions of Theorem 3.5 are satisfied except conditions 
$(i)$, 
$(ii)$ and 
$\boldsymbol {\lambda }$, 
$\boldsymbol {\theta }$, 
$\boldsymbol {\delta }\in \mathcal {D}^{+}_{3}\ (\mathcal {E}^{+}_{3})$. The plot of the ratio of the survival functions of 
$T^{*}_{1:3}(x)$ and 
$T_{1:3}(x)$ is presented in Figure 3, which shows it is not increasing with respect to 
$x$, thus violating the result in Theorem 3.5.
FIGURE 3. Graph of 
$\bar {F}_{T_{1:3}}(x)/\bar {F}_{T^{*}_{1:3}}(x)$ in Counterexample 3.3.
Remark 3.5
(i) Consider the independence survival copula with generator
$\psi (x)=e^{-x}$, $x>0$. In this case, we find
From these expressions, we observe that$$\frac{d}{dx}\left[\frac{\psi'(x)}{\psi(x)}\right]=0,\quad \frac{d}{dx}\left[\frac{1-\psi(x)}{\psi'(x)}\right]=\frac{d}{dx}\left[\frac{1-e^{{-}x}}{-e^{{-}x}}\right]={-}e^{x},\quad \frac{d}{dx}\left[\left[\frac{1-\psi(x)}{\psi'(x)}\right]'\frac{\psi(x)}{\psi'(x)}\right]=e^{x}.$$$\psi$ satisfies all the (generator-based) conditions in Theorems 3.5;(ii) Consider the Ali-Mikhail-Haq survival copula with generator
$\psi (x)={(1-b)}/{(e^{x}-b)}$, $x>0$, $b\in [-1,1)$. In this case, we find
Hence, for$$\frac{d}{dx}\left[\frac{\psi'(x)}{\psi(x)}\right]=\frac{b}{(e^{x}-b)^{2}},\quad \frac{d}{dx}\left[\frac{1-\psi(x)}{\psi'(x)}\right]={-}\frac{(e^{x}-be^{{-}x})}{1-b}.$$$b\in [-1,0],$ $\psi$ is log-concave and ${(1-\psi )}/{\psi '}$ is decreasing. It can be graphically shown that $[{(1-\psi )}/{\psi '}]'[{\psi }/{\psi '}]$ is increasing for $b=-0.1$. Therefore, $\psi$ satisfies all the conditions of Theorem 3.5.
The following corollary is an immediate consequence of Theorem 3.5.
Corollary 3.3 Under the assumptions of Theorem 3.5, and additionally that 
$\delta _1=\cdots =\delta _n=\delta ,$ we have 
$\delta ^{n}\ge e^{\sum _{i=1}^{n}\ln \theta _i}\Rightarrow T_{1:n}\leq _{hr}T^{*}_{1:n}$.
The next theorem shows that weakly supermajorized shape parameter vector yields smaller hazard rate for the smallest claim amount.
Theorem 3.6 Suppose 
$\{X_{1},\ldots ,X_{n}\}$ 
$[\{Y_{1},\ldots ,Y_{n}\}]$ is a set of interdependent random variables such that, for 
$i\in \mathbb {I}_n,$ 
$X_{i}\sim F^{\alpha _i}({(x-\lambda )}/{\theta })$ 
$[Y_{i}\sim F^{\beta _i}({(x-\lambda )}/{\theta })]$ having a common Archimedean survival copula with generator 
$\psi ,$ where 
$F$ is the baseline distribution function. Furthermore, let 
$\{L_{1},\ldots ,L_{n}\}$ 
$[\{L_{1}^{*},\ldots ,L_{n}^{*}\}]$ be a set of independent Bernoulli random variables, independently of 
$X_{i}$'s [
$Y_{i}$'s], with 
$E(L_{i})=p_{i}$ 
$[E(L_{i}^{*})=p_{i}^{*}]$, for 
$i\in \mathbb {I}_n$. Then,
$${\boldsymbol\alpha}\succeq^{w}{\boldsymbol\beta}\Rightarrow T_{1:n}\leq_{hr}T^{*}_{1:n},$$under the following conditions:
(i)
$\psi '/\psi$ and ${(1-\psi )}/{\psi '}$ are decreasing;(ii)
${(1-\psi )\log (1-\psi )}/{\psi '}$ is increasing and convex;(iii)
$\prod _{i=1}^{n}p^{*}_i\geq \prod _{i=1}^{n}p_i$.
Proof. As in Theorem 3.5, it is sufficient to show that 
$X_{1:n}\leq _{hr} Y_{1:n}$. The hazard rate function of 
$X_{1:n}$ is given by
\begin{equation} {r}_{X_{1:n}}(x)\overset{\textrm{def}}{=}S_2(\boldsymbol{\alpha})= \frac{\psi'(\sum_{k=1}^{n}\varepsilon_{k})}{\psi(\sum_{k=1}^{n}\varepsilon_{k})} \sum_{k=1}^{n}\left[\frac{\tilde{r}_X(t)}{\theta\log{F(t)}} \left[\frac{(1-\psi(\varepsilon_{k}))\log(1-\psi(\varepsilon_{k}))}{\psi'(\varepsilon_{k})}\right]\right], \end{equation}where 
$\varepsilon _i=\phi (1-[{F}({(x-\lambda )}/{\theta })]^{\alpha _i})$ and 
$t={(x-\lambda )}/{\theta },$ for 
$i\in \mathbb {I}_n$. The derivative of (3.8) with respect to 
$\alpha _i$, for 
$i\in \mathbb {I}_n$, is given by
\begin{align} \frac{\partial S_2(\boldsymbol{\alpha})}{\partial \alpha_i}& ={-\log F(t)}\frac{1-\psi(\varepsilon_i)}{\psi'(\varepsilon_i)}\left[\frac{d}{dz}\left[\frac{\psi'(z)}{\psi(z)}\right]\right]_{z=\sum_{k=1}^{n}\varepsilon_k}\sum_{k=1}^{n}A_{k}\nonumber\\ & \quad -\left[\frac{\psi'(\sum_{k=1}^{n}\varepsilon_k)}{\psi(\sum_{k=1}^{n}\varepsilon_k)}\right] \left[\frac{\tilde{r}_X(t)}{\theta}\right]\left[\frac{1-\psi(\varepsilon_i)}{\psi'(\varepsilon_i)}\right] \frac{d}{du}\left[\frac{(1-\psi(u))\log(1-\psi(u))}{\psi'(u)}\right]_{u=\varepsilon_i}, \end{align}where
$$A_{k}=\left[\frac{\tilde{r}_X(t)}{\theta\log{F(t)}} \left[\frac{(1-\psi(\varepsilon_{k}))\log(1-\psi(\varepsilon_{k}))}{\psi'(\varepsilon_{k})}\right]\right].$$Now, according to Lemma 2.1 and Theorem A.8 of [Reference Marshall, Olkin and Arnold14], to obtain the desired result, the following conditions need to be verified:
(i)
$S_2(\boldsymbol {\alpha })$ is symmetric and decreasing in $\boldsymbol {\alpha };$(ii) for
$i\neq j$,
(3.10)\begin{equation} (\alpha_i-\alpha_j)\left[\frac{\partial S_2(\boldsymbol{\alpha})}{\partial \alpha_i}-\frac{\partial S_2(\boldsymbol{\alpha})}{\partial \alpha_j}\right]\geq 0. \end{equation}
The first condition can be verified easily. To verify the second condition in (3.10), let us suppose 
$\alpha _i\leq \alpha _j,$ which implies 
$\log F^{\alpha _j}(t)\leq \log F^{\alpha _i}(t)\leq 0$ and 
$\varepsilon _i\geq \varepsilon _j$. Now, the decreasing property of 
$\psi '/\psi$ yields 
$[\psi '/\psi ]'\leq 0$. Moreover, from the assumptions made, 
${(1-\psi )}/{\psi '}$ is decreasing and 
${(1-\psi )\log (1-\psi )}/{\psi '}$ is convex, which yield
\begin{equation} \left[\frac{1-\psi(v)}{\psi'(v)}\right]_{v=\varepsilon_i}\leq \left[\frac{1-\psi(v)}{\psi'(v)}\right]_{v=\varepsilon_j}\leq 0 \end{equation}and
\begin{equation} \frac{d}{du}\left[\frac{(1-\psi(u))\log(1-\psi(u))}{\psi'(u)}\right]_{u=\varepsilon_i}\geq \frac{d}{du}\left[\frac{(1-\psi(u))\log(1-\psi(u))}{\psi'(u)}\right]_{u=\varepsilon_j}\geq 0, \end{equation}respectively. Upon using (3.11) and (3.12), we obtain the following inequalities:
\begin{equation} {-\log F(t)}\frac{1-\psi(\varepsilon_i)}{\psi'(\varepsilon_i)}\left[\frac{d}{dz}\left[\frac{\psi'(z)}{\psi(z)}\right]\right]_{z=\sum_{k=1}^{n}\varepsilon_k}\geq{-\log F(t)}\frac{1-\psi(\varepsilon_j)}{\psi'(\varepsilon_j)}\left[\frac{d}{dz}\left[\frac{\psi'(z)}{\psi(z)}\right]\right]_{z=\sum_{k=1}^{n}\varepsilon_k} \end{equation}and
\begin{align} & \left[\frac{1-\psi(\varepsilon_i)}{\psi'(\varepsilon_i)}\right]\frac{d}{du}\left[\frac{(1-\psi(u))\log(1-\psi(u))}{\psi'(u)}\right]_{u=\varepsilon_i}\nonumber\\ & \quad \leq\left[\frac{1-\psi(\varepsilon_j)}{\psi'(\varepsilon_j)}\right]\frac{d}{du}\left[\frac{(1-\psi(u))\log(1-\psi(u))}{\psi'(u)}\right]_{u=\varepsilon_j}. \end{align} Finally, by combining the inequalities in (3.13) and (3.14), the inequality in (3.10) is obtained. Now, for 
$\alpha _i\geq \alpha _j$, the proof is similar, and is therefore not provided.
Theorem 3.7 Suppose 
$\{X_{1},\ldots ,X_{n}\}$ 
$[\{Y_{1},\ldots ,Y_{n}\}]$ is a set of interdependent random variables such that, for 
$i\in \mathbb {I}_n,$ 
$X_{i}\sim F({(x-\lambda _{i})}/{\theta })$ 
$[Y_{i}\sim F({(x-\mu _{i})}/{\theta })]$ having an Archimedean survival copula with generator 
$\psi ,$ where 
$F$ is the baseline distribution function. Furthermore, let 
$\{L_{1},\ldots ,L_{n}\}$ 
$[\{L_{1}^{*},\ldots ,L_{n}^{*}\}]$ be a set of independent Bernoulli random variables, independently of 
$X_{i}$'s [
$Y_{i}$'s], with 
$E(L_{i})=p_{i}$ 
$[E(L_{i}^{*})=p_{i}^{*}]$, for 
$i\in \mathbb {I}_n$. Then,
$${\boldsymbol\lambda}\succeq^{m}{\boldsymbol\mu}\Rightarrow T_{1:n}\geq_{hr}T^{*}_{1:n},$$provided the following conditions are satisfied:
(i)
$\tilde {r}_X(w)$ is decreasing and concave, and $r_X(w)$ is decreasing;(ii)
$\psi$ is log-concave;(iii)
${(1-\psi )}/{\psi '}$ and ${[{(1-\psi )}/{\psi '}]'}({\psi }/{\psi '})$ are decreasing;(iv)
$\prod _{i=1}^{n}p^{*}_i\leq \prod _{i=1}^{n}p_i$.
Proof. To prove the hazard rate order between 
$T_{1:n}$ and 
$T_{1:n}^{*}$, it is sufficient to show that 
$X_{1:n}\geq _{hr} Y_{1:n}$ holds. The hazard rate function of 
$X_{1:n}$ is given by
\begin{equation} r_{X_{1:n}}(x)\overset{\textrm{def}}{=}S_1(\boldsymbol{\lambda})= \frac{\psi'(\sum_{k=1}^{n}\phi(\bar{F}(\frac{x-\lambda_k}{\theta})))} {\psi(\sum_{k=1}^{n}\phi(\bar{F}(\frac{x-\lambda_k}{\theta})))} \sum_{k=1}^{n}\left[\frac{1}{\theta}\tilde{r}_X\left(\frac{x-\lambda_k}{\theta}\right) \frac{1-\psi(\phi(\bar{F}(\frac{x-\lambda_k}{\theta})))}{\psi'(\phi(\bar{F}(\frac{x-\lambda_k}{\theta})))}\right]. \end{equation} The derivative of (3.15) with respect to 
$\lambda _i,$ for 
$i\in \mathbb {I}_n$, is given by
\begin{align} \frac{\partial S_1(\boldsymbol{\lambda})}{\partial \lambda_i}& ={\frac{1}{\theta} r_X(t_i)}\frac{d}{dz}\left[\frac{\psi'(z)}{\psi(z)}\right]\left[\frac{\psi(\varsigma_{i})}{\psi'(\varsigma_{i})}\right]\left[\sum_{k=1}^{n}\frac{1}{\theta}\tilde{r}_X\left(t_{k}\right)\frac{1-\psi(\varsigma_{k})}{\psi'(\varsigma_{k})}\right]\nonumber\\ & \quad +\left[\frac{1}{\theta}\tilde {r}_X(t_{i}){r}_X(t_{i})\right]\frac{\psi'(z)}{\psi(z)}\left[\left[\frac{{\psi}(v)}{{\psi}'(v)}\right]{\frac{d}{dv}\left[\frac{1-{\psi}(v)}{{\psi}'(v)}\right]}\right]_{v=\varsigma_{i}}\nonumber\\ & \quad -\frac{1}{\theta^{2}}\frac{d}{dw}[\tilde {r}_X(w)]_{w=t_i}\frac{1-\psi(\varsigma_i)}{{\psi'}(\varsigma_i)}\frac{\psi'(z)}{\psi(z)}, \end{align}where 
$z=\sum _{i=1}^{n}\varsigma _i$, 
$\varsigma _i=\phi (\bar {F}({(x-\lambda _i)}/{\theta }))$ and 
$t_i={(x-\lambda _i)}/{\theta }$. Due to Lemma 2.1, in order to prove the required result, the following conditions need to be verified:
(i)
$S_1(\boldsymbol {\lambda })$ is symmetric in $\boldsymbol {\lambda };$(ii) for
$i\neq j,$
(3.17)\begin{equation} (\lambda_i-\lambda_j)\left[\frac{\partial S_1(\boldsymbol{\lambda})}{\partial \lambda_i}-\frac{\partial S_1(\boldsymbol{\lambda})}{\partial \lambda_j}\right]\leq 0. \end{equation}
Clearly, 
$S_1(\boldsymbol {\lambda })$ is symmetric with respect to 
$\boldsymbol {\lambda }$. Then, to verify the second condition, let us assume 
$\lambda _i\geq \lambda _j,$ which implies 
$t_i\leq t_j$ and 
$\varsigma _i\leq \varsigma _j$. Observing the properties of 
$\tilde {r}_X(w)$ and 
$r_X(w)$, we can obtain
\begin{align} [{r}_X(w)]_{w=t_i}& \geq[{r}_X(w)]_{w=t_j}, \end{align}
\begin{align} [\tilde{r}_X(w)]_{w=t_i}& \geq[\tilde{r}_X(w)]_{w=t_j} \end{align}and
\begin{equation} \frac{d}{dw}[ \tilde{r}_X(w)]_{w=t_j}\leq\frac{d}{dw}[\tilde{r}_X(w)]_{w=t_i}\leq 0. \end{equation}Furthermore, from the assumptions made, we have
\begin{align} \left[\frac{\psi(v)}{{\psi}'(v)}\right]_{v=\varsigma_i}& \leq\left[\frac{\psi(v)}{{\psi}'(v)}\right]_{v=\varsigma_j}\leq 0, \end{align}
\begin{align} \left[\frac{1-\psi(v)}{{\psi}'(v)}\right]_{v=\varsigma_j}& \leq\left[\frac{1-\psi(v)}{{\psi}'(v)}\right]_{v=\varsigma_i}\leq 0 \end{align}and
\begin{equation} \left(\frac{\psi(v)}{\psi'(v)}{\frac{d}{dv}\left[\frac{1-\psi(v)}{\psi'(v)}\right]}\right)_{v=\varsigma_i}\geq \left(\frac{\psi(v)}{\psi'(v)}{\frac{d}{dv}\left[\frac{1-\psi(v)}{\psi'(v)}\right]}\right)_{v=\varsigma_j}\geq 0. \end{equation}Moreover, by using (3.18) and (3.21), we obtain the inequality
\begin{equation} {\frac{1}{\theta} r_X(t_i)}\left[\frac{\psi(\varsigma_{i})}{\psi'(\varsigma_{i})}\right] \frac{d}{dz}\left[\frac{\psi'(z)}{\psi(z)}\right] \geq {\frac{1}{\theta} r_X(t_j)}\left[\frac{\psi(\varsigma_{j})}{\psi'(\varsigma_{j})}\right]\frac{d}{dz}\left[\frac{\psi'(z)}{\psi(z)}\right]. \end{equation}On combining (3.18), (3.19) and (3.23), we obtain
\begin{align} & \left[\tilde {r}_X(t_{i}){r}_X(t_{i})\right]\left[\left[\frac{{\psi}(v)}{{\psi}'(v)}\right]{\frac{d}{dv}\left[\frac{1-{\psi}(v)}{{\psi}'(v)}\right]}\right]_{v=\varsigma_{i}}\nonumber\\ & \quad \geq\left[\tilde {r}_X(t_{j}){r}_X(t_{j})\right]\left[\left[\frac{{\psi}(v)}{{\psi}'(v)}\right]{\frac{d}{dv}\left[\frac{1-{\psi}(v)}{{\psi}'(v)}\right]}\right]_{v=\varsigma_{j}}. \end{align}Furthermore, from (3.20) and (3.22), we have
\begin{equation} -\frac{1}{\theta^{2}}\frac{d}{dw}\left[\tilde {r}_X(w)\right]_{w=t_i}\frac{1-\psi(\varsigma_i)}{{\psi}(\varsigma_i)}\frac{\psi'(z)}{\psi(z)}\leq{-}\frac{1}{\theta^{2}}\frac{d}{dw}\left[\tilde {r}_X(w)\right]_{w=t_j}\frac{1-\psi(\varsigma_j)}{{\psi}(\varsigma_j)}\frac{\psi'(z)}{\psi(z)}. \end{equation}Finally, combining Eqs. (3.24)–(3.26), the inequality in (3.17) is obtained. Hence, the theorem proved.
In the preceding result, the scale parameters are taken as same and scalar, and the next theorem regards the scale parameters to be the same but vector-valued. As the proof is similar to that of Theorem 3.7, it is not presented here for conciseness.
Theorem 3.8 Suppose 
$\{X_{1},\ldots ,X_{n}\}$ 
$[\{Y_{1},\ldots ,Y_{n}\}]$ is a set of interdependent random variables such that, for 
$i\in \mathbb {I}_n,$ 
$X_{i}\sim F({(x-\lambda _{i})}/{\theta _{i}})$ 
$[Y_{i}\sim F({(x-\mu _{i})}/{\theta _{i}})]$ having an Archimedean survival copula with generator 
$\psi ,$ where 
$F$ is the baseline distribution function. Furthermore, let 
$\{L_{1},\ldots ,L_{n}\}$ 
$[\{L_{1}^{*},\ldots ,L_{n}^{*}\}]$ be a set of independent Bernoulli random variables, independently of 
$X_{i}$'s [
$Y_{i}$'s], with 
$E(L_{i})=p_{i}$ 
$[E(L_{i}^{*})=p_{i}^{*}]$, for 
$i\in \mathbb {I}_n$. Moreover, let 
$\boldsymbol {\lambda }$, 
$\boldsymbol {\mu }$, 
$\boldsymbol {\theta }\in \mathcal {D}^{+}_{n}\ (\mathcal {E}^{+}_{n})$. Then,
$${\boldsymbol\lambda}\succeq^{m}{\boldsymbol\mu}\Rightarrow T_{1:n}\geq_{hr}T^{*}_{1:n},$$provided the following conditions hold:
(i)
$w\tilde {r}_X(w)$ and $wr_X(w)$ are decreasing, and $\tilde {r}_X(w)$ is concave;(ii)
$\psi$ is log-concave, ${(1-\psi )}/{\psi '}$ and $[{(1-\psi )}/{\psi '}]'({\psi }/{\psi '})$ are decreasing;(iii)
$\prod _{i=1}^{n}p^{*}_i\leq \prod _{i=1}^{n}p_i$.
As 
$(c_1,\ldots ,c_n)\succeq ^{m}(c,\ldots ,c)$ with 
$c=({1}/{n})\sum _{i=1}^{n}c_{i},$ the following corollary readily follows from Theorems 3.6–3.8.
Corollary 3.4 Under the assumptions in
(i) Theorem 3.6, let us take
$\beta _1=\cdots =\beta _n=\beta$. Then, $\beta =({1}/{n})\sum _{i=1}^{n}\alpha _i\Rightarrow T_{1:n}\le _{hr}T_{1:n}^{*}$;(ii) Theorems 3.7 and 3.8, let us take
$\mu _1=\cdots =\mu _n=\mu$. Then, $\mu =({1}/{n})\sum _{i=1}^{n}\lambda _i\Rightarrow T_{1:n}\ge _{hr}T_{1:n}^{*}$.
3.2. Based on a general survival copula
In this subsection, we assume that 
$\{X_{1},\ldots ,X_{n}\}$ and 
$\{Y_{1},\ldots ,Y_{n}\}$ are two heterogeneous sets of random variables of interdependent claims, wherein the claim amounts follow exponentiated location-scale distributions with survival copulas 
$\hat {C}_R$ and 
$\hat {C}^{*}_R$, respectively. Different comparison results are then developed based on the usual stochastic order. The next theorem presents the impact due to the degree of dependence on the comparison of smallest claim amounts in terms of the usual stochastic order when the location parameter vectors are ordered with respect to weakly supermajorization order.
Theorem 3.9 Suppose 
${X_1, \cdots X_n } \,\,{[\{Y_{1},\ldots ,Y_{n}\}]}$ is a set of interdependent random variables such that, for 
$i\in \mathbb {I}_n,$ 
$X_{i}\sim F^{\alpha }({(x-\lambda _{i})}/{\theta })$ 
$[Y_{i}\sim G^{\alpha }({(x-\mu _{i})}/{\theta })]$ with survival copula 
$\hat {C}_R$ 
$[\hat {C}^{*}_R]$, where 
$F\ [G]$ is the baseline distribution function and 
$\alpha \geq 1$. Furthermore, let 
$\{L_{1},\ldots ,L_{n}\}$ 
$[\{L_{1}^{*},\ldots ,L_{n}^{*}\}]$ be a set of independent Bernoulli random variables, independently of 
$X_{i}$'s [
$Y_{i}$'s], with 
$E(L_{i})=p_{i}$ 
$[E(L_{i}^{*})=p_{i}^{*}]$, 
$i\in \mathbb {I}_n$. Moreover, let 
$X\geq _{\textrm {st}}Y,$ 
$f(w)$ or 
$g(w)$ be increasing. Then,
$$\prod_{i=1}^{n}p^{*}_i\leq\prod_{i=1}^{n}p_i,\quad \boldsymbol{\lambda}\preceq^{w}\boldsymbol{\mu},\quad {\hat{C}^{*}_R\prec \hat{C}_R}\Rightarrow T^{*}_{1:n}\leq_{\textrm{st}} T_{1:n}.$$Proof. The reliability functions of 
$T_{1:n}$ and 
$T^{*}_{1:n}$ are, respectively, given by
$$\bar{F}_{T_{1:n}}(x)=\left[\prod_{i=1}^{n}p_{i}\right]{\hat{C}_R}(s(\alpha,\lambda_1,\theta,F),\ldots, s(\alpha,\lambda_n,\theta,F))$$and
$$\bar{F}_{T^{*}_{1:n}}(x)=\left[\prod_{i=1}^{n}p^{*}_{i}\right]{\hat{C}^{*}_R}(l(\alpha,\mu_1,\theta,G),\ldots, l(\alpha,\mu_n,\theta,G)),$$where 
$s(\alpha ,\lambda _i,\theta ,F)=1-F^{\alpha }({(x-\lambda _i)}/{\theta })$ and 
$l(\alpha ,\mu _i,\theta ,G)=1-G^{\alpha }({(x-\mu _i)}/{\theta })$, for 
$i\in \mathbb {I}_n$. From Lemma 2.6, we have
\begin{align} & \left[\prod_{i=1}^{n}p^{*}_{i}\right] {\hat{C}^{*}_R}(l(\alpha,\mu_1,\theta,G),\ldots,l(\alpha,\mu_n,\theta,G))\nonumber\\ & \quad \leq\left[\prod_{i=1}^{n}p^{*}_{i}\right] {\hat{C}_R}(s(\alpha,\mu_1,\theta,G),\ldots,s(\alpha,\mu_n,\theta,G)). \end{align} Furthermore, the increasing property of 
$\hat {C}_R$ and 
$X\geq _{\textrm {st}}Y$ yield
\begin{align} & \left[\prod_{i=1}^{n}p^{*}_{i}\right]{\hat{C}_R}(s(\alpha,\mu_1,\theta,G),\ldots,s(\alpha,\mu_n,\theta,G))\nonumber\\ & \quad \leq \left[\prod_{i=1}^{n}p^{*}_{i}\right] {\hat{C}_R}(s(\alpha,\mu_1,\theta,F),\ldots,s(\alpha,\mu_n,\theta,F)). \end{align}Thus, the required result will get established if the following inequality holds:
\begin{align} & \left[\prod_{i=1}^{n}p^{*}_{i}\right] {\hat{C}_R}(s(\alpha,\mu_1,\theta,F),\ldots,s(\alpha,\mu_n,\theta,F))\nonumber\\ & \quad \leq\left[\prod_{i=1}^{n}p_{i}\right] {\hat{C}_R}(s(\alpha,\lambda_1,\theta,F),\ldots,s(\alpha,\lambda_n,\theta,F)). \end{align}Now, for establishing the inequality in (3.29), according to Lemma 2.2 and Theorem A.8 of [Reference Marshall, Olkin and Arnold14], we need to show that
(i)
$-{\hat {C}_R}$ is decreasing and Schur-convex;(ii)
$s(\alpha ,\lambda ,\theta ,F)$ is increasing concave in $\lambda$;(iii)
$\prod _{i=1}^{n}p^{*}_{i}\leq \prod _{i=1}^{n}p_{i}$.
Under the assumptions made, the first and third conditions follow immediately from Lemma 2.4 and the increasing property of 
$\hat {C}_R$, while the second condition can be shown by Part(i) of Lemma 2.8. Hence, the theorem proved.
The following theorem provides another set of sufficient conditions, under which the usual stochastic order between the smallest claim amounts 
$T_{1:n}$ and 
$T^{*}_{1:n}$ holds. As the proof is similar to that of Theorem 3.9, it is omitted.
Theorem 3.10 Suppose 
$\{X_{1},\ldots ,X_{n}\}$ 
$[\{Y_{1},\ldots ,Y_{n}\}]$ is a set of nonnegative interdependent random variables such that, for 
$i\in \mathbb {I}_n,$ 
$X_{i}\sim F^{\alpha _i}({(x-\lambda )}/{\theta })$ 
$[Y_{i}\sim G^{\beta _i}({(x-\lambda )}/{\theta })]$ having survival copula 
$\hat {C}_R$ 
$[\hat {C}^{*}_R]$, where 
$F\ [G]$ is the baseline distribution function. Furthermore, let 
$\{L_{1},\ldots ,L_{n}\}$ 
$[\{L_{1}^{*},\ldots ,L_{n}^{*}\}]$ be a set of independent Bernoulli random variables, independently of 
$X_{i}$'s [
$Y_{i}$'s], with 
$E(L_{i})=p_{i}$ 
$[E(L_{i}^{*})=p_{i}^{*}]$, for 
$i\in \mathbb {I}_n$. Then,
$$\prod_{i=1}^{n}p^{*}_i\leq\prod_{i=1}^{n}p_i,\quad \boldsymbol{\alpha}\preceq^{w}\boldsymbol{\beta},\quad {\hat{C}^{*}_R}\prec {\hat{C}_R},\quad X\geq_{\textrm{st}}Y\Rightarrow T^{*}_{1:n}\leq_{\textrm{st}} T_{1:n}.$$The following theorem shows that, under some conditions, more heterogeneous (in the sense of weak supermajorization order) scale parameters produce a smaller minimum claim amount in the sense of the usual stochastic order.
Theorem 3.11 Suppose 
$\{X_{1},\ldots ,X_{n}\}$ 
$[\{Y_{1},\ldots ,Y_{n}\}]$ is a set of nonnegative interdependent random variables such that, for 
$i\in \mathbb {I}_n,$ 
$X_{i}\sim F^{\alpha }({(x-\lambda )}/{\theta _i})$ 
$[Y_{i}\sim G^{\alpha }({(x-\lambda )}/{\delta _i})]$ with survival copula 
$\hat {C}_R$ 
$[\hat {C}^{*}_R]$, where 
$F\ [G]$ is the baseline distribution function. Furthermore, let 
$\{L_{1},\ldots ,L_{n}\}$ 
$[\{L_{1}^{*},\ldots ,L_{n}^{*}\}]$ be a set of independent Bernoulli random variables, independently of 
$X_{i}$'s [
$Y_{i}$'s], with 
$E(L_{i})=p_{i}$ 
$[E(L_{i}^{*})=p_{i}^{*}]$, for 
$i\in \mathbb {I}_n$. Moreover, let 
$w^{2}\tilde {r}_X(w)$ or 
$w^{2}\tilde {r}_Y(w)$ be increasing. Then,
$$\prod_{i=1}^{n}p^{*}_i\leq\prod_{i=1}^{n}p_i,\quad \boldsymbol{\theta}\preceq^{w}\boldsymbol{\delta},\quad {\hat{C}^{*}_R\prec \hat{C}_R},\quad X\geq_{\textrm{st}}Y\Rightarrow T^{*}_{1:n}\leq_{\textrm{st}} T_{1:n}.$$ The following remark presents some survival copulas for which the condition 
$\hat {C}^{*}_R\prec \hat {C}_R$ in Theorems 3.9–3.11 is satisfied for 
$n=2$.
Remark 3.6
(i) Consider the Cuadras–Augé family of survival copulas
$\hat {C}_R(u,v)$ and $\hat {C}^{*}_R(u,v)$, such that for $a,b \in (0,1]$,
and$${\hat{C}^{*}_R(u,v)}=[\min(u,v)]^{a}[uv]^{1-a}=\begin{cases} uv^{1-a}, & u\leq v,\\ vu^{1-a}, & u\geq v, \end{cases}$$It can be verified that for$${\hat{C}_R(u,v)}=[\min(u,v)]^{b}[uv]^{1-b}=\begin{cases} uv^{1-b}, & u\leq v,\\ vu^{1-b}, & u\geq v. \end{cases}$$$0\leq a\leq b\leq 1$, $\hat {C}^{*}_R(u,v)\leq \hat {C}_R(u,v)$ (see Example 2.19 in [Reference Nelsen20]). Hence, $\hat {C}^{*}_R\prec \hat {C}_R;$(ii) Consider the Gumbel–Barnett survival copulas
$\hat {C}_R(u,v)$ and $\hat {C}^{*}_R(u,v)$, such that for $a,b\in (0,1],$
It is easy to observe that, for$${\hat{C}_R(u,v)}=uve^{{-}a\log u\log v}\quad \text{and}\quad {\hat{C}^{*}_R(u,v)}=uve^{{-}b\log u\log v}.$$$0\leq a\leq b\leq 1$, $\hat {C}^{*}_R(u,v)\leq \hat {C}_R(u,v)$, and hence $\hat {C}^{*}_R\prec \hat {C}_R$.
In the following result, lower and upper bounds of 
$\bar {F}_{T_{1:n}}(x)$ are presented. As the proof is similar to that of Theorem 3.6 of [Reference Nadeb, Torabi and Dolati17] and Theorem 3.11, it is omitted.
Theorem 3.12 Suppose 
$\{X_{1},\ldots ,X_{n}\}$ is a set of nonnegative interdependent random variables such that, for 
$i\in \mathbb {I}_n,$ 
$X_{i}\sim F^{\alpha }({(x-\lambda )}/{\theta _i})$ having survival copula 
$\hat {C}_R,$ where 
$F$ is the baseline distribution. Furthermore, let 
$\{L_{1},\ldots ,L_{n}\}$ be a set of independent Bernoulli random variables, independently of 
$X_{i}$'s, with 
$E(L_{i})=p_{i}$, for 
$i\in \mathbb {I}_n$. Moreover, let 
$w^{2}\tilde {r}_X(w)$ be increasing and 
$\hat {C}_R$ be Schur-concave. Then,
$$\left[\prod_{i=1}^{n}p_i\right]\delta_{\hat{C}_R}(s(\alpha,\lambda,\theta_{1:n},F))\leq \bar{F}_{T_{1:n}}(x)\leq\left[\prod_{i=1}^{n}p_i\right]\delta_{\hat{C}_R}(s(\alpha,\lambda,\bar{\theta},F)),$$where 
$\bar {\theta }=({1}/{n})\sum _{i=1}^{n}\theta _i$ and 
$\theta _{1:n}=\min \{\theta _1,\ldots ,\theta _n\}$.
The following theorems can all be proved by using the idea of Nadeb et al. [Reference Nadeb, Torabi and Dolati17] along with the results established here. So, their proofs are not presented for conciseness.
Theorem 3.13 Let 
$\hat {C}_R$ be PUOD, and let the assumptions of Theorem 3.12 hold. Then,
$$\left[\prod_{i=1}^{n}p_i\right][s(\alpha,\lambda,\theta_{1:n},F)]^{n}\leq\bar{F}_{T_{1:n}}(x) \leq\left[\prod_{i=1}^{n}p_i\right]s(\alpha,\lambda,\theta_{1:n},F).$$Theorem 3.14 Let 
$\{X_{1},\ldots ,X_{n}\}$ be a set of nonnegative interdependent random variables such that, for 
$i\in \mathbb {I}_n,$ 
$X_{i}\sim F^{\alpha }({(x-\lambda _i)}/{\theta })$ having survival copula 
$\hat {C}_R,$ where 
$F$ is the baseline distribution. Furthermore, let 
$\{L_{1},\ldots ,L_{n}\}$ be a set of independent Bernoulli random variables, independently of 
$X_{i}$'s, with 
$E(L_{i})=p_{i}$, for 
$i\in \mathbb {I}_n$. Moreover, let 
$f(w)$ be increasing and 
$\hat {C}_R$ be Schur-concave. Then,
$$\left[\prod_{i=1}^{n}p_i\right]\delta_{\hat{C}_R}(s(\alpha,\lambda_{1:n},\theta,F))\leq \bar{F}_{T_{1:n}}(x)\leq\left[\prod_{i=1}^{n}p_i\right]\delta_{\hat{C}_R}(s(\alpha,\bar{\lambda},\theta,F)),$$where 
$\bar {\lambda }=({1}/{n})\sum _{i=1}^{n}\lambda _i$ and 
$\lambda _{1:n}=\min \{\lambda _1,\ldots ,\lambda _n\}$.
Theorem 3.15 Let 
$\hat {C}_R$ be PUOD, and let the assumptions of Theorem 3.14 hold. Then,
$$\left[\prod_{i=1}^{n}p_i\right][s(\alpha,\lambda_{1:n},\theta,F)]^{n}\leq\bar{F}_{T_{1:n}}(x)\leq \left[\prod_{i=1}^{n}p_i\right]s(\alpha,\lambda_{1:n},\theta,F).$$Theorem 3.16 Let 
$\{X_{1},\ldots ,X_{n}\}$ be a set of nonnegative interdependent random variables such that, for 
$i\in \mathbb {I}_n,$ 
$X_{i}\sim F^{\alpha _i}({(x-\lambda )}/{\theta })$ having survival copula 
$\hat {C}_R,$ where 
$F$ is the baseline distribution. Furthermore, let 
$\{L_{1},\ldots ,L_{n}\}$ be a set of independent Bernoulli random variables, independently of 
$X_{i}$'s, with 
$E(L_{i})=p_{i}$, for 
$i\in \mathbb {I}_n$. Moreover, let 
$\hat {C}_R$ be Schur-concave. Then,
$$\left[\prod_{i=1}^{n}p_i\right]\delta_{\hat{C}_R}(s(\alpha_{1:n},\lambda,\theta,F))\leq \bar{F}_{T_{1:n}}(x)\leq\left[\prod_{i=1}^{n}p_i\right]\delta_{\hat{C}_R}(s(\bar{\alpha},\lambda,\theta,F)),$$where 
$\bar {\alpha }=({1}/{n})\sum _{i=1}^{n}\alpha _i$ and 
$\alpha _{1:n}=\min \{\alpha _{1},\ldots ,\alpha _n\}$.
Theorem 3.17 Let 
$\hat {C}_R$ be PUOD, and let the assumptions of Theorem 3.16 hold. Then,
$$\left[\prod_{i=1}^{n}p_i\right][s(\alpha_{1:n},\lambda,\theta,F)]^{n}\leq\bar{F}_{T_{1:n}}(x)\leq \left[\prod_{i=1}^{n}p_i\right]s(\alpha_{1:n},\lambda,\theta,F).$$4. Concluding remarks
Due to the close relationship between risk measures and stochastic orders, stochastic orderings of the smallest claim amounts play an important role in finance and insurance. As dependence between random variables is complicated to handle, many researchers have focused on independent and identically distributed random variables for the comparison of extreme claim amounts. However, in practice, this assumption may not be realistic. This paper develops several stochastic comparison results between the smallest claim amounts from two heterogeneous interdependent portfolios of risks, wherein the dependency is modeled by a copula. Two scenarios have been considered: The random variables are modeled by 
$({\rm i})$ an Archimedean survival copula and 
$({\rm ii})$ a general survival copula. When dependent claims are modeled by Archimedean survival copulas, under some conditions, the usual stochastic and hazard rate orders have been developed between the smallest claim amounts of two portfolios of risks. For the case of a general survival copula, the smallest claim amounts have been compared in terms of the usual stochastic order. Various examples and counterexamples have been presented for illustrating the established results. Finally, lower and upper bounds for the reliability functions of the smallest claim amounts have also been presented. It will be of further interest to investigate some variability orders in this setup. We are currently looking into this problem and hope to report the findings in a future paper.
Acknowledgments
The authors thank the Editor in Chief, an Associate Editor and two anonymous reviewers for their positive remarks and useful comments. Sangita Das thanks the MHRD, Government of India, for financial support. Suchandan Kayal acknowledges the partial financial support for this work under the grant MTR/2018/000350, SERB, India.
Conflicts of interest
The authors declared that there is no conflict of interest.
