In the Note published last year [1], bounds and monotonicity of shot-noise and max-shot-noise processes driven by spatial stationary Cox point processes are discussed in terms of some stochastic order. Although all the statements concerning the shot-noise processes remain valid, those concerning the max-shot-noise processes have to be corrected.

First, equations (7) and (9) in Theorem 1 (p. 566) should be replaced by

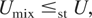
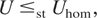
where ≤_st denotes the usual stochastic order; that is, (7) means E f (U_mix) ≤ E f (U) for all increasing f such that the expectations exist. The above (7) and (9) are now verified by checking E f (U) ≤ E f (U_mix) and E f (U_hom) ≤ E f (U), respectively, for any decreasing f.

To prove them, the second assertion in Lemma 1(i) (p. 563) should be replaced by the following: If

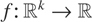
is supermodular [resp. decreasing], then

, defined by

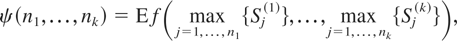
is supermodular [resp. decreasing and componentwise convex]⁽¹⁾; that is, if f is decreasing and supermodular, then ψ is decreasing and dcx (ddcx). Furthermore, the statement at the end of the proof of Theorem 1 (p. 567) should also be replaced by g(x₁,…,x_k) = f (max{x₁,…,x_k}) is decreasing and supermodular for any decreasing f.⁽²⁾ The proofs of ⁽¹⁾ and ⁽²⁾ are provided at the end of this Correction.

According to the above modification, we have along the same lines as in the proof of the article that

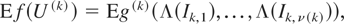
where g^(k) is now ddcx for any decreasing f (note that Lemma 1(ii) still holds even when idcx is replaced by ddcx). Hence, we can show (7) and (9), where the remaining steps in the proof are the same as in the article (note that Lemma 3 can be generalized such that “≤_idcx” is replaced by “≤_ism or “≤_dsm” and Lemma 4 can also be generalized such that “≤_icx” and “≤_idcx” are replaced by “≤_cx” and “≤_dcx” respectively).

On the other hand, in Corollary 1 (p. 569), it would be difficult to fix the statements concerning the Palm version of the max-shot-noise processes with this approach since g(x₀,x₁,…,x_k) = x₀ f (x₁,…,x_k) in the proof of Lemma 5 (p. 569) is no longer supermodular when f is decreasing.

Finally, the statement concerning the max-shot-noise processes in Theorem 2 (p. 570) should be replaced by the following: If

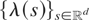
is ≤_ddcx-regular, then U_c is ≤_st-increasing in c (> 0).

Proof of ⁽¹⁾: Let f be supermodular. Then, for nonnegative integers c_i and c_j,

where X_i = max_l=1,…,ni{S_l⁽ⁱ⁾}, A_i = (max_{l=ni+1,…,ni+ci}{S_l⁽ⁱ⁾} − X_i)⁺ ≥ 0, and X_j and A_j are defined similarly.

Next, let f be decreasing. Then since

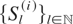
is a sequence of i.i.d. random variables, for nonnegative c_i and d_i,

where X_i = max_l=1,…,ni{S_l⁽ⁱ⁾} and

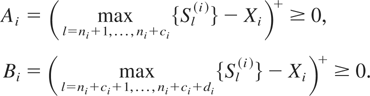
If A_i ≥ B_i, then (*) reduces to −E f (…,X_i + B_i,…) + E f (…,X_i,…) ≥ 0, and if A_i < B_i, then (*) reduces to −E f (…,X_i + A_i,…) + E f (…,X_i,…) ≥ 0 since f is decreasing.

Proof of ⁽²⁾: Let f be decreasing. Then, clearly g is decreasing. Now, for y_i and y_j ≥ 0,

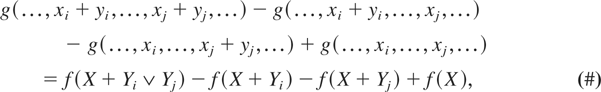
where X = max{…,x_i,…,x_j,…}, Y_i = (x_i + y_i − X)⁺, and Y_j = (x_j + y_j − X)⁺. If Y_i ≥ Y_j, then (#) reduces to −f (X + Y_j) + f (X) ≥ 0, and if Y_i < Y_j, then (#) reduces to −f (X + Y_i) + f (X) ≥ 0 since f is decreasing.