Introduction
In 2006, the Institute of Medicine published Hospital-Based Emergency Care: At the Breaking Point 1 stating that hospitals have limited ability to manage small-scale and, much less, large-scale disasters. Simultaneously, the Society for Academic Emergency Medicine established priorities for the study of surge,Reference Koenig and Kelen2 among which was the ability to predict maximal surge capacity.
Surge capacity is the maximum ability of a health care entity to deliver required resources to handle a significant increase in demand relative to baseline.Reference Kelen and McCarthy3 Components of surge capacity are recognized as staffing, supplies and equipment, beds, and management system.Reference Kelen and McCarthy3-Reference Barbisch6 Developing tools that accurately predict surge capacity will aid hospitals to more effectively prepare for and respond to mass-casualty incidents (MCI) and disasters.
Existing surge models in the published literature consist of a model developed by the Chicago Department of Public Health,7 the FluSurge model developed by the Centers for Disease Control and Prevention,8 and the Hospital Surge Model developed by the Agency for Healthcare Research and Quality (AHRQ).9 The Chicago model estimates the quantity of supplies and equipment required to take care of different numbers of mass casualties resulting from a number of different types of MCIs. The AHRQ model also accounts for staffing and bed requirements, given different MCI scenarios. Neither of these two models takes into account the baseline quantity of resources (beds, staffing, floor, and operative resources) available at a hospital at the time an MCI occurs, or resource utilization by non-MCI patients. The FluSurge model estimates the increase in demand for resources during an influenza pandemic, but is otherwise limited in its estimates of strains on institutional resources.
Burn care is often necessary across different types of MCIs, is highly specialized, and time- and resource-intensive in ways that challenge health care institutions with multiple layers of complexity. Therefore, a simulation model that can account for baseline patient flow and resource utilization while incorporating the effect of a large influx of patients from a burn MCI can serve as a powerful tool that can predict and help address bottlenecks resulting from insufficient resources, before they occur.
The burn model that resulted from this research can serve as an example of a real-time estimation tool for hospital capacity in the setting of MCIs. Ultimately the model can supply decision support for disaster management. Insights from a surge analysis of this type may be applicable across a variety of MCI scenarios.
Methods
Model
Using the simulation software ProModel, version 7.5 (ProModel Corporation, Orem, UT),10 the researchers constructed a mixed model (Markov-Monte Carlo) to estimate the time to bottleneck for different resources required to respond to an MCI involving victims with burns, inhalation injury, or both (Figure 1). The model begins upon arrival of the first casualty to the hospital. Time to bottleneck is defined as the point in time, after the arrival of the first casualty, that a given resource reaches insufficient amounts for further patient care. The analytic horizon for this model is 14 days.

Figure 1 Decision-Analytic Model of Hospital Care Patterns for Patients Brought to a Large Hospital Following a Mass-Casualty Incident
Model inputs include number of mass casualties; inter-arrival time of patients to the hospital; probability distribution for patient age, weight, percent total body surface area (%TBSA) and depth of burns; hospital occupancy; staffing; and floor and operating room resources available beyond average daily hospital use. The model is constructed to predict hospital surge capacity under the worse case scenario; hence, base-case estimates are set to equal the average minimum available resources at the hospital for several parameters.
The model incorporates internal hospital data for resources, where available. Otherwise, input estimates reflect data from either the National Burn Repository (NBR), burn literature, disaster literature, or expert opinion (Table 1). NBR data includes information regarding burn size, hospital length of stay, presence of inhalation injury, and mortality for approximately 1,800 burn cases for the years 2000-2009. University of Michigan Institutional Review Board approval was granted for the study.
Table 1 Base-Case Estimates and Range for Sensitivity Analyses

Abbreviations: ICU, intensive care unit; IHD, internal hospital data; MCI, mass-casualty incident; NA, not applicable; NBR, National Burn Repository; PRBC, packed red blood cells.
aThe unit for this item is the smallest unit of use.
Model outputs include time to bottleneck for hospital beds, floor and operating room resources, and staff utilization. In addition, the researchers estimated the average waiting time in queue for mass casualties to acquire a hospital bed with different size MCIs and patient inter-arrival rates.
Recent burn MCIs typically have produced between 100 and 250 casualties.Reference Welling, Van Harten and Patka11-Reference Ma, Wei and Xia13 The base-case analysis was conducted with the assumption of 100 mass casualties and with resource-availability set at the base-case estimate for all parameters.
Input Assumptions: Central Variables
Age Distribution
The age distribution of mass casualties is based upon the year 2000 US Census data.14 The average age and standard deviation was calculated for the US population age 15 and older and used in the model with the assumption of a normal distribution.
Inter-arrival Rate
Base-case inter-arrival rate of mass casualties to the hospital is assumed to be one patient every three minutes. This rate is based upon a model developed by other authorsReference Christie and Levary15 that simulates the inter-arrival rate of patients from a mass-casualty incident to three different hospitals in a large metropolitan city, given different mass-casualty incident scenarios. In this study, the model demonstrated that patients start experiencing clinically inappropriate average waiting times in queue for inter-arrival rates of three minutes or less. An incident occurring within the proximity of the receiving hospitals would translate into shorter inter-arrival time for casualties, hence less time for hospitals to prepare for receiving casualties and consistent with the intention to design a model to simulate the worse case scenario.
Latest Hospital Arrival Time
Reports from recent MCIs, which occurred in large urban areas, indicate that all transports to the main receiving hospitals were completed in 4-6 hours from the time of the incident. Consistent with the intention to model the worst-case scenario, the model assumes that casualties may arrive up to 24 hours after the incident.
Input Assumptions: Triage and Inpatient Disposition
Triage
The model assumes that triage begins at the site of the MCI and also takes place upon arrival of mass casualties to the hospital. Both approaches have been used in responding to recent mass-casualty incidents and are supported by the State of Michigan's burn disaster plan.Reference de Ceballos, Turégano-Fuentes, Perez-Diaz, Sanz-Sanchez, Martin-Llorente and Guerrero-Sanz16, 17
Distribution of Inhalation Injuries, Depth of Burns, and %TBSA Burns
Among mass casualties, the probabilities of a pure inhalation injury, and an inhalation injury with different %TBSA burns, were based upon the NBR data.18 Based upon historical data reported in the literature,Reference Cassuto and Tarnow19 the model assumes that 2% of mass casualties will have no burns, 24.5% will have second-degree burns, and 73.5% will have third-degree burns. The distribution of %TBSA burns is different for indoor vs. outdoor fires. The size of burns resulting from indoor fires generally has a bimodal %TBSA distribution, with one peak between zero and 30 and another for greater than 80 %TBSA burns. Outdoor fires produce a burn size distribution that is negatively skewed toward burns between zero and 30 %TBSA.Reference Mackie and Koning20 The expected distribution of burn sizes from indoor vs. outdoor fires indicates that an MCI resulting from an indoor fire is likely to be more resource intensive, and is therefore set as the model's base-case scenario.
Admission Criteria
American Burn Association guidelines for patient referral to burn centers21 were used along with expert opinion to construct an algorithm that determines which category of patients presenting from the MCI will be admitted vs. discharged. All patients with partial-thickness burns 30% or greater TBSA, or full-thickness burns with 10% or greater TBSA, and all those with inhalation injuries are admitted. All other patients are assumed to be discharged.
The following guidelines for inpatient disposition were formulated based upon expert recommendations:
Partial-thickness burn: %TBSA burn + age ≥ 75 →Admit to ICU; if <75 admit to floor.
Full-thickness burn: 2 X %TBSA burn + age ≥75→Admit to ICU; if <75 admit to floor.
Input Assumptions: Space Utilization
The research hospital has many different wards and intensive care units. This model assumes that hospital space available to the casualties is restricted to the “surgical space,” which includes the trauma/burn intensive care unit (10 beds), surgery ward (64 beds), the surgical step-down unit (6 beds), and operating rooms (OR, 50).
Baseline Occupancy
The ICU has an average daily occupancy of 82%. The surgery ward has an average daily occupancy of 88%. The surgical step-down unit has a highly variable occupancy, depending upon the day of the week. The average daily occupancy for ICU and surgical floor, and 100% occupancy for the surgical step-down unit, are used as base-case estimates.
Early Discharge of Hospital Patients to Make Beds Available
The model assumes that patients already in the ICU require an ICU bed and neither can be transferred out of the ICU nor discharged home. It is also assumed that some of the patients on the surgical ward who were admitted prior to the MCI will qualify for early discharge. The literature indicates that up to 20% of inpatients are able to be discharged within a few hours of the onset of an MCI.Reference Hick, Hanfling and Burstein22 Data from the hospital indicate that the shortest time from entering a discharge order to actual patient discharge is approximately 30 minutes (average of 3 hours). Based upon this information, the base-case estimates for the percentage of surgical ward patients who qualify for early discharge and the time required to discharge were set at 20% and 2 hours, respectively.
Transfer of Patients Between Defined Spaces Within the Hospital
At the start of the model, all six surgical step-down beds are assumed to be occupied. It is also assumed that all these patients are appropriate for transfer to the surgery ward. Based upon internal hospital data, the shortest transfer time between units is 30 minutes, which was taken as the base-case estimate for patient transfer time from the surgical step-down unit to the ward. Therefore, 30 minutes from the start of the model all six patients in the surgical step-down unit have been transferred to the ward.
Conversion of the Surgical Step-Down Unit to an ICU
It was assumed that 30 minutes from the start of the model all six beds in the surgical step-down unit have been converted to ICU beds. This method of creating additional ICU capacity has been advocated in the surge literature.Reference Rubinson, Hick and Curtis23
Operating Rooms
In the model it is assumed that previously scheduled, elective operations at the hospital will be cancelled in the setting of a large MCI. This method of creating surge capacity with respect to operating rooms and hospital beds is supported in the literature.Reference Barbisch, Haik, Tessone and Hanfling24 Arbitrarily in the model, 10 operating rooms are reserved for emergent cases for non-MCI patients who remain in the facility after the MCI occurs. The remaining 40 operating rooms at the hospital are assumed to be at the disposal of the patients from the MCI.
Input Assumptions: Flow Logic
Days 1-3
Data from the burn repository were used to estimate mortality from different size burns and inhalation injury, and discharge rates for patients with hospital length of stays of one, two, and three days. These estimations were incorporated in the model, reflecting a 10% decrease in the number of patients hospitalized from the MCI during this time interval. Based upon the paradigm of burn surgery, patients with burns are not operated upon until three days after the initial injury.
Days 4-8
Patients from the MCI who require surgery will be operated upon between days 4-8. The number of surgeries that different size burns require has been estimated from the hospital operative reports and reflected in the model. Based upon burn repository data, approximately 5% of MCI patients would be expected to leave the system during this time period.
Days 9-14
Data from the burn repository were used to estimate mortality from different size burns, and to estimate inhalation injury and discharge rates for patients with hospital length of stays of 9-14 days. These estimations were incorporated in the model, reflecting a 5% decrease in the total number of patients hospitalized from the MCI during days 9-14. Based upon the paradigm of burn surgery, patients who require further surgery for their burns will typically not be operated upon until one week after their initial operations. Therefore, in this model no patients from the MCI are operated upon from days 9-14.
Input Assumptions: Floor and Operating Room Resource Utilization
General Logic
To design a model for the worst-case scenario, it was assumed that the MCI occurs at a time when the stores of all the floor and operating room resources are at the minimum levels allowed at the hospital. Hence, all base-case estimates for these items have been set to equal the minimum levels stored.
Data were collected from operative reports at the hospital in order to estimate resource usage for surgery based upon %TBSA burns. The probability distribution for utilization of some of the operative resources was based upon this data. Not every resource included in this model was required during every operation. For most items, usage was weakly correlated with %TBSA burns, demonstrating significant variability in resource utilization. In these cases, expert opinion was used to estimate the amount of operative resources required for different size burns.
Patients with burns are assumed to undergo once daily dressing changes in this model. Therefore, on each day of hospitalization each patient will use one set of resources required for dressing changes depending upon the size of their burns. Patients will utilize a set of resources required for the surgical management of their burns every time they go to the operating room.
Specific Resources
Ventilators: The percentage of patients likely to present with inhalation injury was estimated from the burn repository and incorporated in the model. If a patient is admitted with an inhalation injury they are assumed to require a ventilator for the duration of their hospitalization.
Intravenous fluids: In this model, the Parkland formula was used to predict the volume of Lactated Ringer's solution required in the first 24 hours for the resuscitation of second- and third-degree burns. The formula calls for 4 ml/kg/%TBSA burn.Reference Tricklebank25 Data from the Centers for Disease Control and Prevention on the average and standard deviations for the weight of adults in the United States were used to reflect the distribution of the weight of the mass casualties.26 Other fluid requirements, including resuscitation and the need for maintenance fluids beyond 24 hours, are not accounted for in the model.
Blood products: The distribution of the blood types of the mass casualties is assumed to reflect the general distribution of blood types in the United States.27 The base-case estimate for the number of units of each blood type available at the hospital at the time of the MCI is set at the minimum levels stored at the blood bank.
Albumin: Albumin is used for the resuscitation of difficult-to-resuscitate burn patients; as such, not all casualties will require this resource. According to expert opinion, %TBSA burned does not consistently predict whether a burn patient will require albumin for resuscitation. This model uses the average albumin utilization for burn patients at the research institution to estimate albumin requirements for the casualties where approximately 30% of burn patients are administered an average of 10L of Albumin. For technical simplicity, it was assumed in the model that 100% of the casualties have a 3L albumin requirement.
Input Assumptions: Staff Utilization
Nursing Staff
The ideal nurse-to-patient ratio required for burn care is between 1:1 and 1:2.Reference Huckfeldt28 The base-case estimate for the model assumes that the total number of nurses available is that of a typical shift at the hospital, with a nurse-to-patient ratio of 1:2.
Respiratory Therapists
All patients with inhalation injury are assumed to be on a ventilator and will require a respiratory therapist. In this model the base-case estimate reflects the usual number of respiratory therapists available on a given shift at the hospital, with the usual ratio of respiratory therapist-to-patients at the hospital of 1:5.
Physician Staff
The base-case estimate for physician availability for patient care in the ICU and surgical ward reflects the number of chief residents available at the hospital (including fourth- and fifth-year general surgery residents and surgical, critical-care fellows). The base-case estimate for physician-to-patient ratio reflects the usual daily resident-to-patient ratio at the hospital of approximately 3:50.
Input Assumptions: Sensitivity Analyses
In order to assess whether the model outputs are sensitive to baseline assumptions, sensitivity analyses were conducted across the ranges of parameter values listed in Table 1. A one-way sensitivity analysis was conducted with the amount of each resource kept constant at its base-case estimate while varying the number of mass casualties between 10 and 100. Another set of one-way sensitivity analyses were conducted with the number of mass casualties kept constant at the base-case estimate of 100 while varying each resource across the range for its respective sensitivity analysis. A two-way sensitivity analysis was performed, based upon the results of the one-way sensitivity analysis, on two parameters that were noted to be fundamental in determining the time to bottleneck for different resources; namely, number of mass casualties and the inter-arrival rate of mass casualties to the hospital.
For both of the one-way sensitivity analyses, two MCI scenarios were considered—one resulting from an indoor fire and one from an outdoor fire. The expected distribution of the size of burns resulting from an indoor fire is wider than the distribution from an outdoor fire. Therefore, the model was first run with the assumption of the MCI occurring indoors. Items that produced a bottleneck using the indoor fire scenario were then used to carry out a second analysis with the assumption of an outdoor fire.
Results
Base-Case Analysis
Out of the 100 casualties who present from the MCI, the hospital with 59 surgical beds will be able to admit a total of 21 patients. The limiting factor, apparent within 120 minutes after arrival of the first casualty to the hospital, is that there are a maximum of eight intensive care unit beds and 13 surgery ward beds expected to be available to these mass casualties.
The number of admitted casualties, in turn, determines the utilization of all other resources. The base-case analysis was run with the assumption of the MCI resulting from an indoor fire, with the expected distribution of burn sizes resulting from this type of fire. The following items precipitate a bottleneck: Lactated Ringer's solution, silver sulfadiazine (Silvadene), gauze bandage rolls (Kerlix), bismuth tribromophenate (Xeroform), silver dressing (Acticoat), albumin, and thrombin topical. The minimum amount of each resource remaining, after use by mass casualties, and the time to each bottleneck for limiting resources are listed in Table 2. The amount of each resource required to relieve bottlenecks is indicated by negative numbers in this table.
Table 2 Base-Case Analysis Results

aNegative values imply the amount by which a resource is deficient.
bThe unit for this item is the smallest unit of use.
Abbreviations: ICU, intensive care unit; NA indicates not applicable; PRBC, packed red blood cells.
Ventilators, foams, staplers, antimicrobial non-adherent dressing (Telfa), epinephrine, and packed red blood cells do not induce a bottleneck. Moreover, nursing, respiratory therapist, and physician staffing do not induce bottleneck effects.
One-Way Sensitivity Analyses
Varying the Number of Mass Casualties
A one-way sensitivity analysis was conducted by varying the number of mass casualties between 10 and 100, while keeping the amount of each resource constant at the respective base-case estimate. This analysis was conducted once with the assumption of an MCI resulting from an outdoor fire and once with the assumption of an MCI resulting from an indoor fire.
Results of the analysis for the outdoor fire scenario indicate that thrombin topical is the most limited resource, with insufficient supplies for fewer than 10 mass casualties, followed by albumin, silver sulfadiazine (Silvadene), and type AB packed red blood cells. The respective bottlenecks for 10 vs. 20 mass casualties are reported in Table 3, for an outdoor fire, and in Table 4, for an indoor fire. As with an MCI resulting from an outdoor fire, thrombin topical is the most limited resource for an indoor fire-provoked MCI (Table 4). Additional resources that precipitate a bottleneck for the indoor fire scenario are Lactated Ringer's solution, gauze bandage rolls (Kerlix), bismuth tribromophenate (Xeroform), and silver dressing (Acticoat). Based upon these results, an indoor fire will result in a greater total number of bottlenecks and an earlier time to bottleneck for items that are limited for both scenarios. Nursing, respiratory therapist, and physician staffing do not induce bottleneck effects.
Table 3 Variation in Bottleneck Times for Key Floor and Operating Room Resources for an Outdoor Burn Mass-Casualty Incident for 10 vs 20 Mass Casualties

aPrimarily used in the operating room.
Abbreviations: LR, Lactated Ringer's solution; NB, no bottleneck; PRBC(AB), packed red blood cells type AB.
Table 4 Variation in Bottleneck Times for Key Floor and Operating Room Resources for an Indoor Burn Mass-Casualty Incident for 10 vs. 20 Mass Casualties

aPrimarily used in the operating room.
Abbreviations: LR, Lactated Ringer's solution; NB, no bottleneck; PRBC(AB), packed red blood cells type AB.
Varying Resource Availability
Another set of one-way sensitivity analyses were conducted by varying each resource across the range of expected availability, while keeping the number of mass casualties at the base-case estimate (de facto number of patients = 21). For floor and operating room resource utilization, the researchers compared the results of a one-way sensitivity analysis for an MCI resulting from an indoor fire vs. an MCI resulting from an outdoor fire (Figure 2). Bottlenecks identified for each scenario correspond with those noted in the one-way sensitivity analysis described above. An indoor fire results in a greater number of bottlenecks and a shorter time to bottleneck for items that are limited in both scenarios. Nursing, respiratory therapist, and physician staffing do not induce bottleneck effects.

Figure 2 Results of a One-Way Sensitivity Analysis Comparing Time to Bottleneck for Limiting Resources for Indoor (I) vs. Outdoor (O) Fire Scenarios. Time to bottleneck (in days) is estimated from the time of arrival of the first casualty to the hospital. Number of casualties admitted to the hospital is assumed to be 21, based upon the number of available beds. Resources are varied across the range of their availability.
Two-way Sensitivity Analysis
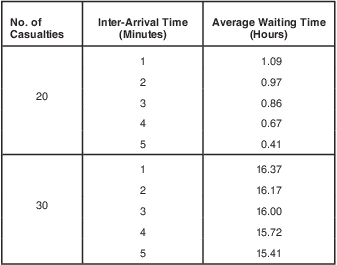
A two-way sensitivity analysis was conducted by varying the number of mass casualties and the inter-arrival rate of mass casualties, to the hospital, concurrently. Among the outputs from this analysis is the average waiting time between arrival of mass casualties to the hospital and the availability of hospital beds. In reality, patients will likely be waiting in the emergency department (ED) to acquire a hospital bed. Therefore, the average waiting time to availability of a hospital bed can be taken as the average ED waiting time. As expected, ED waiting time increases as the inter-arrival rate of patients to the hospital decreases (Table 5).
Table 5 Average Waiting Time from Arrival of Casualties to the Hospital to Availability of Hospital Beds
Discussion
This study analyzes the influence of institutions’ resource, space, and staffing capacity at the time of a burn mass-casualty incident. The study illustrates that a large academic medical center will be quickly constrained in its response by available beds, silver sulfadiazine (Silvadene), albumin, thrombin topical, and type AB packed red blood cells—but not by staff, operating rooms, or many other resources. These items present constraints across the full range of their availability, even if the hospital has maximum stores of each of these items available at the time the MCI occurs.
The model was designed to evaluate resource utilization under the worst-case scenario. Hence, for the base-case analysis, it was assumed that the hospital is at high occupancy at the time of the MCI. In addition, this study assumes that the space available to mass casualties is restricted to the hospital's burn ICU, surgical step-down, and general surgery ward. If other areas of the hospital are recruited, more beds would be available and a greater number of mass casualties would be accommodated. Nevertheless, it was anticipated that a greater number of mass casualties would create additional bottlenecks and shorten the times to bottleneck for the limited burn care and surgical resources identified with this model.
Three findings of note from this new simulation model are generalizable to other (ie, non-exclusively burn-provoked) MCIs. First, a large medical center operating at high occupancy rates (like many hospitals today) will quickly exhaust its capacity to respond to an MCI, accommodating fewer casualties than might be anticipated. This does not mean that hospitals should attempt to operate at lower occupancy rates, because that is not feasible in today's health care economic climate. Rather, the results from this model strongly underscore the imperative for cooperation among hospitals in preparing for and executing a coordinated response to MCIs.
Second, based upon the assumptions of the model, staffing is not a limitation for response to the MCI. This finding is largely because of limitations in beds, restricting to 21 the number of admitted casualties. It is important to note that, if space is not a limiting factor, nurse staffing will induce a bottleneck at about 40 casualties. However, if altered standards of care are instituted in accordance with Michigan's burn disaster plan, a nurse-to-patient ratio of 1:4 will avert this bottleneck. It is not economically advisable for medical facilities to maintain health care provider staffing at levels required to meet maximal demand at all times.Reference Kelen and McCarthy3 On the other hand, studies that have looked at the likelihood of health care providers presenting to work during MCIs and disasters have raised more concerns regarding the ability to meet staffing needs during these periods. One study conducted in Maryland showed that up to 50% of nurses would not make themselves available for duty if a pandemic were to occur.Reference Barnett, Balicer and Thompson29 Another study conducted by the Hawaii Department of Health showed that physicians and nurses have variable attitudes regarding working in makeshift hospitals in the setting of disasters.Reference Lanzilotti, Galanis, Leoni and Craig30 Methods of meeting an increase in demand for health care providers in the setting of MCIs by optimizing the use of existing staff have been advocated by AHRQ.Reference Phillips and Knebel31, 32 Access to a model that accounts for baseline staffing availability, and that allows for identification of the number of mass casualties for which altered standards of care will have to be instituted, with respect to patient-to-healthcare provider ratios, is invaluable in the acute phase of an MCI.
Third, because the beds present a bottleneck so early in MCI response, supply shortages are not as great a challenge as they might be otherwise. Rather, once a hospital knows the volume and type of casualties it has accommodated, it can order supplies that it anticipates will be in shortage soon. This is a critically preferable alternative for hospitals, instead of keeping enough supplies on hand at all times in the event of an MCI.
The Metropolitan Medical Response System (MMRS), an emergency preparedness and response system used in many metropolitan regions in the United States,33 and a related model, the Seamless Emergency Medical Logistics Expansion System (SEMLES), are used to coordinate and integrate local operations and optimize surge capacity in the wake of an MCI or disaster. The first step advocated by SEMLES, in optimization of overall local surge capacity, is optimizing individual health care facility capacity.34 Models such as the one presented here may be used by individual medical facilities to assess their internal surge capacity and needs for outside local, state, or federal aid.
Assessment of bed capacity for individual medical facilities during an MCI is a high priority. Bed availability determines the number of casualties a given hospital is able to absorb, and highlights the need for providing care to patients in alternate and/or unconventional settings such as shuttered hospitals, non-medical buildings, and mobile hospitals.5, 35 This and similar models can aid individual hospitals in the rapid assessment of bed availability, after accounting for baseline hospital occupancy and the unique characteristics of patient flow at each participating hospital. This assessment can be used to guide decisions regarding expanding patient care areas (eg, opening up typical medical wards to surgical patients) within a hospital, transferring patients to other medical facilities, and/or signal the need for mobile medical facilities.
The Joint Commission on Accreditation of Healthcare Organizations requires that hospitals unable to sustain a surge for 96 hours transfer patients to other facilities.36 The ability to identify limiting resources and predict the time to bottleneck allows hospitals to address these bottlenecks before they occur, or make the determination that patients will need to be transferred to other facilities for definitive care. A model that identifies limiting resources, after accounting for baseline resource availability at a given hospital, can be used as a real-time estimation tool for resource requirement in the setting of MCIs. This approach may help avoid the cost of keeping extra stockpiles of materials at medical facilities in anticipation of an ultimately unlikely event.
Data from the University Hospital of the University of Michigan Health System, the National Burn Repository, and empirical data from the literature largely represent the input assumptions of the model. In very few instances did the researchers resort to expert opinion for the input assumptions. Although the input parameters for this model are based primarily upon data from the University Hospital, institution-specific data can be entered into the model to predict resource utilization at any hospital, academic or community. The time to bottleneck will vary based upon each institution's resource availability and flow parameters, however the order of bottlenecks will likely be similar across different institutions for a similar size burn MCI. The researchers plan to incorporate data from other burn centers in the state of Michigan into the current model in order to assess surge capacity for each hospital. Knowing the burn surge capacity for each burn center will allow the assessment of the state's comprehensive burn surge capacity and guide the state Burn Coordinating Center in the management of a burn MCI. Findings from this model have been used to guide state policy regarding hospital preparedness for burn mass casualties. Modifications to the current model will allow application to the pediatric population, and other types of MCIs and disasters.
Limitations
This model is designed to address resource utilization for mass casualties with burns and/or inhalation injuries. Resource utilization for emergent escharotomies, fasciotomies, and traumatic injuries are not included here. Traumatic injuries likely will require surgery immediately, as opposed to delayed surgery for grafting burns, and consequently bottlenecks for operative resources likely will occur earlier. Future iterations of the current model will take mass casualties with mixed burns and traumatic injuries into account.
The average age and standard deviations for the US population were used to predict the likely age distribution of casualties. Clearly, if an incident occurs in a nightclub or nursing home, the age distribution of casualties likely will be skewed in favor of the young or old, respectively. An incident producing older casualties likely will result in a greater number of individuals requiring high-acuity care. Simple modifications to age distribution assumptions in the current model can help predict resource utilization for MCIs primarily affecting young vs. an older population.
The input parameters for hospital length of stay and mortality per %TBSA burns were based upon data from the NBR. The NBR does not distinguish between data for burn patients from MCIs vs. smaller incidents and those involving individuals. It is possible that the volume of casualties from a burn MCI may affect the quality of care that individual burn patients receive during their hospitalization impacting outcomes. Whether or not hospital length of stay and mortality is different for individual burn patients, compared with casualties hospitalized from a MCI, is a compelling matter that deserves further inquiry. The researchers were not able to identify a more robust set of data than the NBR with information about hospital length of stay, mortality, and %TBSA burns for individual burn patients.
Depending upon the type of MCI, some, or all, mass casualties will start receiving care in the emergency department as they await hospital beds. The current model does not account for patient flow and bottlenecks attributable to the emergency department. Other models have been developed looking at patient flow and resource utilization in emergency departments.Reference McCarthy, Zeger, Ding, Aronsky, Hoot and Kelen37, Reference Schweigler, Desmond, McCarthy, Bukowski, Ionides and Younger38 Using such models in tandem with the current model will help facilitate even more detailed forecasting of hospital resource utilization during MCIs.
As with any simulation, the model ultimately reflects the precision of its input parameters. Although hospitals’ available beds and resources necessarily will differ across institutions, this model and the sensitivity analyses illustrate the most critical components of institutional response that will be stressed with any MCI.
This project has modeled a hypothetical scenario, with multiple uncertainties, using best available information from the published literature; historical institutional and National Burn Repository data; and expert opinion. The next step will involve validating this model using information from recent, similar burn MCIs such as the Rhode Island Station Night Club fire where similar numbers of casualties were admitted to Kent County and Rhode Island hospitals.
Conclusion
Experts in the field of disaster medicine have called for modeling surge capacity in a way that accounts for all the vital aspects of surge in a balanced manner.Reference Barbisch, Haik, Tessone and Hanfling24 Space, resources, staff, and management system—the four widely accepted components of surge capacityReference Kelen and McCarthy3—are all included in this model. Outputs from this model can help address the management component of surge capacity. Prediction of average waiting time to admission can help guide management decisions regarding transferring patients to other medical facilities if waiting times are unacceptably long. Designing models tailored to specific institutions, as opposed to one-size-fits-all models, can help more accurately determine individual institutional surge capacity.









