I. INTRODUCTION
In recent years I have been studying the occurrence of crystalline hydrates with the general formula M2+XO4·nH2O that form at low temperatures (at or below the freezing point of ice) with n in the range 7–11. This work is motivated principally by an interest in “planetary” cryohydrates such as MgSO4·11H2O. This substance occurs naturally on Earth as the mineral meridianiite, being found in glacial and periglacial environments (Genceli et al., Reference Genceli, Shinochirou, Yoshinori, Toshimitsu, Hondoh, Kawamura and Witkamp2009) and in a limited number of MgSO4-rich hypersaline lakes during the winter months (Peterson et al., Reference Peterson, Nelson, Madu and Shurvell2007). However, meridianiite may occur globally on Mars, forming a substantial reservoir of bound water in the near-surface regolith (Peterson and Wang, Reference Peterson and Wang2006), and it may also be an important rock-forming mineral inside the icy Galilean moons of Jupiter (Kargel, Reference Kargel1991).
In a series of papers, my colleagues and I reported the results of work to form structural analogues of MgSO4·11H2O in which the cation was replaced by Mn2+, Fe2+, Co2+, Ni2+, Cu2+ or Zn2+ (Fortes et al., Reference Fortes, Browning and Wood2012a, Reference Fortes, Browning and Wood2012b) and the oxyanion was replaced by CrO4 2− (Fortes and Wood, Reference Fortes and Wood2012; Fortes et al., Reference Fortes, Wood and Gutmann2013). These efforts provide information on the response of the structure to chemically induced “internal” stress that are complementary to other means of generating strain in the crystal, such as variable temperature and pressure (cf., Fortes et al., Reference Fortes, Wood and Knight2008, Reference Fortes, Wood and Tucker2009, Reference Fortes, Wood and Fernandez-Alonso2012c). It was determined that only Mg2+ formed an end-member 11-hydrate, although there were some examples of considerable substitution for Mg2+ in the 11-hydrate structure (>50 mol. % by Co2+ and Mn2+ for example). Conversely, it was found that a complete solid solution is possible between 11-hydrate end-members of MgSO4 and MgCrO4. The most surprising discovery was of a new hydration state: crystals containing nine water molecules per formula unit, were obtained from aqueous solutions of (Mg,Ni)SO4, (Mg,Zn)SO4, (Mg,Fe)SO4, and (Mg,Cu)SO4 by rapid quenching in liquid nitrogen. In subsequent work it has proven possible to obtain the end-member enneahydrates MgSO4·9H2O and MgSO4·9D2O (Fortes, Reference Fortes2014).
Given recent interest in highly hydrated sodium sulphate selenates (Weil and Bonneau, Reference Weil and Bonneau2014), which includes the discovery of a new hydration state, Na2SeO4·15/2H2O (Kamburov et al., Reference Kamburov, Schmidt, Voigt and Balarew2014), it seems useful to extend these earlier studies of ion substitution to include Mg-selenate hydrates.
The solid–liquid phase equilibria in the MgSeO4–H2O binary system have been the subject of some disagreement, there being significant differences between the observations of Meyer and Aulich (Reference Meyer and Aulich1928) and those of Klein (Reference Klein1940). In neither instance was the behaviour below the freezing point of ice characterised, the solubility curves and eutectic being found by extrapolation. Up until now, the highest hydrate found in this system, and the phase believed to be in equilibrium at the eutectic (−7 °C), was the heptahydrate, MgSeO4·7H2O. Consequently, an important aspect of this work was to prepare and characterise the heptahydrate, since no crystallographic data on this phase had been reported previously. A single-crystal neutron diffraction experiment was undertaken and the results are reported elsewhere (Fortes and Gutmann, Reference Fortes and Gutmann2014). In brief, MgSeO4·7H2O is orthorhombic, space-group P212121, and is isostructural with the sulphate analogue (epsomite).
A highly productive method to survey the occurrence of both stable and metastable low-temperature hydrates is flash-freezing of aqueous solutions in liquid nitrogen. The work reported here employs this technique, as outlined in the following section.
II. EXPERIMENTAL
A. Sample preparation
An aqueous solution of magnesium selenate was prepared as follows: commercially available aqueous H2SeO4 (Sigma-Aldrich 481513, 40 wt. %) was diluted to 25 wt. % H2SeO4 (1.72 M) with distilled water (Alfa-Aesar, ACS Reagent Grade, 36645), which was then heated to ~70 °C. To this liquid was added a molar excess of powdered MgO (Sigma Aldrich 342793, >99% trace metals basis, −325 mesh); specifically, 6 g of MgO was added to 100 g of hot 1.72 M solution. Since this synthesis, unlike the reaction with basic Mg-carbonate, is quiescent its progress was followed with a Tecpel hand-held pH meter. Once the pH of the solution stabilised at 8.80, the supernatant liquid was decanted, triply filtered and left to stand. Evaporation in the open air led to precipitation of cm-sized crystals of MgSeO4·6H2O from solution. After a further round of re-crystallisation from distilled water the phase purity of the hexahydrate was verified by X-ray powder diffraction. Finally, crystalline Mg-selenate hexahydrate was dissolved in distilled water at concentrations from 25 to 40 wt. % MgSeO4. Quench specimens were prepared in one of two ways; firstly, ~1 cm3 of liquid was poured directly into ~30 cm3 of liquid nitrogen held in a steel cryomortar (Ø = 60 mm, depth = 20 mm), freezing rapidly to form a large white solid lump with regions of transparent (presumably glassy) material in its interior. Secondly, a pipette, filled with aqueous MgSeO4 solution was used to deposit droplets into a pool of liquid nitrogen, which formed spherules from 2 to 6 mm in diameter. Observations made previously on nitrogen-quenched MgSO4 and MgCrO4 solution led me to believe that differences in cooling rates between the larger globules and the smaller spherules might influence the local structure of the solute-rich glass produced by quenching and thereby alter the phase produced on annealing. Once frozen, both the globules and the spherules were pulverised and ground to a powder with a nitrogen-cooled steel pestle.
B. X-ray powder diffraction
X-ray powder diffraction data were collected on a PANalytical X'Pert Pro multipurpose powder diffractometer (using germanium monochromated CoKα1 radiation, λ = 1.788 996 Å, and an X'Celerator multi-strip detector) equipped with a thermoelectrically cooled cold stage (Wood et al., Reference Wood, Hughes, Browning and Fortes2012). This portable cold stage was held in a plastic box filled with dry-ice pellets whilst the powder specimen was prepared and loaded, thereby chilling it to around −80 °C. The samples were transferred to the cold stage with a nitrogen-cooled spoon and the surface was flattened with the flat section of a spoon handle, forming a top-loaded pressed powder specimen. The cover and fan assembly of the cold stage were screwed into place with the body of the stage still embedded in dry ice. In practice, once the power supply to the Peltier element and cooling fans is connected and the stage is screwed onto the diffractometer mounting bracket, the sample temperature rises to −30 °C in under 10 min, eventually equilibrating at −20 to −25 °C (depending on the ambient temperature in the XRD enclosure) within 20 min. Thereafter, the sample temperature remains stable within a degree for many hours. Typically, a 20-min scan in 2θ is carried out during the equilibration period; as described below, this often affords the opportunity to observe transient low-temperature metastable phases (even if they transform during the measurement) that could not be detected otherwise.
Data were collected with variable divergence and receiving slits, converted to fixed-slit geometry with the proprietary X'Pert Pro “HighScore Plus” software package and then exported in an appropriate format for analysis in the GSAS/Expgui package (Larson and Von Dreele, Reference Larson and Von Dreele2000; Toby, Reference Toby2001).
III. RESULTS
As expected, the quenching of aqueous MgSeO4 into either large globules or small spherules produced different results. Figure 1 gives examples of powder diffraction data collected from specimens formed by the two techniques. The globules of aqueous MgSeO4 produced the diffraction pattern shown at the bottom of Figure 1 during the 20-min period of thermal equilibration, which is dominated by Bragg peaks from water ice (phase Ih) and a number of less intense peaks from a crystalline hydrate of MgSeO4. During this brief measurement, the MgSeO4-hydrate underwent a transformation to another phase, which then persisted at −25 °C for the duration of the subsequent measurement (middle pattern in Figure 1). The spherules, on the other hand, produced the diffraction pattern shown at the top of Figure 1, both during the equilibration phase and thereafter, proving to be remarkably stable even when warmed above 0 °C.

Figure 1. (Colour online) Representative X-ray powder diffraction patterns of the three MgSeO4 hydrates observed during this study (see Section III for discussion).
A. Meridianiite-structured MgSeO4 11-hydrate
Neither the top or bottom diffraction patterns shown in Figure 1 resembled any phase seen previously. However, the middle pattern closely resembles (both in terms of peak positions and intensities) the powder diffraction patterns of MgSO4·11H2O and MgCrO4·11H2O reported previously (see figures in Wood et al., Reference Wood, Hughes, Browning and Fortes2012, and Fortes and Wood, Reference Fortes and Wood2012). Since this structure is substantially strained with respect to the analogous sulphate and chromate, it proved necessary to index the Bragg peaks using DICVOL06 (Boultif and Louër, Reference Boultif and Louër2004); the unit cell was subsequently refined by the LeBail method to yield the unit-cell parameters listed in Table I. Both the volume and axial strains caused by replacement of SO4 2− with SeO4 2− are roughly similar to those found on replacement with CrO4 2−, which should not be surprising since the Se–O and Cr–O bond lengths are virtually identical (1.64 Å compared to 1.47 Å for S–O). The chemically induced strains caused by oxyanion exchange in the selenate and chromate analogues of the undecahydrate are highly anisotropic, the most strained direction being along the b-axis. This direction is perpendicular to the corrugated sheets in the MgSO4·11H2O structure, which are connected by a mixture of single and bifurcated hydrogen bonds (Fortes et al., 2008, 2013). Since the data collection for these specimens extended only to 90° 2θ (1.26 Å resolution) and the hydrate represented a little under 40 wt. % of the sample, the remainder being water ice, Rietveld refinement of the structure proved possible only with extremely rigid bond-distance and bond-angle restraints and fixed isotropic displacement parameters. Whilst this demonstrated to my satisfaction that there are no significant differences between the heavy atom structures of MgSeO4·11H2O and its chromate analogue, the accuracy of the atomic coordinates given in Table II is likely to be considerably poorer than for the previously reported MgCrO4·11H2O and MgSO4·11H2O structures (Fortes et al., 2008, 2013; Fortes and Wood, Reference Fortes and Wood2012).
Table I. Comparison of the unit-cell parameters of the three isostructural oxyanion analogues MgXO4·11H2O. Each of these were measured at approximately −22 °C and corrections for sample height were made using water ice as an internal standard using the unit-cell parameters as a function of temperature reported by Röttger et al. (Reference Röttger, Endriss, Ihringer, Doyle and Kuhs1994).

aFortes and Wood (Reference Fortes and Wood2012).
bThis work (cf., Section III.A).
Table II. Refined atomic coordinates (x, y, and z) and fixed isotropic displacement parameters (U iso) for the heavy atoms in the meridianiite-structured MgSeO4·11H2O (cf., Section III.A) compared to those obtained previously for meridianiite-structured MgCrO4·11H2O by neutron time-of-flight diffraction methods (Fortes and Wood, Reference Fortes and Wood2012). This X-ray powder refinement yielded R p = 0.0845 and χ 2 = 2.897 for 57 variables.

B. Unknown MgSeO4 hydrate
The phase that appears prior to the newly discovered MgSeO4·11H2O described above has proven difficult to characterise, since the operation of the Peltier cold stage allows only a brief observation of its powder diffraction pattern whilst it is in the process of transforming to the more stable 11-hydrate, and there is a large variation in temperature during the scan. The most intense Bragg peaks from the meridianiite-structured 11-hydrate, which form a “clump” around 20.70–20.85° 2θ, are marked with an asterisk in Figure 1 and the prevalence of unindexed peaks increases up to the point where the dataset has been truncated. An indexing of the least ambiguous Bragg peaks has been obtained using DICVOL06, but confidence in the accuracy of this result is impossible to determine at present. The indexing yielded a triclinic solution with unit-cell dimensions a = 7.449(5) Å, b = 6.003(4) Å, c = 8.651(6) Å, α = 76.65(8)°, β = 94.79(5)°, γ = 103.86(5)°, and V = 365.30 Å3, the figures of merit M(10) = 55.8 and F(10) = 49.1 (0.0089, 23) (De Wolff, Reference De Wolff1968; Smith and Snyder, Reference Smith and Snyder1979). The volume of this unit cell is very close to half that of the 11-hydrate, which might indicate a novel polymorph of MgSeO4·11H2O with Z = 1 and, necessarily, space-group P1. Tick marks corresponding with this unit cell are shown in Figure 1.
C. Novel MgSeO4 9-hydrate
In contrast with the unknown hydrate described in the previous section the powder pattern observed from the quenched spherules was confidently indexed using DICVOL06 with a monoclinic unit cell: a = 7.271(1) Å, b = 10.509(1) Å, c = 17.408(2) Å, β = 109.46(1)°, and V = 1254.15 Å3, the figures of merit being M(15) = 108.5 and F(15) = 237.3 (0.0023, 27). Additionally, systematic absences were identified that limited the likely space-groups to P21, Pc or P21/c.
Since it was highly likely that this phase was a magnesium selenate hydrate with general formula MgSeO4·nH2O, the problem was then to quantify n. In the absence of single crystals, the specimens being mixtures of an unknown hydrate and water ice, it is not possible to determine the hydration state using thermogravimetric methods. The unit-cell volumes of crystals with the formula MgSeO4·nH2O and n = 0, 2, 4, 4½, 5, and 6 have been reported previously (Snyman & Pistorius, Reference Snyman and Pistorius1964; Stoilova and Koleva, Reference Stoilova and Koleva1995; Kolitsch, Reference Kolitsch2002; Krivovichev, Reference Krivovichev2007); those with n = 7 and 11 have been determined in this and related work (Fortes and Gutmann, Reference Fortes and Gutmann2014). As shown in Figure 2, there is a near linear relationship between the hydration number, n, and the volume per formula unit. The problem now reduces to one of identifying a sensible combination of n and Z that falls on or around this line. The most plausible solution, shown by a red box in Figure 2, has n = 9 and Z = 4. Confidence in this determination is increased by noting that 9-hydrates have been found in quenched specimens of MgSO4 and MgCrO4 (although these have a different monoclinic unit cell to that reported here and are presumably not isostructural), and also that Klein (Reference Klein1940) reported the occurrence of a 9/2-hydrate, the structure of which was determined quite recently by Krivovichev (Reference Krivovichev2007).
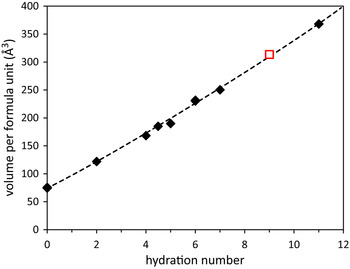
Figure 2. (Colour online) Relationship between hydration number, n, and volume per formula unit amongst the known MgSeO4 hydrates (filled diamonds) and the proposed new 9-hydrate (open square). Based on data in Snyman & Pistorius (1964), Stoilova and Koleva (Reference Stoilova and Koleva1995b), Kolitsch (Reference Kolitsch2002), Krivovichev (Reference Krivovichev2007), Fortes and Gutmann (Reference Fortes and Gutmann2014), and this work.
Perhaps the most convincing argument is the structure solution: the atomic structure was solved as MgSeO4·9H2O in space-group P21/c from the X-ray powder diffraction data using the parallel tempering algorithm implemented in FOX, version 1.9.7.1 (Favre-Nicolin and Černý, Reference Favre-Nicolin and Černý2002, Reference Favre-Nicolin and Černý2004). FOX was initialised with the unit-cell parameters obtained by DICVOL06 and these were refined, along with peak profile coefficients, diffractometer zero-shift and background points by the LeBail method and spline interpolation, respectively. Since ice Ih was present in the specimen, FOX was provided with crystallographic data for this phase (Fortes et al., Reference Fortes, Wood, Grigoriev, Alfredsson, Kipfstuhl, Knight and Smith2004), fitting these Bragg peaks by automatic adjustment of a simple scale factor. For the hydrate, FOX was used to construct ideal MgO6 octahedra with Mg–O distances of 2.06 Å, and ideal SeO4 tetrahedra with Se–O distances of 1.64 Å; these were treated as rigid bodies throughout the solution process. In ten runs of 1 million trials each, the crystal structure was optimised against the powder diffraction data, consistently producing very similar structures with chemically sensible arrangements of the ionic polyhedra. Fourier difference maps phased on these structures revealed three peaks that seemed likely to correspond to the additional water molecules necessary to form a 9-hydrate. When FOX was re-run from scratch with three additional oxygen atoms included, the original structure was reproduced with the extra water oxygen being found in the same positions as the Fourier difference peaks. Ultimately the structure with the lowest overall cost function was exported as a CIF file to form the basis for Rietveld refinement with GSAS.
The sample temperature, −22 °C, was used to obtain appropriate unit-cell parameters for the ice component in the specimen, from a linear interpolation of the values tabulated for H2O ice Ih by Röttger et al. (Reference Röttger, Endriss, Ihringer, Doyle and Kuhs1994). With the ice unit-cell parameters fixed, the specimen height and transparency (SHFT and TRNS parameters in GSAS peak shape function 3) were refined, these quantities being constrained to undergo equal shifts for both phases in the refinement. Sample scale, phase fraction, and six background coefficients were also refined, followed by the specimen unit-cell parameters and the Lorentzian “microstrain” peak profile parameter, LY, and the peak asymmetry parameters S/L and H/L. A degree of preferred orientation in the ice component of the specimen was treated using a 6th-order spherical harmonic model. Given the complexity of the structure, refinement of atomic coordinates was only done after a series of bond-distance and bond-angle restraints were entered; the values employed were intended to produce regular SeO4 tetrahedra with Se–O bond lengths of 1.640 Å and regular MgO6 octahedra with Mg–O bond lengths of 2.065 Å. These values are typical of other MgSeO4-bearing crystals (e.g. Kolitsch, Reference Kolitsch2001). After refinement to convergence of all atomic coordinates and of a common isotropic thermal displacement parameter for all heavy atoms, the locations of the hydrogen atoms were estimated geometrically. Examination of the first coordination shell of the water oxygen revealed a sensible pattern of O···O vectors consistent with hydrogen bonded contacts and so pairs of hydrogen atoms were sited at distances of 0.98 Å from each O atom along these vectors. With U iso for all hydrogen atoms fixed, a further cycle of refinement was carried out, the final χ 2 value for the fit being 7.797, with weighted and unweighted profile R-factors (including the background) of 0.0640 and 0.0805, respectively. Table III reports the final structural parameters of MgSeO4·9H2O: further details of this refinement are contained in a Crystallographic Information File included in the electronic supplement to this article; the reader may inspect the diffraction data using the freely available pdCIFplot software (Toby, Reference Toby2003). The fit to the diffraction data is shown in Figure 3.

Figure 3. (Colour online) X-ray powder diffraction pattern of MgSeO4·9H2O fitted to the newly obtained structure by the Rietveld method. Red circles represent the measured data, the green line is the fit to the data and the purple line underneath the powder pattern is the difference profile. Tick marks show the expected positions of Bragg peaks from the 9-hydrate (upper set) and ice Ih (lower set). The inset depicts a magnified view of the low-2θ range.
Table III. Refined atomic coordinates (x, y, and z) and isotropic displacement parameters (U iso) for the heavy atoms in MgSeO4·9H2O along with hydrogen atom locations estimated on the basis of the observed coordination geometry of neighbouring water oxygen. See also the Supplementary CIF data. (The italics denote the fact that the H-atom positions are geometric estimates rather than being obtained by structure refinement.)

IV. DISCUSSION
The asymmetric unit of MgSeO4·9H2O is shown in Figure 4; bear in mind that the hydrogen atom positions (whilst chemically sensible) are estimated and not directly observed; these serve as predictions for any future neutron powder diffraction or single crystal diffraction study. Selected interatomic distances are listed in Tables IV and V. Despite the fairly light bond-distance restraints, some significant differences have emerged in the Mg–O lengths that are explicable in terms of the coordination of these water molecules. The water molecule with the longest Mg–O distance (Ow6) is the only one of the six Mg-coordinated waters to accept a hydrogen bond (from Ow9). A similar situation occurs in both MgSO4·7H2O and MgSeO4·7H2O, where two of the Mg-coordinated waters accept a hydrogen bond each; these tetrahedrally coordinated waters exhibit Mg–O bond lengths of ~2.10 Å compared with ~2.05 Å for the other trigonally coordinated waters (Baur, Reference Baur1964; Ferraris et al., Reference Ferraris, Jones and Yerkess1973; Fortes and Gutmann, Reference Fortes and Gutmann2014).

Figure 4. (Colour online) The asymmetric unit of MgSeO4·9H2O. Drawn using Diamond (Putz and Brandenburg, Reference Putz and Brandenburg2006). Note that the positions of the hydrogen atoms are inferred on the basis of oxygen coordination geometry and interatomic vectors and are not directly determined from the X-ray powder data.
Table IV. Bond lengths in the polyhedral ions of MgSeO4·9H2O.

Table V. O···O bond lengths in MgSeO4·9H2O. Roman numeral superscripts indicate the symmetry codes listed underneath the table.

(i)2 − x, −0,5 + y, 0.5 − z; (ii)1 + x, y, z; (iii)2 − x, 1 − y, −z; (iv) x, 0.5 − y, −0.5 + z; (v)1 − x, −0.5 + y, 0.5 − z; (vi)1 − x, 1 − y, −z; (vii)2 − x, 0.5 + y, 0.5 − z; (viii)1 − x, 0.5 + y, 0.5 − z; (ix) x, 1.5 − y, −0.5 + z.
The packing of the polyhedral ions and neutral water molecules to form the complete structure is shown perpendicular to the a-axis in Figure 5, the inferred hydrogen bonding being depicted by dashed rods. A less cluttered schematic of the hydrogen bonding is shown in Figure 6, highlighting several salient features. Firstly, three of the Mg-coordinated waters, Ow1, Ow3, and Ow4, engage in H-bonding solely with the selenate oxygen: secondly, all but one of the selenate oxygens accept three H-bonds apiece, whereas O1 only accepts two H-bonds: thirdly, the interstitial water molecules prefer to both donate and accept hydrogen bonds from/to the Mg-coordinated waters and the selenate oxygen, there is only a single H-bond between the Ow7 and Ow8 interstitial waters. None of these features are unusual, being observed also in MgSO4·11H2O (see H-bond scheme in Fortes et al., Reference Fortes, Wood and Knight2008); indeed, between the five interstitial waters of the 11-hydrate there is only one H-bond, the rest being between the Mg-coordinated waters and the sulphate oxygens. In other words, confidence in the structure solution (and the inferred network of hydrogen bonding) is strengthened by the occurrence of these architectural similarities.

Figure 5. (Colour online) Unit cell of MgSeO4·9H2O viewed parallel to the a-axis (i.e. towards the b–c plane) showing the relative arrangement of the Mg(H2O)6 octahedra (green) and the SeO4 tetrahedra (purple). The inferred hydrogen bond framework is illustrated with dashed rods.
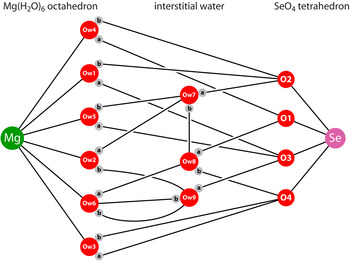
Figure 6. (Colour online) Cartoon illustration of the inferred hydrogen bond scheme in MgSeO4·9H2O.
The O···O distances (Table V) are, with one exception, tightly clustered around 2.8 Å (range 2.73–2.86 Å), which is the expected value for medium strength hydrogen-bonded contacts. The unusually long contact (Ow9–Ow6) forms part of a rather interesting structural element, specifically a square ring or water tetramer (Figure 7). A similar four-sided ring of water molecules occurs in Na2SO4·10H2O; orientational disorder in this ring leads to significant differences in the anisotropic thermal expansion of Na2SO4·10H2O depending on whether this disorder is frozen in by rapid cooling or whether an ordered state is achieved by slow cooling (cf., Brand et al., Reference Brand, Fortes, Wood, Knight and Vočadlo2009). With the current data I cannot rule out the possibility that the water molecules comprising the square ring in MgSeO4·9H2O are orientationally disordered. Future study of the material's thermal expansion and efforts to characterise the structure by single crystal methods must be used in order to establish this.
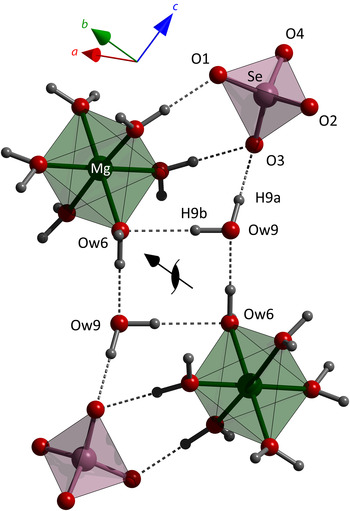
Figure 7. (Colour online) The square ring of hydrogen-bonded water molecules involving Ow6 and Ow9 in relation to one of the 21 screw axes. Note that H6a lies out of the plane of the square ring in front of (top left) and behind (bottom right) Ow6.
V. CONCLUSION
This work reports the discovery of at least two and possibly three new hydrates of MgSeO4 formed by quenching of aqueous solutions in liquid nitrogen and subsequent rapid annealing of the resultant selenate-rich glass. One of these is an undecahydrate that is apparently isostructural with the sulphate analogue, MgSO4·11H2O, but with an anisotropically strained unit cell approximately 4% larger in volume than the sulphate. The second new phase is an enneahydrate, MgSeO4·9H2O; the heavy-atom structure of this compound has been determined from the X-ray powder diffraction data. The third phase appears to be a transient metastable hydrate that rapidly transforms to the more familiar 11-hydrate structure. This may be a low-temperature polymorph of the 11-hydrate but further work is necessary to characterise it better.
The stability of the 9- and 11-hydrates with respect to one another and to the previously known heptahydrate remains to be confirmed. Upon warming, the 11-hydrate has been found to transform (presumably by incongruent melting) to the 9-hydrate. Conversely, crystals of MgSeO4·7H2O stored in a freezer at −20 °C for 2 weeks were discovered to have transformed, both to the intrigue and irritation of the author, entirely to the 9-hydrate. This rather suggests that the 9-hydrate is the stable phase at low temperature and that a re-evaluation of the binary phase diagram is in order.
SUPPLEMENTARY MATERIALS AND METHODS
The supplementary material for this article can be found at http://www.journals.cambridge.org/PDJ.
ACKNOWLEDGEMENT
ADF acknowledges financial support from the Science and Technology Facilities Council, grant numbers PP/E006515/1 and ST/K000934/1.
















