A. Solid-state synthesis

The polycrystalline Na₂ZnB₆O₁₁ sample was prepared by sintering through solid-state reactions. All reagents were of analytical grades. The powders in the appropriate composition of raw materials Na₂CO₃, ZnO, and H₃BO₃ were mixed and ground in an agate mortar, then heated at 300 °C for 10 h after slowly elevating to the specified temperature to avoid the loss of components caused by the volatilization of H₂O and CO₂. After being pressed into a pellet of 12 mm in diameter and 1 to 2 mm in thickness, the sample was sintered at 650 °C for 1 week in a stove. The sintered sample was ground into powders and repeatedly pressed into a pellet and sintered for several times. Then pure NA₂ZnB₆O₁₁ powders were obtained and characterized by powder X-ray diffraction method (XRD).

TABLE I. Crystallographic data, experimental details for powder XRD, and Rietveld refinement for Na₂ZnB₆O₁₁.Footnote ^a

^a R_P=Σ|Y_io−Y_ic|/ΣY_io, R_WP={Σw_i(Y_io−Y_ic)²/Σw_iY _io²}^1/2, R _exp=[(N−P)/Σw_i Y _io²]^1/2, and s=R_WP/R _exp.

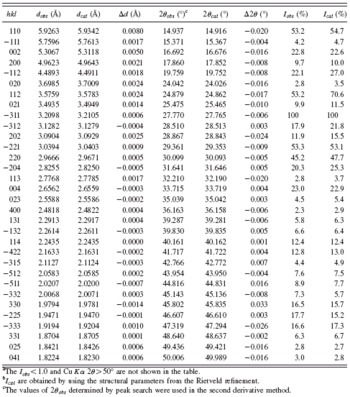
TABLE II. XRD diffraction data for Na₂ZnB₆O₁₁.Footnote ^a,Footnote ^b

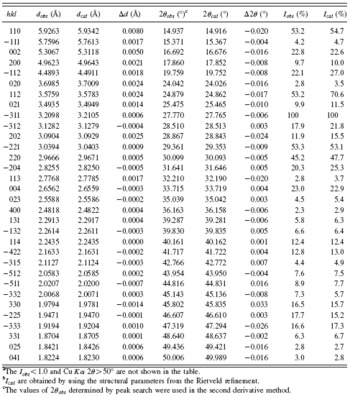
^a The I_obs ≤ 1.0 and Cu Kα 2θ≥50° are not shown in the table.

^b I_cal are obtained by using the structural parameters from the Rietveld refinement.

^c The values of 2θ_obs determined by peak search were used in the second derivative method.

B. X-ray powder diffraction analysis

The XRD data of Na₂ZnB₆O₁₁ used for structure determination and Rietveld refinement were collected at room temperature by a step scan mode on a Rigaku D/Max-2500 diffractometer with a graphite monochrometer. The step width and the sampling time were set as 2θ=0.02° and 2 s per step, respectively. The angular range was set from 2θ=14° to 2θ=120°. Additional technical details are listed in Table I.

C. Vibration spectrum

The infrared absorption spectrum of the sample was measured at room temperature in KBr disks using a SPECORD-751R infrared spectrophotometer in the frequency range of 400 to 4000 cm⁻¹. Wave-number accuracy is within ±2 cm⁻¹ for narrow bands.

A. Automatic indexing of X-ray diffraction data

The powder diffraction peaks were listed as the standard of phase identification (Table II). The diffraction pattern of Na₂ZnB₆O₁₁ was indexed using the DICVOL program (Boultif and Louër, Reference Boultif and Louër2004). It belongs to a monoclinic unit cell with a=10.715(1) Å, b=7.402(2) Å, c=11.465(4) Å, and β=112.088(5)°. The systematic absence rules are the following: hkl with h+k=2n+1, h0l, with l=2n+1(h=2n+1), and 0k0 with k=2n+1; the possible space groups are Cc and C2/c. Since the measured density was about 2.75±0.25 g cm⁻³, it is easy to derive that the number of chemical formula per unit cell, Z, is 4. In other words, a Na₂ZnB₆O₁₁ unit cell contains 8 Na, 4 Zn, 24 B, and 44 O atoms.

B. Vibrational spectrum analysis

The purpose of infrared-spectrum analysis is to obtain the structural information on boron coordination. We can see from Figure 1 that the strongest bonds in the range 1254 to 1464 cm⁻¹ are attributed to the three-coordinated [BO₃]³⁻group and those near 853 and 1020 cm⁻¹ are mainly attributed to the four-coordinated [BO₄]⁵⁻group. The bonds associated with [BO₃]³⁻ groups and [BO₄]⁵⁻ groups bending modes are overlapped and located below 760 cm⁻¹ . The vibrational spectrum shows that the existence of both [BO₃]³⁻

Figure 1. Infrared spectrum of Na₂ZnB₆O₁₁.

groups and [BO₄]⁵⁻ groups and the content of [BO₃]³⁻ groups are considerably greater than that of [BO₄]⁵⁻ groups.

C. Ab initio crystal-structure determination

The correct decomposition of X-ray diffraction profiles is the key to successfully determine crystal structure from powder diffraction data using the single-crystal structure determination method. The profile decomposition was carried out on the experimental X-ray powder diffraction pattern of Na₂ZnB₆O₁₁ using the FULLPROF program (Rodriguez-Carvajal et al., Reference Rodriguez-Carvajal, Fernadez-Diaz and Martinez1991) based on the Le Bail method (Le Bail et al., Reference Le Bail, Duroy and Fourquet1988) with the possible space group Cc. The final agreement factors converged to R_P=10.83%, R_WP=13.42%, and R _exp=5.74%. Structure factors for 624 reflections were extracted in the diffraction range 2θ=14° to 120° and put into the direct methods program SHELXL-97 (Sheldrick, Reference Sheldrick1997). Based on the extracted structure factors, an E map (electronic density map) was obtained. According to the atom distances, six peaks listed in the E map probably corresponded to the correct positions of the atoms, among which one was assigned to the Zn atom, two were assigned to Na atoms, and the other three were assigned to O atoms. Other O and B atoms were located by using difference Fourier synthesis. In this course, once an atom was located, it would be used for the next run of difference Fourier synthesis. Owning to the scattering factor of B is smaller, we failed to reveal all B atoms by the difference Fourier syntheses. However, because the positions of Zn, Na, and O have been determined initially, possible equilibrium positions of B atoms can be analyzed by reported data of bonds and angles of [BO₃]³⁻ groups and [BO₄]⁵⁻ groups. Finally, we determined the positions of B by three parameter equations (two distance equations and one angle equation). So far, all the atomic positions of Na₂ZnB₆O₁₁ have been determined initially. The structural model is used to calculate the X-ray diffraction data by the LAZY program (Klaus et al., Reference Klaus, Wolfgang and Erwin1977); the first six peaks agree well with the experimental data. Then the structure was refined using the Rietveld method (Rietveld, Reference Rietveld1967, Reference Rietveld1969) of the FULLPROF program. There is a total of 96 parameters including 16 profile parameters (five peak-shape

Figure 2. (Color online) Rietveld refinement plots of Na₂ZnB₆O₁₁. Small circles correspond to experimental values, and the solid curve, the calculated pattern. Vertical bars indicate the positions of the Bragg peaks. The bottom curve depicts the difference between the experimental and calculated intensity values.

parameters, three background parameters, four lattice parameters, one asymmetrical parameter, one scale parameter, one zero parameter, and one preference parameter). The March–Dollase model, P_K=(G ₁² cos² ∂+(1/G ₁)sin² ∂)^−3/2, was used to refine the preference parameter (G1 is the refinable parameter and its value is 0.9937) and 80 structural parameters (including 20 temperature factors). The final residual factors converged to R_P=12.26%, R_WP=15.02%, and R _exp=5.75%. Values of R_P and R_WPare slightly large, probably because of crystal imperfection and minor impurities produced during crystal growth by the solid-state reaction process. The refined lattice parameters are a=10.7329(2) Å, b=7.4080(3) Å, c=11.4822(2) Å, and β=112.16(2)°. The final result was put into the PLATON program (Spek, Reference Spek2003) and no additional symmetry was found. Then the final space group was determined as Cc. The Rietveld refinement results are given in Figure 2. The crystallographic data, fractional atomic coordinates, and the thermal parameters (B) are listed in Tables I and III.

D. Description on crystal structure

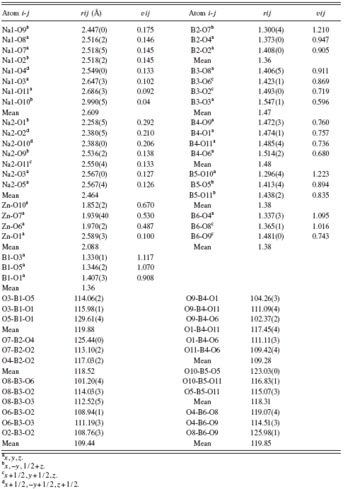
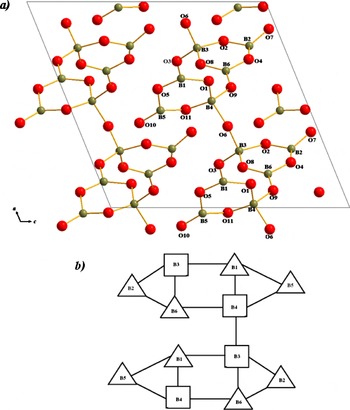
The Na₂ZnB₆O₁₁ compound crystallizes in the space group Cc. The structure perspective of Na₂ZnB₆O₁₁ is shown in Figure 3. The basic structural unit is a double hexagonal ring [B₆O₁₁]⁴⁻ consisting of two BO₄ tetrahedrons and four BO₃ triangles and they are connected by one O atom (see Figure 4), which is consistent with the results obtained from the vibrational spectrum. According to Yuan and Xue (Reference Yuan and Xue2007), it belongs to double-bridge-ring fundamental building blocks (FBBs) and its topology was also given in Figure 4. In this unit, two hexagonal rings formed a certain angle, which is defined by B4, O11, B5, O5, B1, and O1 and by B3, O2, B2, O4, B6, and O8. Values of B–O bonds in the tetrahedral coordination range from 1.406(5) Å to 1.547(1) Å and O–B–O angles from 101.20(4)° to 117.45(4)°; in the triangle coordination the respective ranges are 1.296(4) to 1.438(2) Å

TABLE III. Atomic coordinates and equivalent isotropic displacement parameters for Na₂ZnB₆O₁₁.

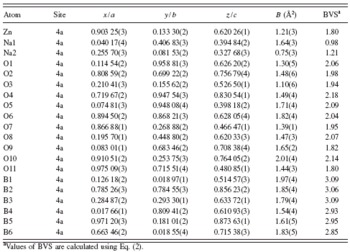
^a Values of BVS are calculated using Eq. (2).

and 113.10(2) to 129.61(4)Å. Values of Na–O, B–O, and Zn–O distances as well as O–B–O angles are listed in Table IV.

The Zn atom is coordinated with four O atoms to form a distorted tetrahedron, as illustrated in Figure 5(a). The ZnO₄ tetrahedron is linked to four different [B₆O₁₁]⁴⁻ groups. Zn–O distances vary from 1.852(2) Å to 2.589(3) Å and O–Zn–O angles between 63.73° and 124.14° suggesting that the tetrahedron is highly distorted.

The coordination surroundings of the Na1 and Na2 atoms are shown in Figures 5(b) and (c). Each Na1 is strongly bonded to five O atoms with distances of 2.447(0) to 2.549(0) Å and also weakly bonded to three other O at distances of 2.647(3) to 2.990(5) Å. Taking all these eight bonds into account, the bond valence sum is equal to 0.98 which is close to the normal bond valence of Na. However, if the O atoms with a longer distance from Na1 are not considered, the BVSs for Na1, O3, and O11 will have a larger deviation from the normal values. Each Na2 is surrounded by seven O

Figure 3. Structure perspective of Na₂ZnB₆O₁₁.

atoms forming an irregular polyhedron. The Na–O distances are 2.447(0) to 2.990(5) Å (average 2.609 Å) for Na1 and 2.258(5) to 2.567(4) Å (average 2.464 Å) for Na2 (Table IV).

As for the 11 unique O atoms, four are three-coordinated, bonded to two B atoms, one Na atom for O4, O5, and O8 or two B atoms, one Zn atom for O6; seven are

Figure 4. (color online)(a) Projection of the [B₆O₁₁]⁴⁻ onto the ac plane. (b) Topology of [B₆O₁₁]⁴⁻.

TABLE IV. Selected bond lengths (Å) and angles (°) for Na₂ZnB₆O₁₁. (The v_ij is the bond valence of a bond between atoms i and j; the r_ij is the corresponding bond distance between the two atoms.)

^a x,y,z.

^b x,−y,1/2+z.

^c x+1/2,y+1/2,z.

^d x+1/2,−y+1/2,z+1/2.

four-coordinated, bonded to two B atoms, two Na atoms for O2, O3, O9, O11 or one B atom, one Zn atom, two Na atoms for O7, O10, O11.

The bond valence sum V_i is useful for checking the reliability of a determined crystal structure. The bond valence and the bond valence sum are defined as follows (Brown and Altermatt, Reference Brown and Altermatt1985; O’Keeffe and Brese, Reference O’Keefe and Brese1991):

The v_ij is the bond valence of a bond between atoms i and j; the r_ij is the corresponding bond distance between the two atoms. The bond valence parameter, r ₀, for Na–O, Zn–O, and B–O ion pairs are 1.803, 1.704, and 1.731, respectively (Brown and Altermatt, Reference Brown and Altermatt1985). The bond valence v_ij between cations and oxygen is listed in Table IV and their sums (BVS) listed in Table III. It shows that the BVS of Na⁺, Zn²⁺, and B³⁺ cations are close to their chemical valences. The BVS for individual O atoms vary from 1.80 to 2.14, which is close to its chemical valence.

Up to now, only hydrate hexaborates were reported in the literature such as Ca₂B₆O₁₁·xH₂O (Clark and Christ, Reference Clark and Christ1957) which crystallizes in the

(a) Coordination environments of Zn in Na₂ZnB₆O₁₁. The tetrahedrons are ZnO₄. (b) Coordination environments of Na1 in Na₂ZnB₆O₁₁. The tetrahedrons are BO₄ and triangles are [BO₃]³⁻ groups. (c) Coordination environments of Na2 in Na₂ZnB₆O₁₁. The tetrahedrons are BO₄ and triangles are [BO₃]³⁻ groups.

triclinic and Mg₂B₆O₁₁·xH₂O (Rumanova and Ashirov, Reference Rumanova and Ashirov1963) which crystallizes in the triclinic and monoclinic. Since there is no reported in the literature for the dehydrated hexaborate, Na₂ZnB₆O₁₁ is a new compound with a new structure type.