I. INTRODUCTION
In recent years, a considerable surge of attention to the porous metal-organic framework (MOF) materials was due to their potential applications in both H2 storage and CO2 capture. However, most MOF materials have low thermal stability as compared to zeolites. Often, one needs to remove solvent or other guest molecules from the pores at elevated temperature, leading to the instability of the framework structure. Therefore, it is important to seek materials with structural stability at elevated temperature. The ‘dhtp’ linker (dhtp = 2,5-dihydroxytetephthalate or 2,5-dihydroxy-1,4-benzenedicarboxylate) is known to form microporous coordination polymers based on the dianionic form of the carboxyl moieties which act as ligands to metal sites. The MII2(dhtp) compounds, also known as the MOF74 family (Rosi et al., Reference Rosi, Kim, Eddaoudi, Chen, O'Keeffe and Yaghi2005), demonstrated stability even after the removal of coordinated water (Dietzel et al., Reference Dietzel, Morita, Blom and Fjellvâg2005).
Extensive research has been performed on the MOF74 family of materials since the first report by Rosi et al. (Reference Rosi, Kim, Eddaoudi, Chen, O'Keeffe and Yaghi2005) on the synthesis and characterization of the Zn-MOF74 analog. For example, Dietzel et al. (Reference Dietzel, Morita, Blom and Fjellvâg2005) carried out an in situ high-temperature single-crystal investigation of Co-MOF74 and hydrogen adsorption studies using Ni-MOF74 (Dietzel, Reference Dietzel, Panella, Hirscher, Blom and Fjellvåg2006). Caskey et al. (Reference Caskey, Wong-Foy and Matzger2008) reported the dramatic tuning of CO2 uptake in the Mg-, Ni-, Co-, and Zn-MOF74 compounds. In the same year, Tranchemontagne et al. (Reference Tranchemontagne, Hunt and Yaghi2008) reported for the first time the room temperature synthesis of Zn-MOF74, and Zhou et al. (Reference Zhou, Wu and Yildirim2008), combining experimental with theoretical efforts, showed that the enhanced H2 adsorption in M-MoF74 (M = Mg, Mn, Co, Ni, Zn) has a strong dependence of the binding strength on the open metal sites. In the following year, Wu et al. (Reference Wu, Zhou and Yildirim2009) illustrated the important role of open metal sites for high-capacity methane storage. As selective binding of CO2 is essential for CO2 capture and natural gas purification, Britt et al. (Reference Britt, Furukawa, Wang, Glover and Yaghi2009) using the Mg-analog show CO2 release at a temperature as low as 80 °C. Wu et al. (Reference Wu, Simmons, Srinivas, Zhou and Yildirim2010) further explored the adsorption sites and binding nature of CO2 in Mg-MOF74 using a combined neutron diffraction and first-principles study. Glover et al. (Reference Glover, Peterson, Schindler, Britt and Yaghi2011) extended the capability of M-MOF74 (M = Mg, Zn, Co, Ni) to the removal of ammonia, cyanogen chloride, and sulfur dioxide from air.
In addition to thermal stability, the MOF74 family of materials also has record setting surface areas coupled with high free volumes. For example, the Mg materials have 8.9 wt% dynamic capacity and exhibit facile CO2 release at a significantly low temperature of 80 °C (Britt et al., 2009). These compounds are also effective sorbents in the low pressure region (0 to 101.3 kPa) for CO2 uptake. Therefore, MOF74 offers a balance between dynamic capacity and regeneration.
As X-ray powder diffraction is a non-destructive method for characterization, X-ray reference diffraction patterns for sorbent materials play an important role for the research community that investigates efficient solid sorbent materials for the CO2 capture process. The goal of this report is two-fold: a brief comparison of the structural features of the MOF74 (M = Mn, Co, Ni, Zn) members, and the determination of their high resolution experimental powder diffraction patterns for inclusion in the Powder Diffraction File (PDF).
II. EXPERIMENTALFootnote 1
Details of the synthesis of the MOF74 samples were reported elsewhere (Zhou et al., Reference Zhou, Wu and Yildirim2008 and references cited in the Supporting Information). Sample loading into the capillaries used for data collection was performed inside a dry box with flowing Ar at room temperature.
High resolution synchrotron X-ray powder diffraction data MOF74 (Mn, Co, Ni, and Zn) were collected at 293 K using beamline 11-BM at the Advanced Photon Source (APS), Argonne National Laboratory using an average wavelength of 0.412 210 Å. Discrete detectors covering an angular range from −6° to 16° with respect to the nominal 2θ were scanned over a 34°2θ range, with data points collected every 0.001° in 2θ at a scan speed of 0.01°/s. The instrumental optics of 11-BM incorporate two platinum-striped mirrors and a double-crystal Si(111) monochromator, where the second crystal has an adjustable sagittal bend (Wang et al., Reference Wang, Toby, Lee, Ribaud, Antao, Kurtz, Ramanathan, Von Dreele and Beno2008). The diffractometer is controlled via EPICS (Dalesio et al., Reference Dalesio, Hill, Kraimer, Lewis, Murray, Hunt, Watson, Clausen and Dalesio1994). A vertical Huber 480 goniometer positions 12 perfect Si(111) analyzers and 12 Oxford-Danfysik LaCl3 scintillators, with a spacing of 2° in 2θ (Lee et al., Reference Lee, Shu, Ramanathan, Preissner, Wang, Beno, Von Dreele, Lynn Ribaud, Antao, Jiao and Toby2008). Capillary samples are mounted by a robotic arm and spun at ≈90 Hz. Data are normalized to incident flux and collected while continually scanning the diffractometer 2θ arm. A mixture of National Institute of Standards and Technology standard reference materials, Si (SRMTM 640c) and Al2O3 (SRMTM 676) is used to calibrate the instrument, where the Si lattice constant determines the wavelength for each detector. Corrections are applied for detector sensitivity, 2θ offset, and small detector wavelength differences, before merging the data into a single set of intensities evenly spaced in 2θ.
The high-resolution patterns of MOF74 were fitted using the Rietveld refinement technique (Rietveld, Reference Rietveld1969) with the software suite GSAS (Larson and von Dreele, Reference Larson and von Dreele1992). For M = Mn, Ni, and Zn, the C8H2O6 dhtp ligand was modeled as a rigid body of half-occupied atoms, with the center of the molecule fixed at the inversion center 1/3, 1/6, 1/6 and only the three orientation angles refined. For M = Co, the C8H2 core of the dhtp ligand was modeled as a rigid body of half-occupied atoms, and distance and angle restraints were applied to the carboxyl and ionized hydroxyl groups. The peak profiles were described using the aniosotropic strain tensor model of GSAS profile function #4. Preferred orientation was modeled using fourth-order spherical harmonics; the texture index varied from 1.015 to 1.128. The background was modeled using a three-term shifted Chebyshev function, and 9–14-term diffuse scattering functions were also included.
The reference X-ray powder patterns were obtained with a Rietveld pattern decomposition technique. In this technique, the reported peak positions are derived from the extracted integrated intensities and positions calculated from the lattice parameters. When peaks are not resolved at the resolution function of the diffractometer, the intensities are summed, and an intensity-weighted d-spacing is reported. Therefore, these patterns represent ideal specimens. They are corrected for systematic errors both in d-spacing and intensity.
III. RESULTS AND DISCUSSION
A. Crystal structure
Figures 1(a)–1(d) show the results of the synchrotron Rietveld refinement of Mn-, Co-, Ni-, and Zn-MOF74 samples. Tick marks indicate peak positions. The difference pattern is plotted on the same scale as the other patterns. In these diagrams, for 2θ values higher than 4°, the scale has been magnified 20 times. At 2θ values are higher than 13°, the scale has been magnified 50 times. The refinement results of the four samples are listed in Table I. No significant impurity phase was found in these samples. Despite the fact that after the samples was loaded into the capillary tubings and was sealed with wax, moisture apparently diffuses into the tubings. The final chemical formula for these compounds was estimated to be [M 2(C8H2O6)(H2O)2]·nH2O, where n = 6.3, 10.0, 6.2, and 6.6 for M = Mn, Co, Ni, Zn. Owing to the disordered situation of water molecules, no attempts were made to locate the hydrogen atoms in the pores.

Figure 1. Rietveld refinement results for (a) M 2(dhtp), M=Mn; (b) M 2(dhtp), M = Co; (c) M 2(dhtp), M = Ni; (d) M 2(dhtp), M = Zn. The row of tick marks indicates the calculated peak positions. The difference pattern is plotted at the same scale as the other patterns up to 5° in 2θ. At 5° 2θ, the scale has been magnified 20 times. At 2θ values greater than 13.5°, the scale has been magnified 50 times.
TABLE I. Rietveld refinement results for M 2(dhtp), M = Mn, Co, Ni, Zn (λ = 0.413 535 Å)
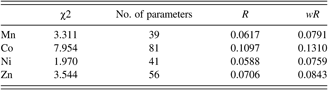
Based on the refinement results, the MOF74 samples are isostructural and the space group was confirmed to be R 3 (No. 148). Table II gives the cell parameters of these phases, and the calculated densities of these phases. The much higher density value for the Co-phase is attributed to the higher number of water molecules in the channels as compared to the remaining three samples. The ionic radii (Shannon, Reference Shannon1976) for Ni2+(VI), Zn2+(VI), Co2+(VI), and Mn2+(VI) are 0.69 Å, 0.74 Å, 0.745 Å, and 0.83 Å, respectively. As Mn2+ has a larger size, it is expected to have larger lattice parameters. The trend of the unit cell volume in Table II follows the trend of the ionic radius of the cations.
TABLE II. Cell parameters for M 2(dhtp) (M=Mn, Co, Zn, Ni); space group R 3, Z = 3

Table III gives the atomic coordinates of the four MOF74 materials. Figures 2 and 3 depict the crystal structure of Zn and Co compounds featuring a three-dimensional coordination polymer with honeycomb topology that contains one-dimensional broad channels. The M-atoms are coordinated in a distorted octahedral fashion by six oxygen atoms. Five of the six oxygen atoms are part of the organic ligand. The sixth one comes from a coordinated water molecule (O18 in the numbering scheme). In general, the pores of the as-synthesized material are occupied with solvent molecules such as H2O which can be removed upon evacuation to generate unsaturated metal sites. Therefore, the coordination number around the M depends on whether the sample is hydrated or not (distorted octahedral or square pyramid, respectively). In the anhydrous state, MOF74 contains open metal sites that are known to play a vital role in enhanced bonding of various gas molecules (H2, CH4, C2H2, NO, CO2, etc.) (Wu et al. Reference Wu, Simmons, Srinivas, Zhou and Yildirim2010). In Figures 2 and 3, only the oxygen atoms of the water molecules are shown. The channels in the honeycomb have a diameter of about 11 Å. The main difference between the Co-analog and the other three is the different number of adsorbed H2O molecules. For example, Co-MOF74 has about 10 water molecules per formula while the other three samples with M = Mn, Ni and Zn have around 6–7. As these three metals have the same charge in the same structure, the polarity/hydrophilicity of the frameworks can be reasonably expected to be similar, and thus the water contents are similar. In Table III, water molecules of hydration are included in the formula. In Mn-MOF74 and Ni-MOF74, O19 of the water molecule is situated on a three-fold axis whereas in Co-MOF74 and Zn-MOF74, no water molecule occupies a three-fold axis. The resulting formulae are M 6(C24H6O18)(H2O)6],·3nH2O (Z = 3, M = Mn, Ni,), and M(C4HO3)(H2O)·nH2O (Z = 18, M = Co and Zn).

Figure 2. The [001] view of the structure of M 2(dhtp) (M = Mn and Ni), showing the large one-dimensional channel pore with partially occupied water molecules (only oxygen atoms are shown). The MO6 groups are represented with yellow octahedra (blue sphere, oxygen; red spheres, C; green spheres, H).

Figure 3. The [001] view of the structure of M 2(dhtp) (M = Co), showing the large one- dimensional channel pore with partially occupied water molecules (only oxygen atoms are shown). The CoO6 groups are represented with yellow octahedra (blue sphere, oxygen; red spheres, C; green spheres, H).
TABLE III. Atomic coordinates and displacement factors (U iso) for M 2(dhtp); space group R 3. In this table, water molecules of hydration are included in the formula. The resulting formulae are M 6(C24H6O18)(H2O)6]·3nH2O (Z = 3, M=Mn, Ni,), or M(C4HO3)(H2O)·nH2O (Z = 18, M = Co and Zn). SOF represents the site occupancy factor.

Table IV gives the pertinent M–O bond distances in the four MOF74 analogs, respectively. The MO6 groups are shown as having a distorted octahedral environment, and the degree of distortion of the MO6 octahedra is similar. In the four MOF74 compounds, four of the M–O distances are shorter than the other two. The water molecule (M–O18) is trans to the longest M–O bond, and its M–O18 distance is also elongated. The distorted geometry of the octahedron is also illustrated by the O–M–O angles. In these compounds, the distorted angles range from 84.7(3)° to 101.5(3)° in the Mn-analog, from 81.8(2)° to 95.8(2)° in the Co-analog, from 73.36(10)° to 103.3(2)° in the Ni-analog, and from 75.00(8)° to 103.10(10)° in the Zn-analog.
TABLE IV. Relevant bond distances found in M 2(dhtp), M = Mn, Co, Ni, Zn. Rigid body distances in the organic moiety have been employed.

The bond valence sum values, V b, for M–O distances were calculated using the Brown–Altermatt empirical expression (Brown and Altermatt, Reference Brown and Altermatt1985; Brese and O'Keeffe, Reference Brese and O'Keeffe1991). The V b of an atom i is defined as the sum of the bond valences v ij of all the bonds from atoms i to atoms j. The most commonly adopted empirical expression for bond valence v ij as a function of the interatomic distance d ij is v ij = exp[(R 0− d ij)/B]. The parameter, B, is commonly taken to be a “universal” constant equal to 0.37 Å. The values for the reference distance R 0 for MnII–O, CoII–O, NiII–O, and ZnII–O are 1.790, 1.692, 1.654, and 1.704 respectively (Brown and Altermatt, Reference Brown and Altermatt1985; Brese and O'Keeffe, Reference Brese and O'Keeffe1991). The V b values for the Mn-, Co-, Ni-, and Zn-analogs around the M sites were calculated to be 2.212, 1.950, 2.077, and 2.234, respectively. The V b values for all four M–O octahedral sites indicate that they are all of 2+ ion. Although Co2+ is under tensile stress or underbonding (in an over-sized cage environment) as V b values (1.950) are smaller than the ideal valence of 2+ for that site, the V b of Mn2+, Ni2+, and Zn2+ are all greater than the value of 2 indicating that they are under compressive stress. As these are isostructural analogs, one possible explanation is that as the Co phase has substantially more water molecules in the channels, there are possible weak intermolecular interactions such as hydrogen bondings between the octahedral apexes (oxygen sites) with the water molecules, giving rise to tensile strain to the octahedral cage.
B. High-resolution X-ray powder diffraction pattern
The high-resolution reference pattern of a representative Mn-MOF74 is given in Table V as an example. In this pattern, the symbols ‘M’ and ‘ + ’ refer to peaks containing contributions from two and more than two reflections, respectively. The symbol * indicates that the particular peak has the strongest intensity of the entire pattern and has been designated a value of ‘999’. The intensity values reported are integrated intensities rather than peak heights. This pattern has been submitted for inclusion in the Powder Diffraction File (PDF).
TABLE V. X-ray diffraction pattern for Ni2(dhtp), (Trigonal R 3, a = 25.8561 (4) Å and c = 6.7119(2) Å, Z = 3). The symbols ‘M’ and ‘ + ’ refer to peaks containing contributions from two and more than two reflections, respectively. The symbol * indicates that the particular peak has the strongest intensity of the entire pattern and is designated a value of ‘999’.

IV. Summary
The M 2(2,5-dihydroxytetephthalate) (M = Ni-, Co-, Mn-, and Zn-) or the MOF74 family of compounds provide more insight into the chemistry of materials which possess coordinatively unsaturated open metal sites and small cylindrical pores. A brief comparison of the structure in terms of relevant bond distances and bond angles around the MO6 octahedral coordination environment of the metal ion shows that four of the M–O distances are shorter than the other two. The water molecule (M–O18) is trans to the longest M–O bond, and its M–O18 distance is also elongated. The bond valence calculations illustrate that while the V b values for the M = Mn, Ni and Zn compounds are all over the value of 2 (compressive stress), the corresponding value for the Co-analog was found to be <2 (tensile stress). In Co-MOF74, the interactions of the coordinated oxygen sites with the larger number of water molecules (hydrogen bonding network) may contribute to this difference. The reference X-ray powder diffraction patterns of these compounds have been submitted for inclusion in the Powder Diffraction File (PDF).
ACKNOWLEDGEMENTS
Use of the Advanced Photon Source at the Argonne National Laboratory was supported by the U. S. Department of Energy, Office of Science, Office of Basic Energy Sciences, under Contract No. DE-AC02-06CH11357. This work utilized facilities supported in part by the National Science Foundation under Agreement No. DMR-0454672. Partial support by ICDD (Grant-in-Aid 09-03) is also acknowledged.










