Hostname: page-component-745bb68f8f-g4j75 Total loading time: 0 Render date: 2025-02-06T12:35:23.818Z Has data issue: false hasContentIssue false
  • English
  • Français

Structure and X-ray powder reference patterns for hexagonal perovskite-related phases, (Sr0.8Ca0.2)5Co4O12 and Sr6Co5O15

Published online by Cambridge University Press:  05 March 2012

W. Wong-Ng ,
J. A. Kaduk  and
G. Liu
W. Wong-Ng*
Affiliation:
Ceramics Division, National Institute of Standards and Technology, Gaithersburg, Maryland 20899
J. A. Kaduk
Affiliation:
Poly Crystallography, Inc., Naperville, Illinois 60540
G. Liu
Affiliation:
Ceramics Division, National Institute of Standards and Technology, Gaithersburg, Maryland 20899
*
a)Author to whom correspondence should be addressed. Electronic mail: winnie.wong-ng@nist.gov
Rights & Permissions [Opens in a new window]

Abstract

Two selected members of the homologous series An+2BBn′O3n+3 (A=Sr and Ca; B and B′=Co) have been investigated for their crystal structures because of their potential applications as thermoelectric materials. A combined Rietveld refinement and spin-polarized magnetic geometry optimization technique was employed for the structural studies. Both the n=3 member, (Sr0.8Ca0.2)5Co4O12, and the n=4 member, Sr6Co5O15, have distorted hexagonal perovskite-related structures that possess one-dimensional cobalt oxide chains separated by alkaline-earth cations. The linear chains consist of one unit of CoO6 trigonal prism alternating with n units of CoO6 octahedra. Crystal structures and reference powder X-ray diffraction patterns of (Sr0.8Ca0.2)5Co4O11 [P3c1, a=9.4196(2) Å, c=19.9857(6) Å, V=825.83 Å3, and Dx=5.358 g/cm3] and Sr6Co5O15 [R32, a=9.497 64(12) Å, c=12.3956(2) Å, V=968.34 Å3, and Dx=5.455 g/cm3] are reported.

Keywords

thermoelectric materialsAn+2BBn′O3n+3 homologous series(Sr0.8Ca0.2)5Co4O12Sr6Co5O15crystal structurereference patterns
Type
Technical Articles
Information
Powder Diffraction , Volume 26 , Issue 1 , March 2011 , pp. 22 - 30
Copyright
Copyright © Cambridge University Press 2011

INTRODUCTION

The efficiency and performance of thermoelectric materials for power generation or cooling applications is related to the dimensionless figure of merit (Z T), given by

where T is the absolute temperature, S is the Seebeck coefficient or thermopower, σ is the electrical conductivity (σ=1/ρ, whereρ is the electrical resistivity), and k is the thermal conductivity (Tritt, Reference Tritt1996; Tritt and Subramanian, Reference Tritt and Subramanian2006). Until recently, only a small number of materials were found to have practical industrial applications. Increased research and development of thermoelectric materials has been mostly driven by the need for more efficient energy utilization and the dramatic increase in Z T values of materials recently discovered (Hsu et al., Reference Hsu, Loo, Guo, Chen, Dyck, Uher, Hogan, Polychroniadis and Kanatzidis2004; Venkatasubramanian et al., Reference Venkatasubramanian, Siivola, Colpitts and O’Quinn2001; Ghamaty and Eisner, Reference Ghamaty and Eisner1999; Dresselhaus et al., Reference Dresselhaus, Chen, Tang, Yang, Lee, Wang, Ren, Fleurial and Gogna2007; Funahashi et al., Reference Funahashi, Urata and Kitawaki2004).

Novel thermoelectric oxides that were discovered within the past decade have been of great interest to the thermoelectric community for high-temperature applications. For example, low dimensional cobaltites NaCoOx (Terasaki et al., Reference Taguchi, Takeda, Kanamaru, Shimada and Koizumi1997), Ca2Co3O6 (Mikami and Funahashi, Reference Mikami and Funahashi2005; Mikami et al., Reference Mikami, Funashashi, Yoshimura, Mori and Sasaki2003), and Ca3Co4O9 (Grebille et al., Reference Grebille, Lambert, Bouree and Petricek2004; Masset et al. Reference Masset, Michel, Maignan, Hervieu, Toulemonde, Studer and Raveau2000; Minami et al., Reference Minami, Itaka, Kawaji, Wang, Koinuma and Lippmaa2002) exhibit coexistence of large thermopower and low electrical resistivity. These compounds also have high electronic anisotropy. In NaCoOx and Ca3Co4O9 (Terasaki et al., Reference Terasaki, Sasago and Uchinokura1997; Grebille et al., Reference Grebille, Lambert, Bouree and Petricek2004; Masset et al. Reference Masset, Michel, Maignan, Hervieu, Toulemonde, Studer and Raveau2000; Minami et al., Reference Minami, Itaka, Kawaji, Wang, Koinuma and Lippmaa2002), the presence of Co-O layers appears to be critical for contributing to the desirable properties. The Ca3Co4O9 phase has the best thermoelectric property among the known oxides due to its distinctive misfit-layered oxide structure that features two penetrating incommensurate lattices with common a and c, and β parameters but with different b (Masset et al., Reference Masset, Michel, Maignan, Hervieu, Toulemonde, Studer and Raveau2000). These misfit layers were thought to scatter phonons, thereby lowering the thermal conductivity. Subsequent to these discoveries, studies of low dimensional cobaltites, including materials with dopants either on Ca or Co sites, have been increasing.

We have previously reported the phase diagram and thermoelectric properties of selected members in the Sr-Ca-Co-O system (Wong-Ng et al., Reference Wong-Ng, Liu, Martin, Thomas, Lowhorn and Kaduk2010). In this system, in addition to the reported (Ca,Sr)3Co4O9 phase, there are two homologous series of compounds, (Ca,Sr)n+2Co′ConO3n+3 and (Sr,Ca)n+2Co′ConO3n+3. While the members of the Can+2ConCo′O3n+3 and Srn+2ConCo′O3n+3 series have reasonably high Seebeck coefficients and relatively low thermal conductivity, the electrical conductivity needs to be increased in order to achieve high Z T values. Although we have determined their solid solution limits for the Can+2ConCo′O3n+3 and Srn+2ConCo′O3n+3 series, the structures of the n=3 (Sr5Co4O12) and n=4 (Sr6Co5O15) members have not been determined definitively. For example, only an ideal structure of Sr5Co4O12 has been derived from high-resolution electron microscopy (Christoffersen et al., 1997; Boulahya et al., Reference Boulahya, Parras and González-Calbet1999a). Structures of related phases such as Ba5CuIr3O12 and (Sr0.75Ba0.25)5NiMn3O12 have been determined to have space groups P321 (Blake et al., Reference Blake, Battle, Sloan, Vent, Darriet and Weill1999) and P-3c1 (Hernando et al., Reference Hernando, Boulahya, Parras, González-Calbet and Amador2003), respectively. It has also been reported that Sr5Co4O12 is isostructural with Sr5Ni4O11 (Lee and Holland, Reference Lee and Holland1991). However, a later report by Abraham et al. (Reference Abraham, Minaud and Renard1994) indicated that Sr5Ni4O11 was actually a mixed-valence compound

TABLE I. Rietveld refinement results of (Sr0.8Ca0.2)5Co4Ox. The R w p and R p values are calculated including the background.

of formula Sr4Ni3O9. For the structure of Sr6Co5O15, there exist two conflicting reported space groups of R32 (Harrison et al., Reference Harrison, Hegwood and Jacobson1995; Iwasaki et al., Reference Iwasaki, Yamane, Kubota, Takahashi and Shimada2003, Reference Iwasaki, Ito, Matsui, Nagasaki, Ohta and Koumoto2006; Rodriguez et al., Reference Rodriguez, Gonzalez, Grenier, Pannetier and Anne1987) and R-3 (Sun et al., Reference Sun, Li, Li, You and Lin2006).

The first goal of this paper is to clarify the structure of the n=3 and n=4 members in the (Sr,Ca)n+2Co′ConO3n+3 series by determining the structure of (Sr0.8Ca0.2)5Co4O11 and Sr6Co5O15 using the combined X-ray Rietveld refinement with a spin-polarized magnetic geometry optimization technique. Currently, the Powder Diffraction File (PDF) of

Figure 1. The structure of the homologous series of compounds, A n+2ConCo′O3n+3 (A=alkali earth elements), with n=1 (Wong-Ng et al., Reference Wong-Ng, Liu, Martin, Thomas, Lowhorn and Kaduk2010; Boulahya et al., Reference Boulahya, Parras and González-Calbet1999a; Boulahya et al., Reference Boulahya, Parras and González-Calbet1999b).

International Centre for Diffraction Data (ICDD) only contains calculated patterns for Sr5Co4O12 (PDF 04-011-1857) (ICDD, Reference Kabekkodu2010) and for Sr6Co5O15

TABLE II. Atomic coordinates of atoms in (Sr0.8Ca0.2)5Co4O12, P3c1. The atomic coordinates for the oxygen ions were obtained from quantum mechanical calculations.

Figure 2. The structure of the homologous series of compounds, A n+2ConCo′O3n+3 (A=alkali earth elements), with n=3 (Wong-Ng et al., Reference Wong-Ng, Liu, Martin, Thomas, Lowhorn and Kaduk2010; Boulahya et al., Reference Boulahya, Parras and González-Calbet1999a; Boulahya et al., Reference Boulahya, Parras and González-Calbet1999b).

(PDF 01-075-3227, 04-009-0961, 01-086-0614, and 01-075-4870 to 4873) (ICDD, Reference Kabekkodu2010). Since X-ray reference powder diffraction patterns are critical for phase characterization, the second goal of this paper is to report the experimental powder patterns for these two phases for an inclusion in the PDF.

EXPERIMENTAL

Sample preparation

Samples were prepared from stoichiometric amounts of CaCO3, Co3O4, and SrCO3 using solid state high-temperature techniques. The starting samples were mixed,

Figure 3. The structure of the homologous series of compounds, A n+2ConCo′O3n+3 (A=alkali earth elements), with n=4 (Wong-Ng et al., Reference Wong-Ng, Liu, Martin, Thomas, Lowhorn and Kaduk2010; Boulahya et al., Reference Boulahya, Parras and González-Calbet1999a; Boulahya et al., Reference Boulahya, Parras and González-Calbet1999b).

Figure 4. The structure of the homologous series of compounds, A n+2ConCo′O3n+3 (A=alkali earth elements), with n=∞ (Wong-Ng et al., Reference Wong-Ng, Liu, Martin, Thomas, Lowhorn and Kaduk2010; Boulahya et al., Reference Boulahya, Parras and González-Calbet1999a; Boulahya et al., Reference Boulahya, Parras and González-Calbet1999b).

pelletized, and annealed at 750 °C for 1 day and subsequently annealed at 850 °C with intermediate grindings and pelletizations for another 7 days. The annealing process was repeated until no further changes were detected in the powder X-ray diffraction patterns.

X-ray powder diffraction

Phase identification

Powder X-ray diffraction was used to investigate the phase purity and establish the phase relationships. These experiments were carried out using a Phillips X-ray powder diffractometer with Cu K α radiation which was equipped with a series of Soller slits and a scintillation counter. The 2θ scanning range was from 10° to 80° and the step interval was

TABLE III. Bond distances in (Sr,Ca)5Co4O12. V b represents bond valence sum (Brese and O’Keeffe, Reference Brese and O’Keeffe1991; Brown and Altermatt, Reference Brown and Altermatt1985). The V b values for the mixed (Sr, Ca) sites were computed based on the respective site occupancy.

Figure 5. (Color online) Observed (crosses) and calculated (solid line) XRD intensity pattern for (Sr0.8Ca0.2)5Co4O12 at 300 K. The row of tick marks indicate the calculated peak positions. The difference pattern is plotted at same scale as the other patterns up to 50°2θ. At between 50 and 100°2θ, the scale has been magnified five times. At 2θ values higher than 100°, the scale has been magnified ten times. An impurity phase of SrCoO3 was determined to be 3.9(2) mass %.

0.03°. The ICDD PDF reference diffraction patterns of the Ca-Sr-Co-O systems were used for performing phase identification.

Crystal structure analysis

The Ca-Sr-Co-O powders were mounted as acetone slurries in silicon zero-background holders. A PANalytical X’Pert Pro MPD diffractometer equipped with a PIXcel position-sensitive detector and a graphite diffracted beam monochromator was used to measure the powder patterns (Cu K α radiation, 40 kV, and 40 mA) from 5 to 148°2θ in 0.013° steps, counting for 0.5 s/step. All data processing and structural refinements were carried out using the Rietveld refinement technique with the GSAS software suite (Larson and von Dreele, Reference Larson and von Dreele1992; Rietveld, Reference Rietveld1969). Included in the refinements were the atomic coordinates and isotropic displacement coefficients, a scale factor, a sample displacement coefficient, and the unit-cell parameters. The peak profiles were described using a pseudo-Voigt function; for (Sr0.8Ca0.2)5Co4O11 the size broadening p t e c and the anisotropic strain broadening terms S x y were refined, and for Sr6Co5O15 the profile Y strain term was refined. The backgrounds of the profiles were described using a six- or nine-term shifted Chebyshev polynomial. To ensure the correctness of structure, a VASP spin-polarized magnetic geometry optimization technique (with fixed lattice parameters) using “normal” precision and a plane wave cutoff energy of 400 eV was performed for optimization of geometry (Kresse and Furthmüller, Reference Kresse and Furthmüller1996a, Reference Kresse and Furthmüller1996b; Kresse and Joubert, Reference Kresse and Joubert1999). GGA-PBE/PAW potentials were used with a 2×2×1 k-point mesh for a spacing of 0.385×0.385×0.314 Å−1.

X-ray reference patterns were obtained with a Rietveld pattern decomposition technique (Larson and von Dreele, Reference Larson and von Dreele1992). Using this technique, the reported peak positions are calculated from the lattice parameters. For overlapped peaks, the intensities are summed, and an intensity-weighted d spacing is reported. Therefore, these patterns represent ideal specimen patterns. They are corrected for systematic errors both in d-spacing and intensity.

Bond valence sums (V b) calculations

The bond valence sum values, V b, of an atom i are defined as the sum of the bond valences v i j of all the bonds from atoms i to atoms j. The most commonly adopted empirical expression for v i j as a function of the interatomic distance d i j is v i j=exp[(R 0−d i j)/B]. The parameter, B, is commonly taken to be a “universal” constant equal to 0.37 Å. V b’s for Sr/Ca and Co are calculated using the Brown-Altermatt empirical expression (Brese and O’Keeffe, Reference Brese and O’Keeffe1991; Brown and Altermatt, Reference Brown and Altermatt1985). The values of the reference distance R 0 for Sr-O and Ca-O are 2.118 and 2.065 Å, respectively (Brese and O’Keeffe, Reference Brese and O’Keeffe1991; Brown and Altermatt, Reference Brown and Altermatt1985). The V b values for the mixed (Sr, Ca) sites were computed based on the respective site occupancy. The R 0 values for Co2+ and Co3+ have been reported to be 1.692 and 1.70 by Brese and O’Keeffe (Reference Brese and O’Keeffe1991), and the approximate value for Co4+ (1.708) has been estimated by extrapolation from the Co2+ and Co3+ values.

RESULTS AND DISCUSSION

The structures of the general A n+2B′B nO3n+3 (A=Sr and Ca; B=Co) homologous series and of two representative members of the series, (Sr0.8Ca0.2)5Co4O12 and Sr6Co5O15, and their reference X-ray powder diffraction patterns are described in the following.

General structure description of A n+2B′B nO3n+3 (A=Sr and Ca; B=Co)

In the formula A n+2B nB′O3n+3, A is an alkaline-earth element, B describes the cobalt ion inside the octahedral cage, and B′ describes the cobalt ion inside a trigonal prism. Srn+2ConCoO3n+3 consists of one-dimensional linear parallel Co2O66− chains, built by successive alternating face-sharing CoO6 trigonal prisms and CoO6 octahedra along the hexagonal c axis (Wong-Ng et al., Reference Wong-Ng, Liu, Martin, Thomas, Lowhorn and Kaduk2010; Boulahya et al., Reference Boulahya, Parras and González-Calbet1999a, Reference Boulahya, Parras and González-Calbet1999b; Stitzer et al., Reference Stitzer, Darriet and zur Loye2001). This face-sharing feature is in contrast with Ca3Co4O9 and NaCo2O4, which consists of edge-sharing CoO6 octahedra (Masset et al., Reference Masset, Michel, Maignan, Hervieu, Toulemonde, Studer and Raveau2000). The Co2O66− chains can be considered as stacking of n number of octahedra alternating with one trigonal prism. The compounds of A n+2ConCo′O3n+3 can also be considered as ordered intergrowth between the n=∞ (ACoO3) and n=1 (A 3Co2O6) end members. These compounds are of interest to the thermoelectric community because it is thought that scattering of heat phonons is perpendicular to the structural Co-O chain directions, which lowers the thermal conductivity.

The structure of the homologous series of compounds, A n+2ConCo′O3n+3 (A=alkali earth elements), with n=1, 3, 4, and ∞, is shown from Figures 1–4 (Wong-Ng et al., Reference Wong-Ng, Liu, Martin, Thomas, Lowhorn and Kaduk2010; Boulahya et al., Reference Boulahya, Parras and González-Calbet1999a, Reference Boulahya, Parras and González-Calbet1999b). Based on our previous study

TABLE IV. Rietveld refinement results of Sr6Co5O15, R32.

of phase equilibria of the SrO-CaO-CoOx system, Ca substitutes in the Sr site for the n=3 and 4 members of the Srn+2ConCo′O3n+3 series to the extent of (Sr0.67Ca0.33)5Co4O11 and (Sr0.725Ca0.275)6Co5Ox, respectively (Wong-Ng et al., Reference Wong-Ng, Liu, Martin, Thomas, Lowhorn and Kaduk2010). The stability of these compounds is related to the size of the alkaline earth. For example, for A=Ca, only n=1 member can be prepared. When A=Sr, n=2, 3, and 4 can be prepared but not with n=1 member under the current processing conditions. For compounds with n>4, only the A=Ba analogs can be made.

Structure of (Sr0.8Ca0.2)5Co4O12

Figure 5 gives the observed (crosses) and calculated (solid line) XRD intensity pattern for (Sr0.8Ca0.2)5Co4O12 at 300 K. Tables I–III give the Rietveld refinement results, the atomic coordinates, and the bond distances of (Sr,Ca)5Co4O12, respectively. The oxygen coordinates that we report are those resulted from the VASP spin-polarized magnetic geometry optimization calculations, as they are more reliable than those from Rietveld refinements.

Based on the refinement results, the space group of (Sr0.8Ca0.2)5Co4O12 was determined to be P3c1 instead of

TABLE V. Atomic coordinates of atoms in Sr6Co5O15.

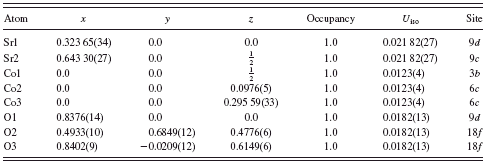
Figure 6. (Color online) Observed (crosses) and calculated (solid line) XRD intensity pattern for Sr6Co5O15 at 300 K. The row of tick marks indicate the calculated peak positions. The difference pattern is plotted at same scale as the other patterns up to 65°2θ. At higher angles, the scale has been magnified five times. An impurity phase of Co3O4 was determined to be 2.1(1) mass fraction %.

P321. The lattice parameters are a=9.4196(2) Å, c=19.9857(6) Å, V=825.83 Å3, and D x=5.358 g/cm3. Ca was confirmed to substitute in the Sr site.

The structure of the n=3 member of (Sr,Ca)n+2ConCo′O3n+3 consists of linear chains of three units of octahedra alternating with one unit of trigonal prism, giving rise to a total of nine octahedra and three trigonal prisms per chain along the c axis within the unit cell (Figure 2). The Co ions in the columns face each other at distances between 2.419(12) and 2.534(4) Å. This relatively short distance will likely produce a large electrostatic repulsion between the metal ions. The oxygen ions of face-shared triangles screen the Coulomb interaction between Co ions and therefore weaken the repulsion. As the distances between the Co ions in the prisms and in the octahedra are only about 2.5 Å, whereas the distances between Co ions in the parallel chains are about 5 Å, there are possible interactions between Co ions in the same chains via superexchange, but these interactions are not likely to occur between the neighboring chains.

At present, there is no conclusive evidence about whether there is charge ordering of Co ions along the chain of A n+2ConCo′O3n+3 (A=alkaline-earth cations). According to Maignan et al. (Reference Maignan, Hébert, Martin and Flahaut2003), in Ca3Co2O6 (n=1 member), no evidence of Co2+/Co4+ ordering (Co2+ ions occupy the prismatic position, while Co4+ occupies the octahedral sites) was detected from high-temperature magnetic susceptibility measurements (Maignan et al., Reference Maignan, Michel, Masset, Martin and Raveau2000). The cobalt species are trivalent, and the larger cation (high-spin Co3+) occupies the trigonal prism site, while the low-spin Co3+ occupies the octahedral site. Fjellvåg et al. (Reference Fjellvåg, Gulbrandsen, Aasland, Olsem and Hauback1996) found the bond valence V b value for the prismatic Co site to be 2.25 while the octahedral Co site to have a much higher valence of 3.35. Therefore, there could be charge ordering of Co2+/Co4+ or ordering of low- and high-spin Co3+ species.

The average valence for the Co ions in (Sr0.8Ca0.2)5Co4O12 was calculated to be 3.5. In (Sr0.8Ca0.2)5Co4O12, if we assume the valence of the three octahedral Co sites to be 4+ and the valence of the Co in the trigonal prism to be 2+, then the charge balanced formula can be written as (Sr,Ca)2+5Co4+3Co2+O122−. As indicated in Table I, the Co sites that are inside the trigonal prisms are labeled as Co1, Co5, and Co9. The values of V b at these trigonal prism sites, while smaller than those of the octahedral sites, are greater than the ideal value of 2.0 (2.758 for Co1, 2.888 for Co5, and 3.145 for Co9) possibly due to the presence of compressive stress (or the size of the cage too small). At the same time the V b values of the octahedral Co sites are all less than the ideal value of 4+ (ranging from 3.433 to 3.714), indicating tensile stress or underbonding because the sizes of the cages where these cations reside are too large. It is also possible that all these Co sites have mixed-valence characters because of metal to metal (Co/Co) interactions along the chains.

The Sr2+/Ca2+ ions have three different types of cage environment or coordination number, namely, one eight-coordination cage (Sr1/Ca1, with average Sr/Ca-O distance of 2.56 Å), three nine-coordination cages (average distances of 2.68 Å for Sr2/Ca2, 2.64 Å for Sr3/Ca3, and 2.64 Å for Sr5/Ca5), and one ten-coordination cage (average distance of 2.74 Å for Sr4/Ca4). The V b values of these sites are all greater than 2.0 (Table III), indicating compressive stress or overbonding.

Structure of Sr6Co5O15

Our refinement results show the structure of Sr6Co5O15 to be R32. The crystal structure of Sr6Co5O15 is shown in Figure 3. Table IV and Figure 6 give the Rietveld refinement

TABLE VI. Bond distances of atoms in Sr6Co5O15. V b represents bond valence sum values (Brese and O’Keeffe, Reference Brese and O’Keeffe1991; Brown and Altermatt, Reference Brown and Altermatt1985).

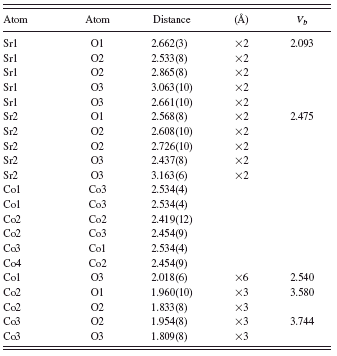
TABLE VII. X-ray reference pattern for (Ca0.2Sr0.8)5Co4O11, P3c1 (No. 165), a=9.4196(2) Å, c=19.9857(6) Å, V=825.83 Å3, and D x=5.358 g/cm3. The symbol d cal refers to calculated d-spacing values, I obs refers to observed integrated intensity value (scaled according to the maximum value of 999; the symbol * indicates the strongest peak), the h k l values are the Miller indexes, and M and + refer to peaks containing contributions from two and more than two reflections, respectively.

results. In Figure 6, the observed (crosses) and calculated (solid line) XRD intensity pattern for Sr6Co5O15 at 295 K are shown. The difference pattern is plotted at the same scale as the other patterns. Tables V and VI provide the atomic coordinates and bond distances of Sr6Co5O15. Similar to (Sr0.8Ca0.2)5Co4O12, the oxygen coordinates that we report are those resulted from the VASP spin-polarized magnetic geometry optimization calculations.

All Co ions in Sr6Co5O15 are six coordinated. Co1 has a trigonal prism environment with all six Co-O distances equal at 2.018(6) Å. Both Co2 and Co3 have a distorted octahedral environment with bond distances ranging from 1.809(8) to 1.960(10) Å. Similar to the structure of (Sr0.8Ca0.2)5Co4O12, the V b values of Co in the trigonal prisms tend to be lower (close to the value of 2.5) than those in the octahedra (3.580 and 3.744). The average oxidation state of Co in Sr6Co5O15 is 3.6. One can achieve charge balance if all the Co’s in the octahedral sites of Sr6Co5O15 have a valence of 4+, and the one Co in the trigonal prism site has a valence of 2+, leading to the formula Sr62+Co44+Co2+O15. The 2.5 value of V b at the trigonal prism Co1 site is possibly due to the presence of compressive stress as compared to the ideal valence state of 2+. In the octahedral Co2 and Co3 sites, both V b values are less than 4+, indicating tensile stress. Similar to (Sr0.8Ca0.2)5Co4O12, the Co…Co distances which range from 2.38(2) to 2.61(2) Å are much shorter than those between chains (about 5 Å); therefore, superexchange between Co ions would not be likely among chains.

Two crystallographically independent Sr environments were found; both are coordinated to ten oxygen atoms (average Sr1-O and Sr2-O distances of 2.09 and 2.48 Å, respectively). By comparing these coordination environments with the (Sr0.8Ca0.2)5Co4O12 structure [containing eight-, nine-, and tenfold (Sr, Ca)-O coordinations], we found that the alkaline-earth oxide cages in Sr6Co5O15 have a relatively larger average cage size. Therefore, as n increases in Srn+2Co′ConO3n+3, the average alkaline-earth cage size increases accordingly. It is clear from our results and those of

TABLE VIII. X-ray reference pattern for Sr6Co5O12, R32 (No. 155), a=9.497 64(12) Å, c=12.3956(2) Å, V=968.34 Å3, and D x=5.455 g/cm3. The symbol d cal refers to calculated d-spacing values, I obs refers to observed integrated intensity value (scaled according to the maximum value of 999; the symbol * indicates the strongest peak), the h k l values are the Miller indexes, and M and + refer to peaks containing contributions from two and more than two reflections, respectively.

the Ca- and Ba-homologous series (Boulahya et al., Reference Boulahya, Parras and González-Calbet1999b; Fjellvåg et al., Reference Fjellvåg, Gulbrandsen, Aasland, Olsem and Hauback1996) that the size of the alkaline-earth cage is important for the stability of the homologous members; the higher the n value is, the larger the cage size is. For example, the coordination number for Ca2+ is 8 in Ca3Co2O6 (n=1 phase) (Fjellvåg et al., Reference Fjellvåg, Gulbrandsen, Aasland, Olsem and Hauback1996) but is greater than 10 around the Ba2+ in Ba8Co7O21 (n=6 member) (Taguchi et al., Reference Taguchi, Takeda, Kanamaru, Shimada and Koizumi1977). The alkaline-earth ions also play a role of adjusting the spacing between chains.

Reference X-ray powder diffraction patterns

The reference X-ray powder diffraction patterns for the phases (Sr,Ca)5Co4O11 and Sr6Co5O15 have been prepared and submitted to the ICDD to be included in the Powder Diffraction File. Tables VII and VIII give the reference patterns for (Sr,Ca)5Co4O11 and Sr6Co5O15, respectively. In these tables, the symbols M and + refer to peaks containing contributions from two and more than two reflections, respectively. The symbol * indicates the particular peak has the strongest intensity of the entire pattern and is designated a value of “999.” The intensity values reported are integrated intensities rather than peak heights.

CONCLUSION

The structures of (Sr,Ca)5Co4O11 and of Sr6Co5O15 in the (Sr,Ca)n+2Co′ConO3n+3 system have been studied because of their potential applications as thermoelectric materials. These structures belong to the n=3 and n=4 members of the homologous series of A n+2ConCo′O3n+3 [A=Sr and (Sr, Ca)]. The salient feature of the structures is the linear chains consisting of alternating CoO6 trigonal prisms with n members of CoO6 octahedra. It is clear from our results and from studies of the Ca- and Ba-homologous series that the size of the alkaline-earth cage is important for the stability of the homologous members; the higher the n value is, the larger the alkaline-earth cage size is. The alkaline-earth ions also play a role of adjusting the spacing between chains. The possible charge ordering along the chain direction still needs to be further studied. The reference X-ray powder diffraction patterns of these two phases have been submitted to the Powder Diffraction File. As cobalt oxides are stable materials at high temperature that possess interesting thermoelectric properties, continuing research efforts in this class of materials in the future are of great interest.

ACKNOWLEDGMENT

The partial financial support from ICDD for the preparation of the reference X-ray powder diffraction patterns is acknowledged.

References

Abraham, F., Minaud, S., and Renard, C. (1994). “Preliminary crystal structure of mixed-valency Sr4Ni3O9, the actual formula of the so-called Sr5Ni4O11,” J. Mater. Chem.JMACEP 4, 1763–1764.10.1039/jm9940401763CrossRefGoogle Scholar
Blake, G. R., Battle, P. D., Sloan, J., Vent, J. F., Darriet, J., and Weill, F. (1999). “Neutron diffraction study of the structures of Ba5CuIr3O12 and Ba16Cu3Ir10O39,” Chem. Mater.CMATEX 11, 1551–1558.10.1021/cm9807844CrossRefGoogle Scholar
Boulahya, K., Parras, M., and González-Calbet, J. M. (1999a). “The A n+2B nB′O3n+3 family (B=B′=Co): Ordered intergrowth between 2H-BaCoO3 and Ca3Co2O6 structures,” J. Solid State Chem.JSSCBI 145, 116–127.10.1006/jssc.1999.8230CrossRefGoogle Scholar
Boulahya, K., Parras, M., and González-Calbet, J. M. (1999b). “Cation deficiency in (Ba,Sr)Co1-xOy hexagonal perovskite related oxides: New members of the A n+2B′B nO3n+3 homologous series,” J. Solid State Chem.JSSCBI 142, 419–427.10.1006/jssc.1998.8057CrossRefGoogle Scholar
Brese, N. E. and O’Keeffe, M. (1991). “Bond-valence parameters for solids,” Acta Crystallogr., Sect. B: Struct. Sci.ASBSDK 47, 192–197.10.1107/S0108768190011041CrossRefGoogle Scholar
Brown, I. D. and Altermatt, D. (1985). “Bond-valence parameters obtained from a systematic analysis of the inorganic crystal structure database,” Acta Crystallogr., Sect. B: Struct. Sci.ASBSDK 41, 244–247.10.1107/S0108768185002063CrossRefGoogle Scholar
Dresselhaus, M. S., Chen, G., Tang, M. Y., Yang, R. G., Lee, H., Wang, D. Z., Ren, Z. F., Fleurial, J. P., and Gogna, P. (2007). “Enhanced thermopower in PbSe nanocrystal quantum dot superlattices,” Adv. Mater.ADVMEW 19, 1043–1053.10.1002/adma.200600527CrossRefGoogle Scholar
Fjellvåg, H., Gulbrandsen, E., Aasland, S., Olsem, A., and Hauback, B. C. (1996). “Crystal structure and possible charge ordering in one-dimensional Ca3Co2O6,” J. Solid State Chem.JSSCBI 124, 190–194.10.1006/jssc.1996.0224CrossRefGoogle Scholar
Funahashi, R., Urata, S., and Kitawaki, M. (2004). “Exploration of n-type oxides by high throughput screening,” Appl. Surf. Sci.ASUSEE 223, 44–48.10.1016/S0169-4332(03)00899-7CrossRefGoogle Scholar
Ghamaty, S. and Eisner, N. B. (1999). “Development of quantum well thermoelectric films,” Proceedings of the 18th International Conference on Thermoelectrics, Baltimore, MD, pp. 485–488.Google Scholar
Grebille, D., Lambert, S., Bouree, F., and Petricek, V. (2004). “Contribution of powder diffraction for structure refinements of aperiodic misfit cobalt oxides,” J. Appl. Crystallogr.JACGAR 37, 823–831.10.1107/S0021889804018096CrossRefGoogle Scholar
Harrison, W. T. A., Hegwood, S. L., and Jacobson, A. L. (1995). “A powder neutron diffraction determination of the structure of Sr6Co5O15, formerly described as the low-temperature hexagonal form of SrCoO3−x,” J. Chem. Soc., Chem. Commun.JCCCAT1953–1954.10.1039/c39950001953CrossRefGoogle Scholar
Hernando, M., Boulahya, K., Parras, M., González-Calbet, J. M., and Amador, U. (2003). “Synthesis and microstructural characterization of two new one-dimensional members of the (A3NiMnO6)α(A3Mn3O9)β homologous series (A=Ba,Sr),” Eur. J. Inorg. Chem.EJICFO2419–2425.10.1002/ejic.200300028CrossRefGoogle Scholar
Hsu, K. F., Loo, S., Guo, F., Chen, W., Dyck, J. S., Uher, C., Hogan, T., Polychroniadis, E. K., and Kanatzidis, M. G. (2004). “Cubic AgPbmSbTe2+m: Bulk thermoelectric materials with high figure of merit,” ChemInform 35 (17).10.1002/chin.200417240CrossRefGoogle Scholar
ICDD (2010). “Powder Diffraction File,’’ edited by Kabekkodu, S., International Centre for Diffraction Data, Newtown Square, Pennsylvania.Google Scholar
Iwasaki, K., Ito, T., Matsui, T., Nagasaki, T., Ohta, S., and Koumoto, K. (2006). “Synthesis of an oxygen nonstoichiometric Sr6Co5O15 phase,” Mater. Res. Bull.MRBUAC 41, 732–739.10.1016/j.materresbull.2005.10.012CrossRefGoogle Scholar
Iwasaki, K., Yamane, H., Kubota, S., Takahashi, J., and Shimada, M. (2003). “Power factors of Ca3Co2O6 and Ca3Co2O6-based solid solutions,” J. Alloys Compd.JALCEU 358, 210–215.10.1016/S0925-8388(03)00041-0CrossRefGoogle Scholar
Kresse, G. and Furthmüller, J. (1996a). “Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set,” Phys. Rev. BPLRBAQ 54, 11169–11186.10.1103/PhysRevB.54.11169CrossRefGoogle ScholarPubMed
Kresse, G. and Furthmüller, J. (1996b). “Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set,” Comput. Mater. Sci.CMMSEM 6, 15–50.10.1016/0927-0256(96)00008-0CrossRefGoogle Scholar
Kresse, G. and Joubert, D. (1999). “From ultrasoft pseudopotentials to the projector augmented-wave method,” Phys. Rev. BPLRBAQ 59, 1758–1775.10.1103/PhysRevB.59.1758CrossRefGoogle Scholar
Larson, A. C. and von Dreele, R. B. (1992). “GSAS-General Structure Analysis system,” U.S. Government contract (W-7405-ENG-36) by the Los Alamos National Laboratory, which is operated by the University of California for the U.S. Department of Energy.Google Scholar
Lee, J. and Holland, G. (1991). “Identification of a new strontium Ni(III) oxide prepared in molten hydroxide,” J. Solid State Chem.JSSCBI 93, 267–271.10.1016/0022-4596(91)90299-WCrossRefGoogle Scholar
Maignan, A., Hébert, S., Martin, C., and Flahaut, D. (2003). “One dimensional compounds with large thermoelectric power factor,” Mater. Sci. Eng., BMSBTEK 104, 1298–1299.10.1016/S0921-5107(03)00183-1CrossRefGoogle Scholar
Maignan, A., Michel, C., Masset, A. C., Martin, C., and Raveau, B. (2000). “Single crystal study of the one dimensional Ca3Co2O6 compound: Five stable configurations for the Ising triangular lattice,” Eur. Phys. J. BEPJBFY 15, 657–663.10.1007/PL00011051CrossRefGoogle Scholar
Masset, A. C., Michel, C., Maignan, A., Hervieu, M., Toulemonde, O., Studer, F., and Raveau, B. (2000). “Misfit-layered cobaltite with an anisotropic giant magnetoresistance: Ca3Co4O9,” Phys. Rev. BPLRBAQ 62, 166–175.10.1103/PhysRevB.62.166CrossRefGoogle Scholar
Mikami, M. and Funahashi, R. (2005). “The effect of element substitution on high-temperature thermoelectric properties of Ca3Co2O6 compounds,” J. Solid State Chem.JSSCBI 178, 1670–1674.10.1016/j.jssc.2005.03.004CrossRefGoogle Scholar
Mikami, M., Funashashi, R., Yoshimura, M., Mori, Y., and Sasaki, T. (2003). “High-temperature thermoelectric properties of single-crystal Ca3Co2O6,” J. Appl. Phys.JAPIAU 94, 6579–6582.10.1063/1.1622115CrossRefGoogle Scholar
Minami, H., Itaka, K., Kawaji, H., Wang, Q. J., Koinuma, H., and Lippmaa, M. (2002). “Rapid synthesis and characterization of (Ca1−xBax)3Co4O9 thin films using combinatorial methods,” Appl. Surf. Sci.ASUSEE 197–198, 442–447.10.1016/S0169-4332(02)00359-8CrossRefGoogle Scholar
Rietveld, H. M. (1969). “A profile refinement method for nuclear and magnetic structures,” J. Appl. Crystallogr.JACGAR 2, 65–71.10.1107/S0021889869006558CrossRefGoogle Scholar
Rodriguez, J., Gonzalez, C. J. M., Grenier, J. C., Pannetier, J., and Anne, M. (1987). “Phase transitions in Sr2Co2O5: A neutron thermodiffracometry study,” Solid State Commun.SSCOA4 62, 231–234.10.1016/0038-1098(87)90801-5CrossRefGoogle Scholar
Stitzer, K. E., Darriet, J., and zur Loye, H. -C. (2001). “Advances in the synthesis and structural description of 2H-hexagonal perovskite-related oxides,” Curr. Opin. Solid State Mater. Sci.COSSFX 5, 535–544.10.1016/S1359-0286(01)00032-8CrossRefGoogle Scholar
Sun, J., Li, G., Li, Z., You, L., and Lin, J. (2006). “Crystal growth and structure determination of oxygen-deficient Sr6Co5O15,” Inorg. Chem.INOCAJ 45, 8394–8402.10.1021/ic060862mCrossRefGoogle ScholarPubMed
Taguchi, H., Takeda, Y., Kanamaru, F., Shimada, M., and Koizumi, M. (1977). “Barium cobalt trioxide,” Acta Crystallogr., Sect. B: Struct. Sci.ASBSDK 33, 1298–1299.10.1107/S0567740877005949CrossRefGoogle Scholar
Terasaki, I., Sasago, Y., and Uchinokura, K. (1997). “Large thermoelectric power in NaCo2O4 single crystals,” Phys. Rev. BPLRBAQ 56, R12685-R12687.10.1103/PhysRevB.56.R12685CrossRefGoogle Scholar
Tritt, T. M. (1996). “Thermoelectrics run hot and cold,” ScienceSCIEAS 272, 1276–1277.10.1126/science.272.5266.1276CrossRefGoogle Scholar
Tritt, T. M. and Subramanian, M. A., guest editors (2006). “Thermoelectric materials, phenomena, and applications: A bird’s eye view,” MRS Bull.MRSBEA 31, 188–195.10.1557/mrs2006.44CrossRefGoogle Scholar
Venkatasubramanian, R., Siivola, E., Colpitts, T., and O’Quinn, B. (2001). “Growth of one-dimensional Si/SiGe heterostructures by thermal CVD,” Nature (London)NATUAS 413, 597–602.10.1038/35098012CrossRefGoogle Scholar
Wong-Ng, W., Liu, G., Martin, J., Thomas, E. L., Lowhorn, N., and Kaduk, J. A. (2010). “Phase compatibility and thermoelectric properties of compounds in the Sr-Ca-Co-O System,” J. Appl. Phys.JAPIAU 107, 033508.10.1063/1.3276158CrossRefGoogle Scholar
Figure 0

TABLE I. Rietveld refinement results of (Sr0.8Ca0.2)5Co4Ox. The Rwp and Rp values are calculated including the background.

Figure 1

Figure 1. The structure of the homologous series of compounds, An+2ConCo′O3n+3 (A=alkali earth elements), with n=1 (Wong-Ng et al., 2010; Boulahya et al., 1999a; Boulahya et al., 1999b).

Figure 2

TABLE II. Atomic coordinates of atoms in (Sr0.8Ca0.2)5Co4O12, P3c1. The atomic coordinates for the oxygen ions were obtained from quantum mechanical calculations.

Figure 3

Figure 2. The structure of the homologous series of compounds, An+2ConCo′O3n+3 (A=alkali earth elements), with n=3 (Wong-Ng et al., 2010; Boulahya et al., 1999a; Boulahya et al., 1999b).

Figure 4

Figure 3. The structure of the homologous series of compounds, An+2ConCo′O3n+3 (A=alkali earth elements), with n=4 (Wong-Ng et al., 2010; Boulahya et al., 1999a; Boulahya et al., 1999b).

Figure 5

Figure 4. The structure of the homologous series of compounds, An+2ConCo′O3n+3 (A=alkali earth elements), with n=∞ (Wong-Ng et al., 2010; Boulahya et al., 1999a; Boulahya et al., 1999b).

Figure 6

TABLE III. Bond distances in (Sr,Ca)5Co4O12. Vb represents bond valence sum (Brese and O’Keeffe, 1991; Brown and Altermatt, 1985). The Vb values for the mixed (Sr, Ca) sites were computed based on the respective site occupancy.

Figure 7

Figure 5. (Color online) Observed (crosses) and calculated (solid line) XRD intensity pattern for (Sr0.8Ca0.2)5Co4O12 at 300 K. The row of tick marks indicate the calculated peak positions. The difference pattern is plotted at same scale as the other patterns up to 50°2θ. At between 50 and 100°2θ, the scale has been magnified five times. At 2θ values higher than 100°, the scale has been magnified ten times. An impurity phase of SrCoO3 was determined to be 3.9(2) mass %.

Figure 8

TABLE IV. Rietveld refinement results of Sr6Co5O15, R32.

Figure 9

TABLE V. Atomic coordinates of atoms in Sr6Co5O15.

Figure 10

Figure 6. (Color online) Observed (crosses) and calculated (solid line) XRD intensity pattern for Sr6Co5O15 at 300 K. The row of tick marks indicate the calculated peak positions. The difference pattern is plotted at same scale as the other patterns up to 65°2θ. At higher angles, the scale has been magnified five times. An impurity phase of Co3O4 was determined to be 2.1(1) mass fraction %.

Figure 11

TABLE VI. Bond distances of atoms in Sr6Co5O15. Vb represents bond valence sum values (Brese and O’Keeffe, 1991; Brown and Altermatt, 1985).

Figure 12

TABLE VII. X-ray reference pattern for (Ca0.2Sr0.8)5Co4O11, P3c1 (No. 165), a=9.4196(2) Å, c=19.9857(6) Å, V=825.83 Å3, and Dx=5.358 g/cm3. The symbol dcal refers to calculated d-spacing values, Iobs refers to observed integrated intensity value (scaled according to the maximum value of 999; the symbol * indicates the strongest peak), the hkl values are the Miller indexes, and M and + refer to peaks containing contributions from two and more than two reflections, respectively.

Figure 13

TABLE VIII. X-ray reference pattern for Sr6Co5O12, R32 (No. 155), a=9.497 64(12) Å, c=12.3956(2) Å, V=968.34 Å3, and Dx=5.455 g/cm3. The symbol dcal refers to calculated d-spacing values, Iobs refers to observed integrated intensity value (scaled according to the maximum value of 999; the symbol * indicates the strongest peak), the hkl values are the Miller indexes, and M and + refer to peaks containing contributions from two and more than two reflections, respectively.