II. EXPERIMENTAL

III. RESULTS AND DISCUSSION

The crystallographic parameters describing the crystal structure of [Co(NH₃)₅Cl]Cl₂ after Rietveld refinement, and the Rietveld agreement factors are summarized in Tables I and II. Figure 1 shows the coordination sphere around the Co(III) ions and the Co(III)—ligand interatomic distances. Figure 2 shows the Rietveld refinement graph.

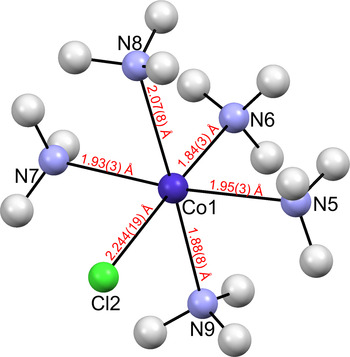
Figure 1. (Color online) The coordination sphere around the Co(III) ions in [Co(NH₃)₅Cl]Cl₂ showing the atom-labeling scheme and selected interatomic distances. Thermal ellipsoids are represented at the 50% probability level. Co³⁺ ions are shown in dark blue, N in light blue, Cl⁻ in green, and H in light gray.

Figure 2. (Color online) Observed (blue circles), calculated (solid red line), and difference (bottom black line) X-ray powder diffraction patterns of [Co(NH₃)₅Cl]Cl₂ refined by the Rietveld method in the space group Pn2₁ a (No. 33), orthorhombic. Vertical bar symbols represent allowed peak positions.

It has been pointed out (Toby, Reference Toby2006) that the best way to judge the correctness of a model from powders is: (1) graphically and carefully observing the experimental and calculated Rietveld profiles; and (2) confirming that the chemical bonding in the model is plausible. For this material, since powder and single-crystal diffraction give rise to crystal structure descriptions in two space groups, Pnma and Pn2₁ a, respectively, and unresolved subtleties in the internal geometry of the coordination complex still remained after the work of Messmer and Amma (Reference Messmer and Amma1968); the Rietveld method was also used to further assess the validity of the published models from single-crystal diffraction (Shigeta et al., Reference Shigeta, Komiyama and Kuroya1963; Messmer and Amma, Reference Messmer and Amma1968), comparing their Rietveld agreement factors and Rietveld graphs with those of the model from powders.

The unit-cell parameters reported in 1963 and 1968 are similar to those found from powders (after Rietveld refinement), and the values from the three models are compared in Table III. The unit-cell parameters determined in 1968 are the closest to those calculated from the powder pattern.

In order to first assess the validity of the model of Shigeta et al. (Reference Shigeta, Komiyama and Kuroya1963), the unit-cell parameters, 2θ zero-error, background coefficients, and peak profile parameters were refined in a model biased Le Bail fit replacing the space group P222 by Pnma, typing the published atomic coordinates and re-adjusting the L _i,j coefficients of the profile function No. 3 (Larson and von Dreele, Reference Larson and vonDreele2004).

In the Rietveld fit that followed, only the scale factor and the background coefficients were initially refined. The calculated pattern showed serious misfits for the most intense peaks and many others. After refining the published atomic coordinates (without bond-length restraints), and the isotropic atomic displacement parameters (subjected to a group constraint), the best agreement factors achieved were R _wp = 10.24%, χ ² = 9.22, R _I = 5.78%, R _p = 7.67% (in all cases significantly larger than those of our model from powders); and although diminished, the misfits persisted (see online Supplementary Figure S2). Moreover, the two nitrogen positions above and below the mirror plane in the unrefined single-crystal model (Shigeta et al., Reference Shigeta, Komiyama and Kuroya1963) split into four, rendering the refined model implausible. The Fourier difference map showed minimum and maximum values of −0.63 and +0.86 e⁻/ų, respectively.

We point out that various factors could have contributed to an erroneous structure (with R = 0.109) reported by Shigeta et al. (Reference Shigeta, Komiyama and Kuroya1963), such as the visual determination of the reflection intensities, the lack of absorption correction, and that the material was simply assumed to be isostructural with a rhodium (III) salt. Individual atomic displacement parameters for each atomic coordinate and hydrogen positions were not reported either.

Towards facilitating the comparison of all three models and their Rietveld refinements, Figure 3 shows the crystal packing in the three models, and Figure 4 shows the reported coordination complex geometry using the labeling scheme of the respective publications (Shigeta et al., Reference Shigeta, Komiyama and Kuroya1963; Messmer and Amma, Reference Messmer and Amma1968). Table IV summarizes the Rietveld agreement factors, Fourier difference residuals, and the number of parameters refined in each fit, all of which were carried out using our synchrotron powder diffraction data (this work).

Figure 3. (Color online) The crystal structure of [Co(NH₃)₅Cl]Cl₂ approximately along the c-axis, with inversion centers shown in orange, 2₁ screw axes in green, and mirror planes in cyan. Glide planes are not shown for clarity; (a) the model of Shigeta et al. (Reference Shigeta, Komiyama and Kuroya1963) in Pnma, (b) the model of Messmer and Amma (Reference Messmer and Amma1968) also in Pnma, and c) the model obtained from powder diffraction in Pn2₁ a (H atoms are not shown for clarity). Co³⁺ ions are shown in dark blue, N in light blue, Cl⁻ in green. The atom labeling shown is that of the original publications (Shigeta et al., Reference Shigeta, Komiyama and Kuroya1963; Messmer and Amma, Reference Messmer and Amma1968). Selected hydrogen bonding is indicated with dashed gray lines and the distances are in Å.

Figure 4. (Color online) The internal geometry of the coordination complex [Co(NH₃)₅Cl]²⁺ with reported interatomic distances in Å and the original labeling scheme in the publications cited. (a) The model of Shigeta et al. (Reference Shigeta, Komiyama and Kuroya1963) in Pnma, (b) the model of Messmer and Amma (Reference Messmer and Amma1968) also in Pnma, and (c) the model obtained from powder diffraction in Pn2₁ a (this work). Co³⁺ ions are shown in dark blue, N in light blue, Cl⁻ in green, and H in light gray (only reported for the model in Pn2₁ a).

The number of restraints only refers to the bond-distance and -angle restraints to refine the positions of hydrogen atoms. Those were included in the powder model (neither single-crystal model reported H atoms), and in the Rietveld-refined model of Messmer and Amma (Reference Messmer and Amma1968), for comparison purposes. The number of constraints is one in all cases, and it corresponds to the isotropic atomic displacement parameters of non-H atoms and H atoms (when included).

Following the procedure described in Scott (Reference Scott1983) for the estimation of standard uncertainties from Rietveld fits, the number of crystallographic parameters (N _C) is the sum of the three lattice parameters, the number of refinable atomic coordinates, and the atomic displacement parameter. The number of profile parameters (N _P) is the sum of 36 background coefficients, the scale factor, the zero-point error, and peak profile parameters (when refined in the last GSAS cycles). The total number of parameters refined (N _T) is the sum of N _C and N _P. The entries in Table IV corresponding to the model from powders in Pn2₁ a were used in the calculation of the standard uncertainties following the procedure described in Scott (Reference Scott1983).

Furthermore, all three structural models are credible from the chemical-bonding point of view; however, the models describe subtleties in the geometry of the [Co(NH₃)₅Cl]²⁺ coordination complex differently. The overall crystal packing in both single-crystal and powder structures is quite similar. The coordination sphere around the Co(III) ion is octahedral, and it is composed of five ammonia molecules and one chloride ion. Viewed approximately along the c-axis, the structures show two alternating horizontal layers, one layer is made of chloride ions, and the second of penta-ammonium cobalt(III) chloride complex ions [Co(NH₃)₅Cl]²⁺, respectively. This is represented in Figure 3 for the single-crystal (Shigeta et al., Reference Shigeta, Komiyama and Kuroya1963; Messmer and Amma, Reference Messmer and Amma1968) and powder structures.

However, both single-crystal models have been defined differently. In both cases, Co³⁺ and three N atoms sit on a mirror plane at y = 1/4, in a 4c special position (x, ¼, z), thus conferring partial planar symmetry to the coordination complex ion [Co(NH₃)₅Cl]²⁺ (see Figure 3). In the model of Shigeta et al. (Reference Shigeta, Komiyama and Kuroya1963), described with eight atomic coordinates and constructed by comparison with the structure of the analogous rhodium salt, N4 and N5 (above and below such mirror plane, respectively) are in 8d general positions [see Figure 3(a)]; while in the model of Messmer and Amma (Reference Messmer and Amma1968), described with seven atomic coordinates derived from a Patterson map, the N3 atom above the mirror plane in a 8d (x, y, z) general position generates N3′ (x, y−½, z) below the mirror plane, within the same complex ion [see Figure 3(b)]. The atomic positions of both models above are summarized in Tables S.I and S.II (online Supplementary material).

Moreover, in both single-crystal structures, the layers of chloride ions are generated by only one crystallographically independent chloride. In the powder structure in Pn2₁ a, the chloride layers are made of two crystallographically independent chloride ions (and a third chloride is coordinated to the cobalt ion). Pn2₁ a does not have inversion symmetry or mirror planes [see Figure 3(c)], and the [Co(NH₃)₅Cl]²⁺ coordination complex does not show sections with planar symmetry.

In order to gather additional information to qualitatively assess the likelihood of observing planar symmetry within the coordination complex, and the credibility of the bond distances resulting from the three models, a search in the Cambridge Structural Database (Allen, Reference Allen2002) version 5.38, November 2016, was conducted to identify minimum, maximum, and average cobalt–NH₃ distances, for structures in which cobalt (this means Co²⁺ or Co³⁺ ions) was bonded to five ammonia molecules and one other residue of any kind. For R < 5%, 69 entries were found resulting in 345 bond-distance observations. Those varied from 1.834 to 2.188 Å, and the average value was (1.966 ± 0.002) Å. Thus, in principle, the bond lengths shown in Figure 1 are deemed valid. Additionally, an analogous planar symmetry section of the coordination complex imposed by the crystal symmetry was not found in any of the above crystal structures. For the four entries hexa-ammine-cobalt(III) dichloride 3-carboxyprop-2-ynoate monohydrate (ASAWUM); (4-methylimidazole-N)-penta-ammine-cobalt(III) trichloride dihydrate (DUSDAW); hexa-ammine-cobalt(III) tris(methanesulfonate) (WEXRIB); and bis[(hexa-ammine)-cobalt(III)] trioxalate tetrahydrate (XEDNAV), in the space groups Pnma, Pna2₁, Pnnm, and Pnnm, respectively, only two of the six ligands in the coordination complex were placed on mirror planes for the three above cases in Pnma and Pnnm. Thus, if the space group of the purpureo salt is actually Pnma, it would be the first structure (after the 69 published) wherein four ligands in [Co(NH₃)₅ R]²⁺ (for R = any residue) are on a mirror plane.

Figure 4 shows the coordination complex geometry reported in the three models, also using the labeling scheme from the publications cited. Messmer and Amma (Reference Messmer and Amma1968) had identified two possible space groups, Pnma and Pn2₁ a; however, they chose to report the structure in Pnma because of the observed correlation between the nitrogen atomic positions above and below the mirror plane (N3 and N3′) in Pn2₁ a refinements, which are symmetry-related in Pnma but crystallographically independent in Pn2₁ a.

One of the reasons for which this structure was revisited by Messmer and Amma (Reference Messmer and Amma1968) was to further investigate the change in bond lengths that occur in metal complexes of this type resulting from trans-directing ligands, such as the electronegative chlorine atom. In the structural description of Shigeta et al. (Reference Shigeta, Komiyama and Kuroya1963), the Co–N1 distance trans to the Co–Cl bond [see Figures 3(a) and 4(a)] is significantly shorter than the four remaining Co–N distances; this is 1.91 vs. 1.97 (×3) and 1.98 Å. On this issue, Messmer and Amma (Reference Messmer and Amma1968) concluded that a significant trans distortion was not observed within the limitations of their data; however, it was confidently determined that one of the Co–N distances [Co–N(4)] was larger than the remaining four; this is 1.998(6) vs. 1.962(4) (×2), 1.946(6), and 1.987(6) Å [see Figures 3(b) and 4(b)]; and that such N atom is likely involved in hydrogen bonding to a chlorine atom [Cl(2)] [see Figure 3(b)], and this likely gives rise to the longest distance observed for Co–N(4), and the shortest N(4)–Cl(2) distance of 3.333(5) Å, among all N–Cl distances.

Thus, three questions to answer using our synchrotron X-ray powder diffraction data have been identified in our work: (1) Is the space group Pnma correct, or the crystal structure is a pseudosymmetry case and it is better described in Pn2₁ a?; (2) Is there a Co–N distance significantly larger than the remaining four, such as Messmer and Amma (Reference Messmer and Amma1968) reported?; and (3) Can a significant trans effect be observed in this compound such as Shigeta et al. (Reference Shigeta, Komiyama and Kuroya1963) did, within the limitations of our powder diffraction data?

Toward answering these questions and further compare the models, we also Rietveld-refined the results of Messmer and Amma (Reference Messmer and Amma1968) using our synchrotron powder pattern. The Rietveld fit obtained is shown in online Supplementary Figure S3, and the agreement factors and other Rietveld refinement details are summarized in Table IV. In this case, the Rietveld refinement renders a chemically plausible model; however, the graphical observation of the Rietveld fit again points to serious model deficiencies (see online Supplementary Figure S3).

One could think that considerable preferred orientation effects could explain why the calculated intensities of a few low-angle peaks [this is (011) around 2θ = 7.129° and (210) at 2θ = 7.186°] are below their observed values. Thus, we observed the powder crystallites under the microscope. The micrographs are shown in Figure 5, and they indicate that the powder crystallites are very small (estimated in the order of 1–10 µm) and of a rather spherical shape; thus, preferred orientation corrections are unlikely to be required.

Figure 5. (Color online) Micrographs of the powder crystallites in the [Co(NH₃)₅Cl]Cl₂ specimen used for X-ray powder diffraction data collection. (a) View at 1 µm resolution showing the absence of large needles or plates, and small microcrystallites (estimated 1–10 µm size); (b) one microcrystallite.

To further test the model of Messmer and Amma (Reference Messmer and Amma1968), the hydrogen positions were added with SHELX (Sheldrick, Reference Sheldrick2008) as implemented through WinGX (Farrugia, Reference Farrugia2012), leading to a considerable improvement of the Rietveld fit (online Figure S4); however, the agreement factors (shown in Table IV) remained higher than those obtained in Pn2₁ a. We must note that Messmer and Amma (Reference Messmer and Amma1968) did not report hydrogen positions, and absorption corrections were not carried out.

Thus, considering all above results, in particular, the lowest agreement factors and Fourier difference residuals obtained for the model from powders in Pn2₁ a, in principle such model seems physically meaningful to us. We believe the analysis of the synchrotron powder diffraction data rather indicates the validity of the Pnma space group choice reported in Messmer and Amma (Reference Messmer and Amma1968) is questionable, and we note that it has been already an arguable choice in 1968, as the authors mentioned. An additional hint toward the structural description in Pn2₁ a is given by evaluating the possibilities of formation of energetically favorable hydrogen-bonding motifs in the crystal packing adopted. It seems reasonable that the partial planarity of the [Co(NH₃)₅Cl]²⁺ coordination complex, as well as bond distances and angles in the Pnma description, can be slightly distorted because of the bonding energy gains resulting from hydrogen bonding of the −NH groups of ammonia to other nitrogen and chloride ions.

Table V shows the hydrogen-bonding distances calculated by PLATON (Spek, Reference Spek2002) and most of the N–Cl distances leading to hydrogen bonding are also shown in Figure 3(c) (a few were omitted for clarity). It is interesting to note that rather than a considerable deviation from planar symmetry for the atoms Cl2, N5, N6, and N7 [see Figure 3(c)], it rather seems that the angles of N9 and N8 with the above atoms considerably deviate from the (90 ± 1)° values observed for the corresponding N3 and N3′ atoms in Figure 3(b), in Pnma. In Pn2₁ a, such angles are not related by mirror symmetry, and their values range from 80 to 100° instead. Since these irregular features in the internal geometry of the coordination complex could be explained by the maximization of lattice energy gains by hydrogen bonding within the crystal, we believe that this is a reasonable chemical reason leading to a better description of the structure in Pn2₁ a, and the structure is a pseudosymmetry case (approximation to a higher symmetry). It must be also mentioned that ADDSYM in the software PLATON (Spek, Reference Spek2002) suggested a space group change to Pnma. However, Spek (Reference Spek2002) indicates that approximations to pseudosymmetry frequently occur in crystal structures; for this reason, the missed symmetry alerts might be false in some cases, and they require careful consideration by the crystallographer analyzing “by hand” the diffraction data.

Thus, our answer to the first question above is that the comparison of the three models using the modern synchrotron powder pattern, including X-ray absorption corrections, calculated hydrogen atom positions, and discarding preferred orientation effects, indicates the correct space group choice is Pn2₁ a, not Pnma. This choice is further supported by the possibilities of formation of energetically more favorable hydrogen-bonding motifs in the lower symmetry space group, leading to a pseudosymmetry.

To answer questions 2 and 3, we must analyze in detail the standard uncertainties of the atomic coordinates from powders, keeping also in mind that the hydrogen positions are only calculated since in the general case, powder diffraction data do not afford their experimental determination. Referring to Figure 4(c), we note that the Co–N8 distance, 2.07(8) Å, is larger than the remaining four, 1.84(3), 1.88(8), 1.93(3), and 1.95(3) Å. Thus, using the calculated standard uncertainties and assuming uncorrelated errors, within two standard deviations (95% confidence level), we cannot say from the powder data that this distance is statistically significantly longer than the rest. However, within one standard deviation (68% confidence level), we could affirm it is (additional details are in the online Supplementary material). This result agrees with the analysis of Messmer and Amma (Reference Messmer and Amma1968), who confidently concluded that one of the distances is longer than the other four.

Concerning the trans effect reported in Shigeta et al. (Reference Shigeta, Komiyama and Kuroya1963), and referring again to Figure 4(c), we see that the Co–N6 distance of 1.84(3)  Å is indeed the shortest among the five Co–N distances leading to a trans effect. However, through the same analysis and assuming uncorrelated errors, we cannot affirm from our powder data that the Co–N6 distance is the shortest distance among the five, giving rise to a statistically significant trans effect with 68% confidence level (additional details are in the online Supplementary material).

In qualitative terms, we assert that the powder data point to the presence of both effects, but the trans effect is less likely than the one reported by Messmer and Amma (Reference Messmer and Amma1968).