I. INTRODUCTION
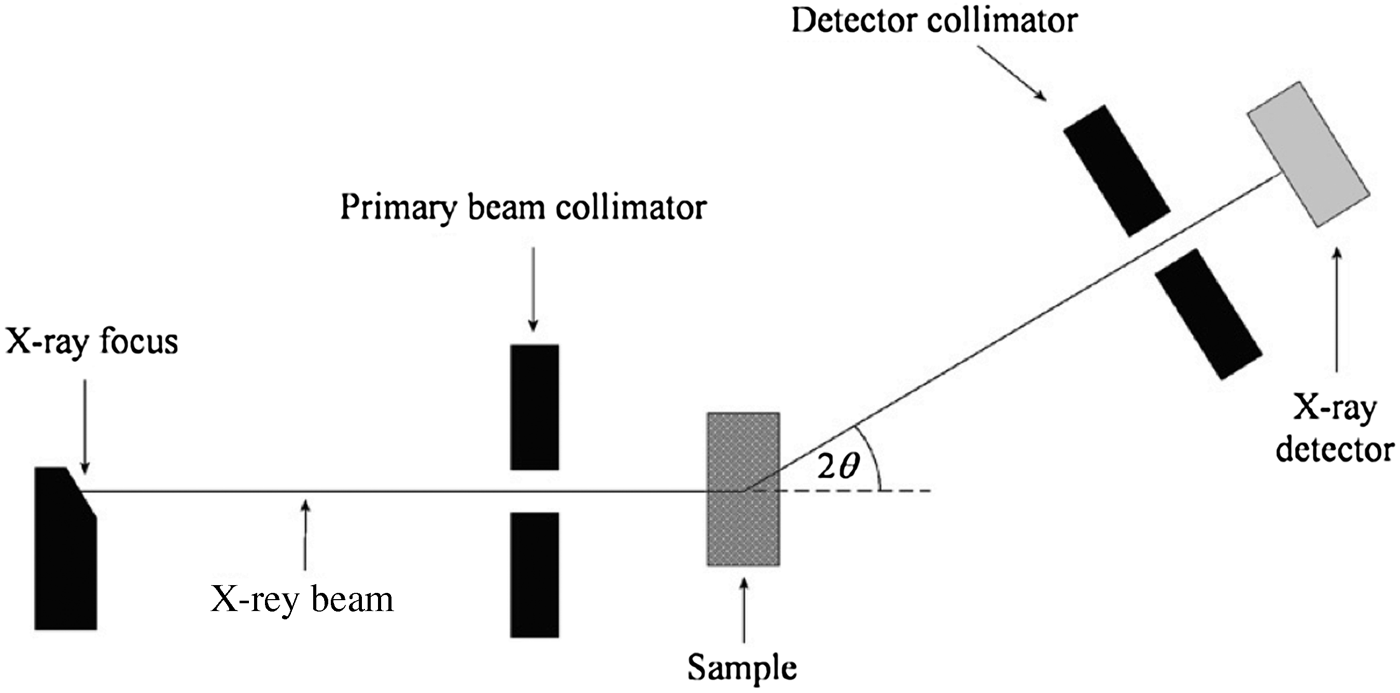
Energy-dispersive X-ray diffraction (EDXRD) is a method for analysing the mineralogical composition of samples containing multiple crystalline phases. An EDXRD analyser measures the energy spectrum of X-rays diffracted through a fixed angle by a crystalline sample. Typically, the instrument is setup in “transmission geometry” as shown in Figure 1, where the X-ray source and detector reside on opposite sides of the sample. The source is typically an X-ray tube, although synchrotron radiation can also be used (Castro et al., Reference Castro, Barroso, de Oliveira and Lopes2005; Scarlett et al., Reference Scarlett, Madsen, Evans, Coelho, McGregor, Rowles, Lanyon and Urban2009; Rowles et al., Reference Rowles, Styles, Madsen, Scarlett, McGregor, Riley, Snook, Urban, Connolley and Reinhard2012). High-resolution solid-state detectors such as high-purity germanium (HPGe), silicon, or cadmium telluride coupled to a multichannel analyser (MCA) are used to collect the energy spectrum of the diffracted X-rays.

Figure 1. Schematic representation of an EDXRD instrument.
The EDXRD method is particularly suited to applications that require automated and/or rapid measurement of unprepared materials. Examples of areas in which EDXRD has found use include the detection of illicit materials in luggage (Luggar et al., Reference Luggar, Farquharson, Horrocks and Lacey1998; Malden and Speller, Reference Malden and Speller2000; Cook et al., Reference Cook, Fong, Horrocks, Wilkinson and Speller2007), routine analysis of pharmaceuticals (Dozier and Anibou, Reference Dozier and Anibou2009), and medical applications such as bone densitometry (Royle and Speller, Reference Royle and Speller1991; Newton et al., Reference Newton, Hukins and Harding1992; Farquharson and Speller, Reference Farquharson and Speller1998) and material-resolved computed tomography (Harding et al., Reference Harding, Kosanetzky and Neitzel1987; Harding and Schreiber, Reference Harding and Schreiber1999). Our focus is on developing analysers capable of performing on-line mineralogical analysis for the minerals processing industry. These instruments are designed to provide rapid mineralogical analysis on the composition of feed process streams for plant control and optimisation.
The performance of an on-line instrument can be measured in a number of ways, depending on the primary function of the analyser. For example, the performance of a baggage inspection device may be measured by the number of false alarms raised. For an on-line mineral phase analyser, it is the accuracy to which the key mineral phases in the process stream can be quantified. Whichever way the performance of an EDXRD analyser is measured, it is determined by a number of instrument design factors. The most influential are:
i. The diffraction angle, θ, which determines the energies of the diffracted X-rays according to
(1)where E = hc/λ, h is the Planck's constant, c is the speed of light, d is the crystal plane spacing, and λ is the X-ray wavelength and equal to 2d sinθ. The angle must be chosen such that the key diffraction peaks reside in a suitable energy region in the diffraction spectrum. $$E=\displaystyle{{h c} \over {2d\sin \theta }}$$
$$E=\displaystyle{{h c} \over {2d\sin \theta }}$$ii. Diffraction peak resolution. This is primarily determined by the opening widths of the X-ray collimators. Good resolution reduces interferences caused by overlapping peaks.
iii. Diffraction peak intensity, which determines the counting statistical accuracy of the measurement. Counting statistics are proportional to
 $\sqrt N$, where N is the number of counts in the peak. Measurement accuracy is therefore improved by increasing the total number of X-rays detected.
$\sqrt N$, where N is the number of counts in the peak. Measurement accuracy is therefore improved by increasing the total number of X-rays detected.
In order to obtain high measurement accuracy, a diffraction spectrum with minimal diffraction peak overlap and a high count-rate is needed. Good resolution requires narrow collimator openings to limit the angular spread of the diffracted beam, which tends to blur the diffraction peaks. On the other hand, a high X-ray throughput requires wide openings to allow more X-rays to reach the detector. The count-rate can of course be increased using a stronger X-ray source or increasing the measurement time; however, this is often not possible for practical or budgetary reasons. Hence, an optimal balance must be found between the resolution and counting efficiency so that the best overall measurement accuracy is achieved.
It is therefore important to fully understand the performance characteristics of an EDXRD instrument during the design phase to ensure that it will deliver the required measurement accuracy. This paper describes a method for predicting the measurement accuracy of an EDXRD mineral phase analyser using Monte Carlo modelling. In our case, we need to determine the accuracy to which the mineral phase abundances can be quantified in industrial mineral samples. The steps we use to estimate the measurement accuracy achievable with an EDXRD design are:
i. Produce a computer model of the proposed design in the Monte Carlo software package XPERT (Tickner, Reference Tickner2005), which includes all of the functional components of the instrument (X-ray source, detector, sample material, and collimators).
ii. Create a suite of samples in XPERT, where the compositions of the samples are representative of the real materials that the instrument will measure. Furthermore, the compositions span the entire range expected to be encountered.
iii. Simulate the diffraction spectrum of each material.
iv. Analyse the diffraction spectra and determine the accuracy to which each of the mineral components can be measured.
In this paper, we use this method to model the measurement accuracy of our laboratory EDXRD mineral analyser for the measurement of potash ore. Potash ore is mined for its potassium-containing minerals, such as KCl (the mineral sylvite). These have many uses, most notably as primary ingredients in fertilisers. Measurements of real potash samples are then carried out with our laboratory EDXRD analyser. The results of the simulated and real measurements are compared to demonstrate that the Monte Carlo method is capable of reliably predicting analysis accuracies obtained using EDXRD.
II. THE LABORATORY EDXRD ANALYSER
The specifications of our laboratory EDXRD mineral phase analyser are as follows. The X-ray source is a Hamamatsu L8121-01 Microfocus X-ray tube and the detector is an Amptek XR-100T-CdTe, which has an energy resolution of approximately 570 eV at 60 keV. The angle between the incident and diffracted beams is 5.5° with collimator opening widths of 0.5 and 1.2 mm for the primary beam and detector collimators, respectively (see Figure 1). The source-to-sample and sample-to-detector distances are both 312 mm. The resulting diffraction peak or d-spacing resolution of the instrument is 4.5% full-width-at-half-maximum (FWHM) for a peak at 46 keV. The peak width is a function of energy, or equivalently d, since it is primarily governed by instrument broadening and the energy resolution of the detector. The angular spread in the beam caused by the instrument Δθ is fixed, hence through Eq. (1) it can be seen that the resolution degrades as the diffraction energy increases. This effect is compounded by the energy resolution of the detector, which also degrades with increasing energy.
III. SAMPLES
The samples used in this investigation were designed to reflect real potash ore as closely as possible. That is, the composition and weight fractions of each mineral were chosen to span that of a typical potash ore deposit as much as possible. A suite of fifteen samples was produced, where each sample contained the minerals halite, sylvite, quartz, anhydrite, gypsum, kaolinite, and hematite in the amounts summarised in Table I. The minerals were obtained from commercial chemical manufactures and had particle sizes ranging from 5 to 200 µm and claimed purities of 99% or better. The samples were prepared placing a carefully weighed amount of each mineral powder into a plastic specimen jar and then vigorously agitating to ensure that the powder distribution was homogeneous. Following this, each powder was transferred to a plastic Petri dish of diameter 70 mm, internal height 15 mm, and wall thickness 1.5 mm. The samples each consisted of 35 g of powder contained with the depths along the axis of the X-ray beam ranged between 6 and 7 mm, depending on the composition.
Table I. Compositions of the potash samples. The maximum, minimum, and mean amount of each mineral contained in the samples is given.

IV. SIMULATION AND MEASUREMENT OF EDXRD SPECTRA
A. Monte Carlo modelling procedure
A computer model of the laboratory instrument was developed in XPERT. The model contained all of the important functional components of the laboratory analyser (X-ray source, detector collimators, and sample). A version of the EGSnrc Monte Carlo code (Kawrakow and Rogers, Reference Kawrakow and Rogers2000) extended to include diffractive scattering (O'Dwyer and Tickner, Reference O'Dwyer and Tickner2007) was used to perform the simulations. The code allows crystalline materials to be included in the simulation and implements the physics of diffractive scattering. The crystal structure parameters of the minerals contained in the samples were obtained from Wyckoff (Reference Wyckoff1963) and diffraction cross-section and form factor data was calculated according to O'Dwyer and Tickner (Reference O'Dwyer and Tickner2007). The plastic Petri dishes that held the mineral powders were treated as purely amorphous polypropylene. Polypropylene does however display significant molecular ordering through strong diffraction peaks at d-spacing values of 6.33, 5.26, 4.81, and 4.46 Å (Weidinger and Hermans, Reference Weidinger and Hermans1961). Treating the polypropylene as purely amorphous is a reasonable approximation given that the Petri dish was mostly outside the measured sample volume and hence primarily contributed to additional attenuation of the X-ray beam.
A source of measurement error not included in the Monte Carlo model is sampling errors caused by the random distribution and orientation of the mineral grains within the sample. For an X-ray to be directed towards the detector and hence measured, the diffracting crystalline plane must be aligned at the Bragg angle relative to the X-ray source and detector. The Monte Carlo model treats the crystallite orientation as perfectly random, however in reality there may be particles preferentially orientated.
Sampling errors were estimated for halite and sylvite by measuring the diffraction spectrum of one of the samples eight times with the laboratory analyser. The X-ray source was operated at a voltage of 120 kV and current of 0.5 mA. During each 2000s measurement, the sample was rotated in the X-ray beam at a speed of approximately 6 rev min−1 using a motorised turntable. Doing this increased the mass of sample measured by approximately 120 times compared to a stationary sample. As such, sampling errors due to inhomogeneity and crystallite orientation were greatly reduced. Between each measurement, the powder was stirred in order to redistribute the particles. Statistical (counting) errors were also estimated using the same method without stirring the powder between acquisitions. Using these measurements, the sampling errors for halite and sylvite were calculated to be 0.35 and 0.40 wt.%, respectively. Sampling errors for the minor components, quartz, anhydrite, gypsum, kaolinite, and hematite, were estimated to be 0.02 wt.%.
The spectra of the samples were modelled in the following way. Two spectra for each sample were modelled: (i) the diffraction spectrum; and (ii) the transmission spectrum of the direct beam, where the compositions included the sampling errors calculated above. The diffraction spectra were fully simulated, however the transmission spectra were calculated using the Lambert–Beer Law,
where I 0 is the intensity of the incident spectrum, μ m and ρ are the mass attenuation coefficient and density of the sample respectively and t is the sample thickness. The X-ray tube output spectrum was calculated (Tucker et al., Reference Tucker, Barnes and Chakraborty1991) based on an operating voltage of 120 kV and tube currents of 0.5 mA and 2 μA (diffraction and transmission, respectively). The transmission spectra were used to calculate normalised diffraction spectra (the diffraction spectrum divided by transmission) in order to account for differences in densities between samples.
The total computation time for each simulation was 1000 min, which was carried out by splitting each simulation into 50 separate runs of 20 min each and combining the results. Statistical noise was added to the final spectra to simulate an acquisition time of 2000s. Finally, a detector response function was applied to each of the spectra to account for detector resolution and efficiency, and to model escape X-rays from the CdTe detector.
B. Laboratory measurements
The above simulations were repeated as real measurements using the laboratory analyser. Each of the 15 samples was analysed. The samples were rotated in the X-ray beam as previously described to reduce sampling errors. Again, two spectra were collected for each sample. The diffraction spectra were measured for a time of 2000s with the X-ray tube set to at operating voltage of 120 kV and current 0.5 mA. The transmission spectra were collected for 200 s with X-ray tube settings of 120 kV and 2 μA. The tube current used for transmission was much lower because of the extremely high intensity of the transmitted beam.
V. RESULTS AND DISCUSSION
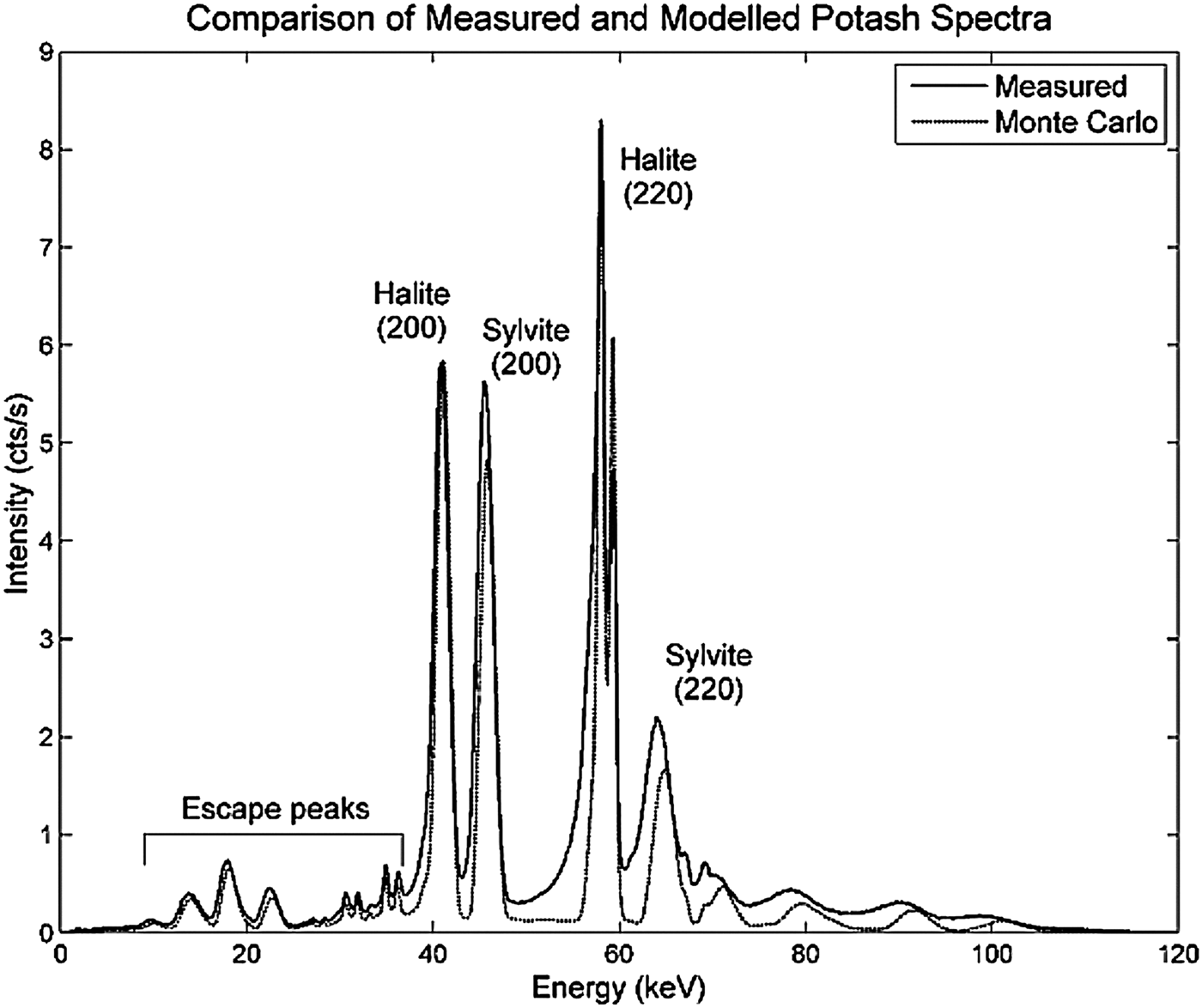
An example of modelled and measured diffraction spectra is shown in Figure 2. The spectra are dominated by the (200) and (220) reflections for both the halite and sylvite phases. The low-energy tails seen on the peaks of the measured data are a result of incomplete charge collection in the CdTe detector (Redus et al., Reference Redus, Huber, Pantazis, Pantazis, Takahashi and Woolf2004). This effect was not included in the detector response function applied to the modelled data and hence tailing is not observed in the Monte Carlo modelled spectrum.

Figure 2. EDXRD spectra of potash sample measured with the laboratory instrument and simulated using Monte Carlo modelling.
Linear regression analysis was used to relate the intensity of a selected set of diffraction peaks for each mineral against the mineral abundances in each sample. The analysis was carried out on the normalised diffraction spectra to account for density variations between samples. An iterative process was used to calculate the composition of the samples. For each of the 15 samples, regression coefficients were calculated using the other 14 samples. These regression coefficients were then applied to the 15th sample to calculate the mineral fractions. Using this method, each sample was effectively unknown to the calibration set and hence reduced the probability of overtraining. For the Monte Carlo data, the mineral masses used to calculate the regression coefficients were those without added sampling errors, so that sampling errors would be part of the total measurement error.
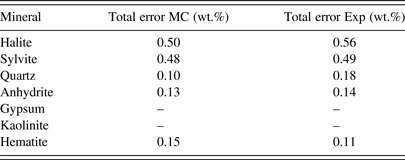
The calculated mineral weight fractions for the measured and simulated data are summarised in Table II. The results are in excellent agreement, showing that Monte Carlo modelling can be used to reliably predict the measurement accuracy achievable with an EDXRD analyser design. Most importantly, this analysis showed that for the instrument used here, two of the key mineral phases, gypsum and kaolinite, could not be accurately analysed and this fact could be predicted by the Monte Carlo model. This ability is vitally important as it allows the instrument designer not only to estimate the measurement accuracy attainable, but also to determine whether a mineral phase can even be measured.
Table II. Comparison of the total errors obtained for the seven mineral components by experiment and Monte Carlo modelling.

The reason why gypsum and kaolinite cannot be measured is because of a combination of their low-peak intensities, the low energies of their strongest lines and an excessive degree of peak overlap. For example, the energy of the strongest diffraction line of gypsum is 16.9 keV at 5.5° 2θ (d = 7.63 Å). At this energy the X-rays are unable to penetrate through the sample. The low-energy cut-off because of attenuation for these samples is approximately 21 keV, thus no diffraction lines are seen below this energy. The only peaks residing below 21 keV are escape peaks produced by X-rays of higher energy. The other two strong lines of gypsum, d = 4.28 and 3.07 Å, are overlapped with quartz and sylvite lines, respectively, and hence cannot be resolved. For kaolinite, the energy of the strongest line, 18.0 keV (d = 7.17 Å), is too low to be measured and its other significant lines are obscured by other peaks. Kaolinite also has a very low diffractive cross-section, which, coupled with the low quantities of kaolinite contained in the samples, results in extremely low-intensity diffraction peaks.
It is not surprising that the two major components, halite and sylvite, could be quantified with good accuracies of approximately 0.6 and 0.5 wt.%, respectively. Such accuracies are attainable because of the strong, free-standing (200), and (220) diffraction peaks. The minor components such as quartz, anhydrite, and hematite can each be measured with good accuracy. Total measurement errors for these components were between 0.1 and 0.2 wt.%. These results are quite good considering that each of these minerals comprised only 1–2 wt.% of the total sample mass. The ability to measure mineral phases present in small amounts is of particular significance to industries where tight control of mineralogical composition is required for optimal process control. Often it is the minerals present below the 5 wt.% level that can cause significant issues with the process efficiency. The capability to measure and track the abundances of these phases is frequently of utmost importance. Using the Monte Carlo method presented here, we can predict whether a particular instrument is able to measure these key phases with the required accuracy.
VI. CONCLUSION
This work has shown that Monte Carlo Modelling can be used to predict the measurement accuracy attainable with an EDXRD mineral phase analyser. A suite of synthetic potash samples were analysed with our laboratory EDXRD instrument and these results were compared to an equivalent set of samples modelled using Monte Carlo simulation. It was found that the accuracies obtained by the laboratory instrument could be replicated by Monte Carlo simulation. An important finding in this study was that the Monte Carlo model can predict whether a material cannot be measured using a particular design setup. The gypsum and kaolinite components of the synthetic potash samples could not be quantified using either the experimental or Monte Carlo data. This is significant because many industrial applications require materials present in small quantities to be measured. Such materials can be difficult to analyse, hence the ability to determine whether it is possible to obtain meaningful measurement data on these materials before an analyser is developed has great time and cost saving benefits. The results of this investigation are therefore important for the development of industrial on-line EDXRD analysers.