INTRODUCTION
Among the three crystallized polymorphs of CaCO3, vaterite is the least stable form under natural conditions, with around 3 kJ/mol difference compared to calcite, and is potentially involved in the first steps of crystallization of the two others (calcite and aragonite). Its complete structural determination would consequently shed important light to understand scaling formation and biomineralization processes. Polymorphs’ formation and modification of inorganic, biogenic, and biomimetic vaterite crystal habits can be induced using special conditions or additives. In vitro crystallization of vaterite was achieved using Mytilus californianus nacre macromolecules and supersaturated solutions (Falini et al., Reference Falini, Albeck, Weiner and Addadi1996). Mg2+ ions (Chen et al., Reference Chen, Neville and Yuan2005) inhibit vaterite formation while NH4+ ions (Gehrke et al., Reference Gehrke, Cölfen, Pinna, Antonietti and Nassif2005) generate hexagonal polydomain vaterite crystals. Surfactants (Dupont et al., Reference Dupont, Portemer and Figlarz1997) and/or polymers (Wei et al., Reference Wei, Shen, Zhao, Wang and Xu2004) also strongly affect crystal habits even in small amounts in the solution. Calcite and aragonite biocrystals, stabilized under organic influences, were shown to exhibit unit-cell and structural distortions (Pokroy et al., Reference Pokroy, Quintana, Caspi, Berner and Zolotoyabko2004, Reference Pokroy, Fitch, Lee, Quintana, Caspi and Zolotoyabko2006, Reference Pokroy, Fieramosca, Von Dreele, Fitch, Caspi and Zolotoyabko2007), depending on the biocrystal habits (Ouhenia et al., Reference Ouhenia, Chateigner, Belkhir and Guilmeau2008a). The vaterite structure might also distort under thermodynamic and/or organic variations, and this would also be the case of other microstructural defects such as microtwins, recently observed in vaterite tablets of freshwater lacklustre pearls (Qiao and Feng, Reference Qiao and Feng2007). Trying to understand the growth of biominerals, our previous results indicated that synthesis of calcium carbonate in the presence of polyacrylic acid (PAA) can shift the chemical equilibrium between the allotropic forms, increasing vaterite and aragonite fractions depending on the temperature used. PAA can also control crystal sizes, quality, and shapes but we also observed such crystal habit variations when no PAA was added (Ouhenia et al., Reference Ouhenia, Chateigner, Belkhir, Guilmeau and Krauss2008b). This led us to a reinvestigation of the vaterite structure under purely inorganic mineral formation and for which only very old experimental atomic coordinates are available in databases (Gražulis et al., Reference Gražulis, Chateigner, Downs, Yokochi, Quirós, Lutterotti, Manakova, Butkus, Moeck and Le Bail2009). In the more accepted CaCO3 vaterite structural model based on single-crystal data (Kamhi, Reference Kamhi1963), the CO32− ions are randomly distributed over three orientations parallel to the c axis (P63/m m c space group, a′=4.13 Å, c′=8.49 Å, and Z=2). However, that model did not take into account the five weak superstructure reflections, leading to a cell having a volume six times larger (a=a′√3, c=2c′, and Z=12). Previously, Meyer (Reference Meyer1959) proposed tentative atomic coordinates in an orthorhombic cell with dimensions a O=4.13 Å, b O=7.15 Å, and c O=8.48 Å and space group P b n m, but this was not checked against any diffraction data. From first-principles calculations and molecular dynamic simulations applied in order to determine the local order, a hexagonal superstructure (P6522) was recently proposed (Wang and Becker, Reference Wang and Becker2009) with Z=18 and cell dimensions of √3 times in a′ and three times in c′. In this latter article, the controversy about the vaterite structure is detailed.
To the best of our knowledge, merohedral or pseudomerohedral microtwinning models have not been considered yet in order to try to explain the single-crystal data with a fully ordered model. We explore this possibility here, giving the highest priority to the fitting of the experimental powder diffraction data by models consistent with plausible interatomic distances, coordinations, and angles and compatible with the previous single-crystal observations, which are obviously prerequisites.
EXPERIMENTAL AND CHECKING PREVIOUS MODELS
The vaterite sample was synthesized using a procedure similar to that of Sato and Matsuda (Reference Sato and Matsuda1969): a 3M solution of CaCl2 in 50 ml of de-ionised water and 1M solution of

Figure 1. (Color online) Le Bail fit with the small hexagonal cell of Kamhi (Reference Kamhi1963) (space group P63/m m c). There are four clear additional peaks noted by vertical arrows which are reproduced by background points (corresponding from lower to larger 2θ angles to the 211, 205, 213, and 401 reflections in the supercell). The fifth supercell reflection seen with the single-crystal data of Kamhi is closely overlapping with an intense reflection of the subcell (∼33°2θ). Calcite is present as very weak impurity; its most intense reflection is indicated. The 00l vaterite reflections are narrower than the others.
K2CO3 in 450 ml of de-ionised water, both preheated at 33 °C, were mixed simultaneously in a beaker and stirred for 20 min at 33 °C. The product was washed actively with water and methanol and then dried in a desiccator under vacuum in the presence of P2O5. The powder pattern was recorded on a PANalytical MPD PRO diffractometer in the Bragg-Brentano geometry, equipped with a X’Celerator detector (Cu K α). From the peak position analysis and indexing efforts with the MCMAILLE software (Le Bail, Reference Le Bail2004), the small hexagonal cell of Kamhi (Reference Kamhi1963) is easily recovered. The supplementary peaks are really few and weak, as seen in Figure 1 from a structureless Le Bail fit (Le Bail, Reference Le Bail2005) using the FULLPROF software (Rodríguez-Carvajal, Reference Rodríguez-Carvajal1993), where they were modelled as belonging to the background. Successful indexing in a new cell that fits these more broadened peaks is not easy. These peaks are present on some of the 13 ICDD PDF cards (ICDD, 2009) obtained by a search on the vaterite mineral name PDF 00-033-0268 (ICDD, Reference Kabekkodu2009), to give one with experimental data). They are also seen in previously reported synthesis (Dupont et al., Reference Dupont, Portemer and Figlarz1997). It was decided to check all the main published models against the powder diffraction data recorded. The CO3 triangles were the subject of soft constraints during refinements.
Meyer (Reference Meyer1959), orthorhombic P, ordered model
The fit of Rietveld (Reference Rietveld1969) by using FULLPROF with the fixed original tentative atomic coordinates from the orthorhombic cell of Meyer (Reference Meyer1959) (Table I) is not very satisfying (R W P=36.3% and R B=25.7%). Refining the atomic coordinates improves the fit significantly (R W P=18.5% and R B=7.90%). However, this cell is unable to explain all the superstructure peaks on the powder pattern and it adds calculated peaks incompatible with the Kamhi hexagonal subcell and the powder data. An orthorhombic cell which would not provide additional reflections has to be C face centered, not primitive, but would still not allow indexing of all the superstructure peaks. It should be recalled that Meyer never checked his structure hypothesis against the experimental data. Moreover, the current fit attempt seems to be the first, though his model continues to be cited as one of the possible structures for vaterite.
Kamhi (Reference Kamhi1963), hexagonal subcell, disordered
A Rietveld refinement in the subcell using Kamhi’s coordinates (Table I) leads to R W P=13.3% and R B=4.57% (Figure 2). Kamhi stated “the crystals are imperfect, and under high magnification can be seen to be aggregates of uniformly oriented hexagonal plates.” This is a feature illustrated more recently in the work of Gehrke et al. (Reference Gehrke, Cölfen, Pinna, Antonietti and Nassif2005). If Kamhi’s remark aimed at underlining the “imperfection” of the crystals, the vaterite aggregates in the work of Gehrke et al., while exhibiting noticeable mosaicity at the TEM scale,
TABLE I. Atomic coordinates for the three main models from the Rietveld refinements.

a Fixed coordinate. The CIF corresponding to model 3 was deposited at the Crystallography Open Database (www.crystallography.net) (Gražulis et al., Reference Gražulis, Chateigner, Downs, Yokochi, Quirós, Lutterotti, Manakova, Butkus, Moeck and Le Bail2009) with entry number 3000002.

Figure 2. (Color online) Rietveld fit with the hexagonal subcell of Kamhi (Reference Kamhi1963). The superstructure peaks (see Figure 1) are modelled by background points.
still give rise to perfect single-crystal diffraction patterns. Later, Meyer (Reference Meyer1969) reused the hexagonal supercell but the proposed coordinates do not allow constructing any reasonable model. So the Kamhi model is still considered to be the best approach to the vaterite crystal structure in spite of the considerable disorder imposed on the CO3 group.
Wang and Becker (Reference Wang and Becker2009), P6522 ordered model by MD annealing
Why propose 3c′ whereas Kamhi experimentally proved that only doubling c accounted for the single-crystal data? Indeed, using the P6522 model and adjusting the predicted cell parameters a=7.29 and c=25.302 Å to the observed ones a=7.16 and c=25.44 Å fails to fit the positions of the additional superstructure peaks and brings a large number of supplementary peaks not observed in any experimental powder pattern data from the literature (nor in Kamhi’s single-crystal data). Rietveld refinements were not attempted in this case. Other first-principles calculations leading to models similar to the orthorhombic cell of Meyer (Reference Meyer1959) were discarded because their cell parameters strongly disagree (up to 10%) with the experimental ones (Medeiros et al., Reference Medeiros, Albuquerque, Maia, Caetano and Freire2007).
TWINNING HYPOTHESIS, STRUCTURE SOLUTION, AND RIETVELD REFINEMENTS
Would it be possible to obtain a fully ordered model which could explain both the powder pattern and the single-crystal data? Various twinning hypotheses by merohedry or pseudomerohedry were tested, targeting those not adding any supplementary reflections to the single-crystal data subcell and supercell. We stayed first in the smallest hexagonal cell (Z=2) from Kamhi (Reference Kamhi1963) and a convincing solution was obtained by following the path of the relation group-subgroup in the hypothesis of a pseudohexagonal symmetry generated from orthorhombic C-centered cells twinned or microtwinned in three domains related by rotation of 120° around the c axis. The occurrence of that twinning law has been encountered many times already, in the β-AlF3 case (Le Bail et al., Reference Le Bail, Jacoboni, Leblanc, De Pape, Duroy and Fourquet1988) for instance. The procedure consisted in extracting the |F obs| from the powder pattern (Le Bail, Reference Le Bail2005) in the various cells and space group hypothesis; then, the extracted |F obs| was used for structure solution attempts in direct space by the ESPOIR software (Le Bail, Reference Le Bail2001), moving

Figure 3. (Color online) The Rietveld fit with the A m a2 fully ordered model. The superstructure peaks (see Figure 1) are modelled by background points.
independently in the cell, by a Monte Carlo process, one or several rigid CO3 groups and the Ca atoms. This twinning hypothesis is able to reconcile the Kamhi hexagonal subcell with the Meyer orthorhombic cell, provided the latter is C centered. Tests were made in C m c m (maximum nonisomorphic subgroup for P63/m m c) and C m c21 space groups without obtaining the expected full order, so the symmetry was finally lowered to monoclinic in the C2/c and C c space groups. A model showing two disordered positions for the CO3 group was obtained in C2/c, and the expected full ordering was obtained in C c with all atoms in the general Wyckoff position 4a. The latter model was convincing for two main reasons: the eightfold Ca coordination satisfied usual interatomic distances and the CO3 group planes were lying all parallel (almost) to the same axis. Checking this model for missing symmetry using PLATON (Spek, Reference Spek2003) finally helped to conclude that A m a2 was the most appropriate space group, for which the Rietveld refinements resulted in R W P=13.4% and R B=5.22% (Figure 3). The obtained reliability factors are comparable to the ones resulting from the hexagonal subcell highly disordered model but with a fully ordered model. The refined atomic coordinates are presented in Table I together with those of the Kamhi and Meyer subcell models. Interatomic distances are in Table II and X-ray diffraction data are in Table III.
TABLE II. Selected geometric parameters (Å, deg) for the vaterite described in A m a2.
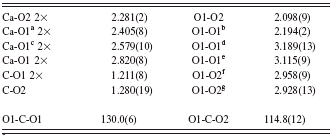
a Symmetry code: x, y, z−1.
b Symmetry code: −x+1/2, y, z.
c Symmetry code: x, y−1/2, z−1/2.
d Symmetry code: −x+1, −y+1, z.
e Symmetry code: −x+1/2, −y+3/2, z−1/2.
f Symmetry code: x, y, z+1.
g Symmetry code: x, y+1/2, z+1/2.
TABLE III. X-ray diffraction data for vaterite indexed in the A m a2 subcell (Cu K α 1).

a Supercell peaks.
DISCUSSION AND CONCLUSION
The A m a2 model is very similar to that of Meyer, as can be seen in Figure 4. The Ca atoms are in a distorted cubic coordination in both cases. The difference lies in the positions of the C atoms for half of them in adjacent possible oxygen triangles. Two edges of the CaO8 cubes are shared by two CO3 triangles, which explain the cube distortion by short O-O distances. The structure is built of CaO8 cubes interconnected by edges like in the CaF2 fluorite structure, but expanding in only two dimensions, forming layers parallel to the b c planes (Figure 5) of the A m a2 model. Each layer is connected by corners (O2 atoms) to the two neighbouring mirror-related layers (Figure 4). The CO3 groups enforce the layers connections, the carbon atom being at the center of the triangle formed by this O2 atom and two O1 atoms from the neighbouring CaO8 cubes in two adjacent layers (Figure 6). This organization builds two neighbouring triangular possibilities for inserting the CO3 group, sharing the oxygen atom O1. If both places were occupied, then C2O5 groups would exist which is impossible. Compared to other CaCO3 polymorphs, there is no edge sharing between the CO3 groups and the calcium CaO6 octahedra in calcite. In the latter compound, only corner sharing is observed both between octahedra themselves and between CO3 groups and octahedra. In aragonite, all three edges of the CO3 groups are common with edges of three different CaO9 polyhedra. In this sense, one can see the vaterite structure as a real intermediate form between calcite and aragonite; these two more stable polymorphs

Figure 4. (Color online) Comparison of the A m a2 model (a) with the P b n m Meyer model (b). Projection along the short axis (4.13 Å) showing the layers of CaO8 cubes interconnected by edges and the CO3 groups ensuring their linkage. The CO3 groups are all pointing in the same direction by O2 in the A m a2 model, and they alternate in opposite directions in the P b n m model.

Figure 5. (Color online) Comparison of the A m a2 model (a) with the P b n m Meyer model (b). Projection along the longer axis (8.47 Å) showing a layer of edge-sharing CaO8 cubes as can be found by selecting a part of the CaF2 fluorite structure.

Figure 6. (Color online) Comparison of the A m a2 model (a) with the P b n m Meyer model (b). Projection along the b axis (7.16 Å) showing the differences in orientation and position of the CO3 groups in a similar matrix of CaO8 cubes interconnected by edges and corners.
correspond to corner and full edge sharing of the CO3 “triangles.” In aragonite, this is operated through a slight but significant displacement of the carbon atom away from the oxygen plane (around 0.05 Å). In the newly proposed vaterite subcell, the lack of edge sharing of CO3 groups is compensated by the stabilization of CaO8 cubes, at the expense of around 2 kJ/mol compared to aragonite. Therefore, the development of vaterite during the first crystallization stages, when surface energy predominates, appears more understandable. The small number of additional weak superstructure reflections indicates that a subtle additional long range ordering modifies the average structure described in the present subcell. Seeing clearly only five peaks when the total number of reflections up to 120°2θ is supposed to increase from 51 to 246 from the hexagonal subcell to the supercell (and more in orthorhombic symmetry), it looks that the task of fully characterizing the supercell will remain uneasy and uncertain for a while. Moreover, an intense microtwinning may involve a non-negligible percentage of the total number of atoms (Figure 7) and be the reason for additional streaks. Faults and microtwinning are favoured by the fluorite-type structure edge-sharing CaO8 cubes being able to develop the observed layers in several space directions, accommodating easily, just like in CaF2. Moreover, on

Figure 7. The twinning hypothesis with three orthorhombic domains (space group A m a2) rotated by 120° along the a axis, regenerating the apparent hexagonal symmetry on a “single crystal.” This implies no change on the Ca atoms, only small oxygen atoms moves, and mainly C atoms positioned at the center of different O3 triangles generated by the edge sharing of the CaO8 cubes. The twin plane may well be orthogonal to the a orthorhombic axis (c in the old hexagonal description) rather than parallel to it.
one side or the other relative to the CaO8 edge-sharing cube layers, the CO3 group order may easily differ because the energy barrier is very small. The stacking may thus show the three orientations at 120° on the same pseudo-single-crystal along the a orthorhombic axis in the A m a2 cell (c axis in the old hexagonal description) as observed by Qiao and Feng (Reference Qiao and Feng2007). Our vaterite particles are globally 4 μm diameter spheres, with SEM-visible substructure as small as acicularlike and radially disposed crystals of typically 50 nm diameter (Ouhenia et al., Reference Ouhenia, Chateigner, Belkhir, Guilmeau and Krauss2008b) and a mean isotropic coherent domain size of 16 nm. Our microtwinning hypothesis then takes place in the formation of these small crystals rather than in an eventual formation of hexagonal-like vaterite platelets as sometimes observed in the literature and is intrinsically linked to the relatively higher energy state, easily transformed into calcite and/or aragonite.












