Hostname: page-component-745bb68f8f-grxwn Total loading time: 0 Render date: 2025-02-11T10:43:43.165Z Has data issue: false hasContentIssue false
  • English
  • Français

Electron density distribution and crystal structure of lithium strontium silicate, Li2SrSiO4

Published online by Cambridge University Press:  29 February 2012

Yoshinori Hirano ,
Tomoyuki Iwata ,
Koichi Momma  and
Koichiro Fukuda
Yoshinori Hirano
Affiliation:
Department of Environmental and Materials Engineering, Nagoya Institute of Technology, Nagoya 466-8555, Japan
Tomoyuki Iwata
Affiliation:
Department of Environmental and Materials Engineering, Nagoya Institute of Technology, Nagoya 466-8555, Japan
Koichi Momma
Affiliation:
Neutron Scattering Group, Quantum Beam Center, National Institute for Materials Science (NIMS), Ibaraki 305-0044, Japan
Koichiro Fukuda*
Affiliation:
Department of Environmental and Materials Engineering, Nagoya Institute of Technology, Nagoya 466-8555, Japan
*
a)Author to whom correspondence should be addressed. Electronic mail: fukuda.koichiro@nitech.ac.jp
Rights & Permissions [Opens in a new window]

Abstract

Crystal structure of Li2SrSiO4 was reinvestigated by laboratory X-ray powder diffraction. The title compound was trigonal with space group P3121, Z=3, unit-cell dimensions a=0.502 281 (4) nm and c=1.245 520(8) nm, and V=0.272 129(3) nm3. The initial structural model was derived by the direct methods and further refined by the Rietveld method. The maximum-entropy method-based pattern fitting (MPF) method was used to confirm the validity of the structural model, in which conventional structure bias caused by assuming intensity partitioning was minimized. The final reliability indices calculated from MPF were Rwp=8.04%, S=1.22, Rp=6.01%, RB=1.50%, and RF=0.66%. Atomic arrangements of the final structural model were in excellent agreement with the three-dimensional electron-density distributions determined by MPF.

Keywords

lithium strontium silicateX-ray powder diffractionRietveld methodmaximum-entropy methodelectron-density distributions
Type
Technical Articles
Information
Powder Diffraction , Volume 25 , Issue 1 , March 2010 , pp. 4 - 8
Copyright
Copyright © Cambridge University Press 2010

I. INTRODUCTION

Eu2+-activated lithium strontium silicate (Li2SrSiO4) exhibits an intense emission peak from yellow to orange-red under a broad excitation band of 400 to 470 nm, and hence attempts have been made to develop white light-emitting diodes (LEDs) through the integration of blue LED chips (Saradhi and Varadaraju, Reference Saradhi and Varadaraju2006; Zhang et al., Reference Zhang, He, Li, Yu and Zou2008; He et al., Reference He, Fu, Wang, Song, Pan, Zhao, Zhang and Cao2008; Kulshreshtha et al., Reference Kulshreshtha, Sharma and Sohn2009a, Reference Kulshreshtha, Shin and Sohn2009b). TheLi2SrSiO4:Eu2+-coated LED showed improved red emission compared to the commercialYAG:Ce3+-coated LED.

Haferkorn and Meyer (Reference Haferkorn and Meyer1998) determined the crystal structure of Li2EuSiO4 [space group P3121, Z=3, and unit-cell dimensions a=0.502 70(5) and c=1.2470(2) nm] by single crystal X-ray diffraction. They also reported the unit-cell dimensions of a=0.502 59(4) [and c=1.2471(1) nm] to conclude that these two compounds are isotypic. Recently, Saradhi and Varadaraju (Reference Saradhi and Varadaraju2006) determined the crystal structure of from laboratory X-ray powder diffraction (XRPD) data by taking Li2EuSiO4 as the initial structural model. The reliability indices of the Rietveld refinement were satisfactory. However, the final structural model can still be improved because the interatomic distances do not agree well with those expected from the ionic radii or bond valence sums. In order to clarify the highly efficient luminescence mechanism and further improve the performance of Li2SrSiO4:Eu2+ phosphor, a more detailed structural study of the host material will be useful.

A combined use of the Rietveld method (Rietveld, Reference Rietveld1967), the maximum-entropy method (MEM) (Takata et al., Reference Takata, Nishibori and Sakata2001) and the MEM-based pattern fitting (MPF) method (Izumi et al., Reference Izumi, Kumazawa, Ikeda, Hu, Yamamoto and Oikawa2001), has enabled us to determine three-dimensional (3D) electron-density distributions (EDDs), which efficiently disclose structural details such as positional disordering of atoms and/or orientational disordering of atomic groups (Izumi, Reference Izumi2004). The Rietveld method and MEM have a drawback in determining the EDD from XRPD data because the observed structure factors, F o (Rietveld), are biased toward the structural model assuming intensity partitioning. On the other hand, the MPF method can minimize the structural bias. Thus, the MEM and MPF analyses are alternately repeated (REMEDY cycle) until the reliability indices reach minima. Crystal structures are represented not by structural parameters but by 3D EDD in MPF.

In the present structural study of Li2SrSiO4, we successfully derived the coordinates of all atoms, including those of Li, using the direct methods and further refined them using the Rietveld method. The validity of the final structural model was confirmed by the 3D EDD determined by MPF.

II. EXPERIMENTAL

A sample of Li2SrSiO4 was prepared from stoichiometric amounts of reagent-grade chemicals Li2CO3, SrCO3, and SiO2. Well-mixed chemicals were pressed into pellets (20 mm diameter and 5 mm thick), heated at 873 K for 3 h, and followed by quenching in air. The densely sintered pellets were finely ground to obtain a powder specimen.

TABLE I. Crystal data for Li2SrSiO4.

A diffractometer (X’Pert PRO Alpha-1, PANalytical B.V., Almelo, The Netherlands), equipped with an incident-beam Ge(111) Johansson monochromator to obtain Cu Kα1 radiation and a high-speed detector, was used in the Bragg-Brentano geometry. The X-ray generator was operated at 45 kV and 40 mA. A variable divergence slit was used to keep a constant illuminated length of 5 mm on the specimen surface. Other experimental conditions were continuous scan, experimental 2θ range from 18.0154° to 148.9314° (an accuracy in 2θ of ±0.0001°) ), 7835 total data points, and 5.5 h total experimental time. The structure data were standardized according to rules formulated by Parthé and Gelato (Reference Parthé and Gelato1984) using the computer program STRUCTURE TIDY (Gelato and Parthé, Reference Gelato and Parthé1987). The crystal-structure models, equidensity isosurfaces of EDD, and two-dimensional (2D) EDD map were visualized with the computer program VESTA (Momma and Izumi, Reference Momma and Izumi2008). Distortion parameters for the coordination polyhedra were found using the computer program IVTON (Balic-Zunic and Vickovic, Reference Balic-Zunic and Vickovic1996).

III. RESULTS AND DISCUSSION

A. Structure refinement

Peak positions of the experimental diffraction pattern were first determined by finding minima in the second derivatives using the computer program PowderX (Dong, Reference Dong1999). The 2θ values of 40 observed peak positions were then used as input data to the automatic indexing computer program TREOR90 (Werner et al., Reference Werner, Eriksson and Westdahl1985). One hexagonal unit cell was found with satisfactory figures of merit: M40/F40=285/415 (0.001 787, 54) (de Wolff, Reference de Wolff1968; Smith and Snyder, Reference Smith and Snyder1979). The derived unit-cell parameters of a=0.502 422(5) and c=1.245 93(1) nm could index all reflections in the observed diffraction pattern.

The observed diffraction peaks were examined to confirm the presence or absence of reflections. Systematic absences l ≠ 3n for hkil reflections were found, suggesting that

TABLE II. Structural parameters for Li2SrSiO4.

Figure 1. (Color online) Crystal structure of Li2SrSiO4. (a) A basic structural unit [Li2SrSiO13]18− viewed along the c axis. (b) Individual units are linked together with formation of a two-dimensional layer parallel to (001). (c) The layers are stacked in the [001] direction to form a three-dimensional structure (perspective view). Atom numbering corresponds to that given in Table II.

possible space groups are P31, P32, P3121, P3121, P3112, P3212, P63/m, and P6322. All these space groups were tested and confirmed using the EXPO2004 package (Altomare et al., Reference Altomare, Burla, Camalli, Carrozzini, Cascarano, Giacovazzo, Guagliardi, Moliterni, Polidori and Rizzi1999). A unit-cell content with [6Li 3Sr 3Si 12O] was used as input data for the search of a crystal-structure model. A promising structural model with the minimum reliability

Figure 2. (Color online) Comparison of the observed diffraction pattern of Li2SrSiO4 (symbol: +) with the corresponding calculated pattern (upper solid line). The difference curve is shown in the lower part of the diagram. Vertical bars indicate the positions of possible Bragg reflections.

index RF (Young, Reference Young and Young1993) of 4.50% was successfully obtained with the space group P3121 in a default run of the program. There were five independent sites (i.e., one Li site located at the Wyckoff position 6c, one Sr site at 3a, one Si site at 3b , and two O sites at 6c )in the unit cell.

Structural parameters of all atoms were refined by the Rietveld method using the computer program RIETAN-FP (Izumi and Momma, Reference Izumi and Momma2007) with the profile intensity data in the 2θ range of 18.0154° to 148.0792° (7784 total data points). A Legendre polynomial with 12 adjustable parameters was fitted to background intensities. The split Pearson VII function (Toraya, Reference Toraya1990) was used to fit the peak profiles. Isotropic displacement (B) parameters were assigned to all atoms. Reliability indices of the Rietveld refinement were

Figure 3. (Color online) Three-dimensional electron-density distributions determined by MPF with the structural model. Isosurfaces expressed in smooth shading style for an equidensity level of 0.002 nm−3.

Figure 4. (Color online) A bird’s eye view of electron densities up to 3.3% of the maximum (0.552 nm−3) on the plane parallel to (110) at the height of Li sites (lower part) with the corresponding atomic arrangements (upper part). Atom numbering corresponds to that given in Table I.

R wp=8.06%, S(=R wp/R e)=1.22, R p=6.01%, R B=1.75% , RF=0.88% , and (Young, Reference Young and Young1993). Crystal data are given in Table I and the final atomic positional and B parameters are given in Table II shows the final structural model, which is isomorphous with that of Li2EuSiO4.

The EDDs with 80×80×198 in the unit cell, the spatial resolution of which is approximately 0.0063 nm, were obtained from the MPF method using the computer programs RIETAN-FP and PRIMA (Izumi and Dilanian, Reference Izumi, Dilanian and Pandalai2002). After one REMEDY cycle, R wp, S, R p, R B, and R F further decreased to 8.04%, 1.22, 6.01%, 1.50%, and 0.66%, respectively. Subtle EDD changes as revealed by MPF significantly improve the

TABLE III. Selected bond lengths (nm) and angles (deg) in Li2SrSiO4.

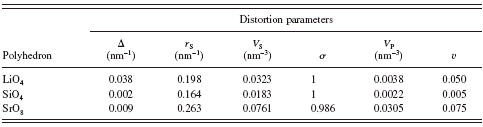
TABLE IV. Polyhedral distortion parameters. Δ=eccentricity; r S=radius of sphere fitted to ligands; V S=sphere volume; σ=sphericity; V P=volume of coordination polyhedron; v=volume distortion; and σ, for coordination number four, is 1 by definition.

R B and R F indices. The decreases in R indices demonstrate that the crystal structure can be seen more clearly from EDD instead from the conventional structural parameters reported in Table II. Observed, calculated, and difference XRPD patterns for the final MPF are plotted in Figure 2). We found the peak positions of EDD from the 3D pixel data and compared them with the coordinates of all atoms that were determined by the Rietveld method. The positional deviations of all atoms in the unit cell were found to be necessarily less than 0.004 nm, which is within the resolution limit of the 3D EDD. We therefore concluded that the present structural model would reasonably and satisfactorily represent the crystal structure of Li2SrSiO4.

B. Structure description

Selected interatomic distances and bond angles, together with their standard deviations, are listed in Table III. The average Li–O bond length in the LiO4 tetrahedra is 0.1982 nm, which is comparable to those of the LiO 4 tetrahedra in Li2EuSiO4 (0.1982 nm), Li2BaSiO4 (0.1979 nm), and Li2CaSiO4 (0.1969 nm) (Haferkorn and Meyer, Reference Haferkorn and Meyer1998; Kim et al., Reference Kim, Ahn, Kulshreshtha, Sohn and Shin2009; Gard and West, Reference Gard and West1973). The average Si–O bond length (0.1635 nm) agrees well with the interatomic distance of 0.164 nm calculated from the ionic radii of Si4+ and O2− in the fourfold coordination {r[Si4+(4)]=0.026 nm and r[O2−(4)]=0.138 nm} (Shannon, Reference Shannon1976). The average value of the O–Si–O angles is 109.5°. These interatomic distance and bond angle are in good agreement with those found in other silicates (Baur, Reference Baur1971). When the volume distortion parameters v (Table IV) are compared between the two types of tetrahedra LiO4 and SiO4, the extent of the distortion is much larger for the former than for the latter.

TheSrO8 polyhedron showed the bond lengths ranging from 0.2572 to 0.2671 nm. Ionic radii of Sr2+ in the eightfold coordination {r[Sr2+(8)=0.126 nm and r[O2−(8)]=0.142 nm} predict the interatomic distance of 0.268 nm for Sr–O. This predicted value is in good agreement with the corresponding average interatomic distance of 0.2631 nm. Ratio of volumes of the circumscribed sphere and the polyhedron (V S/V P) for the SrO8 is 2.493. Because the V S/V P value of the Archimedean square antiprism is 2.4369 and that of square antiprism with maximum volume is 2.3906 (Makovicky and Balic-Zunic, Reference Makovicky and Balic-Zunic1998), the present SrO8 can be described as a distorted Archimedean square antiprism.

Valence bond sums calculated on the basis of bond-strength analysis (Li: 1.00, Sr: 2.01, Si: 3.88) are in good agreement with the expected formal oxidation states of Li+, Sr2+, and Si4+ ions (Brown and Altermatt, Reference Brown and Altermatt1985; Brese and O’Keeffe, Reference Brese and O’Keeffe1991). The average bond lengths of Li–O, Si–O, and Sr–O are in agreement with those expected from the bond valence sums (Li–O: 0.1979 nm, Si–O: 0.1624 nm, Sr–O: 0.2631 nm).

The crystal structure of lithium strontium silicate consists of the three types of polyhedra, LiO4, SiO4, and SrO8. Two LiO4 tetrahedra and one SiO4 tetrahedron are connected via corners to form a [Li2SiO9]−12 ring. This ring and SrO8 polyhedron are joined by sharing faces and edges to build up a basic structural unit [Li2SrSiO13]18− , as shown in Figure 1(a) . Individual units are further linked through oxygen atoms to form layers parallel to (001) [Figure 1(b)]. These layers are stacked in the [001] direction with three layers per unit cell to form a three-dimensional structure [Figure 1(c)]. This compound is isomorphous with Li2EuSiO4 (Haferkorn and Meyer, Reference Haferkorn and Meyer1998).

IV. CONCLUSION

We successfully refined the crystal structure of lithium strontium silicate Li2SrSiO4 , having a trigonal unit cell with space group P3121. The basic units of the crystal structure were [Li2SrSiO13]18− , each comprising three types of polyhedra LiO4, SrO8, and SiO4. These basic units were connected by sharing corners and edges to form layers parallel to (001). These layers were stacked in the [001] direction with three layers per unit cell to form a three-dimensional structure. The validity of the structural model was confirmed by the EDD determined by MPF.

References

Altomare, A., Burla, M. C., Camalli, M., Carrozzini, B., Cascarano, G. L., Giacovazzo, C., Guagliardi, A., Moliterni, A. G. G., Polidori, G., and Rizzi, R. (1999). “EXPO: A program for full powder pattern decomposition and crystal structure solution,” J. Appl. Crystallogr. JACGAR 32, 339–340 .10.1107/S0021889898007729CrossRefGoogle Scholar
Balic-Zunic, T. and Vickovic, I. (1996). “IVTON: Program for the calculation of geometrical aspects of crystal structures and some crystal chemical applications,” J. Appl. Crystallogr. JACGAR 29, 305–306.CrossRefGoogle Scholar
Baur, W. H. (1971). “Prediction of bond length variations in silicon-oxygen bonds,” Am. Mineral. AMMIAY 56, 1573–1599.Google Scholar
Brese, N. E. and O’Keeffe, M. (1991). “Bond-valence parameters for solids,” Acta Crystallogr., Sect. B: Struct. Sci. ASBSDK 47, 192–197 .10.1107/S0108768190011041CrossRefGoogle Scholar
Brown, I. D. and Altermatt, D. (1985). “Bond-valence parameters obtained from a systematic analysis of the inorganic crystal structure database,” Acta Crystallogr., Sect. B: Struct. Sci. ASBSDK 41, 244–247 .10.1107/S0108768185002063CrossRefGoogle Scholar
de Wolff, P. M. (1968). “A simplified criterion for the reliability of a powder pattern indexing,” J. Appl. Crystallogr. JACGAR 1, 108–113 .10.1107/S002188986800508XCrossRefGoogle Scholar
Dong, C. (1999). “PowderX: Windows-95-based program for powder X-ray diffraction data processing,” J. Appl. Crystallogr. JACGAR 32, 838.10.1107/S0021889899003039CrossRefGoogle Scholar
Gard, J. A. and West, A. R. (1973). “Preparation and crystal structure of Li2CaSiO4 and isostructural Li2CaGeO4,” J. Solid State Chem. JSSCBI 7, 422–427 .10.1016/0022-4596(73)90171-0CrossRefGoogle Scholar
Gelato, L. M. and Parthé, E. (1987). “STRUCTURE TIDY: A computer program to standardize crystal structure data,” J. Appl. Crystallogr. JACGAR 20, 139–143 .10.1107/S0021889887086965CrossRefGoogle Scholar
Haferkorn, B. and Meyer, G. (1998). “Li2EuSiO4, an europium(II) lithosilicate. Eu[(Li2Si)O4],” Z. Anorg. Allg. Chem. ZAACAB 624, 1079–1081 .10.1002/(SICI)1521-3749(199807)624:7<1079::AID-ZAAC1079>3.0.CO;2-Y3.0.CO;2-Y>CrossRefGoogle Scholar
He, H., Fu, R., Wang, H., Song, X., Pan, Z., Zhao, X., Zhang, X., and Cao, Y. (2008). “Li2SrSiO4:Eu2+ phosphor prepared by the Pechini method and its application in white light emitting diode,” J. Mater. Res. JMREEE 23, 3288–3294 .10.1557/jmr.2008.0394CrossRefGoogle Scholar
Izumi, F. (2004). “Beyond the ability of Rietveld analysis: MEM-based pattern fitting,” Solid State Ionics SSIOD3 172, 1–6 .10.1016/j.ssi.2004.04.023CrossRefGoogle Scholar
Izumi, F. and Dilanian, R. A. (2002). “Structure refinement based on the maximum-entropy method from powder diffraction data,” in Recent Research Developments in Physics, edited by Pandalai, S. G. (Transworld Research Network, Trivandrum), Vol. 3, Pt. II, pp. 699–726.Google Scholar
Izumi, F., Kumazawa, S., Ikeda, T., Hu, W.-Z., Yamamoto, A., and Oikawa, K. (2001). “MEM-based structure-refinement system REMEDY and its applications,” Mater. Sci. Forum MSFOEP 378–381, 59–64 .10.4028/www.scientific.net/MSF.378-381.59CrossRefGoogle Scholar
Izumi, F. and Momma, K. (2007). “Three-dimensional visualization in powder diffraction,” Solid State Phenom. DDBPE8 130, 15–20 .10.4028/www.scientific.net/SSP.130.15CrossRefGoogle Scholar
Kim, J., Ahn, D., Kulshreshtha, C., Sohn, K.-S., and Shin, N. (2009). “Lithium barium silicate, Li2BaSiO4, from synchrotron powder data,” Acta Crystallogr., Sect. C: Cryst. Struct. Commun. ACSCEE 65, i14–i16.10.1107/S0108270109006118CrossRefGoogle ScholarPubMed
Kulshreshtha, C., Sharma, A. K., and Sohn, K.-S. (2009a). “Effect of local structures on the luminescence of Li2(Sr,Ca,Ba)SiO4:Eu2+,” J. Electrochem. Soc. JESOAN 156, J52–J56.10.1149/1.3065098CrossRefGoogle Scholar
Kulshreshtha, C., Shin, N., and Sohn, K.-S. (2009b). “Decay behavior of Li2(Sr,Ba,Ca)SiO4:Eu2+ phosphors,” Electrochem. Solid-State Lett. ESLEF6 12, J55–J57.10.1149/1.3094051CrossRefGoogle Scholar
Makovicky, E. and Balic-Zunic, T. (1998). “New measure of distortion for coordination polyhedra,” Acta Crystallogr., Sect. B: Struct. Sci. ASBSDK 54, 766–773 .10.1107/S0108768198003905CrossRefGoogle Scholar
Momma, K. and Izumi, F. (2008). “VESTA: A three-dimensional visualization system for electronic and structural analysis,” J. Appl. Crystallogr. JACGAR 41, 653–658 .10.1107/S0021889808012016CrossRefGoogle Scholar
Parthé, E. and Gelato, L. M. (1984). “The standardization of inorganic crystal-structure data,” Acta Crystallogr., Sect. A: Found. Crystallogr. ACACEQ 40, 169–183 .10.1107/S0108767384000416CrossRefGoogle Scholar
Rietveld, H. M. (1967). “Line profiles of neutron powder-diffraction peaks for structure refinement,” Acta Crystallogr. ABCRE6 22, 151–152 .10.1107/S0365110X67000234CrossRefGoogle Scholar
Saradhi, M. P. and Varadaraju, U. V. (2006). “Photoluminescence studies on Eu2+-activated Li2SrSiO4—A potential orange-yellow phosphor for solid-state lighting,” Chem. Mater. CMATEX 18, 5267–5272 .10.1021/cm061362uCrossRefGoogle Scholar
Shannon, R. D. (1976). “Revised effective ionic radii and systematic studies of interatomic distances in halides and chalcogenides,” Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr. ACACBN 32, 751–767 .10.1107/S0567739476001551CrossRefGoogle Scholar
Smith, G. S. and Snyder, R. L. (1979). “FN: A criterion for rating powder diffraction patterns and evaluating the reliability of powder-pattern indexing,” J. Appl. Crystallogr. JACGAR 12, 60–65 .10.1107/S002188987901178XCrossRefGoogle Scholar
Takata, M., Nishibori, E., and Sakata, M. (2001). “Charge density studies utilizing powder diffraction and MEM. Exploring of high c superconductors, C60 superconductors and manganites,” Z. Kristallogr. ZEKRDZ 216, 71–86 .10.1524/zkri.216.2.71.20335CrossRefGoogle Scholar
Toraya, H. (1990). “Array-type universal profile function for powder pattern fitting,” J. Appl. Crystallogr. JACGAR 23, 485–491 .10.1107/S002188989000704XCrossRefGoogle Scholar
Werner, P. E., Eriksson, L., and Westdahl, M. (1985). “TREOR: A semi-exhaustive trial-and-error powder indexing program for all symmetries,” J. Appl. Crystallogr. JACGAR 18, 367–370 .10.1107/S0021889885010512CrossRefGoogle Scholar
Young, R. A. (1993). The Rietveld Method, edited by Young, R. A. (Oxford University Press, Oxford), pp. 1–38.CrossRefGoogle Scholar
Zhang, X., He, H., Li, Z., Yu, T., and Zou, Z. (2008). “Photoluminescence studies on Eu2+ and Ce3+-doped Li2SrSiO4,” J. Lumin. JLUMA8 128, 1876–1879 .10.1016/j.jlumin.2008.05.021CrossRefGoogle Scholar
Figure 0

TABLE I. Crystal data for Li2SrSiO4.

Figure 1

TABLE II. Structural parameters for Li2SrSiO4.

Figure 2

Figure 1. (Color online) Crystal structure of Li2SrSiO4. (a) A basic structural unit [Li2SrSiO13]18− viewed along the c axis. (b) Individual units are linked together with formation of a two-dimensional layer parallel to (001). (c) The layers are stacked in the [001] direction to form a three-dimensional structure (perspective view). Atom numbering corresponds to that given in Table II.

Figure 3

Figure 2. (Color online) Comparison of the observed diffraction pattern of Li2SrSiO4 (symbol: +) with the corresponding calculated pattern (upper solid line). The difference curve is shown in the lower part of the diagram. Vertical bars indicate the positions of possible Bragg reflections.

Figure 4

Figure 3. (Color online) Three-dimensional electron-density distributions determined by MPF with the structural model. Isosurfaces expressed in smooth shading style for an equidensity level of 0.002 nm−3.

Figure 5

Figure 4. (Color online) A bird’s eye view of electron densities up to 3.3% of the maximum (0.552 nm−3) on the plane parallel to (110) at the height of Li sites (lower part) with the corresponding atomic arrangements (upper part). Atom numbering corresponds to that given in Table I.

Figure 6

TABLE III. Selected bond lengths (nm) and angles (deg) in Li2SrSiO4.

Figure 7

TABLE IV. Polyhedral distortion parameters. Δ=eccentricity; rS=radius of sphere fitted to ligands; VS=sphere volume; σ=sphericity; VP=volume of coordination polyhedron; v=volume distortion; and σ, for coordination number four, is 1 by definition.