1 Introduction
How can we elicit honest responses in surveys? Scholars often worry that their survey measurement suffers from social desirability bias (SDB)—systematic misreporting of socially sensitive behavior or attitudes (Zaller and Feldman Reference Zaller and Feldman1992). Along with other techniques, conjoint analysis has become popular among political scientists to elicit honest answers (e.g., Carey, Clayton, and Horiuchi Reference Carey, Clayton and Horiuchi2020; Hankinson Reference Hankinson2018; Teele, Kalla, and Rosenbluth Reference Teele, Kalla and Rosenbluth2018).
Hainmueller, Hopkins, and Yamamoto (Reference Hainmueller, Hopkins and Yamamoto2014) introduced conjoint analysis to political science as an experimental method for causal inference. This sparked numerous applications in political science. Indeed, at least 58 articles using conjoint analysis appeared in leading political science journals between 2014 and 2019 (de la Cuesta, Egami, and Imai Reference de la Cuesta, Egami and Imai2021). In a typical conjoint experiment, respondents evaluate a table containing two hypothetical profiles (columns), each consisting of a set of attributes (rows) that might affect respondents’ evaluations of the profiles. The attributes are randomly varied to form a series of pairwise comparisons. The resulting choice or rating responses are then aggregated to identify respondents’ multidimensional preferences.
A standard conjoint design does not require respondents to state their attitudes on controversial topics directly. Instead, sensitive attitudes are gleaned indirectly through respondents’ evaluations of multiple profiles that randomly vary in many attributes. Consequently, it is widely believed that attitudes elicited using such a design are less susceptible to SDB than those obtained using other designs. Indeed, conjoint analysis has been used to study a range of topics for which traditional approaches might fail to elicit honest opinions. For example, two recent articles explicitly mention that conjoint analysis is appropriate because it “reduces [SDB] by providing many potential reasons for supporting or opposing a proposed [housing] development [e.g., for low-income residents]” (Hankinson Reference Hankinson2018, 479) or because it “lessens the degree to which our results [preferences for female political candidates] are skewed by [SDB]” (Teele, Kalla, and Rosenbluth Reference Teele, Kalla and Rosenbluth2018, 535).
However, systematic evidence supporting the effectiveness of fully randomized conjoint designs in reducing SDB is largely absent.Footnote 1 Some applications of conjoint analysis present results suggesting indirect evidence of SDB mitigation. Hainmueller and Hopkins (Reference Hainmueller and Hopkins2015), for example, show that respondents’ self-monitoring scores do not moderate their preferences for hypothetical immigrants and conclude that responses are not “shaped by social desirability” (Appendix C, Supplementary Material). Hainmueller, Hangartner, and Yamamoto (Reference Hainmueller, Hangartner and Yamamoto2015) show that conjoint designs reproduce the effects of nationality on Swiss citizens’ preferences about naturalization applications estimated from a behavioral benchmark, even though the attribute “raises the specter of potentially strong SDB” (p. 2,396). However, neither study directly estimates the SDB reduction from a fully randomized conjoint design.
In this article, we hypothesize that conjoint analysis reduces SDB via two mechanisms—imperceptibility and rationalization. We then propose a novel experimental design to investigate whether a fully randomized conjoint design mitigates SDB through these mechanisms. Specifically, we compare a standard design against a partially randomized design where only the sensitive attribute varies between the two profiles, removing both the imperceptibility and rationalization mechanisms while maintaining the comparability of preference measurements.
We decompose the difference in average marginal component effects (AMCEs) between these two designs into two components: (1) the reduction in SDB afforded by the fully randomized condition and (2) a “design effect,” which stems from the increased attention respondents pay to the varying attribute in the partially randomized design. The difference in AMCEs observed between the fully and partially randomized conjoint designs in a setting where SDB is expected to be minimal (the control condition) identifies the design effect. By subtracting this estimate of the design effect from the difference in AMCEs observed in the high SDB treatment condition, we estimate the reduction in SDB provided by the fully randomized conjoint design relative to this partially randomized design.
We implement this identification strategy in two original survey experiments. Our two experiments differ in two important ways. First, they test the SDB-reducing ability of conjoint analysis on two different substantive topics: consumers’ preferences for the use of ecofriendly materials (Study 1) and voters’ support for congressional candidates with sexual harassment scandals (Study 2). Both topics represent settings where social norms may conflict with respondents’ honest behavior, and previous research suggests that SDB is likely to be present for at least a subset of respondents on both topics (Klaiman, Ortega, and Garnache Reference Klaiman, Ortega and Garnache2016; Krupnikov, Piston, and Bauer Reference Krupnikov, Piston and Bauer2016).
The social norms targeted by these topics are of great interest to political scientists. The trade-off between achieving a common goal (a better environment) and pursuing personal benefits (e.g., purchasing commodities based on price, style, etc.) is at the heart of many political conflicts. Conjoint designs have been employed to study precisely this trade-off in the context of environmental policies (Bechtel, Genovese, and Scheve Reference Bechtel, Genovese and Scheve2019; Bechtel and Scheve Reference Bechtel and Scheve2013). Similarly, political scientists often worry that respondents will not express attitudes that run counter to social norms, such as gender equality. Candidate choice experiments represent one of the most common uses of conjoint designs to mitigate this concern (e.g., Horiuchi, Smith, and Yamamoto Reference Horiuchi, Smith and Yamamoto2020; Teele, Kalla, and Rosenbluth Reference Teele, Kalla and Rosenbluth2018).
Second, our two studies employ two different procedures for identifying the SDB-prone subgroups of respondents. Recent research suggests that SDB in political science research is typically limited to just a subset of respondents (Blair, Coppock, and Moor Reference Blair, Coppock and Moor2020). On most topics, a large fraction of respondents either do not consider the topic under investigation to be socially sensitive or are not hesitant to express socially undesirable opinions in anonymous surveys. It is thus essential to precisely identify the subgroup of SDB-prone respondents for a given topic. In Study 1, we filter out likely SDB-proof respondents based on theoretically motivated survey items included in a pre-treatment wave. In Study 2, we employ a data-driven, machine-learning approach in a single-shot design.
Overall, our findings suggest that conjoint analysis does mitigate SDB among respondents who view these topics as socially sensitive. Specifically, among the subgroup of SDB-prone respondents, our estimated reduction in SDB for the AMCE of the sensitive attribute afforded by the fully randomized conjoint design is as large as about two-thirds of the AMCE itself in each study. Although these estimates are encouraging, we also caution that our analysis includes a deviation from our preanalysis plan in each study, rendering our evidence exploratory rather than confirmatory. Some of our findings also exhibit a degree of sensitivity to alternative model specifications and parameter choices. To facilitate further confirmatory studies, we discuss suggestions for future researchers who seek to replicate our proposed design on various empirical settings.
Our contribution in this article is thus threefold. First, we propose a novel experimental design for identifying the SDB reduction in a fully random conjoint design. Unlike previous attempts at examining the SDB-reducing potential of factorial survey designs (of which conjoint analysis is an example; see Section A in the Supplementary Materials), our proposed design can distinguish the reduction in SDB from other effects that a survey format might have on survey responses. Second, we provide evidence supportive of the SDB-reducing effect of conjoint analysis among SDB-prone respondents. Although exploratory by nature, our estimates are consistent across two different topics and subgroup-identification strategies. We therefore consider our findings sufficiently strong to be cautiously optimistic about conjoint analysis as a tool to cope with SDB. At the same time, we encourage future confirmatory research, especially given how frequently conjoint analysis is already used for this purpose. Finally, our analysis reveals a high degree of heterogeneity in respondents’ proneness to SDB on each topic. We thus urge future SDB researchers to incorporate this heterogeneity in their study design to avoid false negatives.
2 Social Desirability Bias and Conjoint Analysis
Existing theories about SDB indicate two possible mechanisms through which conjoint analysis can mitigate SDB. The first mechanism is imperceptibility. For SDB to occur, respondents must become aware of the possibility of violating social norms and consciously avoid norm-violating responses (Krumpal Reference Krumpal2013). In a fully randomized conjoint experiment, however, the sensitive attribute is included along with a host of other nonsensitive attributes randomly varied from task to task. Respondents are, therefore, unlikely to perceive the possibility of violating social norms by choosing certain profiles.
For example, suppose that a researcher wants to measure respondents’ preferences about ecofriendly consumer products. Directly asking respondents whether they prefer an ecofriendly product would induce SDB because we expect respondents to respond to the question based on a social norm to protect the environment. However, a fully randomized conjoint experiment makes the researcher’s objective far less obvious because ecofriendliness is only one of many attributes. Although it is still possible that respondents will become captivated by the sensitive attribute (Jenke et al. Reference Jenke, Bansak, Hainmueller and Hangartner2021), this likelihood is certainly reduced relative to direct questioning.
The second mechanism is rationalization. Even if respondents recognize the potential for norm violation in a fully randomized conjoint experiment, they are still more likely to express honest preferences because other attributes enable them to rationalize their evaluations. For example, in a product choice experiment, respondents may recognize a social norm violation if they consider choosing a nonecofriendly product. Still, they may choose to do so if they feel they can justify their decision based on other nonsensitive differences between products, such as price and quality. Therefore, the possibility of rationalization reduces the respondents’ subjective cost of norm-violating responses, further reducing SDB (e.g., Krupnikov, Piston, and Bauer Reference Krupnikov, Piston and Bauer2016).
There exists a well-developed literature examining whether factorial survey designs (Wallander Reference Wallander2009) mitigate SDB through mechanisms similar to the ones discussed above (e.g., Atzmüller and Steiner Reference Atzmüller and Steiner2010). Although conjoint analysis is a specific type of factorial survey, we argue that the existing studies on this topic do not provide sufficient empirical evidence to confirm the SDB-mitigating effect of a fully randomized conjoint design. This is due to shortcomings of these previous studies and specific characteristics of the fully randomized conjoint design. See Section A in the Supplementary Materials for further discussions.
3 Topic Selection
For a topic to be suitable for demonstrating the SDB-reducing effect of conjoint analysis, it must satisfy two conditions. First, the topic must be viewed as socially sensitive by at least a subset of respondents. Second, the honest preference of these respondents must deviate from the socially desirable choice. In other words, they must experience social pressure to misreport their honest preferences.Footnote 2 Based on these requirements, we selected two topics that appear particularly appropriate for our study—attitudes toward environmental protection and vote choice involving candidates with a sexual harassment scandal.Footnote 3
In Study 1, we measured respondents’ attitudes toward environmental protection through hypothetical consumption behavior. The sensitive attribute is whether athletic shoes use ecofriendly materials. We consider this topic to be particularly suitable for our research for three reasons. First, environmental conservation is a classic example of a public good, of which the actions of rational individuals tend to cause under-provisioning due to collective action problems (Ostrom Reference Ostrom1990), and researchers find social pressure to be an effective deterrent for individual free-riding (see Chaudhuri Reference Chaudhuri2011, for a review). Although the direct object of our choice task itself is a private good (i.e., athletic shoes), collective action on climate crucially depends on consumer behavior, such as purchasing environmentally friendly products.
Second, purchasing decisions involve trade-offs between desirable attributes under a budget constraint, where consumers must prioritize certain goods over others. Respondents’ preferences about athletic shoes are likely driven by attributes directly tied to their purchase’s primary objective—owning and wearing the shoes—such as brand, color, and price. Whether ecofriendly materials are used is only incidental for most consumers. Thus, in the absence of SDB, even respondents who favor environmental protection are unlikely to make purchasing decisions solely on the use of ecofriendly materials. Consequently, many respondents would make purchasing decisions different from their honest preference when under social pressure.
Finally, political scientists are often interested in opinions surrounding the environment and worry that SDB could tarnish the measurement of these attitudes. For example, respondents might overstate how much they favor a climate mitigation policy that will increase their energy costs because of SDB (Bechtel, Genovese, and Scheve Reference Bechtel, Genovese and Scheve2019). Moreover, there is a known disconnect between how likely consumers state they are to purchase products made with ecofriendly materials in surveys and aggregate sales data, suggesting that SDB is a significant concern (e.g., Carrigan and Attalla Reference Carrigan and Attalla2001).
In Study 2, we administered a candidate choice experiment and used whether a hypothetical candidate is involved in sexual harassment scandals as the sensitive attribute. There are several reasons why we consider this topic to be useful for our purpose. First, candidate choice conjoint experiments are very common in political science (e.g., Horiuchi, Smith, and Yamamoto Reference Horiuchi, Smith and Yamamoto2020; Teele, Kalla, and Rosenbluth Reference Teele, Kalla and Rosenbluth2018), and many existing candidate choice studies indeed investigate the influence of corruption allegations and other scandals on voters’ preferences (e.g., Incerti Reference Incerti2020).
Second, this setting relies on norms of gender equality and ethical behavior among elected officials that are believed to be a common source of SDB in political science applications. Such norms are distinct from those at work in Study 1, that is, norms surrounding the provision of public goods.
Finally, a discrepancy has arisen in recent years between polling results, which suggest that many voters are unwilling to support candidates accused of sexual harassment, and the continued success of candidates from both parties facing such allegations. For example, both Presidents Trump and Biden were elected despite facing such allegations. Consequently, we believe an exploration of the effect of SDB on this topic will be of particular interest to political scientists.
4 Identification Strategy
To estimate the size of the response bias avoided in conjoint experiments due to the mechanisms discussed in Section 2, we propose an identification strategy that involves three innovations. First, we randomly assign respondents to one of two conjoint designs. The two designs are almost identical: we ask respondents to complete a series of paired conjoint evaluation tasks involving a sensitive attribute. However, they are different in terms of how we generate the profiles. Namely, in the fully randomized design, all attributes vary so that the aforementioned mechanisms will mitigate the influence of SDB on the AMCEs. In the partially randomized design, only one attribute varies between each pair of conjoint profiles so that respondents will focus on just that attribute.
We intend our fully randomized design to be similar to conjoint experiments typically employed in political science so that our results speak to the SDB-mitigating ability of such designs. On the other hand, we use the partially randomized design to “turn off” the two SDB-reducing mechanisms from the standard conjoint design while maintaining the comparability of our estimand (i.e., the AMCE). Specifically, this design blocks the imperceptibility mechanism because the objective of the study will be apparent to respondents and the potential for norm violation will be just as noticeable as in direct questioning. Similarly, displaying pairs of profiles that differ only in the sensitive attribute provides respondents with no additional information to base their evaluations on, blocking the rationalization mechanism.
However, the difference between the two designs is potentially confounded by a factor that we call the design effect—the increase in the AMCE of any varying attribute under the partially randomized design due to focused attention on that attribute. In the partially randomized design, respondents will need to evaluate profiles solely based on a single varying feature, amplifying its average effect. Therefore, we theorize that the difference in AMCEs between the fully and partially randomized designs is the sum of the reduction in SDB afforded by these two mechanisms and the design effect.
The second innovation in our experimental approach is the introduction of a control condition to remove this design effect. In each study, we include a control condition that replicates the contrast between the partially and fully randomized conjoint designs in a setting where we expect little SDB to be present. In this condition, SDB will be low under both the partially and fully randomized designs, so the difference in AMCEs between these designs will represent the design effect. Consequently, we estimate the reduction in SDB facilitated by the fully random conjoint design by subtracting this estimate of the design effect (in the low SDB condition) from the difference in AMCEs in the high SDB condition. The result is a difference-in-differences estimator.Footnote 4
Table 1 summarizes these four design conditions. We construct the sensitive and control conditions differently in each study. In Study 1, we utilize a nonsensitive placebo attribute, gel cushioning, for which we expect no SDB to be present. In Study 2, we randomly assign an SDB-increasing prime to half of the respondents and use the un-primed group as the low SDB control condition. We provide further details in Section 5.
Table 1 Summary of design conditions in two studies.
Under the “partial” conditions, only the key attribute varies between profiles in each pair of conjoint profiles. Under the “full” conditions, all attributes vary randomly. The “sensitive” and “control” conditions differ in terms of the expected level of SDB.
The third innovation in our empirical strategy is the construction of an SDB-prone subgroup tailored for each of the substantive topics. We are motivated to focus on these subgroups by the emergent body of empirical research suggesting that SDB is much less common than political scientists often fear and is frequently local to respondents with background characteristics specific to particular contexts. For example, Blair, Coppock, and Moor (Reference Blair, Coppock and Moor2020) conducted a systematic review looking for evidence of SDB in political science applications and identified only four settings with convincing evidence of SDB in the full sample.
Despite the growing literature suggesting that concerns about SDB might be somewhat exaggerated, there are good reasons to believe that SDB poses a threat to inference when the attitudes of particular subgroups of respondents are important. For example, even if only strong Democrats exaggerated their unwillingness to support a candidate accused of sexual harassment, it would still have significant implications for understanding what types of candidates likely win a Democratic primary. Similarly, even if just a small proportion of environmentally conscious consumers overstated their interest in buying ecofriendly products, it could still lead researchers to overestimate the market size for such goods.
Consequently, in each of our studies, we focus on a subset of SDB-prone respondents who are expected to exhibit SDB on these topics. We take different approaches to identifying SDB-prone respondents in Studies 1 and 2. In Study 1, we employ a two-wave survey design to condition our main analysis on a preregistered set of covariates we identify in the baseline wave. In Study 2, we use a single-wave design but apply a machine-learning algorithm to identify SDB prone respondents. We explain both approaches in Section 6.
5 Survey Designs
In this section, we describe our two empirical studies, each of which implements the general identification strategy presented in Section 4.Footnote 5
5.1 Study 1
We use a two-wave survey design for Study 1. In Wave 1, we asked questions about respondents’ demographic attributes and their political attitudes. We also included a battery of items to measure proneness to SDB in general and on this topic specifically (see Section C of the Supplementary Materials). We measured these variables in the pretreatment wave to avoid priming respondents. Making respondents aware of our primary interest in ecofriendly consumption preferences or SDB would draw their attention to our treatment attribute regardless of the design conditions, undermining our empirical strategy’s validity. To the same end, we presented our study to the respondents as a survey about online shopping in general. We also added several distracter questions about other attributes that we would include in the conjoint tasks in Wave 2.
At the beginning of Wave 2, we randomly assigned respondents into one of the four conjoint designs. In each condition, we asked respondents to complete twenty paired conjoint evaluation tasks.Footnote 6 In each task, we asked respondents how likely they were to purchase each of the shoes using two separate 7-point Likert scales.
The four conditions constitute a two-by-two factorial design, implementing our general identification strategy (Table 1). Namely, the partial-sensitive design keeps all attributes constant in each profile pair except for the sensitive attribute, Ecofriendly Materials, directing respondent attention to just that attribute, and eliminating the SDB-reducing mechanisms. The partial-control design instead keeps all attributes constant except for the placebo attribute, Gel Cushioning, allowing us to estimate the design effect of focusing respondents’ attention on just one nonsensitive attribute. In contrast, the full-sensitive and full-control designs generate tables composed of attributes that vary randomly between the two profiles, much like a standard fully randomized conjoint experiment.Footnote 7 The remaining attributes in the design are filler attributes not directly used in the analyses. We included them to activate SDB-mitigating mechanisms and to maintain the realism of the conjoint tasks. See Section C.2 of the Supplementary Materials for the details of our estimation strategy, and Section C.3 for the full list of attributes used in Study 1.
5.2 Study 2
In Study 2, we implement our identification strategy in a typical candidate choice experiment. We asked respondents to evaluate ten pairs of hypothetical congressional candidates and to indicate their likelihood of voting for each candidate using two separate 7-point Likert scales. The sensitive attribute is Scandal. Although most respondents will genuinely prefer candidates not involved in sexual harassment scandals, SDB should drive this difference even larger. Just as in Study 1, the AMCE for the Scandal attribute should be smaller under the fully randomized design than under the partially randomized design both because of the two SDB-mitigating mechanisms and the design effect.
In Study 1, we use a placebo, nonsensitive attribute to subtract the design effect from our SDB-reduction estimate. A limitation of this approach is that the sensitive and placebo attributes might differ not only in their social sensitivity, but also in their design effects. Although the sensitive and placebo conditions are identical in every way except these attributes, we cannot rule out the possibility that the partially and fully randomized designs create larger attention differentials for one attribute than the other. To address this possible threat to inference, in Study 2, we take a different approach to constructing high and low SDB conditions. Namely, we employ a randomized intervention to prime respondents’ social sensitivity.
Our intervention draws upon the literature suggesting that SDB is larger in in-person interviews than online surveys (e.g., Tourangeau and Yan Reference Tourangeau and Yan2007, 863–871). Specifically, before the conjoint tasks, we showed a random half of respondents (i.e., the treatment, sensitive group) a paragraph stating that we might contact them again for a follow-up survey with an invitation to complete a face-to-face interview (Figure 1). The other half (i.e., the control group) were given no such treatment and proceeded directly to the conjoint tasks.Footnote 8 We expect that respondents exposed to this prime will have completed the conjoint evaluation tasks with the possibility of added scrutiny during a face-to-face interview in mind, inducing SDB. Existing studies suggest that small changes to survey designs can succeed in inducing SDB in respondents. For example, subtle primes of a religious identity make respondents less likely to admit to some sensitive behaviors (Rodriguez, Neighbors, and Foster Reference Rodriguez, Neighbors and Foster2014). Similarly, Eck et al. (Reference Eck, Hatz, Crabtree and Tago2021) show that even a subtle intervention reminding respondents about the possibility of government surveillance can lead to biased responses.
Figure 1 Experimental stimulus for priming social desirability bias (SDB) in Study 2. In the actual stimulus, an image depicting a stick figure interviewing another also appeared directly above the text (see https://columbian.gwu.edu/person-interviews-yield-best-outcomes; last accessed on June 18, 2020).
Study 2 follows our general identification strategy, constituting the two-by-two factorial design shown in Table 1. We randomly assigned respondents to one of the four conditions. In the full-sensitive condition, respondents received our stimulus before completing conjoint tasks with fully randomized attributes. In the partial-sensitive condition, respondents received the same stimulus but completed conjoint tasks consisting of partially randomized attributes where we only varied the Scandal attribute within each pair. In the full-control and partial-control conditions, subjects received no SDB-priming stimulus before completing their fully and partially randomized conjoint tasks, respectively. For all four experimental conditions, the conjoint tasks involved eight attributes of hypothetical congressional candidates, including the sensitive attribute (see Section D.2 in the Supplementary Materials).
5.3 Deviations from the Preanalysis Plans
Before presenting our empirical findings, we note that the results of our analysis reported below involve some deviations from the preanalysis plans included in our research preregistrations. Our results should therefore be regarded as exploratory by nature, rather than confirmatory. We describe the specific deviations here.
In the analysis of Study 1 reported below, we use a standard difference-in-means estimator for our primary result (as described in Section 4), as opposed to the difference-in-ratios estimator originally prespecified. The deviation was necessary because we discovered after collecting the data that the difference-in-ratios estimator behaved unstably across specification changes and we also confirmed this behavior under realistic sample sizes using simulations. The result exactly following the originally specified procedure was null, although we have a low level of trust in this result because of the instability.
In Study 2, we originally prespecified the difference-in-differences test unconditional on respondent characteristics, as opposed to the conditional analysis on the SDB-prone subgroup of respondents as reported below. Our original conjecture was that the effect of our SDB-priming stimulus would be large and homogeneous enough to detect the SDB reduction even unconditionally, given the supposed strength and universality of the social norms against sexual harassment. Our result using the full sample, however, turned out to be statistically insignificant. We therefore proceeded with the conditional analysis described in Section 6.2. Although our workflow renders our reported estimates exploratory, our subsetting strategy uses a machine-learning approach to guard against overfitting and the false discovery of statistically significant results, as discussed later.
6 Results
In this section, we describe the results of our two studies. Overall, both results indicate that the fully randomized conjoint design reduces SDB relative to the partially randomized design among the subgroup of respondents who are prone to SDB in the given substantive setting.
6.1 Study 1
We fielded the first wave of Study 1 on December 1 and 2, 2018, on 3,417 respondents recruited from Amazon’s Mechanical Turk (MTurk) platform. The second wave was conducted approximately one week after the conclusion of Wave 1 (from December 8 to 14, 2018). We successfully obtained responses from 90% of the Wave 1 participants, yielding the final sample size of 3,075. Although some research suggests possible quality issues with Mturk respondents (Kennedy et al. Reference Kennedy, Clifford, Burleigh, Waggoner, Jewell and Winter2020), other research demonstrates that survey experiments conducted on MTurk can produce results similar to those obtained from nationally representative population-based samples (Berinsky, Huber, and Lenz Reference Berinsky, Huber and Lenz2012; Mullinix et al. Reference Mullinix, Leeper, Druckman and Freese2016).
Our primary empirical analysis focuses on respondents whom we label as SDB-prone. This group excludes respondents for whom we expect little SDB based on the covariates measured in Wave 1. First, we exclude those who score low on questions directly asking respondents how much they care about the environment. Respondents who openly admit their lack of interest in protecting the environment should have no reason to feel social pressure to choose ecofriendly products. Second, we exclude respondents who score low on our general measure of SDB. We specified the exact criteria for the subsetting in our preanalysis plan before we conducted any analysis on the data. After subsetting to SDB-prone respondents and attrition, the sample for our main analysis consists of 1,444 respondents (47% of the Wave 2 respondents).
Figure 2 shows our results. The plot presents our estimated AMCEs for the four design conditions (solid circles/triangles) along with their 95% confidence intervals based on standard errors robust to clustering at the respondent level (vertical bars). The outcome variable is a 7-point Likert Scale measure of preference about purchasing hypothetical athletic shoes (least likely to buy
$=1$
; most likely to buy
$=7$
), which we treat as a continuous variable in the analysis. For the nonsensitive placebo attribute (gel cushioning), the AMCEs are substantially larger under the partially randomized design than the fully randomized design. The estimated AMCE for gel cushioning (vs. no gel cushioning) is 1.28 (with the 95% confidence interval of
$[1.13, 1.43]$
) on the 7-point scale when only that attribute varies between the two profiles in each pair. However, the AMCE for the same attribute drops to 0.43
$[0.34, 0.51]$
when the other attributes also vary. This gap indicates a substantial design effect due to forced attention on a single varying attribute.
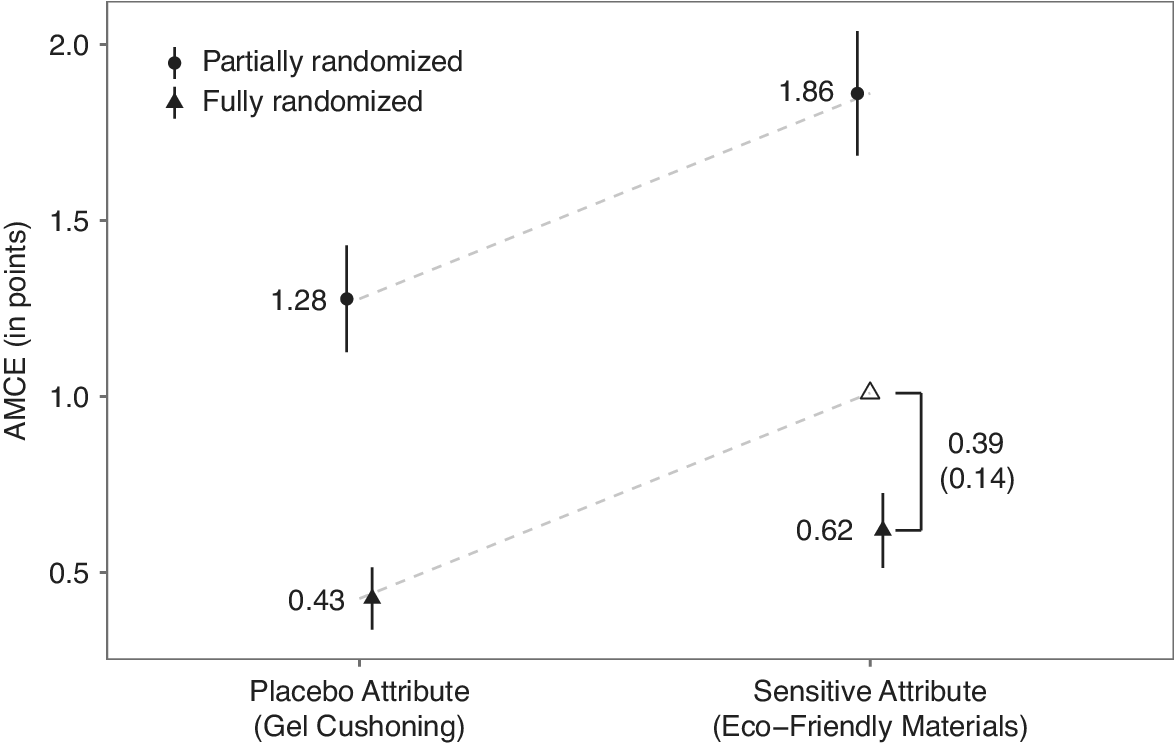
Figure 2 Average marginal component effects (AMCEs) for the sensitive and placebo attributes under the partial and fully randomization designs in Study 1. The hollow triangle visualizes the AMCE from the partially randomized condition after subtracting our estimated reduction in SDB. The vertical distance between the hollow triangle and the bottom-right solid triangle below represents our difference-in-differences estimate (with a cluster-robust standard error in parentheses) of the reduction in SDB, net of design effects.
Although the same pattern holds for the sensitive attribute (ecofriendly materials), the gap between the partially and fully randomized designs is larger than for the placebo attribute. The estimated AMCE for shoes made of 100% ecofriendly materials (vs. no ecofriendly material) is 1.86
$[1.68, 2.04]$
under the partially randomized design, but it is only 0.62
$[0.51, 0.73]$
under the fully randomized design. The estimated difference between the two differences (i.e.,
$[1.86-0.62] - [1.28-0.43] = 0.39$
) is significantly different from zero with the 95% confidence interval of
$[0.12, 0.66]$
, representing a reduction in SDB almost as large as two-thirds of the AMCE estimate itself. This result is consistent with our expectation that the fully randomized conjoint design can reduce SDB for the sensitive attribute.
Remarkably, this result disappears when we perform the same analysis on the rest of our sample, the subset of respondents who we excluded from the group of SDB-prone respondents (see Section C.4 of the Supplementary Materials). This finding further confirms the validity of our pre-registered subsetting strategy and indicates that the SDB-mitigating ability of the fully randomized conjoint design should be local to respondents for whom SDB exists.
6.2 Study 2
For Study 2, we fielded a single-wave survey on a sample recruited by Prolific from December 3 to December 6, 2020. We used the Prolific platform to address possible quality problems with respondents recruited directly through MTurk.Footnote 9 We collected a total of 2,000 respondents, excluding those who failed our quality checks.Footnote 10
For this study, we use a machine-learning algorithm to identify a subset of respondents for which the prime successfully induced SDB. This approach has several advantages relative to the two-wave design in Study 1. First, it allows us to avoid the cost of fielding a baseline wave and direct our resources entirely on a single large sample for the main analysis. Second, it also allows us to flexibly model which pre-treatment covariates best identify a subset of respondents for which the prime successfully induced SDB, avoiding the risk of preregistering a set of conditioning variables that do not ultimately predict biased responding. A potential drawback of such data-driven approaches is the risk of overfitting and post-hoc data dredging. However, recent advances in methods for estimating causal heterogeneity (e.g., Künzel et al. Reference Künzel, Sekhon, Bickel and Yu2019; Wager and Athey Reference Wager and Athey2018) enable us to avoid those problems.
Specifically, we use a procedure that adapts the causal forest (Wager and Athey Reference Wager and Athey2018) for our experimental design.Footnote 11 Among several alternative methods for analyzing heterogeneous causal effects, the causal forest particularly suits our purpose for several reasons. First, it employs sample splitting to avoid inferential problems due to overfitting, while emphasizing performance on out-of-bag predictions. This allows us to generate valid estimates for respondents’ SDB proneness while minimizing the loss of efficiency. Second, unlike many machine-learning algorithms, the causal forest has been formally shown to have desirable asymptotic properties (Athey, Tibshirani, and Wager Reference Athey, Tibshirani and Wager2019).
Our analysis proceeds as follows. First, we randomly select a subset of the respondents in the partially randomized condition as the training set. The remaining respondents (the remainder of the partially randomized group and the entire fully randomized group) constitute the test set. We then fit a model using respondents in the training set to predict the priming effect on the AMCE of the Scandal attribute given a set of pretreatment covariates.Footnote 12 Then, we use this model to generate predictions of the respondent-level priming effect— the difference in their (dis)preference toward candidates with sexual harassment scandals between the primed and unprimed partially randomized conditions—for the test set. Because we randomly assign respondents to the training and test sets, these predictions for effect heterogeneity are statistically independent of those respondents’ actual responses. Therefore, we can condition our main analysis on these predictions without biasing the resulting estimates.Footnote 13 The algorithm repeats this sample splitting procedure many times and then averages the predictions for each respondent, resulting in an estimate of SDB-proneness.Footnote 14 Finally, we label respondents who rank among the top 10% on the SDB-proneness score as SDB-prone.
Once we identify the subgroup of SDB-prone respondents, we proceed to our difference-in-differences analysis on this subgroup (see Section D.5 in the Supplementary Materials for details). The results are presented in the left panel of Figure 3. The outcome variable is a 7-point Likert Scale measure of preference for hypothetical candidates (least likely to vote for
$=1$
; most likely to vote for
$=7$
). For the SDB-prone group identified using the causal forest, the resulting AMCEs are
$-2.46$
(with the 95% confidence interval of
$[-2.92, -1.99]$
) under the partially randomized condition and
$-2.17 [-2.63, -1.70]$
under the fully randomized condition without the prime. The difference of
$-0.29$
is the estimated design effect. With the prime, this difference expands substantially. The AMCEs are
$-3.41 [-3.91, -2.90]$
under the partially randomized condition and
$-1.86 [-2.30, -1.42]$
under the fully randomized condition. The difference-in-differences estimate (i.e.,
$[-3.41-(-1.86) - (-2.46-(-2.17))] = -1.26$
) is statistically significant with the 95% confidence interval of
$[-2.20, -0.31]$
. Compared to the baseline AMCE of the scandal attribute under the primed, fully randomized condition, our estimate of the SDB reduction is roughly two-thirds of the effect itself. That is, if the fully randomized design hypothetically did not reduce SDB, the AMCE of the sensitive attribute would be biased away from zero by 68 percentage points. Thus, in Study 2, we largely replicate the substantive finding in Study 1, which employed a different topic and a different strategy for identifying the SDB-prone subgroup.
Figure 3 Average marginal component effects (AMCEs) for the sensitive attribute under the partial and fully randomization designs with and without the social desirability bias (SDB)-inducing prime in Study 2. See the caption for Figure 2 and the main text for the explanations of the graph elements.
Although the causal forest is our preferred procedure on theoretical grounds, alternative approaches for flexibly modeling heterogeneous treatment effects exist. Given the exploratory nature of our analysis (and the accompanying researcher degrees of freedom), an important concern is that our result might be dependent on the choice of the subset-identifying procedure. Thus, we conduct extensive robustness checks to investigate how sensitive our estimate is to different model specifications. Of the plausible alternative algorithms, the S-learner appears to be particularly appropriate. The S-learner is one of the meta-algorithms proposed by Künzel, Walter, and Sekhon (Reference Künzel, Walter and Sekhon2019), who suggest that it is best suited to cases when the overall treatment effects are mostly zero (also see Künzel, Walter, and Sekhon Reference Künzel, Walter and Sekhon2019), as is the case in our experiment. One limitation of the algorithm for our purpose, however, is that it does not readily generate out-of-bag predictions. To cope with this issue, we use a 10-fold sample-splitting procedure, which uses data less efficiently than the causal forest algorithm.
The result using the S-learner is presented on the right panel of Figure 3. The estimated AMCEs exhibit a pattern similar to those using the causal forest, although our finding is somewhat weaker. That is, the difference in AMCEs between the partially and fully random designs is
$0.79$
without the prime, but increases to
$1.20$
with the prime. This implies an estimated change in SDB of
$-0.41$
with the 95% confidence interval of
$[-1.37, 0.54]$
. Although the estimate is smaller in magnitude and statistically insignificant at the conventional threshold, it is still qualitatively similar to that obtained with the causal forest approach.
In summary, our primary analysis shows evidence of SDB reduction by the fully randomized conjoint design that is remarkably similar to the finding in Study 1, and the result is moderately robust to alternative model specifications. Sections D.6, D.7, and D.8 in the Supplementary Materials show additional (nonpreregistered) analyses probing alternative specifications, and the results corroborate our overall conclusion: individual estimates are somewhat variable and weaker under some specifications, but they largely point in the same direction. Of particular note, Figure D.2 presents estimates for the reduction in SDB achieved using different thresholds for the SDB-prone group. We observe that, at least for the causal forest procedure, the estimates generally behave as we would expect: estimates based on higher thresholds are larger but less precise than estimates that use lower thresholds.
7 Conclusion
Conjoint analysis has become a popular tool for analyzing preferences when SDB is a concern. Because conjoint analysis does not directly ask about respondents’ socially undesirable preferences, there is a strong theoretical basis for believing that it will reduce SDB. Yet, there has been little systematic evidence showing its appropriateness for this task. To address this gap in the literature, we designed two original survey experiments: one on attitudes toward environmental protection and another about preferences about congressional candidates involved in a sexual harassment scandal.
Overall, our results are largely consistent with the common belief held by many applied researchers: the fully randomized conjoint design reduces SDB. In each study, we observe that the difference in effect sizes between the partially and fully randomized conjoint designs is larger under the condition where respondents experienced social pressure to misreport their honest preferences. However, these results are best viewed as preliminary and should be interpreted with caution. First, our analyses involve some deviations from the pre-registered analysis plans. This renders our estimates exploratory in nature rather than confirmatory. Second, our robustness checks for Study 2 reveal a moderate degree of sensitivity to alternative model specifications, although the direction of the estimates remains generally consistent.
Substantively, our results add a degree of credibility to the past research that employs conjoint designs to study preferences about socially sensitive topics in domains related to our two empirical studies, including studies on public support for more sustainable policies (e.g., Bechtel and Scheve Reference Bechtel and Scheve2013) and support for political candidates (e.g., Teele, Kalla, and Rosenbluth Reference Teele, Kalla and Rosenbluth2018). Since we find remarkably similar results between our two studies once we subset our sample to SDB-prone respondents using our preferred specification, we are cautiously optimistic about the generalizability our conclusion—that the fully randomized conjoint design reduces SDB—to a broader set of application areas.
Given the exploratory nature of our empirical findings, we urge future researchers to replicate our proposed design in other substantive domains. A key consideration that emerges from our empirical applications is the importance of identifying a SDB-prone subgroup of respondents specific to the substantive topic. Our analysis indicates that the susceptibility to SDB is highly heterogeneous and application-specific, as illustrated by the null full-sample results in both Studies 1 and 2. This article uses two alternative empirical strategies for identifying such SDB-prone respondents: a two-wave design with the specification of subsetting criteria in between (Study 1) or a machine-learning algorithm tailored for avoiding overfitting problems (Study 2). Either way, domain-specific substantive knowledge will play a crucial role for a successful confirmatory analysis.
It will also be useful to assess how the results might vary depending on survey design features, such as the number of attributes, cross-attribute constraints, other ways to measure outcome responses, and so forth. Our results suggest that SDB reduction is due to the fully randomized conjoint design’s ability to draw respondents’ attention away from the sensitive attribute. Therefore, we would expect an even greater SDB reduction for designs that include a larger number of attributes. Our result also suggests that when a primary motivation for adopting a conjoint design is to mitigate SDB, researchers might want to avoid designs involving restrictions on atypical profiles if such restrictions lead to a considerable reduction in the variability of nonsensitive attributes.Footnote 15
Although topics for future inquiry abound, we believe that our exploratory findings provide useful initial evidence that conjoint analysis is suitable for the crucial task of measuring preferences when SDB is a concern. Given the widespread use of conjoint analysis as a research method in political science, applied researchers can take heart from these results, while they are encouraged to follow further methodological debates concerning conjoint analysis.
Data Availability Statement
Replication code for this article is available at Horiuchi, Markovich, and Yamamoto (Reference Horiuchi, Markovich and Yamamoto2021) at https://doi.org/10.7910/DVN/4WDVDB.
Supplementary Material
For supplementary material accompanying this article, please visit https://doi.org/10.1017/pan.2021.30.
