Introduction
Maize (Zea mays L.) genetic resources are the raw materials for building breeding populations of this important food staple worldwide. Information about breeding traits of individual maize accessions, particularly those available in genebanks may not be always thoroughly assessed, thereby reducing their use in crop genetic enhancement. The link between conservation and use of maize genetic resources could be strengthened by providing accurate and precise information to plant breeders of the most important traits available in the genebank. Maize genetic resources include a diverse set of accessions at the population level, and are often held as public goods or common heritage resources by many farmers worldwide (Brush, Reference Brush1998).
The cost and logistics of phenotyping impose limits on sample size. Hence, allocation of resources needs to consider the number of testing environments and replications therein. The estimates of the variance components can be used to help improve the design of future field trials. In this regard, variance components have been useful for determining the optimum resource allocation for cassava (Dixon and Nukenine, Reference Dixon and Nukenine2000), navy beans (Butler et al., Reference Butler, Redden, DeLacy and Usher2000), plantain (Ortiz and De Cauwer, 1998/Reference Ortiz and De Cauwer1999), sorghum (Obilana and El-Rouby, Reference Obilana and El-Rouby1980) and tomato multi-location trials (Ortiz, Reference Ortiz1991) or comparing potato breeding approaches (Ortiz et al., Reference Ortiz, Peloquin, Freyre and Iwanaga1991). The aim of this research was to use variance components to calculate phenotypic variances and the allocation of resources (number of both environments and replications) for precise phenotyping of vegetative and reproductive traits in a set of Peruvian highland maize genetic resources.
Materials and methods
Plant material
A total of 59 accessions from Peruvian highland maize landraces were evaluated using two planting dates (normal, October; and late, December) in two consecutive years at one site (Carhuaz, Ancash, northern Peruvian highlands, within the inter-Andean valley of the Callejón de Huaylas). The experimental design was a randomized complete block with data recorded in at least two replications per environment for reproductive traits, and a maximum of four replications for vegetative traits. Data were recorded for ten plants per replication.
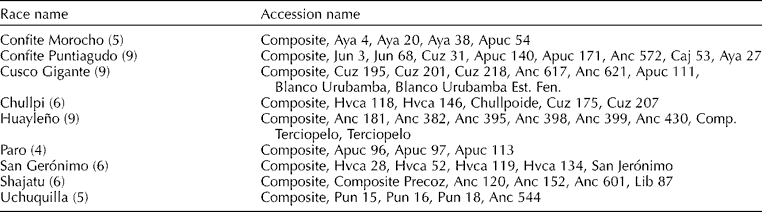
The nine races were Confite Morocho, Confite Puntiagudo, Cusco Gigante, Chullpi, Huayleño, Paro, San Gerónimo, Shajatu and Uchuquilla (Grobman et al., Reference Grobman, Salhuana, Sevilla and Mangelsdorf1961). Different numbers of accessions were used for each race (Table 1).
Table 1 Name of the accessions of nine Peruvian highland maize races
Number of accessions indicated in parentheses after race name.
The vegetative traits recorded were plant height (cm), ear height (cm), leaf number, leaf number above ear, leaf length (cm) and leaf width (cm), whereas the reproductive traits were pith and cob diameters (cm), glume length (cm) and texture, and cupule length and width (cm). The methods for measuring each of the 12 traits are given in Grobman et al. (Reference Grobman, Salhuana, Sevilla and Mangelsdorf1961).
Estimating variance components for precision
Assuming an experiment of accessions of a specific race planted in ‘e’ environments and ‘r’ replications in each of the ‘e’ environments, the variance components for accessions within race pooled across all races (
), environments (
) and accession within race × environment interaction (
) can be estimated using restricted maximum-likelihood method (REML) (SAS, 1999). The phenotypic variance of an accession mean 
was estimated as 
. Optimum number of replications and environments can be found using the estimated REML variance components from the data. To examine the influence of experimental design on results in future experiments, the variance components for vegetative and reproductive traits were therefore assumed to be stable while the denominator coefficients ‘e’ (number of environments) and ‘r’ (replications) vary. This technique was used previously to examine the sensitivity of the standard error of soybean strains to changing allocations of replications, locations and years (Schutz and Bernard, Reference Schutz and Bernard1967).
Results
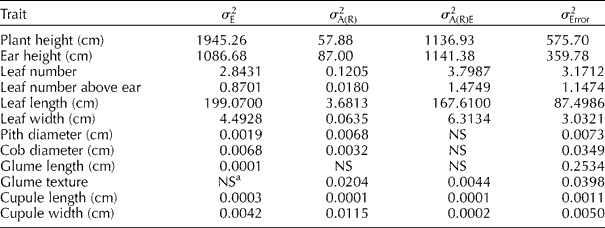
The variance components estimated for accessions within races are shown in Table 2. The variability of the accessions within races in different environments (
) was also of sizeable magnitude for vegetative traits, which was mainly due to the later December planting. By contrast, 
was non-significant (P>0.05) or very small for most reproductive traits. The results of this research are not surprising since heritability was previously found to be higher for reproductive than vegetative traits (Goodman and Paterniani, Reference Goodman and Paterninani1969; Sánchez et al., Reference Sánchez, Goodman and Rawlings1993; Ortiz and Sevilla, Reference Ortiz and Sevilla1997).
Table 2 Variance components for plant and internal ear traits recorded in Peruvian highland maize accessions
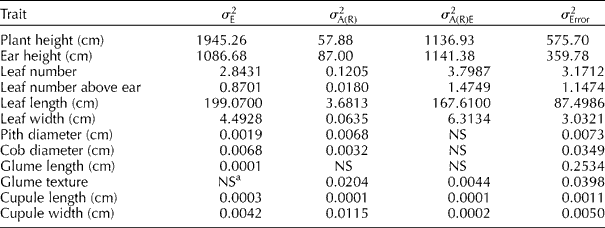
a NS indicates that the non-significant source of variation had a negative component of variance ( ≈ 0).
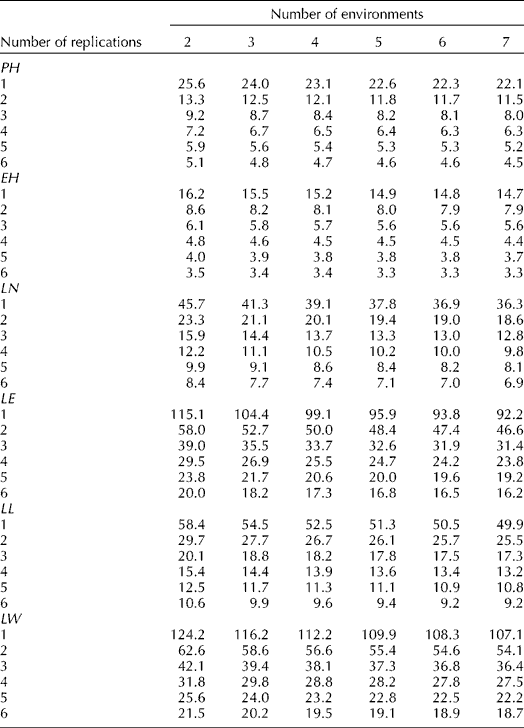
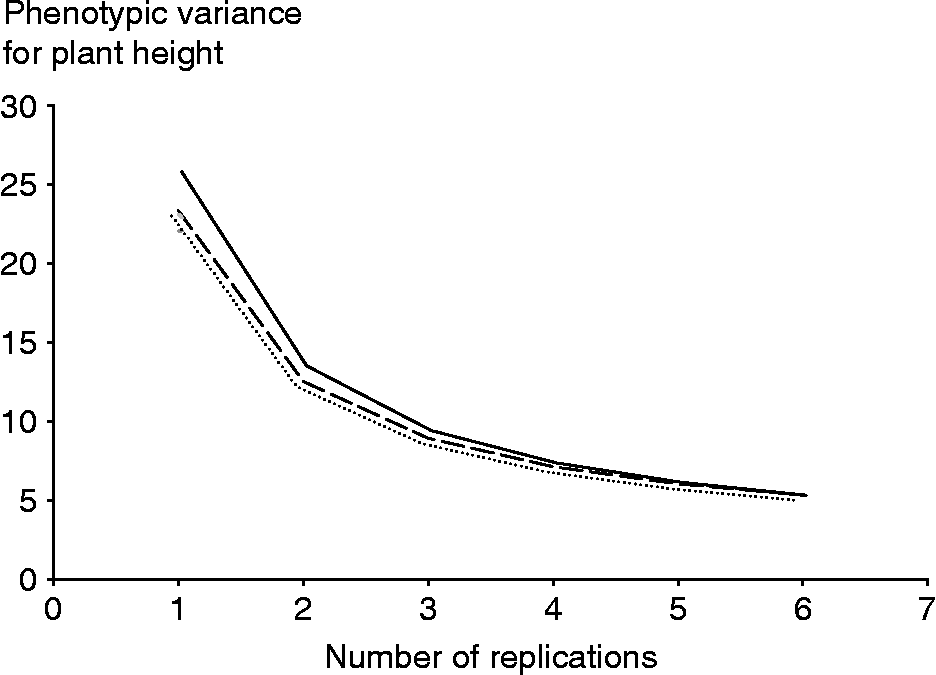
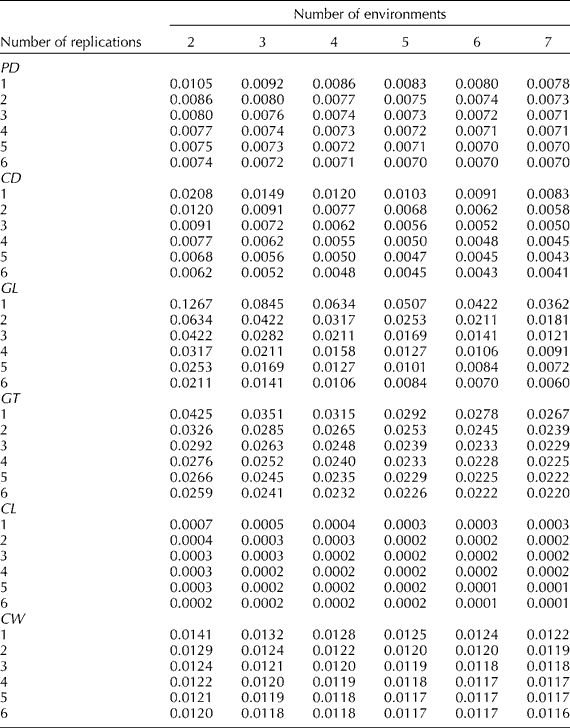
The effect of the number of replicates and environments on the precision by which the phenotypic means of accessions are estimated is examined in the changes of 
. The optimum option, therefore, is to use the least number of environments and replications that will not affect the precision of phenotyping. Results indicated that the decrease in the phenotypic variance of an accession mean will be negligible for vegetative traits beyond six environments (Table 3). These results are shown for plant height in Fig. 1, where the number of environments and replications required to estimate low values of phenotypic variance components and thus to increase the estimate of heritability are plotted. The critical point was achieved as the curve starts to plateau because beyond this point an increase in the number of testing environments and replications provides only a negligible gain in phenotyping precision. The phenotypic variance of vegetative traits can decrease further if one increases the number of replications, though it will be more costly. Table 3 provides a means for balancing the number of environments and replications therein since increasing the number of one of them can be offset by reducing the other and could provide guidance for Peruvian highland maize researchers to allocate resources for assessing variation in plant traits. For example, by using six environments and five reps, the variance of plant traits may decrease on average by an additional 50% than by just using three reps in three environments.
Table 3 Phenotypic variance components of an accession mean (
) for plant height (PH), ear height (EH), leaf number (LN), leaf number above the ear (LE), leaf length (LL) and leaf width (LW), and different number of replicates and environments for eight highland Peruvian maize races
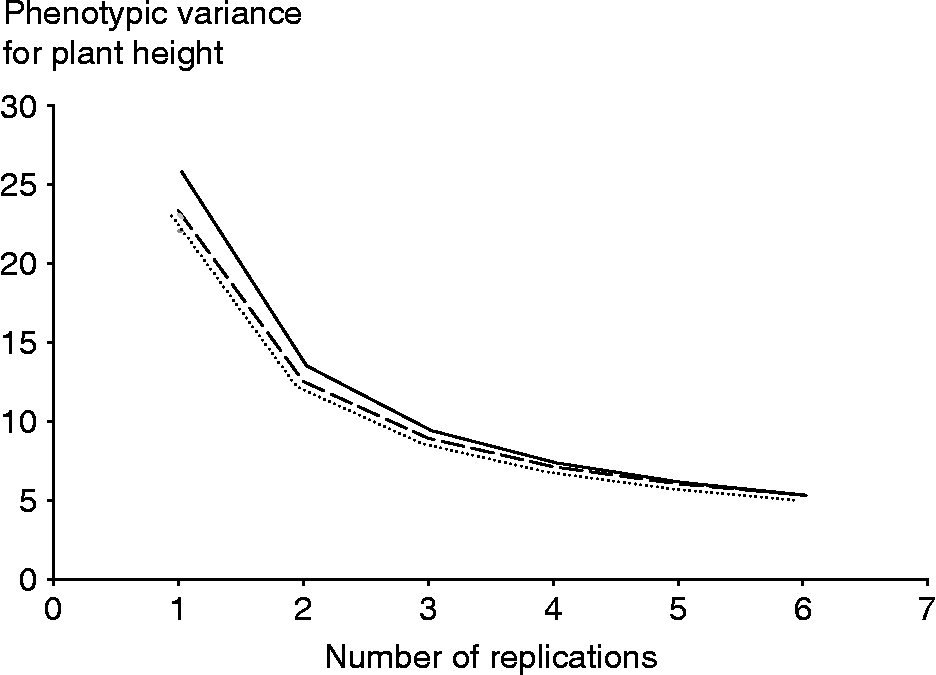
Fig. 1 Plot of the phenotypic variance of an accession mean against number of replicates for two (—), four (- - -) and five (…) environments for plant height.
Similarly, Table 4 provides the estimates of phenotypic variation for reproductive traits. The phenotypic variance decreases as the number of environments increases to six. Additional environments do not greatly reduce the phenotypic variance of reproductive traits. For example, with six environments and four reps, the variation may decrease up to 50% vis-à-vis using two environments and two reps for assessing reproductive traits. The lesser number of replications for minimizing phenotypic variation in reproductive traits vis-à-vis vegetative traits was not surprising since reproductive traits have a higher heritability than vegetative traits.
Table 4 Phenotypic variance components of an accession mean (
) for pith diameter (PD), cob diameter (CD), glume length (GL), glume texture (GT), cupule length (CL) and cupule width (CW), and different number of replicates and environments for eight highland Peruvian maize races
Discussion
Although these variance components are estimations from a set of plants within accessions and accessions within races, their sample sizes should be sufficient to draw conclusions that can be applied to these populations of different Peruvian highland maize races. In general, with the use of an appropriate experimental design for controlling local variability, and with the fit of an appropriate spatial analysis for controlling possible local and global trends in the field, a few replications may be required, which agreed with previous suggestions for assessing maize grain yield (Machado et al., Reference Machado, Alvarez, Estigarribia, Molinas, Sevilla and Espinoza1990). Furthermore, virtually all maize breeding trials of the multi-national private sector use single-rep, multiple-location trials for grain yield (a trait with lower heritability than those included in this research). Most of their plots are standardized to two rows: 2 m × 5 m with about 50 plants per plot.
The objective of an experimental design for estimating entry means is to minimize the error variance (
) for a given cost. However, the optimum number of environments to be used for testing accessions of different races is debatable and depends on factors such as the range of adaptation of each race, the target population of environments where enhanced germplasm from that race could be adapted and scope of the accession × environment interaction, among other factors. Nonetheless, the results of our research suggest that the Peruvian highland races should be tested with fewer replications for reproductive than vegetative traits.
This research addressed an important topic completing previous reports regarding what traits to be used for characterizing and classifying maize races (Goodman and Paterniani, Reference Goodman and Paterninani1969; Sánchez et al., Reference Sánchez, Goodman and Rawlings1993; Ortiz and Sevilla, Reference Ortiz and Sevilla1997). However, there are still other areas needing research such as where should data be recorded, as well as how many appropriate locations, years and number of accessions are needed for recording reliable data for characterizing and classifying maize germplasm.
