1 Introduction
Phonological theories (of the ‘free-standing’ variety; Prince Reference Prince2007) make typological claims, predictions about what are and what are not possible phonological patterns. Much work has been devoted to questions concerning the expressivity of a given phonological theory. Is the theory powerful enough to correctly predict the existence of a given attested pattern?; if not, how can its expressive power be appropriately extended? Is the theory so powerful that it incorrectly predicts the existence of an unattested, potentially ‘pathological’ pattern?; if so, how can its expressive power be appropriately constrained?
Recent work has approached this question from the perspective of formal language theory, aiming to characterise particular attested or unattested phonological patterns in terms of well-defined, theory-independent computational classes of string sets (formal languages) or mappings between string sets (string functions): any given pattern can be characterised by the minimum level of complexity (expressivity) required to capture it. The larger goal of this work is to formally delimit the boundary between possible and impossible grammatical patterns, as evidenced by attested and unattested language patterns. Heinz (Reference Heinz2011a, Reference Heinzb, Reference Heinz, Hyman and Plank2018), Heinz & Lai (Reference Heinz, Lai, Kornai and Kuhlmann2013) and Jardine (Reference Jardine2016), among others, have advanced the broad hypothesis that phonological patterns are subregular, meaning that they can be characterised by computational classes that are strictly less expressive than the class of regular string relations, which characterises the expressivity of ordered SPE-style rewrite rules (Johnson Reference Johnson1972, Kaplan & Kay Reference Kaplan and Kay1994). Figure 1 summarises some subregular function classes and gives some relevant examples, including the one that is the empirical focus of this article, Tutrugbu ATR harmony (McCollum & Essegbey Reference McCollum and Essegbey2018, Essegbey Reference Essegbey2019).

Figure 1 Some regions of the subregular hierarchy of string-to-string mappings, with phonological examples. Examples of Input Strictly Local functions include nasal place assimilation and metathesis (Chandlee 2014); examples of subsequential functions include unidirectional harmony (Heinz & Lai 2013) and dissimilation (Payne 2017); examples of weakly deterministic functions include bidirectional harmony (Heinz & Lai 2013); examples of nondeterministic functions include unbounded circumambient processes (Jardine 2016); examples of regular relations include optional iterativity (Heinz 2018).
Chandlee (Reference Chandlee2014: §7.1) and Heinz (Reference Heinz, Hyman and Plank2018: §6.2.1) note that the vast majority of phonological patterns appear to be contained within the innermost, least expressive classes of the subregular hierarchy. However, there are some patterns that are relatively more complex, and Heinz & Lai (Reference Heinz, Lai, Kornai and Kuhlmann2013) and Jardine (Reference Jardine2016) contend that the most complex segmental patterns require no more expressivity than what is afforded by weakly deterministic regular functions. These types of patterns include prototypical bidirectional harmony processes. In contrast, Jardine (Reference Jardine2016) demonstrates that a number of tonal spreading patterns are more complex than this. These patterns all require at least non-deterministic regular functions to be described, and all exhibit unbounded circumambience, a dependence on information (e.g. spreading triggers and blocking conditions) that are an unbounded distance from the spreading target in both directions.Footnote 1
The unbounded circumambient nature of the Tutrugbu ATR harmony pattern can be seen in the comparison between the pairs of forms in (1). [ATR] spreads leftwards from the root to prefixes, targeting both [+high] and [―high] vowels (1a, b). When the initial prefix vowel is [+high], however, harmony is blocked by [―high] vowels (1d). In other words, the surface realisation of the medial vowels in (1) depends on both the [ATR] value of the root and the presence or absence of an initial-syllable [+high] vowel. We demonstrate below that this pattern is non-deterministic in exactly the same way that the tonal spreading patterns discussed by Jardine (Reference Jardine2016) are, because this pattern also satisfies Jardine's criteria for unbounded circumambience.Footnote 2
(1)

We introduce ATR harmony in Tutrugbu in §2, and in §3 we show that it satisfies Jardine's definition of an unbounded circumambient process. We introduce the computational machinery necessary to account for unbounded circumambient processes in §4, providing examples for three complexity classes within the subregular hierarchy: subsequential, weakly deterministic and non-deterministic. We provide a finite-state analysis of Tutrugbu ATR harmony in §5, and show that it is non-deterministic. In §6 we discuss other examples of unbounded circumambient segmental patterns, and the implications of our findings for explaining the typology of complexity and evaluating phonological theories, before concluding in §7.
2 Tutrugbu ATR harmony
Tutrugbu is a Ghana-Togo Mountain language (Kwa), spoken in southeastern Ghana. The data for this article come from formal elicitation, as well as a documentary corpus of natural speech. Data-collection practices are described in Essegbey (Reference Essegbey2019: 11–13). Almost all of the data presented here were collected by James Essegbey over the course of around 15 years of fieldwork in Ghana, with only recent collaboration with the first author of this paper. The pattern described here was first presented in Essegbey (Reference Essegbey2009), and more extensively discussed in McCollum & Essegbey (Reference McCollum and Essegbey2018) and Essegbey (Reference Essegbey2019: 36–39). Example data are found throughout Essegbey (Reference Essegbey2019), and, to the best of our knowledge, are representative of the entire speech community, without exceptions or variation, except as described in §2.2.Footnote 3
2.1 Data
Tutrugbu has an inventory of nine oral vowels, /a ɔ o ʊ u ɛ e ɪ i/, with contrasts in height, backness, rounding and ATR. As Essegbey (Reference Essegbey2009) notes, there are only seven surface vowels in the language. The vowels we transcribe as high [―ATR] vowels, /ʊ/ and /ɪ/, always surface as the mid vowels [ɔ] and [ɛ], but pattern as high vowels. To reflect their phonological status, we will transcribe them as [ʊ] and [ɪ] throughout (see McCollum & Essegbey Reference McCollum and Essegbey2018, Reference McCollum and Essegbey2020 for a different approach). We defend this abstract analysis in §2.3.2 below. Nasal counterparts of these oral vowels are also phonemic in the language, and behave just like oral vowels with respect to ATR harmony. ATR harmony proceeds from right to left in Tutrugbu, from roots to prefixes. Suffixation is rare, and suffixes do not generally undergo harmony.
Observe the ATR pairings demonstrated by regressive harmony on noun class prefixes in (2). In (2a), prefixal [a] alternates with [e], while in (b), [ɔ] alternates with [o]. In (c), [ɪ] alternates with [i], and finally, in (d), [ʊ] alternates with [u]. Note that [ɛ] does not occur in affixes. We analyse [+ATR] as the active (or dominant) feature value in the language, and assign affixes a [―ATR] value underlyingly.
(2)

Noun-class prefixes undergo ATR harmony, but concatenating more prefixes to a nominal root is not possible. Verbal morphology, on the other hand, allows for more complexity. In (3) we see that words with only [+high] prefix vowels show full harmony. In (3a–c), [―ATR] roots are preceded by [―ATR] prefixes, while in (3d–f), [+ATR] roots are preceded by [+ATR] prefixes.
(3)

Full harmony also obtains when all prefix vowels are [―high], as in (4). In (4d–f), [+ATR] roots propagate their [+ATR] feature to the left edge of the word. Note also in (4c, f) that [―high] round vowels in the initial syllable trigger progressive rounding harmony in the preverbal domain (McCollum & Essegbey Reference McCollum and Essegbey2020). Rounding harmony is triggered by and targets [―high] vowels; [+high] vowels are transparent.
(4)

In (3) and (4), all prefix vowels agree in [±high]. Harmony in forms with prefix vowels of differing values of [high] is illustrated in (5). The initial-syllable vowel is [―high] in these examples, as it is in (4), and harmony obtains throughout the word.
(5)

In contrast to the previous examples, [―high] vowels block harmony if the vowel in the initial syllable is [+high]. Regardless of the root's [ATR] value, the vowel of the [―high] future prefix and all preceding vowels surface as [―ATR] under this condition, as shown in (6).
(6)

These examples show that the [―high] vowel blocks harmony when the initial-syllable vowel is [+high]. The [―high] vowel immediately precedes the root in (6), but Tutrugbu does allow at least one [+high] prefix to intervene between a root and a [―high] vowel. In words with a [+ATR] root, a [+high] initial-syllable vowel and a medial [―high] prefix vowel (satisfying the two conditions necessary to block harmony), a [+high] prefix vowel intervening between the root and the medial [―high] vowel undergoes harmony. In (7a) and (b), the itive prefix alternates based on the [ATR] value of the root, establishing that this particular morpheme regularly undergoes harmony. In (7c) and (d), this prefix is the only one to undergo harmony. In essence, harmony spreads as far as the blocking [―high] vowel, and then stops.
(7)

The data above show that [―high] vowels are conditional blockers: they block harmony only in the presence of an initial-syllable [+high] vowel. Two [+high] vowel prefixes do not block harmony, as in (3), and two [―high] vowel prefixes do not block harmony, as in (4) and (5). It is only the combination of an initial-syllable [+high] vowel and a medial [―high] vowel that blocks harmony. In other words, the realisation of a [―high] prefix vowel depends not only on the [ATR] value of the vowel in the immediately following morpheme (the root, or a prefix closer to the root), but also on the [high] value of the initial-syllable vowel.
In (6) and (7), the initial-syllable [+high] vowel and the medial [―high] vowel are in adjacent syllables. In (8) we see that harmony is blocked by the co-occurrence of these two conditions, even when separated by intervening syllables.
(8)

ATR harmony is blocked only when two conditions are met: (i) the initial-syllable vowel is [+high], and (ii) another prefix vowel is [―high], as in (c)–(g). When only one of these conditions is met, as in (a), (b) and (h), harmony obtains. In (c), the [+high] initial-syllable vowel and the [―high] prefix vowel are adjacent, and harmony fails. In (d)–(g), one, two, three and four syllables intervene between these two interacting conditions on harmony. Thus the blocking of regressive ATR harmony depends on decidedly non-local information – the [high] value of the initial-syllable vowel – and the presence of a [―high] prefix vowel, which may occur a number of syllables from the initial syllable, with no principled upper bound.
2.2 Variation
Before we move on to the analysis, there is an additional aspect of the pattern worth noting. Essegbey (Reference Essegbey2009: 40) describes variation in the blocking context. When an initial-syllable [+high] prefix is followed by a medial [―high] prefix, as in (9a), the [―high] prefix and all preceding prefixes may surface as [―ATR]. But the initial-syllable [+high] prefix may also surface as [+ATR], even though the following [―high] prefix is [―ATR]. Finally, as in (9b), the [―high] vowel undergoes harmony when the initial-syllable vowel is [―high], just as in our data above, with no variation. (As noted in §2.1, we use /ɪ/ and [ɪ] rather than Essegbey's /ɛ/ and [ɛ].)
(9)

In the pattern most widely attested in our data, the medial [―high] vowel conditionally blocks harmony, preventing [+ATR] from spreading to prefixes further from the root. For the alternative form, Essegbey suggests that harmony skips the [―high] vowel to target the initial-syllable [+high] vowel. This in turn suggests that, for these speakers, the medial [―high] vowel is (optionally) conditionally transparent. We have very few data on conditional transparency when more than one [+high] vowel occurs to the left of medial /a/, but preliminary data suggest that all [+high] vowels are realised as [+ATR] for speakers exhibiting conditional transparency. In any event, note that for both patterns the realisation of medial /a/ depends on both the initial-syllable vowel to its left and the root vowel to its right, even when either or both of these dependencies is long-distance.
2.3 Analysis
2.3.1 Active value
Determining which feature value is active, as van der Hulst & van de Weijer (Reference Harry van der, van de Weijer and Goldsmith1995: 504) note, can be challenging in patterns of root-controlled harmony. That being said, several facts point to [+ATR] being the active feature value in Tutrugbu (see also Casali Reference Casali2012 on diagnosing feature-value activity). First, when a vowel is not assimilated to the [ATR] value of the root, it always surfaces as [―ATR]. In (8c–g), for example, all prefix vowels surface as [―ATR], because both parts of the blocking condition are present. Additionally, morphemes to the right of the root do not generally undergo harmony, surfacing as [―ATR]. In (10a, b), the plural suffix, which may only attach to human roots, surfaces as [-alɪ], regardless of the root's [ATR] value. In (10c–f), the definite enclitic surfaces as [﹦Í], irrespective of the root's [ATR] value.
(10)

In other words, when harmony does not apply, affix vowels surface as [―ATR], which is good evidence that [+ATR] is active. For Akan, Casali (Reference Casali2012) suggests that cross-word harmony and the form of the independent pronouns provide further support for the activity of [+ATR]. As in Akan, [+ATR] may optionally spread across word boundaries in Tutrugbu, as in (11).
(11)

As far as we are aware, this phrasal ATR harmony may only target [+high] vowels. In (11a) the [+ATR] root /bwi/ triggers harmony on the prefix /kɪ-/, and in (b) the same root triggers harmony on both its prefix and the preceding object pronoun, /mɪ/. Observe that the verb /bʰɪtɪ/ is unaffected by phrasal harmony here, and is realised with its underlying [―ATR] specification. And yet, in (11c), /bwi/ triggers harmony on its prefix and the preceding verb, /bʰɪtɪ/. In this context, the underlyingly [―ATR] vowels of the verb are assimilated to the [+ATR] value of /bwi/. Similarly, in (d), the verb /sɪ/ is unaffected by the [ATR] value of the following root, surfacing as [―ATR]. In (11e), though, this verb undergoes harmony from the following verb root /ɖi/, and is pronounced as [si]. In both sets of examples, verbs that are underlyingly [―ATR] optionally undergo phrasal [+ATR] harmony. While phrasal [+ATR] spreading is widespread in our data, [―ATR] spreading is unattested.
Casali (Reference Casali2012) also considers the independent form of the personal pronouns to be indicative of the underlying [ATR] value of harmonic affixes more generally. Independent pronouns occur as separate words, while their dependent counterparts occur as prefixes. In Akan, the independent forms are all [―ATR], supporting the claim that [―ATR] is the unmarked underlying form of alternating affixes. This same generalisation holds for Tutrugbu. Independent pronouns are very similar to their dependent (prefixal) counterparts in segmental form, and in all cases surface with [―ATR] vowels, as in (12). According to Casali's diagnostics, the [―ATR] status of the independent pronouns lends further support to [+ATR] spreading.
(12)

2.3.2 Abstract vowels
As noted in §2.1, we assume that Tutrugbu has a nine-vowel inventory requiring two abstract [+high, ―ATR] vowels, /ɪ ʊ/, which are phonetically realised as mid [ɛ ɔ], but which we consistently represent as [ɪ ʊ]. This abstract analysis is justified for several reasons.
First, these vowels pattern consistently as [+high] with respect to rounding harmony. In (5b, e), even the [―ATR] allomorph of the negation prefix, which is phonetically mid (but transcribed in (5b) as [tÍ]), does not undergo progressive rounding harmony, and we can attribute this to the fact that rounding harmony only targets [―high] vowels. Rounding harmony is also only triggered by [―high] vowels, so the abstract high vowel /ʊ/ of the 1st person plural prefix does not trigger rounding harmony on the future prefix in (6b) or (7d), despite being phonetically mid.
Along with their inertness as triggers and targets of rounding harmony, the phonological status of these vowels is evident in their actual ATR alternations. For example, the 2nd person singular prefix alternates between phonetic [ɔ] and [o], while the 1st person plural prefix alternates between phonetic [bɔ] and [bu] (our phonological surface [bʊ] and [bu]). If, as we argued in §2.3.1, [―ATR] is the underlying feature value, its [+ATR] counterpart is not able to be inferred from its faithful phonetic realisation. Specifically, which phonetic [ɔ] alternates with [o], and which alternates with [u]? This problem appears insurmountable if both surface [ɔ] vowels are treated equivalently.
We have thus chosen to mark the vowels that alternate with [+high, +ATR] vowels as [+high], but this is not the only possible analysis. One alternative is to specify the underlying vowels we have analysed as /ɪ ʊ/ as [+ATR] /i u/. Possible support for this alternative comes from speakers who (optionally) produce the pattern of conditional transparency described in §2.2. Recall that when a medial [―high] vowel and an initial-syllable [+high] vowel co-occur, these speakers may produce the [+high] vowel(s) as [+ATR], despite the [―high] vowel surfacing as [―ATR] [a]. A possible alternative to the conditional transparency analysis is that in this context, prefix vowels to the left of blocking [a] may surface in accordance with their underlying [ATR] specifications. For these speakers at least, there would be a seven-vowel system, with [+high] vowels underlyingly specified as [+ATR], in contrast with the [―high] vowels. Note that, regardless of whether the conditional transparency analysis or this alternative is correct, the generalisation holds that harmony is blocked when an initial-syllable [+high] vowel co-occurs with a medial [―high] vowel, in unbounded circumambient fashion.
A seven-vowel analysis with underlying /i u/ cannot account for the phrasal [+ATR] harmony described in (11), however. As noted above, in all these examples the verb roots are clearly [―ATR], but may surface as [+ATR] if followed by a [+ATR] word. Since these are roots, not affixes, we cannot simply stipulate that the vowels in a word like /bʰɪtɪ/ are [+ATR]. This verb root is always preceded by [―ATR] prefixes in our data, even in (11c), where it undergoes phrasal [+ATR] harmony. This brings us back to the original point: we cannot infer the [+ATR] counterpart of the vowels in question if they are underlyingly specified as [―high, ―ATR]. If the vowels in /bʰɪtɪ/ are simply [―high, ―ATR], then why do these vowels surface as [i], and not [e], when affected by phrasal [+ATR] harmony? To account for these facts, we must analyse these vowels as underlyingly [+high]. Since phrasal harmony prevents us from assuming that they are [+high, +ATR], the best analysis requires a nine-vowel inventory, with two abstract [+high, ―ATR] vowels.
One final typological point is worth mentioning here. As an anonymous reviewer notes, African languages in which the [+high] vowels exhibit ATR contrasts show almost exclusive [+ATR] dominance, whereas languages in which the [+high] vowels exhibit no [ATR] contrasts show no clear typological tendencies (Casali Reference Casali2003, Reference Casali2008, Reference Casali2012, Rose Reference Rose, Gallagher, Gouskova and Yin2018). Despite historical changes to its vowel inventory, Tutrugbu vowels pattern like those of neighbouring Tafi, which has maintained what we take to be the proto-language's nine-vowel inventory, with an ATR contrast among the high vowels (see also Essegbey Reference Essegbey2009: 40). The structure of the [―high] portion of the inventory is somewhat distinct from canonical African nine-vowel systems: the low vowel /a/ pairs with mid /e/, whereas in most nine-vowel systems the low vowel has no harmonic counterpart. If the presence of contrastive [ATR] values for the [+high] vowels is predictive of feature-value activity, our nine-vowel analysis is consistent with the expected dominance of [+ATR] in an African language with nine phonological vowels.
3 Unbounded circumambience
The Tutrugbu ATR harmony pattern described in the previous section instantiates what Jardine (Reference Jardine2016) dubs an unbounded circumambient process, defined in (13).
(13)

In Tutrugbu, the surface quality of prefix vowels is dependent on three factors: the [ATR] value of the root, the height of the initial prefix vowel and the presence or absence of a medial non-high prefix vowel. As shown in (8), there appears to be no bound on the potential distance between these three factors; the only constraint on their distance is the productivity of the language's morphology. For these reasons, Tutrugbu ATR harmony satisfies the criteria for unbounded circumambience.
Compared to the patterns previously identified as unbounded circumambient, Tutrugbu ATR harmony stands out as a segmental, rather than a tonal process. In fact, for Jardine (Reference Jardine2016), one reason to single out unbounded circumambient processes as a class is to characterise a typological asymmetry between tonal and segmental phenomena, namely that unbounded circumambience is more prevalent (if not unique) among tonal processes than among segmental processes. Jardine attributes this asymmetry to the computational expressivity required to describe unbounded circumambient patterns. He argues that tonal patterns are capable of commanding greater computational expressivity than segmental patterns, and concludes that tone should be viewed as an exception to hypotheses concerning the upper bound on the expressivity of phonology. In the following section, we briefly review these hypotheses, and introduce the computational machinery necessary to capture unbounded circumambient processes.
4 Computational requirements for unbounded circumambience
The expressivity of phonological grammars comprising ordered SPE-style rewrite rules (Chomsky & Halle Reference Chomsky and Halle1968) corresponds to the class of regular string relations (Johnson Reference Johnson1972, Kaplan & Kay Reference Kaplan and Kay1994). However, many phonological input–output maps do not require the full expressivity of regular relations. Synchronically attested metathesis, partial reduplication, consonant harmony and dissimilation patterns are all subsequential (Chandlee et al. Reference Chandlee, Athanasopoulou and Heinz2012, Chandlee & Heinz Reference Chandlee and Heinz2012, Luo Reference Luo2017, Payne Reference Payne2017). Moreover, Chandlee's (Reference Chandlee2014) analysis of PBase (Mielke Reference Mielke2007), a database of phonological patterns, shows that most are describable using a highly restricted subclass of the subsequential functions.Footnote 4 Finally, the vowel-harmony patterns analysed in Nevins (Reference Nevins2010) have also been shown to be subsequential (Gainor et al. Reference Gainor, Lai and Heinz2012), with the sole exception of bidirectional harmony in Woleaian. For this reason, Gainor et al. argue that a more restrictive hypothesis better captures the minimum computational expressivity necessary to describe phonological patterns: the subsequential hypothesis (see also Heinz Reference Heinz, Hyman and Plank2018).
Under this hypothesis, the most complex computational machinery necessary to model phonological patterns is that of subsequential functions (perhaps first proposed by Mohri Reference Mohri1997: 279). However, Heinz & Lai (Reference Heinz, Lai, Kornai and Kuhlmann2013) demonstrate that bidirectional stem-controlled and dominant-recessive vowel-harmony patterns are not subsequential, and propose instead that phonological patterns are at most weakly deterministic, a class they tentatively define in terms of a restriction on compositions of two subsequential functions.
Jardine (Reference Jardine2016) discusses a number of tonal patterns that are neither subsequential nor weakly deterministic, and shows that this class of unbounded circumambient tonal patterns requires the strictly greater expressivity of non-deterministic regular functions. Most significantly in the present context, Jardine argues that there is a computational difference between tonal and segmental phonology: while segmental phonology may be restricted to the class of subsequential functions and their weakly deterministic compositions, tonal phonology requires the expressive power of non-deterministic regular functions.
Regular relations and their subclasses can be represented in many ways, including ordered SPE-style rewrite rules, suitably restricted Optimality Theory grammars (Riggle Reference Riggle2004) and finite-state transducers (FSTs). In this paper we represent such mappings as FSTs, for two related reasons: much work characterising regular relations and their subclasses uses this formalism, and consequently, so does existing work on the complexity of phonology. FSTs represent string-to-string functions in a way that emphasises incremental calculation, proceeding symbol by symbol from one end of the input string to the other, and restricting the amount of information about the observed prefix of the input that can be ‘remembered’ while deciding what to output at each step. Such differences in the amount and type of information a transducer is able to store can define more vs. less expressive classes of transducers, which can in turn be used to describe differences in the amount and type of information required to express different phonological patterns. For more detailed introductions to FSTs and their relation to phonology, we refer the reader to Kaplan & Kay (Reference Kaplan and Kay1994), Mohri (Reference Mohri1997) and Jardine (Reference Jardine2016). In the next three subsections we review definitions, key properties and attendant phonological examples of subsequential functions, weakly deterministic regular functions and non-deterministic regular functions.
4.1 Subsequentiality
A subsequential FST τ can be defined by the seven parameters in (14).
(14)

Intuitively, a subsequential transducer is an FST whose incremental behaviour is always deterministic. That is, state transitions and output strings are deterministic functions of the current state and input symbol, and the string-to-string function τ:Σ﹡ → Δ﹡ defined by a subsequential FST is also a deterministic mapping: every full input string is associated with at most one full output string.
Subsequential FSTs can be divided into two partially overlapping classes, based on the directionality of their computation (Chandlee Reference Chandlee2014: ch. 3). Left-subsequential FSTs read input strings from left to right, while right-subsequential FSTs read input strings from right to left. When using subsequential FSTs to model vowel-harmony patterns, this distinction in directionality of computation maps intuitively onto the directionality of the harmony pattern. Canonical progressive harmony patterns are modelled with left-subsequential FSTs, and canonical regressive harmony patterns are modelled with right-subsequential FSTs.
Some data exhibiting the progressive rounding harmony pattern found in Turkish are shown in (15). Rounding spreads left to right from roots to suffixes; [+high] vowels undergo harmony (15f, g) while [―high] vowels block harmony (15h–j).
(15)

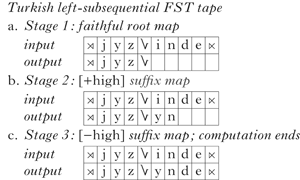
Appendix A1 gives an example of a left-subsequential FST which models this pattern,Footnote 6 and in (16) we provide a ‘running tape’ representation of the mapping performed by the FST, using the word [jyzynde] to illustrate both rounding harmony and its blocking, Since harmony is stem-controlled in the language, the FST outputs all segments to the left of the root–suffix boundary (symbolised as Â) without modification (16a). Note that the FST does not as its first operation map the entire substring ⋊jyz to itself; it processes each input symbol incrementally. To save space, we do not show each of the first five steps separately, and adopt the same strategy in later examples.
(16)

The FST then reads a suffix with a [+high] vowel, and, since the roundness of the root vowel is known, the output function emits a vowel matching the roundness of the root in (16b). (Again, the two symbols of the suffix are technically processed incrementally. Since consonants do not participate in the harmony process, they are always mapped faithfully; we do not show these steps separately.)
Next, the FST reads an input suffix with a [―high] vowel. This vowel is mapped faithfully, since [―high] vowels block rounding harmony. The end of the word is then reached and the computation ends (16c).
In this way, progressive harmony patterns can be modelled with left-subsequential FSTs – and in similar fashion, regressive harmony patterns can be modelled with right-subsequential FSTs. In the next subsection, we define and discuss weakly deterministic regular functions, characterised by a restricted composition of left- and right-subsequential FSTs.
4.2 Weak determinism
The ordering of rewrite rules ρ₁ < ρ₂< … < ρn in an SPE-style analysis corresponds to the ordered composition of associated string-to-string functions φρₙ ∘ … ∘ φρ₂ ∘ φρ₁. While the composition of any two subsequential functions going in the same direction can only yield another subsequential function (Mohri Reference Mohri1997), a function defined by the composition of subsequential functions going in opposite directions can capture any regular function, as detailed in the next subsection. Weakly deterministic regular functions (see Fig. 1) are described by Heinz & Lai (Reference Heinz, Lai, Kornai and Kuhlmann2013) as those FSTs that can be defined as the composition of two subsequential functions going in opposite directions, such that the two functions do not use an intermediate alphabet containing symbols not present in the input alphabet; see (17).Footnote 7
(17)

This definition of weakly deterministic regular functions is designed to pick out functions with two notable properties. First, this class of functions is able to capture bidirectional patterns that no right- or left-subsequential function can on its own. Second, the increased expressivity of this class is constrained by a restriction: no extra intermediate symbols. This is ensured by the condition that the output alphabet of the first (‘inner’) subsequential function, I, is the same as the input alphabet of both functions. Without such a restriction, the composition of two subsequential functions is guaranteed to be a function, but not necessarily a subsequential one (Elgot & Mezei Reference Elgot and Mezei1965). In a weakly deterministic function, the behaviour of the second (‘outer’) function does not depend on any form of ‘mark-up’ deposited by the first function into the intermediate representation, and the restrictiveness of this class of patterns is intended to follow from the definition's prohibition of an intermediate alphabet with extra symbols. Without this restriction, the inner function could use additional symbols to effectively provide unbounded look-ahead for the outer function, allowing the outer function to behave deterministically, given this marked-up version of the input string.
At this juncture, it is important that we clarify that splitting a phonological process into the composition of multiple finite transductions does not impact the formal status or complexity of the overall transduction. In formalisms that use cyclic rule application or level-ordering, derivational stages of input–output maps are given formal interpretations and theoretical significance. In contrast, no formal status is given to the non-surface outputs of intermediate transductions in current work exploring the subregular hierarchy (Chandlee & Heinz Reference Chandlee and Heinz2018, Chandlee et al. Reference Chandlee, Heinz and Jardine2018). In this way, the formal language theory adopted here is similar to Optimality Theory, where the analytical focus is on properties of holistic input–output maps, regardless of whether they are characterised as multiple independent processes in other formalisms; here, too, only properties of the total input–output mapping are relevant to a pattern's complexity. However, unlike Optimality Theory, the way in which inputs are mapped to their final output in formal language theory can vary, and therefore requires explication and justification. To this end, breaking a pattern into multiple transductions serves two interrelated purposes which are orthogonal to the minimum expressivity required to describe the overall pattern: (i) to aid human interpretability and reasoning about the overall transduction, and (ii) to validate that the simplest overall transduction has been selected (for example, by showing that a pattern can be generated as the composition of multiple single-direction subsequential transductions, we substantiate the claim that the pattern is subsequential). Although some individual transductions in a composition may resemble what would be considered an independent process in other formalisms, it is critical to keep in mind that this is for convenience and interpretability, and that these individual transductions do not have the same formal status as independent processes in other analytical frameworks.
For example, Heinz & Lai (Reference Heinz, Lai, Kornai and Kuhlmann2013) show that weakly deterministic functions are capable of describing bidirectional harmony patterns, such as the ATR harmony pattern found in Degema (Kari Reference Kari1997, Archangeli & Pulleyblank Reference Archangeli and Pulleyblank2007). The pattern in Degema differs from that in Turkish in two key respects: the harmonising feature and directionality. First, the feature which participates in harmony is [ATR], resulting in the alternations /i–ɪ/, /u–ʊ/, /e–ɛ/, /o–ɔ/ and /ə–a/. Second, affixes on both sides of a root agree in [ATR] with the root, as shown in (18).Footnote 8 (FSTs modelling the Degema pattern can be found in Appendix A2.)
(18)

In (19) and (20) we provide a running tape representation of the mapping, using the word [ubiə] in (18b). We begin with the left-subsequential function.Footnote 9
(19)

Following the prefix vowel, the FST encounters the prefix–root boundary, notated here with the symbol √. The transducer progresses through the input string, and faithfully outputs all symbols between the two root-boundary symbols (19b). In (19c), the FST reaches a suffix vowel. Because the [ATR] value of the root is known, the FST outputs [ə] from input /a/.
Following the application of this inner function, we see that affixes to the right of the root have been appropriately harmonised, but affixes to the left of the root have not. To capture the bidirectionality of harmony in Degema, we compose the left-subsequential function with the right-subsequential function, taking the output of (19c) and applying the right-subsequential function to it. To keep track of the derivation, we add another tape to our running tape representation below. The top tape represents the initial input, prior to application of the left-subsequential function; the middle, intermediate, tape represents the output of the left-subsequential function and the input of the right-subsequential function. The new bottom tape represents the final output of the computation.
The right-subsequential function in (20a) mirrors the left-subsequential function that was previously applied. The computation begins from the right end of the input string, and upon reaching the first vowel in the string, the vowel is output faithfully.
(20)

Following the suffix vowel, the FST encounters the root–suffix boundary symbol, and the transducer outputs all characters between the root-boundary characters faithfully (20b). Finally, in (20c) the FST reaches the initial prefix vowel, which is currently disharmonic. The [ATR] value of the root is known at this point, and the FST outputs a vowel matching the root value for the harmonic feature.
The computation is now complete, and the initial input has been successfully harmonised to the final output form observed in Degema. The analysis of this harmony pattern requires the composition of two subsequential functions, but maintains the alphabet size of the initial input throughout the application of both functions, satisfying the definition of a weakly deterministic function given by Heinz & Lai (Reference Heinz, Lai, Kornai and Kuhlmann2013). In the next subsection, we describe non-deterministic functions and a set of phonological maps which require non-determinism to be described – unbounded circumambient patterns.
4.3 Non-determinism
As noted in §4.1, a subsequential transducer τ:X﹡ → Y﹡ defines a string-to-string function that is deterministic in its input string and has state transition and output functions that are deterministic in the current state and input symbol: every input string w ∈ X﹡ is mapped by τ to at most one string in Y﹡ and any given (state, input symbol) pair is mapped by δ and ω to at most one state and at most one output string respectively. If τ can map at least one input string to more than one output string, then τ is a non-deterministic function on strings; it is a string relation. In contrast, a transducer that maps every input string to at most one output string is said to be functional or single-valued. If there are any (state, input symbol) pairs such that a transducer can ‘choose’ from among a set of two or more states to transition to, or from among a set of two or more strings to output, then that transducer's transition and/or output functions are non-deterministic.
Following Heinz (Reference Heinz, Hyman and Plank2018: §6.2.5), we use the term regular relations to refer exclusively to the most general class of string-to-string mappings definable using FSTs – the class that includes transducers which are not functional. We also follow Heinz in using non-deterministic regular functions to refer to the class of transducers that are functional, but can have non-deterministic state and/or output functions. Such transducers can have temporarily and incrementally ambiguous input strings, but the point of disambiguation may be an unbounded distance away from the location of the read/write head at the moment of ambiguity. As Elgot & Mezei (Reference Elgot and Mezei1965) show, any regular function can be decomposed into two subsequential functions going in opposite directions, as long as the first function in the composition is allowed to enlarge the input alphabet, as shown in (21).
(21)

As mentioned in the previous subsection, the intuition is that the first, inner function can effectively perform unbounded look-ahead for the second function by ‘marking up’ intermediate strings with extra information (in the form of extra symbols that are in Y but not in X) that the second, outer function can then use to behave in a manner that is incrementally deterministic.
Jardine (Reference Jardine2016) conjectures that unbounded circumambient processes are a class of patterns which require non-determinism, the full expressivity of regular relations.Footnote 10 For this reason, to introduce this complexity class, we walk through Jardine's analysis of tonal spreading in Copperbelt Bemba.
In Copperbelt Bemba (Bickmore & Kula Reference Bickmore and Kula2013, Kula & Bickmore Reference Kula and Bickmore2015; see also Pater Reference Pater2018 for discussion), a high tone spreads unboundedly to the right word edge in phrase-final forms (22a). However, if another high tone intervenes between the first high tone and the word edge, then bounded ternary spreading takes place instead (22b).
(22)

We schematise this pattern in (23).Footnote 11
(23)

In (24) and (25) we show ternary spreading with a running tape representation of the input string /HLLLH/. The input–output mapping here is composed of a left-subsequential FST, as well as a right-subsequential FST that reads the output of the left-subsequential FST as its input, and outputs the actual attested form (FSTs modelling the mapping can be found in Appendix A3). The order between the two FSTs is not arbitrary: the left-subsequential FST adds mark-up that the right-subsequential FST then takes advantage of.Footnote 12
Generally speaking, the left-subsequential FST outputs all L tones without modification until encountering a H tone, at which point the H ‘spreads’ to two following L tones. For all following L tones, the FST outputs a distinct symbol (notated as Ψ here) not contained in the input alphabet, because it cannot determine whether the output should be an L (or an H) tone until it does (or does not) encounter another H tone later in the word. Since a second H tone may in principle occur an unbounded distance from the first, the FST cannot ‘wait’, and so instead outputs the placeholder Ψ symbol, indicating that the preceding context matches the lefthand side of the structural description for unbounded spreading. The FST iteratively outputs all subsequent input L tones as Ψ until it encounters either an input H, which is output without modification, or the right word edge.
With the input /HLLLH/, the inner left-subsequential FST first reads the word-initial H tone, and initiates ternary spreading to the immediately following two L tones (24a).
(24)

Next, the FST reads the third L tone from the input, but cannot determine at this point whether to output an H or an L tone, because the presence or absence of a following H tone is unknown. The FST thus outputs a new symbol not contained in the input alphabet, Ψ (24b). This new symbol will ultimately provide the outer right-subsequential FST with the information necessary to determine all tone values for the word. Progressing through the input string, the inner FST continues as described above. In (24c), the FST reads a second input H tone and maps it faithfully, and then reaches the right edge.
The outer right-subsequential FST now reads the output just produced by the inner left-subsequential FST as its input, and completes the input–output mapping. Generally speaking again, the outer FST outputs all input L and H tones without modification, but maps intermediate Ψ according to the previously read context. Proceeding from right to left, if the FST reads an H tone, then it outputs all Ψ as L; if it does not encounter H, then it outputs all Ψ as H. The outer FST is able to discern whether a second H tone is present in the word, and uses the mark-up passed from the inner FST to determine whether ternary or unbounded spreading occurs.
This is shown in (25) for the more specific form under discussion. First, the outer right-subsequential FST reads the word-final H tone, and outputs it faithfully.
(25)

Since an input H has been encountered, the FST outputs all Ψ as L in (25b) and all H faithfully in (25c). The result in this case is thus ternary, rather than unbounded, spreading from the initial H.
Unbounded circumambient processes like tone spreading in Copperbelt Bemba can thus be analysed as regular non-deterministic maps, either in the form of a single non-deterministic FST, as in Jardine (Reference Jardine2016), or as the composition of two subsequential functions that may use an enlarged alphabet containing some symbols not present in the initial input alphabet.
4.4 Summary
The three levels of expressivity defined and exemplified in this section can be summarised as follows. Subsequential regular functions can describe unidirectional processes with bounded look-ahead (and unbounded ‘look-behind’), as in Turkish harmony. Weakly deterministic functions are intended to be able to describe bidirectional processes where the first ‘pass’ is not allowed to behave as look-ahead for, or otherwise affect the behaviour of, the second pass, as in Degema. Non-deterministic regular functions can describe compositions of unidirectional processes going in opposite directions, where the first pass may serve as unbounded look-ahead for, or otherwise affect the behaviour of, the second pass, as in Copperbelt Bemba.
Jardine (Reference Jardine2016: §5.4) acknowledges two attested cases of apparent unbounded circumambience in segmental phonology, Sanskrit n-retroflexion (Ryan Reference Ryan2017) and Yaka height harmony (Hyman Reference Hyman1998). He does not consider them equivalent to tonal patterns, however, claiming that such segmental patterns are ‘extremely rare’. He suggests that the harmony patterns in Sanskrit and Yaka may not actually be unbounded. In §5 we analyse ATR harmony in Tutrugbu, which provides a further challenge to the claim that segmental phonology is at most weakly deterministic. Looking ahead, we identify a number of other cases in §6.2 as evidence that unbounded circumambient vowel-harmony patterns are more widely attested than previously thought.
5 Finite-state analysis of Tutrugbu ATR harmony
This section presents a finite-state analysis of ATR harmony and conditional blocking in Tutrugbu. We demonstrate that this pattern requires the same expressivity as tonal spreading in Copperbelt Bemba.
Since ATR harmony in Tutrugbu is regressive, the analysis begins with a right-subsequential FST that starts at the right edge of the input string and moves leftwards. We first demonstrate a simple attempt at modelling ATR harmony in (26), using the example /i-tɪ-wu/ [itíwu] from (8b). Since harmony is regressive and root-controlled in the language, all segments to the right of the root–prefix boundary (represented by √) are output without modification (26a).
(26)

In (26b), the FST reads a prefix vowel and outputs it according to the [ATR] value of the root.Footnote 13 The right-subsequential FST outputs prefix vowels further away from the root in the same way. The output [ATR] value for a given prefix vowel depends on the output [ATR] value of the nearest following output vowel. In (26c), the 1st person singular prefix /ɪ-/ is, like the vowel of the negation prefix /tÍ-/, output as [+ATR]. The next symbol read is the left word-edge symbol, and the computation is complete.
The input–output mapping shown in (26) models harmony when both blocking conditions are not met. If, however, an initial [+high] prefix and a medial [―high] prefix co-occur, then this right-subsequential FST cannot on its own properly determine whether a given prefix vowel will be realised as [+ATR] based solely on the nearest vowel to the right. Compare the forms in (27). In (a), the future prefix is [+ATR] before the root /wu/, but in (b), the same prefix is [―ATR], even though it occurs before the same root.
(27)

Since the right-subsequential FST does not have access to information to the left of the target vowel (which can in principle be an unbounded distance away), it cannot determine which allomorph of the future morpheme should surface, [ba] or [be]. This indeterminacy precludes a subsequential analysis of Tutrugbu. If, however, we mimic the structure of the analysis provided for Copperbelt Bemba in §4.3, where the first FST is able to introduce intermediate mark-up into the derivation, the Tutrugbu pattern is analysable.
Generally speaking, the first, right-subsequential FST proceeds leftward, outputting all high vowels in accordance with the root's [ATR] value. If, after reading a [+ATR] root, the FST reads an input [―high] vowel, the transducer first outputs Ψ and then all subsequent vowels as either Ψ (for further [―high] vowels) or Ê (for [+high] vowels). By doing so, this first FST passes information about the [ATR] value of the root and the presence of a potential blocker to the second, left-subsequential FST.
This analysis is illustrated in (28) with the example [ɪbawu]. First, the right-subsequential FST faithfully maps the root, starting from the right edge of the input.
(28)

Next, this inner FST encounters a prefix with a [―high] vowel (28b). Having not yet determined the height of the initial prefix vowel, the [―high] prefix vowel is output with the new symbol Ψ, which encodes its height and leaves its [ATR] value to be determined by the outer, left-subsequential FST. The inner FST then encounters a prefix with a [+high] vowel (28c). It happens to be the initial prefix in this case, but as with all [+high] prefix vowels, it is output with Ê, which encodes its height and leaves its [ATR] value to be determined. The left edge is then reached, and this pass ends.
The outer left-subsequential FST then proceeds from left to right, using the output of the inner FST as its input, as in (29).
(29)

Upon encountering a Ê in the initial syllable, the outer FST ‘knows’ that the conditions for blocking have been met, because initial Ê indicates both that the root is [+ATR] and that there is a medial [―high] prefix vowel. Because Ê is in the initial syllable, this FST outputs all Ê and Ψ as [ɪ] and [a] respectively. With the introduction of additional symbols into the derivation, this analysis of Tutrugbu parallels the non-deterministic analysis of Copperbelt Bemba in §4.3.
As noted earlier in §4.3, a subsequential FST can utilise ‘wait’ states to achieve (bounded) look-ahead without increasing expressivity, but the maximum number of wait states (here equivalent to the amount of look-ahead) must be known and fixed a priori. Given that the context to the left of a target [―high] vowel in Tutrugbu may be unboundedly long, then there is no single number of ‘waiting’ transition states that can model all of the possible data and capture the principled generalisation describing it. In (8) we demonstrated that [―high] vowels could be separated from the initial syllable by a number of syllables with no principled upper bound. The generalisation is that the realisation of [ATR] on [―high] prefix vowels depends on both the [ATR] value of the root and the height value of the initial syllable. Furthermore, a given [―high] vowel may occur a potentially unbounded distance from both the root and the initial syllable. The conditional blocking pattern in Tutrugbu is thus unbounded circumambient, like the tonal processes analysed in Jardine (Reference Jardine2016).
6 Discussion
Formal language theory offers a valuable framework-independent metalanguage for comparing linguistic formalisms and classifying phonological patterns in terms of formally well-characterised and independently motivated categories of computational complexity and expressivity (Heinz Reference Heinz, Hyman and Plank2018). While the subregular programme has excelled at identifying salient categories for phonological typology, we think the programme is at its weakest when it comes to predicting and explaining typology. It has primarily done so by positing, on a post hoc basis, innate categorical constraints on the hypothesis space that human learners apply to phonology via a phonology-specific learning mechanism. In the subsections below we present evidence that segmental phonology is substantially more expressive than previously predicted, outlining what a more productive relationship between formal language theoretic phonology and typological explanation could look like, and how phonological theories should be evaluated.
6.1 How complex is phonology?
The first counterexamples to the subregular hypothesis articulated in Heinz (Reference Heinz2011a, Reference Heinzb, Reference Heinz, Hyman and Plank2018) came from the tonal patterns in Jardine (Reference Jardine2016), which require the expressivity of non-deterministic regular functions. To uphold the subregular hypothesis, Jardine (Reference Jardine2016) adds a qualification: segmental phonology is subregular, but tonal phonology is not constrained in the same way. Heinz (Reference Heinz, Hyman and Plank2018) writes:
Jardine's result [i.e. the existence of unbounded circumambient phonological patterns] is perhaps the most serious challenge to the Subsequential Hypothesis (or a revised Weakly Deterministic hypothesis) because the best characterization of Yaka vowel harmony seems to be that it is circumambient unbounded (Hyman Reference Hyman1998). However, this is the only known example of this type, and it is probably premature to reject the hypothesis on these grounds alone.
In addition to the Tutrugbu pattern detailed above, we consider in §6.2 a comparable number of segmental phenomena requiring the same level of expressivity as the tonal patterns discussed by Jardine (Reference Jardine2016), as well as those in Yaka, adding more counterexamples to any proposed subregular upper bound on the complexity of phonology (see Avcu Reference Avcu2018 for experimental evidence for the learnability of more complex patterns). This evidence shows that segmental phonology, like tonal phonology, is more expressive than previously thought, requiring the expressivity of non-deterministic regular functions.
In fact, there is some evidence that segmental patterns may require strictly more expressivity than the non-deterministic regular functions. As Heinz (Reference Heinz, Hyman and Plank2018: §6.2.5) notes, optional processes require non-deterministic mappings that are, unlike the Copperbelt Bemba and Tutrugbu patterns, non-functional (recall the discussion at the beginning of §4.3). Optional processes thus require the more expressive class of regular relations. In the face of optionality, Heinz (Reference Heinz, Hyman and Plank2018: 175) suggests that optionality may be ‘handled at a higher level of control than the individual transformation’. Although offloading optionality to some other part of the grammar effectively downplays the significance of these potential counterexamples to the subregular hypothesis, patterns of optionality like those listed in Vaux (Reference Vaux, Vaux and Nevins2008) and others like iterative optionality in Icelandic umlaut (Anderson Reference Anderson1974) present challenges to the strong claim that segmental phonology is categorically subregular. In particular, in cases where an iterative process may be optional, there is no a priori bound on the number of potential alternations (Mohri Reference Mohri1997).
Moreover, some recent work suggests that segmental phonology may require more expressivity than the regular relations: Bowler (Reference Bowler2013) and Bowler & Zymet (Reference Bowler and Zymet2019) demonstrate from a corpus of Warlpiri nouns that disharmonic nouns exhibit optional ‘majority rules’ harmony (Lombardi Reference Lombardi1999, Baković Reference Baković2000), a pattern that numerous linguists have claimed to be unattested, impossible and pathological, given that it requires even more expressivity than the regular relations (Riggle Reference Riggle2004, Heinz & Lai Reference Heinz, Lai, Kornai and Kuhlmann2013, Hulden Reference Hulden2017, Heinz Reference Heinz, Hyman and Plank2018, Lamont Reference Lamont, Hout, Mai, McCollum, Rose and Zaslansky2019). Whatever conclusion future work comes to about the significance of the last two pieces of evidence, these patterns suggest that there is presently no clear subregular cap on the empirically observed expressivity of phonology – segmental or tonal.
6.2 Additional unbounded circumambient segmental patterns
In §6.2.1–§6.2.4 we briefly describe four additional cases of unbounded circumambient segmental patterns, all involving ATR harmony: Tafi, Turkana, Karimojong and Liko. A few other segmental patterns whose unboundedness is less clear are discussed in §6.2.5. The ATR harmony patterns of Tutrugbu, Tafi, Turkana, Karimojong and Liko all quite clearly meet Jardine's (Reference Jardine2016) definition of unbounded circumambience in (13). Jardine's claim that unbounded circumambient segmental patterns are significantly rarer than their tonal counterparts, and that they are therefore not within the computational bounds of segmental phonology, thus appears to have been premature.
6.2.1 Tafi
We have claimed that Tafi (Kwa), a closely related language, exhibits the same pattern of harmony as Tutrugbu. Bobuafor (Reference Bobuafor2013) does not give an explicit description of conditional blocking in Tafi, but its existence is clear from the data presented, as illustrated in (30) (from Bobuafor Reference Bobuafor2013 and Mercy Bobuafor (personal communication)). Harmony obtains when a [+ATR] verb is preceded by only [+high] prefixes (30a) or only [―high] prefixes (30b). It is also found when a [+ATR] root is preceded by vowels of both heights, and the initial-syllable vowel is [―high] (30c). However, when the initial-syllable vowel is [+high] and is followed by a [―high] vowel, harmony is blocked by the [―high] vowel, just as in Tutrugbu (30d, e). The additional examples in (30f, g) demonstrate that blocking occurs at longer distances, since in these examples the initial-syllable high vowel and medial non-high vowel are not syllable-adjacent.Footnote 14
(30)

6.2.2 Turkana
Besides Tutrugbu and Tafi, Turkana (Nilotic) also features a vowel-harmony pattern that is unbounded circumambient (Dimmendaal Reference Dimmendaal1983, Baković Reference Baković2000).Footnote 15 In Turkana, [+ATR] spreads bidirectionally from a dominant root or suffix, as shown in (31). Prefix and other recessive vowels alternate, but the behaviour of /ɑ/ depends on whether it is to the left or the right of a dominant vowel: /ɑ/ to the left is opaque to harmony and does not alternate (as shown by the gerundial prefix in these examples), while /ɑ/ to the right alternates between the [+low, ―ATR] vowel [ɑ] and the [―low, +ATR] vowel [o], with [o] occurring after [+ATR] dominant vowels (as shown by the epipatetic vowel in these examples).Footnote 16
(31)

A small subset of dominant suffixes in Turkana are [―ATR], and when a dominant [―ATR] suffix co-occurs with a [+ATR] root, the realisation of the epipatetic vowel between them is neither [+low, ―ATR] [ɑ] nor [―low, +ATR] [o], but rather [―low, ―ATR] [ɔ], as shown in (32). As above, in (32a) the epipatetic vowel surfaces as [o] after the [+ATR] root /ibus/ when no dominant [―ATR] suffix vowel follows. However, in (32b), a dominant [―ATR] suffix occurs to the right of the epipatetic vowel, which surfaces as [ɔ].
(32)

The surface quality of a suffixal low vowel is thus not determinable based solely on whether there is an [+ATR] vowel to its left; it also depends on the presence or absence of a dominant [―ATR] suffix to its right. In other words, the realisation of a suffixal low vowel depends on information a potentially unbounded distance away in both directions (see Appendix A5), and the realisation of a suffix low vowel is therefore non-deterministic. ATR harmony in Turkana is thus unbounded circumambient.
6.2.3 Karimojong
The pattern described above for Turkana is also attested in Karimojong (Nilotic; Novelli Reference Novelli1985, Lesley-Neuman Reference Lesley-Neuman2012). As in Turkana, the low vowel suffix alternates between [ɑ] and [o] for [ATR]. Note specifically the alternation of the frequentive suffix, /-ɑn/, in (33a, b). There are also dominant [―ATR] suffixes, like the itive suffix /ɔr/, shown in (33c, d). In (33c), the dominant [―ATR] itive suffix attaches to the right of the root, spreading its [―ATR] value to the root. Moreover, the itive suffix causes both the frequentive suffix and the root to surface as [―ATR] in (d). Similarly to Turkana, the surface quality of the frequentive suffix depends on both the [ATR] value of the root and the presence or absence of a dominant [―ATR] suffix, surfacing as [ɑn], [ɔn] or [on].
(33)

In (33d), the frequentive suffix exhibits a dependency on the [ATR] value of two syllable-adjacent vowels. Longer-distance dependencies are also reported in Karimojong. In reduplicated stems, an epenthetic vowel is inserted immediately before suffixes. In (34a, b), the epenthetic vowel (which Novelli Reference Novelli1985: 224 calls the ‘stem-enlarging vowel’) alternates based on the quality of the root: it surfaces as [ɔ] after the reduplicated stem /dɔŋɔdɔŋ/, but as [o] after /doŋidoŋ/. Thus the stem-enlarging vowel is like the frequentive in (33). Like the frequentive suffix, the epenthetic vowel takes on the [―ATR] value of a following itive suffix (34c). Yet, in (34d, e), both the stem-enlarging vowel and the itive suffix take on the value of a following dominant [+ATR] suffix. In other words, the surface quality of the stem-enlarging vowel is conditioned by the potentially non-local [ATR] values of dominant morphemes on both its left and its right.
(34)

6.2.4 Liko
Liko (Bantu) displays a slightly different pattern of unbounded circumambience (de Wit Reference Wit2015). ATR harmony is typically controlled by roots in Liko. Rightward harmony affects all vowels, while leftward harmony affects only the first prefix. In (35a), all affixes surface with their underlying, i.e. [―ATR] feature values, while in (35b) the [+ATR] root causes input /a/ to surface as [o]. The unboundedness of rightward harmony is seen in the three suffix alternations in (35c) (de Wit Reference Wit2015: 77, 82).
(35)

Like the other languages discussed in this section, Liko possesses dominant [+ATR] and dominant [―ATR] morphemes. The negative enclitic, /﹦gʊ/, is invariantly [―ATR] in (36). In (36a), the enclitic does not undergo harmony from a [+ATR] root, although the preceding [+high] suffix does. When preceded by an underlying /a/, though, the enclitic not only resists [+ATR] harmony, but also prevents preceding low vowels from undergoing harmony (36b, c). In (b), the enclitic blocks harmony on a single preceding /a/, and in (c), the negative enclitic blocks harmony on both preceding low vowels (de Wit Reference Wit2015: 94–96).
(36)

De Wit (Reference Wit2015) argues that [+ATR] is the active feature value in the language, further arguing that alternating vowels are specified as [―ATR] underlyingly. In examples like (36b, c), the root value for [ATR] is not sufficient to determine whether suffixal /a/ undergoes harmony to [o]. The presence or absence of a dominant enclitic must be known in order to map low suffix vowels to their attested output forms.
One might object to treating Turkana, Karimojong and Liko in the same way as Tutrugbu and Tafi, since ATR harmony with conditional blocking in the first two is, at least intuitively, a single pattern. In the other three languages, on the other hand, spreading of [+ATR] and the more restricted pattern of [―ATR] spreading are – again, at least intuitively – two distinct patterns, as in existing analyses (Dimmendaal Reference Dimmendaal1983, Baković Reference Baković2000, Lesley-Neuman Reference Lesley-Neuman2012). Recall, however, that the question of interest is the minimum level of complexity required to describe complete input–output mappings (Heinz Reference Heinz, Hyman and Plank2018: §2). Thus the object of study is not the complexity of a particular pattern isolated from the larger phonology in a language, but rather the function that maps inputs to outputs comprising all relevant patterns. As a consequence of this framing, the multiple [ATR] spreading patterns in Turkana, Karimojong and Liko are together comparable in complexity to the single pattern found in Tutrugbu or Tafi.
6.2.5 Other cases
There are other apparent cases of circumambient harmony described in the literature, but these are less clear, and we cannot say with certainty that they are both unbounded and circumambient. Hyman (Reference Hyman1998) argues that in Yaka (Bantu), high suffix vowels lower if they are preceded and followed by mid vowels, thus exhibiting some similarity to unbounded tone plateauing. Although the harmony extends over several syllables, Jardine (Reference Jardine2016) doubts the unboundedness of this pattern. But as far as we can tell, harmony in Yaka satisfies all three of Jardine's (Reference Jardine2016: 250) stated criteria in (37).
(37)

In addition to Yaka, Jardine (Reference Jardine2016: §2.3.1) questions the status of retroflex harmony in Sanskrit (Indo-Aryan), based on Ryan (Reference Ryan2017). In Sanskrit, a retroflex consonant triggers retroflexion of a following /n/ as long as another retroflex consonant is not present later in the word. Ryan (Reference Ryan2017: §4) finds no examples of blocking across more than one syllable, a point which Jardine uses to question the boundedness of harmony. But Ryan shows evidence of triggering across intervening segments and blocking across one, two or three segments, which, in our estimation, suggests that the pattern may be unbounded.
Teso (Nilotic; Rottland & Otaala Reference Rottland, Otaala, Voßen and Bechhaus-Gerst1983), Toposa (Nilotic; Schröder & Schröder Reference Schröder and Schröder1987) and Bondu-So (Dogon; Hantgan & Davis Reference Hantgan and Davis2012) may also exhibit unbounded circumambience. These languages all exhibit patterns of conflicting [ATR] dominance, like Turkana and Karimojong, but triggering morphemes in extant descriptions always immediately precede or follow the relevant suffix, so we cannot determine the unboundedness of these harmony patterns. If these are in fact bounded, then they parallel other cases of bounded circumambient harmony, like those described in Kalinowski (Reference Kalinowski2009) and Lionnet (Reference Lionnet2016).
6.2.6 Summary
We contend that claims about the frequency of complex segmental phenomena relative to tonal phenomena are at best premature. As further support for a computational distinction between segmental and tonal processes, Heinz (Reference Heinz, Hyman and Plank2018) and Jardine (Reference Jardine2016) claim that unbounded circumambient tonal processes are relatively common and equivalent segmental mappings are at most ‘extremely rare’. In support of this, Jardine adduces nine potential examples of such tonal processes, but only two unbounded circumambient segmental processes, Sanskrit n-retroflexion and Yaka height harmony. In our view, the difference between two and nine examples is not persuasive evidence of a difference in typological frequency. As Piantadosi & Gibson (Reference Piantadosi and Gibson2014) contend (and as we elaborate in §6.3), outside particular cases of carefully framed questions and statistical reasoning, we do not currently – nor will we soon – have descriptions of enough languages to draw strong conclusions about what properties are categorically impossible (e.g. non-deterministic segmental phonological patterns) for natural languages to have on the basis of simple comparisons of frequency counts. Furthermore, we simply do not have enough data to even know how many languages have tone, or how many have vowel harmony. At best, we have very rough ballpark estimates. For instance, Yip (Reference Yip2002: 1) notes that ‘by some estimates as much as 60–70 per cent of the world's languages are tonal’. Such rough estimates demonstrate how much we have to learn before we can evaluate the frequency of unbounded circumambient tonal patterns and their segmental equivalents.
Even if the foregoing were not the case, of the nine tonal patterns marshalled as evidence in Jardine (Reference Jardine2016), at least two (Digo and Xhosa) are not actually unbounded circumambient – see Appendix B for a left-subsequential analysis. Moreover, we have identified in this subsection at least four examples of unbounded circumambient segmental patterns in addition to our main example of Tutrugbu ATR harmony. We discuss these patterns, not to make typological claims about the frequency of these patterns relative to similarly complex tonal processes, but instead to demonstrate that they must be dealt with seriously, and not swept aside as outliers.
6.3 How should we establish and explain typological generalisations?
The empirical data from Tutrugbu (§2) and the additional languages described in §6.2 provide strong reasons to revise the typological claims in Jardine (Reference Jardine2016), outlined in §3. Additionally, we would like to point out problems with the approach to typology advanced by existing work on the subregular hypothesis (e.g. Heinz & Idsardi Reference Heinz and Idsardi2011, Chandlee & Heinz Reference Chandlee and Heinz2012, Reference Chandlee and Heinz2018, Chandlee et al. Reference Chandlee, Athanasopoulou and Heinz2012, Gainor et al. Reference Gainor, Lai and Heinz2012, Heinz & Lai Reference Heinz, Lai, Kornai and Kuhlmann2013, Jardine Reference Jardine2016) and summarised in (38).
(38)

In the particular case of segmental and tonal pattern, even granting both points in (38), our discussion of the vowel-harmony patterns in Tutrugbu and in §6.2 shows that a non-trivial number of unbounded circumambient patterns exist in segmental phonology, just as they do in tonal phonology.
More generally, contemporary literature on typology and linguistic theory offers four reasons for rejecting (38b). First, Piantadosi & Gibson (Reference Piantadosi and Gibson2014) show that, in general, the number of independent languages that linguists need to observe to achieve reasonable statistical confidence that a particular type of feature or phenomenon is categorically impossible is far higher than they are likely to observe and document for many generations. Second, even if we had both detailed descriptions and computational analyses for the phonology of every language currently spoken, this would only constitute a small and likely unrepresentative fraction of all human languages spoken in the last 100,000–200,000 years (Plank Reference Plank2007, Bowern Reference Bowern2011). Third, even if we had reasonably complete analyses on both current and past human languages, for these data to be strongly informative about what is likely or even possible in potential future human languages requires either good reasons to believe such data are representative of all possible human languages or a dynamic model of how languages change over long timescales that would allow us to make such predictions (see e.g. Maslova Reference Maslova2000, Daniel Reference Daniel2007, Bickel Reference Bickel2011, Croft et al. Reference Croft, Bhattacharya, Kleinschmidt, Eric Smith and Florian Jaeger2011, Cysouw Reference Cysouw2011).
The final reason for rejecting (38b) is that it doesn't have a good track record. Work on the subregular hypothesis has not predicted the typology of complexity; instead, the particular choice of exactly which class is hypothesised to be an upper bound has been post hoc, and driven by the most complex phenomena known to researchers at the time. The strengths of formal language theoretic methods lie in picking out well-defined classes of patterns and functions, and identifying formal conditions under which such patterns and functions are efficiently learnable. In order to make typological predictions, these strengths must be coupled with other linking hypotheses, which in previous literature have been nativist (38b). Nevertheless, since an empirically adequate theory must predict that actually attested languages do exist, these methods are metatheoretically useful for identifying what a well-specified theory should predict to be possible.
While it may traditionally have been considered a virtue in generative linguistics to attempt to predict all and only observed typological data, in the context of model selection the phenomenon of ‘memorising’ observed data and failing to make correct generalisations that predict future data is called overfitting – regardless of whether the inductive learner in question is that of a child reasoning about an unknown but partially observed ‘set of possible strings’ or that of a scientist reasoning about a ‘set of possible human languages’ (see Perfors et al. Reference Perfors, Tenenbaum and Regier2011, Piantadosi & Gibson Reference Piantadosi and Gibson2014 and Rasin et al. Reference Rasin, Berger, Lan and Katzirms for review, as well as discussion of the relevance of model selection to the role of typology and/or nativism in linguistic theory development and comparison). In either case, such hypotheses should, ceteris paribus, be normatively dispreferred relative to simpler hypotheses that predict as yet unobserved data – or at least don't rule it out.
We offer the following suggestions in place of (38b). First, rather than assuming that the absence of some type of phenomenon is best explained by arbitrary innate constraints, linguists should preferentially consider explanations that offer an independently motivated reason for that absence. Second, per the conclusions of Piantadosi & Gibson (Reference Piantadosi and Gibson2014) and Tily & Jaeger (Reference Tily and Florian Jaeger2011), multiple methodologies should be used to identify and test putative linguistic universals, and any linguistic universal proposed should be presented alongside an explicit measure of evidential strength.
Turning to (38a), contemporary literature on typology and its relation to linguistic theory has shown the value of considering phylogenetic and areal effects (see e.g. discussion of word-order typology in Bickel Reference Bickel2007: 241), language-specific historical contingencies (Nichols Reference Nichols1992, Blevins Reference Blevins2004, Hansson Reference Hansson2008, Harris Reference Harris and Good2008) and differential learnability (e.g. Hayes & Wilson Reference Hayes and Wilson2008, Culbertson Reference Culbertson2012, Moreton & Pater Reference Moreton and Pater2012, Stanton Reference Stanton2016)Footnote 17 as productive alternatives to innate constraints. We independently need explanations and theories of each of these domains, and each is a strictly simpler type of explanation of typological commonality and rarity than the non-specific, catch-all assumption of innate knowledge or constraints.
It may traditionally have been considered a virtue for generative linguistic theories to explain as much about observed typological data as possible. However, in light of all of the mechanisms we now know can and do affect observed linguistic typology and how little we know about the origins of long-distance phonological processes in particular, it would be surprising if a recently explored dimension of typological variation were entirely or largely explained by just one factor. This is especially the case when that factor is an innate constraint whose existence and specificity are not independently motivated or well-evidenced. In the language of model selection, (i) each previously mentioned non-nativist cause is a hypothesis with higher prior probability than a phonology-specific innate constraint of arbitrary complexity and weak independent motivation, and (ii) each of these non-nativist causes is constrained in terms of what kind of data it predicts and can explain, whereas an innate constraint could be invoked to explain almost any typological observation (see e.g. discussion of the ‘size principle’ in Tenenbaum & Griffiths Reference Tenenbaum and Griffiths2001).Footnote 18 We conclude that phonologists interested in explaining the typology of complex long-distance phonological processes would profit from exploring hypotheses about why they arise in the first place in the languages that have them and why they have the relative distributions they do (Bickel Reference Bickel2007).
6.4 Evaluating phonological theories and computational phonology
Independent of explaining typology per se, exactly fitting observed typology has been commonly used for evaluating generative linguistic theories. We argue that there are better ways of evaluating theories than the all-and-only criterion. We also emphasise that computational phonology has a key role to play: while the goal of identifying maximally restrictive theories of grammar has commonly been used to frame the significance of contemporary work on the subregular hierarchies of languages and relations, this sells short what contemporary work in computational phonology has to offer theory development and evaluation. For this reason, the question of how to evaluate theories of grammar without the all-and-only criterion is particularly relevant to this article.
In terms of model selection (Perfors et al. Reference Perfors, Tenenbaum and Regier2011, Rasin et al. Reference Rasin, Berger, Lan and Katzirms), the all-and-only criterion neglects consideration of both a theory's prior probability as a scientific hypothesis, plus the non-typological predictions it makes. Relevant sources of evidence for evaluating grammatical theories include results and debates concerning psychologically plausible representations and architectures (e.g. Marslen-Wilson Reference Marslen-Wilson1973, Marslen-Wilson & Tyler Reference Marslen-Wilson, Tyler and Garfield1987, Tanenhaus et al. Reference Tanenhaus, Spivey-Knowlton, Eberhard and Sedivy1995), computational learnability and predictions of learning errors (Tesar Reference Tesar1995, Heinz et al. Reference Heinz, Kobele and Riggle2009, Perfors et al. Reference Perfors, Tenenbaum and Regier2011, Rogers & Pullum Reference Rogers and Pullum2011, Chandlee et al. Reference Chandlee, Eyraud and Heinz2014, Piantadosi et al. Reference Piantadosi, Tenenbaum and Goodman2016, among many others), as well as linguistically significant distinctions (e.g. ‘Do phonological grammars count beyond two?’). Significantly, these are all sources of evidence already in use: phonologists bereft of the all-and-only criterion are hardly without other means of theory evaluation.
7 Conclusion
Jardine (Reference Jardine2016) claims that the minimum expressivity required to describe tonal patterns exhibiting unbounded circumambience is categorically greater than that needed to represent any patterns of segmental phonology, which are claimed to require at most weakly deterministic regular functions. Existing evidence for potentially unbounded circumambient segmental processes in Yaka and Sanskrit has been minimised, and these patterns have been construed as aberrant (Jardine Reference Jardine2016, Heinz Reference Heinz, Hyman and Plank2018). We have shown that ATR harmony in Tutrugbu clearly satisfies the definition of unbounded circumambience according to the criteria laid out in Jardine (Reference Jardine2016). Moreover, we have noted a variety of other languages that exhibit segmental patterns requiring similar expressivity. Altogether, there is strong evidence that segmental patterns require no less expressivity than tonal patterns.
The claim advanced in this article, that segmental phonology requires the same expressivity as tonal phonology, has significant implications for the continued evaluation of the subregular hypothesis and the expressivity of phonology more generally. Formal language theory provides a framework within which to frame these questions and address issues like the computational properties of human sound patterns. Moreover, we recognise that work like Heinz (Reference Heinz2011a, Reference Heinzb), Heinz & Lai (Reference Heinz, Lai, Kornai and Kuhlmann2013) and Jardine (Reference Jardine2016) has stimulated a growing body of work examining phonology from a different point of view, and we hope further discussion of empirical patterns like ATR harmony in Tutrugbu and others noted here will facilitate a deeper understanding of human sound patterns, their expressivity and their distribution among the world's languages.