1. Introduction and Examples

It's difficult to say precisely what thought experiments are. Luckily, it's also unimportant. We know them when we see them, and that's enough to make discussion possible. A few features are obvious. Thought experiments are carried out in the mind and involve something akin to experience; that is, we typically see something happening in a thought experiment. Often there is more than mere observation. As in a real experiment, there might be calculating, some application of theory, guesswork, and conjecture. The best way to get a grip on what thought experiments are is to simply look at lots of examples. For the sake of illustration, I'll briefly give a few.

One of the most beautiful early examples is from De rerum natura; Lucretius attempts to show that space is infinite. If there is a boundary to the universe, we can toss a spear at it (see Figure 1). If the spear flies through, then it isn't a boundary after all. And if the spear bounces back, then there must be something beyond the supposed edge of space, a cosmic brick wall that is itself in space, that stopped the spear. Either way, there is no edge of the universe; space is infinite.

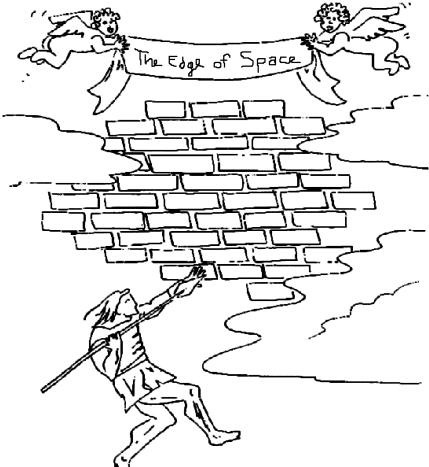
Figure 1. Throwing a spear at the edge of the universe.

This example nicely illustrates many of the common features of thought experiments: We visualize some situation; we carry out an operation; we see what happens. Though we use empirical concepts, we often can't carry out an empirical test. It also illustrates their fallibility. In this case we've learned how to conceptualize space so that it is both finite and unbounded.

Galileo showed that all bodies fall at the same speed, with a brilliant thought experiment that started by destroying the then reigning Aristotelian account. Aristotle and common sense hold that heavy bodies fall faster than light ones. (Symbolize this as $H> L$.) But consider Figure 2, where a heavy canon ball is attached to a light musket ball ( $H+L$); it must fall faster than the cannon ball alone ( $H+L> H$). Yet the compound object must also fall slower, since the lighter part will act as a drag on the heavier part ( $H+L< H$). Now we have a contradiction ( $H+L> H$ and $H+L< H$). That's the end of Aristotle's theory. But we can go further. The right account of free fall is now obvious: they all move at the same speed ( $H=L=H+L$).

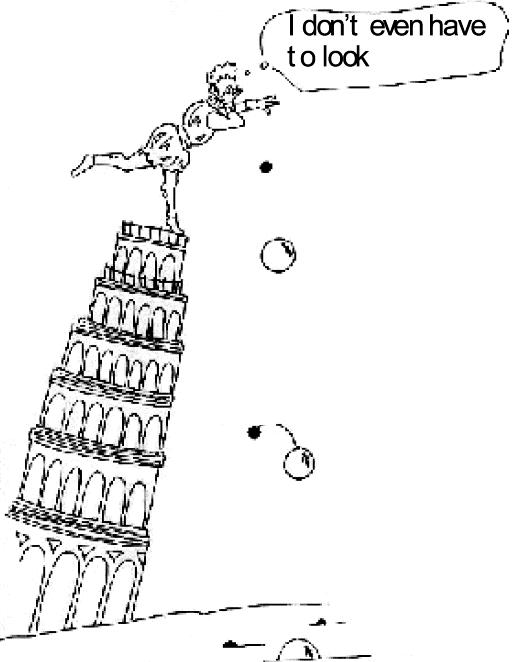
Figure 2. Galileo determining rates of fall.

Newton's bucket is one of the most famous thought experiments ever. It's also perfectly doable as a real experiment, as I'm sure most know from personal experience. The two-spheres example (described in the famous scholium to definition 8 of the Principia; see Figure 3) is not actually doable. So let's consider it. We image the universe completely empty except for two spheres connected by a cord. The spheres are of a material such that they neither attract nor repel one another. There is a tension in the cord joining them, but the spheres are not moving toward one another under the force in the cord. Why not? Newton offers an explanation: They are rotating with respect to space itself; their inertial motion keeps them apart. And so, Reference Newton and CohenNewton concludes, absolute space exists.

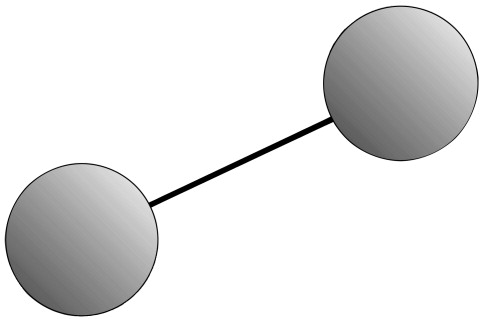
Figure 3. Newton's spheres in otherwise empty space.

2. Some Morals

Even with only a few examples, we can begin to draw some conclusions. For one thing, thought experiments can mislead us, not unlike real experiments. The Lucretius example leads us to infinite space, but we have since learned how to conceive of an unbounded but still finite space. Some thought experiments couldn't be actually performed. Newton's two-spheres thought experiment is impossible, since we can't get rid of the entire universe to try it out. On the other hand, the thought experiment of Galileo comes close to being doable. Of course, not exactly, but we can approximate it rather well. This, I think, shows that being able or not being able to perform a thought experiment is rather unimportant to understanding them. The so-called counterfactual nature of thought experiments is overstressed.

More interesting is the different roles they play. Some play a negative or refuting role. The aim of Schrödinger's cat is to show that quantum orthodoxy leads to absurdity. Newton's spheres thought experiment does not so much give us a new result, but rather gives us a remarkable phenomenon, something that needs explaining. The thought experiment establishes a phenomenon; the explanation comes later. And the best explanation, according to Newton, is the existence of absolute space. This way of looking at it is confirmed, it seems to me, by the way Berkeley and Reference Mach and McCormackMach reacted to the thought experiment. Instead of denying that rotation with respect to absolute space is the best explanation for the tension in the cord, they denied there would be any tension in the first place; or, if there were a tension, then the two spheres would move together. That is, they didn't challenge the explanation of the thought experiment, they challenged the alleged phenomenon the thought experiment tried to establish.

The most interesting example is surely Galileo's. This seems to play a negative role—it refutes Aristotle by means of a reductio—then, in a positive vein, it establishes a new theory of motion. There are lots of wonderful thought experiments, but only a small number work in this way. Elsewhere I called them Platonic (Brown Reference Brown1991; see also Reference Brown, Hull, Forbes and Okruhlik1993a, Reference Brown1993b, Reference Brown1999, Reference Brown and Hitchcock2004Reference Brown). I think they are rather remarkable—they provide us with a priori knowledge of nature.

My reasons for claiming this thought experiment provides a priori knowledge are rather simple and straightforward. For one thing, though it is true that empirical knowledge is present in this example, there are no new empirical data being used when we move from Aristotle's to Galileo's theory of free fall. It is not a logical truth, either. After all, objects could fall on the basis of their color, say, with red things falling faster than blue things. If this were the case, then Galileo's thought experiment wouldn't be effective. After all, sticking two red things together doesn't make one thing that is even redder.

In a different, though similar, context Galileo remarked: “Without experiment, I am sure that the effect will happen as I tell you, because it must happen that way” (Reference Galilei[1638] 1974, 145). This indicates the kind of confidence he had in thought experiments. The great French historian, Alexandre Koyré once remarked, “Good physics is made a priori” (Reference Koyré and Koyré[1960] 1968, 88), and he claimed for Galileo “the glory and the merit of having known how to dispense with [real] experiments” (Reference Koyré and Koyré[1960] 1968, 75). This remarkable assessment of Galileo is surely right. Some thought experiments do transcend empirical sensory experience.

3. Gendler, McAllister, and Norton

Thomas Kuhn (Reference Kuhn[1964] 1977) and Tamar Szabó Gendler (Reference Gendler1998, Reference Gendler2004) both maintain that thought experiments can provoke conceptual change. They focus on the effects of a thought experiment on a conceptual framework. I think there is something deeply right in their view. The empiricist-minded might go so far as to claim that this is an empiricist view. However, the thought experiment induces a gestalt switch from duck to rabbit, without any new empirical data. Could this be assimilated into an empiricist account? I doubt it. Empiricism is usually taken to hold that concepts are derived from experience, whereas in the gestalt analogy, concepts are being imposed on, rather than drawn from, the world. Where do the new concepts come from? It seems that the thought experiment prods the new concepts into consciousness. I doubt Norton's empiricist-inspired account (to be discussed below) will do full justice to this important feature, and I endorse Gendler's critique of his view.

But I contend that even more is going on in this example than is allowed in the Kuhn-Gendler account. Why, for example, does what happens in Galileo's thought experiment seem so different from a mere gestalt switch? We can shift back and forth between duck and rabbit without feeling like one is right and the other wrong. Yet the transition from Aristotle's theory of motion to Galileo's seems both inevitable and a genuine improvement. As Kuhn and Gendler say, we are provoked into conceptual change. But they haven't told us why this is a change for the better.

The kinds of consideration I have outlined (see Brown Reference Brown1991 for more detail) could certainly be resisted by any dedicated empiricist. They are plausible considerations in support of an a priori account of science, but no more than plausible. There is a second kind of consideration I now want to sketch. It depends on two things: mathematical Platonism and a realist view of laws of nature. I will for the moment be dogmatic about both, merely outlining my assumptions.

In the philosophy of mathematics, Platonism is the view that mathematical objects and facts exist independently from us. Our statements about these abstract entities are objectively true or false. Our knowledge of these facts is based in part on intuitions. We are able to grasp or perceive these objects and facts. We also conjecture axioms or postulates and test them against further intuitions. This is a fallible process, but it is a priori in the sense that the physical senses cannot fully account for this knowledge acquisition; some sort of intellectual perception must also be at work. In recent times Gödel has been the most prominent champion of such a view.

The second assumption I make is realism about the laws of nature. I take laws to be relations among properties. These are abstract entities, outside of space and time, that somehow necessitate the regularities we experience in the empirical world. This is a very anti-Humean view. Current champions of this outlook on laws include: Armstrong, Dretske, and Tooley. It is Tooley's Platonistic version that I especially favor (see Tooley Reference Tooley1977).

Now let's put these two assumptions together and tie them to thought experiments. According to mathematical Platonism we can perceive the abstract entities of mathematics. Not all, of course, but we do have intuitions of some of them. So, it's possible to perceive abstract entities, at least some. Usually we learn laws empirically, by seeing instances. But laws are abstract entities, so they could be perceivable, too. How could we have an intuition of a law of nature? The obvious thing to conjecture is that we grasp them via thought experiments. Laws and numbers are both outside of space and time. If we can see one, then we should be able to see the other. Thought experiments are telescopes into the abstract realm. Not all laws can be seen, but the odd one here and there can be perceived in this a priori way.

Before proceeding, a few remarks about James McAllister's views (Reference McAllister1996, Reference McAllister2004). He wants to historicize thought experiments. That is, he thinks that the evidential significance of a thought experiment is historically conditioned. I entirely agree. I have not addressed this issue before, but I take his view to be a sophisticated extension (in some respects) of what I have already claimed. McAllister himself thinks there is a significant conflict between his view and mine (and Norton's, too, for that matter). He takes both of us to be normative in some fundamental way that he is not. I see the situation somewhat differently, though I find myself in sympathy with him to a large extent. Thought experiments are no different than real ones in many respects. A particular thought experiment might be rightly used one way in one historical situation and wrongly used in another.

I have repeatedly stressed the fallibility of thought experiments. Following McAllister I would also stress their historical conditioning. I part with him, however, in holding that they do have genuine objective evidential significance, even though this significance will vary from context to context. He goes so far as to say that thought experiments may have no epistemic significance at all in some contexts. I allow that this is logically possible, but the onus is surely on those who would deny it. Thought experiments have been consistently used since antiquity in all sorts of contexts. The status of thought experiments is not unlike the status of empirical observation, both are legitimate sources of evidence. What he calls “phenomena” I take to be present at all times, whether recognized or not. Of course, someone might deny any role whatsoever for empirical observation. Parmenides did. But I take such a view to be implausible, to put it mildly. In the case of observation and thought experiments, neither needs a justification before we can proceed with doing science. The burden of proof is on Parmenides and the opponents of thought experiments. I'll turn now to my main target.

My own account of thought experiments is just about as antinaturalist as anything could be. John Norton, by contrast, is an empiricist and has given an empiricist-inspired account of thought experiments (see Norton Reference Norton1991, Reference Norton1993, Reference Norton1996, Reference Norton2004a, Reference Norton and Hitchcock2004b). It's the kind of account that would appeal to contemporary naturalists. It is elegant and straightforward, and being empiricist, it is very much in the spirit of naturalism. The principal idea is simple: thought experiments are arguments. Being an empiricist, Norton then adds that the premises are (or ought to be) empirically justified and the inference to the conclusion is sanctioned by logic (deductive logic or empirically acceptable inductive logic, liberally understood). I should stress that strictly speaking Norton's account of thought experiments involves only the argument ingredient. As he would say, he is also an empiricist and this motivates his account, but it is possible to reject empiricism and still hold that all thought experiments are (possibly disguised) arguments and nothing more. There are other features that give a thought experiment the air of experimentation, but they play an inessential, heuristic role, or perhaps no role at all. Actual thought experiments may not look like arguments, but that only means the true structure is hidden, but it can, on reconstruction, be revealed. Thought experiments can be good ones or bad, says Norton, depending on how well the premises are justified and how correct the inference to the conclusion is.

A way of seeing an important difference between Norton and myself is to consider first, real experiments. We would agree (as would most people) that a real experiment carries us from a perception (and some possible background propositions) to a proposition. The so-called experimental result may be the culmination of a great deal of theorizing and calculating, but somewhere along the way the experimenter has to look at something, e.g., a thermometer. I hold that a thought experiment has a similar structure. The only difference is that the perception is not sense perception, but rather an intuition, a case of seeing with the mind's eye. In other words, thought experiments (at least some of them) carry us from a perception (and some possible background propositions) to a proposition. Norton would deny this similarity with real experiments and instead claim that a thought experiment carries us from a proposition (and some possible background propositions) to a proposition. It is argument and inference all the way; there is no perception of any kind involved during the thought experiment.

Norton has two important considerations in favor of his deflationary view. One is that it involves only unproblematic ingredients, i.e., empirical observations and empirically acceptable inference patterns. The naturalist-minded take a view such as mine involving intuitions of abstract entities to be highly problematic and the idea of seeing with the mind's eye they regard as hopeless. Second, every thought experiment Norton has so far examined he has managed to reconstruct into the argument pattern he champions. There seem to be no counterexamples. These two considerations make Norton's view very plausible.

Norton has been able to refashion some of my favorites into straightforward derivations. This in itself is an impressive accomplishment, but it is not decisive. Even if every thought experiment could be reconstructed in Norton's argument form, this would not guarantee that this is what thought experiments essentially are. Norton calls it the “elimination thesis.” It says: “Any conclusion reached by a (successful) scientific thought experiment will also be demonstrable by a non-thought-experimental argument” (Reference Norton1991Reference Horowitz and Massey, 131). This claim—bold though it is—may be true without thought experiments actually being arguments, disguised or not. For instance, most of us would say that we make judgements of the relative size of other people based on our perception of their geometric characteristics. Suppose Norton claimed this is not so, and that what we really do is count molecules. He then showed us that every time we judge that A is bigger than B, it turns out that on his (laborious) reconstruction, A has more molecules than B. Even a success rate of 100% in reconstructing judgements of size does not refute the commonsense claim that we judge size by means of visual geometry, not arithmetic.

There is no denying that such reconstructions would be significant. But for Norton to make his case for arguments, mere reconstruction is not enough. He must also make the case that a thought experiment gives some sort of clue to the (hidden) argument; perhaps it's there in a sketchy or embryonic form and can be readily grasped. Norton acknowledges this point. Outlining the generalized logic of argument, he remarks that “we should expect the schema of this logic not to be very complicated, so that they can be used tacitly” (Reference Norton and Hitchcock2004b, 54). Otherwise, there must be something else going on of great epistemic significance. This, of course, is what I think, even if a Norton-type reconstruction is possible in every case.

4. Mathematical Thinking

In mathematics itself, the common view is that pictures and diagrams can be psychologically useful, but they do not constitute a genuine proof. For that we must have a verbal/symbolic proof. Yet there are examples that seriously challenge this. Consider the following simple picture proof of a number theory theorem.

Theorem. $1+2+3+\cdots +n=n^{2}/2+n/2$.

Proof.

Examples such as this last one are getting very close to thought experiments, as I wish to understand them. That is, they are about abstract entities, yet the proof, the evidence, is visual. You might, like Norton, grant that the picture works, but only because there is a traditional proof that we can give of this theorem. That is, we can reconstruct such pictorial evidence with proper proofs, in this case a proof by mathematical induction. Such a proof would, of course, be an argument in Norton's sense (though I greatly doubt it is embryonic in the picture). What I need in order to counter Norton's claims is an example that he can't reconstruct, even in principle. That's what I'll next try to produce. To be precise, I am going to give an example that cannot, in principle, be reconstructed into an argument starting from established empirical or mathematical premises. Somewhere along the line there must be an intuition, a kind of intellectual perception that allows us to arrive at the final result.

5. Refuting the Continuum Hypothesis

Christopher Freiling (Reference Freiling1986) produced a remarkable result that has gone largely unnoticed by philosophers. He refuted the continuum hypothesis. Really refuted the continuum hypothesis? That's hard to say. The standards for success in such a venture are not the normal mathematical ones, since the continuum hypothesis (CH) is independent of the rest of set theory. So any “proof” or “refutation” will be based on considerations outside current mathematics. Because of this, Freiling calls his argument “philosophical.”

Imagine throwing darts at the real line, specifically at the interval [0, 1]. Two darts are thrown and they are independent of one another. The point is to select two random numbers (see Figure 4). As background, we assume ZFC (Zermelo-Frankel set theory with the axiom of choice), which implies that every set can be well ordered (i.e., every subset of a well-ordered set has a first element). If CH is true, then the points on the line can be well-ordered so that for each $q\in [ 0,\,1] $, the set $S_{q}=\{ p\in [ 0,\,1] \thinspace{:}\thinspace p< q\} $ is countable. (Note that < is the well-ordering relation, not the usual less than.) The existence of a well ordering is guaranteed by ZFC; the fact that the set is countable stems from the nature of an ordering of any set that has cardinality ℵ₁. To get a feel for this, imagine the set of natural numbers. It is infinite, but if you pick a number in the ordering, there will be only finitely many numbers earlier—and infinitely many numbers later. Similarly, pick a number in a well-ordered set that is ℵ₁ in size and you will get a set of earlier members that is at most ℵ₀ in size and possibly even finite. Suppose the first throw hits point p and the second hits q. Either $p< q$, or vice versa; we'll assume the first. Thus, $p\in S_{q}$ and S _q is a countable subset of points on the line. Since the two throws were independent, we can say the throw landing on q defines the set S _q “before” the throw that picks out p. The measure of any countable set is 0. So, according to standard probability theory, the probability of landing on a point in S _q is 0. While logically possible, this sort of thing is almost never the case. Yet it will happen every time there is a pair of darts thrown at the real line. Consequently, we should abandon CH, that is, the assumption that the number of points on the line is the first uncountable cardinal number.

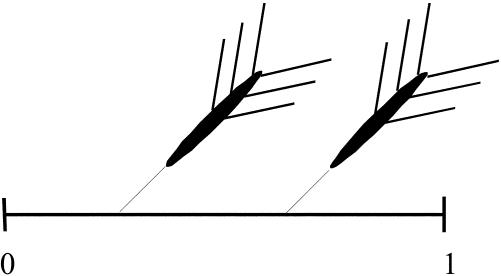
Figure 4. Darts picking out random real numbers.

If the cardinality of the continuum is ℵ₂ or greater, then there is no problem (at least as set out here), since the set of points S _q earlier in the well ordering need not be countable, and so would not automatically lead to a zero probability of hitting a point in it. (Freiling actually goes on to show that there are infinitely many cardinal numbers between ℵ₀ and the continuum.) This line of reasoning cannot be reformulated within standard mathematics as an argument in the strict sense (i.e., a derivation from established premises). Many sketchy arguments that appeal to vague intuitions can be rigorously reconstructed. But this one cannot. If we tried to recast this in purely mathematical terms we would violate established mathematical principles. CH is, after all, demonstrably independent of the rest of standard mathematics.

What morals for thought experiments, if any, can we draw from this startling example? I wish to draw two. The first moral is a negative one concerning Norton's argument view. The second is a positive one supporting the claims I made above about a priori intuitions. To make these morals manifest we need some analysis of what is going on in the thought experiment. We cannot get ∼CH from ZFC alone, but we seem to be able to get it via the thought experiment. What has been added? We seem to have the result $\mathrm{ZFC}\,+X\Rightarrow $ ∼CH. So the relevant question is: What are X and ⇒?

We know from the mere fact that CH is independent from ZFC that X is not any established mathematical principle and ⇒ is not ordinary entailment. There are other possibilities to consider, too. Perhaps X is some existing bit of mathematics and ⇒ is an inductive connection. This seems highly unlikely, since the thought-experimental reasoning doesn't seem like any known inductive style of reasoning such as enumerative induction, or inference to the best explanation, and so on. Yet another possibility is that X is empirical and ⇒ is normal deduction. (Though Norton is an empiricist, his strict claim about thought experiments would only require that X be known independently and not be acquired essentially from the thought experiment.) This, too, seems quite implausible, since picking out individual real numbers with darts is physically impossible, and, moreover, one cannot literally see the symmetry of the two tosses. Idealization and perception with the mind's eye are central to the thought experiment. They are not discovered empirically or in any other way independent from the thought experiment. When we run through the various candidates for X and ⇒, we find that none will plausibly satisfy the Norton criteria.

My contention is quite different from his. I hold that X is a cluster of intuitions acquired in the thought experiment. These are intuitions about (1) the randomness of the darts, hence the randomness of p and q, (2) the independence of p and q, and (3) the symmetry of p and q. These intuitions support a proposition that I will call Freiling's Symmetry Axiom:

Here f is a function defined on the reals with a countable range. Once we have FSA, ⇒ is just ordinary entailment. Here's the theorem and the proof which is carried out in ZFC.

In conclusion, my case for an a priori view of (some) thought experiments rests on three considerations. The first of these concerns facts such as that there is no new empirical evidence playing a role in thought-experimental reasoning. The second concerns the Platonistic framework involving both mathematics and laws of nature, and how nicely thought experiments fit into this framework. The third and final consideration is the refutation of CH which cannot be reconstructed into the argument form that Norton advocates. All in all, this makes for a pretty strong case for a priori knowledge of nature via (some) thought experiments.

Naturally there are worries. For instance, does the CH thought experiment actually work? Only a very small number of mathematicians have actually been persuaded. I'm inclined to think this is because of the very unusual style of argument; nevertheless, it's an important point. Moreover, it's a mathematics example, so the connection to natural science is questionable. Again, the point is conceded. Its real worth is as a model of how intuitions can work. It's also a problem for Norton, regardless, since his claim about thought experiments is that they are all arguments from independently given premises no matter what the subject matter. At the very least the Freiling example deserves further study. It suggests to me, and I hope to others, that the epistemology of thought experiments is very exciting for those of us with a fondness for the old-fashioned rationalists who hankered after a priori knowledge of nature.