1. Introduction

Among other things, causal hypotheses predict how the world will respond to an intervention. How much will we reduce our risk of stroke by switching to a low-fat diet? How will the chances of another terrorist attack change if the U.S. invades Iraq next week? Over the last two decades, philosophers, statisticians, and computer scientists have converged on the fundamental outline of a theory of causal representation and causal inference (Spirtes, Glymour, and Scheines Reference Spirtes, Glymour and Scheines2000; Pearl Reference Pearl2000). Some conditions and assumptions under which reliable inference about the effects of manipulations is possible have been precisely characterized; other conditions and assumptions under which reliable inference about the effects of manipulations is not possible have also been characterized. Different researchers give slightly different accounts of the idea of a manipulation, or an intervention, but all assume that when we intervene ideally to directly set the value of exactly one variable, how we set it does not matter in predicting how the rest of the system will respond. This assumption turns out to be problematic, primarily because it often does matter how one sets the value of a variable one is manipulating. In this paper we explain the nature of the problem and how it affects the theory of causal representation and causal inference. We begin by describing the source of the problem, defined variables. We illustrate how manipulations on defined variables can be ambiguous, and how this ambiguity affects prediction. We describe the theory of causal inference when it is assumed that manipulations are not ambiguous, and we describe how admitting the possibility of ambiguous manipulations affects causal inference. Finally, we illustrate with an example involving both an ambiguous and then an unambiguous manipulation.

2. Defined Variables

In causal modeling, sometimes variables are deliberately introduced as defined functions of others variables. More interestingly, sometimes two or more measured variables are deterministic functions of one another, not deliberately, but because of redundant measurements, or underlying lawlike connections. When all of the variables are measured, the second sort of dependency sometimes shows up as complete statistical dependence, or in the case of linear relationships, a correlation equal to one. A very high correlation of causal variables, or “multicollinearity,” creates problems for data analysis for which there are a variety of more or less ad hoc data analysis procedures. Perhaps the most principled response is to divide the analysis into several subanalyses in none of which are variables deterministically related. But the most interesting case is much more interesting

Consider the following hypothetical example. An observational study leads researchers to hypothesize that high cholesterol levels cause heart disease. They recommend lower-cholesterol diets to prevent heart disease. But, unknown to them, there are two sorts of cholesterol: LDL cholesterol causes heart disease, and HDL cholesterol prevents heart disease. Low-cholesterol diets differ, in the proportions of the two kinds of cholesterol. Consequently, experiments with low-cholesterol regimens can differ considerably in their outcomes.

In such a case the variable identified as causal—total cholesterol—is actually a deterministic function of two underlying factors, one of which is actually causal, the other preventative. The manipulations (diets) are actually manipulations on the underlying factors, but in different proportions. When specification of the value of a variable, such as total cholesterol, underdetermines the values of underlying causal variables, such as LDL cholesterol and HDL cholesterol, we will say that manipulation of that variable is ambiguous. How are such causal relations to be represented, what relationships between causal relations and probability distributions are there in such cases, and how should one conduct a search when the systems under study may, for all one knows, have this sort of hidden structure? These issues seem important to understanding possible reasons for disagreements between observational and experimental studies, nonrepeatability of experimental studies (and not only in medicine—psychology presents many examples), and in understanding the value and limitations of metanalysis.

3. Causal Inference When Manipulations Are Assumed Unambiguous

There are two fundamentally different operations that transform probability distributionsFootnote ¹ into other probability distributions. The first is conditioning, which corresponds roughly to changing a probability distribution in response to finding out more information about the state of the world (or seeing). The second is manipulating, which corresponds roughly to changing a probability distribution in response to changing the state of the world in a specified way (or doing). An important feature of conditioning is that each conditional distribution is completely determined by the joint distribution (except when conditioning on sets of measure 0). In contrast to conditioning, a manipulated probability distribution is not a distribution in a subpopulation of an existing population, but is a distribution in a (possibly hypothetical) population formed by externally forcing a value upon a variable in the system.

In some cases the conditional probability is equal to the manipulated probability, and in other cases the conditional probability is not equal to the manipulated probability. In general, if conditioning on the value of a variable X raises the probability of a given event, manipulating X to the same value may raise, lower, or leave the same the probability of a given event. Similarly if conditioning on a given value of a variable lowers or leaves the probability of a given event the same, the corresponding manipulated probability may be higher, lower, or the same, depending upon the domain.

In contrast to conditioning, the results of manipulating depend upon more than the joint probability distribution. The “more than the joint probability distribution” are causal relationships between variables. Thus discovering the causal relations between variables is a necessary step to correctly inferring the effects of manipulations.

Conditional probabilities are typically of interest in those situations where the values of some variables (e.g.. what bacteria are in your blood stream) are difficult to measure, but the values of other variables (e.g., what your temperature is, whether you have spots on your face) are easy to measure; in that case one can find out about the probability distribution of the value of the variable that is hard to measure by conditioning upon the values of the variables that are easy to measure.

Manipulated distributions are typically of interest in those situations where a decision is to be made, or a plan to be formulated. The possible actions that are considered in decision theory are typically manipulations, and hence the probability distributions that are relevant to the decision are manipulated probabilities, not conditional probabilities (although, as we have noted, in some cases they may be equal).

First, we will consider inference in the case where all manipulations are assumed to be unambiguous. The general setup is described at length in Spirtes et al. Reference Spirtes, Glymour and Scheines2000;we illustrate it with the following example. It is assumed that HDL cholesterol (HDL) causes Disease 1, LDL cholesterol (LDL) causes Disease 2, and that HDL and LDL cause heart disease (HD). This causal structure can be represented by the directed acyclic graph shown in Figure 1.

Figure 1

A directed graph G is the causal graph for a causal system C when there is an edge from A to B in G if and only if A is a direct cause of B relative to C. Note that for a causal system C over a set of variables V there is a unique causal graph for C. We assume that the set of variables in a causal graph is causally sufficient, i.e., if V is the set of variables in the causal graph, that there is no variable L not in V that is a direct cause (relative to $\mathbf{V}\cup \{ L\} $) of two variables in V. However, we do not assume that the set of measured variables is causally sufficient.

In order to make causal inferences from data samples, it is necessary to have some principles that connect causal relations to probability distributions. We make the following assumption that is widely, if often implicitly, assumed in a number of sciences. In order to state the principle the following definitions are needed. In a graph G, X is a parent of Y if and only if G contains an edge $X\rightarrow Y$. Y is a descendant of X in a graph G if and only if either $X=Y$, or there is a directed path from X to Y.

In the example, the causal Markov principle entails that HD is independent of {Disease 1, Disease 2} conditional on {HDL, LDL}, HDL is independent of {LDL, Disease 2}, LDL is independent of {HDL, Disease 1}, Disease 1 is independent of {HD, LDL, Disease 2} conditional on HDL, and Disease 2 is independent of {HD, HDL, Disease 1} conditional on LDL.

The justification (and limitations) of the causal Markov principle is discussed at length in Spirtes et al. Reference Spirtes, Glymour and Scheines2000. One justification is that if each variable is a function of its parents in the causal graph, together with some independent random noise term, then the causal Markov principle is guaranteed to hold.

The causal Markov principle is equivalent to the following factorization principle. X is an ancestor of Y in a graph if there is a directed path from X to Y, or $X=Y$. Parents(G, Y) is the set of parents of Y in graph G. If G is a directed graph over S, and $\mathbf{X}\subseteq \mathbf{S}$, X is an ancestral set of vertices relative to G if and only if every ancestor of X in G is in X. A joint probability distribution (or in the case of continuous variables a joint density function) $P(\mathbf{V}) $ factors according to a directed acyclic graph (DAG) G when for every $\mathbf{X}\subseteq \mathbf{V}$ that is an ancestral set relative to G,

In the example, this entails that

This factorization entails that the entire joint distribution can be specified in the following way (where the numbers have been chosen simply for the purposes of illustration):

1. P(HDL = High) = .2

2. P(LDL = High) = .4

3. P(Disease 1 = Present|HDL = Low) = .2

4. P(Disease 1 = Present|HDL = High) = .9

5. P(Disease 2 = Present|LDL = Low) = .3

6. P(Disease 2 = Present|LDL = High) = .8

1. P(HD = Present|HDL = Low, LDL = Low) = .4

2. P(HD = Present|HDL = High, LDL = Low) = .1

3. P(HD = Present|HDL = Low, LDL = High) = .8

4. P(HD = Present|HDL = High, LDL = High) = .3

We will take a joint manipulation $\{ \mathrm{Man}\,(P_{1}(X_{1})),\,\ldots,\,\mathrm{Man}\,(P_{n}(X_{n})) \} $ for a set of variables $X_{i}\in \mathbf{X}$ as primitive. Intuitively, this represents a randomized experiment where the distribution $P^{\prime }(\mathbf{X}) =\prod_{X_{i}\in \mathbf{X}}P^{\prime }_{i}(X_{i}) $ is forced upon the variables X. We will also write $\{ \mathrm{Man}\,(P^{\prime }_{1}(X_{1})),\,\ldots,\,\mathrm{Man}\,(P^{\prime }_{n}(X_{n})) \} $ as $\mathrm{Man}\,(P^{\prime }(\mathbf{X})) $. We assume X can be manipulated to any distribution over the values of X, even those that have zero probability in the population distribution over X, as long as the members of X are jointly independent in the manipulated distribution. For a set of variables $\mathbf{V}\supseteq \mathbf{X}$, a manipulation $\mathrm{Man}\,(P^{\prime }(\mathbf{X})) $ transforms a distribution $P(\mathbf{V}) $ into a manipulated distribution over V denoted as $P(\mathbf{V}\Vert P^{\prime }(\mathbf{X})) $, where the double bar (Lauritzen Reference Lauritzen, Barndorff-Nielsen, Cox and Kluppenlberg2001) denotes that the manipulation $\mathrm{Man}\,(P^{\prime }(\mathbf{X})) $ has been performed.

For example, suppose that LDL was manipulated so that $P^{\prime }(\mathrm{LDL}\,=\mathrm{Low}\,) =.5$ and $P^{\prime }(\mathrm{LDL}\,=\mathrm{High}\,) =.5$, while simultaneously HDL was manipulated so that $P^{\prime }(\mathrm{HDL}\,=\mathrm{Low}\,) =.5$ and $P^{\prime }(\mathrm{HDL}\,=\mathrm{High}\,) =.5$. This could be done for each person by flipping two independent fair coins, one determining the value to be given to LDL and the other determining the value to be given to HDL. Consider then $P(\mathrm{HD}\,\vert \mathrm{Disease}\,\,1) $ in the hypothetical population after the two manipulations. It is denoted in this notation by $P(\mathrm{HD}\,\vert \mathrm{Disease}\,\,1\Vert P^{\prime }(\mathrm{HDL}\,) \times P^{\prime }(\mathrm{LDL}\,)) $, where the term to the left of the double bar represents the quantity of interest, and the term to the right of the double bar specifies the joint distribution that the manipulated variables have been assigned.

A DAG G represents a causal system among a set of variables V when $P^{\prime }(\mathbf{V}) $ factors according to G, and for every manipulation $\mathrm{Man}\,(P^{\prime }(\mathbf{X})) $ of any subset X of V

For example, if HD is manipulated to have the value Present, i.e., $P^{\prime }(\mathrm{HD}\,=\mathrm{Present}\,) =1$, then the joint manipulated distribution is:

and

Note that the distribution of HDL after manipulation of HD to Present, i.e., $P(\mathrm{HDL}\,\Vert P^{\prime }(\mathrm{HD}\,=\mathrm{Present}\,)) $ is not equal to the probability of HDL conditional on HD = Present, i.e., $P(\mathrm{HDL}\,\vert \mathrm{HD}\,=\mathrm{Present}\,) $.

The causal Markov principle allows some very limited causal inferences to be made. For example, suppose {X, Y} is causally sufficient. A causal graph that contains no edge between X and Y entails that X is independent of Y, and hence is not compatible with any distribution in which X and Y are dependent. However, if it is not known whether {X, Y} is causally sufficient, then assuming just the causal Markov principle, no (point) conclusions about the effects of a manipulation can be reliably drawn. For example, suppose the causal relationship between X and Y is known to be linear, and the correlation between X and Y is r. Let the linear coefficient that describes the effect of X on Y be c (i.e., a unit change in X produces a change of c in Y). Then regardless of the value of r, for any specified c there is a causal model in which the correlation between X and Y is r, and the effect of X on Y is c. That is, the observed statistical relation (r) places no constraints at all on the causal relation (c). This negative result generalizes the case where more than two variables are measured. Even when {X, Y} is known to be causally sufficient, the causal Markov principle does not suffice to produce a unique prediction about the mean effect of manipulating X on Y no matter what variables are measured, as long as X and Y are dependent.

We will make a second assumption that is commonly, if implicitly, made in the statistical literature.

Applying the causal faithfulness principle to the DAG in Figure 1 entails that the only conditional independence relations that hold in the population are the ones entailed by the causal Markov principle: i.e., that HD is independent of {Disease 1, Disease 2} conditional on {HDL, LDL}, HDL is independent of {LDL, Disease 2}, LDL is independent of {HDL, Disease 1}, Disease 1 is independent of {HD, LDL, Disease 2} conditional on HDL, and Disease 2 is independent of {HD, HDL, Disease 1} conditional on LDL.

The justification for the causal faithfulness principle (as well as descriptions of cases where it should not be assumed) is discussed at length in Spirtes et al. Reference Spirtes, Glymour and Scheines2000. One justification is that for a variety of parametric families, the causal faithfulness principle is only violated for a set of parameters that have measure 0 (with respect to Lebesgue measure, and hence with respect to any of the usual priors placed over the parameters of the model).

Given the causal Markov principle and the causal faithfulness principle, there are algorithms that in the large sample limit reliably infer some of the causal relations among the random variables, and reliably predict the effects of some manipulations, even if it is not known whether the measured variables are causally sufficient. For those causal relations that cannot be inferred, and those effects of manipulations that cannot be predicted, the algorithms will return “can't tell.” See Spirtes et al. Reference Spirtes, Glymour and Scheines2000 for details. Examples of inferences that can be reliably made, and inferences that cannot be reliably made, are described in Section 4.

4. Causal Inference When Manipulations May Be Ambiguous

We now consider the case where it is not known whether a manipulation is ambiguous or not. Consider what kinds of dependency structures can emerge in a few hypothetical examples. (More details and proofs are available in Spirtes and Scheines Reference Spirtes and Scheines2003.)

4.1. Example 1

Consider an extension of the hypothetical Example 1, shown in Figure 2, in which the concentration of total cholesterol is defined in terms of the concentrations of high-density lipids and low-density lipids. This is indicated in the figure by the bold-faced arrows from HDL and LDL to TC. The other arrows indicate causal relationships. Suppose that high levels of HDL tend to prevent HD, while high levels of LDL tend to cause HD. We have the following parameters for Example 1 (again chosen for the purpose of illustration).

1. HDL = Low, LDL = Low → TC = Low

2. HDL = Low, LDL = High → TC = Medium

3. HDL = High, LDL = Low → TC = Medium

4. HDL = High, LDL = High → TC = High

1. P(HDL = High) = .2

2. P(LDL = High) = .4

3. P(Disease 1 = Present|HDL = Low) = .2

4. P(Disease 1 = Present|HDL = High) = .9

5. P(Disease 2 = Present|LDL = Low) = .3

6. P(Disease 2 = Present|LDL = High) = .8

1. P(HD = Present|HDL = Low, LDL = Low) = .4

2. = P(HD = Present|TC = Low)

3. P(HD = Present|HDL = High, LDL = Low) = .1

4. P(HD = Present|HDL = Low, LDL = High) = .8

5. P(HD = Present|HDL = High, LDL = High) = .3

6. = P(HD = Present|TC = High)

Manipulation of TC is really a manipulation of HDL and LDL. However, even after an exact level of TC is specified as the target of a manipulation, there are different possible manipulations of HDL and LDL compatible with that target. For example, if a manipulation sets TC to Medium, then this could be produced by manipulating HDL to Low and LDL to High, or by manipulating HDL to High and LDL to Low. Thus, even after the manipulation of TC is completely specified (e.g., to Medium), the effect of the manipulation on HD is indeterminate (i.e., if the manipulation is HDL to High and LDL to Low, then after the manipulation $P(\mathrm{HD}\,) $ is .1, but if the manipulation is HDL to Low and HDL to High, then after the manipulation $P(\mathrm{HD}\,) $ is .8). Hence a manipulation of TC to Medium might either lower the probability of HD (compared to the population rate), or it might raise the probability of HD. It is quite plausible that, in many instances, someone performing a manipulation upon TC would not know about the existence of the underlying variables HDL and LDL, and would not know that the manipulation they performed was ambiguous with respect to underlying variables. For example, manipulation of TC could be produced by the administration of several different drugs that affect HDL and LDL in different ways, and produce different effects on HD.

Figure 2

What is the correct answer to the question, “What is the effect of manipulating TC to Medium on HD”? Suppose that we manipulate TC to Medium, i.e., $P^{\prime }(\mathrm{TC}\,=\mathrm{Medium}\,) =1$. Without further information, the most informative answer that could be given is to give the entire range of effects of manipulating TC to Medium (i.e., either $P(\mathrm{HD}\,\Vert P^{\prime }(\mathrm{TC}\,)) =.8$ or $P(\mathrm{HD}\,\Vert P^{\prime }(\mathrm{TC}\,)) =.1$). Another possible answer is to simply output “can't tell” because the answer is indeterminate from the information given. A third, but misleading, answer would be to output one of the many possible answers (e.g., $P(\mathrm{HD}\,\Vert P^{\prime }(\mathrm{TC}\,)) =.1$). This answer is misleading as long as it contains no indication that this is merely one of a set of possible different answers, and an actual manipulation of TC to Medium might lead to a completely different result. Note that it is the third, misleading, kind of answer that would be produced by performing a randomized clinical trial on TC; there would be nothing in the trial to indicate that the results of the trial depended crucially upon details of how the manipulation was done. A fourth possibility is open to Bayesians: put a prior distribution down on the underlying manipulations, and then calculate the posterior probability of the effect of a manipulation.

In the examples described below, we take the second alternative, and output “can't tell” in some instances. However, there can be a variety of reasons that the effects of a manipulation are underdetermined by the evidence (e.g., the possibility of latent variables or the possibility of an ambiguous manipulation) and when “can't tell” is output, we make no attempt here to determine if it is possible to find the reason for the underdetermination.

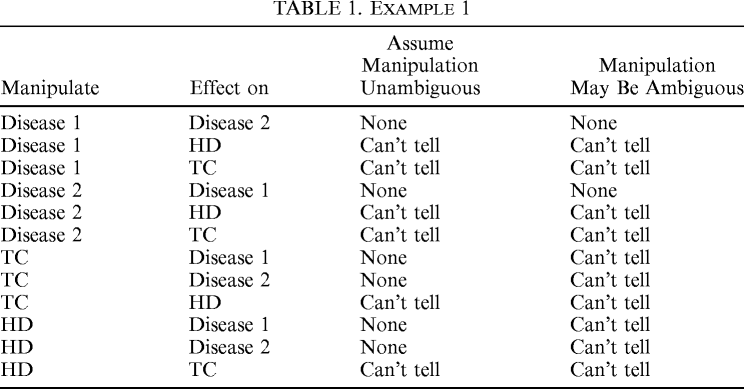
Suppose now that Disease 1, Disease 2, TC, and HD are the measured variables, and we assume the causal Markov and faithfulness principles (extended to graphs with definitional links), but allow that there may be hidden common causes. What reliable (pointwise consistent)Footnote ² inferences can be drawn from samples of the distribution described in Example 1? We will contrast two cases: the case where it is assumed that all manipulations are unambiguous manipulations of underlying variables and the case where the possibility that a manipulation may be ambiguous is allowed. The general effect of weakening the assumption of no ambiguous manipulations is to introduce more “can't tell” entries. The results for Example 1 are given in Table 1. Proofs of these results are given in Spirtes and Scheines Reference Spirtes and Scheines2003.

Table 1. Example 1

Manipulate	Effect on	Assume Manipulation Unambiguous	Manipulation May Be Ambiguous
Disease 1	Disease 2	None	None
Disease 1	HD	Can't tell	Can't tell
Disease 1	TC	Can't tell	Can't tell
Disease 2	Disease 1	None	None
Disease 2	HD	Can't tell	Can't tell
Disease 2	TC	Can't tell	Can't tell
TC	Disease 1	None	Can't tell
TC	Disease 2	None	Can't tell
TC	HD	Can't tell	Can't tell
HD	Disease 1	None	Can't tell
HD	Disease 2	None	Can't tell
HD	TC	Can't tell	Can't tell

4.2. Example 2

We will now consider what happens when the example is changed slightly. In Example 2 (results given in Table 2), suppose that the effect of HDL and LDL on the probability of HD actually is completely determined by TC. Example 2 is the same as Example 1, except that we have changed the distribution of HD in the following way:

1. P(HD = Present|HDL = Low, LDL = Low) =

2. P(HD = Present|TC = Low) = .1

1. P(HD = Present|HDL = High, LDL = Low) =

2. P(HD = Present|HDL = Low, LDL = High) =

3. P(HD = Present|TC = Medium) = .3

1. P(HD = Present|HDL = High, LDL = High) =

2. P(HD = Present|TC = High) = .8

In this case, while manipulating TC to Medium represents several different possible manipulations of the underlying variables HDL and LDL, each of the different manipulations of HDL and LDL compatible with manipulating TC to Medium produces the same effect on HD (i.e., $P(\mathrm{HD}\,\Vert P^{\prime }(\mathrm{TC}\,)) $ equals

prior to manipulation, which is .3). In this case we say that the effect of manipulating TC on HDL is determinate. (Note that the effect of manipulating TC on Disease 1 is not determinate, because it depends upon how the manipulation of TC is done. So manipulating a variable may have determinate effects on some variables, but not on others.)

Table 2. Example 2

Manipulate	Effect on	Assume Manipulation Unambiguous	Manipulation May Be Ambiguous
Disease 1	Disease 2	None	None
Disease 1	HD	Can't tell	Can't tell
Disease 1	TC	Can't tell	Can't tell
Disease 2	Disease 1	None	None
Disease 2	HD	Can't tell	Can't tell
Disease 2	TC	Can't tell	Can't tell
TC	Disease 1	None	Can't tell
TC	Disease 2	None	Can't tell
TC	HD	= P(HD|TC)	= P(HD|TC)
HD	Disease 1	None	None
HD	Disease 2	None	None
HD	TC	None	None

Interestingly, the causal faithfulness assumption actually entails that the effect of TC on HD is not determinate. This is because if the effect of manipulating TC on HD is determinate, then LDL and HDL are independent of HD conditional on TC, which is not entailed by the structure of the causal graph, but instead holds only for certain values of the parameters, i.e., those values for which

Hence, in these cases we make a modified version of the causal faithfulness principle, which allows for the possibility of just these kinds of determinate manipulations.

What reliable (pointwise consistent) inferences can be drawn from samples of the distribution described in Example 2? Because there are conditional independence relations that hold in Example 2 that do not hold in Example 1, more pointwise consistent estimates of manipulated quantities can be made under the assumption that manipulations may be ambiguous, than could be made in the previous example.