1. Introduction
It is widely accepted in philosophy of science that having multiple lines of evidence and multiple independent lines of evidence for a hypothesis, model, or parameter value is preferable and in some cases necessary. Cosmologists have taken this adage to heart. In the last 3 decades, they have relied on various types of astrophysical and cosmological observations, as well as terrestrial experiments to produce evidence constraining the cosmological concordance model, ΛCDM.
The relevance of these terrestrial experiments to cosmology is not always obvious. For example, there are experiments underway that use experimental methods from high-energy particle physics to investigate dark matter (see below) or technology from atomic physics to investigate dark energy (see, e.g., Hamilton et al. Reference Hamilton, Jaffe, Haslinger, Simmons, Müller and Khoury2015). Meanwhile, all available astrophysical and cosmological evidence supporting dark matter indicates that, if constituted by a (class of) particle(s), it is unlike any other particle studied by high-energy particle physics so far. Dark energy fares worse: although there is extensive evidence from cosmological observations for its effect on the expansion of the universe, its other properties are a complete mystery. Current theorizing about dark matter and dark energy, aside from their respective effects on cosmological and astrophysical scales, excels in the negative: many possibilities have been excluded, none have been supported by empirical evidence.
Given that it is widely accepted that dark matter and dark energy are fundamentally different from any particle or entity that high-energy physics or atomic physics have studied in the past, it is puzzling that methods from these respective disciplines are employed to learn more about their properties. How can these experiments be justified? How do particle physicists argue that their experimental methods will be effective in probing dark matter, despite dark matter not being constituted by any particles in the current standard model of particle physics?
In this article, my primary goal is to answer this question of justification: I expose a new logic to structure the justification for a particular method choice. This logic differs from the logic that is often assumed, in that it is method driven rather than target driven. I argue that the method-driven logic plays a crucial role when knowledge of the target is minimal, as is the case for dark matter or dark energy. Exposing the method-driven logic brings to the forefront some questions about the availability of robustness arguments and methodological pluralism more generally. A secondary goal of the article is to begin unearthing these questions in the context of dark matter searches.
I begin by providing necessary terminological clarification as groundwork (sec. 2). I then explain the common target-driven logic of method choice, and I contrast it with the less familiar method-driven logic in section 3. Section 4 contains a discussion of contemporary dark matter research as a detailed illustration of the latter. Before concluding, I draw implications for triangulation arguments in section 5.
2. Methods, Target Systems, and Their Features
In order to get a better handle on this method-driven logic, it will be useful to take a step back and determine what constitutes a particular method. By ‘method’, I do not mean anything akin to a ‘unified scientific method’ like Mill’s methods or the logical positivists’ hypothetico-deductivism.Footnote 1 ‘Method’ here refers to something much more specific: a method is any activity that generates empirical evidence, where that activity can be applied in various research contexts and to various target systems. A method should be describable such that it is transferable across target systems and specific enough such that any misapplication can be identified.
The use of the term ‘activity’ in the definition is purposefully vague: methods span a wide range of scientific practices, across disciplines and scales. Often, they will appear as (sets of) protocols in the ‘method’ sections of scientific research papers. Perhaps the most useful characterization here comes in the form of some paradigmatic examples: a method can be anything from radiometric dating for fossils to using particle colliders and assorted data processing to search for new elementary particles or from using optical telescopes to observe sunspots and the moons of Jupiter to randomized controlled clinical trials in medicine. All these activities or clusters of activities consist of a protocol that uses some empirical input to produce data and ultimately a line of evidence for a particular phenomenon.Footnote 2 ‘Conducting an experiment on a target system’ does not qualify as a specific method, however, since it is too general to specify in what contexts this method can reliably relate to a target and in what contexts it cannot.
Regardless of the specifics of the protocol, a method should be applicable in various research contexts and to various target systems.Footnote 3 A method should be such that it is not tied down to one specific phenomenon or research context, even if the method in practice appears to be tied to a unique event. For example, while cosmologists can observe only one cosmic microwave background (CMB), their methods—using specific types of telescopes or radio receivers, among others—used in the mapping of the CMB are transferable to other targets.
The goal of the types of methods under consideration here, finally, is to generate empirical data that can be used as evidence for hypotheses about the target system. Whether that is good evidence will depend on how the method was applied to the target system and how the subsequent data processing happened—‘using a scientific method’ does not imply success.
A second term in need of clarification is that of a ‘target system’. The target system is that system in the world about which a scientist’s research aims to generate knowledge. The scientist’s goal is to explore and model the features and causal interactions of the target system.Footnote 4
At first sight, this definition may strike one as circular: wouldn’t scientists only know what they are investigating after they have finished the investigation? For example, didn’t researchers at CERN only know what the 125 GeV Higgs boson was after they had discovered it? The circularity is only apparent. It is true that some definition of the target system needs to be accepted before an investigation of the target system can commence, just like particle physics already had a hypothetical description of the Higgs boson and its role in the standard model before the discovery. That description or local theory can be minimal and independent of the new features that a particular experiment is investigating. Nonetheless, it still plays a crucial role in the justification of method choice, as I show below.
To clarify the cluster of concepts, consider the following examples. A current high-profile set of experiments in physics attempts to measure the neutron lifetime (see Yue et al. Reference Yue, Dewey, Gilliam, Greene, Laptev, Nico, Snow and Wietfeldt2013; Pattie et al. Reference Pattie2018). The target system is the neutron as described by nuclear physics. This description includes an estimate of the neutron mass, size, and magnetic moment, as well as the feature of nuclear β-decay, the process that determines the mean lifetime of the neutron τn (the precise value of τn affects the helium-to-hydrogen ratio generated by Big Bang nucleosynthesis in the early universe, and it might help constrain extensions to the standard model of particle physics—hence its importance). Two types of methods are used to measure τn: one traps neutrons in a gravito-magnetic ‘bottle’ for an extended period of time and counts the decay products after various time intervals. Another method uses a focused neutron beam and traps and counts decay products along the beam line.
Mitchell and Gronenborn (Reference Mitchell and Gronenborn2017) provide an example from biology. Current molecular biology aims to determine the folding structure of various proteins. In this case, the target systems are the various proteins, and their feature of interest is their folding structure. Mitchell and Gronenborn describe how that folding structure can be measured through nuclear magnetic resonance (NMR) or X-ray crystallography and in what ways the two methods are independent from one another—despite sharing some common assumptions about the protein’s primary structure, the sequence of amino acids.
3. Choosing the Right Method
How is a particular method choice justified? In other words, given a particular target, how do scientists argue that a (set of) method(s) will be effective when trying to learn more about the target and its features? Or, when multiple methods are available and scientists can only run a limited number of experiments, how do they argue that one (set of) method(s) will be more effective when trying to learn more about the target and its features than another (set)?
I propose that two types of logic of method choice can be at play in answering these questions: a target-driven logic and a method-driven logic. (The use of ‘logic’ here merely indicates that there is a general schema that can be codified and applied broadly.) Both logics can be used to justify why a particular method can be used to construct a new line of evidence for a particular feature of a target system. The former, more common logic relies primarily on preexisting knowledge of the target to justify the method choice. The latter, less familiar logic is prevalent in situations in which this preexisting knowledge is sparse and can therefore not be relied on in the justification. For the purpose of this article, I assume that the methods under consideration are well developed and that their common sources of error are generally known, as this is the case for the dark matter experiments discussed in section 4.
3.1. Target-Driven Method Choice
Very often, method choice follows a target-driven logic, where the justification relies on previous knowledge of the target as the prime differentiating factor between methods. “Knowledge” here indicates that the target and its various features are described by a well-established, empirically confirmed scientific theory. Target-driven method choice adheres to the following structure:Footnote 5
| Given a target system T, with known features A and B. |
| Method 1 uses feature A of possible targets to uncover potential new feature X. |
| Method 2 uses feature B of possible targets to uncover potential new feature X. |
| Method 3 uses feature C of possible targets to uncover potential new feature X. |
| The preferred methods to uncover a potential new feature X of T will be methods 1 and 2, while method 3 remains out of consideration (for now). |
In short, when a given method adheres to a feature that the target is known to have, it will be preferred over methods that adhere to features either the target does not have or for which it is unclear whether the target has them. Of course, since the accepted theory about the target can evolve, the specifics that are substituted for ‘method 1’ or ‘feature A’ can also evolve over time—hence the bracketed caveat in the conclusion.
To see this abstract logic in action, consider again the two examples from the previous section. First, the neutron lifetime experiments:
| Given the neutron, which decays through nuclear β-decay, which has mass and a magnetic moment, and which has a radius of approximately
|
| Bottle experiments trap ultra-cold neutrons through their mass and magnetic moment and count the remaining neutrons that have not yet undergone β-decay at various times t to derive τn from the exponential decay function
|
| Beam experiments use a focused beam of cold neutrons that moves continuously through a proton trap and count the number of neutrons N in a well-defined volume of the beam, as well as the rate of neutron decay
|
| Optical microscopy uses a minimal resolution of the order of 10−7m to magnify optical features of small objects. |
| Bottle and beam experiments can both be used to measure τn. Optical microscopy uses length scales much larger than the size of a neutron and can therefore not be used to determine an individual neutron’s properties. |
Although the example of the optical microscope is contrived, my hope is that it conveys the structure of target-driven logic here: methods are selected on the basis of preexisting knowledge of the target and on whether the methods in question employ features the target is known to have.
Along with neutron lifetime experiments, the target-driven logic of method choice also applies to the various protein-folding structure experiments:
| Given proteins, which are made up of atoms that have a nucleus and an electron cloud. |
| NMR experiments use the magnetic moment of atomic nuclei to determine the nuclei’s and therefore the atoms’ positions. |
| X-ray crystallography uses the diffraction of X-rays by electron clouds to determine the electron clouds’ density and therefore the atoms’ positions. |
| NMR and X-ray crystallography can both be used to determine the folding structure of proteins. |
Again, particular methods are chosen on the basis of preexisting knowledge of the target system. It is the preexisting knowledge of the target that determines whether an established method can reasonably be expected to be effective for investigating a new feature X.
3.2. Method-Driven Method Choice
The above target-driven method choice may be a familiar one, but it is not the only logic of method choice. Scientists are sometimes confronted with target systems where the definition is so thin that the target-driven logic cannot be employed to justify particular experimental explorations of new features of the target system. For example, in case of dark energy, its only commonly accepted features are that it is a majority contribution to the current energy density of the universe and that it causes the universe’s expansion to accelerate. In the words of the Dark Energy Task Force, “Although there is currently conclusive observational evidence for the existence of dark energy, we know very little about its basic properties. It is not at present possible, even with the latest results from ground and space observations, to determine whether a cosmological constant, a dynamical fluid, or a modification of general relativity is the correct explanation. We cannot yet even say whether dark energy evolves with time” (Albrecht et al. Reference Albrecht2006, 1). Without a well-developed, empirically confirmed theory of dark energy that describes its basic properties, it is impossible to apply the target-driven logic explained in the previous section. There are not enough known features to latch onto to uncover new features of the target system.
While the target-driven logic cannot be employed, it is not the case that scientists are left completely in the dark and cannot justify their choice of methods. Rather, they employ a different logic: a method-driven logic. This method-driven logic has a similar setup as the target-driven logic, namely,
| Given a target system T. |
| Method 1 uses feature A of possible targets to uncover new feature X. |
| Method 2 uses feature B of possible targets to uncover new feature X. |
| Method 3 uses feature C of possible targets to uncover new feature X. |
However, unlike for the target-driven logic, it is now not stated from the beginning that the target T has features A, B, or C that are used by methods 1, 2, or 3 to uncover a new feature X. Thus, the next step in the method-driven logic needs to be different:
| If T has feature A, method 1 can be used to uncover new feature X. |
| If T has feature B, method 2 can be used to uncover new feature X. |
| If T has feature C, method 3 can be used to uncover new feature X. |
With this different setup compared to the method-driven logic, another premise is needed to complete the justification of the method choice: Which of the antecedent clauses in the above set of premises can plausibly be triggered?
| It is possible and plausible that T has features A and B, but it is either impossible or implausible (but possible) that T has feature C. |
| The preferred methods to uncover a potential new feature X will be methods 1 and 2, while method 3 remains out of consideration (for now). |
In the method-driven logic, the justification of the method choice primarily appeals to what features the target would need to have in order for various established methods to be effective in probing its features. Rather than appealing to an established theory of the target, the justification primarily appeals to preexisting knowledge of the available methods. This guides what assumptions about the target need to be made for that method to produce reliable evidence about various features of the target.
Using the method-driven logic in a responsible manner requires that these assumptions are plausible (and at minimum possible), but it does not require sufficient empirical evidence to accept the assumption as ‘known’ or empirically well confirmed. It is at this point that the preexisting knowledge of the target system T still plays a role in the context of the method-driven logic. In the most ideal situation, the preexisting knowledge allows scientists to construct a plausibility argument for T having a specific feature, turning the assumptions from an ‘allowed’ to an ‘educated’ guess, at best. But at minimum, the preexisting knowledge of T delineates what additional assumptions about the target are possible and which ones are already excluded. For example, dark energy cannot be any known form of matter, since it counteracts gravity. Similarly, dark matter cannot be constituted entirely by standard model particles. Any method that uses those respective features is therefore already excluded for dark energy or dark matter research.
One important qualification to the discussion is in order here.Footnote 6 So far, I have introduced the distinction between the target- and the method-driven logic as a dichotomy. However, the two logics lie on a continuous spectrum. It is possible to reformulate the general structure of the target-driven logic such that it is almost identical with the method-driven logic, except for the final premise. Rather than it being possible or plausible that the target has a particular assumed feature, this premise would read that there is very high confidence that the target has a particular assumed feature (which I indicated as ‘known’ in sec. 3.1). The cases I discuss here all lie on one or another extreme of the spectrum—this allows me to showcase important implications of the method-driven logic for the interpretation of the results (see sec. 5).
Finally, let me also briefly touch on the relation between my distinction here and the literature on exploratory experimentation. Exploratory experiments are commonly defined as contrasting with confirmatory experiments: while confirmatory experiments aim to test a particular hypothesis, exploratory experiments do not (see, e.g., Franklin Reference Franklin2005). It is sometimes argued that they are particularly attractive for discovering new phenomena whenever theoretical frameworks are in turmoil or underdeveloped—something I have also indicated as a reason to use a method-driven logic.
I take my distinction between target- and method-driven logic to be orthogonal to the confirmatory/exploratory experimentation distinction, however. I follow Karaca (Reference Karaca2017) and Colaço (Reference Colaço2018) in that the theory of the target system and the method plays a role in confirmatory and exploratory experiments alike. Colaço (Reference Colaço2018, 2) explicitly identifies “determin[ing] that the system is an appropriate candidate for the application of a technique” as one role for theory in the context of exploratory experiments. My discussion here focuses specifically on how this task is fulfilled in light of that available theory, whereas the difference between confirmatory and exploratory experiments focuses on the further aim of the resulting experiment (confirmatory experiments aim to test the theory of the target, whereas exploratory experiments do not). It is therefore entirely possible for exploratory experiments to be target driven (I take Colaço’s cases from brain research to be examples of this) or method driven (the dark matter example discussed below might qualify as such).
Before discussing the implications of the use of the method-driven logic, more needs to be said to elucidate this method-driven logic itself. What does it mean to ‘make assumptions plausible’ without having empirical evidence for them? What can scientists conclude, if anything at all, if their experiments using methods 1, 2, or both lead to a positive result? And what if the contrary is the case? To answer these and other questions about the method-driven logic further, I now turn toward contemporary dark matter research.
4. Method-Driven Choices in Dark Matter Research
The method-driven logic underlies several research projects in cosmology, including different searches for dark matter particles. I first explain why dark matter was introduced and how the reasons for its introduction define dark matter as a target. This definition is thin, however, and provides very little in terms of properties of dark matter to use as in the target-driven logic above. Instead, particle physicists have justified dark matter searches with a method-driven logic.
4.1. Defining the Target System of Dark Matter
An abundance of cosmological and astrophysical evidence supports the presence of an additional, nonbaryonic matter component contributing to the energy density of the universe. The first observations in support of dark matter date back to the 1930s, to Zwicky’s observations of velocity dispersion in the Coma Cluster (Zwicky Reference Zwicky2009). In the 1980s, Rubin’s observations of flat galaxy rotation curves became the first widely accepted source of evidence for dark matter (Rubin and Ford Reference Rubin and Ford1970; Rubin, Ford, and Rubin Reference Rubin, Ford and Rubin1973). Other evidence comes from lensing events like the Bullet Cluster (Clowe et al. Reference Clowe, Bradac, Gonzalez, Markevitch, Randall, Jones and Zaritsky2006), weak lensing surveys, theories of cosmological structure formation (White and Rees Reference White and Rees1978), and the CMB anisotropy power spectrum (Planck Collaboration Reference Collaboration2020).
In the course of the past 4 decades, it has become abundantly clear that astrophysical and cosmological evidence only gets scientists so far in learning more about dark matter. The available evidence supports dark matter’s gravitational effects and puts the dark matter contribution to the current energy density of the universe at approximately 26%. It also constrains what the particle properties of the constituents of dark matter can be: dark matter is nonbaryonic (i.e., it is not constituted by particles in the standard model of particle physics), its coupling to standard model particles through the strong or electromagnetic interaction is very limited or nonexisting, and its self-interaction cross-section is limited. It is this small set of properties that defines dark matter as a target: a form of nonbaryonic matter that acts gravitationally and where there are strong upper limits on various possible couplings to standard model particles, as well as on its self-interaction cross-section.
That definition is remarkably thin. For all that the cosmological and astrophysical evidence reveals about what features dark matter cannot have, it does not indicate much about what the particle properties of dark matter are. It does not reveal what the coupling mechanism of dark matter particles to standard model physics is. Worse, it does not even reveal whether there is such a coupling in the first place.
Nonetheless, the thin definition plays a crucial role in dark matter research for three reasons. First, the different dark matter experiments described below all share this common definition of the target. This makes it at least possible that, despite their different search strategies and further assumptions about dark matter, all experiments are probing the same target (although I raise some issues with this in sec. 5). Relatedly, the thin definition constrains the space of possibilities for any further theorizing about dark matter: any more elaborate model for dark matter particles better adhere to the properties above, if it wants to claim to describe dark matter. Models proposing standard model neutrinos cannot describe dark matter, for example, since cosmological structure formation excludes neutrinos as a credible dark matter candidate. Finally, the definition of dark matter provides some resources for formulating possibility and plausibility arguments that can help guide the method-driven research.
Within the constraints from cosmology and astrophysics, a variety of experiments have been proposed and executed in the search for dark matter. These range from searches at accelerators like the Large Hadron Collider (LHC), to looking for nuclear recoils of dark matter particles with heavy atomic nuclei, to finding annihilation products in astrophysical observations. The candidate particle favored by most so far is the weakly interacting massive particle (WIMP), a (class of) particle(s) with a mass of the order of O(100 GeV) coupling through the weak interaction.Footnote 7 This because of the so-called WIMP miracle: including WIMPs in a standard Big Bang nucleosynthesis scenario would automatically obtain the dark matter abundance derived from observations of the CMB and structure formation. WIMPs are therefore considered plausible dark matter candidates (although failure to turn up any positive detection result has recently started to put pressure on the WIMP hypothesis). Regardless of what happens to the WIMP hypothesis in the future, it is useful to examine in detail how physicists have tried to find WIMPs.
For present purposes, I focus on two sets of experiments: current production searches at the LHC and the early days of direct detection experiments (see also fig. 1). Both approaches have had to make additional assumptions about the particle properties of dark matter without having empirical evidence for them. The most basic assumption is depicted in figure 1: dark matter particles (χ) must couple to standard model particles (f) through some mediator (dashed line). How that coupling is modeled and exploited varies between the different experimental approaches.
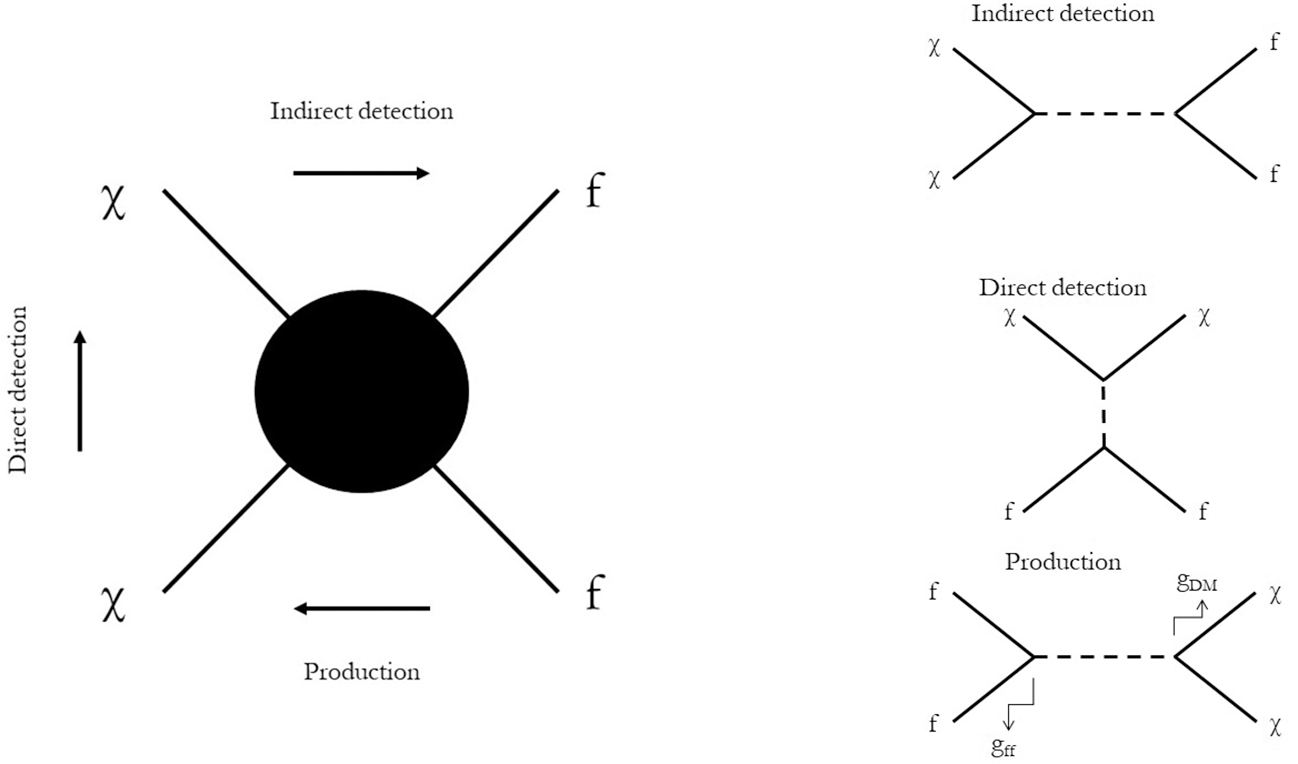
Figure 1. Overview of three types of searches for dark matter particles (represented by χ), all based on interactions with standard model particles (represented by f). The three Feynman diagrams on the right are specifications of the diagram on the left, where the arrows on the left diagram indicate the direction in which the diagram should be read. On the right, the dashed lines represent the mediator, and gff and g DM are the coupling strengths at the standard model and dark matter vertex, respectively.
4.2. Production Experiments
Production experiments, mostly conducted at the LHC, aim to produce dark matter through collisions of standard model particles in an accelerator.Footnote 8 The hope is that dark matter will be the result of another successful LHC search to uncover previously unobserved physics, similar to the discovery of the Higgs boson, and the general methodology behind it is very similar. The LHC looks for elementary particles by colliding proton beams at very high energy levels. These collisions generate approximately 600 million collisions per second, of which only a small fraction are recorded for further analysis.Footnote 9 After going through trigger systems, data reductions, and background reductions, new physics presents itself as a detected excess signal, or as excess missing energy, above the background. A discovery is claimed if the excess can be calculated as having a high enough statistical significance and if all known sources of systematic error have been excluded to a satisfactory degree.
Two types of dark matter searches are conducted at the LHC. The first type searches for particles described by specific extensions of the standard model, for example, supersymmetry (SUSY). The hope is that there is a supersymmetric particle that also constitutes dark matter. If this assumption is correct, then SUSY particles, and therefore dark matter, can be found at the LHC (specifically by searching for a final state signature that is rich in jets and that has a significant amount of missing transverse energy).
The second type of search is more general and less dependent on proposed extensions of the standard model of particle physics. Rather than focusing on constraining the properties of the dark matter particle itself, these searches focus on the mediator for the coupling of the ‘dark sector’ (the collection of all dark matter particles to standard model particles). One possible mediator is the Higgs boson: current constraints on the branching ratios of the different Higgs decay channels still allow for a significant ‘invisible Higgs’ sector, leaving room for possible couplings to the dark sector.
These so-called model-independent searches are not tied to the actual production of dark matter—they could equally well detect the mediator particle on the basis of its decay into the standard model particles.Footnote 10 The decay products of the mediator can be either (1) missing energy, if it decays into dark matter, or (2) unaccounted for but detected standard model particles. The goal of the model-independent searches is primarily to discover an unknown mediator to physics beyond the standard model and to exploit this new gateway to subsequently search for dark matter candidates. One benefit of this approach is that it potentially mitigates the worry about distinguishing dark matter from neutrinos, another particle species presenting itself as missing energy.
Production experiments thus instantiate the method-driven logic as follows.
| Given dark matter as described and defined in section 4.1. |
| Accelerator experiments use the coupling of new particle species to standard model particles to detect new particles or couplings in the form of excess events above the known background. |
| If dark matter is made up of SUSY particles, or it couples to standard model particles through a mediator (invisible Higgs or otherwise), accelerator experiments can be used to search for signatures of dark matter particles or dark matter mediators. |
| It is possible and plausible that dark matter is made up of SUSY particles or that it couples to standard model particles through a mediator (invisible Higgs or otherwise). |
| Accelerator experiments can be used to search for signatures of dark matter particles or dark matter mediators. |
Important here is that there is no independent evidence for SUSY particles constituting dark matter, or even for the coupling between dark matter and standard model particles. Again, given the cosmological and astrophysical evidence for dark matter, it is entirely possible that dark matter does not couple to standard model particles at all. Accelerator experiments would be useless in the search for dark matter in that case: they require some nongravitational coupling to standard model particles to detect a signature. Luckily, the cosmological and astrophysical evidence does not exclude nongravitational coupling either. Independent arguments in favor of SUSY or invisible Higgs physics then provide a plausibility argument in favor of the assumptions that are required to make accelerator experiments effective dark matter probes.
4.3. Direct Detection Experiments
My brief discussion of production experiments provided a first example of how the method-driven logic can be implemented in practice. They are not the sole type of search currently under way; direct detection experiments are another. The early days of direct detection experiments also provide a nice example of scientific practice appealing to the method-driven logic.
Direct detection searches like LUX, CoGeNT, CRESST, or CDMS look for signals of dark matter particles that scatter off heavy nuclei like xenon. The basic principle behind the experiments is the same as that behind neutrino searches: a scattering event results in recoil energy being deposited, which can be transformed into a detectable signal. Similarly, direct detection searches look for evidence of a scattering event of a dark matter particle off a heavy nucleus. According to the WIMP hypothesis, that scattering happens through the weak interaction. Should a WIMP scatter off one of the xenon nuclei in the detector, it would deposit some recoil energy that can be detected using scintillators and photomultiplier tubes, for example.
Even from this brief summary, it becomes clear that the justification for direct detection experiments is following a method-driven logic. The justification runs as follows:
| Given dark matter as described and defined in section 4.1. |
| Neutrino-detection type experiments use the weak coupling of (extraterrestrial) particles to detect their presence by their deposited energy in scattering events of those particles from atomic nuclei. |
| If dark matter particles are weakly interacting, have a mass of the order of 100 GeV, and exist stably in the galactic halo, detectors similar to those used for neutrino detection can be used to search for signatures of dark matter particles existing in the halo of the Milky Way. |
| It is plausible that dark matter particles are weakly interacting, have a mass of the order of 100 GeV, and exist stably in the galactic halo. |
| Detectors similar to those used for neutrino detection can be used to search for signatures of dark matter particles existing in the halo of the Milky Way. |
To fully explore the justification for the various premises and the argument structure as a whole, let me return to the early days of direct detection experiments, in the late 1980s. Of particular interest here is a review article by Primack, Seckel, and Sadoulet (Reference Primack, Seckel and Sadoulet1988) that summarizes arguments for the effectiveness of direct detection experiments.
First, the authors use astrophysical and cosmological evidence to establish that dark matter exists and that it must be nonbaryonic (the first premise above). The authors appeal to flat galaxy rotation curves as evidence for dark matter.Footnote 11 The nonbaryonic nature of dark matter is then established by first appealing to galaxy formation theories and Big Bang nucleosynthesis constraints on the baryonic energy density component of the universe and then comparing this limit to (admittedly very weak) constraints on the total energy density of the universe.
The second premise, on neutrino detection techniques, is not explicitly addressed in the review paper. Instead, the authors refer to previous papers on neutrino detectors by Goodman and Witten (Reference Goodman and Witten1985) and Wasserman (Reference Wasserman1986). The two papers both first describe neutrino detectors and subsequently argue that those neutrino detectors might be effective for dark matter as well. For example, Goodman and Witten write that “dark galactic halos may be clouds of elementary particles so weakly interacting or so few and massive that they are not conspicuous. … Recently, Drukier and Stodolsky proposed a new way of detecting solar and reactor neutrinos. The idea is to exploit elastic neutral-current scattering of nuclei by neutrinos. … The principle of such a detector has already been demonstrated. In this paper, we will calculate the sensitivity of the detector … to various dark-matter candidates” (Reference Goodman and Witten1985, 3059). Similarly, Wasserman writes that “recently, a new type of neutrino detector, which relies on the idea that even small neutrino energy losses (
![]() ) in cold material (
) in cold material (
![]() ) with a small specific heat could produce measurable temperature changes, has been proposed. … The purpose of this paper is to examine the possibility that such a detector can be used to observe heavy neutral fermions (
) with a small specific heat could produce measurable temperature changes, has been proposed. … The purpose of this paper is to examine the possibility that such a detector can be used to observe heavy neutral fermions (
![]() ) in the Galaxy. Such particles, it has been suggested, could be a substantial component of the cosmological missing mass, and would be expected to condense gravitationally, in particular, into galactic halos” (Reference Wasserman1986, 2071). Both papers start out from the established effectiveness of neutrino detection techniques. They then immediately move on to the third premise: determining what would be required to make these neutrino detectors effective dark matter probes.
) in the Galaxy. Such particles, it has been suggested, could be a substantial component of the cosmological missing mass, and would be expected to condense gravitationally, in particular, into galactic halos” (Reference Wasserman1986, 2071). Both papers start out from the established effectiveness of neutrino detection techniques. They then immediately move on to the third premise: determining what would be required to make these neutrino detectors effective dark matter probes.
This also becomes the prime focus of Primack et al., and in their investigation of what properties dark matter would need to have, they immediately formulate arguments for the plausibility of these assumptions. The authors start out by listing various dark matter candidates. The list includes axions and light neutrinos, but the main focus lies on WIMPs.Footnote 12 Listed WIMP candidates include the lightest supersymmetric particle and the now-abandoned cosmion proposal.Footnote 13 Setting up terrestrial detection experiments requires fine-grained assumptions about dark matter: “In order to evaluate the proposed WIMP detection techniques, one must know the relevant cross sections [for the interaction of WIMPs with ordinary matter]” (Primack et al. Reference Primack, Seckel and Sadoulet1988, 762). The required detail is made plausible by appealing to possible cosmological scenarios that determine the dark matter abundance. The authors consider two:
1. The dark matter abundance today is determined by freeze-out as per the WIMP miracle. In this scenario, dark matter is formed thermally in the early universe, just like baryonic matter, during Big Bang nucleosynthesis. In order for the correct abundance of dark matter to be generated, stringent constraints are placed on the allowed cross-section.
2. The dark matter abundance today is determined by a so-called “initial asymmetry” (763). This scenario posits the dark matter-abundance as an initial condition for the evolution of the universe, which means that “only a lower bound may be placed on the cross sections from requiring that annihilation be efficient enough to eliminate the minority species” (763).
The main purpose of both arguments is to investigate what assumptions about dark matter can plausibly be made such that direct detection experiments can be set up. Primack et al. conclude from the cross-section determination that “the exciting possibility exists of detecting WIMPs in the laboratory” (768).
The remaining sections of the paper focus on details of the experimental setup. The discussion shifts from justifying the use of neutrino detection techniques for dark matter to concerns about background mitigation and signal detection optimization. This discussion shows that making assumptions about the target system in order to justify why a particular method might detect it does not exclude the usual experimental process of then minimizing systematic errors or maximizing the signal-to-noise ratio.
4.4. Taking Stock
Let me take stock. I have explored the particle physicists’ approach to dark matter experiments, and I have argued that these follow a method-driven (rather than a target-driven) logic for the justification of their effectiveness as dark matter searches. Specifically, physicists make additional assumptions about the particle properties of dark matter, most notably about its nongravitational interactions (illustrated in fig. 1). If dark matter has those properties, the various experiments could plausibly detect it.
What are the implications of relying on a method-driven logic? A first consequence is that the interpretation of the results is muddled. Suppose a direct detection experiment detects nuclear recoil by a dark matter particle from the galactic halo. That evidence could support two things: the fact that such a detected dark matter particle exists, as well as the assumptions that were required to justify the method choice in the first place. However, the detection can only provide evidence for the assumption that was required to get the evidence going in the first place, if it is plausible that no other unknown features of the target or the method could give rise to the signal. A second consequence is that the method-driven logic raises some problems for the appeal to common motivations for methodological pluralism in the context of dark matter searches.
5. Implications: Questions about Methodological Pluralism
In the previous section, I described two types of dark matter searches, each generating a separate line of evidence. This pursuit of multiple lines of evidence is common in scientific practice, and for good reason. One type of argument concludes that it is better to have multiple lines of evidence than not. For one, increasing the empirical basis for an inductive inference is usually taken to strengthen the conclusion of that inference. Increasing the pool of evidence can also resolve local underdetermination problems and related issues in theory choice (see, e.g., Laudan and Leplin Reference Laudan and Leplin1991; Stanford Reference Stanford and Zalta2017)—even if breaking so-called global underdetermination remains a lost cause. Another motivation comes from the literature on robustness.
Specifically for measurement results, Woodward (Reference Woodward2006) defines “measurement robustness” as a concurrence of measurement results for the determination of the same quantity through different measurement procedures. A robust empirical result is a result that has been found to be invariant for at least a range of different measurement processes and conditions, where a failure of invariance for certain other conditions or processes can be explained (Wimsatt Reference Wimsatt2007).Footnote 14 Perrin’s determination of Avogadro’s number is a classic example of such a robust result. If different experimental procedures, with independent sources of systematic error, all deliver the same value for a given parameter, the general argument goes, it is highly unlikely that the agreement is the result of different systematic errors all lining up, rather than that the result is tracking an actual physical effect. For example, in the neutron lifetime example from section 3.1, the bottle and beam methods come with different sources of systematic error. Thus, if their outcomes agree, it is likely that the determined value of the neutron lifetime is accurate.Footnote 15
Although this is not always explicitly stated, a crucial condition for measurement robustness is that the same parameter or quantity is being measured by the different experiments. This is where the definition of a target system comes in: the definition of the target system remains fixed under the employment of different methods. It provides, in other words, a common core that might underlie multiple methods attempting to probe the same target. Without this agreement on the common core, it is not obvious that methods that detect different phenomena are still probing the same target system and that measurement robustness arguments therefore apply. While the common core does not guarantee that the same target is probed, I submit it is a necessary condition that this common core can be identified. Of course, the fact that the definition of the target system needs to remain fixed across various methods being applied to it does not mean that it has to remain fixed over time. Rather, the common core can evolve, but that evolution needs to be shared across the different methods applied.
A second set of arguments concludes that there are contexts in which methodological pluralism is not merely desirable insofar as possible but in fact necessary to gain understanding of a complex target system and its workings in different environments. This idea of methodological integration is quite common in the life sciences. For example, O’Malley and Soyer (Reference O’Malley and Soyer2012) describe how systems biology can be understood in terms of methodological integration, and O’Malley (Reference O’Malley2013) argues that various difficulties in phylogeny originate in a failure to apply multiple methods. Mitchell and Gronenborn (Reference Mitchell and Gronenborn2017) use the development of protein science over the last 5 decades as an exemplar of how the hope for one experimental strategy to replace all others is futile. Kincaid (Reference Kincaid1990, Reference Kincaid1997) formulates similar views with respect to both molecular biology and the social sciences. Finally, Currie (Reference Currie2018) describes the use of multiple methods as an integral aspect of developing an evidential basis for historical sciences.
Both motivations are at play in the dark matter searches. On the one hand, any result claiming to have found dark matter will only be accepted if multiple experiments belonging to multiple types of searches are able to find it. This is in part why the DAMA/Libra result, after several decades of claiming the sole positive result in dark matter searches, remains controversial in the larger physics world (see Castelvecchi [Reference Castelvecchi2018] for a recent update). On the other hand, different types of dark matter searches need to be employed to search as much area of parameter space as possible: production experiments are typically sensitive in a lower mass range than direct detection experiments, where the deposited energy in the scattering interaction would be too small to pick up on. Direct detection and production experiments (along with the indirect detection experiments that were not discussed here) are therefore sometimes referred to as being “complementary.”Footnote 16
However, the use of the method-driven logic introduces a complication, both for measurement robustness and for methodological pluralism more broadly in the context of dark matter searches. To draw out this concern, let me recapitulate and bring together different points of the discussion so far. Recall that production and direct detection experiments require different assumptions about dark matter for the justification of their potential effectiveness. Moreover, the two types of searches are clearly two distinct methodologies to search for dark matter particles. In case of a positive detection, the two types of experiments could try to pick up the same signal, giving the basis for a typical measurement robustness argument. In the meantime, while such an uncontroversial positive result remains elusive, the two types can rule out complementary regions of parameter space. So where lies the problem for measurement robustness and methodological pluralism?
The situation is not quite as straightforward: complementarity comes at a cost. Direct detection experiments, unlike model-independent production experiments, can only search for one type of dark matter candidate at a time, with already specified coupling constants. Thus, direct detection experiments only constrain two free parameters: the interaction cross-section σ and the dark matter mass m χ. Model-independent production experiments constrain four free parameters: the mass of the mediator particle m mediator, the dark matter mass m χ, the coupling at the standard model-vertex gff, and the coupling at the dark matter vertex g DM (see fig. 1). The interaction cross-section σ depends on all four of these parameters. To make results from production and direct detection experiments comparable—specifically, to translate production experiment results into constraints on m χ σ-parameter space—requires making assumptions about two of the four free parameters, usually the coupling strengths gff and g DM. These assumptions are again based on theoretical plausibility arguments, but they do pose a significant weakness for constraints from production experiments on specific dark matter models, since the translation of the production experiment results can be very sensitive to these assumed parameter values.Footnote 17
6. Conclusion
I have proposed a new logic for justifying scientific method choice, which I called a method-driven logic. This logic begins from a common core that describes a target system but then looks at the method for guidance as to what further assumptions about a target system might need to be made in order for a method to be effective to discover new features of the target system. I submit that this logic is an interesting deviation from the more common target-driven logic.
The method-driven logic helps to understand why certain cosmological experiments have a chance at being successful, despite not being conducted on cosmological scales. It also raises an important puzzle for classic measurement robustness arguments in contexts in which the method-driven logic is employed: because of the use of the method-driven logic, robustness arguments are not always readily available. This is because of the different assumptions that are required to start the experiment in the first place.
The puzzle for robustness and complementarity points toward some further puzzles: How should results, positive and negative, from method-driven experiments be interpreted in the first place? What do they provide evidence for (with regard to both the positive result and the assumed feature of the target)? These questions only come to the forefront, once the crucial role of the method-driven logic is recognized.



