TRANSMISSION CYCLE

For the basic transmission cycle, the definitive hosts are dogs with sheep being the intermediate hosts (Fig. 1). However, a number of other intermediate hosts, such as goats, cattle, pigs horses or camels, can readily be substituted into the cycle, or form their own specific cycle, and these alternative hosts are important in some localities (Thompson & McManus, 2002). Man is normally represented as an accidental intermediate host and, because humans rarely are involved in transmission, can be considered an ecologically aberrant host. The transition between different groups depends on the transmission dynamics of the system. For example, the transition between non-infected and infected dogs depends on the frequency of feeding offal to dogs, the prevalence of infection in sheep and the age of the sheep being fed to the dogs. These all contribute to the infection pressure to dogs. Likewise the transition from infected to non-infected dogs depends on the life expectancy of the parasite, host immunity and the frequency of anthelmintic treatment. If the prevalence and abundance of infection is constant (i.e. in a steady state) then the transition rate between non-infected dogs to infected dogs will equal the rate at which infected dogs lose their infection. The rate at which sheep become infected will depend upon the prevalence in dogs, the intensity of infection in dogs, the contact rate between dogs and sheep and the level of host immunity in sheep, which all contribute to the infection pressure to sheep. Once sheep are infected, they generally remain infected for life, although a proportion of cysts will not become fertile (such as when they calcify).

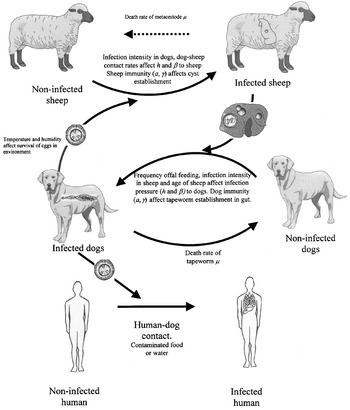
Fig. 1. Transmission of Echinococcus granulosus between dogs, sheep and man. © Institute of Parasitology, University of Zurich.

IMMUNITY

Immunity in both definitive and intermediate hosts is an important consideration in the transmission dynamics of E. granulosus. Immunity will partially or fully prevent infection or superinfection of the host with the parasite. Protective immunity may be stimulated by exposure to the parasite and may have a different significance in the definitive or intermediate host.

Early studies by Sweatman et al. (1963) suggested that a large number of eggs were required to stimulate immunity in sheep to the metacestode. The experimental design consisted of oral challenge infection 9 months after the initial infection and the sheep were not exposed to E. granulosus eggs between the two challenges. Therefore, any immunity stimulated by ingestion of a small number of eggs could have been lost in the intervening 9 months. Supportive evidence for an absence of immunity due to natural challenge in the intermediate host has been reported in a number of studies. These studies demonstrated a linear increase in hydatid cysts with the age of the sheep (Roberts et al. 1986; Gemmell, 1990; Ming et al. 1992a; Cabrera et al. 1995; Torgerson, Williams & Abo-Shehada, 1998; Dueger & Gilman, 2001; Torgerson et al. 2003a). Likewise in the definitive host, experimental studies have suggested that it required repeated exposure on several occasions to stimulate protective immunity in the dog (Gemmell, Lawson & Roberts, 1986). However, these latter experimental infections were terminated by anthelmintics after a relatively short time. Heath & Lawrence (1991) showed that dogs could develop a degree of immunity to a large infection of protoscoleces (88000), and after an initial release of eggs, the egg production was completely suppressed. However, the worms were not rejected and remained as immature worms in the dog's small intestine. There is ample experimental evidence that immune responses occur in other hosts to adult tapeworms, but the mechanisms are complex and the effectiveness is variable (reviewed by Andreassen, 1997). For example, in experimental dogs it has been demonstrated that there is significant cellular and humoral immune responses to protoscolex or adult worm antigens 35 days after a primary infection with E. granulosus (Deplazes et al. 1994). However, it was suggested that there were few if any density-dependent constraints on transmission in the life cycle (reviewed by Gemmell, 1990) and a field study from China (Ming et al. 1992b) supported the idea that protective immunity in the dog was poor. A consequent theoretical conclusion from this is that the parasite is able to maintain itself with a basic reproductive ratio (R₀) of just above 1. However, more recent data from Tunisia and Kazakhstan (Lahmar, Kilani & Torgerson, 2001; Torgerson et al. 2003b) provides substantial evidence for significant definitive host immunity in regions of high infection pressure as young dogs have significantly higher worm burdens then old dogs. Likewise young foxes are more heavily parasitised with E. multilocularis then old foxes (Hofer et al. 2000). Thus definitive host immunity may provide a density-dependent constraint and result in a higher reproductive ratio for E. granulosus than previously thought possible.

Despite the apparent lack of naturally-induced protective immunity against the metacestode in the intermediate host, a highly effective vaccine has been developed for sheep, goats and cattle that induces protective immunity against challenge (Heath & Lawrence, 1996; Lightowlers et al. 1996; Lightowlers & Gauci, 2001). The host protective antigens appear to be extracellular proteins associated with the oncosphere surface membrane (Holcman et al. unpublished). Thus, the vaccine stimulates protection against invading oncospheres but has little effect against established cysts. In view of this, the role of naturally-induced immunity in the intermediate host may also need to be reassessed. It is possible that the increase in parasites with age is an artefact caused by a wide variance in the development times of individual hydatid cysts following a high exposure to eggs as lambs. Heath & Lawrence (1981) showed that serum from sheep infected orally, and which harboured 100–300 cysts, was lethal to oncospheres in vitro even 12 months after infection. However, these levels of infection are rare in the field, and as Sweatman et al. (1963) found, only heavy infections induced protection that lasted for 9 months Also, Dueger & Gilman (2001) found that the mean number of small, but normal hydatid cysts did not decrease with age. This suggested that either cysts obtained early in life failed to grow or new infections occur throughout life.

BIOTIC POTENTIAL

The biotic potential is an important biological parameter of a parasite. In the case of taeniid parasites the biotic potential will influence the extent that it can contaminate the environment with infective stages (i.e. eggs) which will influence the dynamics of transmission to the intermediate host as well as the risk of human infection. E. granulosus has a relatively low biotic potential in the definitive host particularly when compared to other taeniid species. Thus a single adult parasite will produce on average approximately 42 eggs per day compared to 38 000 for Taenia hydatigena (estimates from Gemmell et al. 1986, 1987). However, this is compensated to a certain extent by the intensity of infection. In highly endemic areas dogs may be infected with hundreds or even thousands of parasites on average. For example, in Tunisia infected dogs had a mean intensity of infection of 2543 E. granulosus compared to a mean intensity of 1·52 T. hydatigena (Lahmar et al. 2001). Thus a dog heavily infected with E. granulosus has the potential to cause widespread contamination of the environment. Gemmell et al. (1986) and Gemmell, Lawson & Roberts (1987) suggested that the number of eggs that appear to be able to transform into viable cysts is somewhat lower than other taeniid parasites with only about 0·33% of E. granulosus eggs developing into cysts compared to 7·1% of eggs of T. hydatigena. However, a much higher proportion of eggs of E. granulosus developed into cysts in primary challenges undertaken in lambs by Sweatman et al. (1963). Similarly, Yong, Heath & Van Knapen (1984) suggest a higher proportion of eggs are able to develop into cysts. Groups of five lambs were given 10, 100 or 1000 freshly collected eggs of either E. granulosus, T. hydatigena or T. ovis. The percentage of eggs developing into live or dead cysts was estimated at necropsy 1 year later. For E. granulosus, the respective percentages were 48%, 43% and 32% and all cysts were viable. For T. hydatigena the figures were 8%, 6% and 4% and most but not all cysts were dead. For T. ovis the figures were 30%, 4% and 5% and, like T. hydatigena, many of the cysts were dead. The discrepancies in these results may be due to the fact that no consistent method to assess egg viability prior to experimental infection of sheep was used between the different trials.

Wachira, MacPherson & Gathuma (1991) reported that the number of eggs per proglottid in E. granulosus appears to be unaffected by the worm burdens of the dog. Likewise the rate of development is independent of worm numbers (Gemmell et al. 1986). However, Heath & Lawrence (1991) found that one dog which harboured 3000 mature worms was passing 45 000 eggs each day in the faeces, while another which harboured 13 000 mature worms was passing only 15 000 eggs per day. Thus there appears to be conflicting evidence on a crowding effect in the definitive host.

The viability of the metacestodes will also affect the parasite's biotic potential. Studies have shown that 74% of T. hydatigena cysticerci will develop into viable adult tapeworms compared to only 5% of E. granulosus protoscoleces (Gemmell et al. 1986, 1987). However, a single fertile hydatid cyst may have hundreds or thousand of protoscoleces compared to the single protoscolex in a T. hydatigena cysticercus.

PREPATENT AND PATENT PERIODS

The time which the parasite takes to reach potency in the definitive or intermediate host and the parasite's life-span are both important parameters when considering the transmission dynamics. The prepatent period in the dog has been established for a long time and is generally considered to be approximately 6 weeks. It is for this reason that 6 weeks is often chosen as the period between anthelmintic treatments of dogs. However, some strains of E. granulosus have been shown to have a prepatent period in dogs of less than 6 weeks (Thompson & McManus, 2001). The life-span of the parasite in the definitive host is less well-defined and has been estimated both through mathematical modelling (Roberts et al. 1986; Ming et al. 1992b; Torgerson et al. 2003b) and through experimental infections of dogs (Aminzhanov, 1976; Sweatman & Williams 1963). These studies have suggested that the patent period is between 6 and 22 months with the most likely value at about 10–12 months.

The latent period for the metacestode is considerably longer. Gemmell et al. (1986) suggested that it took an average of 6·5 years before protoscoleces were present in hydatid cysts in sheep, although in a few animals they appeared as early as two years after infection. However, this is somewhat longer than the figure suggested by other workers and a figure of 1·5–2 years seems more likely (Sweatman & Williams, 1963; Aminzhanov, 1976; Heath & Lawrence, 1978; Harris et al. 1980). The shorter time to cyst maturity is supported by field studies such as Dueger & Gilman (2001) who found over one third of all cysts in three-year-old sheep to be fertile and over 68% in sheep in excess of 6 years. The number of brood capsules, and the number of protoscoleces within brood capsules tend to continue to increase during the life of an infective cyst. Thus, old sheep assume a greater importance in the transmission than young sheep.

DISPERSAL AND LONGEVITY IN THE ENVIRONMENT

Most of the eggs (91%) are released from the proglottids before they pass out of the hosts (Wachira et al. 1991). From the faecal pat the eggs can directly contaminate herbage which is then available to grazing animals. Intermediate hosts such as sheep do not normally eat dog faeces so some emigration of eggs from the faecal pat is likely to occur. Experimental evidence of this has been provided by the grazing of sentinal sheep in paddocks that were adjacent to dog kennels but to which dogs had no access (Lawson & Gemmell, 1983). Local dispersal is likely to be by insects such as blowflies (Lawson & Gemmell, 1990), birds or other wildlife. The potential for transmission of taeniid eggs over considerable distances has been demonstrated by the finding of T. hydatigena cysts in a population of feral sheep on a remote Scottish island despite the complete absence of any dogs on the island. The nearest definitive hosts were some 40 km distant. Thus, it is hypothesised that eggs were dispersed by mechanical means such as birds (Torgerson et al. 1995).

An example of the infectious ability of an infected dog was obtained near the end of the hydatid eradication programme in New Zealand. A sheep farm in 1991 had 7000 sheep, and hydatid cysts were reported when old sheep were sent to the abattoir. An examination of randomly-selected sheep from each age class revealed that only 4-year-old and older sheep were infected: 53% of 1850 sheep had hydatid cysts. Viable cysts were found in 33% of the total, and 16% of the total sheep had cysts that contained protoscoleces. There were no infected sheep found on surrounding farms, so the infections were attributed to a dog that had been fed infected offal but had escaped for a short time the highly-regimented 6-weekly treatment with praziquantel of all farm dogs in New Zealand (1975–91). In another example from a farm in Xinjiang Province of China, 30 lambs were necropsied. The animals were shown to have been exposed to two natural field infections: one occurred at 6 months of age, and another about 12 months of age. Necropsy was at 18 months of age. Fifty percent were infected with 1–50 cysts. This farm attempts to dose all dogs monthly to protect against cestode infections, but clearly the procedure is not fully effective (Heath, D. D., unpublished data). In another area of Xinjiang Province of China, a 3-year study of the epidemiology of echinococcosis showed that infections were associated with late autumn-early winter return of flocks to their winter quarters, and again in late winter, early spring. This was assumed to be when guard dogs, who live with their flocks, would pass eggs from fresh infections obtained as a result of the early winter slaughter of old sheep that might not survive the winter (Heath, Jensen & Lightowlers, 2002).

Once in the environment eggs will remain viable for a variable time depending on local conditions of temperature and humidity. At 4 °C the life-span of the eggs for a variety of taeniid species is 300 days or more (reviewed by Lawson & Gemmell, 1983). Increasing the temperature gradually decreases the life-span of the eggs to 2–14 day at 37–39 °C. Eggs are much more tolerant to extreme cold, but storage of eggs at −70 °C for 24 hours appears to be lethal (Colli & Williams, 1972). Humidity is also important. The maximum life-span is only achieved when eggs are kept in cool conditions with a high relative humidity. Lower humidity decreased the lifespan dramatically.

Transmission to man is either directly or indirectly from dogs. Close association with dogs is an obvious important factor for transmission. When dogs were experimentally infected with T. hydatigena large numbers of eggs could be recovered from the perianal region and under the tail (Deplazes & Eckert, 1988). Although 85% of eggs recovered were from these locations, the other 15% were recovered from other anatomical locations such as the nose, flank and paws (Fig. 2). With such widespread contamination of the dog's coat shown to occur with experimental infection of tapeworms, the risk for transmission to man from the intimate contact with infected pet dogs must be considered high. Nevertheless a number of studies have suggested that dog ownership is not always a risk factor for human echinococcosis (Carmona et al. 1998; Bai et al. 2002; Wang et al. 2001; Dowling, Abo-Shehada & Torgerson, 2000). Therefore indirect transmission may be important in some circumstances. Reports from Uruguay, Jordan, Argentina and Kyrgystan have all indicated that human infection with E. granulosus may be associated with the water supply (Carmona et al. 1998; Dowling et al. 2000; Larrieu et al. 2002; Torgerson et al. 2003c). In addition, because of the mechanisms for egg dispersal already discussed, contamination of vegetables and fruit with eggs of Echinococcus either directly or indirectly may also be important (Carmona et al. 1998). Several analyses of risk factors for human infection have been carried out in western Sichuan where echinococcosis is intensely endemic. In a single variate analysis old subjects were more likely to have cysts than young subjects. The nomadic lifestyle, keeping sheep or yaks, playing with dogs and not protecting food from flies were all associated with an increased risk of CE. Re-running the analysis as a multiple logistic analysis suggested that only age, raising livestock and playing with dogs were important risk factors (Wang et al. 2001). Hygiene factors such as washing hands before eating, had no effect in protecting against infection. There would appear to be a level of environmental contamination with eggs above which the risk of infection is very high, and cannot be avoided by hygiene measures. It would not be surprising if serological tests on humans from these environments showed that most were serologically positive to oncosphere antigens, indicating regular ingestion of Echinococcus spp. eggs.

Fig. 2. Taeniid eggs recovered per cm2 from a dog experimentally infected with Taenia hydatigena. © Institute of Parasitology, University of Zurich.

MATHEMATICAL MODELS OF THE TRANSMISSION DYNAMICS

Mathematical models have been developed to describe the transmission dynamics of E. granulosus (Roberts et al. 1986, 1987; Torgerson et al. 2002). Ideally, mathematical models should be able to describe and predict the epidemiology of these parasites. Furthermore, for them to be useful and widely applicable, they should be simple to understand, but robust under a variety of different systems. To be of practical use models should be able to predict future events given the model and basic information. For example, models could be used to predict the outcomes of intervention such as periodic anthelmintic prophylaxis in dogs as part of a disease control programme. Assuming a model is based on theoretical ideas of parasite–host relationships, they can be tested using actual data and departures from the theoretical model can be used to define better models and thus gain a better insight into the parasite biology. To formulate a working model of the transmission dynamics of E. granulosus, a knowledge of the parasite's biology together with observational studies of its epidemiology are required.

AGE INTENSITY AND AGE PREVALENCE MODELS

Roberts et al. (1986) derived a model that described the variation of parasite prevalence with the age of the host. From these models important information about the transmission of the parasite (such as the infection pressure) in the different hosts in the life cycle can be deduced. A set of 4 differential equations was proposed to model the variation in the proportion of hosts infected but immune, infected but not immune, not infected and immune and not infected and not immune (see equations A1–A4 in Roberts et al. 1986). From these equations it was possible to derive general equations for the variation of the prevalence of infection with age in sheep and dogs, and the variation of abundance with age in sheep. Thus, the of prevalence of infection, p(t) with E. granulosus in the absence of protective immunity, was reported to vary with age (t) of the dog according to the equation:

where β=the infection pressure (in terms of insults per unit time) and μ=the rate at which hosts lose their parasite. The asymptotic prevalence was reported as:

Roberts et al. (1986) also reported that in the presence of protective immunity the asymptotic prevalence is:

where γ=rate of loss of immunity; δ=death rate of host; α=probability of immunity on exposure in infected dogs; and α₀=probability of immunity on exposure in non infected dogs. Thus, when immunity is present the asymptotic prevalence is always reduced by a factor less than 1. When this mathematical relationship is plotted it produces Fig. 3 (top, the exact shape of the curve depends upon the values assigned to the parameters μ and β). The curve does have a number of properties. As the age increases so does the prevalence, eventually reaching an asymptote when there is no further increase. The affect of immunity, if described by equation (2) is to decrease the asymptote, but old dogs still have a greater prevalence than young dogs. The difference in prevalence between old and young animals will depend upon the infection pressure. If the infection pressure is high the asymptotic prevalence will be reached more quickly than if it is low. Data has been fitted to this equation on two occasions. Data from Australasia gave a good fit when only the data from young dogs was used (Roberts et al. 1986). Likewise, Ming et al. (1992b) fitted data from China, which again gave a good fit with young dogs.

Fig. 3. Variation in prevalence of E. granulosus and the proportion of dogs susceptible to infection with age. Top: 0·44 infections each year and the absence of immunity on exposure. Middle: infection pressure of 2 infections per year with an 80% probability of immunity on exposure and 20% probability of loss of immunity each year. Bottom: 0·44 infection every year with a 0·30 probability of immunity on exposure and 0·02 probability of loss of immunity (MLE estimates of farm dogs from Kazakhstan). All simulations assume a parasite life expectancy of about 1 year.

Similarly, in the intermediate host, the variation in prevalence in the absence of host immunity was proposed as:

where β is the infection pressure in infectious insults per year. The variation of abundance m(t) with age t was defined as:

where h is the infection pressure in parasites per year, a is an immunity parameter which depends on the rate of acquisition of immunity (also ah in equation (3)=αβ; Roberts et al. 1987) which in the absence of protective host immunity becomes:

Likewise the proportion of animals susceptible to infection S(t) varies with age t according to the equation:

Torgerson et al. (2003b) derived a more general equation for the variation of abundance m(t) with age t of the definitive host:

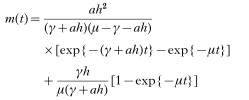
This equation was derived from the assumptions made by Roberts et al. (1986) and hence can be applicable to both hosts in the life cycle.

By substituting the Taylor expansion:

into (7) it can be shown that as μ→0, this becomes equation (4). Also from (7) it can be shown that in the absence of immunity (a=0) then this simplifies to:

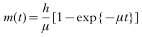
Thus in the definitive host the variation of abundance with age in the absence of immunity is only dependent on the prevailing infection pressure and the death rate (or life expectancy) of the parasite. In the intermediate host the parasite is long lived. By substituting (8) into (9) and setting μ=0 the variation of abundance with age becomes equation (5).

It can be shown that more general equations can be derived for the variation of prevalence with age and abundance with age in both life cycle hosts. By summing equation A2 in Roberts et al. (1986), from 0 to infinity, the rate of change of the proportion Y of animals infected, but immune to further infection is:

where α is the probability of immunity on exposure and β is the infection pressure in infectious insults per year. Likewise, by summing equation A1 in Roberts et al. (1986) from 0 to infinity, the variation in the proportion X infected but not immune can be shown to be:

Because ah=αβ (see Roberts et al. 1986, 1987) the variation of the proportion of animals that are susceptible with age is also:

Although equation for the variation of prevalence P(t) with age can be derived analytically from these equations (as P=X+Y), the solution is not straightforward and takes the form of:

where K₁, K₂, K₃ and K₄ are relationships between α, β, γ and μ.

In the absence of protective host immunity (α=0) the solution can be shown to be identical to equation (1). In addition if the death rate of the parasite is 0 (i.e. μ=0), then this becomes equation (3) reported by Roberts et al. (1986). An important property of equation (13) is that it predicts that when there is significant host immunity it allows for a lower prevalence in old animals compared to young animals. Equation (2) only allows for a decrease in the asymptotic prevalence. This can easily be shown using the ODE function of PopTools software (CSIRO Australia) which uses a 4^th order Runge–Kutta alogarithm to integrate the series of differential equations (equations 10–12) (Fig. 3, middle and bottom). From these it can be clearly seen that if immunity is present it is highly likely that the prevalence in the older age classes will be lower than in young dogs. In the absence of immunity the prevalence approaches an asymptote with the older dogs having the highest prevalence. The importance of this result is that the presence of herd immunity can be demonstrated not only from the collection of abundance data (as in Torgerson et al. 2003b) but also in prevalence data. The latter is more easily collected by using techniques such as coproantigen whereas abundance data needs either necropsy data or data from purgation with arecoline. A decrease in the prevalence of Echinococcus in old dogs has been observed in Tunisia (Lahmar et al. 2001) and indeed was suggested in data reported in Roberts et al. (1986). Using a binomial likelihood function with the ODE function of PopTools it is possible to estimate the parameters. This suggested that the maximum likelihood estimate (MLE) of the infection pressure in Tunisia was 5·3 infections per year and the likelihood of developing immunity on exposure was 0·53. The MLE of the life expectancy of the parasite was 7 months which is biologically reasonable. Attempting to fit the data to the model without immunity gives a poor fit (see Lahmar et al. 2001).

If the death rate of the parasite is 0, which has been suggested for E. granulosus in the intermediate host, then the asymptotic prevalence will be 1. However, in the theory of egg maturation proposed by Gemmell (1990), only a proportion of taeniid eggs to which the host is exposed to will develop into cysts. However, some of the eggs that do not develop are still capable of stimulating the immune response. In this scenario, eggs that start to develop and stimulate the immune response must be modelled as a parasite with a short life expectancy and will result in a lower prevalence with a proportion of hosts immune through exposure, but with no mature metacestode cysts. Alternatively, immature parasitic larvae that fail to develop after penetration of the intestinal wall will have a similar effect. Either is consistent with observational studies of T. hydatigena in sheep and goats in Jordan where the asymptotic prevalence in old animals was 0·27 and 0·54 respectively (Torgerson et al. 1998).

These equations have been used to make deductions about the transmission dynamics of the parasite. Using this equation (1) data from New Zealand (Roberts et al. 1986) suggested that the mean time to exposure in dogs was calculated as 5·3 years whilst the mean survival time of infection of adult parasites was reported as 3·9 years. Likewise in China these parameters were calculated as 2·2 and 1·5 years respectively (Ming et al. 1992b). In Tunisia this model optimum fit, using equation 1, was a mean time to exposure of 0·2 years and mean survival of the infection of 0·02 years. The latter figure in particular is not consistent with the biology of the parasite. When analysis was re-run, but the parameter for the life expectancy (1/μ) was constrained to a value described experimentally, the mean time to infection was calculated as 1·47 years and mean survival time of 0·8 years (Lahmar et al. 2001). Because the data from Tunisia in particular had a lower prevalence in old dogs and thus would not give a better fit, even to equation (2), an alternative mathematical description of the variation of prevalence and abundance proposed above may be more appropriate (see above).

Using data from Kazakhstan, the full abundance model (equation 7) gave a better fit to the data than the nested abundance model (equation 9) (Torgerson et al. 2003b). This indicated that there was likely to be parasite-induced host immunity under conditions of high infection pressure. However, under conditions of low infection pressure, the nested model without immunity, gave a better fit. This is consistent with E. granulosus stimulating immunity when there is high infection pressure but not in conditions of low infection pressure. The results agree with the idea that herd immunity is likely to be less under conditions of low infection pressure as suggested by Anderson & May (1985). Thus, in farm dogs in rural Kazakhstan, the model suggested herd immunity is present with an estimated infection pressure of 3000 parasites per dog year compared to just 30 parasites per dog per year in village dogs. In addition, the maximum likelihood value of the life expectancy of the parasite given the model and the data were very close to that observed experimentally. The confidence limits were wide, but by re-running the analysis using experimental data that reflect the variation in experimentally observed potency times, it was possible to define the confidence limits of all the parameters in the model more precisely. In Morocco, some quantitative data are available (Ouhelli et al. 1997). In contrast to the data from Tunisia and farm dogs in Kazakhstan, there appear to be greater numbers of parasites in old dogs than young dogs. This would be consistent with a lack of immunity. If the life expectancy of the parasite is around 1 year (as suggested by experimental studies), then the data reported from Morocco would reflect an infection pressure of around about 200 parasites per dogs per year. This is somewhat lower than the farm dogs in Kazakhstan and thus there may be insufficient parasites to stimulate immunity in Moroccan dogs.

THE INTERMEDIATE HOST

The models derived by Roberts et al. (1986, 1987) to describe the variations of age intensity and prevalence in the intermediate host have already been described. This also depended on the same parameters as the definitive host (i.e. infection pressure, life expectancy of the parasite, and the rate of acquisition and loss of immunity). In the intermediate host the parasite is assumed to have a greater life expectancy than the definitive host and the assumption is made that, once infected, the intermediate host will remain infected for life. Therefore the death rate is μ=0. Consequently, in the absence of immunity the variation of prevalence with age is only dependent on the infection pressure β and can be described by equation (3). Thus sheep will gradually accumulate hydatid cysts and in the oldest age groups of animals the asymptotic prevalence approaches 1. The model predicts that in the intermediate host, if immunity is absent, then the numbers of hydatid cysts will increase with age in a linear fashion. This is indeed in agreement with a number of observational studies (Roberts et al. 1986; Gemmell, 1990; Ming et al. 1992a; Cabrera et al. 1995; Dueger & Gilman, 2001; Torgerson et al. 1998, 2003a).

There have been a number of studies that have used these models to gain an idea of the infection pressure in sheep in the environment, the numbers of infection insults per year and the numbers of cysts produced by each infection insult. A characteristic of all these studies is that there is no evidence of parasite-induced immunity in the intermediate host. In all cases there was a linear increase in the numbers of cysts with age in each of the species of intermediate host studied (sheep, goats and horses). These studies are summarised in Table 1. The terms endemic and hyperendemic were introduced by Roberts et al. (1986) to describe the levels of herd immunity in the intermediate host when infected by taeniid cestodes. Essentially the parasite was defined as being endemic if there was no evidence of parasite-induced immunity in the intermediate host. E. granulosus appears to be in an endemic steady state in all areas that have been studied except possibly western Sichuan. Other cestodes (e.g. T. hydatigena) appear to stimulate more readily intermediate host immunity by exposure to natural infections of eggs. With this parasite, the increase in numbers of metacestodes with age is not linear with young animals having similar parasite abundances to older animals. Field observations are consistent with this hypothesis with ovine cysticercosis (see Cabrera et al. 1995; Torgerson et al. 1998). Likewise, the asymptotic prevalence is depressed below 1, so even in the oldest age groups of sheep, the prevalence is usually much less than 1. On this definition, hyperendemic cysticercosis has been recorded a number of times (e.g. Roberts et al. 1987; Cabrera et al. 1995; Torgerson et al. 1998), but there have been no convincing accounts of hyperendemic echinococcosis in sheep, cattle, goats or horses. However, as shown in Table 2, a study of E. granulosus infections in yaks in Sichuan province of China suggest an asymptotic prevalence of less than 100%, which might indicate a ‘hyperendemic’ status. Although references have been made to ‘hyperendemic’ echinococcosis, it is important not to confuse reports that have data that support intermediate host immunity rather than the parasite being highly prevalent. Even in China, where Zhang et al. (2001) discussed the possibility of a decline in hydatid infections in older sheep in Xingjiang, an evaluation of the original data that was cited from Chi et al. (1990) suggests an asymptotic prevalence approaching 1 (96% of sheep age 6 years were infected).

AGGREGATION

In both the intermediate host and particularly the definitive host, there is a large degree of aggregation of parasites. Thus, some hosts harbour a large number of parasites whilst a large proportion of the population harbour few, if any parasites. This can be modelled by a negative binomial distribution with the degree of aggregation indicated by the negative binomial constant k which can be estimated as:

where x is the sample mean and s² is its variance. Thus when x=s², k=∞, the distribution becomes Poisson (random). There are a number of reasons for this aggregated distribution. The aggregation of infective stages can explain a large part of the distribution in hosts. Thus eggs in the environment might be expected to be aggregated close to the location of dog faeces. Consequently when sheep (or other intermediate hosts) are infected, an infectious insult is unlikely to consist of a single egg but many eggs. In goats this has been demonstrated to a certain extent by Torgerson et al. (1998). Using the models of transmission it is possible to transform numbers of cysts in goats to infectious insults. In most age classes of goats this resulted in a Poisson (and hence random) distribution of infectious insults. The same was not true of sheep so therefore it is likely that there are other process occurring, the most likely of which is a variation in host resistance to infection which then results in further aggregation of parasites. In the definitive host infectious stages are always likely to be aggregated as a fertile hydatid cyst can contain large numbers of protoscoleces. No studies have been done to indicate if a random distribution would result by transforming the numbers of parasites per dog into infectious insults, but it is likely that there would still be an aggregated distribution as there have been some experimental studies to indicate aggregation of parasites in dogs following experimental infection (Gemmell et al. 1986). With a number of other host–parasite systems there is evidence that the degree of aggregation increases with decreasing prevalence (Shaw, Grenfell & Dobson, 1998). If such a relationship could be confirmed in dog populations infected with E. granulosus and data reported in Table 3 suggests it may exist, this would be an important result to use in surveillance studies.

Presently, it is only as possible to obtain quantitative data by arecoline purgation or necropsy studies. The former is labour intensive, hazardous and underestimates the true parasite burden. The latter technique can only be undertaken on stray dogs. Copro-antigen techniques can be used for detecting the infection qualitatively. If the negative binomial constant were to have a relationship with the parasite prevalence, it would be possible to estimate the mean parasite abundance of the dog population from prevalence studies as the prevalence p is related to the mean abundance of parasites m by the equation:

where k is the negative binomial constant. However, further data need to be obtained to confirm this.

When fitting the data to the models described above it is important to ensure that the aggregation is taken into account when calculating the parameters. Thus, the negative binomial function should be used as a description of the error variance, together with maximum likelihood techniques to establish the most likely value for the parameters (Torgerson et al. 2003a,b). A failure to use such an analytical approach gives an increase in the likelihood of type 1 or type 2 statistical errors (Wilson, Grenfell & Shaw, 1996) or can lead to inaccurate estimation of model parameters.

INFERENCES FROM THE MODELS

Important epidemiological data can be gained by using these models on data. When data are fitted to the model then the parameters can be estimated. This includes the potential exposure of the hosts to the parasites and thus the infection pressure. This can be combined with data from the biotic potential of the parasite to calculate the numbers of infectious stages of the parasite that the host is likely to be exposed to. For example, the numbers of eggs the intermediate host is consuming can be calculated (e.g. Ming et al. 1992a; Cabrera et al. 1995; Torgerson et al. 1998; Dueger & Gilman, 2001). This can then be used to estimate the level of environmental contamination with eggs as well as indicate likely control feasibility. The model has also been used on one occasion to demonstrate the lower level of exposure to eggs by goats compared to sheep grazing in the same herds. Torgerson et al. (1998) reported that sheep had a greater abundance of hydatid cysts compared to goats but fewer metacestodes of T. hydatigena. By modelling the age related distribution it could be shown that the increase in T. hydatigena metacestodes was actually likely to be due to reduced host immunity resulting in greater numbers of cysts compared to sheep despite a lower infection pressure. Because E. granulosus appeared not to stimulate immunity in either intermediate host then the lower numbers of hydatid cysts was related directly to the infection pressure. This observation was hypothesised to be due to the fact that goats are browsers and thus more likely to consume the extremities of the herbage. Here eggs are likely to be at lower concentrations and have a lower viability due to greater exposure to desiccation and ultraviolet radiation. This was confirmed experimentally by Heath (unpublished). Oral infection of 14 Merino lambs and 14 Cashmere kids with identical numbers of eggs was undertaken in Xinjiang and the mean number of cysts found on subsequent necropsy was 7·9 cysts in the lambs compared to 5·6 cysts for the kids (not significant).

BASIC REPRODUCTION RATIO (R₀)

This is an important concept in infectious diseases as the level of this figure will give an indication of the agent's stability in the population. R₀ is a measure of the reproductive rate of the parasite in the absence of density-dependent constraints. R₀ must be a value of 1 or greater for the parasite to maintain itself in the population. A value of little more than 1 would indicate that the parasite is in an endemic steady state with little regulation of the population by intermediate host immunity. A value much greater than 1 indicates that there is some regulation by herd immunity on parasite abundance. The calculation of R₀ has been attempted on a number of occasions (e.g. Roberts et al. 1986; Cabrera et al. 1995; Torgerson et al. 1998). However, there are some problems, especially if the assumption is that there are no density-dependent constraints in the life cycle. This would indicate that R₀ can never be any value other than 1 as the entire population will always remain susceptible. Indeed, Roberts et al. (1986) indicated that R₀=1/S₀ where S₀ is the equilibrium proportion of the population that is susceptible to infection. Because the population of sheep will always have S₀=1, an alternative method was suggested as R₀=1+L/A where L is the life expectancy of the host and A is the average age of infection. With T. hydatigena, Torgerson et al. (1998) suggested that R₀ could be defined from the age prevalence curves. Indeed Roberts et al. (1986) demonstrated that the proportion S of animals in a population susceptible to infection varies with age according to equation (6). Thus by fitting this equation to age abundance data it is possible to estimate the parameters γ, a and h and thus S and hence R₀. However, this can be done with T. hydatigena (see Torgerson et al. 1998), but in E. granulosus, the parameter a has always been 0, hence R₀ would be=1.

Assuming the intermediate host does not have immunity, then it may be that the density-dependent constraint occurs at the level of the definitive host. Evidence for this comes from studies in Kazakhstan (Torgerson et al. 2003b) and Tunisia (Lahmar et al. 2001). Thus the equation (4) can be used to estimate parameters a, h and γ; but in the definitive host. In farm dog populations in Kazakhstan, a, h and γ were estimated as 3·03×10⁻⁴, 3070 and 0·0193 respectively. If the mean age of the dog population is assumed to be equal to the mean age of the dogs that were sampled, R₀ can be estimated to be approximately 3·0 in these dog populations in Kazakhstan using this technique. This is somewhat higher than the estimates based on sheep populations such as in New Zealand, Uruguay and Jordan (Roberts et al. 1987; Cabrera et al. 1995; Torgerson et al. 1998) and reflects a possible significant density dependant constraint in transmission due to parasite-induced host immunity in the dog population.

SIMULATION OF CONTROL PROGRAMMES

Possibly the most important use of modelling is the potential to model control intervention. In the case of cystic echinococcosis, the equations that define transmission reported have been used to develop a spread-sheet model that could be utilized to predict the possible outcomes of intervention. This is reported in more detail in Torgerson (2003). A spread-sheet model was built round cell entries for prevalence and abundance of the host populations based on the equations reported above. Simulation of control was undertaken by assuming an intervention strategy would change one or more of the base-line parameters in the model. Precontrol parameters are first obtained by surveillance data (Table 4) such as that reported by Torgerson et al. (2003a,b) in Kazakhstan.

Once base-line information is obtained for a particular locality, control can be simulated by changing the parameters (Table 5, Torgerson, 2003). For example, if treatment of dogs with anthelmintic is undertaken every 6 weeks (the prepatent period for the G1 strain) then the mean survival time of a patent infection (1/μ) is reduced to 0. However, other less intense (and cheaper) programmes can be modelled such as 3 or 6-monthly anthelmintic treatment. In modelling intervention it must be assumed that 100% compliance is rarely if ever achieved. In China, frequently less than 80% of dogs were treated in a control programme (Liu, 1993), whilst in Turkana Kenya only 59% of dogs could be treated (MacPherson et al. 1986). Less than 100% compliance is modelled by increasing the life expectancy of the parasite to a larger value than would occur if there was 100% anthelmintic treatment. The decrease in parasites in dogs caused by anthelmintic treatment will result in a lowered infection pressure in sheep. The numbers of cysts in sheep will begin to decline but not change the infection pressure in dogs for some time because of the longevity of cysts in the older sheep. Thus delay is included in the model to allow time for older sheep with their parasite population to be removed from the system. The length of the delay depends on the time to cyst maturity. In addition some of the parameters relating to immunity were assumed to change as control of the parasite population progressed. For example, as the prevalence in dogs becomes lower the probability of immunity on exposure is decreased. This models the relaxation of herd immunity as a result of lower infection pressure. Data for this concept can be found in Torgerson et al. (2003b), where it was demonstrated that herd immunity was significant when the prevalence in the dog population was 23% but absent when the prevalence was only 5·8% in a separate population of dogs.

A vaccination campaign can be modelled as a reduction in the numbers of new fertile cysts from the date of vaccination. Thus, sheep that are vaccinated with a 100% effective vaccine will develop no further cysts from continued exposure to Echinococcus eggs. However, infection acquired before vaccination can still be transmitted to dogs; thus there will be some delay until all the cysts disappear from the sheep population. Likewise, an education campaign may reduce the rate at which offal is fed to dogs and this can be modelled as a reduction in the infection pressure in dogs.

There is significant variability in some of the parameters suggested by different experimental work and in the possible capture rates of dogs in the populations. There will also be additional variability in the base-line surveillance data obtained for the precontrol parameters. To model this variability in the simulations, Monte-Carlo routines have also been written into the spreadsheet model to account for this. Thus, variability in the capture rate of dogs between the best case (say 90% treated) and worse case (say 60% treated) can be modelled. This is particularly important in the absence of accurate dog population figures and would give best and worse case scenarios if a target capture rate or compliance rate of 75% was assumed.

A number of hypothetical scenarios were investigated using this simulation model. The conclusion was that if anthelmintic treatment is used as the main strategy, then generally a minimum of treatment every 3 months is required assuming at least 60% of the dogs in the population are treated. Vaccination of sheep is effective, provided that a large proportion of the population is vaccinated (over 90%). Interestingly, the most effective intervention was a combination of vaccinating sheep and anthelmintic treatment. Using this strategy it was possible to reduce levels of echinococcosis in both principal life cycle hosts to very low levels. If there is vaccine cover of about 75% of the sheep population, anthelmintic treatment in dogs can be reduced to six monthly intervals. Such a less intensive approach would have advantages in terms of cost, and may also increase compliance. In any case, by using an integrated approach, a low level of compliance would still result in acceptable levels of control.

An economic analysis of control options is shown in Table 6, and indicates that significant benefits can be obtained by using vaccination combined with treating dogs with anthelmintics strategically twice a year to control E. granulosus.