Hostname: page-component-745bb68f8f-s22k5 Total loading time: 0 Render date: 2025-02-06T16:07:00.483Z Has data issue: false hasContentIssue false
  • English
  • Français

A stochastic model for the aggregation of Onchocerca volvulus in nodules

Published online by Cambridge University Press:  31 July 2001

H. P. DUERR ,
K. DIETZ ,
D. W. BÜTTNER  and
H. SCHULZ-KEY
H. P. DUERR
Affiliation:
Department of Medical Biometry, University of Tübingen, Germany Institute of Tropical Medicine, University of Tübingen, Germany
K. DIETZ
Affiliation:
Department of Medical Biometry, University of Tübingen, Germany
D. W. BÜTTNER
Affiliation:
Bernhard Nocht Institute of Tropical Medicine, Hamburg, Germany
H. SCHULZ-KEY
Affiliation:
Institute of Tropical Medicine, University of Tübingen, Germany
Rights & Permissions [Opens in a new window]

Abstract

A model is presented which describes the aggregation of female Onchocerca volvulus in nodules and their distribution in the human population. The basic model is based on a single parameter, the formation probability q, which represents the probability with which incoming larvae form a new nodule. This parameter describes parasite behaviour which cannot easily be recognized in available data without modelling. The estimate for the average formation probability of μq = 0.39 suggests an attraction of the invading infective larvae to already existing nodules or resident worms with probability 0.61. No significant difference in μq was found between the forest and savanna parasite strains. The model can be used inversely to estimate the worm burden of persons from palpation data. The observed variance in the number of nodules per person requires the assumption of a variance-increasing mechanism which was implemented by heterogeneity within the host population (extended model with 2 parameters). Possible reasons for this heterogeneity are presented and its implications concerning the reproductive biology of the parasite are discussed.

Keywords

Onchocerca volvulussavanna and forest strainsaggregationmodellingonchocercomatanodule formation
Type
Research Article
Information
Parasitology , Volume 123 , Issue 2 , August 2001 , pp. 193 - 201
Copyright
2001 Cambridge University Press

INTRODUCTION

Onchocerciasis is a parasitic infection caused by nematodes of the genus Onchocerca. The adult worms (macrofilariae) are mostly located in the subcutaneous tissue of their specific hosts. These comprise ungulates and, exceptionally, also man. Several species are obligatorily located in a capsule consisting of host tissue so as to form a nodule, the onchocercoma, which is also characteristic for the human parasite, Onchocerca volvulus. The onchocercoma seems to be induced predominantly or even exclusively by the female parasite, which remains sessile after settlement. While the intranodular parasite species of animals usually remain solitary in nodules of more or less similar size, the human parasite shows a typical accumulation of worms in the onchocercomata with a considerable range of sizes (Schulz-Key & Albiez, 1977). Young, old and degenerated worms may be found in the same nodule, with the average number of female O. volvulus per nodule increasing with total worm burden. Ten female worms per nodule are often found, with some nodules harbouring even more than 40 worms (Albiez, Büttner & Duke, 1988; Büttner et al. 1988).

The biological reason behind this unusual aggregation pattern – atypical for the genus Onchocerca – of O. volvulus in the human host is not yet known. But the advantage it confers in terms of facilitating the meeting and mating of dioeceous parasites should be obvious. This suggestion is supported by the observation that younger male worms regularly leave the nodules. They migrate freely within the host tissue and visit female worms, which require several inseminations per year at distinct intervals (Schulz-Key & Karam, 1986). The sex-finding mechanism of tissue-dwelling nematodes still needs clarification, but a chemotactic attraction may be suspected, either induced by pheromones of the sessile female worm, by other excretory or secretory parasite products, or by the tissue of the nodule itself. In addition, the composition of the worm burden in big nodules and the observation of satellite nodules with smooth and thin capsules, usually containing young worms, indicates a gradual growth of the nodules that accompanies large worm burdens.

The present investigation describes a model mimicking stochastically the nodule forming process of O. volvulus and it seeks to clarify the question if the assumption of an attraction of the incoming larvae to resident worms is required to explain the observed parasite's aggregation pattern.

MATERIALS AND METHODS

Sources of data and parasitological procedures

The data derive from 2 nodulectomy campaigns in villages of the West African countries of Liberia (rain forest) and Burkina Faso (savanna), conducted, respectively, in 1976/77 and 1977/78. Both regions were hyperendemic for onchocerciasis at the time of nodulectomy. After extirpation, the nodules were digested with collagenase (for parasitological procedures see Schulz-Key, Albiez & Büttner, 1977) so that the number of worms per nodule could be precisely assessed. Descriptive aspects of these data sets, the worm burden, the relation of palpable to impalpable nodules, and the incidence of different worm stages were published elsewhere (Schulz-Key & Albiez, 1977; Albiez, 1983; Albiez, Büttner & Schulz-Key, 1984). The absolute numbers listed in Table 1 may differ slightly from those given in these publications due to the fact that it was impossible to reconstruct the exactly identical subset of persons. The villages included in this analysis are Mauwa, Sungbeta, Wodee, Yeahmeah and Meningee (located east of St Paul River in southern Bong and in Montserrado counties, Liberia), and Kourougbele, Hemkoa, and Yabar (located south of the Bougouriba River in the region of Gaoua, Burkina Faso). For the present investigation, all individuals operated on and showing at least 1 female adult worm were included in the analysis. Since male worms seem to play a minor role in the nodule forming process (Collins et al. 1982), only female worms of all stages are taken into consideration.

Description of the basic model

The methods used to generate the distribution of the number of worms per nodule have recently been described in terms of a stochastic aggregation process (Duerr & Dietz, 2000). Fig. 1 depicts the basic idea of the probability tree that enables mathematical handling of the sequential process of infection, and Table 2 explains parameters as used in the following. After infection, developing female larvae form a new nodule with formation probability q or else join an already existing nodule with invasion probability p = 1−q. The model assumptions are that both probabilities are independent of: (1) N, the number of female worms per person, and (2) the size of the nodules (measured as the number of females per nodule).

Fig. 1. Representation of the stochastic model describing formation of different nodule sizes after sequential infection with Onchocerca volvulus. Arrows indicate branches as based on the formation probability q and the invasion probability p = 1−q. The last 2 lines demonstrate that the number of nodules minus 1 follows a binomial distribution.

The aggregation process leads to a binomial distribution of the number of nodules K per person. Since the female larvae of the initial (primary) infection invariably form the first nodule, the distribution has parameters q and N−1, with mean and variance

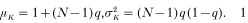
Thus, the average number of nodules per person is a linear function of N, and the formation probability of female worms within an individual host i can be estimated by

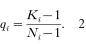
Since this relation is derived from the mean of the binomial distribution, qi is not only the moment estimator but also the maximum likelihood estimator.

Implementation of heterogeneity in the model

As the variance of the binomial distribution is too low to explain the observed variance in the number of nodules per individual, we allow q to vary between individuals, instead of fixing it, as in the case of the binomial distribution. This accounts for an assumed variability on the part of hosts to react with differential intensity of encapsulation to the presence of parasites. Defining q to be beta distributed, as described by Duerr & Dietz (2000), the number of nodules per person therefore follows a beta binomial distribution with parameters N−1, α and β:

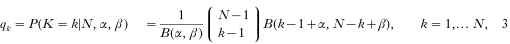
where B(ξ1, ξ2) is the beta function.

The average formation probability and the corresponding variance in this case are

and the expected number of nodules and the corresponding variance is given by

The distribution of nodule sizes

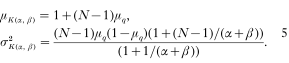
Given the individual worm burden Ni and the probability that k nodules occur, qk, the probabilities for the expected nodule sizes can be calculated from the probability generating function (pgf) of the partition distribution

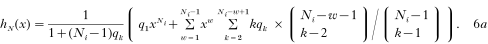
where x is the dummy variable of the pgf (for details see Duerr & Dietz, 2000). The coefficients of xw yield then the probability that w female worms per nodule can be found. Fitting these probabilities to data can be done in two ways as follows.

(A) In the basic model, with a binomially distributed number of nodule numbers, qk is replaced by the binomial probabilities

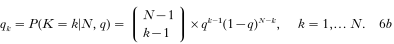
so that we obtain

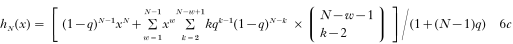
Replacing in this stage parameters N and q with the individual parameters (i.e. N = Ni, q = qi) results in a fit which is in its parametrization closest to the observations. This fit will be called in the following ‘individual-based fit’.

(B) For the extended model with implemented heterogeneity, qk is given by the beta binomial distribution (equation (3)) and substituted into equation (6a). Since these probabilities are based on the population parameters α and β this fit will be called in the following ‘parametric fit’.

Parameter estimation

Parameters α and β were determined by maximum likelihood estimation, using Powell's algorithm (Press et al. 1992) in combination with varying initial values. Confidence limits for μq were derived from the isolines of the 2-dimensional log-likelihood function lnL(α, β): since μq = 1/(1+β/α) depends only on the ratio β/α the slopes of the 2 tangents to the isoline of lnL(α, β)−3.84/2 determine the lower and upper confidence limits (according to a likelihood ratio test with 1 degree of freedom, the 95% quantile is χ2 = 3.84).

Predicting the number of female worms from palpation or surgery data

As shown above the number of nodules Ki of individuals with a total worm burden of Ni female worms can be described by the beta binomial distribution with probability P(ki[mid ]Ni = ni). From this we can inversely calculate the probability that an individual i has ni female worms given ki excised nodules. Since this probability is conditioned on Ki, the prediction may not be deduced from the relationship as shown in Fig. 3. Instead, Bayes' theorem must be applied as follows:

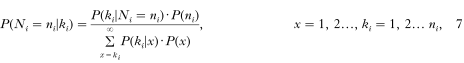
where the denominator normalizes the probabilities. P(ni) is the probability that ni female worms per person can be found. This can be fitted by the geometric distribution from the population data according to P(ni) = (1/m)(1−1/m)ni-1 (with parameter estimates mforest = 25.6 and msavanna = 24.0, which are the average number of worms (including live and dead worms) per person as given in Table 1).

Approximation by the Waring distribution

As shown by Duerr & Dietz (2000), the partition distribution of the number of worms per nodule with a beta binomially distributed number of nodules per host converges to a zero-truncated Waring distribution (Wimmer & Altmann, 1999) when N→∞. The distribution of nodule sizes for heavily infected people can therefore be approximated by the Waring distribution, and the probability that w female worms per nodule are found is given then by

where Γ is the Gamma function and α, β are the parameters of the beta distribution. Mean and variance of this distribution are μ

W

= 1+β/(α−1) and σ

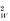
= μW(μ

W

−1)α/(α−2), respectively.

RESULTS

Parameter estimates

Table 3 shows the parameter estimates of the beta distributed formation probabilities with corresponding means and variances for the examined individuals in Liberia (forest strain) and Burkina Faso (savanna strain). Overlapping confidence intervals for μq indicate that the average formation probabilities of both strains do not differ significantly, so that a common distribution can be assumed. Fig. 2 shows the density functions for these estimates.

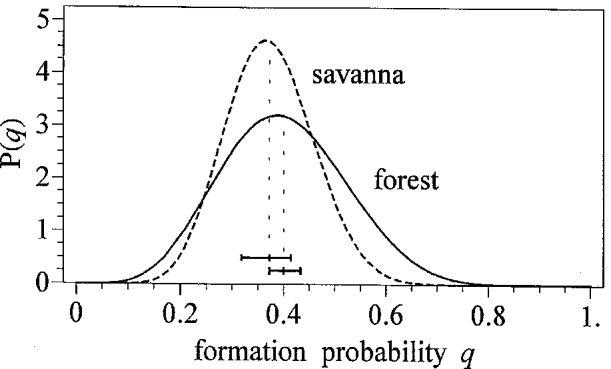
Fig. 2. The beta-distributions of the formation probability q; 95%-confidence limits of the mean μq are illustrated as bars above the q-axis.

Fig. 3 shows the observed numbers of female worms and nodules for individuals in villages of Liberia (forest strain) and Burkina Faso (savanna strain) with the average number of nodules as a function of the total female worm burden. The 95% regions of tolerance cover, respectively, 96% and 94% of the observations in Liberia and Burkina Faso, and therefore explain the observed variability very well.

Fig. 3. Comparison between observed data and model prediction. Each point represents the number of female worms and nodules per person. Bold line: mean μK(α, β) according to the beta binomial distribution; thin line: discrete 95% region of tolerance.

Validation of the model

Since the model makes use of distributions based on the finite support N, individual hosts contribute specifically to the distribution of nodules per person in the host population (dependent on their total female worm burden Ni). Accordingly, the host population must be described in terms of the mixture of these individual distributions. In practical terms this means that all theoretical, individual-specific distributions of the number of excised nodules per person were summed up, resulting in the expected distribution for the population. This was done analogously for the distribution of the number of worms per nodule, either using the individual-specific values for Ni and qi (individual-based fit, see above) or using Ni in combination with the parametric formation probability based on the population parameters α and β (parametric fit).

As shown in Fig. 4 this mixture of individual beta binomial distributions yields a good prediction of the observed distribution of excised nodules per person in both forest and savanna settings. Fig. 5 shows the predicted nodule size represented by the parametric and the individual-based fit. The logarithmic scale is added, to show the low frequencies of large nodule sizes. χ2-tests on the individual-based fit cannot be performed, because the number of qi reduces the number of the degrees of freedom below zero. χ2-tests on the other fits show significant results due to mixed influences from outliers, underestimation of the observations (Fig. 5) and variability in the observations (Fig. 4).

Fig. 4. Comparison of the observed distribution of nodule numbers per person ([bull ]) with the theoretically expected distribution (—) (the latter is the sum of beta binomial distributions (equation (3)) of all individuals, calculated on the basis of α, β and the individual Ni).

Fig. 5. Comparison of the observed distribution of nodule sizes ([bull ]) with the theoretically expected distribution (sum of the partition distributions). Dashed line: parametric fit, calculated on the basis of α, β and Ni (equation (6a) with (3)) Solid line: individual-based fit, calculated on the basis of qi and Ni (equation (6c)). Graphs in the right column show the logarithmic representation of the same data as in the left column.

Predicting the number of female worms from palpation or surgery data

The quantiles shown in Fig. 6 demonstrate the expected variability if the numbers of live and dead female worms per person are deduced from surgery data. Using the chart requires consideration of the following 3 points. (1) To obtain the expected number of live female worms from the chart it is necessary to subtract the percentage of dead female worms. The data do not show a significant decline or increase in the proportion of dead females with increasing total female worm burden. Therefore for practical purposes the values can be set constant and they amount to 12.2% and 15.2% for the forest and savanna strains, respectively (Table 1). (2) If the chart is used to predict the number of live female worms from palpation data the number of palpated nodules must first be multiplied by 1.6 (forest strain) or 1.25 (savanna strain) to get the number of nodules expected in a nodulectomy (Albiez, 1983). However, it is important to note that in this case the variance given in the chart is only a lower estimate, because the variance caused by palpation is not considered. (3) Finally, it should be noticed that the numbers of female worms predicted from the chart refer to the number found in the nodulectomy trial, in which the presence of deep nodules was not examined. A crude approximation to the expected real number of parasites is given by multiplication with factor 3.5 (forest strain) (Duke, 1993), which is the only available figure for considering deep nodules.

Fig. 6. Quantiles for the predicted number of live and dead female worms as based on the number of palpated nodules. Central, bold line: median, wrapped by the 50%, 75%, 90% and 95% regions of tolerance (thin lines). The discrete, stepwise functions were smoothed.

DISCUSSION

Biological implications

The results deduced from this model show an aggregation of female O. volvulus in nodules explained by a probabilistic process based on a single parameter, the formation probability q, or its counterpart, the invasion probability p = 1−q. The estimates for the average formation probabilities μq = 0.40 (forest strain) and μq = 0.37 (savanna strain) clearly indicate that female infective larvae tend to join existing nodules rather than forming new ones. This suggestion is also supported by the small proportion of female worms found living solitary in a nodule, with 16% in forest and 18% in savanna localities of West Africa.

In 40% of the operated persons the total number of males exceeded the number of nodules, suggesting that the aggregation of females might facilitate mating due to the abovementioned necessity for repeated insemination (Schulz-Key & Karam, 1986). However, this is not the only possible explanation for worm aggregation. Bovine O. ochengi, living in intradermal nodules, is the closest relative of the human parasite, showing many morphological and genetic similarities. It is suggested that humans acquired the parasite when commencing cattle husbandry thousands of years ago (Bain, 1981). Both Onchocerca species still share the same vectors and have a similar reproductive biology such as repeated inseminations and migration of male worms (Schulz-Key & Karam, 1986). However, females of O. ochengi do not at all aggregate in nodules, being usually solitary (nevertheless nodules accumulate in a small area of the ventral part of the host). This inconsistency between the behaviour of O. volvulus and O. ochengi raises questions as to the role and formation of the nodule and as to the nature of the mechanism responsible for sexual attraction and for attraction of female larvae to already existing nodules.

It is supposed that intranodular species are more specialized and phylogenetically younger than those that do not form nodules (Bain, 1981). In addition, the morphology of these onchocercomata is not uniform. Mobile female worms are found in cystic nodules (e.g. O. jakutensis, Plenge-Bönig, Krömer & Büttner, 1995) or else closely and tightly embedded in connective tissues as in the human parasite. It is suggested that nodule formation is actively induced by still unknown stimuli from the parasite.

The natural host spectrum of the genus Onchocerca is principally represented by ungulates with humans (or primates) being atypical hosts. This fact supports the hypothesis of human onchocerciasis originating from a zoonosis. Since the parasite–host relationship of the human species seems to be evolutionarily much younger than that of its bovine counterpart, it is also suspected to be less balanced. Zoonoses often induce severe immune reactions and pathologies. This might result in exceptionally strong and exaggerated nodule formation in human onchocerciasis.

There are several conceivable factors which might be responsible for the attraction of invading filarial larvae. For example, products secreted or released by the resident female worm might allure other worms; or less probably, the larva might be guided by a chemical gradient derived from the reactive tissue of the host. In contrast, sexual attraction should be caused by pheromones irrespective of the existence of a nodule. These products released by the female worms might be excreted or derived from the uterine fluid which extravasates during release of microfilariae. The actual reproductive state of the female is suspected to play an important role in signalling readiness to mate.

The degree of clustering of female parasites is increased by the formation of conglomerates of nodules with adherent young satellite nodules (Albiez, 1983; Albiez et al. 1988; Büttner et al.1988). No relevant dependence of the average size of the nodules on the number of satellites was found. However, the distribution of formation probabilities for those persons who show only weak conglomeration, has greater variance (analysis not shown, further aspects see below). A comparison of the aggregation patterns does not reveal striking differences between the forest and the savanna strain of O. volvulus, because of overlapping confidence limits for the average formation probability.

The assumptions of the model are that a developing female larva joins or invades a nodule independently of the sizes of existing nodules and independently of the total female worm burden of a host. The first assumption implies that the attraction effect of a nodule on a developing larva would not depend on the number of females located in it. With respect to chemotaxis, this would mean that a developing female larva recognizes females in a nodule qualitatively but not quantitatively. The model prediction suggests this as a plausible explanation for the observation of smaller nodule sizes. However, the lack of the fit for higher nodule sizes indicates that there should exist a factor that weakly supports the formation of large nodules. The model cannot discriminate between a more heterogeneous or a preferred invasion of large nodules. Descriptive analysis suggests the first of these 2 possibilities (see below). According to the second assumption, the aggregation pattern is not altered by N, the total worm burden of a host. The pattern seems to be stable as given by the model and its partition distribution. This is also in agreement with the findings of Albiez et al. (1988) that the number of live female worms per nodule does not depend on the endemicity level.

To explain the observed variability of the data, it was assumed that the average formation probability for developing larvae depends on the host. This dependence is interpreted as a more or less intense host-specific reaction to worm encapsulation. A possible factor for this heterogeneity is the time lag before the parasite is encapsulated by the immunological response of the host. Analysis of covariance does not show host age or sex to affect the formation probability, so that a plausible reason for this variability is the differing immunological states of the individual hosts. It would be worthwhile to verify experimentally these speculations in order to clarify the rationale underlying this parasite behaviour.

Statistical considerations

The basic model with a binomially distributed number of nodules and the same parameter q for all individuals cannot result in an acceptable fit of the data. In Fig. 5, for example, nodule sizes would be predicted from this model by a geometric distribution (linear decrease in logarithmic representation), of which the variance is too low. Thus, it is essential to implement variance-increasing effects in the individual-based distributions of nodule sizes. This can be achieved either by introducing heterogeneity on the level of the population or by implementing the formation probability as a linearly increasing function of the nodule size. Since both approaches yield the same distribution, it is theoretically impossible to estimate their impact simultaneously (Duerr & Dietz, 2000). We therefore decided that the variance-increasing effect shall be attributed solely to heterogeneity, which is a fundamental and widespread characteristic of parasitic infections. Should there exist a dependency with respect to the nodule size, then this contribution is incorporated and compensated by the aspect of heterogeneity.

In comparison to the individual-based fit, the parametric fit in Fig. 5 shows an underestimation of large nodule sizes. A χ2-test shows a significant result which has to be attributed to mixed influences from outliers, variability in the observations and underestimation of the observations. To interpret the latter means that individual qi's contribute a greater variance than the parametric beta distribution. This additional variance might be attributed to the data-based observation that persons who show only a weak degree of conglomeration have a greater variance in their distribution of qi's. However, as stated before, a possible dependency from the nodule size cannot be excluded. The intention of this work focussed on modelling with a minimal set of parameters and, although the derivation of the model requires some effort, it does suggest only a simple, plausible explanation for the genesis of the data. Discrepancies between model prediction and observed data may provide a stimulus for further discussion of the aggregation behaviour of O. volvulus.

The authors are grateful to M. Eichner and H. H. Diebner for fruitful collaboration and to M. G. Basáñez for suggesting the use of the model to estimate worm burden from nodule palpation. This work was supported by the Fortüne grant no. 528 of the University Hospital, Tübingen, Germany and by a grant from the Deutsche Forschungsgemeinschaft, Graduiertenkolleg Lebensstile, soziale Differenzen und Gesundheitsförderung.

References

ALBIEZ, E. J. (1983). Studies on nodules and adult Onchocerca volvulus during a nodulectomy trial in hyperendemic villages in Liberia and Upper Volta. I. Palpable and impalpable onchocercomata. Tropenmedizin und Parasitologie 34, 54–60.Google Scholar
ALBIEZ, E. J., BÜTTNER, D. W. & SCHULZ-KEY, H. (1984). Studies on nodules and adult Onchocerca volvulus during a nodulectomy trial in hyperendemic villages in Liberia and Upper Volta. II. Comparison of the macrofilaria population in adult nodule carriers. Tropenmedizin und Parasitologie 35, 163–166.Google Scholar
ALBIEZ, E. J., BÜTTNER, D. W. & DUKE, B. O. L. (1988). Diagnosis and extirpation of nodules in human onchocerciasis. Tropical Medicine and Parasitology 39 (Suppl. IV), 331–346.Google Scholar
BAIN, O. (1981). Le genre Onchocerca: hypothèses sur son évolution et clé dichotomique des espèces. Annales de Parasitologie 56, 503–526.CrossRefGoogle Scholar
BÜTTNER, D. W., ALBIEZ, E. J., VON ESSEN, J. & ERICHSEN, J. (1988). Histological examination of adult Onchocerca volvulus and comparison with the collagenase technique. Tropical Medicine and Parasitology 39 (Suppl. IV), 390–417.Google Scholar
COLLINS, R. C., LUJAN, R., FIGUEROA, H. & CAMPBELL, C. C. (1982). Early formation of the nodule in Guatemalan onchocerciasis. American Journal of Tropical Medicine and Hygiene 31, 267–269.CrossRefGoogle Scholar
DUERR, H. P. & DIETZ, K. (2000). Stochastic models for aggregation processes. Mathematical Biosciences 165, 135–145.CrossRefGoogle Scholar
DUKE, B. O. L. (1993). The population dynamics of Onchocerca volvulus in the human host. Tropical Medicine and Parasitology 44, 61–68.Google Scholar
PLENGE-BÖNIG, A., KRÖMER, M. & BÜTTNER, D. W. (1995). Light and electron microscopy studies on Onchocerca jakutensis and O. flexuosa of red deer show different host–parasite interactions. Parasitology Research 81, 66–73.Google Scholar
PRESS, W. H., TEUKOLSKY, S. A., VETTERLING, W. T. & FLANNERY, B. P. (1992). Numerical Recipes in C, 2nd Edn. Cambridge University Press, Cambridge.
SCHULZ-KEY, H. & ALBIEZ, A. J. (1977). Worm burden of Onchocerca volvulus in a hyperendemic village of the rain-forest in West Africa. Tropenmedizin und Parasitologie 28, 409–560.Google Scholar
SCHULZ-KEY, H., ALBIEZ, E. J. & BÜTTNER, D. W. (1977). Isolation of adult Onchocerca volvulus from nodules. Tropenmedizin und Parasitologie 28, 428–430.Google Scholar
SCHULZ-KEY, H. & KARAM, M. (1986). Periodic reproduction of Onchocerca volvulus. Parasitology Today 2, 284–286.CrossRefGoogle Scholar
WIMMER, G. & ALTMANN, G. (1999). Thesaurus of Univariate Discrete Probability Distributions. Stamm, Essen, Germany.
Figure 0

Table 1. Summary of data for nodulectomy trials of Onchocerca volvulus in West African localities (see text for sources of data)

Figure 1

Fig. 1. Representation of the stochastic model describing formation of different nodule sizes after sequential infection with Onchocerca volvulus. Arrows indicate branches as based on the formation probability q and the invasion probability p = 1−q. The last 2 lines demonstrate that the number of nodules minus 1 follows a binomial distribution.

Figure 2

Table 2. Parameter notation and definition

Figure 3

Fig. 2. The beta-distributions of the formation probability q; 95%-confidence limits of the mean μq are illustrated as bars above the q-axis.

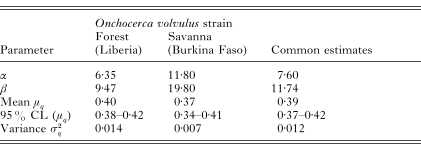
Figure 4

Table 3. Estimates for the parameters of the beta-distributed formation probabilities with corresponding means and variances

Figure 5

Fig. 3. Comparison between observed data and model prediction. Each point represents the number of female worms and nodules per person. Bold line: mean μK(α, β) according to the beta binomial distribution; thin line: discrete 95% region of tolerance.

Figure 6

Fig. 4. Comparison of the observed distribution of nodule numbers per person ([bull ]) with the theoretically expected distribution (—) (the latter is the sum of beta binomial distributions (equation (3)) of all individuals, calculated on the basis of α, β and the individual Ni).

Figure 7

Fig. 5. Comparison of the observed distribution of nodule sizes ([bull ]) with the theoretically expected distribution (sum of the partition distributions). Dashed line: parametric fit, calculated on the basis of α, β and Ni (equation (6a) with (3)) Solid line: individual-based fit, calculated on the basis of qi and Ni (equation (6c)). Graphs in the right column show the logarithmic representation of the same data as in the left column.

Figure 8

Fig. 6. Quantiles for the predicted number of live and dead female worms as based on the number of palpated nodules. Central, bold line: median, wrapped by the 50%, 75%, 90% and 95% regions of tolerance (thin lines). The discrete, stepwise functions were smoothed.