INTRODUCTION
The vast majority of modelling approaches to host–pathogen or host–parasite interactions, commencing with the model of smallpox by Bernoulli (Reference Bernoulli1760), has been concerned with infections of humans, or to a lesser extent, of livestock. Nevertheless, the same broad principles of epidemiological modelling apply equally well to wildlife as they do to diseases of humans or livestock. The starting point for modelling microparasites such as viruses and bacteria is the Susceptible – Exposed – Infected – Recovered (S E I R) compartmental framework (Anderson and May, Reference Anderson and May1979; May and Anderson, Reference May and Anderson1979) and the basis of models of macroparasite (typically helminth) dynamics was likewise developed by Anderson and May (Anderson and May, Reference Anderson and May1978; May and Anderson, Reference May and Anderson1978) and involves modelling the number of hosts, the number of parasites and, critically, the frequency distribution of parasites within the host population.
There are three fundamental differences between modelling wildlife diseases and those of humans and livestock. First, wildlife disease modellers inevitably work in a data poor environment in comparison with those working on livestock and human disease. It is not unusual for human disease modellers to have datasets available with high spatial and temporal precision covering decades (for example, Grenfell et al. Reference Grenfell, Bjørnstad and Kappey2001). No wildlife disease dataset of such resolution exists. This means that models of wildlife disease must inevitably be simpler, because sufficient data are unavailable to parameterize or fit complex and detailed models.
Second, in wildlife disease problems, modelling the effect that the pathogen or parasite has on the host population is often the key problem of interest. In conservation biology, for example, determining the circumstances under which infectious disease may cause extinction is a fundamental issue (de Castro and Bolker, Reference de Castro and Bolker2005; McCallum, Reference McCallum2012). For most human disease problems, the population size or density is determined extrinsically or is considered constant, rather than being driven by the host–pathogen interaction. In livestock disease management, the population density of the host may be considered as a variable able to be manipulated to manage the level of infection (Ferguson et al. Reference Ferguson, Donnelly and Anderson2001) but it is rarely driven by the dynamics of the interaction. The dynamic nature of population size or density in wildlife disease models means that understanding the way in which transmission scales with population size is especially important. Transmission is often dichotomized as being either frequency- or density-dependent (McCallum et al. Reference McCallum, Barlow and Hone2001), but evidence is increasing that transmission may often depend on population density somewhere between these two extremes (Smith et al. Reference Smith, Telfer, Kallio, Burthe, Cook, Lambin and Begon2009) and that the relationship between density and transmission may depend on spatial scale(Cross et al. Reference Cross, Creech, Ebinger, Manlove, Irvine, Henningsen, Rogerson, Scurlock and Creel2013).
A third distinction between modelling human disease dynamics, in contrast with modelling dynamics of both livestock and wildlife, is that certain experimental manipulations are not ethical when applied to human infections. There are, of course, significant ethical issues when dealing with wildlife (McCallum and Hocking, Reference McCallum and Hocking2005; Minteer and Collins, Reference Minteer and Collins2005; Parris et al. Reference Parris, McCall, McCarthy, Minteer, Steele, Bekessy and Medvecky2010; Jones et al. Reference Jones, Hamede, McCallum, Banks, Lunney and Dickman2012), but they are qualitatively different from those faced by human epidemiologists. For example, the transmission rate of a parasite or pathogen and its relationship to host density is fundamental to understand host–parasite interactions (McCallum et al. Reference McCallum, Barlow and Hone2001). In both livestock and wildlife it is possible to perform direct transmission experiments. Such experiments are not impossible with human infections but are clearly not ethical with highly pathogenic organisms. Transmission dynamics in human infections therefore, usually need to be inferred from observation of epidemic time series (for example, Ferrari et al. Reference Ferrari, Bjornstad and Dobson2005). Similarly, direct experiments to determine the rate of the parasite induced death are clearly not possible with human populations, although there are also ethical issues with wildlife.
Here, I critically review the application of models in management of wildlife disease. I do not attempt to provide an exhaustive review of the application of models to wildlife disease in general, which has been extensively covered elsewhere (Roberts et al. Reference Roberts, Smith, Grenfell, Grenfell and Dobson1995; Dobson and Foufopoulos, Reference Dobson and Foufopoulos2000; Tompkins et al. Reference Tompkins, Dunn, Smith and Telfer2011; Restif et al. Reference Restif, Hayman, Pulliam, Plowright, George, Luis, Cunningham, Bowen, Fooks, O'Shea, Wood and Webb2012). Rather, I concentrate on evaluating the role that models have played, or could play, in providing guidance for developing practical management strategies for pathogens and parasites in wildlife populations, with a particular emphasis on terrestrial vertebrates.
OBJECTIVES OF MODELLING
There is little point in modelling any ecological interaction without a clear purpose in mind. The most appropriate modelling approach is entirely dependent on the purpose for which the model is intended. So the first critical question is why you might need to manage wildlife diseases. As has been pointed out by a number of authors (e.g. Daszak et al. Reference Daszak, Cunningham and Hyatt2000; Joseph et al. Reference Joseph, Mihaljevic, Arellano, Kueneman, Preston, Cross and Johnson2013), emerging infectious diseases of wildlife are threats to biodiversity, agricultural production and human health. In most situations, the objective of managing wildlife disease is therefore to reduce disease impact, either in wildlife populations themselves, or in livestock and human populations. There is, however, one important situation in which the objective may be to maximize disease impact. Infectious disease can also be an effective means of biological control of pest wildlife species, for example myxomatosis in rabbits (Fenner and Fantini, Reference Fenner and Fantini1999).
Where the objective is to reduce disease impact, management goals may be: (i) preventing spread to currently uninfected areas or populations; (ii) eliminating parasites or pathogens from currently infected populations; (iii) reducing the prevalence or intensity of infection; or (iv) enabling the population to better persist in the presence of infection. The tools available to achieve these goals are limited. Broadly, they are: (i) development of strategies such as fencing and movement controls to prevent spread to currently uninfected populations; (ii) development and dissemination of vaccines or treatments; (iii) culling (whether of infected animals only or irrespective of infection); (iv) dissemination of resistant or tolerant genotypes; and (v) habitat modification to limit transmission (Wobeser, Reference Wobeser2002; McCallum and Jones, Reference McCallum and Jones2006). For each of these strategies, models can be applied to assess their feasibility and to assist in the design of optimal approaches, but they have been especially important in the design of vaccination strategies and of culling programs. Preventing or limiting spillover may be the goal for managing threats to livestock and for managing zoonoses (infections transferred from a non-human host to humans). The process of spillover itself is under modelled (Lloyd-Smith et al. Reference Lloyd-Smith, George, Pepin, Pitzer, Pulliam, Dobson, Hudson and Grenfell2009), but there has been extensive modelling effort directed at strategies to reduce prevalence or eliminate disease in wildlife reservoirs. Management of spillover may also be important when dealing with threats to biodiversity, given that most parasites or pathogens that threaten host extinction have one or more reservoir species that are relatively tolerant to infection, within which the parasite can persist at relatively high prevalence (McCallum, Reference McCallum2012).
If pathogens are proposed as biological control agents, the fundamental management goal is to maximize the impact on the host population whilst avoiding detrimental impacts on other species. For ‘classical’ biological control, the agent will not already be present in the target population, although if the proposed agent is genetically modified, a ‘wild type’ strain may be present. Models to predict the impact of the proposed agent on the host population, its persistence, and the impact of selection on the agent and the host are critical. Models may also be required to design optimal release strategies.
MODELS TO DETERMINE THE IMPACT OF INFECTIOUS DISEASES ON HOST POPULATIONS
Assessing the impact that a parasite or pathogen may have on a host population is a critical first step. This is important whether the management objective is to reduce the impact of a pathogen or to maximize it (as is the case with biological control), and is important whether or not the pathogen is already present. The simple presence of a parasite or pathogen in a population is not evidence that it poses a threat to the population and indeed parasites and other infectious agents present endemically at very high prevalence in a population are likely not to be having a major impact on population size (McCallum and Dobson, Reference McCallum and Dobson1995), unless the disease affects fecundity and not survival. Very simple models suggest that higher prevalence or intensity of infection in morbid or dying animals than in the general population is an indicator of potential disease impact, but observational data alone cannot determine the direction of causation.
In cases when a highly virulent pathogen spreads into previously naive populations, such as the chytrid fungus Batrachochytrium dendrobatidis spreading through frog populations (Berger et al. Reference Berger, Speare, Daszak, Green, Cunningham, Goggin, Slocombe, Ragan, Hyatt, McDonald, Hines, Lips, Marantelli and Parkes1998; Lips et al. Reference Lips, Brem, Brenes, Reeve, Alford, Voyles, Carey, Livo, Pessier and Collins2006) or Tasmanian devil facial tumour disease (McCallum et al. Reference McCallum, Jones, Hawkins, Hamede, Lachish, Sinn, Beeton and Lazenby2009), the combination of massive population declines, spatial spread and clinical signs of disease in many individuals is sufficient to identify a disease threat without a dynamic model.
The situation is less straightforward when dealing with enzootic infections. In the absence of replicated experimental interventions, assessing the impact of infectious disease on a population is not easy (Tompkins et al. Reference Tompkins, Dunn, Smith and Telfer2011). The Bradford Hill criteria, originally applied to identify smoking as a cause of lung cancer (Hill, Reference Hill1965) may also be helpful in distinguishing causation from association in infective diseases of wildlife (Plowright et al. Reference Plowright, Sokolow, Gorman, Daszak and Foley2008).
Field studies, using radio telemetry or mark recapture can be used to estimate the survival and fecundity of infected and uninfected animals. It remains possible, however, that some third factor such as nutritional stress may be responsible for both high parasite burdens and reduced fitness. Even where it is reasonable to assume that the disease is responsible for reduced fitness of individuals, this may not directly translate into impact on population size because of density-dependent factors. For example, Joly and Messier (Reference Joly and Messier2005) used radio telemetry to conclude that brucellosis and bovine tuberculosis (TB) led to a decreased survival and fecundity in a declining population of Wood Buffalo Bison bison athabascae. However, they cautioned against a simplistic conclusion that these diseases were responsible for the decline. In a separate modelling study (Joly and Messier, Reference Joly and Messier2004) they showed that it was likely that the disease interacted with density-dependent predation in determining population size.
MODELLING VACCINATION STRATEGIES IN ENDANGERED SPECIES
Vaccines have been pivotal in managing human infectious diseases and are widely used in livestock. It is not surprising that a vaccine is often suggested as the obvious solution to manage the threat to wildlife of an emerging infectious disease. Examples where development and delivery of a vaccine have been proposed include chlamydial infection in koalas (Kollipara et al. Reference Kollipara, George, Hanger, Loader, Polkinghorne, Beagley and Timms2012), Tasmanian devil facial tumour disease (Woods et al. Reference Woods, Kreiss, Belov, Siddle, Obendorf and Muller2007; Pinfold et al. Reference Pinfold, Brown, Bettiol and Woods2014) and chytridiomycosis in frogs (Cashins et al. Reference Cashins, Grogan, McFadden, Hunter, Harlow, Berger and Skerratt2013). In each of these cases, a vaccine capable of successfully immunizing hosts, even in a laboratory setting, has yet to be successfully developed.
Models have an important role in identifying the properties a vaccine capable of effectively managing disease would need to possess and how it would need to be delivered. At the most general level, simple models show that eliminating a disease by administering a vaccine requires making a fraction P > (1 − 1/R 0) resistant, where R 0 is the basic reproductive number of the pathogen (Anderson and May, Reference Anderson and May1992).
There have been relatively few attempts to model the effects of a yet to be developed wildlife vaccine. An exception is a model of a koala chlamydia vaccine (Craig et al. Reference Craig, Hanger, Loader, Ellis, Callaghan, Dexter, Jones, Beagley, Timms and Wilson2014). They used an individual-based stochastic model, parameterized using a Latin hypercube process. Parameter sets that allowed the population to increase at the highest rate that the authors found in the literature were retained as ‘realistic’. Disease related parameters were estimated by retaining those that caused the population to halve in between 5 and 10 years (as appears to be the case for some Southeast Queensland populations). The parameterization and calibration thus presumed that chlamydial infection was the primary cause of population decline, and that populations would recover in the absence of infection. The model suggested that a vaccine with 75% efficiency delivered to 10% of the population each year would be able to arrest population decline. Setting targets for vaccine efficiency and delivery prior to vaccine production and field trials is highly desirable, but a limitation in this case is that the prediction is conditional on the presumption that disease is the primary driver of population decline.
Vaccination programmes to manage wildlife diseases to date have almost entirely used vaccines that have been developed for livestock or domestic animals. The investment of time and money in research and development that is necessary to develop an effective vaccine for a pathogen is considerable and few, if any, vaccines for pathogens found only in wildlife have yet been fully developed. If the management strategy is to reduce or eliminate infection in the wildlife population, the key challenge with an existing vaccine is delivery to that population and design of the vaccination programme. Models have an important role here.
Rabies is almost uniformly lethal to humans and produces very high mortality in most mammals, but an effective vaccine does exist. Proposals to vaccinate entire populations of threatened canids have, however, been controversial because of the possible negative consequences of capture and handling (Burrows et al. Reference Burrows, Hofer and East1994; Gascoyne and Laurenson, Reference Gascoyne and Laurenson1994; Dye, Reference Dye1996). Haydon et al. (Reference Haydon, Randall, Matthews, Knobel, Tallents, Gravenor, Williams, Pollinger, Cleaveland, Woolhouse, Sillero-Zubiri, Marino, Macdonald and Laurenson2006) developed a model to assess a targeted vaccination strategy for Ethiopian wolves (Canis simensis), an endangered species for which rabies is a major threat. Their study population comprised several subpopulations connected by narrow corridors of suitable habitat. The wolves are highly territorial and within pack transmission occurs at a much higher rate than between pack transmission. Haydon et al. (Reference Haydon, Randall, Matthews, Knobel, Tallents, Gravenor, Williams, Pollinger, Cleaveland, Woolhouse, Sillero-Zubiri, Marino, Macdonald and Laurenson2006) developed a spatially explicit stochastic SEIR model, which suggested that reactive vaccination of populations in which outbreaks were detected and in connecting corridors would be effective in preventing catastrophic population crashes. This example illustrates how modelling spatial structure and heterogeneity can help design vaccination strategies.
MODELLING VACCINATION TO MANAGE SPILLOVER
The previous section considered strategies to manage disease in the populations being vaccinated. A somewhat different situation arises when vaccination is used to manage spillover. First, models are important to determine the direction of the spillover, particularly for diseases of carnivores such as rabies and canine distemper. In the Serengeti ecosystem in Tanzania, lions have suffered several severe epizootics of canine distemper virus in the last few decades (Viana et al. Reference Viana, Cleaveland, Matthiopoulos, Halliday, Packer, Craft, Hampson, Czupryna, Dobson, Dubovi, Ernest, Fyumagwa, Hoare, Hopcraft, Horton, Kaare, Kanellos, Lankester, Mentzel, Mlengeya, Mzimbiri, Takahashi, Willett, Haydon and Lembo2015). The virus also infects a range of other carnivores, in particular dogs living around the periphery of the national park. The strains of canine distemper virus affecting lions were similar to those present in the dog populations. One option for managing the threats to wildlife is to mass vaccinate domestic dog populations (Cleaveland et al. Reference Cleaveland, Kaare, Knobel and Laurenson2006), although the cost effectiveness of this strategy has been debated, particularly if the dog population is not in fact an important reservoir (Viana et al. Reference Viana, Cleaveland, Matthiopoulos, Halliday, Packer, Craft, Hampson, Czupryna, Dobson, Dubovi, Ernest, Fyumagwa, Hoare, Hopcraft, Horton, Kaare, Kanellos, Lankester, Mentzel, Mlengeya, Mzimbiri, Takahashi, Willett, Haydon and Lembo2015). Viana et al. (Reference Viana, Cleaveland, Matthiopoulos, Halliday, Packer, Craft, Hampson, Czupryna, Dobson, Dubovi, Ernest, Fyumagwa, Hoare, Hopcraft, Horton, Kaare, Kanellos, Lankester, Mentzel, Mlengeya, Mzimbiri, Takahashi, Willett, Haydon and Lembo2015) used a Bayesian State Space model based on more than 30 years of serological data and determined that the dynamics were largely driven by dog to lion transmission rather than the reverse. Despite the amount of data available, the authors did not think that a mechanistic susceptible-infected-resistant (SIR) model was capable of being adequately parameterized. They therefore used a more statistically-based approach: an autoregressive model in which the prevalence of disease in lions in year t was predicted by the prevalence in lions in both year t-1 and year t-2, together with a cross-infection term from dogs at time t-1. The prevalence in dogs was similarly predicted, with the exception that there was the possibility of a direct vaccination effect. In addition, measurement error (false serological positives and negatives) was also accounted for. This example emphasizes the importance of an appropriate level of complexity for the question at hand. Determining the direction of spillover is possible without a full dynamic model, whereas modelling the effectiveness of intervention such as vaccination or culling would not be.
For rabies infecting humans, the direction of the spillover is not in question. Models have been widely used to determine optimum vaccination strategies for wildlife such as foxes and raccoons to limit spillover of this fatal disease to human populations. The effective elimination of rabies in foxes from most of western and central Europe in the last three decades, using bait delivered vaccination, is probably the most successful example of management of infectious disease in wild animals (Freuling et al. Reference Freuling, Hampson, Selhorst, Schroder, Meslin, Mettenleiter and Muller2013). A similar genetically modified poxvirus is also being developed to vaccinate prairie dogs (Cynomys spp.) in the USA against plague (Rocke et al. Reference Rocke, Kingstad-Bakke, Berlier and Osorio2014; Tripp et al. Reference Tripp, Rocke, Streich, Abbott, Osorio and Miller2015). Models should play a role in determining the likely success of this vaccine in controlling epizootics and also in optimal bait delivery strategies.
Managing a vaccination programme as eradication is approached is critical. Continuing a broad-scale baiting programme, long after eradication is achieved, is clearly a waste of resources, but scaling back a program too soon risks disease re-emergence. Models have contributed to addressing this problem. Tischendorf et al. (Reference Tischendorf, Thulke, Staubach, Muller, Jeltsch, Goretzki, Selhorst, Muller, Schluter and Wissel1998) used a simulation model that combined a conventional compartmental epidemic model on a two-dimensional (2D) spatial grid with occasional individual-based long-distance dispersal events. The model suggested that low-level persistence with moving foci of infection was possible even at high vaccination levels and that therefore scaling back the vaccination program, as had been suggested at that time, would be inadvisable. More recently, models have been used to suggest optimal rabies eradication strategies in regions where it remains endemic (Sterner and Smith, Reference Sterner and Smith2006; Townsend et al. Reference Townsend, Lembo, Cleaveland, Meslin, Miranda, Putra, Haydon and Hampson2013).
In eastern North America, the issue has been limiting the epidemic spread of rabies in raccoon populations over the last 40 years, in contrast to the eradication of an endemic infection. Disease dynamics can be well modelled with an S.E.I.R framework (Childs et al. Reference Childs, Curns, Dey, Real, Feinstein, Bjornstad and Krebs2000). An oral vaccine has been successful in limiting spread in some areas. An individual-based spatial model (Rees et al. Reference Rees, Pond, Tinline and Belanger2013) showed that low levels of vaccination in heterogeneous landscape could in fact be counter-productive, shifting the disease dynamics from epidemic burnout, in which the disease dies out by rapidly eliminating susceptible hosts, to endemic persistence. This is an example of successful use of a complex spatially explicit stochastic model, which produced this apparently counterintuitive result that vaccination could make the spillover risk worse. However, the understanding that large epidemics can produce disease burnout in finite populations can be derived from much simpler models (e.g. Keeling and Grenfell, Reference Keeling and Grenfell1997).
Pathogens can also spillover from humans to wild populations, especially those of great apes (Ryan and Walsh, Reference Ryan and Walsh2011). Rushmore et al. (Reference Rushmore, Caillaud, Hall, Stumpf, Meyers and Altizer2014) used empirically derived contact networks to simulate disease transmission in a population of chimpanzees. They found that by vaccinating the most connected individuals, they could reduce the amount of vaccination necessary to prevent large epidemics by up to 35%. In practice, such a strategy would be expensive because of the need to derive the contact network for any population threatened by disease. However, they also found that vaccination strategies based on the traits of the most highly connected individuals (such as being a member of a large family group or being a high-ranking male) would still reduce the amount of vaccination required by at least 18%.
MODELLING CULLING FOR CONSERVATION
Culling of all animals that may possibly have been exposed to infection is often the immediate veterinary response to an outbreak of an exotic infectious disease in a livestock population. When an infectious disease emerges in a population of conservation significance, however, such indiscriminate culling is a less suitable option. A common approach is to remove only those animals that are infected, a strategy known as ‘test-and-cull’ in the veterinary literature. There have been several applications of modelling to evaluate the effectiveness of this approach for diseases of conservation concern.
Tasmanian devil facial tumour disease (DFTD) is an infectious cancer that threatens to cause the extinction of the largest surviving marsupial carnivore (McCallum, Reference McCallum2008). The disease is almost uniformly lethal once signs of infection are detected and transmission appears to be frequency dependent, meaning that there is no threshold host density for disease maintenance and that therefore this host specific pathogen is potentially capable of causing the extinction of the Tasmanian devil (McCallum et al. Reference McCallum, Jones, Hawkins, Hamede, Lachish, Sinn, Beeton and Lazenby2009).
When the disease entered the almost isolated Forestier Peninsula, an attempt was made to eliminate the disease by removing all individuals captured with detectable infection. Population decline continued unarrested and, more critically, there was no evidence that culling reduced the force of infection to which undiseased devils were exposed (Lachish et al. Reference Lachish, McCallum, Mann, Pukk and Jones2010). More than 150 infected animals were removed during quarterly trapping sessions over more than 5 years. Clearly, a range of other culling strategies would be possible, involving more trapping effort, more frequent trapping sessions etc., but to exhaustively test a range of strategies would be both time-consuming and prohibitively expensive. Beeton and McCallum (Reference Beeton and McCallum2011) investigated whether any feasible removal strategy would be capable of controlling or eliminating the disease in a closed population. A very simple deterministic Susceptible – Exposed – Infected model identified that there are two threshold removal rates of diseased animals. One rate of removal, ρ1 is sufficient to eliminate disease, and a lower rate ρ2 will not eliminate disease but, if applied indefinitely, will allow the persistence of a devil population in the presence of infection. This simple model could not provide quantitative estimates of the necessary removal rates because of time delays introduced by age structure in the devil population and the existence of a poorly known incubation or latent period. We therefore developed the age-structured deterministic model shown schematically in Fig. 1.

Fig. 1. An age structured model to investigate the feasibility of culling as a strategy to control Tasmanian devil facial tumour disease. Key features of the host–pathogen interaction that needed to be modelled to generate quantitative estimates of appropriate removal rates to control disease are that animals between the ages of 0 and 1 year do not become infected and do not reproduce, whereas animals between the ages of 1 and 2 both become infected and reproduce at a substantially lower rate than those of 2 years and older. Reproduction is seasonal with most births occurring within the month of March (the Austral autumn). There is a latent period between being exposed to infection and both showing symptoms and becoming infectious. Anecdotal evidence suggests this may be lengthy (perhaps as much as 9 months) but the frequency distribution of the latent period is poorly known.
How time delays are modelled is important when constructing host-parasite models. One approach is simply to use a separate differential equation to represent the susceptible, exposed and infectious individuals in each age class, with rate parameters describing transitions between age classes and infection states. The difficulty with this approach is that it implicitly assumes that the time delays are exponentially distributed. This is plainly unrealistic, particularly for transitions between age classes. At the other extreme, time delays may be fixed, so that all individuals leave a class exactly the same time after entering it. An intermediate possibility is to use multiple differential equations, each with exponential delays within each class, leading to time delays with a gamma distribution. Parameters can be adjusted to allow for widely or tightly distributed time delays (Wearing et al. Reference Wearing, Rohani and Keeling2005). We applied each of these possible approaches to investigate how sensitive our conclusions about removal rates were to the method of modelling time delays.
Generating quantitative estimates of removal rates requires appropriate estimates of demographic and epidemiological parameters. Fecundity, age-specific mortality and disease induced mortality were available from extensive mark recapture datasets (Lachish et al. Reference Lachish, Jones and McCallum2007, Reference Lachish, McCallum and Jones2009). Information on the rate at which prevalence increases in newly infected populations (McCallum et al. Reference McCallum, Jones, Hawkins, Hamede, Lachish, Sinn, Beeton and Lazenby2009) enabled us to estimate the transmission rate. We needed to conduct extensive sensitivity analysis on the latent period because of lack of reliable data.
Figure 2 shows a simplified version of the results for the most likely combination of both infection rate and latent period. Most Tasmanian devils are very trappable: mark recapture analysis suggested that with the number of traps used over a 10 day trapping session, a devil present in the trappable population had between a 57 and 94% chance of being trapped (Beeton and McCallum, Reference Beeton and McCallum2011). However, DNA analysis suggested that a substantial proportion of the population was not trappable (Menna Jones, personal communication.). The modelling therefore supported the empirical observation that quarterly trapping was incapable of eliminating the disease, but furthermore showed that the removal rates necessary to eliminate disease, with more frequent or intense trapping, are likely to be unachievable. Figure 2 shows that this conclusion is relatively invariant to the way in which the time delay has been modelled.
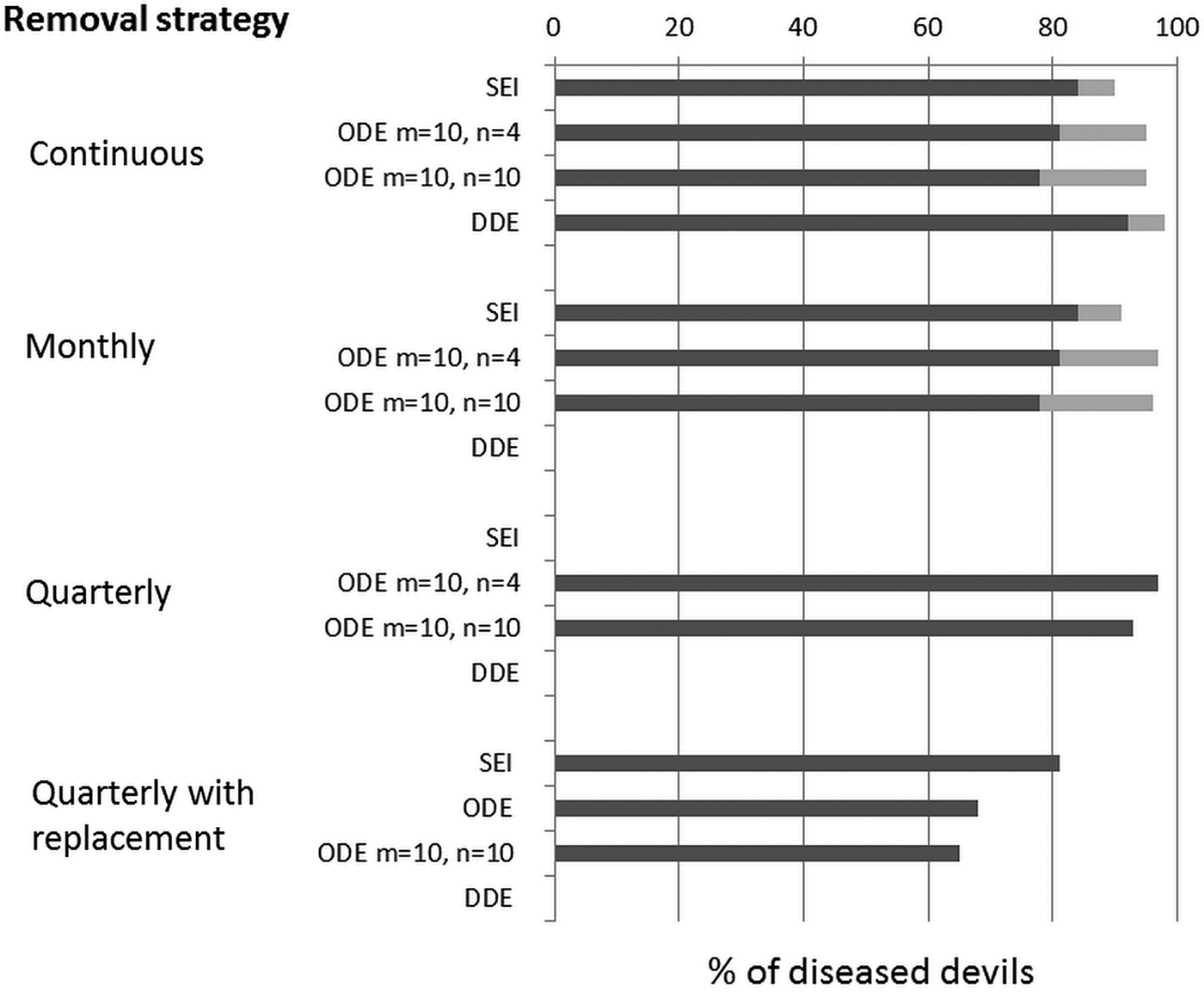
Fig. 2. Removal rates necessary to control Tasmanian devil facial tumour disease. Dark bars show ρ 2 the removal rate necessary to prevent devil extinction, but not to eliminate disease, whereas the additional removal rate ρ 1 necessary to eliminate disease is shown in the grey bars. Four ways of modelling the time delay are shown: SEI – simple exponentially distributed delays; ODE m = 10, n = 4 – tightly distributed maturation, but a broadly distributed latent period; ODE m = 10, n = 10 – tightly distributed maturation and a tightly distributed latent period; DDE – delay differential equations. Four removal strategies are shown: continuous, where trapping occurs continually; monthly; quarterly, the strategy used in practice; and quarterly with replacement where diseased animals are replaced with captive reared disease free individuals. Abbreviation: ODE, Ordinary Differential Equation.
Chronic wasting disease (CWD) is a prion disease of wild cervids in North America. Whether prions can be considered as parasites or pathogens is perhaps debatable, but this is one of the few systems in which models have been used to investigate culling a species to reduce or eliminate an infectious agent in that same species. CWD has a fundamental difference in epidemiology from DFTD, in that infections progress relatively slow. This means that a discrete-time approach can be used to model its dynamics, with semi-annual time steps (May–October and November–April). Gross and Miller (Reference Gross and Miller2001) used an individual-based model to conclude that test-and-cull was better able to control the disease than indiscriminate culling. For most parameter sets explored, removing 20% or more of diseased animals would eliminate disease, but over a time scale of several decades. A field investigation suggested that higher rates of selective culling of up to 50% were technically feasible (but at substantial cost) and the model suggested that this could reduce prevalence in the approximately 350 deer from 8 to 2% in 10–15 years (Wolfe et al. Reference Wolfe, Miller and Williams2004). A more recent model (Wasserberg et al. Reference Wasserberg, Osnas, Rolley and Samuel2009) used a deterministic matrix model including both sex and age structure. The model compared the effect of non-selective culling under frequency and density-dependent transmission. Not surprisingly, it predicted that control was easier to achieve with density-dependent transmission than frequency dependent transmission, with eradication possible at high and sustained culling levels provided transmission was density-dependent. Eradication of disease if transmission was frequency dependent also resulted in extinction of the host.
In contrast, an Ordinary Differential Equation (ODE) model developed by Potapov et al. (Reference Potapov, Merrill and Lewis2012) showed that it is theoretically possible for non-selective culling to eliminate a disease with frequency dependent transmission without causing host extinction. The preconditions are that recruitment is density-dependent and also sufficiently high at low host density. Culling removes both infected and uninfected hosts, but these are then replaced by newborns, which are uninfected. For appropriate parameter combinations, this may reduce disease prevalence sufficiently and for long enough to enable eradication.
White-nose syndrome is an emerging fungal disease threatening North American hibernating bats (Frick et al. Reference Frick, Pollock, Hicks, Langwig, Reynolds, Turner, Butchkoski and Kunz2010). Culling, either of infected hibernacula or infected bats within hibernacula, is a potential control strategy. A discrete-time simulation model, in which infection was spread by dispersal across a 2D array of arenas suggested that no culling strategy was capable of controlling white-nose syndrome in wild bat populations (Hallam and McCracken, Reference Hallam and McCracken2011).
These three examples, emphasise the importance of modelling when contemplating to control an infectious disease by culling a population of conservation value. No conservation manager would wish to be characterized as the US army officer who said (perhaps apocryphally) during the Vietnam War of the village of Ben Tre ‘It became necessary to destroy the town to save it’. Culling has the obvious potential to be counterproductive, test-and-cull is inevitably expensive and too many alternative culling strategies exist to test them all experimentally. Models enable the effects of a range of culling intensities and strategies to be investigated. The examples presented are not encouraging about the feasibility of culling as a control strategy. Only in the case of the very slowly progressing CWD is there a suggestion that an intensive test-and-cull strategy may be feasible, and then only in a relatively small closed population. As with all modelling exercises, the results are only as good as the input parameters and adequate parameterization of the transmission process remains a major challenge.
MODELLING CULLING TO MANAGE SPILLOVER
Culling of wildlife reservoirs is widely proposed as a strategy to prevent spillover of pathogens to both human and livestock populations. If the wildlife reservoir is not of conservation significance, then culling irrespective of infection status, even to the point of extinction, may be acceptable. For example, bovine TB was reduced to undetectable levels by the near eradication of the introduced swamp buffalo Bubalus bubalis in northern Australia. Bradshaw et al. (Reference Bradshaw, McMahon, Miller, Lacy, Watts, Verant, Pollak, Fordham, Prowse and Brook2012) developed a model linking a population viability analysis on an annual time step for the buffalo to a shorter time step epidemiological model for TB to demonstrate that current rates of culling of sentinels are inadequate both to detect low levels of TB infection and to maintain effective control. An important aspect of this model is that it provides a solution to the problem that the time scale on which transmission of many infectious diseases operates is much faster than the annual time step typically used in stochastic and individual-based models of large vertebrates. It used the software package MetaModel Manager (Pollak and Lacy, Reference Pollak and Lacy2014) to link an epidemic model to the annual time step of the Vortex population viability analysis programme.
There are several examples in which culling of the reservoir species to reduce spillover has produced unexpected consequences. The best known and most controversial of these is badger culling to reduce spillover of bovine TB to cattle in the UK. Whilst large-scale badger culling can reduce the disease risk in cattle, spillover increases in areas around the edge of the culling zone and also increases if culling occurs on a small-scale (Donnelly et al. Reference Donnelly, Woodroffe, Cox, Bourne, Cheeseman, Clifton-Hadley, Wei, Gettinby, Gilks, Jenkins, Johnston, Le Fevre, McInerney and Morrison2006). The mechanism is that culling increases badger movement rates (Pope et al. Reference Pope, Butlin, Wilson, Woodroffe, Erven, Conyers, Franklin, Delahay, Cheeseman and Burke2007) and thus contacts and transmission. There have been a number of models of varying levels of complexity developed of this system. The simplicity of the deterministic model developed by Cox et al. (Reference Cox, Donnelly, Bourne, Gettinby, McInerney, Morrison and Woodroffe2005) enabled them to make considerable progress analytically. When parameterized with available data, it showed that R 0 in British cattle was relatively close to 1, suggesting that achieving control should be possible. With the available data, however, the model was incapable of determining the role that badger to cattle transmission plays in maintaining the epidemic. A series of individually-based stochastic simulation models (Smith et al. Reference Smith, Cheeseman, Clifton-Hadley and Wilkinson2001, Reference Smith, McDonald and Wilkinson2012; Wilkinson et al. Reference Wilkinson, Smith, Delahay and Cheeseman2004) has emphasized the importance of determining how the extent of social disruption of badger territories relates to culling intensity.
A recent suggestion is that a combination of selective culling of TB positive badgers and vaccination and release of TB negative animals might both be more acceptable to the conservation community and avoid the problems of increased movements and transmission following culling. A modification of the previously developed simulation models (Smith et al. Reference Smith, Budgey and Delahay2013) investigated this possibility and found that its effectiveness to reduce spillover to cattle depended critically on the extent to which the relatively low removal rate in such a strategy resulted in social perturbation. Unfortunately, empirical analysis of the existing data was inadequate to determine the rate of badger removal that may trigger substantial social perturbation (Bielby et al. Reference Bielby, Donnelly, Pope, Burke and Woodroffe2014).
Simple models show that there are other circumstances in which culling may be counter-productive. If there is density-dependent compensation to culling that leads to an increased birth rate, a pathogen which confers lifelong immunity may increase in prevalence (Choisy and Rohani, Reference Choisy and Rohani2006) because animals with immunity are replaced by naive recruits. Streicker et al. (Reference Streicker, Recuenco, Valderrama, Gomez Benavides, Vargas, Pacheco, Condori Condori, Montgomery, Rupprecht, Rohani and Altizer2012) found increased rabies prevalence in vampire bats following culling and suggested this as the mechanism. Prentice et al. (Reference Prentice, Marion, White, Davidson and Hutchings2014) provide a general framework for modelling these ‘perturbation effects’ on pathogen prevalence.
Multiple pathogen strains may also lead to increased pathogen prevalence following culling. Bolzoni and De Leo (Reference Bolzoni and De Leo2013) modelled two strains of pathogen, one more virulent than the other, circulating in the same host population. Within the host, the more virulent strain replicates more rapidly and therefore will replace the less virulent strain if co-infection occurs (the process of superinfection). If transmission is density-dependent, a more pathogenic strain requires a higher threshold host density in order to persist in a population (Anderson and May, Reference Anderson and May1979). Without superinfection, the less virulent strain would always replace the more virulent one, but superinfection can allow for co-existence. If that is the case without culling, reducing population density will lead to increasing selection in favour of the less virulent strain. In some conditions, culling will therefore lead to an overall increase in the fraction of the reservoir hosts infected, thus increasing risks of spillover. Parameterizing their model for classical swine fever in wild boar in Italy (which spills over into domestic hogs), Bolzoni and De Leo (Reference Bolzoni and De Leo2013) showed that a culling rate of around 15% per year could lead to a near doubling of disease prevalence in boar.
MODELLING PATHOGENS AS BIOCONTROL AGENTS
The previous examples have aimed to reduce the level of infectious disease. Sometimes, disease may be managed to maximize impact on a population, as a control agent for a pest species. Modelling should have an essential role in evaluating potential control agents and in managing their use.
The classical example of biological control using a pathogen is the myxoma virus, which was introduced to control rabbit populations in Australia, France, the UK and New Zealand (Fenner and Fantini, Reference Fenner and Fantini1999). When myxoma was introduced into Australia in 1952, mortality in infected rabbits was initially close to 100%, but in less than a decade, rabbits had developed some resistance to the virus and highly pathogenic strains of the virus were largely replaced by strains of intermediate virulence. A similar co-evolutionary trajectory was followed in the UK (Fenner and Fantini, Reference Fenner and Fantini1999). Simple deterministic models (May and Anderson, Reference May and Anderson1983) and a more complex simulation approach (Dwyer et al. Reference Dwyer, Levin and Buttel1990) are able to explain this observed outcome, largely through a trade-off between virulence and transmissibility. Although rabbit populations in Australia did not approach pre-myxomatosis levels, numbers increased and other pathogen-based biological control options were considered. Rabbit haemorrhagic disease virus (RHDV), was imported to Australia in early 1995 for trials on an offshore island, but rapidly emerged on the mainland and subsequently spread (Cooke and Fenner, Reference Cooke and Fenner2002). Virally vectored immunocontraception (using a genetically modified avirulent strain of myxoma) was also the subject of a major research program from 1992 to 2005 (Saunders et al. Reference Saunders, Cooke, McColl, Shine and Peacock2010).
The effectiveness of RHDV as a control of rabbit populations has been variable both spatially and temporally in Australia. It has substantially reduced rabbit populations in arid areas, but effects have been much more variable in wetter regions (Mutze et al. Reference Mutze, Bird, Cooke, Henzell, Alves, Ferrand and Hacklander2008). Further, there is evidence that populations have recovered in some areas where control was previously effective (Mutze et al. Reference Mutze, Sinclair, Peacock, Capucci and Kovaliski2014). Several different hypotheses have been suggested to account for this variable effect, including co-evolutionary forces acting on both virus and host, the existence of avirulent endemic strains that may effectively vaccinate rabbits against more virulent strains, the presence of maternal antibodies in juveniles, and age dependent pathogenicity, with juvenile rabbits being less likely to develop fatal infections. Understanding the relative importance of these hypotheses is critical in managing the pathogen for effective control. Modelling is important both in assessing these hypotheses and in developing optimal management strategies. A number of models of RHDV dynamics have been published (Barlow and Kean, Reference Barlow and Kean1998; Fa et al. Reference Fa, Sharples, Bell and DeAngelis2001; Barlow et al. Reference Barlow, Barron and Parkes2002; White et al. Reference White, Norman and Hudson2002). Few have explicitly included the potential influence of maternal antibodies in juveniles and/or lower pathogenicity of the virus in juvenile rabbits. Barlow and Kean (Reference Barlow and Kean1998) used a differential equation model with juvenile immunity and seasonally-forced reproduction and found that juvenile immunity enhanced persistence. Calvete (Reference Calvete2006) developed a model from the perspective of trying to limit the impact of the virus in European rabbit populations, rather than maximizing its impact, as is the objective in the Australian situation. Recently, Wells et al. (Reference Wells, Brook, Lacy, Mutze, Peacock, Sinclair, Schwensow, Cassey, O'Hara and Fordham2015) developed an individual-based stochastic model of both myxomatosis and rabbit haemorrhagic disease in a population of rabbits in South Australia. The model suggested that interplay between seasonal reproductive pulses and maternal antibodies were important in driving disease outbreaks and determining the impact on rabbit populations.
Calvete's (Reference Calvete2006) numerical model produces some tantalizing results that would be well-worth following up with more detailed theoretical analysis and parameterization for Australian conditions. The model suggests that there may be alternative stable states at intermediate rabbit carrying capacities and that co-existence of the virus with rabbits at high population density is possible. These predictions neither require the existence of an avirulent immunizing strain nor co-evolution of host and pathogen. The mechanism is that at high densities, rabbits are exposed to infection earlier, at an age when mortality is relatively low, resulting in high proportions of resistant adults, the females then passing antibodies through to the offspring. Whether the parameter range in which this occurs applies in the Australian situation and how robust these conclusions are have yet to be fully tested. They are broadly consistent with the observation that in wetter areas, where density is usually higher, RHDV is a relatively ineffective control measure, whereas in drier areas outcomes are more variable. The possibility is that intensive management manipulations could shift the system from the high host density quasi stable state to a low host density quasi stable state.
With the benefit of hindsight, it is instructive to re-evaluate the contribution of modelling to the failed attempt to develop a disseminating virally-vectored immunocontraceptive for rabbits in Australia. Simple models were developed relatively early in the programme (Barlow, Reference Barlow1994, Reference Barlow1997). Although Barlow's models were explicitly directed towards development of an immunocontraceptive to control brushtail possums (Trichosurus vulpecula, a serious pest in New Zealand), their results are more broadly applicable. In line with general epidemiological theory (McCallum and Dobson, Reference McCallum and Dobson1995), they show that a disease that suppresses fertility is likely to have greater ultimate effect on population density than one that increases mortality, because decreasing fertility does not directly decrease R 0 , in contrast to the effect of increasing mortality. However, decreasing fertility will act more slowly than increasing mortality, suggesting that some form of integrated control, combining initial culling with fertility control might be more effective. As basic theory would suggest, a sexually transmitted pathogen, which would be likely to have frequency-dependent transmission, would be likely to achieve better control than one with density-dependent transmission. Barlow also pointed out the possibility that some form of compensatory effects of reduced density (such as increased reproductive output) might inhibit the control exerted by a sterilizing pathogen. Indeed in the case of rabbits, it was subsequently shown that reproductive output did not diminish until upwards of 80% of all females in a population were experimentally tubally ligated (Williams et al. Reference Williams, Davey, Moore, Hinds, Silvers, Kerr, French, Hood, Pech and Krebs2007). This is a nice example of how a simple result from a mathematical model has led to an important ecological experiment.
Barlow (Reference Barlow1997) also considered the question of whether a genetically modified fertility-depressing strain would be able to outcompete a wild strain of a pathogen. In a non-spatial system, this can approximately be answered by asking whether R 0 in the wild strain exceeds that of the modified strain, in which case the wild strain will outcompete the modified one. For a pathogen that increases mortality, this will almost certainly be the case, as the wild strain is likely to have evolved towards an optimum R 0 (May and Anderson, Reference May and Anderson1983) and any increase in pathogenicity is likely to lead to a decreased R 0. This will not necessarily be the case if the pathogen decreases fertility, although increased ‘genetic baggage’ associated with the genetic modification might be expected to reduce R 0. In a spatial context, however, a strain that reduces population density by whatever means is likely to have a reduced R 0 relative to a wild strain, provided there is any density dependent component to transmission. This is because a patch infected by the strain that reduces density will be locally surrounded by a reduced population density, relative to the density surrounding a patch infected by the wild strain (Hood et al. Reference Hood, Chesson and Pech2000). There is an extensive literature using spatially explicit models predicting that pathogens may evolve reduced virulence when there is low dispersal (Wild et al. Reference Wild, Gardner and West2009; Lion and Boots, Reference Lion and Boots2010), but this has concentrated on pathogens that increase mortality rather than reduce fecundity. Both theoretical models (O'Keefe and Antonovics, Reference O'Keefe and Antonovics2002) and limited empirical data (Szilagyi et al. Reference Szilagyi, Scheuring, Edwards, Orivel and Yu2009) show that spatial structure similarly may reduce the selective advantage of sterilizing pathogens. This is an issue that needs to be considered when developing models for biological control via fertility suppression.
DISCUSSION: GAPS IN CURRENT MODELS AND PROSPECTS FOR FUTURE APPLICATIONS
Models for Macroparasites
Almost all of the above examples have been concerned with microparasites: viruses, bacteria or protozoa – with the exception of Tasmanian devil facial tumour disease and CWD. Nevertheless, all of them have been approached with variants on the SIR framework. There is, however, a large class of parasites for which this model framework is less appropriate. These are the macroparasites, typically helminths, which cannot complete an entire life cycle within one individual host, meaning that the level of infection is substantially determined by the number of infective stages a host has encountered and the impacts on the host individual are largely determined by the parasite burden.
Although the basic framework for macroparasite models was established nearly 40 years ago (Anderson and May, Reference Anderson and May1978; May and Anderson, Reference May and Anderson1978), macroparasite models are less widely used than the SIR framework. Modelling of the effects of macroparasites on wildlife populations remains under-studied. There are certainly some well-established cases of helminths having substantial impacts on wildlife population. For example, the meningeal worm Parelaphostrongylus tenuis has threatened translocations of elk Cervus elaphus (Samuel et al. Reference Samuel, Pybus, Welch and Wilke1992; Lankester, Reference Lankester2010). One of the best examples of simple models of macroparasite infection producing predictions that were subsequently empirically verified is the experimental removal of cycles in red grouse (Lagopus lagopus scoticus) populations by treating the birds with anthelmintic to remove the nematode Trichostrongylus tenuis (Hudson et al. Reference Hudson, Dobson and Newborn1998).
Nevertheless, macroparasites are probably under-recognized as drivers of wildlife population dynamics. Given the substantial impacts that high helminth infections can have on human morbidity, including cognitive ability (Ezeamama et al. Reference Ezeamama, McGarvey, Hogan, Lapane, Bellinger, Acosta, Leenstra, Olveda, Kurtis and Friedman2012; Bundy et al. Reference Bundy, Walson and Watkins2013), more attention to understand the impact of helminth infections on wildlife is warranted. There is also increasing evidence that helminth infections may influence hosts’ susceptibility to microparasites (Jolles et al. Reference Jolles, Ezenwa, Etienne, Turner and Olff2008), which needs to be taken into account when constructing host-parasite models.
The macroparasite models of Anderson and May are inherently more complex than their microparasite equivalents, as they require keeping track of the distribution of parasites amongst hosts in addition to the number of hosts and the mean parasite burden. Further, parasite burdens within individual hosts are regulated by at least three interacting factors: parasite induced host mortality, a partially effective immune response and within-host density-dependent constraints on parasite survival, growth and fecundity. Whilst considerable progress has been made incorporating some of these factors into differential equation-based models (Fenton and Perkins, Reference Fenton and Perkins2010), macroparasites are more likely to require individually-based models (Cornell, Reference Cornell2005) from which it is difficult to draw general conclusions and for which parameterization and sensitivity analysis are difficult problems.
Modelling assisted selection
Accelerating the co-evolutionary processes that lead to increased resistance and tolerance in host populations and decreased virulence in parasites or pathogens has been suggested as a long term solution to otherwise intractable infectious disease threats to biodiversity (Wobeser, Reference Wobeser2002; McCallum and Jones, Reference McCallum and Jones2006; Scheele et al. Reference Scheele, Hunter, Grogan, Berger, Kolby, McFadden, Marantelli, Skerratt and Driscoll2014; Maslo and Fefferman, Reference Maslo and Fefferman2015). There are many models of host-pathogen co-evolution in the literature (May and Anderson, Reference May and Anderson1983; Woolhouse et al. Reference Woolhouse, Webster, Domingo, Charlesworth and Levin2002; Bennett and Bowers, Reference Bennett and Bowers2008; Gandon et al. Reference Gandon, Hochberg, Holt and Day2013), but relatively few have concentrated on modelling strategies to accelerate selection of resistance or tolerance in the wild, which remains a gap that requires filling. An exception is Maslo and Fefferman (Reference Maslo and Fefferman2015), who used a population viability analysis approach to explore how best to maintain bat populations infected with white-nose syndrome until resistance could develop in those populations. The other management scenario is that it may be possible to accelerate evolution towards lower virulence in a pathogen. Simple models suggest that this may not be straightforward for ‘virulence management’ of human diseases (Ebert and Bull, Reference Ebert and Bull2003). The circumstances in which virulence management may be able to increase the viability of a wildlife population threatened by emerging disease warrant further exploration.
Appropriate levels of complexity
Deciding on the appropriate level of complexity to develop a model to approach any management issue is a critical question. As a general principle, the simpler a model can be whilst still answering the questions asked of it, the better. The previous examples have shown that much can be gained from deterministic ODE models. Even though only the most trivial of these can be solved analytically, a simple model with relatively few parameters can shed more light on the factors that influence the qualitative behaviour of a system than can highly complex individually based stochastic models. Nevertheless, deterministic ODEs are not sufficient to answer every question in wildlife disease management. Time delays and age structure, as is shown by the Tasmanian devil example, are essential to predict the impact of some management interventions. There are also substantial difficulties in estimating parameters for very simple models. Empirical estimates of birth and death will almost always be age specific. When a population has reached a stable or stationary age distribution, single parameters describing both birth and death rates, will be those of the ‘average’ individual. However, the ‘average’ individual is a function of the age structure, which in turn is determined by the dynamics of the interaction, the age specific birth and death rates and possibly management interventions. An age structured model is therefore necessary to appropriately link empirical data with a model.
Models that explicitly include contact network and spatial structure have become increasingly widely used for wildlife disease (Davis et al. Reference Davis, Abbasi, Shah, Telfer and Begon2015). The structure of a contact network is potentially important for disease management for at least two reasons – it influences R 0 , with heterogeneous contact networks having higher R 0 than homogeneous equivalents with the same average number of contacts; and also contact networks can identify superspreaders against which interventions can be concentrated. However, contact networks are difficult to obtain for field populations, with a particular issue being ensuring that contacts are epidemiologically relevant. Whether the additional complexity of network models is justified will depend on both the host-parasite system and the purpose of the modelling exercise.
Some important questions in wildlife disease management are inherently stochastic in nature. Extinction of a host population and the equivalent process of fade out in a pathogen population are probabilistic events. Further, whilst stochasticity can sometimes be understood as random ‘fuzz’ around a deterministic skeleton stochastic models can sometimes have qualitatively different behaviours from those of their deterministic analogues (Coulson et al. Reference Coulson, Rohani and Pascual2004). An advantage of individually-based models is that they permit description of ecological processes as they actually occur, without the constraints of needing to ensure mathematical tractability. The difficulty is that these models are so complex that estimating the parameters for all the modelled processes and understanding how the dynamics of the system respond to the range of parameter sets within the plausible biological range is not straightforward. If it is as difficult to understand why a complex model behaves as it does as it is to understand the empirical dynamics of the real system, then little progress has been made.
A particular challenge with modelling infectious disease systems in vertebrates is that the time scale on which host dynamics change is very much longer than the time scale for pathogen dynamics. The population dynamics of large vertebrates are typically modelled on a yearly time step using discrete matrix-based approaches (Caswell, Reference Caswell1989) or their stochastic equivalents (Lacy, Reference Lacy1993). For any but the most slowly developing infections, a yearly time step is too long. One approach is to assume that epidemics run to completion rapidly within one individual time step (for example, Gerber et al. Reference Gerber, McCallum, Lafferty, Sabo and Dobson2005), which can allow for considerable progress to be made analytically. A second, simulation based approach is to link a discrete-time stochastic model for the hosts to a shorter time frame simulation model for the pathogen (for example, Bradshaw et al. Reference Bradshaw, McMahon, Miller, Lacy, Watts, Verant, Pollak, Fordham, Prowse and Brook2012).
Most wildlife management problems will need to be modelled with a range of different approaches. These will sometimes be determined by the stage of investigation: following the model guided fieldwork paradigm (Restif et al. Reference Restif, Hayman, Pulliam, Plowright, George, Luis, Cunningham, Bowen, Fooks, O'Shea, Wood and Webb2012), simple models will be used in the early iterations of the investigation, when empirical data are limited and the objective is to understand the broad qualitative features of the interaction and to identify those parameters to which system is most sensitive. Later in the process, more detailed and complex models are likely to be appropriate. Even when a complex model is necessary, it is helpful to construct simpler analogues to help identify why the model behaves as it does.
The disadvantage of overly complex models was nicely summarized in the paper by Cox et al. (Reference Cox, Donnelly, Bourne, Gettinby, McInerney, Morrison and Woodroffe2005) on simple models of badger culling:
‘Quasirealistic models… aim to get much closer to reality by representing, almost inevitably in a model implemented by computer rather than by mathematical analysis, as many features of reality as is feasible. Despite the attractions of greater realism, a common problem with such models is the need to specify the values of a considerable number of forms of dependence and the numerical values of unknown parameters, often… aspects about which little is known. The consequent need for extensive and systematic sensitivity analyses may undermine the usefulness of such models’
Parameterization and sensitivity analysis
The preceding quote leads onto the critical issue of linking models to data: parameterization and assessing the sensitivity of the model outcomes to uncertainty in the values of parameters and functional forms. The qualitative conclusions from very general models sometimes do not rely on detailed parameterization. As the previous examples have shown, if models are used to guide management, the objective is usually to identify the necessary minimum vaccination level, culling level or similar control strategy to reach a specified management target. This means that numerical estimates of the important parameters of the model are required and that it is essential to assess the sensitivity of the results to uncertainty in those parameter estimates.
If sufficient analytic progress can be made with a model so that some results can be presented algebraically, then inspection of the results can, in practice, amount to a sensitivity analysis. Where only numerical results are available, a formal sensitivity analysis is essential. Simply varying each parameter in turn across its range of uncertainty, keeping all the others at what is believed to be their most likely value, is not sufficient. Where only two parameters are subject to substantial uncertainty, a straightforward grid search across the plausible range of variation in each may be possible. This rapidly becomes impractical where there are multiple uncertain parameters. In this case, one approach is to use Latin hypercube sampling (Iman and Conover, Reference Iman and Conover1980), which uses parameters sampled without replacement across their plausible range. A number of software packages, such as ‘lhs’ in R implement this approach. Rushton et al. (Reference Rushton, Gurnell, Lurz and Fuller2002) used the method in a model to develop control strategies for grey squirrels.
Deriving parameter estimates and plausible ranges for them is critical, but rarely straightforward. Usually wildlife disease models use estimates from a variety of sources, including literature, unpublished data and expert opinion (see, for example, Bradshaw et al. Reference Bradshaw, McMahon, Miller, Lacy, Watts, Verant, Pollak, Fordham, Prowse and Brook2012). This may often be all that is possible and it is arguable that formal models based on informally derived parameters are preferable to simply relying on intuition. Nevertheless, the more rigorous the parameter estimation process, the more defensible will be the results. Recent developments in statistical analysis have enabled empirical data and dynamic models to be linked much more closely than has been possible in the past.
A perennial problem in ecology is that the variables we can observe or measure are in fact not those that are actually driving the dynamics, but merely estimates of them, subject to observational error. For example, in many wildlife disease systems it is possible to observe prevalence in a sample of individuals at points in time and space, but what we would like to infer would be the force of infection in time and space, although it is impossible to directly measure when and where individuals were exposed. Problems of this type can be approached using Bayesian–Monte Carlo–Markov chain methods.
Heisey et al. (Reference Heisey, Osnas, Cross, Joly, Langenberg and Miller2010a ) describe the application of these methods to estimate the force of infection of CWD in a population of white-tailed deer. This paper generated considerable controversy (Heisey et al. Reference Heisey, Osnas, Cross, Joly, Langenberg and Miller2010b ; Hodges, Reference Hodges2010; LaDeau, Reference LaDeau2010; Lele, Reference Lele2010; Waller, Reference Waller2010), with the suggestion that the approach was over-complex for the problem and that the statistical properties of the models were too poorly understood. These methods have enormous potential, but are potentially a minefield for ecologists and require specialist statistical collaborators. The combination of measurement and process error also occurs where the objective is to estimate parameters for a dynamical disease model from observations of observed cases through time. If the state of the system can often be considered as determined by its state in a previous time step, then the process can be modelled as a Markov chain, although the actual state (the real number of cases) cannot directly be observed. This is then a Partially Observed Markov Process, or state–space model. Methods to estimate epidemiological parameters from time series data have been developed and tested on human cholera data (Ionides et al. Reference Ionides, Breto and King2006). More recently, Blackwood et al. (Reference Blackwood, Streicker, Altizer and Rohani2013) used this methodology to parameterize an SEIR model of rabies in vampire bats using field data collected from Peru.
A third approach with much promise that also uses Bayesian approaches and Monte Carlo methods is Approximate Bayesian Computation (Toni et al. Reference Toni, Welch, Strelkowa, Ipsen and Stumpf2009). This is a way of deriving a posterior distribution for a parameter set without the necessity of being able to calculate a formal likelihood. In its simplest form, parameter sets are repeatedly selected from a proposal distribution (a prior) and used to simulate datasets from a model. If the simulated output is sufficiently close to the observed data, the parameter set is considered plausible. Otherwise, it is rejected and the procedure is repeated. After a sufficiently large number of such trials, this process will generate a posterior distribution of plausible values of the parameters. An obvious issue here is how ‘sufficiently close’ to the observed data is defined, and it is necessary to construct some form of distance function (which might be as simple as Euclidean distance) to measure the discrepancy between the observed and simulated data. There are a number of variations on this basic scheme to make it more efficient, several of which are implemented in an R package (Csilléry et al. Reference Csilléry, François and Blum2012).
Toni et al. (Reference Toni, Welch, Strelkowa, Ipsen and Stumpf2009) applied one of the variations on Approximate Bayesian Computation, a sequential Monte Carlo approach, to a small dataset giving the number of infected and recovered individuals with the common cold following an outbreak on the isolated island of Tristan da Cunha. Of interest to wildlife disease modellers is that this process was applied to a dataset of only 20 observations: this is not a method that can be used only with very large datasets. Approximate Bayesian Computation does not appear yet to have been widely applied to wildlife disease problems, although a recent paper uses the approach on data from bovine TB outbreaks in cattle in the UK (Brooks-Pollock et al. Reference Brooks-Pollock, Roberts and Keeling2014).
CONCLUSIONS
In conclusion, management requires selecting from a range of potential management actions (bearing in mind that deciding to ‘do nothing’ is a management action). In turn, this requires predicting how the system may respond to each of the potential actions. Inevitably, a model is always involved in prediction, although it may not necessarily be a formal mathematical model. The advantage of mathematical modelling is that assumptions are clearly written down, rather than being implicit, as is the case with more informal modelling approaches. This review has shown that a broad range of modelling approaches can be constructively applied to support decision-making in wildlife management problems. No single approach is inherently superior to all others and most systems will need to be modelled using a range of methods, often with complexity increasing iteratively as more data are available and the system is understood more fully (Restif et al. Reference Restif, Hayman, Pulliam, Plowright, George, Luis, Cunningham, Bowen, Fooks, O'Shea, Wood and Webb2012). The maxim that a model should no more be complex than is necessary to fulfil its function remains true – although modern computing power allows the construction of very complex simulations, they are not necessarily the best approach to all problems. Connecting models to data and confronting model predictions with data (Hilborn and Mangel, Reference Hilborn and Mangel1997) remains a major challenge, although recently developed tools have the potential to revolutionize model parameterization and fitting.
ACKNOWLEDGEMENTS
This paper was largely written during a period as a Visiting Research Scholar in the Department of Ecology and Evolutionary Biology, Princeton University.
FINANCIAL SUPPORT
My modelling of wildlife disease is supported by grants from the Australian Research Council (DP110102656, LP130101073) and US National Science Foundation (DEB1316549).





