INTRODUCTION
It is well recognized that reliable maps of the spatial distribution of parasitic diseases are required to help plan and evaluate disease control, and during the last decade there has been growing research interest in modelling disease risk (Hay et al. 2000, 2006). Most studies have modelled point prevalence data (Thomson et al. 1999; Kleinschmidt et al. 2001; Brooker et al. 2001, 2006; Clements et al. 2006) since this is an easily collected and readily available indicator. However, although prevalence data are often used for making recommendations for the need for control, data on the intensity of infection has greater relevance to the transmission dynamics of a given host-parasite system and for understanding the occurrence of morbidity (Anderson and May, 1991).
The modelling of infection intensity is nonetheless complicated by the fact that parasite distributions are highly aggregated within communities (Woolhouse et al. 1998; Shaw et al. 1998; Basáñez and Boussinesq, 1999) and by the presence of spatial correlation. In addition to parasite distributions, aggregated – or so-called overdispersed – distributions are a characteristic of several epidemiological phenomena including social networks (Zheng et al. 2006), infection exposure (Woolhouse et al. 1998) and wildlife distributions (Thogmartin et al. 2004). Aggregated distributions can often be fitted by the negative binomial distribution (Anderson, 1993) and previous analysis has employed negative binomial regression modelling to investigate the relationship between intensity of parasitic infection and a range of individual- and group-level risk factors (Nodtvedt et al. 2002; Yapi et al. 2005).
Studies modelling the spatial distribution of parasitic diseases have increasingly adopted a fully Bayesian geostatistical approach (Diggle et al. 2002; Carabin et al. 2003; Gemperli et al. 2004, 2006; Raso et al. 2005, 2006; Yang et al. 2005; Clements et al. 2006). This approach explicitly incorporates the spatial correlation structure of the data, the ability to include covariate effects and the comprehensive representation of uncertainty in the model outputs. Recently, Alexander and others (Alexander et al. 2000, 2003) have presented a negative binomial spatial model, which incorporates spatial correlation and adjusts for individual-level covariates such as age and sex. Their analysis, however, was explicative rather than predictive (limiting its utility for disease control decision-making), conducted on a small geographical scale and, unlike the Bayesian geostatistical modelling studies described above, did not include environmental factors which may have helped explain some of the observed heterogeneity.
In the present study, we extend the approach of Alexander and colleagues to model the spatial distribution of the intensity of Schistosoma mansoni infection in East Africa. The modelling of intensity of infection, as measured by quantitative faecal egg counts, has particular relevance for the targeting of control activities since intensity is related to schistosome transmission dynamics and is a key determinant of schistosome-related morbidity with high levels likely to induce greater morbidity. Our adopted approach provides estimates of the effects of various factors influencing infection patterns including individual-level variables, such as age and sex, and location-level environmental variables. We then follow a Bayesian geostatistical approach to generate predictive maps of infection intensity across the region, and assess uncertainty associated with predictions.
PATIENTS AND METHODS
Data sources
Individual-level data on intensity of Schistosoma mansoni infection were obtained from cross-sectional random samples of schoolchildren from dedicated school surveys conducted between 1999 and 2004 at 459 locations by national research teams under the auspices of the Schistosomiasis Control Initiative (SCI) in Tanzania (Clements et al. 2006) and in Uganda (Kabatereine et al. 2004) and by research projects in western Kenya (Brooker et al. 2001; Clarke et al. 2005). The locations of surveyed schools are shown in Fig. 1 and details of the studies are shown in Table 1. These data cover a large contiguous area of East Africa covering an area of approximately 1260 km (North/South)×590 km (East/West) and, to our knowledge, represent some of the most comprehensive geo-referenced data on the intensity of infection for any parasitic disease. No previous mass treatment had been undertaken in any of the schools. The details of the survey design, data collection and acquisition of ethical approval are reported in the original publications. Intensity of infection was based on the microscopic examination of 2 Kato-Katz smears derived from a single stool specimen, and expressed as eggs per gram of faeces (epg). As well as information on quantitative egg counts, individual-level factors including age and sex were also included in the final dataset.

Fig. 1. Distribution of school surveys and observed intensity of Schistosoma mansoni (as measured by the mean number of eggs per gram faeces in each location) in 31458 school children aged 5–22 years at 459 locations in East Africa conducted between 1999 and 2004. Locations of major lakes are also indicated.

Long-term climatic data (1982–2000) were obtained from the National Oceanographic and Atmospheric Administration's (NOAA) Advanced Very High Radiometer (AVHRR) which provides indirect estimates of land surface temperature (LST) and normalized difference vegetation index (NDVI). Estimates of elevation were obtained from an interpolated digital elevation model from the Global Land Information System (GLIS) of the United States Geological Survey (http://edcwww.cr.usgs.gov/landdaac/gtopo30/) and the location of inland water-bodies, obtained from the US National Imagery and Mapping Agency (NIMA) and transformed by FAO/GIS at the Food and Agriculture Organisation (FAO). For each school, Euclidian distance to in-land water bodies was calculated. The degree of urbanization, categorized into urban, periurban, rural and extreme rural, was derived from Tatem and colleagues (Tatem et al. 2005). These data were imported into the GIS ArcMap 8.1 (ESRI, Redlands, CA) and linked by geographical location to the parasitological data.
Statistical analysis
Initial analysis indicated that the distribution of egg counts were not Poisson distributed, with a predominance of zero and low values, such that the median egg count was 0 epg and the variance was 3·6×105, clearly indicative of overdispersion. This justified a multi-variable regression approach (to account for some of the additional sources of heterogeneity) using the negative binomial distribution (to model the overdispersion) in our statistical modelling and prediction. Negative binomial regression models were fitted in Stata/SE version 8.1 (Stata Corporation, College Station, Texas). Initially, univariate analyses were conducted and variables with Wald's P>0·2 were excluded from further analyses. With the remaining variables, backwards-stepwise regression was conducted using Wald's P>0·1 as the exit criterion and P[les ]0·05 as the entry criterion. In the final model, sex was included as an individual-level covariate and elevation and distance to perennial water bodies were included as school-level covariates. Modelling either the overdispersion parameter as a function of a range of covariates or the zero values separately from the positive values (using a zero-inflated model) did not improve the overall fit, justifying the subsequent use of a standard negative binomial regression model with a fixed value for the overdispersion parameter.
To provide an explanation of the overdispersion in the data and in particular to assess whether the overdispersion is spatially structured, we followed the approach of Alexander et al. (2000). In this, the total egg count of each individual was modelled as a negative binomial variate with overdispersion parameter k>0 which incorporates extra-Poisson variation. Larger values of k indicate less variability, with the limiting case k=∞ corresponding to the Poisson distribution. We model the logarithm of the mean of the distribution as an additive function of the individual-level covariate sex, the two school-level covariates elevation and distance to nearest inland perennial water body and a spatially-structured school-level random-effect. The spatial random-effect was modelled as a stationary Gaussian process with mean 0, variance σ2 and correlation function exp(−dij/α), where dij is the distance between villages i and j and the parameter α measures the rate at which the spatial correlation decays over distance, with α log 2 being a characteristic length, which we call the ‘half-distance’, over which the correlation reduces by half, and 3 α being the distance at which the correlation reduces to 0·05.
Bayesian inference was implemented via a Markov chain Monte Carlo algorithm using the model-based geostatistics framework of Diggle et al. (1998). For the particular application considered in this paper the specification of prior distributions for the model parameters was done along the lines of the work described by Alexander et al. (2000) and Diggle et al. (2002). Specifically, the prior distribution for k was chosen to be gamma with density proportional to k(1·5–1) exp(−0·01k) so that, a priori, k had a high variance. We chose independent improper uniform prior distributions for all the regression coefficients associated with the covariates and the constant term. For the parameters σ2 and α we adopted the following vague priors: f(σ2)∝1/σ2 and f(α)∝1/α2. In the absence of any prior knowledge about the model parameters, the choice of non-informative improper priors was dictated by practical considerations, e.g. convergence issues and allowing the data to have a greater influence in determining the posterior.
We simulated realizations from the posterior distributions by means of a single-component Metropolis-Hastings algorithm. The parameters were updated by using a random-walk Metropolis algorithm with a Gaussian proposal density for the regression parameters, log(σ2), log(α) and log(k). At each iteration, the updating of σ2 and α required the inversion of the n×n covariance matrix of the spatial effect, where n is the number of locations. In our example, n=459. The Markov chain was run for 110000 iterations. After an initial burn-in of 10000 iterations, the chain was sampled every 20th iteration to yield a sample of 5000 values from the posterior distribution of each of the model parameters. The convergence was judged by looking at the MCMC traces of the model parameters and also by computing the Monte Carlo errors. The traces differed in the extent to which they showed good mixing, but they all exhibited a reasonable degree of convergence to a stationary distribution. Spatial prediction was undertaken on a fine grid of 3304 locations with a grid-spacing of 12 km. At each prediction location 5000 values were simulated using the method outlined by Diggle et al. (1998). The Bayesian inference and prediction were undertaken using a program custom-written in the C language.
RESULTS
Intensity data were available for 31458 school children (15904 boys and 15554 girls) aged 5–22 years (mean age 11·5 years, median age 12 years, 90% aged between 6 and 16 years). The median prevalence of S. mansoni infection was 3·3% ranging from 0 to 97·2% by school. The overall mean egg count was 116 epg (ranging from 0 to 3234 epg faeces by school) (Table 1). Figure 1 displays the spatial variation in infection intensity and shows that intensity was highest along the shores of the major lakes and in Uganda, along the river Nile.
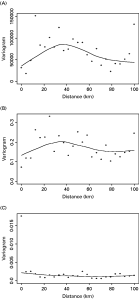
The results of the Bayesian geostatistical model are presented in Table 2. Model coefficients indicate that females had significantly lower egg counts than males and that higher egg counts are found in areas at low elevations and close to perennial water. The posterior mean of 0·137∗122≈16·7 km for α, the range of spatial correlation, corresponds to a ‘half-distance’ for correlation of 16·7∗log2≈11·6 km, with 3×16·7≈50·1 km being the distance at which the correlation reduces to 0·05. The 95% posterior interval for α of (11·1, 24·2) km indicates that the residual spatial variation operates on a small scale. This is in agreement with the empirical variogram of the mean number of eggs in each location in Fig. 2A which exhibits a rising trend up to a distance of around 40 km. The posterior mean value of the overdispersion parameter was 0·060, confirming that the data were highly overdispersed even after accounting for spatial correlation. In addition, the estimate of the overdispersion parameter for the non-spatial model was 0·031, suggesting that inclusion of the spatial random-effect accounted for some of the overdispersion and, despite similar posterior mean values, the Bayesian credible intervals were narrower for the non-spatial model than the spatial model. All the parameters have mostly symmetric posterior distributions excepting σ2 and α which are slightly positively skewed. The empirical variogram of the Pearson residuals from the fitted non-spatial regression model in Fig. 2B is quite similar to the variogram in Fig. 2A. This indicates that the non-spatial regression model is inadequate in explaining the short-range spatial structure, whereas the variogram of the residuals from the spatial model shown in Fig. 2C is essentially flat.

Fig. 2. (A) Empirical variogram of the mean number of eggs in each location. (B) Empirical variogram of the average of the Pearson residuals for each location from the non-spatial model. (C) Empirical variogram of the average of the Pearson residuals for each location from the spatial model. The curves were produced using a Loess smoother.

The map of the posterior mean predicted intensity value is presented in Fig. 3. Model predictions of infection intensity indicate a high intensity in areas adjacent to Lakes Victoria, Kyoga, Albert and the northern part of Lake Edward as well as along the Nile River valley in Uganda. Low intensity areas were predicted in northeast and southwest Uganda and much of northwest Tanzania away from the lakeshore. Fig. 4 presents the standard deviations of the modelled intensities. As expected, a lower level of uncertainty was apparent in locations close to observed data points and a higher level of uncertainty was apparent in locations distant from observed data points. Since observed data were well distributed across the region, most areas were characterized by a reasonable level of prediction certainty. An exception to this was northeast Uganda and areas between Lakes Victoria, Albert and Edward in western Uganda, areas which are too arid and too high, respectively to support transmission of S. mansoni, and therefore were not sampled.

Fig. 3. Predicted intensity of infection (epg) with Schistosoma mansoni in East Africa, adjusted for covariates (distance to perennial water body and elevation).

Fig. 4. Posterior standard deviations of the model predictions of the intensity of infection with Schistosoma mansoni in East Africa.
DISCUSSION
This study presents a novel application of Bayesian geostatistical modelling to predict intensity of infection with S. mansoni, a highly aggregated parasitological index. Results identify the role of environmental risk factors in explaining geographical heterogeneity in infection intensity and show how these factors can be used to develop a predictive map. Such a map provides an empirical basis for identifying priority areas when implementing control and for predicting the potential impact of control.
The observed risk factors are already well known and are consistent and interpretable with the epidemiology of infection and known biology of freshwater snails, the intermediate hosts for S. mansoni. Malacological studies confirm that Biomphalaria snail species in East Africa tend to prefer large water body habitats (Prentice et al. 1972; Lwambo et al. 1999). Furthermore, individuals living on or near the shore are more likely to undertake risky water contact behaviour, increasing their exposure to infection. Observed differences among males and females may also be exposure-related, although it is also suggested that hormonal differences between males and females may account for higher infection rates in males than females (Webster et al. 1997). The role of other host-specific factors, such as genetics, immunity, nutrition, hygienic behaviour and education, as risk factors is also recognized. Climatic conditions, primarily temperature and rainfall, have been shown to influence the distribution and density of snails and the rate of schistosomal development in the snail host (Appleton, 1978; Sturrock, 1993). At high altitudes, low temperatures cause snails to die before the cercariae mature from sporocysts, limiting transmission (Pflüger, 1980).
Our predictive map of schistosome transmission is less affected by seasonality than other, more seasonally dynamic, parasitic diseases, such as malaria. Although seasonal dynamics in schistosome transmission may occur, such fluctuations may be of little significance to the overall parasite equilibrium within communities. This is because the life-span of adult worms is typically much longer (1–10 years) than the periods in the year during which the basic reproductive number (Ro) is less than unity, and Ro will on average be greater than one, maintaining overall endemicity (Anderson, 1982).
Previous studies predicting parasitic diseases in Africa on the basis of published data suffer from certain methodological problems including dissimilar age groupings of surveys and use of different diagnostic techniques to assess infection (e.g. Kleinschmidt et al. 2001). The inclusion of survey data from comparable age groups collected using the same diagnostic method (Kato-Katz quantitative smear) reduces this inherent variability. However, methodological problems related to the limited sensitivity and specificity of single stool samples to detect light infection (de Vlas et al. 1993) constitutes a limitation of the current analysis and may widen the prediction errors by introducing greater variability into the estimates of infection intensity.
Our approach highlights a number of key methodological limitations and areas for further work. First, the current model does not account for anisotropic and non-stationary spatial variation. Data are currently being collected in other countries with SCI-supported control programmes, including Zambia in southern Africa and Burkina Faso, Mali and Niger in west Africa. These data cover wide areas with marked environmental diversity. Hence, there is scope of investigating the possible presence of anisotropy and non-stationarity in observed spatial variation. Second, there is the possibility that the degree of parasite aggregation may vary between endemic populations, reflecting area-specific differences in host exposure and immunity (Guyatt et al. 1994). We did not observe any variation in aggregation patterns with host age, presumably reflective of the relatively narrow age range of individuals included in the analysis, or according to environmental covariates. Third, zero-truncated negative binomial distribution has previously been used to describe patterns of Wuchereria bancrofti (Grenfell et al. 1990), Onchocerca volvulus (Filipe et al. 2005) and Loa loa (Pion et al. 2006) and may provide an alternative approach to modelling aggregated distributions. This would involve using a mixture model, i.e. a negative binomial distribution with an extra point mass at zero. Over the next few years improved approaches to modelling geostatistical processes and transmission dynamics will iteratively improve our ability to predict disease patterns for geographical targeting of interventions.
As well as identifying areas where population-based morbidity control, using praziquantel, is most warranted (Brooker and Michael, 2000; Brooker, 2002), spatial predictions of infection intensity can also help define the frequency of treatment required to reduce morbidity and to model the potential impact of treatment. Mathematical models of transmission dynamics (Chan et al. 1995) use mean intensity of infection to predict rates of re-infection over fixed time-intervals, and provide estimates of infections and heavy infections prevented each year and the number of morbidity cases/year prevented. The integration of Bayesian geostatistical modelling with transmission dynamics models will provide an important analytical platform to help better understand the epidemiology of schistosomiasis and provide a more robust evidence-based approach to implementing and evaluating control.
This project was supported by the Schistosomiasis Control Initiative which is generously supported by the Bill and Melinda Gates Foundation. S. B. is supported by a Wellcome Trust Advanced Training Fellowship (073656). We thank the many field workers who carried out the field surveys. We also thank Drs Narcis Kabateriene, Nicholas Lwambo, Sian Clarke, Benson Estambale and Njagi Kiambo for providing access to the survey data, Dr Simon Hay for providing the satellite data and Professor Alan Fenwick for his support and contributions.