Our object of study is a rational map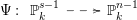 defined by homogeneous forms
defined by homogeneous forms 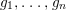 $g_{1},\ldots ,g_{n}$ , of the same degree
$g_{1},\ldots ,g_{n}$ , of the same degree 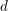 $d$ , in the homogeneous coordinate ring
$d$ , in the homogeneous coordinate ring 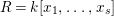 $R=k[x_{1},\ldots ,x_{s}]$ of
$R=k[x_{1},\ldots ,x_{s}]$ of 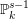 $\mathbb{P}_{k}^{s-1}$ . Our goal is to relate properties of
$\mathbb{P}_{k}^{s-1}$ . Our goal is to relate properties of 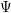 $\unicode[STIX]{x1D6F9}$ , of the homogeneous coordinate ring
$\unicode[STIX]{x1D6F9}$ , of the homogeneous coordinate ring 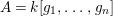 $A=k[g_{1},\ldots ,g_{n}]$ of the variety parameterized by
$A=k[g_{1},\ldots ,g_{n}]$ of the variety parameterized by 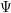 $\unicode[STIX]{x1D6F9}$ , and of the Rees algebra
$\unicode[STIX]{x1D6F9}$ , and of the Rees algebra  ${\mathcal{R}}(I)$ , the bihomogeneous coordinate ring of the graph of
${\mathcal{R}}(I)$ , the bihomogeneous coordinate ring of the graph of 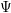 $\unicode[STIX]{x1D6F9}$ . For a regular map
$\unicode[STIX]{x1D6F9}$ . For a regular map 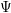 $\unicode[STIX]{x1D6F9}$ , for instance, we prove that
$\unicode[STIX]{x1D6F9}$ , for instance, we prove that  ${\mathcal{R}}(I)$ satisfies Serre’s condition
${\mathcal{R}}(I)$ satisfies Serre’s condition  $R_{i}$ , for some
$R_{i}$ , for some 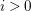 $i>0$ , if and only if
$i>0$ , if and only if  $A$ satisfies
$A$ satisfies 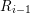 $R_{i-1}$ and
$R_{i-1}$ and  $\unicode[STIX]{x1D6F9}$ is birational onto its image. Thus, in particular,
$\unicode[STIX]{x1D6F9}$ is birational onto its image. Thus, in particular, 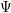 $\unicode[STIX]{x1D6F9}$ is birational onto its image if and only if
$\unicode[STIX]{x1D6F9}$ is birational onto its image if and only if 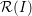 ${\mathcal{R}}(I)$ satisfies
${\mathcal{R}}(I)$ satisfies  $R_{1}$ . Either condition has implications for the shape of the core, namely,
$R_{1}$ . Either condition has implications for the shape of the core, namely,  $\text{core}(I)$ is the multiplier ideal of
$\text{core}(I)$ is the multiplier ideal of 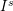 $I^{s}$ and
$I^{s}$ and  $\text{core}(I)=(x_{1},\ldots ,x_{s})^{sd-s+1}.$ Conversely, for
$\text{core}(I)=(x_{1},\ldots ,x_{s})^{sd-s+1}.$ Conversely, for 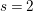 $s=2$ , either equality for the core implies birationality. In addition, by means of the generalized rows of the syzygy matrix of
$s=2$ , either equality for the core implies birationality. In addition, by means of the generalized rows of the syzygy matrix of 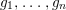 $g_{1},\ldots ,g_{n}$ , we give an explicit method to reduce the nonbirational case to the birational one when
$g_{1},\ldots ,g_{n}$ , we give an explicit method to reduce the nonbirational case to the birational one when  $s=2$ .
$s=2$ .
 $C^{(n)}$
$C^{(n)}$
 $F$-PURITY VERSUS LOG CANONICITY FOR POLYNOMIALS
$F$-PURITY VERSUS LOG CANONICITY FOR POLYNOMIALS