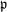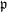1 Introduction
This work concerns duality phenomena in various triangulated categories of modules over Gorenstein algebras. By a Gorenstein algebra, we mean here an algebra
$A$
, finite dimensional over a field
$k$
, with the property that
$A$
has finite injective dimension both as a left module and a right module over itself. For such an
$A$
, the derived Nakayama functor is an equivalence:
$$\begin{eqnarray}\unicode[STIX]{x1D708}:\mathsf{D}^{\text{b}}(\operatorname{mod}A)\stackrel{{\sim}}{\longrightarrow }\mathsf{D}^{\text{b}}(\operatorname{mod}A)\quad \text{where }\unicode[STIX]{x1D708}(X)=\operatorname{Hom}_{k}(A,k)\otimes _{A}^{\mathbf{L}}X.\end{eqnarray}$$
Happel [Reference Happel19] proved that for perfect complexes
$X,Y$
, there is a natural isomorphism
$$\begin{eqnarray}\operatorname{Hom}_{k}(\operatorname{Hom}_{\mathsf{D}}(X,Y),k)\cong \operatorname{Hom}_{\mathsf{D}}(Y,\unicode[STIX]{x1D708}X),\end{eqnarray}$$
where
$\mathsf{D}:=\mathsf{D}^{\text{b}}(\operatorname{mod}A)$
. In other words, the Nakayama functor on
$\mathsf{D}$
restricts to a Serre functor, in the sense of Bondal and Kapranov [Reference Bondal and Kapranov12], on the full subcategory of perfect complexes.
In this work, we discover that Happel’s result is only the tip of an iceberg: it is a special case of a duality on all of
$\mathsf{D}$
, analogous to Grothendieck’s local duality for commutative Gorenstein algebras. The duality on
$\mathsf{D}$
also involves a graded-commutative algebra, namely the Hochschild cohomology
$\operatorname{HH}^{\ast }(A/k)$
of
$A$
over
$k$
that acts on
$\mathsf{D}$
via canonical homomorphisms of
$k$
-algebras
$$\begin{eqnarray}\operatorname{HH}^{\ast }(A/k)\longrightarrow \operatorname{Ext}_{A}^{\ast }(X,X)\quad \text{for each }X\in \mathsf{D}.\end{eqnarray}$$
In this way,
$\mathsf{D}$
acquires a structure of an
$\operatorname{HH}^{\ast }(A/k)$
-linear category.
In the remainder of Section 1, we fix a homogeneous
$k$
-subalgebra
$R$
of
$\operatorname{HH}^{\ast }(A/k)$
that is finitely generated as a
$k$
-algebra. To simplify the exposition, we assume
$R^{0}=k$
. This is not a great loss of generality for given any
$R$
as above, we can drop down to the subring
$k\oplus R^{{\geqslant}1}$
without sacrificing the finite generation. A natural choice for
$R$
is
$k\oplus \operatorname{HH}^{{\geqslant}1}(A/k)$
, assuming it is finitely generated, but, for example, when
$A$
is a Hopf algebra (such as the group algebra of a finite group), it is more natural to take
$R=\operatorname{Ext}_{A}^{\ast }(k,k)$
, the cohomology ring of
$A$
, for this is functorial in the ring argument, whilst the Hochschild cohomology is not.
Fix a homogeneous prime ideal
$\mathfrak{p}$
of
$R$
. Let
$\unicode[STIX]{x1D6FE}_{\mathfrak{p}}(\mathsf{D})$
be the triangulated category obtained from
$\mathsf{D}$
by localizing the graded morphisms at
$\mathfrak{p}$
and then taking the full triangulated subcategory of objects such that the graded endomorphisms are
$\mathfrak{p}$
-torsion. By construction,
$\unicode[STIX]{x1D6FE}_{\mathfrak{p}}(\mathsf{D})$
is an
$R_{\mathfrak{p}}$
-linear category, where
$R_{\mathfrak{p}}$
denotes the homogeneous localization of
$R$
at
$\mathfrak{p}$
. The Nakayama functor induces an equivalence
$$\begin{eqnarray}\unicode[STIX]{x1D708}_{\mathfrak{p}}:\unicode[STIX]{x1D6FE}_{\mathfrak{p}}(\mathsf{D})\xrightarrow[{}]{{\sim}}\unicode[STIX]{x1D6FE}_{\mathfrak{p}}(\mathsf{D}).\end{eqnarray}$$
Let
$\operatorname{Spec}^{+}(R)$
denote the set of homogeneous prime ideals in
$R$
not containing
$R^{{\geqslant}1}$
, the unique maximal homogeneous ideal of
$R$
. For each
$\mathfrak{p}$
in
$\operatorname{Spec}^{+}(R)$
, we write
$I(\mathfrak{p})$
for the injective hull of the graded
$R$
-module
$R/\mathfrak{p}$
. Our local Serre duality statement reads as follows.
Theorem 1.1. Let
$\mathfrak{p}$
be in
$\operatorname{Spec}^{+}(R)$
and let
$d$
be the Krull dimension of
$R/\mathfrak{p}$
. Then
$\unicode[STIX]{x1D6F4}^{-d}\circ \unicode[STIX]{x1D708}_{\mathfrak{p}}$
is a Serre functor for
$\unicode[STIX]{x1D6FE}_{\mathfrak{p}}(\mathsf{D})$
, in that, for all
$X,Y$
in
$\unicode[STIX]{x1D6FE}_{\mathfrak{p}}(\mathsf{D})$
, there are natural isomorphisms
$$\begin{eqnarray}\operatorname{Hom}_{R_{\mathfrak{p}}}(\operatorname{Hom}_{\unicode[STIX]{x1D6FE}_{\mathfrak{ p}}(\mathsf{D})}^{\ast }(X,Y),I(\mathfrak{p}))\cong \operatorname{Hom}_{\unicode[STIX]{x1D6FE}_{\mathfrak{p}}(\mathsf{D})}(Y,\unicode[STIX]{x1D6F4}^{-d}\unicode[STIX]{x1D708}_{\mathfrak{p}}(X)).\end{eqnarray}$$
This result is proved toward the end of Section 5 from a more general statement concerning the category
$\operatorname{GProj}A$
of (possibly infinite dimensional) Gorenstein projective modules. These are
$A$
-modules
$M$
with the property that
$\operatorname{Ext}_{A}^{i}(M,P)=0$
for
$i\geqslant 1$
and projective
$A$
-module
$P$
. The connection to
$\mathsf{D}$
is through its subcategory,
$\operatorname{Gproj}A$
, consisting of finite dimensional modules. These are precisely the maximal Cohen–Macaulay
$A$
-modules, in the terminology of Buchweitz [Reference Buchweitz14].
The stable category,
$\text{}\underline{\operatorname{GProj}}A$
, of
$\operatorname{GProj}A$
is a compactly generated triangulated category, with compact objects equivalent to
$\text{}\underline{\operatorname{Gproj}}A$
, the stabilization of
$\operatorname{Gproj}A$
. Buchweitz [Reference Buchweitz14] proved that there is an equivalence of triangulated categories
$$\begin{eqnarray}\text{}\underline{\operatorname{Gproj}}A\stackrel{{\sim}}{\longrightarrow }\mathsf{D}_{\text{sg}}(A):=\mathsf{D}^{\text{b}}(\operatorname{mod}A)/\mathsf{D}^{\text{b}}(\operatorname{proj}A),\end{eqnarray}$$
where
$\mathsf{D}_{\text{sg}}(A)$
is the singularity category, also known as the stable derived category, of
$A$
. There is a natural
$R$
-action on
$\text{}\underline{\operatorname{GProj}}A$
and the equivalence above is compatible with the induced
$R$
-actions. For each prime ideal
$\mathfrak{p}$
in
$\operatorname{Spec}^{+}(R)$
, the canonical functors induce equivalences of triangulated categories
$$\begin{eqnarray}\unicode[STIX]{x1D6FE}_{\mathfrak{p}}(\text{}\underline{\operatorname{Gproj}}A)\xrightarrow[{}]{~\sim ~}\unicode[STIX]{x1D6FE}_{\mathfrak{p}}(\mathsf{D})\xrightarrow[{}]{~\sim ~}\unicode[STIX]{x1D6FE}_{\mathfrak{p}}(\mathsf{D}_{\text{sg}}(A))\end{eqnarray}$$
compatible with
$R_{\mathfrak{p}}$
-actions, by Lemma 5.5. Thus, to prove Theorem 1.1, it suffices to prove the corresponding statement for
$\text{}\underline{\operatorname{Gproj}}A$
and, equivalently, for the singularity category of
$A$
. This also explains the title of this paper.
To that end, we consider the subcategory
$\unicode[STIX]{x1D6E4}_{\mathfrak{p}}(\text{}\underline{\operatorname{GProj}}A)$
of
$\text{}\underline{\operatorname{GProj}}A$
consisting of the
$\mathfrak{p}$
-local
$\mathfrak{p}$
-torsion modules. These are the Gorenstein projective
$A$
-modules
$M$
with the property that for each finite dimensional
$A$
-module
$C$
, every element of
$\text{}\underline{\operatorname{Hom}}_{A}^{\ast }(C,M)$
, the graded
$R$
-module of morphisms in
$\text{}\underline{\operatorname{GProj}}A$
, is annihilated by some power of
$\mathfrak{p}$
, and the natural map
$\text{}\underline{\operatorname{Hom}}_{A}^{\ast }(C,M)\rightarrow \text{}\underline{\operatorname{Hom}}^{\ast }(C,M)_{\mathfrak{p}}$
is bijective. Then
$\unicode[STIX]{x1D6E4}_{\mathfrak{p}}(\text{}\underline{\operatorname{GProj}}A)$
is also a compactly generated triangulated category and the full subcategory of compact objects is equivalent, up to direct summands, to
$\unicode[STIX]{x1D6FE}_{\mathfrak{p}}(\text{}\underline{\operatorname{Gproj}}A)$
. There is an idempotent functor
$\unicode[STIX]{x1D6E4}_{\mathfrak{p}}:\text{}\underline{\operatorname{GProj}}A\rightarrow \text{}\underline{\operatorname{GProj}}A$
with image the
$\mathfrak{p}$
-local
$\mathfrak{p}$
-torsion modules; see Section 3 for details. The central result of this work is a local duality theorem for this category.
Theorem 1.2. Let
$\mathfrak{p}$
be in
$\operatorname{Spec}^{+}(R)$
and let
$d$
be the Krull dimension of
$R/\mathfrak{p}$
. Let
$X,Y$
be Gorenstein projective
$A$
-modules and suppose that
$X$
is finite dimensional. Then there is a natural isomorphism
$$\begin{eqnarray}\operatorname{Hom}_{R}(\operatorname{Ext}_{A}^{\ast }(X,Y),I(\mathfrak{p}))\cong \text{}\underline{\operatorname{Hom}}_{A}(Y,\unicode[STIX]{x1D6FA}^{d}\unicode[STIX]{x1D6E4}_{\mathfrak{p}}\operatorname{GP}\unicode[STIX]{x1D708}(X)).\end{eqnarray}$$
Here
$\operatorname{GP}$
is the Gorenstein projective approximation functor and
$\unicode[STIX]{x1D6FA}$
is the syzygy functor; see Section 2 for details. The theorem above is contained in Theorem 5.1.
Theorems 1.1 and 1.2 are formulated in terms of an arbitrary (but fixed) subalgebra
$R$
of the Hochschild cohomology of
$A$
. It is thus natural to ask how these results are related as we vary
$R$
. This point is addressed in Remark 5.8. Another issue is what transpires in Theorem 1.1 if we set
$\mathfrak{p}=R^{{\geqslant}1}$
. When the ring
$R$
is such that, in addition to being Noetherian, the
$R$
-module
$\operatorname{Ext}_{A}^{\ast }(X,X)$
is finitely generated for each
$X\in \mathsf{D}$
, the subcategory
$\unicode[STIX]{x1D6E4}_{\mathfrak{m}}(\mathsf{D})$
is precisely the subcategory of perfect complexes and the analogue of Theorem 1.1 is Happel’s duality; see Remark 5.6.
The duality statements above are modeled on, and extensions of, analogous results for representation of modules over finite group schemes established in [Reference Benson, Iyengar, Krause and Pevtsova11]. In that context, the stable category of (finite dimensional) Gorenstein projectives is the stable category of (finite dimensional) representations. We refer to that work for antecedents of these results and for applications, notably, the existence of AR-triangles in
$\unicode[STIX]{x1D6FE}_{\mathfrak{p}}(\mathsf{D})$
. The proof of the results in op. cit. exploited the tensor structure on the module categories in question, but, in fact, the arguments can be readily adapted to deal with the general case, as we do here. In doing so, it became clear that local duality is a feature of Gorenstein algebras in general.
2 Gorenstein algebras
In this section, we recall basic notions and results from the homological theory of Gorenstein algebras, mainly pertaining to duality. The main result we are working toward is Theorem 2.9. This result is well known, in principle, but unavailable in the literature in the form we need; so a complete proof is given.
Throughout this work,
$k$
will be a field and
$A$
a finite dimensional
$k$
-algebra.
Let
$\operatorname{Mod}A$
be the category of all (left)
$A$
-modules and
$\operatorname{mod}A$
its full subcategory consisting of finitely generated
$A$
-modules. The full subcategory of
$\operatorname{Mod}A$
consisting of projective
$A$
-modules is denoted by
$\operatorname{Proj}A$
, and we set
$\operatorname{proj}A:=\operatorname{Proj}A\cap \operatorname{mod}A$
. The injective analogues are denoted by
$\operatorname{Inj}A$
and
$\operatorname{inj}A$
, respectively. In what follows for
$A$
-modules
$M,N$
, we set
$$\begin{eqnarray}\displaystyle \text{}\underline{\operatorname{Hom}}_{A}(M,N) & := & \displaystyle \operatorname{Hom}_{A}(M,N)/\{\unicode[STIX]{x1D719}\mid \unicode[STIX]{x1D719}\text{ factors through a projective}\}\nonumber\\ \displaystyle \overline{\operatorname{Hom}}_{A}(M,N) & := & \displaystyle \operatorname{Hom}_{A}(M,N)/\{\unicode[STIX]{x1D719}\mid \unicode[STIX]{x1D719}\text{ factors through an injective}\}.\nonumber\end{eqnarray}$$
When
$M$
and
$N$
are finitely generated, it suffices to consider maps
$\unicode[STIX]{x1D719}$
that factor through
$\operatorname{proj}A$
and
$\operatorname{inj}A$
, respectively.
2.1 Vector space duality
For any
$A$
-module
$M$
, we set
$$\begin{eqnarray}DM:=\operatorname{Hom}_{k}(M,k),\end{eqnarray}$$
viewed as an
$A^{\text{op}}$
-module. The assignment
$M\mapsto DM$
induces an equivalence
$$\begin{eqnarray}(\operatorname{mod}A)^{\text{op}}\xrightarrow[{}]{~\sim ~}\operatorname{mod}A^{\text{op}}\end{eqnarray}$$
which restricts to an equivalence
$(\operatorname{proj}A)^{\text{op}}\xrightarrow[{}]{{\sim}}\operatorname{inj}A^{\text{op}}$
. The functor
$D$
also extends to an equivalence between the corresponding bounded derived categories:
$$\begin{eqnarray}D:{\mathsf{D}^{\text{b}}(\operatorname{mod}A)}^{\text{op}}\xrightarrow[{}]{~\sim ~}\mathsf{D}^{\text{b}}(\operatorname{mod}A^{\text{op}}).\end{eqnarray}$$
Let
$\mathsf{D}^{\text{b}}(\operatorname{proj}A)$
denote the bounded derived category of
$\operatorname{proj}A$
. We identify it with the subcategory of
$\mathsf{D}^{\text{b}}(\operatorname{mod}A)$
consisting of perfect complexes.
2.2 The Nakayama functor
Observe that
$DA$
is an
$A$
-bimodule. The functor
$\unicode[STIX]{x1D708}:\operatorname{Mod}A\rightarrow \operatorname{Mod}A$
that assigns to each
$A$
-module
$M$
the
$A$
-module
$$\begin{eqnarray}\unicode[STIX]{x1D708}M:=DA\otimes _{A}M\end{eqnarray}$$
is called the Nakayama functor. The functor
$\unicode[STIX]{x1D708}^{-}:=\operatorname{Hom}_{A}(DA,-)$
is its right adjoint. Both functors preserve all products and coproducts since
$DA$
is a finitely presented module on either side. The Nakayama functor is an equivalence if
$A$
is self-injective but not in general. However, one has the following result. In the sequel, given an
$A$
-module
$X$
, we write
$\operatorname{Add}X$
for the full subcategory of
$\operatorname{Mod}A$
consisting of direct summands of coproducts of copies of
$X$
and
$\operatorname{Prod}X$
where products are used instead of coproducts.
Lemma 2.1. For any finite dimensional
$k$
-algebra
$A$
, one has
$\operatorname{Proj}A=\operatorname{Prod}A$
and
$\operatorname{Inj}A=\operatorname{Add}DA$
, and
$\unicode[STIX]{x1D708}$
restricts to an equivalence
$\operatorname{Proj}A\xrightarrow[{}]{{\sim}}\operatorname{Inj}A$
.
Proof. Adjunction yields an isomorphism of functors
$\operatorname{Hom}_{A}(-,DA)\cong \operatorname{Hom}_{k}(-,k)$
. Thus, the
$A$
-module
$DA$
is a faithful injective. As
$A$
is Noetherian, this implies that
$\operatorname{Inj}A=\operatorname{Add}DA$
; see [Reference Cartan and Eilenberg15, Chapter I, Exercise 8]. Hence,
$\unicode[STIX]{x1D708}$
restricts to a functor
$\operatorname{Proj}A\rightarrow \operatorname{Inj}A$
. Here we are using the fact that also
$\operatorname{Proj}A=\operatorname{Add}A$
. Moreover,
$\unicode[STIX]{x1D708}A=DA$
and
$\unicode[STIX]{x1D708}^{-}DA=A$
; the latter is by adjunction. Since
$\unicode[STIX]{x1D708}$
and
$\unicode[STIX]{x1D708}^{-}$
preserve coproducts, it follows that the unit
$\operatorname{id}\rightarrow \unicode[STIX]{x1D708}^{-}\unicode[STIX]{x1D708}$
and counit
$\unicode[STIX]{x1D708}\unicode[STIX]{x1D708}^{-}\rightarrow \operatorname{id}$
of the adjunction are isomorphisms, and, hence,
$\unicode[STIX]{x1D708}$
and
$\unicode[STIX]{x1D708}^{-}$
are equivalences of categories:
Finally,
$\operatorname{Inj}A=\operatorname{Prod}DA$
since
$DA$
is a faithful injective, and
$\unicode[STIX]{x1D708}^{-}$
preserves products, so the equivalence above yields
$\operatorname{Proj}A=\operatorname{Prod}A$
.
2.3 The singularity category
Buchweitz [Reference Buchweitz14] introduced the stable derived category of
$A$
as the Verdier quotient
$$\begin{eqnarray}\mathsf{D}_{\text{sg}}(A):=\mathsf{D}^{\text{b}}(\operatorname{mod}A)/\mathsf{D}^{\text{b}}(\operatorname{proj}A).\end{eqnarray}$$
This category was rediscovered by Orlov [Reference Orlov22], who called it the singularity category of
$A$
, and our notation reflects this terminology. When the global dimension of
$A$
is finite, one has
$\mathsf{D}_{\text{sg}}(A)=0$
, so the singularity category is one measure of the deviation of
$A$
from finite global dimension.
The singularity category can be realized (in more than one way) as a stabilization of a subcategory of
$\operatorname{mod}A$
. This is described next.
2.4 Gorenstein algebras
Henceforth, the
$k$
-algebra
$A$
will be Gorenstein (also known as Iwanaga–Gorenstein): the injective dimension of
$A$
as a left
$A$
-module and as a right
$A$
-module is finite. In this case, the injective dimensions are the same; this was proved by Zaks [Reference Zaks25]. Evidently, when
$A$
is Gorenstein, so is
$A^{\text{op}}$
, the opposite algebra of
$A$
. The Gorenstein condition on
$A$
is equivalent to the following. An
$A$
-module has finite projective dimension if and only if it has finite injective dimension; see, for example, [Reference Buchweitz14, Lemma 5.1.1]. This implies that the equivalence (2.1) restricts to an equivalence
$\mathsf{D}^{\text{b}}(\operatorname{proj}A)^{\text{op}}\xrightarrow[{}]{{\sim}}\mathsf{D}^{\text{b}}(\operatorname{proj}A^{\text{op}})$
and hence induces an equivalence
$$\begin{eqnarray}D:{\mathsf{D}_{\text{sg}}(A)}^{\text{op}}\xrightarrow[{}]{~\sim ~}\mathsf{D}_{\text{sg}}(A^{\text{op}}).\end{eqnarray}$$
This will be used often in the sequel.
2.5 Gorenstein projective and Gorenstein injective modules
An
$A$
-module
$X$
is Gorenstein projective if
$$\begin{eqnarray}\operatorname{Ext}_{A}^{i}(X,P)=0\quad \text{for each projective }P\text{ and each }i\geqslant 1.\end{eqnarray}$$
Since
$\operatorname{Proj}A=\operatorname{Prod}A$
, by Lemma 2.1, the condition above is equivalent to
$$\begin{eqnarray}\operatorname{Ext}_{A}^{i}(X,A)=0\quad \text{for each }i\geqslant 1.\end{eqnarray}$$
We write
$\operatorname{GProj}A$
for the category of Gorenstein projective
$A$
-modules and set
$$\begin{eqnarray}\operatorname{Gproj}A:=\operatorname{GProj}A\cap \operatorname{mod}A.\end{eqnarray}$$
These are the maximal Cohen–Macaulay
$A$
-modules in Buchweitz’s terminology.
Standard arguments (following, e.g., [Reference Happel19, Section 9]) yield that
$\operatorname{GProj}A$
is a Frobenius exact category with projective objects the projective
$A$
-modules. We write
$\text{}\underline{\operatorname{GProj}}A$
for the corresponding stable category; it is a triangulated category. Its thick subcategory consisting of the finitely generated modules is denoted by
$\text{}\underline{\operatorname{Gproj}}A$
, for it identifies with the stabilization of
$\operatorname{Gproj}A$
.
On
$\operatorname{GProj}A$
, the syzygy functor
$\unicode[STIX]{x1D6FA}$
has an inverse, denoted by
$\unicode[STIX]{x1D6FA}^{-1}$
, that is well defined up to projective summands. This is the translation on
$\text{}\underline{\operatorname{GProj}}A$
.
An
$A$
-module
$Y$
is Gorenstein injective if
$$\begin{eqnarray}\operatorname{Ext}_{A}^{i}(Q,Y)=0\quad \text{for each injective }Q\text{ and each }i\geqslant 1.\end{eqnarray}$$
Again, Lemma 2.1 implies that the condition above is equivalent to
$$\begin{eqnarray}\operatorname{Ext}_{A}^{i}(DA,Y)=0\quad \text{for each }i\geqslant 1.\end{eqnarray}$$
We write
$\operatorname{GInj}A$
for the category of Gorenstein injective modules and set
$\operatorname{Ginj}A:=\operatorname{GInj}A\cap \operatorname{mod}A$
. The stabilization of
$\operatorname{GInj}A$
is denoted by
$\overline{\operatorname{GInj}}A$
, and the subcategory of finitely generated modules is
$\overline{\operatorname{Ginj}}A$
. These are triangulated categories, where the translation
$\unicode[STIX]{x1D6F4}Y$
of a
$Y\in \operatorname{GInj}A$
is the cokernel of an embedding into an injective
$A$
-module:
$$\begin{eqnarray}0\longrightarrow Y\longrightarrow I\longrightarrow \unicode[STIX]{x1D6F4}Y\longrightarrow 0.\end{eqnarray}$$
The equivalence
$D:(\operatorname{mod}A)^{\text{op}}\xrightarrow[{}]{{\sim}}\operatorname{mod}A^{\text{op}}$
restricts to equivalences
$$\begin{eqnarray}(\operatorname{Gproj}A)^{\text{op}}\xrightarrow[{}]{~\sim ~}\operatorname{Ginj}A^{\text{op}}\qquad \text{and}\qquad (\operatorname{proj}A)^{\text{op}}\xrightarrow[{}]{~\sim ~}\operatorname{inj}A^{\text{op}}\end{eqnarray}$$
and hence induces an equivalence of triangulated categories
$$\begin{eqnarray}D:\text{}\underline{\operatorname{Gproj}}A\xrightarrow[{}]{~\sim ~}\overline{\operatorname{Ginj}}A^{\text{op}}.\end{eqnarray}$$
Here is the result on realizing the singularity category as a stabilization.
Proposition 2.2. The inclusions
$\operatorname{Gproj}A\rightarrow \mathsf{D}^{\text{b}}(\operatorname{mod}A)$
and
$\operatorname{Ginj}A\rightarrow \mathsf{D}^{\text{b}}(\operatorname{mod}A)$
induce triangle equivalences
$$\begin{eqnarray}p:\text{}\underline{\operatorname{Gproj}}A\xrightarrow[{}]{{\sim}}\mathsf{D}_{\text{sg}}(A)\qquad \text{and}\qquad q:\overline{\operatorname{Ginj}}A\xrightarrow[{}]{{\sim}}\mathsf{D}_{\text{sg}}(A).\end{eqnarray}$$
Proof. The first equivalence is [Reference Buchweitz14, Theorem 4.4.1], and the second equivalence follows from that statement applied to
$A^{\text{op}}$
and dualities (2.4).
2.6 Approximations
The following result—see [Reference Buchweitz14, Lemma 5.1.1]—is straightforward to verify.
Lemma 2.3. Let
$X$
be a Gorenstein projective module.
-
(1)
$\operatorname{Ext}_{A}^{i}(X,F)=0$
for any module
$F$
of finite projective dimension and
$i\geqslant 1$
. -
(2) If an
$A$
-linear map
$X\rightarrow N$
factors through a module of finite projective dimension, then it factors through a projective module.
The analogous statements for Gorenstein injective modules also hold. ◻
This has the following consequence.
Lemma 2.4. If
$X$
is Gorenstein projective and
$Y$
is Gorenstein injective, then
$$\begin{eqnarray}\text{}\underline{\operatorname{Hom}}_{A}(X,Y)=\overline{\operatorname{Hom}}_{A}(X,Y).\end{eqnarray}$$
Proof. Given Lemma 2.3, one has to verify that a map
$f:M\rightarrow N$
factors through a module of finite projective dimension if and only if it factors through a module of finite injective dimension. This is a tautology as these categories coincide.
The following result is due to Auslander and Buchweitz and is the cornerstone of their theory of maximal Cohen–Macaulay approximations. There is an analogous statement involving Gorenstein injectives.
Proposition 2.5. Every finite dimensional
$A$
-module
$M$
fits into exact sequences
$$\begin{eqnarray}0\rightarrow F_{M}\rightarrow X_{M}\rightarrow M\rightarrow 0\qquad \text{and}\qquad 0\rightarrow M\rightarrow F^{M}\rightarrow X^{M}\rightarrow 0,\end{eqnarray}$$
where
$X_{M},X^{M}$
are in
$\operatorname{Gproj}A$
and
$F_{M},F^{M}$
have finite projective dimension. For
$X\in \operatorname{Gproj}A$
and
$F$
of finite projective dimension, these sequences induce bijections
$$\begin{eqnarray}\text{}\underline{\operatorname{Hom}}_{A}(X,X_{M})\xrightarrow[{}]{{\sim}}\text{}\underline{\operatorname{Hom}}_{A}(X,M)\qquad \text{and}\qquad \text{}\underline{\operatorname{Hom}}_{A}(F^{M},F)\xrightarrow[{}]{{\sim}}\text{}\underline{\operatorname{Hom}}_{A}(M,F).\end{eqnarray}$$
Proof. This is part of [Reference Buchweitz14, Theorems 5.1.2, 5.1.4]; see also [Reference Auslander and Buchweitz4, Theorems 1.8, 2.8].
We write
$\operatorname{GP}(M):=X_{M}$
for the Gorenstein projective approximation of
$M$
. It follows from the preceding result that
$X_{M}$
is well defined in
$\text{}\underline{\operatorname{Gproj}}A$
.
Lemma 2.6. The Gorenstein projective approximation
$\operatorname{GP}$
induces a triangle equivalence
$\overline{\operatorname{Ginj}}A\xrightarrow[{}]{{\sim}}\text{}\underline{\operatorname{Gproj}}A$
satisfying
$q\cong p\circ \operatorname{GP}$
, where
$p,q$
are the functors in Proposition 2.2.
Proof. Since
$pF=0$
for any
$A$
-module
$F$
of finite projective dimension, Proposition 2.5 implies
$qY\cong p\operatorname{GP}(Y)$
for any Gorenstein injective module
$Y$
. This yields also that
$\operatorname{GP}$
is a triangle equivalence since
$p,q$
are triangle equivalences.
Remark 2.7. When
$A$
is self-injective, the projective and injective
$A$
-modules coincide and hence
$\operatorname{GProj}A=\operatorname{GInj}A$
. Conversely, when the (projective) module
$A$
is Gorenstein injective,
$A$
is self-injective. Consider an exact sequence
$$\begin{eqnarray}0\longrightarrow A\longrightarrow I\longrightarrow \unicode[STIX]{x1D6F4}A\longrightarrow 0,\end{eqnarray}$$
where
$I$
is injective. If
$A$
is Gorenstein injective, then so is
$\unicode[STIX]{x1D6F4}A$
, and hence the sequence above splits, as the injective dimension of
$A$
is finite. Thus,
$A$
is injective.
Example 6.3 describes a Gorenstein algebra that is not self-injective and identifies modules that are Gorenstein projective but not Gorenstein injective.
2.7 The Nakayama functor again
The Nakayama functor restricts to equivalences
Therefore, one gets an induced equivalence
$\unicode[STIX]{x1D708}:\text{}\underline{\operatorname{Gproj}}A\xrightarrow[{}]{{\sim}}\overline{\operatorname{Ginj}}A$
. In particular, one has
$\unicode[STIX]{x1D708}\unicode[STIX]{x1D6FA}^{-1}X\simeq \unicode[STIX]{x1D6F4}\unicode[STIX]{x1D708}X$
for each
$X$
in
$\text{}\underline{\operatorname{Gproj}}A$
.
The derived Nakayama functor, which we also denote
$\unicode[STIX]{x1D708}$
, is also an equivalence:
$$\begin{eqnarray}\unicode[STIX]{x1D708}:\mathsf{D}^{\text{b}}(\operatorname{mod}A)\stackrel{{\sim}}{\longrightarrow }\mathsf{D}^{\text{b}}(\operatorname{mod}A)\quad \text{where }M\mapsto DA\otimes _{A}^{\mathbf{L}}M.\end{eqnarray}$$
On the other hand, since the complexes of finite projective dimension are the same as those of finite injective dimension (because
$A$
is Gorenstein),
$DA$
is in the thick subcategory of
$\mathsf{D}^{\text{b}}(\operatorname{mod}A^{\text{op}})$
generated by
$A$
, and, hence, by duality,
$A$
is in the thick subcategory of
$\mathsf{D}^{\text{b}}(\operatorname{mod}A)$
generated by
$DA$
, that is to say, by
$\unicode[STIX]{x1D708}A$
. It follows that the derived Nakayama functor satisfies
$$\begin{eqnarray}\unicode[STIX]{x1D708}(\mathbf{D}^{\text{b}}(\operatorname{proj}A))=\mathbf{D}^{\text{b}}(\operatorname{proj}A).\end{eqnarray}$$
This is the essence of Happel duality. It induces an equivalence
$\bar{\unicode[STIX]{x1D708}}$
on the singularity category that makes the following square commutative:
The vertical equivalences are from Proposition 2.2.
2.8 The Auslander transpose
Let
$X$
be a finite dimensional Gorenstein projective
$A$
-module. In what follows, we will often need the fact that the
$A^{\text{op}}$
-module
$\operatorname{Hom}_{A}(X,A)$
is also Gorenstein projective. This can be verified directly from the definition; see, for example, [Reference Buchweitz14, Lemma 4.2.2]. Any projective presentation
$$\begin{eqnarray}P_{1}\longrightarrow P_{0}\longrightarrow X\longrightarrow 0\end{eqnarray}$$
induces an exact sequence of
$A^{\text{op}}$
-modules.
$$\begin{eqnarray}0\longrightarrow \operatorname{Hom}_{A}(X,A)\longrightarrow \operatorname{Hom}_{A}(P_{0},A)\longrightarrow \operatorname{Hom}_{A}(P_{1},A)\longrightarrow \operatorname{Tr}X\longrightarrow 0.\end{eqnarray}$$
The
$A^{\text{op}}$
-module
$\operatorname{Tr}X$
is the Auslander transpose of
$X$
, and it depends only on
$X$
up to projective summands. It is a Gorenstein projective
$A^{\text{op}}$
-module since it identifies with
$\operatorname{Hom}_{A}(\unicode[STIX]{x1D6FA}^{2}X,A)$
. Applying
$D$
yields an exact sequence of
$A$
-modules
$$\begin{eqnarray}0\longrightarrow D\operatorname{Tr}X\longrightarrow \unicode[STIX]{x1D708}P_{1}\longrightarrow \unicode[STIX]{x1D708}P_{0}\longrightarrow \unicode[STIX]{x1D708}X\longrightarrow 0.\end{eqnarray}$$
Since
$\operatorname{Tr}X$
is Gorenstein projective over
$A^{\text{op}}$
, the
$A$
-module
$D\operatorname{Tr}X$
is Gorenstein injective and the exact sequence above implies that there is an isomorphism
$$\begin{eqnarray}\unicode[STIX]{x1D6F4}^{2}(D\operatorname{Tr}X)\cong \unicode[STIX]{x1D708}X\end{eqnarray}$$
in
$\overline{\operatorname{Ginj}}A$
.
2.9 Auslander–Reiten duality
We are ready to state the main results of this section. For similar statements, we refer to [Reference Amiot1, Reference Auslander and Reiten6].
Proposition 2.8. Let
$A$
be a Gorenstein algebra and
$X,Y$
Gorenstein projective
$A$
-modules. When
$X$
is finite dimensional, there is a natural isomorphism
$$\begin{eqnarray}D\text{}\underline{\operatorname{Hom}}_{A}(X,Y)\cong \text{}\underline{\operatorname{Hom}}_{A}(Y,\unicode[STIX]{x1D6FA}^{-1}\operatorname{GP}(D\operatorname{Tr}X)).\end{eqnarray}$$
Proof. The exact sequence
$0\rightarrow \unicode[STIX]{x1D6FA}Y\rightarrow P\rightarrow Y\rightarrow 0$
with
$P$
projective induces the first of the following isomorphisms:
$$\begin{eqnarray}\displaystyle D\text{}\underline{\operatorname{Hom}}_{A}(X,Y) & \cong & \displaystyle D\operatorname{Ext}_{A}^{1}(X,\unicode[STIX]{x1D6FA}Y)\nonumber\\ \displaystyle & \cong & \displaystyle \overline{\operatorname{Hom}}_{A}(\unicode[STIX]{x1D6FA}Y,D\operatorname{Tr}X)\nonumber\\ \displaystyle & \cong & \displaystyle \text{}\underline{\operatorname{Hom}}_{A}(\unicode[STIX]{x1D6FA}Y,D\operatorname{Tr}X)\nonumber\\ \displaystyle & \cong & \displaystyle \text{}\underline{\operatorname{Hom}}_{A}(\unicode[STIX]{x1D6FA}Y,\operatorname{GP}(D\operatorname{Tr}X))\nonumber\\ \displaystyle & \cong & \displaystyle \text{}\underline{\operatorname{Hom}}_{A}(Y,\unicode[STIX]{x1D6FA}^{-1}\operatorname{GP}(D\operatorname{Tr}X)).\nonumber\end{eqnarray}$$
The second isomorphism is Auslander–Reiten duality [Reference Auslander3, Proposition I.3.4], whilst the third isomorphism is from Lemma 2.4 since
$\unicode[STIX]{x1D6FA}Y$
is Gorenstein projective and
$D\operatorname{Tr}X$
is Gorenstein injective. The fourth isomorphism follows from Proposition 2.5, and the final one is clear since
$\unicode[STIX]{x1D6FA}$
is an equivalence on
$\text{}\underline{\operatorname{Gproj}}A$
.
As in Bondal and Kapranov [Reference Bondal and Kapranov12, Section 3], a Serre functor on a
$k$
-linear, Hom-finite, additive category
$\mathsf{C}$
is an equivalence
$F:\mathsf{C}\rightarrow \mathsf{C}$
along with natural isomorphisms
$$\begin{eqnarray}D\operatorname{Hom}_{\mathsf{C}}(X,Y)\cong \operatorname{Hom}_{\mathsf{C}}(Y,FX)\end{eqnarray}$$
for all objects
$X,Y$
in
$\mathsf{C}$
.
The following result subsumes the formula for the Serre functor on the stable module category of a self-injective algebra.
Theorem 2.9. Let
$A$
be a Gorenstein algebra. Then
$$\begin{eqnarray}\unicode[STIX]{x1D6FA}\circ \operatorname{GP}\circ \unicode[STIX]{x1D708}:\text{}\underline{\operatorname{Gproj}}A\xrightarrow[{}]{{\sim}}\text{}\underline{\operatorname{Gproj}}A\qquad \text{and}\qquad \unicode[STIX]{x1D6F4}^{-1}\circ \bar{\unicode[STIX]{x1D708}}:\mathsf{D}_{\text{sg}}(A)\xrightarrow[{}]{{\sim}}\mathsf{D}_{\text{sg}}(A)\end{eqnarray}$$
are Serre functors.
Proof. For any Gorenstein projective
$A$
-module
$X$
, one has a sequence of isomorphisms in
$\text{}\underline{\operatorname{Gproj}}A$
, where the first and the last one are by construction,
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FA}^{-1}\operatorname{GP}(D\operatorname{Tr}X) & = & \displaystyle \unicode[STIX]{x1D6F4}\operatorname{GP}(D\operatorname{Tr}X)\nonumber\\ \displaystyle & \cong & \displaystyle \operatorname{GP}(\unicode[STIX]{x1D6F4}D\operatorname{Tr}X)\nonumber\\ \displaystyle & \cong & \displaystyle \operatorname{GP}(\unicode[STIX]{x1D6F4}^{-1}\unicode[STIX]{x1D708}X)\nonumber\\ \displaystyle & \cong & \displaystyle \unicode[STIX]{x1D6F4}^{-1}(\operatorname{GP}\unicode[STIX]{x1D708}X)\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D6FA}(\operatorname{GP}\unicode[STIX]{x1D708}X).\nonumber\end{eqnarray}$$
The second and the fourth isomorphisms hold because
$\operatorname{GP}$
is a triangle functor, and the third one is by (2.6). Thus, Proposition 2.8 yields that
$\unicode[STIX]{x1D6FA}\circ \operatorname{GP}\circ \unicode[STIX]{x1D708}$
is a Serre functor on
$\text{}\underline{\operatorname{GProj}}A$
, as claimed. The description of the Serre functor on
$\mathsf{D}_{\text{sg}}(A)$
is then a consequence of Lemma 2.6 and (2.5).
2.10 Compact generation
So far, the results have mostly dealt with the categories
$\text{}\underline{\operatorname{Gproj}}A$
and
$\overline{\operatorname{Ginj}}A$
consisting of finite dimensional modules. To prove the local duality theorem announced in Section 1, we need to work in larger categories,
$\text{}\underline{\operatorname{GProj}}A$
and
$\overline{\operatorname{GInj}}A$
. To this end, we recall the following result, which is well known at least for self-injective algebras.
Proposition 2.10. The stable categories
$\text{}\underline{\operatorname{GProj}}A$
and
$\overline{\operatorname{GInj}}A$
are compactly generated triangulated categories, and the full subcategories of compact objects identify with
$\text{}\underline{\operatorname{Gproj}}A$
and
$\overline{\operatorname{Ginj}}A$
, respectively.
Proof. The Nakayama functor induces a triangle equivalence
$\text{}\underline{\operatorname{GProj}}A\xrightarrow[{}]{{\sim}}\overline{\operatorname{GInj}}A$
, identifying
$\text{}\underline{\operatorname{Gproj}}A$
with
$\overline{\operatorname{Ginj}}A$
; the quasi-inverse is given by
$\operatorname{Hom}_{A}(D(A),-)$
. It thus suffices to verify the assertions about
$\overline{\operatorname{GInj}}A$
.
It follows from [Reference Iyengar and Krause20, Section 5] that
$\overline{\operatorname{GInj}}A$
is compactly generated; it remains to identify the compact objects. If
$X$
is a finite dimensional module, then
$\overline{\operatorname{Hom}}_{A}(X,-)$
preserves direct sums. Thus, every module in
$\overline{\operatorname{Ginj}}A$
is compact in
$\overline{\operatorname{GInj}}A$
.
On the other hand, for any nonzero module
$Y$
in
$\overline{\operatorname{GInj}}A$
, there exists a finite dimensional module
$M$
such that
$\overline{\operatorname{Hom}}_{A}(M,Y)\neq 0$
; this is because
$Y$
is not injective. Choose a Gorenstein injective approximation
$M\rightarrow W$
, using the analogue of Proposition 2.5 for Gorenstein injective modules. Then
$$\begin{eqnarray}\overline{\operatorname{Hom}}_{A}(W,Y)\cong \overline{\operatorname{Hom}}_{A}(M,Y)\neq 0,\end{eqnarray}$$
which implies that
$\overline{\operatorname{Ginj}}A$
is all the compact objects of
$\overline{\operatorname{GInj}}A$
.
3 Cohomology and localization
In this section, we recall basic notions and constructions concerning certain localization functors on triangulated categories with ring actions. The material is needed to state and prove the results in Sections 4 and 5. The main triangulated category of interest is the stable category of Gorenstein projective modules. Primary references for the material presented here are [Reference Benson, Iyengar and Krause7, Reference Benson, Iyengar and Krause8].
3.1 Triangulated categories with central action
Let
$\mathsf{T}$
be a triangulated category with suspension
$\unicode[STIX]{x1D6F4}$
. Given objects
$X$
and
$Y$
in
$\mathsf{T}$
, consider the graded abelian groups
$$\begin{eqnarray}\operatorname{Hom}_{\mathsf{T}}^{\ast }(X,Y)=\bigoplus _{i\in \mathbb{Z}}\operatorname{Hom}_{\mathsf{T}}(X,\unicode[STIX]{x1D6F4}^{i}Y)\qquad \text{and}\qquad \operatorname{End}_{\mathsf{T}}^{\ast }(X)=\operatorname{Hom}_{\mathsf{T}}^{\ast }(X,X).\end{eqnarray}$$
Composition makes
$\operatorname{End}_{\mathsf{T}}^{\ast }(X)$
a graded ring and
$\operatorname{Hom}_{\mathsf{T}}^{\ast }(X,Y)$
a left-
$\operatorname{End}_{\mathsf{T}}^{\ast }(Y)$
right-
$\operatorname{End}_{\mathsf{T}}^{\ast }(X)$
module.
Let
$R$
be a graded-commutative ring. We say the triangulated category
$\mathsf{T}$
is
$R$
-linear or that
$R$
acts on
$\mathsf{T}$
, if for each
$X$
in
$\mathsf{T}$
, there is a homomorphism of graded rings
$\unicode[STIX]{x1D719}_{X}:R\rightarrow \operatorname{End}_{\mathsf{T}}^{\ast }(X)$
such that the induced left and right actions of
$R$
on
$\operatorname{Hom}_{\mathsf{T}}^{\ast }(X,Y)$
are compatible in the following sense. For any
$r\in R$
and
$\unicode[STIX]{x1D6FC}\in \operatorname{Hom}_{\mathsf{T}}^{\ast }(X,Y)$
, one has
$$\begin{eqnarray}\unicode[STIX]{x1D719}_{Y}(r)\unicode[STIX]{x1D6FC}=(-1)^{|r||\unicode[STIX]{x1D6FC}|}\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D719}_{X}(r).\end{eqnarray}$$
In what follows, we fix a compactly generated
$R$
-linear triangulated category
$\mathsf{T}$
and write
$\mathsf{T}^{c}$
for its full subcategory of compact objects.
3.2 Graded modules
In the remainder of this section,
$R$
will be a graded-commutative Noetherian ring. We will only be concerned with homogeneous elements and ideals in
$R$
. In this spirit, “localization” will mean homogeneous localization, and
$\operatorname{Spec}R$
will denote the set of homogeneous prime ideals in
$R$
.
Given graded
$R$
-modules
$M$
and
$N$
, we denote by
$\operatorname{Hom}_{R}(M,N)$
the
$R$
-linear maps
$\unicode[STIX]{x1D719}:M\rightarrow N$
such that
$\unicode[STIX]{x1D719}(M^{i})\subseteq N^{i}$
for all
$i\in \mathbb{Z}$
, and
$$\begin{eqnarray}\operatorname{Hom}_{R}^{\ast }(M,N)=\bigoplus _{i\in \mathbb{Z}}\operatorname{Hom}_{R}(M,N[i])\end{eqnarray}$$
where
$N[i]^{p}=N^{i+p}$
for all
$i,p\in \mathbb{Z}$
.
3.3 Localization
Fix an ideal
$\mathfrak{a}$
in
$R$
. An
$R$
-module
$M$
is
$\mathfrak{a}$
-torsion if
$M_{\mathfrak{q}}=0$
for all
$\mathfrak{q}$
in
$\operatorname{Spec}R$
with
$\mathfrak{a}\not \subseteq \mathfrak{q}$
. Analogously, an object
$X$
in
$\mathsf{T}$
is
$\mathfrak{a}$
-torsion if the
$R$
-module
$\operatorname{Hom}_{\mathsf{T}}^{\ast }(C,X)$
is
$\mathfrak{a}$
-torsion for all
$C\in \mathsf{T}^{c}$
. The full subcategory of
$\mathfrak{a}$
-torsion objects
$$\begin{eqnarray}\unicode[STIX]{x1D6E4}_{{\mathcal{V}}(\mathfrak{a})}\mathsf{T}:=\{X\in \mathsf{T}\mid X\text{ is }\mathfrak{a}\text{-torsion}\}\end{eqnarray}$$
is localizing and the inclusion
$\unicode[STIX]{x1D6E4}_{{\mathcal{V}}(\mathfrak{a})}\mathsf{T}\subseteq \mathsf{T}$
admits a right adjoint, denoted by
$\unicode[STIX]{x1D6E4}_{{\mathcal{V}}(\mathfrak{a})}$
.
Fix a
$\mathfrak{p}$
in
$\operatorname{Spec}R$
. An
$R$
-module
$M$
is
$\mathfrak{p}$
-local if the localization map
$M\rightarrow M_{\mathfrak{p}}$
is invertible, and an object
$X$
in
$\mathsf{T}$
is
$\mathfrak{p}$
-local if the
$R$
-module
$\operatorname{Hom}_{\mathsf{T}}^{\ast }(C,X)$
is
$\mathfrak{p}$
-local for all
$C\in \mathsf{T}^{c}$
. Consider the full subcategory of
$\mathsf{T}$
of
$\mathfrak{p}$
-local objects
$$\begin{eqnarray}\mathsf{T}_{\mathfrak{p}}:=\{X\in \mathsf{T}\mid X\text{ is }\mathfrak{p}\text{-local}\}\end{eqnarray}$$
and the full subcategory of
$\mathfrak{p}$
-local and
$\mathfrak{p}$
-torsion objects
$$\begin{eqnarray}\unicode[STIX]{x1D6E4}_{\mathfrak{p}}\mathsf{T}:=\{X\in \mathsf{T}\mid X\text{ is }\mathfrak{p}\text{-local and }\mathfrak{p}\text{-torsion}\}.\end{eqnarray}$$
Note that
$\unicode[STIX]{x1D6E4}_{\mathfrak{p}}\mathsf{T}\subseteq \mathsf{T}_{\mathfrak{p}}\subseteq \mathsf{T}$
are localizing subcategories. The inclusion
$\mathsf{T}_{\mathfrak{p}}\rightarrow \mathsf{T}$
admits a left adjoint
$X\mapsto X_{\mathfrak{p}}$
, while the inclusion
$\unicode[STIX]{x1D6E4}_{\mathfrak{p}}\mathsf{T}\rightarrow \mathsf{T}_{\mathfrak{p}}$
admits a right adjoint. We denote by
$\unicode[STIX]{x1D6E4}_{\mathfrak{p}}:\mathsf{T}\rightarrow \unicode[STIX]{x1D6E4}_{\mathfrak{p}}\mathsf{T}$
the composition of those adjoints; it is the local cohomology functor with respect to
$\mathfrak{p}$
(see [Reference Benson, Iyengar and Krause7, Reference Benson, Iyengar and Krause8] for explained notions and details).
The following observation is clear.
Lemma 3.1. For any element
$r$
in
$R\setminus \mathfrak{p}$
, say of degree
$n$
, and
$\mathfrak{p}$
-local object
$X$
, the natural map
$X\xrightarrow[{}]{r}\unicode[STIX]{x1D6F4}^{n}X$
is an isomorphism. ◻
3.4 Koszul objects
Fix objects
$X,Y$
in
$\mathsf{T}$
. Any element
$b$
in
$R^{d}$
induces a morphism
$X\rightarrow \unicode[STIX]{x1D6F4}^{d}X$
and let
$X/\!/b$
denote its mapping cone. This gives a morphism
$X\rightarrow \unicode[STIX]{x1D6F4}^{-d}(X/\!/b)$
. For a sequence of elements
$\mathbf{b}:=b_{1},\ldots ,b_{n}$
in
$R$
set
$X/\!/\mathbf{b}:=X_{n}$
, where
$$\begin{eqnarray}X_{0}:=X\qquad \text{and}\qquad X_{i}:=X_{i-1}/\!/b_{i}\quad \text{for }1\leqslant i\leqslant n.\end{eqnarray}$$
It is easy to check that for
$s=\sum _{i}|b_{i}|$
, there is an isomorphism
$$\begin{eqnarray}\operatorname{Hom}_{\mathsf{T}}(X,Y/\!/\mathbf{b})\cong \operatorname{Hom}_{\mathsf{T}}(X/\!/\mathbf{b},\unicode[STIX]{x1D6F4}^{s+n}Y).\end{eqnarray}$$
3.5 Injective cohomology objects
Given an object
$C$
in
$\mathsf{T}^{\mathsf{c}}$
and an injective
$R$
-module
$I$
, Brown representability yields an object
$T(C,I)$
in
$\mathsf{T}$
such that
$$\begin{eqnarray}\operatorname{Hom}_{R}^{\ast }(\operatorname{Hom}_{\mathsf{T}}^{\ast }(C,-),I)\cong \operatorname{Hom}_{\mathsf{T}}^{\ast }(-,T(C,I)).\end{eqnarray}$$
This yields a functor
$$\begin{eqnarray}T:\mathsf{T}^{\mathsf{c}}\times \operatorname{Inj}R\longrightarrow \mathsf{T}.\end{eqnarray}$$
For each
$\mathfrak{p}$
in
$\operatorname{Spec}R$
, we write
$I(\mathfrak{p})$
for the injective hull of
$R/\mathfrak{p}$
and set
$$\begin{eqnarray}T_{\mathfrak{p}}:=T(-,I(\mathfrak{p})),\end{eqnarray}$$
viewed as a functor
$\mathsf{T}^{\mathsf{c}}\rightarrow \mathsf{T}$
. For objects
$C$
and
$D$
in
$\mathsf{T}^{\mathsf{c}}$
, applying (3.2) twice, one gets a natural
$R$
-linear isomorphism
$$\begin{eqnarray}\operatorname{Hom}_{\mathsf{T}}^{\ast }(T(C,I),T(D,I))\cong \operatorname{Hom}_{R}^{\ast }(\operatorname{Hom}_{R}^{\ast }(\operatorname{Hom}_{\mathsf{T}}^{\ast }(C,D),I),I).\end{eqnarray}$$
4 Hochschild and Tate cohomology
Let
$k$
be a field and
$A$
a finite dimensional Gorenstein
$k$
-algebra. The enveloping algebra of
$A$
is the
$k$
-algebra
$A^{e}:=A\otimes _{k}A^{\text{op}}$
; it is also Gorenstein, by Proposition 6.1, but this observation does not play a role in the sequel. The Hochschild cohomology of the
$k$
-algebra
$A$
is
$$\begin{eqnarray}\operatorname{HH}^{\ast }(A/k):=\operatorname{Ext}_{A^{e}}^{\ast }(A,A).\end{eqnarray}$$
This is a graded-commutative
$k$
-algebra.
When
$X$
and
$Y$
are Gorenstein projective
$A$
-modules, we set
$$\begin{eqnarray}\text{}\underline{\operatorname{Hom}}_{A}^{\ast }(X,Y)=\bigoplus _{i\in \mathbb{Z}}\text{}\underline{\operatorname{Hom}}_{A}(X,\unicode[STIX]{x1D6FA}^{-i}Y).\end{eqnarray}$$
This is the Tate cohomology of
$X,Y$
. There is a canonical homomorphism
$$\begin{eqnarray}\operatorname{Ext}_{A}^{\ast }(X,Y)\longrightarrow \text{}\underline{\operatorname{Hom}}_{A}^{\ast }(X,Y),\end{eqnarray}$$
of graded abelian groups, induced from the canonical morphism
$\mathbf{t}X\rightarrow \mathbf{p}X$
from a complete projective resolution to a projective resolution of
$X$
; see [Reference Buchweitz14, 6.2]. In particular, this map is surjective in degree
$0$
and bijective in positive degrees.
4.1 Action on
$\operatorname{GProj}A$
For any
$A$
-module
$M$
, there is a canonical map
$$\begin{eqnarray}\operatorname{HH}^{\ast }(A/k)\xrightarrow[{}]{-\otimes _{A}M}\operatorname{Ext}_{A}^{\ast }(M,M)\end{eqnarray}$$
that is a morphism of graded
$k$
-algebras. When
$X$
is Gorenstein projective, composing the map above with the one in (4.1), one gets a homomorphism of
$k$
-algebras
$$\begin{eqnarray}\unicode[STIX]{x1D719}_{X}:\operatorname{HH}^{\ast }(A/k)\longrightarrow \text{}\underline{\operatorname{Hom}}_{A}^{\ast }(X,X)\end{eqnarray}$$
and this induces an action of
$\operatorname{HH}^{\ast }(A/k)$
on
$\text{}\underline{\operatorname{GProj}}A$
, in the sense of Section 3. It follows from the construction of the action that for any element
$b\in \operatorname{HH}^{\ast }(A/k)$
and morphism
$f:X\rightarrow Y$
in
$\text{}\underline{\operatorname{GProj}}A$
, there is a natural morphism
$f/\!/b:X/\!/b\rightarrow Y/\!/b$
. This observation will be used often in the sequel.
Assumption 4.1. We fix a homogeneous
$k$
-subalgebra
$R$
of
$\operatorname{HH}^{\ast }(A/k)$
such that
-
(1)
$R^{0}=k$
; -
(2)
$R$
is finitely generated as a
$k$
-algebra.
Condition (1) implies that
$R^{{\geqslant}1}$
is the unique maximal ideal of
$R$
, which allows us to import the results from [Reference Benson, Iyengar, Krause and Pevtsova11]. Imposing it is not a loss of generality. Indeed,
$A$
decomposes as a direct product of connected algebras, and for a connected algebra
$A$
, the ring
$\operatorname{HH}^{0}(A/k)$
, being the center of
$A$
, is a finite dimensional local ring; so the inclusion
$R^{0}\subseteq \operatorname{HH}^{0}(A/k)$
induces a bijection on spectra.
The finite generation of the
$k$
-algebra
$R$
is equivalent to the condition that the ring
$R$
is Noetherian; see [Reference Bruns and Herzog13, Proposition 1.5.4]. Since the
$\operatorname{HH}^{\ast }(A/K)$
-action on
$\text{}\underline{\operatorname{GProj}}A$
restricts to an
$R$
-action, the Noetherian property of
$R$
allows one to invoke the constructions and results presented in Section 3.
4.2 Base change
Let
$K/k$
be an extension of fields and set
$$\begin{eqnarray}A_{K}:=K\otimes _{k}A.\end{eqnarray}$$
This is a finite dimensional
$K$
-algebra, and extension of scalars
$$\begin{eqnarray}\operatorname{Mod}A\longrightarrow \operatorname{Mod}A_{K},\qquad X\mapsto X_{K}=K\otimes _{k}X\end{eqnarray}$$
and restriction
$$\begin{eqnarray}\operatorname{Mod}A_{K}\longrightarrow \operatorname{Mod}A,\qquad X\mapsto X\downarrow _{A}=\operatorname{Hom}_{K}(K,X)\end{eqnarray}$$
form an adjoint pair of exact functors. The result below is standard.
Lemma 4.2. For
$A$
-modules
$X$
and
$Y$
, the canonical
$K$
-linear map
$$\begin{eqnarray}K\otimes _{k}\operatorname{Hom}_{A}(X,Y)\longrightarrow \operatorname{Hom}_{A_{K}}(X_{K},Y_{K})\end{eqnarray}$$
is a isomorphism when
$X$
, or
$K$
, is finite dimensional over
$k$
.◻
Lemma 4.3. Extension and restriction preserve projectivity and injectivity; in particular, the
$K$
-algebra
$A_{K}$
is Gorenstein. Moreover, extension and restriction preserve Gorenstein projectivity.
Proof. We will use without mention that both extension and restriction preserve coproducts. Extension of scalars takes
$A$
to
$A_{K}$
and hence projective
$A$
-modules to projective
$A_{K}$
-modules. Moreover, since
$A$
is finite dimensional over
$k$
, the natural map
$\operatorname{Hom}_{k}(A,k)_{K}\rightarrow \operatorname{Hom}_{K}(A_{K},K)$
is an isomorphism, by Lemma 4.2. It follows from Lemma 2.1 that
$(-)_{K}$
restricts to a functor
$\operatorname{Inj}A\rightarrow \operatorname{Inj}A_{K}$
.
Viewed as an
$A$
-module,
$A_{K}$
is a (possibly) infinite direct sum of copies of
$A$
and, in particular, projective. It follows that restriction preserves projectivity. That it also preserves injectivity follows from the fact that it is right adjoint to extension of scalars, which is an exact functor.
If
$X$
is a Gorenstein projective
$A$
-module, then the
$A_{K}$
-module
$X_{K}$
is Gorenstein projective, for one has
$$\begin{eqnarray}\operatorname{Ext}_{A_{K}}^{i}(X_{K},A_{K})\cong \operatorname{Ext}_{A}^{i}(X,A_{K}\downarrow _{A})\cong 0\quad \text{for }i\geqslant 1.\end{eqnarray}$$
The first isomorphism is adjunction and the second one holds because
$A_{K}$
is projective as an
$A$
-module.
The
$A_{K}$
-module
$\operatorname{Hom}_{k}(K,A)$
is isomorphic to
$\operatorname{Hom}_{k}(K,k)\otimes _{k}A$
, and, hence, it is projective. Thus, if
$X$
is a Gorenstein projective
$A_{K}$
-module, one gets
$$\begin{eqnarray}\operatorname{Ext}_{A}^{i}(X\downarrow _{A},A)\cong \operatorname{Ext}_{A_{K}}^{i}(X,\operatorname{Hom}_{k}(K,A))\cong 0\quad \text{for }i\geqslant 1,\end{eqnarray}$$
where the first isomorphism is again by adjunction. It follows that
$X\downarrow _{A}$
is Gorenstein projective.
There are isomorphisms of
$K$
-algebras
$$\begin{eqnarray}(A_{K})^{e}\cong (A^{e})_{K}\qquad \text{and}\qquad \operatorname{HH}^{\ast }(A_{K}/K)\cong K\otimes _{k}\operatorname{HH}^{\ast }(A/k).\end{eqnarray}$$
Thus, extension of scalars yields a ring homomorphism
$\operatorname{HH}^{\ast }(A/k)\rightarrow \operatorname{HH}^{\ast }(A_{K}/K)$
, and setting
$R_{K}:=K\otimes _{k}R$
, one gets a ring homomorphism
$$\begin{eqnarray}R\longrightarrow R_{K}.\end{eqnarray}$$
Observe that the
$K$
-subalgebra
$R_{K}$
of
$\operatorname{HH}^{\ast }(A_{K}/K)$
satisfies the conditions in Assumption 4.1.
The action of Hochschild cohomology on
$\text{}\underline{\operatorname{GProj}}A$
is compatible with extension of scalars and restriction, in that, for any
$X,Y\in \text{}\underline{\operatorname{GProj}}A$
, the natural map
$$\begin{eqnarray}\text{}\underline{\operatorname{Hom}}_{A}(X,Y)\longrightarrow \text{}\underline{\operatorname{Hom}}_{A_{K}}(X_{K},Y_{K})\end{eqnarray}$$
of graded abelian groups, induced by Lemma 4.2, is compatible with the homomorphism
$\operatorname{HH}^{\ast }(A/k)\rightarrow \operatorname{HH}^{\ast }(A_{K}/K)$
, as is the adjunction isomorphism
$$\begin{eqnarray}\text{}\underline{\operatorname{Hom}}_{A}(X,Z\downarrow _{A})\cong \text{}\underline{\operatorname{Hom}}_{A_{K}}(X_{K},Z)\end{eqnarray}$$
for any
$Z$
in
$\text{}\underline{\operatorname{GProj}}A_{K}$
. The following result is a special case of [Reference Benson, Iyengar and Krause9, Theorem 7.7]; a proof tailored to the present context is provided for readability.
Lemma 4.4. Let
$\mathfrak{a}$
be an ideal in
$R$
and
$\mathfrak{b}$
an ideal in
$R_{K}$
.
-
(1) For
$X$
in
$\text{}\underline{\operatorname{GProj}}A$
, there is a natural isomorphism
$$\begin{eqnarray}(\unicode[STIX]{x1D6E4}_{{\mathcal{V}}(\mathfrak{a})}X)_{K}\cong \unicode[STIX]{x1D6E4}_{{\mathcal{V}}(\mathfrak{a}R_{K})}(X_{K}).\end{eqnarray}$$
-
(2) If
$Y$
in
$\text{}\underline{\operatorname{GProj}}A_{K}$
is
$\mathfrak{b}$
-torsion, then
$Y\downarrow _{A}$
is
$(\mathfrak{b}\cap R)$
-torsion.
Proof. (1) Suppose
$\mathfrak{a}=(r_{1},\ldots ,r_{n})$
. There is then a natural isomorphism of functors
$\unicode[STIX]{x1D6E4}_{{\mathcal{V}}(\mathfrak{a})}\cong \unicode[STIX]{x1D6E4}_{{\mathcal{V}}(r_{1})}\circ \cdots \circ \unicode[STIX]{x1D6E4}_{{\mathcal{V}}(r_{n})}$
; see [Reference Benson, Iyengar and Krause7, Proposition 6.1]. Thus, we can assume
$\mathfrak{a}=(r)$
, a principal ideal. Since
$(-)_{K}$
preserves coproducts, the statement follows from an explicit description of
$\unicode[STIX]{x1D6E4}_{{\mathcal{V}}(r)}$
in terms of homotopy colimits; see [Reference Benson, Iyengar and Krause8, Proposition 2.9].
(2) Let
$C$
be a compact object in
$\text{}\underline{\operatorname{GProj}}A$
, that is to say, a finite dimensional (over
$k$
) Gorenstein projective
$A$
-module; see Proposition 2.10. The
$A_{K}$
-module
$C_{K}$
is evidently finite dimensional over
$K$
; it is also Gorenstein projective, by Lemma 4.3. In particular,
$\text{}\underline{\operatorname{Hom}}_{A_{K}}(C_{K},Y)$
is
$\mathfrak{b}$
-torsion. It remains to recall what was noted above: the adjunction isomorphism
$$\begin{eqnarray}\text{}\underline{\operatorname{Hom}}_{A}(C,Y\downarrow _{A})\cong \text{}\underline{\operatorname{Hom}}_{A_{K}}(C_{K},Y)\end{eqnarray}$$
is compatible with the homomorphism
$R\rightarrow R_{K}$
.
As usual,
$\operatorname{Spec}^{+}(R)$
denotes the set of prime ideals that do not contain
$R^{{\geqslant}1}$
. Next, we recall a construction from [Reference Benson, Iyengar, Krause and Pevtsova10] of a field extension
$K/k$
and a closed point in
$\operatorname{Spec}^{+}(R)_{K}$
lying over a given point in
$\operatorname{Spec}^{+}(R)$
.
Construction 4.5. Let
$R$
be a finitely generated, graded
$k$
-algebra with
$R^{0}=k$
. Fix a point
$\mathfrak{p}$
in
$\operatorname{Spec}^{+}(R)$
, and let
$d$
be the Krull dimension of
$R/\mathfrak{p}$
.
Choose elements
$\mathbf{a}:=a_{0},\ldots ,a_{d-1}$
in
$R$
of the same degree such that their image in
$R/\mathfrak{p}$
is algebraically independent over
$k$
and
$R/\mathfrak{p}$
is finitely generated as a module over the subalgebra
$k[\mathbf{a}]$
. Set
$K:=k(t_{1},\ldots ,t_{d-1})$
, the field of rational functions in indeterminates
$t_{1},\ldots ,t_{d-1}$
and
$$\begin{eqnarray}b_{i}:=a_{i}-a_{0}t_{i}\quad \text{for }i=1,\ldots ,d-1\end{eqnarray}$$
viewed as elements in
$R_{K}$
. Let
$\mathfrak{p}^{\prime }$
denote the extension of
$\mathfrak{p}$
to
$R_{K}$
, and set
$$\begin{eqnarray}\mathfrak{q}:=\mathfrak{p}^{\prime }+(\mathbf{b})\qquad \text{and}\qquad \mathfrak{m}:=\sqrt{\mathfrak{q}}.\end{eqnarray}$$
The following statements hold:
-
(1)
$\mathfrak{m}$
is a closed point in
$\operatorname{Spec}^{+}(R)_{K}$
with the property that
$\mathfrak{m}\cap R=\mathfrak{p}$
; -
(2) the induced extension of fields
$k(\mathfrak{p})\xrightarrow[{}]{~\cong ~}k(\mathfrak{m})$
is an isomorphism.
The first part is contained in [Reference Benson, Iyengar, Krause and Pevtsova10, Theorem 7.7]. The second one holds by construction; see [Reference Benson, Iyengar, Krause and Pevtsova10, Lemma 7.6, and (7.2)].
We record the following observation for later use. Since the
$a_{i}$
are not in
$\mathfrak{p}$
, when
$Y$
in
$\text{}\underline{\operatorname{GProj}}A$
is
$\mathfrak{p}$
-local, Lemma 3.1 yields a natural isomorphism
$$\begin{eqnarray}\unicode[STIX]{x1D6FA}^{s}Y\cong Y\quad \text{where }s=\mathop{\sum }_{i}|a_{i}|=\mathop{\sum }_{i}|b_{i}|.\end{eqnarray}$$
This algebraic construction has the following representation theoretic avatar.
Lemma 4.6. If
$X$
in
$\text{}\underline{\operatorname{GProj}}A$
is
$\mathfrak{p}$
-torsion, then
$X_{K}/\!/\mathbf{b}$
in
$\text{}\underline{\operatorname{GProj}}A_{K}$
is
$\mathfrak{m}$
-torsion and
$(X_{K}/\!/\mathbf{b})\downarrow _{A}$
, its restriction to
$A$
, is
$\mathfrak{p}$
-local and
$\mathfrak{p}$
-torsion.
Proof. Since
$\unicode[STIX]{x1D6E4}_{{\mathcal{V}}(\mathfrak{p})}X\cong X$
, one gets the first isomorphism below
$$\begin{eqnarray}X_{K}\cong (\unicode[STIX]{x1D6E4}_{{\mathcal{V}}(\mathfrak{p})}X)_{K}\cong \unicode[STIX]{x1D6E4}_{{\mathcal{V}}(\mathfrak{p}^{\prime })}(X_{K});\end{eqnarray}$$
the second one is by Lemma 4.4(1). In other words,
$X_{K}$
is
$\mathfrak{p}^{\prime }$
-torsion and hence
$X_{K}/\!/\mathbf{b}$
is
$(\mathfrak{p}^{\prime }+\mathfrak{b})$
-torsion; that is to say, it is
$\mathfrak{m}$
-torsion since
$\mathfrak{m}$
is the radical of
$\mathfrak{p}^{\prime }+\mathfrak{b}$
. The claim about the restriction of
$X_{K}/\!/\mathbf{b}$
to
$A$
follows from Lemma 4.4(2).
Fix an object
$X$
in
$\text{}\underline{\operatorname{GProj}}A$
. The sequence of elements
$\mathbf{b}$
in
$R_{K}$
yields a morphism
$X_{K}\rightarrow \unicode[STIX]{x1D6FA}^{s}(X_{K}/\!/\mathbf{b})$
. Adjunction gives a morphism
$$\begin{eqnarray}f_{X}:X\longrightarrow \unicode[STIX]{x1D6FA}^{s}(X_{K}/\!/\mathbf{b})\downarrow _{A}.\end{eqnarray}$$
When
$X$
is
$\mathfrak{p}$
-torsion, the target of
$f_{X}$
is
$\mathfrak{p}$
-local, by Lemma 4.6; so the map factors through localization at
$\mathfrak{p}$
and yields a natural morphism
$$\begin{eqnarray}g_{X}:\unicode[STIX]{x1D6E4}_{\mathfrak{p}}X=X_{\mathfrak{p}}\longrightarrow \unicode[STIX]{x1D6FA}^{s}(X_{K}/\!/\mathbf{b})\downarrow _{A}\cong (X_{K}/\!/\mathbf{b})\downarrow _{A}.\end{eqnarray}$$
The isomorphism holds by (4.2), which applies by Lemma 4.6. Here, we have implicitly used the fact that passing to syzygies commutes with restriction.
The following result extends [Reference Benson, Iyengar, Krause and Pevtsova11, Theorem 3.4] that concerns modules over finite group schemes, but the argument is essentially the same.
Theorem 4.7. Let
$X$
be a Gorenstein projective
$A$
-module. When
$X$
is
$\mathfrak{p}$
-torsion, the natural morphism
$g_{X}$
constructed above is an isomorphism:
$$\begin{eqnarray}g_{X}:\unicode[STIX]{x1D6E4}_{\mathfrak{p}}X\xrightarrow[{}]{~\cong ~}(X_{K}/\!/\mathbf{b})\downarrow _{A}.\end{eqnarray}$$
For an arbitrary
$X$
, the morphism
$g_{X}$
induces a natural isomorphism
$$\begin{eqnarray}\unicode[STIX]{x1D6E4}_{\mathfrak{p}}X\xrightarrow[{}]{~\cong ~}\unicode[STIX]{x1D6E4}_{\mathfrak{m}}(X_{K}/\!/\mathbf{b})\downarrow _{A}.\end{eqnarray}$$
Proof. The
$\mathfrak{p}$
-torsion modules
$X$
for which
$g_{X}$
is an isomorphism form a localizing subcategory of
$\text{}\underline{\operatorname{GProj}}A$
. Moreover, by [Reference Benson, Iyengar and Krause8, Proposition 2.7], the
$\mathfrak{p}$
-torsion modules form a localizing subcategory of
$\text{}\underline{\operatorname{GProj}}A$
generated by the modules
$X/\!/\mathfrak{p}$
, for
$X$
in
$\operatorname{Gproj}A$
. It thus suffices to verify the desired isomorphism for such modules, that is to say that the map
$g_{X/\!/\mathfrak{p}}$
is an isomorphism. This is proved in [Reference Benson, Iyengar, Krause and Pevtsova10, Theorem 8.8] for the case of finite group schemes and
$X=k$
, the trivial representation. The argument uses [Reference Benson, Iyengar, Krause and Pevtsova10, Proposition 6.2(2)] that should be substituted by Lemma 4.4.
Let
$X$
be an arbitrary Gorenstein projective
$A$
-module and
$\mathfrak{p}^{\prime }$
the ideal in Construction 4.5. Since
$Y:=\unicode[STIX]{x1D6E4}_{{\mathcal{V}}(\mathfrak{p})}X$
is
$\mathfrak{p}$
-torsion,
$g_{Y}$
is an isomorphism. This is the second isomorphism below:
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E4}_{\mathfrak{p}}X & \cong & \displaystyle (\unicode[STIX]{x1D6E4}_{{\mathcal{V}}(\mathfrak{p})}X)_{\mathfrak{p}}\nonumber\\ \displaystyle & \cong & \displaystyle ((\unicode[STIX]{x1D6E4}_{{\mathcal{V}}(\mathfrak{p})}X)_{K}/\!/\mathbf{b})\downarrow _{A}\nonumber\\ \displaystyle & \cong & \displaystyle (\unicode[STIX]{x1D6E4}_{{\mathcal{V}}(\mathfrak{p}^{\prime })}(X_{K})/\!/\mathbf{b})\downarrow _{A}\nonumber\\ \displaystyle & \cong & \displaystyle (\unicode[STIX]{x1D6E4}_{{\mathcal{V}}(\mathfrak{p}^{\prime })}(X_{K}/\!/\mathbf{b}))\downarrow _{A}\nonumber\\ \displaystyle & \cong & \displaystyle (\unicode[STIX]{x1D6E4}_{{\mathcal{V}}(\mathfrak{p}^{\prime }+(\mathbf{b}))}(X_{K}/\!/\mathbf{b}))\downarrow _{A}\nonumber\\ \displaystyle & \cong & \displaystyle (\unicode[STIX]{x1D6E4}_{\mathfrak{m}}(X_{K}/\!/\mathbf{b}))\downarrow _{A}.\nonumber\end{eqnarray}$$
The third one is by Lemma 4.4, applied to the functor
$K\otimes _{k}(-)$
from
$\text{}\underline{\operatorname{GProj}}A$
to
$\text{}\underline{\operatorname{GProj}}A_{K}$
. The next one is standard, while the penultimate one holds because
$X_{K}/\!/\mathbf{b}$
is
$(\mathbf{b})$
-torsion.
5 The Gorenstein property
Let
$F:\text{}\underline{\operatorname{Gproj}}A\rightarrow \text{}\underline{\operatorname{Gproj}}A$
be the Serre functor from Theorem 2.9, given by
$$\begin{eqnarray}F(X)=(\unicode[STIX]{x1D6FA}\circ \operatorname{GP}\circ \,\unicode[STIX]{x1D708})(X).\end{eqnarray}$$
Given the description of
$F$
, the following result contains Theorem 1.2. It extends [Reference Benson, Iyengar, Krause and Pevtsova11, Theorem 5.1], which deals with the case where
$A$
is the group algebra of a finite group scheme and
$R=\operatorname{Ext}_{A}^{\ast }(k,k)$
, its cohomology ring.
Theorem 5.1. Let
$k$
be a field,
$A$
a finite dimensional Gorenstein
$k$
-algebra and
$R\subseteq \operatorname{HH}^{\ast }(A/k)$
as in Assumption 4.1. Fix
$\mathfrak{p}\in \operatorname{Spec}^{+}(R)$
, and let
$d$
be the Krull dimension of
$R/\mathfrak{p}$
. On
$\text{}\underline{\operatorname{Gproj}}A$
, there is a natural isomorphism of functors
$$\begin{eqnarray}\unicode[STIX]{x1D6E4}_{\mathfrak{p}}\circ F\cong \unicode[STIX]{x1D6FA}^{-d+1}\circ T_{\mathfrak{ p}}.\end{eqnarray}$$
Thus, for any object
$X$
in
$\operatorname{Gproj}A$
, there is a natural isomorphism
$$\begin{eqnarray}\text{}\underline{\operatorname{Hom}}_{A}(-,\unicode[STIX]{x1D6FA}^{d-1}\unicode[STIX]{x1D6E4}_{\mathfrak{p}}F(X))\cong \operatorname{Hom}_{R}(\operatorname{Ext}_{A}^{\ast }(X,-),I(\mathfrak{p})).\end{eqnarray}$$
This result is proved further below, following some preparatory remarks.
Remark 5.2. Let
$X,Y$
be Gorenstein projective
$A$
-modules. The natural map
$$\begin{eqnarray}\operatorname{Ext}_{A}^{\ast }(X,Y)\rightarrow \text{}\underline{\operatorname{Hom}}_{A}^{\ast }(X,Y)\end{eqnarray}$$
is compatible with the action of
$\operatorname{HH}^{\ast }(A/k)$
and hence of
$R$
. The map is surjective in degree zero, with kernel
$\operatorname{PHom}_{A}(X,Y)$
, the maps from
$X$
to
$Y$
that factor through a projective
$A$
-module. Since it is bijective in positive degrees, one gets an exact sequence of graded
$R$
-modules
$$\begin{eqnarray}0\longrightarrow \operatorname{PHom}_{A}(X,Y)\longrightarrow \operatorname{Ext}_{A}^{\ast }(X,Y)\longrightarrow \text{}\underline{\operatorname{Hom}}_{A}^{\ast }(X,Y)\longrightarrow C\longrightarrow 0\end{eqnarray}$$
with
$C^{i}=0$
for
$i\geqslant 0$
. For degree reasons, the
$R$
-modules
$\operatorname{PHom}_{A}(X,Y)$
and
$C$
are
$R^{{\geqslant}1}$
-torsion; so for
$\mathfrak{p}$
in
$\operatorname{Spec}^{+}(R)$
, the induced localized map is an isomorphism:
$$\begin{eqnarray}\operatorname{Ext}_{A}^{\ast }(X,Y)_{\mathfrak{ p}}\xrightarrow[{}]{{\sim}}\text{}\underline{\operatorname{Hom}}_{A}^{\ast }(X,Y)_{\mathfrak{ p}}.\end{eqnarray}$$
It follows from Lemma 4.3 that the functor
$F$
is compatible with base change.
Lemma 5.3. Let
$K/k$
be a field extension and
$F_{K}:\text{}\underline{\operatorname{Gproj}}A_{K}\rightarrow \text{}\underline{\operatorname{Gproj}}A_{K}$
the corresponding Serre functor. For
$X$
in
$\operatorname{Gproj}A$
, there is a natural isomorphism
$F_{K}(X_{K})\cong F(X)_{K}$
.◻
The following argument is a direct adaptation of the one for [Reference Benson, Iyengar, Krause and Pevtsova11, Theorem 5.1].
Proof of Theorem 5.1.
The proof uses the following observation. For any
$A$
-modules
$X,Y$
that are
$\mathfrak{p}$
-local and
$\mathfrak{p}$
-torsion, there is an isomorphism
$X\cong Y$
in
$\text{}\underline{\operatorname{GProj}}A$
if and only if there is a natural isomorphism
$$\begin{eqnarray}\text{}\underline{\operatorname{Hom}}_{A}(M,X)\cong \text{}\underline{\operatorname{Hom}}_{A}(M,Y)\end{eqnarray}$$
for
$\mathfrak{p}$
-local and
$\mathfrak{p}$
-torsion
$A$
-modules
$M$
. This follows from Yoneda’s lemma.
In anticipation of using the preceding remark, we note that
$\unicode[STIX]{x1D6E4}_{\mathfrak{p}}(X)$
and
$T_{\mathfrak{p}}(X)$
are
$\mathfrak{p}$
-local and
$\mathfrak{p}$
-torsion. This is clear for
$\unicode[STIX]{x1D6E4}_{\mathfrak{p}}(X)$
and follows for
$T_{\mathfrak{p}}(X)$
from the fact that
$I(\mathfrak{p})$
is a
$\mathfrak{p}$
-local and
$\mathfrak{p}$
-torsion
$R$
-module. Another observation is that, by (5.2), for any
$\mathfrak{p}$
-local
$R$
-module
$I$
, there is an isomorphism
$$\begin{eqnarray}\operatorname{Hom}_{R}(\operatorname{Ext}_{A}^{\ast }(X,-),I)\cong \operatorname{Hom}_{R}(\text{}\underline{\operatorname{Hom}}_{A}^{\ast }(X,-),I).\end{eqnarray}$$
Consequently, one can rephrase the defining isomorphism (3.2) for the object
$T_{\mathfrak{p}}(X)$
as a natural isomorphism
$$\begin{eqnarray}\text{}\underline{\operatorname{Hom}}_{A}(-,T_{\mathfrak{p}}(X))\cong \operatorname{Hom}_{R}(\operatorname{Ext}_{A}^{\ast }(X,-),I(\mathfrak{p})).\end{eqnarray}$$
Our task is to verify that, on
$\text{}\underline{\operatorname{Gproj}}A$
, there is an isomorphism of functors
$$\begin{eqnarray}\unicode[STIX]{x1D6E4}_{\mathfrak{p}}F\cong \unicode[STIX]{x1D6FA}^{-d+1}T_{\mathfrak{ p}}.\end{eqnarray}$$
We verify this when
$\mathfrak{p}$
is closed and then use a reduction to closed points.
Claim.
The desired isomorphism holds when
$\mathfrak{m}$
is a closed point in
$\operatorname{Spec}^{+}(R)$
.
The injective hull,
$I(\mathfrak{m})$
, of the
$R$
-module
$R/\mathfrak{m}$
is the same as that of the
$R_{\mathfrak{m}}$
-module
$k(\mathfrak{m})$
, viewed as an
$R$
-module via restriction of scalars along the localization map
$R\rightarrow R_{\mathfrak{m}}$
. Let
$Y$
be a Gorenstein projective
$A$
-module that is
$\mathfrak{m}$
-local and
$\mathfrak{m}$
-torsion. The claim is a consequence of the following computation:
$$\begin{eqnarray}\displaystyle \text{}\underline{\operatorname{Hom}}_{A}(Y,\unicode[STIX]{x1D6E4}_{\mathfrak{m}}(FX)) & \cong & \displaystyle \text{}\underline{\operatorname{Hom}}_{A}(Y,FX)\nonumber\\ \displaystyle & \cong & \displaystyle \operatorname{Hom}_{k}(\text{}\underline{\operatorname{Hom}}_{A}(X,Y),k)\nonumber\\ \displaystyle & \cong & \displaystyle \operatorname{Hom}_{R_{\mathfrak{m}}}(\text{}\underline{\operatorname{Hom}}_{A}^{\ast }(X,Y),I(\mathfrak{m}))\nonumber\\ \displaystyle & \cong & \displaystyle \operatorname{Hom}_{R}(\text{}\underline{\operatorname{Hom}}_{A}^{\ast }(X,Y),I(\mathfrak{m}))\nonumber\\ \displaystyle & \cong & \displaystyle \text{}\underline{\operatorname{Hom}}_{A}(Y,T_{\mathfrak{m}}(X)).\nonumber\end{eqnarray}$$
The first isomorphism holds because
$Y$
is
$\mathfrak{m}$
-torsion; the second is Serre duality, Proposition 2.8, and the next one is by [Reference Benson, Iyengar, Krause and Pevtsova11, Lemma A.2], which applies because
$\text{}\underline{\operatorname{Hom}}_{A}^{\ast }(X,Y)$
is
$\mathfrak{m}$
-local and
$\mathfrak{m}$
-torsion as an
$A$
-module.
Let
$\mathfrak{p}$
be a point in
$\operatorname{Spec}^{+}(R)$
that is not closed, and let
$K$
,
$\mathbf{b}$
and
$\mathfrak{m}$
be as in Construction 4.5. Recall that
$\mathfrak{m}$
is a closed point in
$R_{K}$
lying over
$\mathfrak{p}$
.
Claim.
In
$\text{}\underline{\operatorname{GProj}}A$
, there is an isomorphism of
$A$
-modules
$$\begin{eqnarray}(T_{\mathfrak{m}}(X_{K})/\!/\mathbf{b})\downarrow _{A}\cong \unicode[STIX]{x1D6FA}^{-d+1}T_{\mathfrak{ p}}(X),\end{eqnarray}$$
where
$d$
is the Krull dimension of
$R/\mathfrak{p}$
.
Let
$Y$
be an
$A$
-module that is
$\mathfrak{p}$
-local and
$\mathfrak{p}$
-torsion. Then we have the following:
$$\begin{eqnarray}\displaystyle \text{}\underline{\operatorname{Hom}}_{A}(Y,\unicode[STIX]{x1D6FA}^{d-1}(T_{\mathfrak{m}}(X_{K})/\!/\mathbf{b})\downarrow _{A}) & \cong & \displaystyle \text{}\underline{\operatorname{Hom}}_{A_{K}}(Y_{K},\unicode[STIX]{x1D6FA}^{d-1}(T_{\mathfrak{m}}(X_{K})/\!/\mathbf{b}))\nonumber\\ \displaystyle & \cong & \displaystyle \text{}\underline{\operatorname{Hom}}_{A_{K}}(Y_{K}/\!/\mathbf{b},T_{\mathfrak{m}}(X_{K}))\nonumber\\ \displaystyle & \cong & \displaystyle \operatorname{Hom}_{R_{K}}(\text{}\underline{\operatorname{Hom}}_{A_{K}}^{\ast }(X_{K},Y_{K}/\!/\mathbf{b}),I(\mathfrak{m}))\nonumber\\ \displaystyle & \cong & \displaystyle \operatorname{Hom}_{R}(\text{}\underline{\operatorname{Hom}}_{A_{K}}^{\ast }(X_{K},Y_{K}/\!/\mathbf{b}),I(\mathfrak{p}))\nonumber\\ \displaystyle & \cong & \displaystyle \operatorname{Hom}_{R}(\text{}\underline{\operatorname{Hom}}_{A}^{\ast }(X,(Y_{K}/\!/\mathbf{b})\downarrow _{A}),I(\mathfrak{p}))\nonumber\\ \displaystyle & \cong & \displaystyle \operatorname{Hom}_{R}(\text{}\underline{\operatorname{Hom}}_{A}^{\ast }(X,Y),I(\mathfrak{p}))\nonumber\\ \displaystyle & \cong & \displaystyle \text{}\underline{\operatorname{Hom}}_{A}(Y,T_{\mathfrak{p}}(X)).\nonumber\end{eqnarray}$$
The first and fifth isomorphisms are by adjunction. The second one is a direct computation using (3.1) and (4.2). The next one is by definition and the fourth isomorphism is by [Reference Benson, Iyengar, Krause and Pevtsova11, Lemma A.3], applied to the homomorphism
$R\rightarrow R_{K}$
; it applies as the
$R_{K}$
-module
$\text{}\underline{\operatorname{Hom}}_{A_{K}}^{\ast }(X_{K},Y_{K}/\!/\mathbf{b})$
is
$\mathfrak{m}$
-torsion. The sixth isomorphism is by Theorem 4.7, and the last one by definition. This justifies the claim.
Consider now the chain of isomorphisms:
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E4}_{\mathfrak{p}}F(X) & \cong & \displaystyle \unicode[STIX]{x1D6E4}_{\mathfrak{m}}(F(X)_{K}/\!/\mathbf{b})\downarrow _{A}\nonumber\\ \displaystyle & \cong & \displaystyle \unicode[STIX]{x1D6E4}_{\mathfrak{m}}(F_{K}(X_{K})/\!/\mathbf{b})\downarrow _{A}\nonumber\\ \displaystyle & \cong & \displaystyle (\unicode[STIX]{x1D6E4}_{\mathfrak{m}}(F_{K}(X_{K}))/\!/\mathbf{b})\downarrow _{A}\nonumber\\ \displaystyle & \cong & \displaystyle (T_{\mathfrak{m}}(X_{K})/\!/\mathbf{b})\downarrow _{A}\nonumber\\ \displaystyle & \cong & \displaystyle \unicode[STIX]{x1D6FA}^{-d+1}T_{\mathfrak{p}}(X).\nonumber\end{eqnarray}$$
The first isomorphism is by Theorem 4.7, the second by Lemma 5.3, the third is clear, the fourth follows from the first claim since
$\mathfrak{m}$
is a closed point for
$A_{K}$
and the last one follows from the second claim.
This completes the proof that the functors
$\unicode[STIX]{x1D6E4}_{\mathfrak{p}}\circ F$
and
$\unicode[STIX]{x1D6FA}^{-d+1}\circ T_{\mathfrak{p}}$
are isomorphic. Given this and the alternative description of
$T_{\mathfrak{p}}$
above, the last isomorphism in the statement follows.
Next, we record a corollary of Theorem 5.1 concerning
$\unicode[STIX]{x1D6FE}_{\mathfrak{p}}(\text{}\underline{\operatorname{Gproj}}A)$
, the
$\mathfrak{p}$
-torsion objects in the
$\mathfrak{p}$
-localization of
$\text{}\underline{\operatorname{Gproj}}A$
; see [Reference Benson, Iyengar, Krause and Pevtsova11, Section 7] and the references therein for details of this construction. The
$R$
-linear triangle equivalences
$$\begin{eqnarray}\unicode[STIX]{x1D708}:\text{}\underline{\operatorname{Gproj}}A\rightarrow \overline{\operatorname{Ginj}}A\qquad \text{and}\qquad \operatorname{GP}:\overline{\operatorname{Ginj}}A\rightarrow \text{}\underline{\operatorname{Gproj}}A\end{eqnarray}$$
induce
$R_{\mathfrak{p}}$
-linear triangle equivalences
compatible with the localization functor; see [Reference Benson, Iyengar, Krause and Pevtsova11, Remark 7.1]. The following result can be interpreted as the statement that the category
$\unicode[STIX]{x1D6FE}_{\mathfrak{p}}(\text{}\underline{\operatorname{Gproj}}A)$
, and hence also
$\unicode[STIX]{x1D6FE}_{\mathfrak{p}}(\overline{\operatorname{Ginj}}A)$
, has a Serre functor.
Corollary 5.4. For
$X,Y$
in
$\mathsf{C}:=\unicode[STIX]{x1D6FE}_{\mathfrak{p}}(\text{}\underline{\operatorname{Gproj}}A)$
, there is a natural isomorphism
$$\begin{eqnarray}\operatorname{Hom}_{R_{\mathfrak{p}}}(\text{}\underline{\operatorname{Hom}}_{\mathsf{C}}^{\ast }(X,Y),I(\mathfrak{p}))\cong \text{}\underline{\operatorname{Hom}}_{\mathsf{C}}(Y,\unicode[STIX]{x1D6FA}^{d}\operatorname{GP}_{\mathfrak{ p}}\unicode[STIX]{x1D708}_{\mathfrak{p}}(X)).\end{eqnarray}$$
Proof. Up to direct summands, the categories
$\mathsf{C}$
and
$\unicode[STIX]{x1D6E4}_{\mathfrak{p}}(\text{}\underline{\operatorname{GProj}}A)^{\mathsf{c}}$
are equivalent, and the compact objects in
$\unicode[STIX]{x1D6E4}_{\mathfrak{p}}(\text{}\underline{\operatorname{GProj}}A)$
are of the form
$M_{\mathfrak{p}}$
, for some
$M\in \text{}\underline{\operatorname{Gproj}}A$
that is
$\mathfrak{p}$
-torsion; see [Reference Benson, Iyengar, Krause and Pevtsova11, Remark 7.2]. We obtain the desired isomorphism by reinterpreting the isomorphisms in Theorem 5.1, as follows.
Fix
$\mathfrak{p}$
-torsion objects
$M,N$
in
$\text{}\underline{\operatorname{Gproj}}A$
. One has the first isomorphism below because
$M$
is finite dimensional:
$$\begin{eqnarray}\displaystyle \operatorname{Hom}_{R_{\mathfrak{p}}}(\text{}\underline{\operatorname{Hom}}_{A}^{\ast }(M_{\mathfrak{p}},N_{\mathfrak{p}}),I(\mathfrak{p})) & \cong & \displaystyle \operatorname{Hom}_{R_{\mathfrak{p}}}(\text{}\underline{\operatorname{Hom}}_{A}^{\ast }(M,N)_{\mathfrak{p}},I(\mathfrak{p}))\nonumber\\ \displaystyle & \cong & \displaystyle \operatorname{Hom}_{R_{\mathfrak{p}}}(\operatorname{Ext}_{A}^{\ast }(M,N)_{\mathfrak{p}},I(\mathfrak{p}))\nonumber\\ \displaystyle & \cong & \displaystyle \operatorname{Hom}_{R}(\operatorname{Ext}_{A}^{\ast }(M,N),I(\mathfrak{p})).\nonumber\end{eqnarray}$$
The second one is by (5.2) and the last one is by adjunction.
On the other hand, since
$M$
is
$\mathfrak{p}$
-torsion, so is
$F(M)$
, and, hence, one has the first isomorphism below:
$$\begin{eqnarray}\unicode[STIX]{x1D6FA}^{d-1}\unicode[STIX]{x1D6E4}_{\mathfrak{p}}F(M)\cong \unicode[STIX]{x1D6FA}^{d-1}F(M)_{\mathfrak{ p}}\cong \unicode[STIX]{x1D6FA}^{d-1}(\unicode[STIX]{x1D6FA}\operatorname{GP}\unicode[STIX]{x1D708}(M))_{\mathfrak{ p}}\cong \unicode[STIX]{x1D6FA}^{d}\operatorname{GP}_{\mathfrak{ p}}\unicode[STIX]{x1D708}_{\mathfrak{p}}(M_{\mathfrak{p}}).\end{eqnarray}$$
The second one is by the definition of
$F$
and the third one follows by the discussion around (5.4). Applying
$\text{}\underline{\operatorname{Hom}}_{A}(N,-)$
to the composition yields the first isomorphism below, whilst the second one holds as the covariant argument is
$\mathfrak{p}$
-local:
$$\begin{eqnarray}\displaystyle \text{}\underline{\operatorname{Hom}}_{A}(N_{\mathfrak{p}},\unicode[STIX]{x1D6FA}^{d}\operatorname{GP}_{\mathfrak{p}}\unicode[STIX]{x1D708}_{\mathfrak{p}}(M_{\mathfrak{p}})) & \cong & \displaystyle \text{}\underline{\operatorname{Hom}}_{A}(N_{\mathfrak{p}},\unicode[STIX]{x1D6FA}^{d-1}\unicode[STIX]{x1D6E4}_{\mathfrak{p}}F(M))\nonumber\\ \displaystyle & \cong & \displaystyle \text{}\underline{\operatorname{Hom}}_{A}(N,\unicode[STIX]{x1D6FA}^{d-1}\unicode[STIX]{x1D6E4}_{\mathfrak{p}}F(M)).\nonumber\end{eqnarray}$$
The isomorphisms above and Theorem 5.1, applied with
$X=M$
and
$Y=N$
, yield the desired result.
Lemma 5.5. For any
$\mathfrak{p}\in \operatorname{Spec}^{+}(R)$
, the quotient functor
$\mathsf{D}^{\text{b}}(\operatorname{mod}A)\rightarrow \mathsf{D}_{\text{sg}}(A)$
induces equivalences
$$\begin{eqnarray}{\mathsf{D}^{\text{b}}(\operatorname{mod}A)}_{\mathfrak{p}}\xrightarrow[{}]{~\sim ~}{\mathsf{D}_{\text{sg}}(A)}_{\mathfrak{p}}\qquad \text{and}\qquad \unicode[STIX]{x1D6FE}_{\mathfrak{p}}(\mathsf{D}^{\text{b}}(\operatorname{mod}A))\xrightarrow[{}]{~\sim ~}\unicode[STIX]{x1D6FE}_{\mathfrak{p}}(\mathsf{D}_{\text{sg}}(A))\end{eqnarray}$$
compatible with the
$R_{\mathfrak{p}}$
actions.
Proof. The quotient functor is essentially surjective and hence so is its
$\mathfrak{p}$
-localization
${\mathsf{D}^{\text{b}}(\operatorname{mod}A)}_{\mathfrak{p}}\rightarrow {\mathsf{D}_{\text{sg}}(A)}_{\mathfrak{p}}$
. The latter is also fully faithful, by (5.2), and so is an equivalence of categories. It is also
$R_{\mathfrak{p}}$
-linear, by construction. Given this, it is immediate from the definition that the
$\mathfrak{p}$
-torsion subcategories are equivalent.
Proof of Theorem 1.1.
Recall that
$A$
is a finite dimensional Gorenstein algebra and
$R$
is a finitely generated, homogeneous,
$k$
-subalgebra of
$\operatorname{HH}^{\ast }(A/k)$
with
$R^{0}=k$
. Also,
$\mathsf{D}:=\mathsf{D}^{\text{b}}(\operatorname{mod}A)$
. We fix a homogeneous prime ideal
$\mathfrak{p}$
in
$\operatorname{Spec}^{+}(R)$
. We want to verify that for all
$X,Y$
in
$\unicode[STIX]{x1D6FE}_{\mathfrak{p}}(\mathsf{D})$
, there are natural isomorphisms
$$\begin{eqnarray}\operatorname{Hom}_{R_{\mathfrak{p}}}(\operatorname{Hom}_{\unicode[STIX]{x1D6FE}_{\mathfrak{ p}}(\mathsf{D})}^{\ast }(X,Y),I(\mathfrak{p}))\cong \operatorname{Hom}_{\unicode[STIX]{x1D6FE}_{\mathfrak{p}}(\mathsf{D})}(Y,\unicode[STIX]{x1D6F4}^{-d}\unicode[STIX]{x1D708}_{\mathfrak{p}}(X))\end{eqnarray}$$
with
$d$
the Krull dimension of
$R/\mathfrak{p}$
. Lemma 5.5 gives the second equivalence as follows:
$$\begin{eqnarray}\unicode[STIX]{x1D6FE}_{\mathfrak{p}}(\text{}\underline{\operatorname{Gproj}}A)\xrightarrow[{}]{~\sim ~}\unicode[STIX]{x1D6FE}_{\mathfrak{p}}(\mathsf{D})\xrightarrow[{}]{~\sim ~}\unicode[STIX]{x1D6FE}_{\mathfrak{p}}(\mathsf{D}_{\text{sg}}(A)),\end{eqnarray}$$
whereas the first one is induced by Proposition 2.2, and both these are compatible with the
$R_{\mathfrak{p}}$
actions. It remains to recall Corollary 5.4.
5.1 The (Fg) condition
Let
$R\subseteq \operatorname{HH}^{\ast }(A/k)$
be a
$k$
-subalgebra as in (4.1). Assume, in addition, that for each
$M\in \operatorname{mod}A$
, the
$R$
-module
$\operatorname{Ext}_{A}^{\ast }(M,M)$
is finitely generated. Said otherwise, the algebra
$A$
satisfies the (Fg) condition with respect to
$R$
, introduced in [Reference Erdmann, Holloway, Taillefer, Snashall and Solberg16]. As noted in [Reference Solberg24, Proposition 5.7], this condition implies that the Hochschild cohomology algebra
$\operatorname{HH}^{\ast }(A/k)$
is finitely generated. The (Fg) condition holds for several interesting classes of finite dimensional Hopf algebras, including group algebras of finite groups (or group schemes), small quantum groups, and also for finite dimensional commutative complete intersection rings; see [Reference Erdmann, Holloway, Taillefer, Snashall and Solberg16, Reference Ginzburg and Kumar18, Reference Mastnak, Pevtsova, Schaunberg and Witherspoon21, Reference Solberg24].
When
$A$
satisfies the (Fg) condition, it follows from Corollary 5.4 that the triangulated category
$\unicode[STIX]{x1D6FE}_{\mathfrak{p}}(\text{}\underline{\operatorname{Gproj}}A)$
, and hence also anything equivalent to it, has AR-triangles. This is explained in [Reference Benson, Iyengar, Krause and Pevtsova11, Section 7], to which we refer the reader also for other consequences of Serre duality.
Remark 5.6. Assume that the algebra
$A$
satisfies the (Fg) condition with respect to
$R$
and set
$\mathfrak{r}:=R^{{\geqslant}1}$
, the homogeneous maximal ideal of
$R$
. Set
$\mathsf{D}:=\mathsf{D}^{\text{b}}(\operatorname{mod}A)$
.
Claim.
The triangulated category
$\unicode[STIX]{x1D6FE}_{\mathfrak{r}}(\mathsf{D})$
is equivalent to
$\mathsf{D}^{\mathsf{b}}(\operatorname{proj}A)$
.
Indeed, by definition,
$\unicode[STIX]{x1D6FE}_{\mathfrak{r}}(\mathsf{D})$
consists of complexes
$M\in \mathsf{D}$
for which
$\operatorname{Ext}_{R}^{\ast }(M,M)$
is
$\mathfrak{r}$
-torsion as an
$R$
-module; equivalently,
$\operatorname{Ext}_{R}^{\ast }(M,N)$
is
$\mathfrak{r}$
-torsion for each
$N\in \mathsf{D}$
. In particular,
$\operatorname{Ext}_{R}^{\ast }(M,A/J)$
is
$\mathfrak{r}$
-torsion, where
$J$
is the Jacobson radical of
$A$
. As the
$R$
-module
$\operatorname{Ext}_{R}^{\ast }(M,A/J)$
is finitely generated, by the (Fg) condition, this last property is equivalent to
$\operatorname{Ext}_{R}^{\ast }(M,A/J)=0$
for
$i\gg 0$
, that is to say,
$M$
is perfect.
Given this claim, one gets a Serre duality on
$\unicode[STIX]{x1D6FE}_{\mathfrak{r}}(\mathsf{D})$
: for perfect complexes
$X,Y$
from [Reference Happel19], we get the second isomorphism below:
$$\begin{eqnarray}\displaystyle \operatorname{Hom}_{R}(\operatorname{Hom}_{\mathsf{D}}^{\ast }(X,Y),I(\mathfrak{r})) & \cong & \displaystyle \operatorname{Hom}_{k}(\operatorname{Hom}_{\mathsf{D}}^{\ast }(X,Y),k)\nonumber\\ \displaystyle & \cong & \displaystyle \operatorname{Hom}_{\mathsf{D}}(Y,\unicode[STIX]{x1D708}(X)).\nonumber\end{eqnarray}$$
The first one is by adjunction as
$I(\mathfrak{r})=\operatorname{Hom}_{k}(R,k)$
; see [Reference Benson, Iyengar, Krause and Pevtsova11, Lemma A.2]. Thus, Theorem 1.1 may be seen as an extending, in this case, the known Serre duality to cover the other (homogeneous) prime ideals in
$R$
.
Remark 5.7. Concerning the claim in Remark 5.6: even when
$A$
does not satisfy the (Fg) condition with respect to
$R$
, the subcategory
$\unicode[STIX]{x1D6FE}_{\mathfrak{r}}(\mathsf{D})$
contains the perfect complexes, but it is possible that it contains more. To see what is at stake, consider the special case that
$A$
is self-injective. Let
$M\in \operatorname{mod}A$
be a module containing
$A$
as a direct summand and satisfying
$\operatorname{Ext}_{A}^{i}(M,M)=0$
for all
$i>0$
. It is easy to verify that
$M$
is in
$\unicode[STIX]{x1D6FE}_{\mathfrak{r}}(\mathsf{D})$
. However, it is still unknown, and a conjecture of Auslander and Reiten [Reference Auslander and Reiten5], whether such an
$M$
has finite projective dimension, equivalently that
$M$
is projective.
Remark 5.8. Let
$k$
be a field and
$A$
a finite dimensional, Gorenstein,
$k$
-algebra. Let
$R$
and
$S$
be
$k$
-subalgebras of the Hochschild cohomology algebra
$\operatorname{HH}^{\ast }(A/k)$
satisfying Assumption 4.1. Theorem 5.1, and so also its corollaries, applies to the action of
$R$
, and also of
$S$
, on
$\text{}\underline{\operatorname{GProj}}A$
. In reconciling the two, one can replace
$S$
by the
$k$
-subalgebra of
$\operatorname{HH}^{\ast }(A/k)$
generated by
$R$
and
$S$
and assume
$R\subseteq S$
. Then one has an induced map
$\unicode[STIX]{x1D711}:\operatorname{Proj}S\rightarrow \operatorname{Spec}^{+}(R)$
defined by the assignment
$\mathfrak{q}\mapsto \mathfrak{q}\cap R$
.
Given
$\mathfrak{q}$
in
$\operatorname{Proj}S$
, it is clear that there is an inclusion
$$\begin{eqnarray}\unicode[STIX]{x1D6E4}_{\mathfrak{q}}(\text{}\underline{\operatorname{GProj}}A)\subseteq \unicode[STIX]{x1D6E4}_{\mathfrak{p}}(\text{}\underline{\operatorname{GProj}}A)\quad \text{where }\mathfrak{p}=\mathfrak{q}\cap R.\end{eqnarray}$$
So the version of Theorem 5.1 for the action of
$S$
may be seen as a refinement of the one for the action of
$R$
. Indeed, in the extremal case
$R=k$
, one has
$\mathfrak{p}=0$
for any
$\mathfrak{q}$
in
$\operatorname{Spec}S$
and
$\unicode[STIX]{x1D6E4}_{\mathfrak{p}}(\text{}\underline{\operatorname{GProj}}A)=\text{}\underline{\operatorname{Gproj}}A$
.
A more interesting situation occurs when
$S$
is finite as an
$R$
-module. Then there are only finitely many primes
$\mathfrak{q}$
in
$\operatorname{Proj}S$
lying over a given
$\mathfrak{p}\in \operatorname{Spec}^{+}(R)$
, and [Reference Benson, Iyengar and Krause9, Corollary 7.10] yields a direct sum decomposition
$$\begin{eqnarray}\unicode[STIX]{x1D6E4}_{\mathfrak{p}}(\text{}\underline{\operatorname{GProj}}A)\cong \bigoplus _{\mathfrak{q}\in \unicode[STIX]{x1D711}^{-1}(\mathfrak{p})}\unicode[STIX]{x1D6E4}_{\mathfrak{q}}(\text{}\underline{\operatorname{GProj}}A).\end{eqnarray}$$
This decomposition thus reflects the ramification, in the sense of commutative algebra, of the inclusion
$R\subseteq S$
.
6 Examples
In this section, we describe some examples of Gorenstein algebras. To begin with, gentle algebras, introduced by Assem and Skowroński [Reference Assem and Skowroński2], are Gorenstein. This was proved by Geiß and Reiten [Reference Geiß and Reiten17]. Their result also shows that the injective dimension of a gentle algebra can be arbitrary. One can construct new examples of Gorenstein algebras using tensor products. This is explained below.
Throughout,
$k$
will be a field. The injective dimension of a finite dimensional
$k$
-algebra
$A$
is the injective dimension of
$A$
viewed as a (left) module over itself; we denote it by
$\operatorname{inj.dim}A$
. This is also the projective dimension of the
$A$
-module
$\operatorname{Hom}_{k}(A,k)$
. The last assertion in the result below is well known, but we could not find a reference for the equality of injective dimensions, so a proof is provided.
Proposition 6.1. Let
$\unicode[STIX]{x1D6E4}$
and
$\unicode[STIX]{x1D6EC}$
be finite dimensional
$k$
-algebras. The finite dimensional
$k$
-algebra
$\unicode[STIX]{x1D6E4}\otimes _{k}\unicode[STIX]{x1D6EC}$
satisfies
$$\begin{eqnarray}\operatorname{inj.dim}(\unicode[STIX]{x1D6E4}\otimes _{k}\unicode[STIX]{x1D6EC})=\operatorname{inj.dim}\unicode[STIX]{x1D6E4}+\operatorname{inj.dim}\unicode[STIX]{x1D6EC}.\end{eqnarray}$$
In particular,
$\unicode[STIX]{x1D6E4}\otimes _{k}\unicode[STIX]{x1D6EC}$
is Gorenstein if and only if both
$\unicode[STIX]{x1D6E4}$
and
$\unicode[STIX]{x1D6EC}$
are Gorenstein.
Proof. Set
$M:=\operatorname{Hom}_{k}(\unicode[STIX]{x1D6E4},k)$
and
$N:=\operatorname{Hom}_{k}(\unicode[STIX]{x1D6EC},k)$
. Let
$P$
,
$Q$
be minimal projective resolutions of
$M$
,
$N$
, respectively. Then
$P\otimes _{k}Q$
is a minimal projective resolution of
$M\otimes _{k}N$
by Lemma 6.2. It remains to observe that the latter is isomorphic to
$\operatorname{Hom}_{k}(\unicode[STIX]{x1D6E4}\otimes _{k}\unicode[STIX]{x1D6EC},k)$
, as modules over
$\unicode[STIX]{x1D6E4}\otimes _{k}\unicode[STIX]{x1D6EC}$
.
Lemma 6.2. Let
$P$
,
$Q$
be minimal projective resolutions of modules
$M$
,
$N$
over finite dimensional algebras
$\unicode[STIX]{x1D6E4}$
,
$\unicode[STIX]{x1D6EC}$
, respectively. Then
$P\otimes _{k}Q$
is a minimal projective resolution of the
$\unicode[STIX]{x1D6E4}\otimes _{k}\unicode[STIX]{x1D6EC}$
-module
$M\otimes _{k}N$
.
Proof. With
$J(-)$
denoting the Jacobson radical,
$J(\unicode[STIX]{x1D6E4})\otimes _{k}\unicode[STIX]{x1D6EC}+\unicode[STIX]{x1D6E4}\otimes _{k}J(\unicode[STIX]{x1D6EC})$
is a nilpotent two-sided ideal in
$\unicode[STIX]{x1D6E4}\otimes _{k}\unicode[STIX]{x1D6EC}$
, and, therefore, it is contained in
$J(\unicode[STIX]{x1D6E4}\otimes _{k}\unicode[STIX]{x1D6EC})$
. So for any projective
$\unicode[STIX]{x1D6E4}$
-module
$U$
and projective
$\unicode[STIX]{x1D6EC}$
-module
$V$
, we have
$$\begin{eqnarray}\operatorname{Rad}(U)\otimes _{k}V+U\otimes _{k}\operatorname{Rad}(V)\subseteq \operatorname{Rad}(U\otimes _{k}V)\end{eqnarray}$$
as
$\unicode[STIX]{x1D6E4}\otimes _{k}\unicode[STIX]{x1D6EC}$
-modules. The lemma follows from the fact that a projective resolution is minimal if and only if the image of each differential lands in the radical.
Using the result above, one can construct Gorenstein algebras of any given injective dimension as long as we find one whose injective dimension is one. The next example describes such an algebra. In particular, its class of Gorenstein projective modules is not the same as the class of Gorenstein injective modules; confer Remark 2.7. Another noteworthy feature of the algebra is that it is not of finite global dimension.
Example 6.3. Let
$k$
be a field,
$k[\unicode[STIX]{x1D700}]$
the
$k$
-algebra of dual numbers and set
$$\begin{eqnarray}\unicode[STIX]{x1D6EC}:=k[\unicode[STIX]{x1D700}]\otimes _{k}\unicode[STIX]{x1D6E4}\quad \text{where }\unicode[STIX]{x1D6E4}=\left[\begin{array}{@{}cc@{}}k & k\\ 0 & k\end{array}\right].\end{eqnarray}$$
The
$k$
-algebra
$\unicode[STIX]{x1D6EC}$
has injective dimension one over itself and can be realized as the path algebra of the quiver
modulo the relations
$$\begin{eqnarray}\unicode[STIX]{x1D700}_{1}^{2}=0=\unicode[STIX]{x1D700}_{2}^{2}\qquad \text{and}\qquad \unicode[STIX]{x1D6FC}\unicode[STIX]{x1D700}_{1}=\unicode[STIX]{x1D700}_{2}\unicode[STIX]{x1D6FC}.\end{eqnarray}$$
The algebra
$\unicode[STIX]{x1D6EC}$
is representation finite and has precisely nine indecomposable modules. There are two simple modules corresponding to the vertices
$1$
and
$2$
. The following diagram shows the Auslander–Reiten quiver. The vertices represent the indecomposables via their composition series. There is a solid arrow
$X\rightarrow Y$
if there is an irreducible morphism, and a dotted arrow
$X{\dashrightarrow}Y$
when
$Y=D\operatorname{Tr}X$
.
The Gorenstein projectives have a bold frame, the Gorenstein injectives are shaded and the modules of finite projective and injective dimension have rectangular shape. A module belongs to all three classes if and only if it is projective and injective; there is a unique indecomposable with this property.
One way to justify these computations is via [Reference Ringel and Zhang23, Theorem 2] due to Ringel and Zhang that sets up a bijection between indecomposable nonprojective Gorenstein projective modules over
$k[\unicode[STIX]{x1D700}]\otimes _{k}kQ$
and the indecomposable
$kQ$
-modules, for any quiver
$Q$
.
Acknowledgments
We are grateful to the American Institute of Mathematics in San Jose, California for supporting this project by their “Research in Squares” program. Our thanks also to a referee for reading this document with care and offering constructive criticism.
