1 Introduction
Let  $X$ be a complex manifold and
$X$ be a complex manifold and  $Y$ be a complex submanifold of codimension
$Y$ be a complex submanifold of codimension  $r$. Our interest is in the analytic structure of a neighborhood of
$r$. Our interest is in the analytic structure of a neighborhood of  $Y$ when the normal bundle
$Y$ when the normal bundle  $N_{Y/X}$ is unitary flat. We say that a holomorphic vector bundle
$N_{Y/X}$ is unitary flat. We say that a holomorphic vector bundle  $E$ on
$E$ on  $Y$ is unitary flat if
$Y$ is unitary flat if
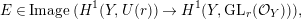 $$\begin{eqnarray}E\in \text{Image}\,(H^{1}(Y,U(r))\rightarrow H^{1}(Y,\text{GL}_{r}({\mathcal{O}}_{Y}))),\end{eqnarray}$$
$$\begin{eqnarray}E\in \text{Image}\,(H^{1}(Y,U(r))\rightarrow H^{1}(Y,\text{GL}_{r}({\mathcal{O}}_{Y}))),\end{eqnarray}$$ or equivalently, the transition matrices of  $E$ can be chosen to be
$E$ can be chosen to be  $U(r)$-valued locally constant functions, where
$U(r)$-valued locally constant functions, where  $U(r)$ is the set of
$U(r)$ is the set of  $r\times r$ unitary matrices. A unitary flat vector bundle
$r\times r$ unitary matrices. A unitary flat vector bundle  $E$ admits a flat connection whose monodromy
$E$ admits a flat connection whose monodromy  $\unicode[STIX]{x1D70C}_{E}$ is a unitary representation of the fundamental group
$\unicode[STIX]{x1D70C}_{E}$ is a unitary representation of the fundamental group  $\unicode[STIX]{x1D70B}_{1}(Y,\ast )$ of
$\unicode[STIX]{x1D70B}_{1}(Y,\ast )$ of  $Y$ (see Section 2.1 for the details). Our interest is in a sort of the linearizability problem of a neighborhood of
$Y$ (see Section 2.1 for the details). Our interest is in a sort of the linearizability problem of a neighborhood of  $Y$. In other words, we are interested in comparing a neighborhood of
$Y$. In other words, we are interested in comparing a neighborhood of  $Y$ in
$Y$ in  $X$ and of the zero section in
$X$ and of the zero section in  $N_{Y/X}$. One main goal of this paper is to investigate the existence of a holomorphic foliation
$N_{Y/X}$. One main goal of this paper is to investigate the existence of a holomorphic foliation  ${\mathcal{F}}$ of codimension
${\mathcal{F}}$ of codimension  $r$ on a neighborhood of
$r$ on a neighborhood of  $Y$ which includes
$Y$ which includes  $Y$ as a leaf with
$Y$ as a leaf with  $\text{Hol}_{{\mathcal{F}},Y}=\unicode[STIX]{x1D70C}_{N_{Y/X}}$, where
$\text{Hol}_{{\mathcal{F}},Y}=\unicode[STIX]{x1D70C}_{N_{Y/X}}$, where  $\text{Hol}_{{\mathcal{F}},Y}$ is the holonomy of
$\text{Hol}_{{\mathcal{F}},Y}$ is the holonomy of  ${\mathcal{F}}$ along
${\mathcal{F}}$ along  $Y$.
$Y$.
In [Reference Arnol’dA], Arnol’d studied a neighborhood of an elliptic curve  $Y$ by applying a linearizing technique as in [Reference SiegelSi]. In [Reference UedaU], Ueda studied the case where
$Y$ by applying a linearizing technique as in [Reference SiegelSi]. In [Reference UedaU], Ueda studied the case where  $Y$ is any compact complex curve and
$Y$ is any compact complex curve and  $r=1$. For such a pair
$r=1$. For such a pair  $(Y,X)$, Ueda posed the Ueda class
$(Y,X)$, Ueda posed the Ueda class  $u_{n}(Y,X)\in H^{1}(Y,N_{Y/X}^{-n}):=H^{1}(Y,{\mathcal{O}}_{Y}(N_{Y/X}^{\otimes -n}))$ as an obstruction of the linearization of a neighborhood of
$u_{n}(Y,X)\in H^{1}(Y,N_{Y/X}^{-n}):=H^{1}(Y,{\mathcal{O}}_{Y}(N_{Y/X}^{\otimes -n}))$ as an obstruction of the linearization of a neighborhood of  $Y$ in
$Y$ in  $n$-jet along
$n$-jet along  $Y$ (
$Y$ ( $n\geqslant 1$). The pair
$n\geqslant 1$). The pair  $(Y,X)$ is of infinite type if
$(Y,X)$ is of infinite type if  $u_{n}(Y,X)=0$ holds for each
$u_{n}(Y,X)=0$ holds for each  $n\geqslant 1$. When
$n\geqslant 1$. When  $(Y,X)$ is of infinite type, Ueda generalized the result of Arnol’d. He showed that an infinite type pair
$(Y,X)$ is of infinite type, Ueda generalized the result of Arnol’d. He showed that an infinite type pair  $(Y,X)$ admits the foliation
$(Y,X)$ admits the foliation  ${\mathcal{F}}$ as above if
${\mathcal{F}}$ as above if  $N_{Y/X}$ is a torsion element of
$N_{Y/X}$ is a torsion element of  ${\mathcal{P}}(Y):=\text{Image}\,(H^{1}(Y,U(1))\rightarrow H^{1}(Y,{\mathcal{O}}_{Y}^{\ast }))$, or satisfies the following Diophantine-type condition: there exists a constant
${\mathcal{P}}(Y):=\text{Image}\,(H^{1}(Y,U(1))\rightarrow H^{1}(Y,{\mathcal{O}}_{Y}^{\ast }))$, or satisfies the following Diophantine-type condition: there exists a constant  $A>0$ such that
$A>0$ such that  $d(\mathbb{I}_{Y}^{(1)},N_{Y/X}^{m})\geqslant (2m)^{-A}$ holds for any
$d(\mathbb{I}_{Y}^{(1)},N_{Y/X}^{m})\geqslant (2m)^{-A}$ holds for any  $m\geqslant 1$. Here
$m\geqslant 1$. Here  $\mathbb{I}_{Y}^{(1)}$ is the holomorphically trivial line bundle on
$\mathbb{I}_{Y}^{(1)}$ is the holomorphically trivial line bundle on  $Y$ and
$Y$ and  $d$ is an invariant distance on
$d$ is an invariant distance on  ${\mathcal{P}}(Y)$ ([Reference UedaU, Theorem 3], see [Reference UedaU, Section 4.1] for the details). Note that the proof of [Reference UedaU, Theorem 3] works not only when
${\mathcal{P}}(Y)$ ([Reference UedaU, Theorem 3], see [Reference UedaU, Section 4.1] for the details). Note that the proof of [Reference UedaU, Theorem 3] works not only when  $Y$ is a curve, but also when
$Y$ is a curve, but also when  $Y$ is a compact complex manifold of arbitrary dimension if the codimension of
$Y$ is a compact complex manifold of arbitrary dimension if the codimension of  $Y$ is one.
$Y$ is one.
We generalize Ueda’s theory to the case where the codimension  $r$ of
$r$ of  $Y$ is greater than
$Y$ is greater than  $1$. We will define the obstruction class
$1$. We will define the obstruction class
 $$\begin{eqnarray}u_{n}(Y,X)\in H^{1}(Y,N_{Y/X}\otimes S^{n+1}N_{Y/X}^{\ast })\end{eqnarray}$$
$$\begin{eqnarray}u_{n}(Y,X)\in H^{1}(Y,N_{Y/X}\otimes S^{n+1}N_{Y/X}^{\ast })\end{eqnarray}$$ as a straightforward generalization of the Ueda class and generalize [Reference UedaU, Theorem 3] to the pair  $(Y,X)$ of infinite type with
$(Y,X)$ of infinite type with  $N_{Y/X}\in {\mathcal{E}}_{0}^{(r)}(Y)\cup {\mathcal{E}}_{1}^{(r)}(Y)$. Here we denote by
$N_{Y/X}\in {\mathcal{E}}_{0}^{(r)}(Y)\cup {\mathcal{E}}_{1}^{(r)}(Y)$. Here we denote by  $S^{n+1}N_{Y/X}^{\ast }$ the
$S^{n+1}N_{Y/X}^{\ast }$ the  $n+1$th symmetric tensor bundle,
$n+1$th symmetric tensor bundle,  ${\mathcal{E}}_{0}^{(r)}(Y)$ the set
${\mathcal{E}}_{0}^{(r)}(Y)$ the set  $\{E_{\unicode[STIX]{x1D70C}}\mid \#(\text{Image}\,\unicode[STIX]{x1D70C})<\infty \}$, and by
$\{E_{\unicode[STIX]{x1D70C}}\mid \#(\text{Image}\,\unicode[STIX]{x1D70C})<\infty \}$, and by  ${\mathcal{E}}_{1}^{(r)}(Y)$ the set
${\mathcal{E}}_{1}^{(r)}(Y)$ the set
 $$\begin{eqnarray}\displaystyle & & \displaystyle \{\!E_{\unicode[STIX]{x1D70C}}|\unicode[STIX]{x1D70B}^{\ast }E_{\unicode[STIX]{x1D70C}}\in {\mathcal{S}}_{A}^{(r)}(\widetilde{Y})\nonumber\\ \displaystyle & & \displaystyle \text{for some finite normal covering}~\unicode[STIX]{x1D70B}:\widetilde{Y}\rightarrow Y~\text{and}~A>0\!\},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \{\!E_{\unicode[STIX]{x1D70C}}|\unicode[STIX]{x1D70B}^{\ast }E_{\unicode[STIX]{x1D70C}}\in {\mathcal{S}}_{A}^{(r)}(\widetilde{Y})\nonumber\\ \displaystyle & & \displaystyle \text{for some finite normal covering}~\unicode[STIX]{x1D70B}:\widetilde{Y}\rightarrow Y~\text{and}~A>0\!\},\nonumber\end{eqnarray}$$ where  $E_{\unicode[STIX]{x1D70C}}$ is the unitary flat vector bundle of rank
$E_{\unicode[STIX]{x1D70C}}$ is the unitary flat vector bundle of rank  $r$ which corresponds to a unitary representation
$r$ which corresponds to a unitary representation  $\unicode[STIX]{x1D70C}$ of
$\unicode[STIX]{x1D70C}$ of  $\unicode[STIX]{x1D70B}_{1}(Y,\ast )$ (see Section 2.1 for the correspondence) and
$\unicode[STIX]{x1D70B}_{1}(Y,\ast )$ (see Section 2.1 for the correspondence) and  ${\mathcal{S}}_{A}^{(r)}(\widetilde{Y})$ is the set
${\mathcal{S}}_{A}^{(r)}(\widetilde{Y})$ is the set
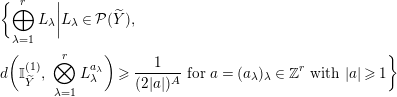 $$\begin{eqnarray}\displaystyle & & \displaystyle \bigg\{\!\bigoplus _{\unicode[STIX]{x1D706}=1}^{r}L_{\unicode[STIX]{x1D706}}\bigg|L_{\unicode[STIX]{x1D706}}\in {\mathcal{P}}(\widetilde{Y}),\nonumber\\ \displaystyle & & \displaystyle d\biggl(\mathbb{I}_{\widetilde{Y}}^{(1)},~\bigotimes _{\unicode[STIX]{x1D706}=1}^{r}L_{\unicode[STIX]{x1D706}}^{a_{\unicode[STIX]{x1D706}}}\biggr)\geqslant \frac{1}{(2|a|)^{A}}~\text{for}~a=(a_{\unicode[STIX]{x1D706}})_{\unicode[STIX]{x1D706}}\in \mathbb{Z}^{r}~\text{with}~|a|\geqslant 1\bigg\}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \bigg\{\!\bigoplus _{\unicode[STIX]{x1D706}=1}^{r}L_{\unicode[STIX]{x1D706}}\bigg|L_{\unicode[STIX]{x1D706}}\in {\mathcal{P}}(\widetilde{Y}),\nonumber\\ \displaystyle & & \displaystyle d\biggl(\mathbb{I}_{\widetilde{Y}}^{(1)},~\bigotimes _{\unicode[STIX]{x1D706}=1}^{r}L_{\unicode[STIX]{x1D706}}^{a_{\unicode[STIX]{x1D706}}}\biggr)\geqslant \frac{1}{(2|a|)^{A}}~\text{for}~a=(a_{\unicode[STIX]{x1D706}})_{\unicode[STIX]{x1D706}}\in \mathbb{Z}^{r}~\text{with}~|a|\geqslant 1\bigg\}\nonumber\end{eqnarray}$$ ( $|a|:=a_{1}+a_{2}+\cdots +a_{r}$).
$|a|:=a_{1}+a_{2}+\cdots +a_{r}$).
Theorem 1.1. Let  $X$ be a complex manifold and
$X$ be a complex manifold and  $Y$ be a compact complex submanifold of codimension
$Y$ be a compact complex submanifold of codimension  $r$ with
$r$ with  $N_{Y/X}\in {\mathcal{E}}_{0}^{(r)}(Y)\cup {\mathcal{E}}_{1}^{(r)}(Y)$. Assume that the pair
$N_{Y/X}\in {\mathcal{E}}_{0}^{(r)}(Y)\cup {\mathcal{E}}_{1}^{(r)}(Y)$. Assume that the pair  $(Y,X)$ is of infinite type (i.e.
$(Y,X)$ is of infinite type (i.e.  $u_{n}(Y,X)=0$ for each
$u_{n}(Y,X)=0$ for each  $n\geqslant 1$). Then the following holds:
$n\geqslant 1$). Then the following holds:
(i) There uniquely exists a nonsingular holomorphic foliation
 ${\mathcal{F}}$ of codimension
${\mathcal{F}}$ of codimension  $r$ on some neighborhood
$r$ on some neighborhood  $V$ of
$V$ of  $Y$ which includes
$Y$ which includes  $Y$ as a leaf with
$Y$ as a leaf with  $\text{Hol}_{{\mathcal{F}},Y}=\unicode[STIX]{x1D70C}_{N_{Y/X}}$.
$\text{Hol}_{{\mathcal{F}},Y}=\unicode[STIX]{x1D70C}_{N_{Y/X}}$.(ii) Suppose that there exists a hypersurface
 $S$ such that
$S$ such that  $Y\subset S$ and
$Y\subset S$ and  $N_{Y/S}$ is unitary flat. Then there exists a nonsingular holomorphic foliation
$N_{Y/S}$ is unitary flat. Then there exists a nonsingular holomorphic foliation  ${\mathcal{G}}_{S}$ of codimension
${\mathcal{G}}_{S}$ of codimension  $1$ on
$1$ on  $V$ with the following properties by shrinking
$V$ with the following properties by shrinking  $V$ if necessary:
$V$ if necessary:  ${\mathcal{G}}_{S}$ includes
${\mathcal{G}}_{S}$ includes  $S\cap V$ as a leaf with
$S\cap V$ as a leaf with  $U(1)$-linear holonomy, and each leaf of
$U(1)$-linear holonomy, and each leaf of  ${\mathcal{F}}$ is holomorphically immersed into a leaf of
${\mathcal{F}}$ is holomorphically immersed into a leaf of  ${\mathcal{G}}_{S}$. Especially,
${\mathcal{G}}_{S}$. Especially,  $S\cap V$ is the union of leaves of
$S\cap V$ is the union of leaves of  ${\mathcal{F}}$.
${\mathcal{F}}$.
Note that the assertion (i) in Theorem 1.1 implies the existence of a deformation family of  $Y$ when
$Y$ when  $N_{Y/X}\in {\mathcal{E}}_{0}^{(r)}(Y)$. Note also that, for each unitary flat subbundle
$N_{Y/X}\in {\mathcal{E}}_{0}^{(r)}(Y)$. Note also that, for each unitary flat subbundle  $E\subset N_{Y/X}$, the assertion (i) implies the existence of a submanifold
$E\subset N_{Y/X}$, the assertion (i) implies the existence of a submanifold  $Z\subset V$ with
$Z\subset V$ with  $Y\subset Z$ and
$Y\subset Z$ and  $N_{Y/Z}=E$ (see Remark 2.6). Especially, when
$N_{Y/Z}=E$ (see Remark 2.6). Especially, when  $N_{Y/X}$ admits a direct decomposition to
$N_{Y/X}$ admits a direct decomposition to  $r$ unitary flat line bundles, it is observed from Theorem 1.1(i) that
$r$ unitary flat line bundles, it is observed from Theorem 1.1(i) that  $Y$ is realized as a transversal intersection of
$Y$ is realized as a transversal intersection of  $r$ nonsingular hypersurfaces of a neighborhood of
$r$ nonsingular hypersurfaces of a neighborhood of  $Y$ in
$Y$ in  $X$ if
$X$ if  $N_{Y/X}\in {\mathcal{E}}_{0}^{(r)}(Y)\cup {\mathcal{E}}_{1}^{(r)}(Y)$ and the pair
$N_{Y/X}\in {\mathcal{E}}_{0}^{(r)}(Y)\cup {\mathcal{E}}_{1}^{(r)}(Y)$ and the pair  $(Y,X)$ is of infinite type. As the pair
$(Y,X)$ is of infinite type. As the pair  $(Y,X)$ is always of infinite type when
$(Y,X)$ is always of infinite type when  $H^{1}(Y,N_{Y/X}\otimes S^{n+1}N_{Y/X}^{\ast })=0$ for each
$H^{1}(Y,N_{Y/X}\otimes S^{n+1}N_{Y/X}^{\ast })=0$ for each  $n\geqslant 1$, Theorem 1.1(i) can be applied to the case where, for example,
$n\geqslant 1$, Theorem 1.1(i) can be applied to the case where, for example,  $Y$ is an elliptic curve and
$Y$ is an elliptic curve and  $N_{Y/X}\in {\mathcal{E}}_{1}^{(r)}(Y)$. In this sense, Theorem 1.1(i) can be also regarded as a generalization of the result of Arnol’d for elliptic curves.
$N_{Y/X}\in {\mathcal{E}}_{1}^{(r)}(Y)$. In this sense, Theorem 1.1(i) can be also regarded as a generalization of the result of Arnol’d for elliptic curves.
Theorem 1.1(ii) can be applied to the semipositivity problem (the existence problem of a  $C^{\infty }$ Hermitian metric with semipositive curvature) on a holomorphic line bundle, since the assertion (ii) implies the unitary flatness of the line bundle
$C^{\infty }$ Hermitian metric with semipositive curvature) on a holomorphic line bundle, since the assertion (ii) implies the unitary flatness of the line bundle  $[S]$ on
$[S]$ on  $V$.
$V$.
Corollary 1.2. Let  $X$ be a complex manifold of dimension
$X$ be a complex manifold of dimension  $n$ and
$n$ and  $L$ be a holomorphic line bundle on
$L$ be a holomorphic line bundle on  $X$. Take
$X$. Take  $D_{1},D_{2},\ldots ,D_{n-1}\in |L|$. Assume that
$D_{1},D_{2},\ldots ,D_{n-1}\in |L|$. Assume that  $C:=\bigcap _{\unicode[STIX]{x1D706}=1}^{n-1}D_{\unicode[STIX]{x1D706}}$ is a smooth elliptic curve,
$C:=\bigcap _{\unicode[STIX]{x1D706}=1}^{n-1}D_{\unicode[STIX]{x1D706}}$ is a smooth elliptic curve,  $L|_{C}\in {\mathcal{E}}_{1}^{(1)}(C)$, and
$L|_{C}\in {\mathcal{E}}_{1}^{(1)}(C)$, and  $\{D_{\unicode[STIX]{x1D706}}\}_{\unicode[STIX]{x1D706}=1}^{n-1}$ intersects transversally along
$\{D_{\unicode[STIX]{x1D706}}\}_{\unicode[STIX]{x1D706}=1}^{n-1}$ intersects transversally along  $C$. Then
$C$. Then  $L$ is semipositive (i.e.
$L$ is semipositive (i.e.  $L$ admits a
$L$ admits a  $C^{\infty }$ Hermitian metric with semipositive curvature).
$C^{\infty }$ Hermitian metric with semipositive curvature).
Note that  $L$ as in Corollary 1.2 has
$L$ as in Corollary 1.2 has  $C$ as a stable base locus:
$C$ as a stable base locus:  $C=\text{SB}(L):=\bigcap _{m\geqslant 1}\text{Bs}\,|L^{m}|$. Corollary 1.2 can be applied to the example of the blow-up of a del Pezzo manifold at a general point as follows:
$C=\text{SB}(L):=\bigcap _{m\geqslant 1}\text{Bs}\,|L^{m}|$. Corollary 1.2 can be applied to the example of the blow-up of a del Pezzo manifold at a general point as follows:
Corollary 1.3. Let  $(V,L)$ be a del Pezzo manifold of degree
$(V,L)$ be a del Pezzo manifold of degree  $1$ (i.e.
$1$ (i.e.  $V$ is a projective manifold of dimension
$V$ is a projective manifold of dimension  $n$ and
$n$ and  $L$ is an ample line bundle on
$L$ is an ample line bundle on  $V$ with
$V$ with  $K_{V}^{-1}\cong L^{n-1}$ and the self-intersection number
$K_{V}^{-1}\cong L^{n-1}$ and the self-intersection number  $(L^{n})$ is equal to
$(L^{n})$ is equal to  $1$), and
$1$), and  $C\subset V$ be an intersection of general
$C\subset V$ be an intersection of general  $n-1$ elements of
$n-1$ elements of  $|L|$. For each point
$|L|$. For each point  $q\in C$ with
$q\in C$ with  $L|_{C}\otimes [-q]\in {\mathcal{E}}_{1}^{(0)}(C)\cup {\mathcal{E}}_{1}^{(1)}(C)$, the anticanonical bundle of the blow-up of
$L|_{C}\otimes [-q]\in {\mathcal{E}}_{1}^{(0)}(C)\cup {\mathcal{E}}_{1}^{(1)}(C)$, the anticanonical bundle of the blow-up of  $V$ at
$V$ at  $q$ is semipositive.
$q$ is semipositive.
We remark that Corollary 1.3 can be regarded as a generalization of the known phenomena for the blow-up of  $\mathbb{P}^{2}$ at general nine points ([Reference Arnol’dA], [Reference BrunellaB], [Reference UedaU], see also [Reference DemaillyD2, Section 1]), or the blow-up of
$\mathbb{P}^{2}$ at general nine points ([Reference Arnol’dA], [Reference BrunellaB], [Reference UedaU], see also [Reference DemaillyD2, Section 1]), or the blow-up of  $\mathbb{P}^{3}$ at general eight points ([Reference KoikeK2, Corollary 1]. Note that this result can be re-proved by using [Reference Koike and OgawaKO, Theorem 1.4, Remark 3.12], which is a corrected form of [Reference KoikeK2, Theorem 1]).
$\mathbb{P}^{3}$ at general eight points ([Reference KoikeK2, Corollary 1]. Note that this result can be re-proved by using [Reference Koike and OgawaKO, Theorem 1.4, Remark 3.12], which is a corrected form of [Reference KoikeK2, Theorem 1]).
The organization of the paper is as follows. In Section 2, we summarize some fundamental facts and notations on the unitary flat vector bundles on a compact complex manifold and local defining functions of compact submanifolds. In Section 3, we give the definitions of the obstruction class  $u_{n}(Y,X)$ and the type of the pair
$u_{n}(Y,X)$ and the type of the pair  $(Y,X)$. In Section 4, we prove Theorem 1.1. In Section 5, we show Corollary 1.2. In Section 6, we give some examples. Here we will prove Corollary 1.3. In Section 7, we list some remaining problems.
$(Y,X)$. In Section 4, we prove Theorem 1.1. In Section 5, we show Corollary 1.2. In Section 6, we give some examples. Here we will prove Corollary 1.3. In Section 7, we list some remaining problems.
2 Preliminaries
2.1 Unitary flat vector bundles on compact complex manifolds
Let  $Y$ be a compact complex manifold and
$Y$ be a compact complex manifold and  $E$ be a holomorphic vector bundle on
$E$ be a holomorphic vector bundle on  $Y$. We say that
$Y$. We say that  $E$ is unitary flat if
$E$ is unitary flat if
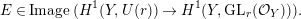 $$\begin{eqnarray}E\in \text{Image}\,(H^{1}(Y,U(r))\rightarrow H^{1}(Y,\text{GL}_{r}({\mathcal{O}}_{Y}))).\end{eqnarray}$$
$$\begin{eqnarray}E\in \text{Image}\,(H^{1}(Y,U(r))\rightarrow H^{1}(Y,\text{GL}_{r}({\mathcal{O}}_{Y}))).\end{eqnarray}$$ It means that, for a suitable choice of an open covering  $\{U_{j}\}$ of
$\{U_{j}\}$ of  $Y$ and a local frame
$Y$ and a local frame  $e_{j}=(e_{j}^{1},e_{j}^{2},\ldots ,e_{j}^{r})$ of
$e_{j}=(e_{j}^{1},e_{j}^{2},\ldots ,e_{j}^{r})$ of  $E$ on each
$E$ on each  $U_{j}$, the transition matrix
$U_{j}$, the transition matrix  $T_{jk}$ of
$T_{jk}$ of  $\{(U_{j},e_{j})\}$ on each
$\{(U_{j},e_{j})\}$ on each  $U_{jk}:=U_{j}\cap U_{k}$ can be a locally constant function values in
$U_{jk}:=U_{j}\cap U_{k}$ can be a locally constant function values in  $U(r)$: i.e. for some
$U(r)$: i.e. for some  $T_{jk}\in U(r)$, it holds that
$T_{jk}\in U(r)$, it holds that  $e_{j}=T_{jk}e_{k}$, or equivalently,
$e_{j}=T_{jk}e_{k}$, or equivalently,  $e_{j}^{\unicode[STIX]{x1D706}}=\sum _{\unicode[STIX]{x1D707}=1}^{r}(T_{jk})_{\unicode[STIX]{x1D707}}^{\unicode[STIX]{x1D706}}\cdot e_{k}^{\unicode[STIX]{x1D707}}$. Here we denote by
$e_{j}^{\unicode[STIX]{x1D706}}=\sum _{\unicode[STIX]{x1D707}=1}^{r}(T_{jk})_{\unicode[STIX]{x1D707}}^{\unicode[STIX]{x1D706}}\cdot e_{k}^{\unicode[STIX]{x1D707}}$. Here we denote by  $(T_{jk})_{\unicode[STIX]{x1D707}}^{\unicode[STIX]{x1D706}}$ the
$(T_{jk})_{\unicode[STIX]{x1D707}}^{\unicode[STIX]{x1D706}}$ the  $(\unicode[STIX]{x1D706},\unicode[STIX]{x1D707})$th entry of
$(\unicode[STIX]{x1D706},\unicode[STIX]{x1D707})$th entry of  $T_{jk}$. For a unitary flat vector bundle
$T_{jk}$. For a unitary flat vector bundle  $E$, we can define a unitary flat metric
$E$, we can define a unitary flat metric  $h$ on
$h$ on  $E$ by regarding each
$E$ by regarding each  $e_{j}$ as an orthonormal frame. By using this
$e_{j}$ as an orthonormal frame. By using this  $h$, we obtain:
$h$, we obtain:
Lemma 2.1. Let  $a_{j,\unicode[STIX]{x1D706}}:U_{j}\rightarrow \mathbb{C}$ be a holomorphic function. Assume that
$a_{j,\unicode[STIX]{x1D706}}:U_{j}\rightarrow \mathbb{C}$ be a holomorphic function. Assume that  $\{(U_{j},\sum _{\unicode[STIX]{x1D706}=1}^{r}a_{j,\unicode[STIX]{x1D706}}\cdot e_{j}^{\unicode[STIX]{x1D706}})\}$ glue up to define a holomorphic global section
$\{(U_{j},\sum _{\unicode[STIX]{x1D706}=1}^{r}a_{j,\unicode[STIX]{x1D706}}\cdot e_{j}^{\unicode[STIX]{x1D706}})\}$ glue up to define a holomorphic global section  $a$ of
$a$ of  $E$. Then
$E$. Then  $a_{j,\unicode[STIX]{x1D706}}$ is a locally constant function on each
$a_{j,\unicode[STIX]{x1D706}}$ is a locally constant function on each  $U_{j}$.
$U_{j}$.
Proof. (See also the proof of [Reference SeshadriSe, Section 1, Proposition 1]) By applying the maximal principle to the psh (plurisubharmonic) function  $|a|_{h}^{2}$, we obtain
$|a|_{h}^{2}$, we obtain  $|a|_{h}^{2}\equiv C$ for some constant
$|a|_{h}^{2}\equiv C$ for some constant  $C$. As it holds that
$C$. As it holds that  $|a_{j,\unicode[STIX]{x1D706}}|^{2}=C-\sum _{\unicode[STIX]{x1D706}\not =\unicode[STIX]{x1D707}}|a_{j,\unicode[STIX]{x1D707}}|^{2}$ on each
$|a_{j,\unicode[STIX]{x1D706}}|^{2}=C-\sum _{\unicode[STIX]{x1D706}\not =\unicode[STIX]{x1D707}}|a_{j,\unicode[STIX]{x1D707}}|^{2}$ on each  $U_{j}$, we conclude that
$U_{j}$, we conclude that  $|a_{j,\unicode[STIX]{x1D706}}|^{2}$ is pluriharmonic for each
$|a_{j,\unicode[STIX]{x1D706}}|^{2}$ is pluriharmonic for each  $\unicode[STIX]{x1D706}=1,2,\ldots ,r$, which proves the lemma.◻
$\unicode[STIX]{x1D706}=1,2,\ldots ,r$, which proves the lemma.◻
By considering the monodromy of the Chern connection of  $h$, we obtain a unitary representation
$h$, we obtain a unitary representation  $\unicode[STIX]{x1D70C}=\unicode[STIX]{x1D70C}_{E}:\unicode[STIX]{x1D70B}_{1}(Y,\ast )\rightarrow U(r)$. Conversely, for a given unitary representation
$\unicode[STIX]{x1D70C}=\unicode[STIX]{x1D70C}_{E}:\unicode[STIX]{x1D70B}_{1}(Y,\ast )\rightarrow U(r)$. Conversely, for a given unitary representation  $\unicode[STIX]{x1D70C}:\unicode[STIX]{x1D70B}_{1}(Y,\ast )\rightarrow U(r)$, we can construct a unitary flat vector bundle
$\unicode[STIX]{x1D70C}:\unicode[STIX]{x1D70B}_{1}(Y,\ast )\rightarrow U(r)$, we can construct a unitary flat vector bundle  $E_{\unicode[STIX]{x1D70C}}$ by
$E_{\unicode[STIX]{x1D70C}}$ by
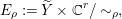 $$\begin{eqnarray}E_{\unicode[STIX]{x1D70C}}:=\widetilde{Y}\times \mathbb{C}^{r}/{\sim}_{\unicode[STIX]{x1D70C}},\end{eqnarray}$$
$$\begin{eqnarray}E_{\unicode[STIX]{x1D70C}}:=\widetilde{Y}\times \mathbb{C}^{r}/{\sim}_{\unicode[STIX]{x1D70C}},\end{eqnarray}$$ where  $\widetilde{Y}\rightarrow Y$ is the universal covering of
$\widetilde{Y}\rightarrow Y$ is the universal covering of  $Y$ and
$Y$ and  ${\sim}_{\unicode[STIX]{x1D70C}}$ is the relation defined by
${\sim}_{\unicode[STIX]{x1D70C}}$ is the relation defined by  $(z,v){\sim}_{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D6FE}z,\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE})v)$ for each
$(z,v){\sim}_{\unicode[STIX]{x1D70C}}(\unicode[STIX]{x1D6FE}z,\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE})v)$ for each  $(z,v)\in \widetilde{Y}\times \mathbb{C}^{r}$ and
$(z,v)\in \widetilde{Y}\times \mathbb{C}^{r}$ and  $\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D70B}_{1}(Y,\ast )$.
$\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D70B}_{1}(Y,\ast )$.
Proposition 2.2. The above gives  $1:1$-correspondence between the image of the natural map
$1:1$-correspondence between the image of the natural map  $H^{1}(Y,U(r))\rightarrow H^{1}(Y,\text{GL}_{r}({\mathcal{O}}_{Y}))$ and the set
$H^{1}(Y,U(r))\rightarrow H^{1}(Y,\text{GL}_{r}({\mathcal{O}}_{Y}))$ and the set  $\{\unicode[STIX]{x1D70C}:U(r)\text{-representation of}~\unicode[STIX]{x1D70B}_{1}(Y,\ast )\}/\sim$, where
$\{\unicode[STIX]{x1D70C}:U(r)\text{-representation of}~\unicode[STIX]{x1D70B}_{1}(Y,\ast )\}/\sim$, where  $\unicode[STIX]{x1D70C}\sim \unicode[STIX]{x1D70C}^{\prime }$ means that there exists
$\unicode[STIX]{x1D70C}\sim \unicode[STIX]{x1D70C}^{\prime }$ means that there exists  $A\in \text{GL}_{r}(\mathbb{C})$ such that
$A\in \text{GL}_{r}(\mathbb{C})$ such that  $A^{-1}\cdot \unicode[STIX]{x1D70C}\cdot A=\unicode[STIX]{x1D70C}^{\prime }$ holds.
$A^{-1}\cdot \unicode[STIX]{x1D70C}\cdot A=\unicode[STIX]{x1D70C}^{\prime }$ holds.
For proving Proposition 2.2, we need the following:
Lemma 2.3. Let  $E$ and
$E$ and  $F$ be unitary flat vector bundles on
$F$ be unitary flat vector bundles on  $Y$. Assume that
$Y$. Assume that  $E$ and
$E$ and  $F$ are isomorphic to each other as holomorphic vector bundles. Then the image of
$F$ are isomorphic to each other as holomorphic vector bundles. Then the image of  $E$ and
$E$ and  $F$ by the natural map
$F$ by the natural map
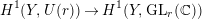 $$\begin{eqnarray}H^{1}(Y,U(r))\rightarrow H^{1}(Y,\text{GL}_{r}(\mathbb{C}))\end{eqnarray}$$
$$\begin{eqnarray}H^{1}(Y,U(r))\rightarrow H^{1}(Y,\text{GL}_{r}(\mathbb{C}))\end{eqnarray}$$coincide with each other.
Proof. The lemma is shown by applying Lemma 2.1 to a global section of the unitary flat vector bundle  $\text{Hom}(E,F)\cong E^{\ast }\otimes F$. See the proof of [Reference SeshadriSe, Section 1, Proposition 1] for the details.◻
$\text{Hom}(E,F)\cong E^{\ast }\otimes F$. See the proof of [Reference SeshadriSe, Section 1, Proposition 1] for the details.◻
Proof of Proposition 2.2.
Let  $E$ be a unitary flat vector bundle. Take
$E$ be a unitary flat vector bundle. Take  $\{(U_{j},e_{j})\}$ and
$\{(U_{j},e_{j})\}$ and  $\unicode[STIX]{x1D70C}=\unicode[STIX]{x1D70C}_{E}$ as above. Let
$\unicode[STIX]{x1D70C}=\unicode[STIX]{x1D70C}_{E}$ as above. Let  $\{(U_{j},f_{j}=(f_{j}^{1},f_{j}^{2},\ldots ,f_{j}^{r}))\}$ be another local frame of
$\{(U_{j},f_{j}=(f_{j}^{1},f_{j}^{2},\ldots ,f_{j}^{r}))\}$ be another local frame of  $E$ with
$E$ with  $f_{j}=S_{jk}f_{k}$ on each
$f_{j}=S_{jk}f_{k}$ on each  $U_{jk}$ (
$U_{jk}$ ( $S_{jk}\in U(r)$), and
$S_{jk}\in U(r)$), and  $\unicode[STIX]{x1D70C}^{\prime }:\unicode[STIX]{x1D70B}_{1}(Y,\ast )\rightarrow U(r)$ be the monodromy defined by using
$\unicode[STIX]{x1D70C}^{\prime }:\unicode[STIX]{x1D70B}_{1}(Y,\ast )\rightarrow U(r)$ be the monodromy defined by using  $f_{j}$ as an orthonormal frame on each
$f_{j}$ as an orthonormal frame on each  $U_{j}$. By Lemma 2.3, we can take
$U_{j}$. By Lemma 2.3, we can take  $A_{j}\in \text{GL}_{r}(\mathbb{C})$ for each
$A_{j}\in \text{GL}_{r}(\mathbb{C})$ for each  $j$ with
$j$ with  $A_{j}S_{jk}=T_{jk}A_{k}$. Then, for each loop
$A_{j}S_{jk}=T_{jk}A_{k}$. Then, for each loop  $\unicode[STIX]{x1D6FE}$ of
$\unicode[STIX]{x1D6FE}$ of  $Y$ with a base point
$Y$ with a base point  $\ast \in U_{j}$, we can calculate that
$\ast \in U_{j}$, we can calculate that  $\unicode[STIX]{x1D70C}([\unicode[STIX]{x1D6FE}])=A_{j}\cdot \unicode[STIX]{x1D70C}^{\prime }([\unicode[STIX]{x1D6FE}])\cdot A_{j}^{-1}$, which proves
$\unicode[STIX]{x1D70C}([\unicode[STIX]{x1D6FE}])=A_{j}\cdot \unicode[STIX]{x1D70C}^{\prime }([\unicode[STIX]{x1D6FE}])\cdot A_{j}^{-1}$, which proves  $\unicode[STIX]{x1D70C}\sim \unicode[STIX]{x1D70C}^{\prime }$.
$\unicode[STIX]{x1D70C}\sim \unicode[STIX]{x1D70C}^{\prime }$.
Conversely, let  $\unicode[STIX]{x1D70C}$ and
$\unicode[STIX]{x1D70C}$ and  $\unicode[STIX]{x1D70C}^{\prime }$ be two
$\unicode[STIX]{x1D70C}^{\prime }$ be two  $U(r)$-representations of
$U(r)$-representations of  $\unicode[STIX]{x1D70B}_{1}(Y,\ast )$ with
$\unicode[STIX]{x1D70B}_{1}(Y,\ast )$ with  $\unicode[STIX]{x1D70C}\sim \unicode[STIX]{x1D70C}^{\prime }$. Take
$\unicode[STIX]{x1D70C}\sim \unicode[STIX]{x1D70C}^{\prime }$. Take  $A\in \text{GL}_{r}(\mathbb{C})$ such that
$A\in \text{GL}_{r}(\mathbb{C})$ such that  $A^{-1}\cdot \unicode[STIX]{x1D70C}\cdot A=\unicode[STIX]{x1D70C}^{\prime }$. Define the map
$A^{-1}\cdot \unicode[STIX]{x1D70C}\cdot A=\unicode[STIX]{x1D70C}^{\prime }$. Define the map  $F:\widetilde{Y}\times \mathbb{C}^{r}\rightarrow \widetilde{Y}\times \mathbb{C}^{r}$ by
$F:\widetilde{Y}\times \mathbb{C}^{r}\rightarrow \widetilde{Y}\times \mathbb{C}^{r}$ by  $F(z,v):=(z,A^{-1}\cdot v)$. Then it is easily observed that
$F(z,v):=(z,A^{-1}\cdot v)$. Then it is easily observed that  $F$ induces an isomorphism
$F$ induces an isomorphism  $E_{\unicode[STIX]{x1D70C}}\cong E_{\unicode[STIX]{x1D70C}^{\prime }}$, which proves the proposition.◻
$E_{\unicode[STIX]{x1D70C}}\cong E_{\unicode[STIX]{x1D70C}^{\prime }}$, which proves the proposition.◻
Remark 2.4. The definition of the relation  ${\sim}$ in Proposition 2.2 can be replaced by the following one: we say
${\sim}$ in Proposition 2.2 can be replaced by the following one: we say  $\unicode[STIX]{x1D70C}\sim \unicode[STIX]{x1D70C}^{\prime }$ if there exists
$\unicode[STIX]{x1D70C}\sim \unicode[STIX]{x1D70C}^{\prime }$ if there exists  $U\in U(r)$ such that
$U\in U(r)$ such that  $U^{-1}\cdot \unicode[STIX]{x1D70C}\cdot U=\unicode[STIX]{x1D70C}^{\prime }$ holds. It is because, for each
$U^{-1}\cdot \unicode[STIX]{x1D70C}\cdot U=\unicode[STIX]{x1D70C}^{\prime }$ holds. It is because, for each  $A\in \text{GL}_{r}(\mathbb{C})$ and
$A\in \text{GL}_{r}(\mathbb{C})$ and  $S\in U(r)$ with
$S\in U(r)$ with  $A^{-1}\cdot S\cdot A\in U(r)$, it holds that
$A^{-1}\cdot S\cdot A\in U(r)$, it holds that  $A^{-1}\cdot S\cdot A=U_{A}^{-1}\cdot S\cdot U_{A}$, where
$A^{-1}\cdot S\cdot A=U_{A}^{-1}\cdot S\cdot U_{A}$, where  $U_{A}$ is the unitary part of the polar decomposition
$U_{A}$ is the unitary part of the polar decomposition  $A=U_{A}\cdot P_{A}$. Therefore, by the same argument as in the proof of Proposition 2.2, we obtain that the image of
$A=U_{A}\cdot P_{A}$. Therefore, by the same argument as in the proof of Proposition 2.2, we obtain that the image of  $H^{1}(Y,U(r))\rightarrow H^{1}(Y,\text{GL}_{r}({\mathcal{O}}_{Y}))$ is naturally isomorphic to
$H^{1}(Y,U(r))\rightarrow H^{1}(Y,\text{GL}_{r}({\mathcal{O}}_{Y}))$ is naturally isomorphic to  $H^{1}(Y,U(r))$, or equivalently, the natural map
$H^{1}(Y,U(r))$, or equivalently, the natural map  $H^{1}(Y,U(r))\rightarrow H^{1}(Y,\text{GL}_{r}({\mathcal{O}}_{Y}))$ is injective.
$H^{1}(Y,U(r))\rightarrow H^{1}(Y,\text{GL}_{r}({\mathcal{O}}_{Y}))$ is injective.
Remark 2.5. Here we give another (more direct) proof of the injectivity of the natural map  $i:H^{1}(Y,U(r))\rightarrow H^{1}(Y,\text{GL}_{r}({\mathcal{O}}_{Y}))$, which was taught by Professor Tetsuo Ueda. Let
$i:H^{1}(Y,U(r))\rightarrow H^{1}(Y,\text{GL}_{r}({\mathcal{O}}_{Y}))$, which was taught by Professor Tetsuo Ueda. Let  $E:=\{(U_{jk},T_{jk})\}$ and
$E:=\{(U_{jk},T_{jk})\}$ and  $F:=\{(U_{jk},S_{jk})\}$ be elements of
$F:=\{(U_{jk},S_{jk})\}$ be elements of  $H^{1}(Y,U(r))$ with
$H^{1}(Y,U(r))$ with  $i(E)=i(F)$. By Lemma 2.3, we can take
$i(E)=i(F)$. By Lemma 2.3, we can take  $A_{j}\in \text{GL}_{r}(\mathbb{C})$ for each
$A_{j}\in \text{GL}_{r}(\mathbb{C})$ for each  $j$ such that
$j$ such that  $S_{jk}A_{k}=A_{j}T_{jk}$ holds. Denote by
$S_{jk}A_{k}=A_{j}T_{jk}$ holds. Denote by  $A_{j}=P_{j}U_{j}$ the polar decomposition of
$A_{j}=P_{j}U_{j}$ the polar decomposition of  $A_{j}$, where
$A_{j}$, where  $P_{j}$ is the positive definite Hermitian part and
$P_{j}$ is the positive definite Hermitian part and  $U_{j}$ is the unitary part. Then we have
$U_{j}$ is the unitary part. Then we have  $(S_{jk}P_{k}S_{jk}^{-1})\cdot (S_{jk}U_{k})=P_{j}\cdot (U_{j}T_{jk})$. By the uniqueness of the polar decomposition, we obtain
$(S_{jk}P_{k}S_{jk}^{-1})\cdot (S_{jk}U_{k})=P_{j}\cdot (U_{j}T_{jk})$. By the uniqueness of the polar decomposition, we obtain  $S_{jk}U_{k}=U_{j}T_{jk}$.
$S_{jk}U_{k}=U_{j}T_{jk}$.
Remark 2.6. Let  $F$ be a holomorphic subbundle of a unitary flat vector bundle
$F$ be a holomorphic subbundle of a unitary flat vector bundle  $E$ on
$E$ on  $Y$. Then it follows from the same argument as in the proof of Lemma 2.3 that
$Y$. Then it follows from the same argument as in the proof of Lemma 2.3 that  $F$ is a unitary flat subbundle of
$F$ is a unitary flat subbundle of  $E$: i.e.
$E$: i.e.  $F$ is the unitary flat vector bundle which corresponds to a unitary subrepresentation of
$F$ is the unitary flat vector bundle which corresponds to a unitary subrepresentation of  $\unicode[STIX]{x1D70C}_{E}$.
$\unicode[STIX]{x1D70C}_{E}$.
2.2 Local defining functions
Let  $X$ be a complex manifold
$X$ be a complex manifold  $X$ and
$X$ and  $Y$ be a compact complex submanifold of codimension
$Y$ be a compact complex submanifold of codimension  $r$ with unitary flat normal bundle. Take a sufficiently fine open covering
$r$ with unitary flat normal bundle. Take a sufficiently fine open covering  $\{U_{j}\}$ of
$\{U_{j}\}$ of  $Y$. In this paper, we always assume that
$Y$. In this paper, we always assume that  $\#\{U_{j}\}<\infty$ and that
$\#\{U_{j}\}<\infty$ and that  $U_{j}$ and
$U_{j}$ and  $U_{jk}$ are simply connected and Stein for each
$U_{jk}$ are simply connected and Stein for each  $j$ and
$j$ and  $k$. Denote by
$k$. Denote by  $z_{j}$ a coordinate of
$z_{j}$ a coordinate of  $U_{j}$. Take a sufficiently small tubular neighborhood
$U_{j}$. Take a sufficiently small tubular neighborhood  $V$ of
$V$ of  $Y$ in
$Y$ in  $X$ and an open covering
$X$ and an open covering  $\{V_{j}\}$ of
$\{V_{j}\}$ of  $V$ with
$V$ with  $V_{j}\cap Y=U_{j}$ for each
$V_{j}\cap Y=U_{j}$ for each  $j$. By shrinking
$j$. By shrinking  $V$ and
$V$ and  $V_{j}$’s if necessary, we may assume that
$V_{j}$’s if necessary, we may assume that  $U_{jk}\not =\emptyset$ if and only if
$U_{jk}\not =\emptyset$ if and only if  $V_{jk}\not =\emptyset$.
$V_{jk}\not =\emptyset$.
Take a defining functions system  $w_{j}=(w_{j}^{1},w_{j}^{2},\ldots ,w_{j}^{r})$ of
$w_{j}=(w_{j}^{1},w_{j}^{2},\ldots ,w_{j}^{r})$ of  $U_{j}$ in
$U_{j}$ in  $V_{j}$. We regard
$V_{j}$. We regard  $(z_{j},w_{j})$ as a coordinates system of
$(z_{j},w_{j})$ as a coordinates system of  $V_{j}$. Note that, here we denote by the same letter
$V_{j}$. Note that, here we denote by the same letter  $z_{j}$ an extension of
$z_{j}$ an extension of  $z_{j}$ to
$z_{j}$ to  $V_{j}$. In what follows, we always use the same
$V_{j}$. In what follows, we always use the same  $z_{j}$’s even though we often change
$z_{j}$’s even though we often change  $w_{j}$’s and shrink
$w_{j}$’s and shrink  $V$ and
$V$ and  $V_{j}$’s. More precisely, we fix a local projection
$V_{j}$’s. More precisely, we fix a local projection  $p_{j}:V_{j}\rightarrow U_{j}$ and, for any function
$p_{j}:V_{j}\rightarrow U_{j}$ and, for any function  $f$ defined on
$f$ defined on  $U_{j}$, we always use the pull back
$U_{j}$, we always use the pull back  $p_{j}^{\ast }$ for extending
$p_{j}^{\ast }$ for extending  $f$ to
$f$ to  $V_{j}$ and denote
$V_{j}$ and denote  $p_{j}^{\ast }f$ by the same letter
$p_{j}^{\ast }f$ by the same letter  $f(z_{j})$.
$f(z_{j})$.
As  $N_{Y/X}$ is unitary flat, we can take a local frame
$N_{Y/X}$ is unitary flat, we can take a local frame  $e_{j}=(e_{j}^{1},e_{j}^{2},\ldots e_{j}^{r})$ of the conormal bundle
$e_{j}=(e_{j}^{1},e_{j}^{2},\ldots e_{j}^{r})$ of the conormal bundle  $N_{Y/X}^{\ast }$ on
$N_{Y/X}^{\ast }$ on  $U_{j}$ with
$U_{j}$ with  $e_{j}=T_{jk}e_{k}$ for each
$e_{j}=T_{jk}e_{k}$ for each  $j$,
$j$,  $k$ (
$k$ ( $T_{jk}\in U(r)$). By changing
$T_{jk}\in U(r)$). By changing  $w_{j}$ if necessary, we may assume that
$w_{j}$ if necessary, we may assume that  $dw_{j}=e_{j}$ holds on each
$dw_{j}=e_{j}$ holds on each  $U_{j}$ (consider a new defining functions system
$U_{j}$ (consider a new defining functions system  $M_{j}(z_{j})\cdot w_{j}$ if
$M_{j}(z_{j})\cdot w_{j}$ if  $e_{j}=M_{j}(z_{j})\cdot dw_{j}|_{U_{j}}$). In what follows, we always assume this condition for the system
$e_{j}=M_{j}(z_{j})\cdot dw_{j}|_{U_{j}}$). In what follows, we always assume this condition for the system  $\{w_{j}\}$. Then it follows that the expansion of the function
$\{w_{j}\}$. Then it follows that the expansion of the function  $(\sum _{\unicode[STIX]{x1D707}=1}^{r}(T_{jk})_{\unicode[STIX]{x1D707}}^{\unicode[STIX]{x1D706}}\cdot w_{k}^{\unicode[STIX]{x1D707}})|_{V_{jk}}$ in the variables
$(\sum _{\unicode[STIX]{x1D707}=1}^{r}(T_{jk})_{\unicode[STIX]{x1D707}}^{\unicode[STIX]{x1D706}}\cdot w_{k}^{\unicode[STIX]{x1D707}})|_{V_{jk}}$ in the variables  $w_{j}$ is in the form of
$w_{j}$ is in the form of  $\sum _{\unicode[STIX]{x1D707}=1}^{r}(T_{jk})_{\unicode[STIX]{x1D707}}^{\unicode[STIX]{x1D706}}\cdot w_{k}^{\unicode[STIX]{x1D707}}=w_{j}^{\unicode[STIX]{x1D706}}+O(|w_{j}|^{2})$, where we denote by
$\sum _{\unicode[STIX]{x1D707}=1}^{r}(T_{jk})_{\unicode[STIX]{x1D707}}^{\unicode[STIX]{x1D706}}\cdot w_{k}^{\unicode[STIX]{x1D707}}=w_{j}^{\unicode[STIX]{x1D706}}+O(|w_{j}|^{2})$, where we denote by  $O(|w_{j}|^{2})$ the higher order terms. Let us denote this expansion by
$O(|w_{j}|^{2})$ the higher order terms. Let us denote this expansion by
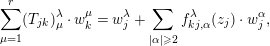 $$\begin{eqnarray}\mathop{\sum }_{\unicode[STIX]{x1D707}=1}^{r}(T_{jk})_{\unicode[STIX]{x1D707}}^{\unicode[STIX]{x1D706}}\cdot w_{k}^{\unicode[STIX]{x1D707}}=w_{j}^{\unicode[STIX]{x1D706}}+\mathop{\sum }_{|\unicode[STIX]{x1D6FC}|\geqslant 2}f_{kj,\unicode[STIX]{x1D6FC}}^{\unicode[STIX]{x1D706}}(z_{j})\cdot w_{j}^{\unicode[STIX]{x1D6FC}},\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{\unicode[STIX]{x1D707}=1}^{r}(T_{jk})_{\unicode[STIX]{x1D707}}^{\unicode[STIX]{x1D706}}\cdot w_{k}^{\unicode[STIX]{x1D707}}=w_{j}^{\unicode[STIX]{x1D706}}+\mathop{\sum }_{|\unicode[STIX]{x1D6FC}|\geqslant 2}f_{kj,\unicode[STIX]{x1D6FC}}^{\unicode[STIX]{x1D706}}(z_{j})\cdot w_{j}^{\unicode[STIX]{x1D6FC}},\end{eqnarray}$$ where  $\unicode[STIX]{x1D6FC}=(\unicode[STIX]{x1D6FC}_{1},\unicode[STIX]{x1D6FC}_{2},\ldots ,\unicode[STIX]{x1D6FC}_{r})\in (\mathbb{Z}_{{\geqslant}0})^{r}$,
$\unicode[STIX]{x1D6FC}=(\unicode[STIX]{x1D6FC}_{1},\unicode[STIX]{x1D6FC}_{2},\ldots ,\unicode[STIX]{x1D6FC}_{r})\in (\mathbb{Z}_{{\geqslant}0})^{r}$,  $|\unicode[STIX]{x1D6FC}|:=\unicode[STIX]{x1D6FC}_{1}+\unicode[STIX]{x1D6FC}_{2}+\cdots +\unicode[STIX]{x1D6FC}_{r}$, and
$|\unicode[STIX]{x1D6FC}|:=\unicode[STIX]{x1D6FC}_{1}+\unicode[STIX]{x1D6FC}_{2}+\cdots +\unicode[STIX]{x1D6FC}_{r}$, and  $w_{j}^{\unicode[STIX]{x1D6FC}}:=\prod _{\unicode[STIX]{x1D706}=1}^{r}(w_{j}^{\unicode[STIX]{x1D706}})^{\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D706}}}$. We also denote this expansion by
$w_{j}^{\unicode[STIX]{x1D6FC}}:=\prod _{\unicode[STIX]{x1D706}=1}^{r}(w_{j}^{\unicode[STIX]{x1D706}})^{\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D706}}}$. We also denote this expansion by
 $$\begin{eqnarray}T_{jk}w_{k}=w_{j}+\mathop{\sum }_{|\unicode[STIX]{x1D6FC}|\geqslant 2}f_{kj,\unicode[STIX]{x1D6FC}}(z_{j})\cdot w_{j}^{\unicode[STIX]{x1D6FC}},\end{eqnarray}$$
$$\begin{eqnarray}T_{jk}w_{k}=w_{j}+\mathop{\sum }_{|\unicode[STIX]{x1D6FC}|\geqslant 2}f_{kj,\unicode[STIX]{x1D6FC}}(z_{j})\cdot w_{j}^{\unicode[STIX]{x1D6FC}},\end{eqnarray}$$where
 $$\begin{eqnarray}w_{j}=\left(\begin{array}{@{}c@{}}w_{j}^{1}\\ w_{j}^{2}\\ \vdots \\ w_{j}^{r}\end{array}\right),\quad f_{kj,\unicode[STIX]{x1D6FC}}=\left(\begin{array}{@{}c@{}}f_{kj,\unicode[STIX]{x1D6FC}}^{1}\\ f_{kj,\unicode[STIX]{x1D6FC}}^{2}\\ \vdots \\ f_{kj,\unicode[STIX]{x1D6FC}}^{r}\end{array}\right).\end{eqnarray}$$
$$\begin{eqnarray}w_{j}=\left(\begin{array}{@{}c@{}}w_{j}^{1}\\ w_{j}^{2}\\ \vdots \\ w_{j}^{r}\end{array}\right),\quad f_{kj,\unicode[STIX]{x1D6FC}}=\left(\begin{array}{@{}c@{}}f_{kj,\unicode[STIX]{x1D6FC}}^{1}\\ f_{kj,\unicode[STIX]{x1D6FC}}^{2}\\ \vdots \\ f_{kj,\unicode[STIX]{x1D6FC}}^{r}\end{array}\right).\end{eqnarray}$$ We denote by  $e_{j}^{\ast }=(e_{j,1}^{\ast },e_{j,2}^{\ast },\ldots ,e_{j,r}^{\ast })$ the dual of
$e_{j}^{\ast }=(e_{j,1}^{\ast },e_{j,2}^{\ast },\ldots ,e_{j,r}^{\ast })$ the dual of  $e_{j}$ and regard it as a local frame of
$e_{j}$ and regard it as a local frame of  $N_{Y/X}$. For each
$N_{Y/X}$. For each  $\unicode[STIX]{x1D6FC}$ with
$\unicode[STIX]{x1D6FC}$ with  $|\unicode[STIX]{x1D6FC}|=n$, we denote by
$|\unicode[STIX]{x1D6FC}|=n$, we denote by  $e_{j}^{\unicode[STIX]{x1D6FC}}$ the local section
$e_{j}^{\unicode[STIX]{x1D6FC}}$ the local section  $\prod _{\unicode[STIX]{x1D706}=1}^{r}(e_{j}^{\unicode[STIX]{x1D706}})^{\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D706}}}$ of the symmetric tensor bundle
$\prod _{\unicode[STIX]{x1D706}=1}^{r}(e_{j}^{\unicode[STIX]{x1D706}})^{\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D706}}}$ of the symmetric tensor bundle  $S^{n}N_{Y/X}^{\ast }$. Then
$S^{n}N_{Y/X}^{\ast }$. Then  $\{e_{j}^{\unicode[STIX]{x1D6FC}}\}\text{}_{|\unicode[STIX]{x1D6FC}|=n}$ forms a local frame of
$\{e_{j}^{\unicode[STIX]{x1D6FC}}\}\text{}_{|\unicode[STIX]{x1D6FC}|=n}$ forms a local frame of  $S^{n}N_{Y/X}^{\ast }$ on
$S^{n}N_{Y/X}^{\ast }$ on  $U_{j}$. On each
$U_{j}$. On each  $U_{jk}$, it holds that
$U_{jk}$, it holds that  $e_{j}^{\unicode[STIX]{x1D6FC}}=\prod _{\unicode[STIX]{x1D706}=1}^{r}(\sum _{\unicode[STIX]{x1D707}=1}^{r}(T_{jk})_{\unicode[STIX]{x1D707}}^{\unicode[STIX]{x1D706}}\cdot e_{k}^{\unicode[STIX]{x1D707}})^{\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D706}}}$. Let us denote by
$e_{j}^{\unicode[STIX]{x1D6FC}}=\prod _{\unicode[STIX]{x1D706}=1}^{r}(\sum _{\unicode[STIX]{x1D707}=1}^{r}(T_{jk})_{\unicode[STIX]{x1D707}}^{\unicode[STIX]{x1D706}}\cdot e_{k}^{\unicode[STIX]{x1D707}})^{\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D706}}}$. Let us denote by  $\unicode[STIX]{x1D70F}_{jk,\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D6FC}}$ the coefficient of
$\unicode[STIX]{x1D70F}_{jk,\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D6FC}}$ the coefficient of  $e_{k}^{\unicode[STIX]{x1D6FD}}$ in the expansion of the right hand side: i.e.
$e_{k}^{\unicode[STIX]{x1D6FD}}$ in the expansion of the right hand side: i.e.
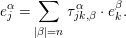 $$\begin{eqnarray}e_{j}^{\unicode[STIX]{x1D6FC}}=\mathop{\sum }_{|\unicode[STIX]{x1D6FD}|=n}\unicode[STIX]{x1D70F}_{jk,\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D6FC}}\cdot e_{k}^{\unicode[STIX]{x1D6FD}}.\end{eqnarray}$$
$$\begin{eqnarray}e_{j}^{\unicode[STIX]{x1D6FC}}=\mathop{\sum }_{|\unicode[STIX]{x1D6FD}|=n}\unicode[STIX]{x1D70F}_{jk,\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D6FC}}\cdot e_{k}^{\unicode[STIX]{x1D6FD}}.\end{eqnarray}$$Remark 2.7. Note that the matrix  $(\unicode[STIX]{x1D70F}_{jk,\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D6FC}})$ need not be unitary when
$(\unicode[STIX]{x1D70F}_{jk,\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D6FC}})$ need not be unitary when  $r>1$, however the vector bundle
$r>1$, however the vector bundle  $S^{n}N_{Y/X}^{\ast }$ itself is unitary flat. Here we explain the unitary flat structure of
$S^{n}N_{Y/X}^{\ast }$ itself is unitary flat. Here we explain the unitary flat structure of  $S^{n}N_{Y/X}^{\ast }$ induced from the orthonormal frames
$S^{n}N_{Y/X}^{\ast }$ induced from the orthonormal frames  $\{(U_{j},e_{j})\}$ of
$\{(U_{j},e_{j})\}$ of  $N_{Y/X}^{\ast }$. Let us consider the local sections
$N_{Y/X}^{\ast }$. Let us consider the local sections
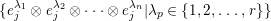 $$\begin{eqnarray}\{e_{j}^{\unicode[STIX]{x1D706}_{1}}\otimes e_{j}^{\unicode[STIX]{x1D706}_{2}}\otimes \cdots \otimes e_{j}^{\unicode[STIX]{x1D706}_{n}}|\unicode[STIX]{x1D706}_{p}\in \{1,2,\ldots ,r\}\}\end{eqnarray}$$
$$\begin{eqnarray}\{e_{j}^{\unicode[STIX]{x1D706}_{1}}\otimes e_{j}^{\unicode[STIX]{x1D706}_{2}}\otimes \cdots \otimes e_{j}^{\unicode[STIX]{x1D706}_{n}}|\unicode[STIX]{x1D706}_{p}\in \{1,2,\ldots ,r\}\}\end{eqnarray}$$ of  $\bigotimes ^{n}N_{Y/X}^{\ast }:=N_{Y/X}^{\ast }\otimes N_{Y/X}^{\ast }\otimes \cdots \otimes N_{Y/X}^{\ast }$ and regard it as a local frame on each
$\bigotimes ^{n}N_{Y/X}^{\ast }:=N_{Y/X}^{\ast }\otimes N_{Y/X}^{\ast }\otimes \cdots \otimes N_{Y/X}^{\ast }$ and regard it as a local frame on each  $U_{j}$. Then, as the transition matrix on
$U_{j}$. Then, as the transition matrix on  $U_{jk}$ is equal to
$U_{jk}$ is equal to  $S_{jk}\otimes S_{jk}\otimes \cdots \otimes S_{jk}\in U(r^{n})$, this local frame can be regarded as an orthonormal frame of the unitary flat metric induced from that of
$S_{jk}\otimes S_{jk}\otimes \cdots \otimes S_{jk}\in U(r^{n})$, this local frame can be regarded as an orthonormal frame of the unitary flat metric induced from that of  $N_{Y/X}^{\ast }$. By regarding each symmetric section of
$N_{Y/X}^{\ast }$. By regarding each symmetric section of  $\bigotimes ^{n}N_{Y/X}^{\ast }$ as a section of
$\bigotimes ^{n}N_{Y/X}^{\ast }$ as a section of  $S^{n}N_{Y/X}^{\ast }$ in the usual manner, we can regard
$S^{n}N_{Y/X}^{\ast }$ in the usual manner, we can regard  $S^{n}N_{Y/X}^{\ast }$ as a unitary flat subbundle of
$S^{n}N_{Y/X}^{\ast }$ as a unitary flat subbundle of  $\bigotimes ^{n}N_{Y/X}^{\ast }$ with an orthonormal frame
$\bigotimes ^{n}N_{Y/X}^{\ast }$ with an orthonormal frame  $\{\sqrt{n!/\unicode[STIX]{x1D6FC}!}\cdot e_{j}^{\unicode[STIX]{x1D6FC}}\}\text{}_{\unicode[STIX]{x1D6FC}}$ on each
$\{\sqrt{n!/\unicode[STIX]{x1D6FC}!}\cdot e_{j}^{\unicode[STIX]{x1D6FC}}\}\text{}_{\unicode[STIX]{x1D6FC}}$ on each  $U_{j}$, which induces the unitary flat structure of
$U_{j}$, which induces the unitary flat structure of  $S^{n}N_{Y/X}$ (
$S^{n}N_{Y/X}$ ( $\unicode[STIX]{x1D6FC}!:=\prod _{\unicode[STIX]{x1D706}=1}^{r}\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D706}}!$).
$\unicode[STIX]{x1D6FC}!:=\prod _{\unicode[STIX]{x1D706}=1}^{r}\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D706}}!$).
3 The obstruction classes and the type of the pair  $(Y,X)$
$(Y,X)$
3.1 Definition of the obstruction classes
Take  $\{(U_{j},z_{j})\},\{(V_{j},(z_{j},w_{j}))\},\{e_{j}\}$, and
$\{(U_{j},z_{j})\},\{(V_{j},(z_{j},w_{j}))\},\{e_{j}\}$, and  $\{(U_{jk},T_{jk})\}$ as in Section 2.2. In this section, we will define the obstruction class
$\{(U_{jk},T_{jk})\}$ as in Section 2.2. In this section, we will define the obstruction class  $u_{n}(Y,X)$ as a straightforward generalization of the Ueda class.
$u_{n}(Y,X)$ as a straightforward generalization of the Ueda class.
Definition 3.1. We say that the system  $\{(V_{j},w_{j})\}$ is of type
$\{(V_{j},w_{j})\}$ is of type  $n$ (
$n$ ( $n\geqslant 1$) if the coefficient function
$n\geqslant 1$) if the coefficient function  $f_{kj,\unicode[STIX]{x1D6FC}}$ in the expansion (1) is equal to
$f_{kj,\unicode[STIX]{x1D6FC}}$ in the expansion (1) is equal to  $0$ for any
$0$ for any  $\unicode[STIX]{x1D6FC}$ with
$\unicode[STIX]{x1D6FC}$ with  $|\unicode[STIX]{x1D6FC}|\leqslant n$ on each
$|\unicode[STIX]{x1D6FC}|\leqslant n$ on each  $U_{jk}$.
$U_{jk}$.
Let  $\{(V_{j},w_{j})\}$ be a system of type
$\{(V_{j},w_{j})\}$ be a system of type  $n$. Then, by definition, the expansion (1) can be written as follows:
$n$. Then, by definition, the expansion (1) can be written as follows:  $T_{jk}w_{k}=w_{j}+\sum _{|\unicode[STIX]{x1D6FC}|\geqslant n+1}f_{kj,\unicode[STIX]{x1D6FC}}(z_{j})\cdot w_{j}^{\unicode[STIX]{x1D6FC}}$. For
$T_{jk}w_{k}=w_{j}+\sum _{|\unicode[STIX]{x1D6FC}|\geqslant n+1}f_{kj,\unicode[STIX]{x1D6FC}}(z_{j})\cdot w_{j}^{\unicode[STIX]{x1D6FC}}$. For
 $$\begin{eqnarray}f_{kj,n+1}=\left(\begin{array}{@{}c@{}}f_{kj,n+1}^{1}\\ f_{kj,n+1}^{2}\\ \vdots \\ f_{kj,n+1}^{r}\end{array}\right):=\mathop{\sum }_{|\unicode[STIX]{x1D6FC}|=n+1}\left(\begin{array}{@{}c@{}}f_{kj,\unicode[STIX]{x1D6FC}}^{1}\\ f_{kj,\unicode[STIX]{x1D6FC}}^{2}\\ \vdots \\ f_{kj,\unicode[STIX]{x1D6FC}}^{r}\end{array}\right)\cdot e_{j}^{\unicode[STIX]{x1D6FC}},\end{eqnarray}$$
$$\begin{eqnarray}f_{kj,n+1}=\left(\begin{array}{@{}c@{}}f_{kj,n+1}^{1}\\ f_{kj,n+1}^{2}\\ \vdots \\ f_{kj,n+1}^{r}\end{array}\right):=\mathop{\sum }_{|\unicode[STIX]{x1D6FC}|=n+1}\left(\begin{array}{@{}c@{}}f_{kj,\unicode[STIX]{x1D6FC}}^{1}\\ f_{kj,\unicode[STIX]{x1D6FC}}^{2}\\ \vdots \\ f_{kj,\unicode[STIX]{x1D6FC}}^{r}\end{array}\right)\cdot e_{j}^{\unicode[STIX]{x1D6FC}},\end{eqnarray}$$we can show the following:
Lemma 3.2. The system  $\{(U_{jk},\sum _{\unicode[STIX]{x1D706}=1}^{r}e_{j,\unicode[STIX]{x1D706}}^{\ast }\otimes f_{kj,n+1}^{\unicode[STIX]{x1D706}})\}$ satisfies the
$\{(U_{jk},\sum _{\unicode[STIX]{x1D706}=1}^{r}e_{j,\unicode[STIX]{x1D706}}^{\ast }\otimes f_{kj,n+1}^{\unicode[STIX]{x1D706}})\}$ satisfies the  $1$-cocycle condition: i.e.
$1$-cocycle condition: i.e.
 $$\begin{eqnarray}\bigg\{\biggl(U_{jk},\mathop{\sum }_{\unicode[STIX]{x1D706}=1}^{r}e_{j,\unicode[STIX]{x1D706}}^{\ast }\otimes f_{kj,n+1}^{\unicode[STIX]{x1D706}}\biggr)\bigg\}\in {\check{Z}}^{1}(Y,N_{Y/X}\otimes S^{n+1}N_{Y/X}^{\ast }).\end{eqnarray}$$
$$\begin{eqnarray}\bigg\{\biggl(U_{jk},\mathop{\sum }_{\unicode[STIX]{x1D706}=1}^{r}e_{j,\unicode[STIX]{x1D706}}^{\ast }\otimes f_{kj,n+1}^{\unicode[STIX]{x1D706}}\biggr)\bigg\}\in {\check{Z}}^{1}(Y,N_{Y/X}\otimes S^{n+1}N_{Y/X}^{\ast }).\end{eqnarray}$$Proof. The lemma can be shown by summing the expansions of  $T_{jk}w_{k}-w_{j}$,
$T_{jk}w_{k}-w_{j}$,  $T_{jk}\cdot (T_{k\ell }w_{\ell }-w_{k})$, and
$T_{jk}\cdot (T_{k\ell }w_{\ell }-w_{k})$, and  $T_{j\ell }\cdot (T_{\ell j}w_{j}-w_{\ell })$ on
$T_{j\ell }\cdot (T_{\ell j}w_{j}-w_{\ell })$ on  $V_{jk\ell }$ and comparing the terms with
$V_{jk\ell }$ and comparing the terms with  $w_{j}^{\unicode[STIX]{x1D6FC}}$ of the both hand sides for each
$w_{j}^{\unicode[STIX]{x1D6FC}}$ of the both hand sides for each  $\unicode[STIX]{x1D6FC}$ with
$\unicode[STIX]{x1D6FC}$ with  $|\unicode[STIX]{x1D6FC}|=n+1$.◻
$|\unicode[STIX]{x1D6FC}|=n+1$.◻
Definition 3.3. For a system  $\{(V_{j},w_{j})\}$ of type
$\{(V_{j},w_{j})\}$ of type  $n$, we denote by
$n$, we denote by  $u_{n}(Y,X)=u_{n}(Y,X;\{w_{j}\})$ the class
$u_{n}(Y,X)=u_{n}(Y,X;\{w_{j}\})$ the class  $[\{(U_{jk},\sum _{\unicode[STIX]{x1D706}=1}^{r}e_{j,\unicode[STIX]{x1D706}}^{\ast }\otimes f_{kj,n+1}^{\unicode[STIX]{x1D706}})\}]\in H^{1}(Y,N_{Y/X}\otimes S^{n+1}N_{Y/X}^{\ast })$ and call it the
$[\{(U_{jk},\sum _{\unicode[STIX]{x1D706}=1}^{r}e_{j,\unicode[STIX]{x1D706}}^{\ast }\otimes f_{kj,n+1}^{\unicode[STIX]{x1D706}})\}]\in H^{1}(Y,N_{Y/X}\otimes S^{n+1}N_{Y/X}^{\ast })$ and call it the  $n$th obstruction class.
$n$th obstruction class.
Lemma 3.4. Let  $\{(V_{j},w_{j})\}$ be a system of type
$\{(V_{j},w_{j})\}$ be a system of type  $n$ with
$n$ with  $dw_{j}|_{U_{j}}=e_{j}$ for each
$dw_{j}|_{U_{j}}=e_{j}$ for each  $j$. Assume
$j$. Assume  $u_{n}(Y,X;\{w_{j}\})=0$. Then there exists a system
$u_{n}(Y,X;\{w_{j}\})=0$. Then there exists a system  $\{(U_{j},\widehat{w}_{j})\}$ of type
$\{(U_{j},\widehat{w}_{j})\}$ of type  $n+1$ with
$n+1$ with  $d\widehat{w}_{j}|_{U_{j}}=e_{j}$ for each
$d\widehat{w}_{j}|_{U_{j}}=e_{j}$ for each  $j$.
$j$.
Proof. From the assumption  $u_{n}(Y,X;\{w_{j}\})=0$, we can take
$u_{n}(Y,X;\{w_{j}\})=0$, we can take
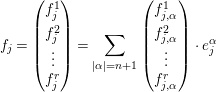 $$\begin{eqnarray}f_{j}=\left(\begin{array}{@{}c@{}}f_{j}^{1}\\ f_{j}^{2}\\ \vdots \\ f_{j}^{r}\end{array}\right)=\mathop{\sum }_{|\unicode[STIX]{x1D6FC}|=n+1}\left(\begin{array}{@{}c@{}}f_{j,\unicode[STIX]{x1D6FC}}^{1}\\ f_{j,\unicode[STIX]{x1D6FC}}^{2}\\ \vdots \\ f_{j,\unicode[STIX]{x1D6FC}}^{r}\end{array}\right)\cdot e_{j}^{\unicode[STIX]{x1D6FC}}\end{eqnarray}$$
$$\begin{eqnarray}f_{j}=\left(\begin{array}{@{}c@{}}f_{j}^{1}\\ f_{j}^{2}\\ \vdots \\ f_{j}^{r}\end{array}\right)=\mathop{\sum }_{|\unicode[STIX]{x1D6FC}|=n+1}\left(\begin{array}{@{}c@{}}f_{j,\unicode[STIX]{x1D6FC}}^{1}\\ f_{j,\unicode[STIX]{x1D6FC}}^{2}\\ \vdots \\ f_{j,\unicode[STIX]{x1D6FC}}^{r}\end{array}\right)\cdot e_{j}^{\unicode[STIX]{x1D6FC}}\end{eqnarray}$$such that
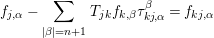 $$\begin{eqnarray}f_{j,\unicode[STIX]{x1D6FC}}-\mathop{\sum }_{|\unicode[STIX]{x1D6FD}|=n+1}T_{jk}f_{k,\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D70F}_{kj,\unicode[STIX]{x1D6FC}}^{\unicode[STIX]{x1D6FD}}=f_{kj,\unicode[STIX]{x1D6FC}}\end{eqnarray}$$
$$\begin{eqnarray}f_{j,\unicode[STIX]{x1D6FC}}-\mathop{\sum }_{|\unicode[STIX]{x1D6FD}|=n+1}T_{jk}f_{k,\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D70F}_{kj,\unicode[STIX]{x1D6FC}}^{\unicode[STIX]{x1D6FD}}=f_{kj,\unicode[STIX]{x1D6FC}}\end{eqnarray}$$ holds on  $U_{jk}$ for each
$U_{jk}$ for each  $\unicode[STIX]{x1D6FC}$ with
$\unicode[STIX]{x1D6FC}$ with  $|\unicode[STIX]{x1D6FC}|=n+1$. Define a new system
$|\unicode[STIX]{x1D6FC}|=n+1$. Define a new system  $\{\widehat{w}_{j}\}$ by
$\{\widehat{w}_{j}\}$ by
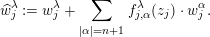 $$\begin{eqnarray}\widehat{w}_{j}^{\unicode[STIX]{x1D706}}:=w_{j}^{\unicode[STIX]{x1D706}}+\mathop{\sum }_{|\unicode[STIX]{x1D6FC}|=n+1}f_{j,\unicode[STIX]{x1D6FC}}^{\unicode[STIX]{x1D706}}(z_{j})\cdot w_{j}^{\unicode[STIX]{x1D6FC}}.\end{eqnarray}$$
$$\begin{eqnarray}\widehat{w}_{j}^{\unicode[STIX]{x1D706}}:=w_{j}^{\unicode[STIX]{x1D706}}+\mathop{\sum }_{|\unicode[STIX]{x1D6FC}|=n+1}f_{j,\unicode[STIX]{x1D6FC}}^{\unicode[STIX]{x1D706}}(z_{j})\cdot w_{j}^{\unicode[STIX]{x1D6FC}}.\end{eqnarray}$$ Then it follows from a simple computation that the system  $\{\widehat{w}_{j}\}$ is of type
$\{\widehat{w}_{j}\}$ is of type  $n+1$ with
$n+1$ with  $d\widehat{w}_{j}|_{U_{j}}=dw_{j}|_{U_{j}}$, which proves the lemma.◻
$d\widehat{w}_{j}|_{U_{j}}=dw_{j}|_{U_{j}}$, which proves the lemma.◻
Remark 3.5. Here we consider the case where  $N_{Y/X}$ admits a direct decomposition
$N_{Y/X}$ admits a direct decomposition  $N_{Y/X}=N_{1}\oplus N_{2}\oplus \cdots \oplus N_{r}$ such that each
$N_{Y/X}=N_{1}\oplus N_{2}\oplus \cdots \oplus N_{r}$ such that each  $N_{\unicode[STIX]{x1D706}}$ is a unitary flat line bundle on
$N_{\unicode[STIX]{x1D706}}$ is a unitary flat line bundle on  $Y$. It follows from Schur’s lemma that such
$Y$. It follows from Schur’s lemma that such  $N_{\unicode[STIX]{x1D706}}$’s are unique up to ordering and isomorphism (note that, as we mentioned in Remark 2.4, two unitary flat line bundles are isomorphic to each other if and only if the corresponding unitary representations coincide, see also [Reference UedaU, Proposition 1(2)]). In this case, the transition matrix
$N_{\unicode[STIX]{x1D706}}$’s are unique up to ordering and isomorphism (note that, as we mentioned in Remark 2.4, two unitary flat line bundles are isomorphic to each other if and only if the corresponding unitary representations coincide, see also [Reference UedaU, Proposition 1(2)]). In this case, the transition matrix  $T_{jk}$ is written in the form
$T_{jk}$ is written in the form  $T_{jk}=\text{diag}\,(t_{jk}^{1},t_{jk}^{2},\ldots ,t_{jk}^{r})$ (
$T_{jk}=\text{diag}\,(t_{jk}^{1},t_{jk}^{2},\ldots ,t_{jk}^{r})$ ( $t_{jk}^{\unicode[STIX]{x1D706}}\in U(1)$). Then it holds that
$t_{jk}^{\unicode[STIX]{x1D706}}\in U(1)$). Then it holds that
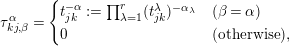 $$\begin{eqnarray}\unicode[STIX]{x1D70F}_{kj,\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D6FC}}=\left\{\begin{array}{@{}ll@{}}t_{jk}^{-\unicode[STIX]{x1D6FC}}:=\mathop{\prod }_{\unicode[STIX]{x1D706}=1}^{r}(t_{jk}^{\unicode[STIX]{x1D706}})^{-\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D706}}}\quad & (\unicode[STIX]{x1D6FD}=\unicode[STIX]{x1D6FC})\\ 0\quad & (\text{otherwise}),\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70F}_{kj,\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D6FC}}=\left\{\begin{array}{@{}ll@{}}t_{jk}^{-\unicode[STIX]{x1D6FC}}:=\mathop{\prod }_{\unicode[STIX]{x1D706}=1}^{r}(t_{jk}^{\unicode[STIX]{x1D706}})^{-\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D706}}}\quad & (\unicode[STIX]{x1D6FD}=\unicode[STIX]{x1D6FC})\\ 0\quad & (\text{otherwise}),\end{array}\right.\end{eqnarray}$$which induces a direct decomposition
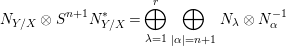 $$\begin{eqnarray}N_{Y/X}\otimes S^{n+1}N_{Y/X}^{\ast }=\bigoplus _{\unicode[STIX]{x1D706}=1}^{r}\bigoplus _{|\unicode[STIX]{x1D6FC}|=n+1}N_{\unicode[STIX]{x1D706}}\otimes N_{\unicode[STIX]{x1D6FC}}^{-1}\end{eqnarray}$$
$$\begin{eqnarray}N_{Y/X}\otimes S^{n+1}N_{Y/X}^{\ast }=\bigoplus _{\unicode[STIX]{x1D706}=1}^{r}\bigoplus _{|\unicode[STIX]{x1D6FC}|=n+1}N_{\unicode[STIX]{x1D706}}\otimes N_{\unicode[STIX]{x1D6FC}}^{-1}\end{eqnarray}$$ ( $N_{\unicode[STIX]{x1D6FC}}:=\bigotimes _{\unicode[STIX]{x1D706}=1}^{r}N_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D706}}}$). Accordingly, we have a decomposition
$N_{\unicode[STIX]{x1D6FC}}:=\bigotimes _{\unicode[STIX]{x1D706}=1}^{r}N_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D706}}}$). Accordingly, we have a decomposition
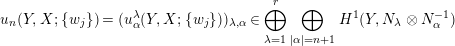 $$\begin{eqnarray}u_{n}(Y,X;\{w_{j}\})=(u_{\unicode[STIX]{x1D6FC}}^{\unicode[STIX]{x1D706}}(Y,X;\{w_{j}\}))_{\unicode[STIX]{x1D706},\unicode[STIX]{x1D6FC}}\in \bigoplus _{\unicode[STIX]{x1D706}=1}^{r}\bigoplus _{|\unicode[STIX]{x1D6FC}|=n+1}H^{1}(Y,N_{\unicode[STIX]{x1D706}}\otimes N_{\unicode[STIX]{x1D6FC}}^{-1})\end{eqnarray}$$
$$\begin{eqnarray}u_{n}(Y,X;\{w_{j}\})=(u_{\unicode[STIX]{x1D6FC}}^{\unicode[STIX]{x1D706}}(Y,X;\{w_{j}\}))_{\unicode[STIX]{x1D706},\unicode[STIX]{x1D6FC}}\in \bigoplus _{\unicode[STIX]{x1D706}=1}^{r}\bigoplus _{|\unicode[STIX]{x1D6FC}|=n+1}H^{1}(Y,N_{\unicode[STIX]{x1D706}}\otimes N_{\unicode[STIX]{x1D6FC}}^{-1})\end{eqnarray}$$ of the  $n$th obstruction class in this case. It is easily observed that
$n$th obstruction class in this case. It is easily observed that  $u_{\unicode[STIX]{x1D6FC}}^{\unicode[STIX]{x1D706}}(Y,X;\{w_{j}\})=[\{(U_{jk},f_{kj,\unicode[STIX]{x1D6FC}}^{\unicode[STIX]{x1D706}})\}]\in H^{1}(Y,N_{\unicode[STIX]{x1D706}}\otimes N_{\unicode[STIX]{x1D6FC}}^{-1})$.
$u_{\unicode[STIX]{x1D6FC}}^{\unicode[STIX]{x1D706}}(Y,X;\{w_{j}\})=[\{(U_{jk},f_{kj,\unicode[STIX]{x1D6FC}}^{\unicode[STIX]{x1D706}})\}]\in H^{1}(Y,N_{\unicode[STIX]{x1D706}}\otimes N_{\unicode[STIX]{x1D6FC}}^{-1})$.
3.2 Well-definedness of the obstruction classes and the type of the pair  $(Y,X)$
$(Y,X)$
Take  $\{U_{j}\},\{V_{j}\}$,
$\{U_{j}\},\{V_{j}\}$,  $\{e_{j}\},\{w_{j}\}$, and
$\{e_{j}\},\{w_{j}\}$, and  $\{T_{jk}\}$ as in Section 2.2. In this subsection, we study the dependence of the
$\{T_{jk}\}$ as in Section 2.2. In this subsection, we study the dependence of the  $n$th obstruction class
$n$th obstruction class  $u_{n}(Y,X;\{w_{j}\})$ on a system
$u_{n}(Y,X;\{w_{j}\})$ on a system  $\{(V_{j},w_{j})\}$ of type
$\{(V_{j},w_{j})\}$ of type  $n$.
$n$.
Lemma 3.6. Let  $\{(V_{j},w_{j})\}$ and
$\{(V_{j},w_{j})\}$ and  $\{(V_{j},\widehat{w}_{j})\}$ be systems of type
$\{(V_{j},\widehat{w}_{j})\}$ be systems of type  $n$ such that
$n$ such that  $dw_{j}=d\widehat{w}_{j}=e_{j}$ holds on each
$dw_{j}=d\widehat{w}_{j}=e_{j}$ holds on each  $U_{j}$. Then,
$U_{j}$. Then,  $u_{n}(Y,X;\{w_{j}\})=u_{n}(Y,X;\{\widehat{w}_{j}\})$.
$u_{n}(Y,X;\{w_{j}\})=u_{n}(Y,X;\{\widehat{w}_{j}\})$.
Proof. Let
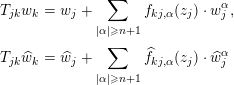 $$\begin{eqnarray}\displaystyle T_{jk}w_{k} & = & \displaystyle w_{j}+\mathop{\sum }_{|\unicode[STIX]{x1D6FC}|\geqslant n+1}f_{kj,\unicode[STIX]{x1D6FC}}(z_{j})\cdot w_{j}^{\unicode[STIX]{x1D6FC}},\nonumber\\ \displaystyle T_{jk}\widehat{w}_{k} & = & \displaystyle \widehat{w}_{j}+\mathop{\sum }_{|\unicode[STIX]{x1D6FC}|\geqslant n+1}\widehat{f}_{kj,\unicode[STIX]{x1D6FC}}(z_{j})\cdot \widehat{w}_{j}^{\unicode[STIX]{x1D6FC}}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle T_{jk}w_{k} & = & \displaystyle w_{j}+\mathop{\sum }_{|\unicode[STIX]{x1D6FC}|\geqslant n+1}f_{kj,\unicode[STIX]{x1D6FC}}(z_{j})\cdot w_{j}^{\unicode[STIX]{x1D6FC}},\nonumber\\ \displaystyle T_{jk}\widehat{w}_{k} & = & \displaystyle \widehat{w}_{j}+\mathop{\sum }_{|\unicode[STIX]{x1D6FC}|\geqslant n+1}\widehat{f}_{kj,\unicode[STIX]{x1D6FC}}(z_{j})\cdot \widehat{w}_{j}^{\unicode[STIX]{x1D6FC}}\nonumber\end{eqnarray}$$ be the expansions as in (1). It holds from the assumption  $dw_{j}=d\widehat{w}_{j}$ that the expansion of
$dw_{j}=d\widehat{w}_{j}$ that the expansion of  $\widehat{w}_{j}$ in
$\widehat{w}_{j}$ in  $w_{j}$ is in the form of
$w_{j}$ is in the form of  $\widehat{w}_{j}^{\unicode[STIX]{x1D706}}=w_{j}^{\unicode[STIX]{x1D706}}+\sum _{|\unicode[STIX]{x1D6FC}|\geqslant 2}a_{j,\unicode[STIX]{x1D6FC}}^{\unicode[STIX]{x1D706}}(z_{j})\cdot w_{j}^{\unicode[STIX]{x1D6FC}}$, which in what follows we will denote by
$\widehat{w}_{j}^{\unicode[STIX]{x1D706}}=w_{j}^{\unicode[STIX]{x1D706}}+\sum _{|\unicode[STIX]{x1D6FC}|\geqslant 2}a_{j,\unicode[STIX]{x1D6FC}}^{\unicode[STIX]{x1D706}}(z_{j})\cdot w_{j}^{\unicode[STIX]{x1D6FC}}$, which in what follows we will denote by
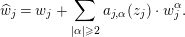 $$\begin{eqnarray}\widehat{w}_{j}=w_{j}+\mathop{\sum }_{|\unicode[STIX]{x1D6FC}|\geqslant 2}a_{j,\unicode[STIX]{x1D6FC}}(z_{j})\cdot w_{j}^{\unicode[STIX]{x1D6FC}}.\end{eqnarray}$$
$$\begin{eqnarray}\widehat{w}_{j}=w_{j}+\mathop{\sum }_{|\unicode[STIX]{x1D6FC}|\geqslant 2}a_{j,\unicode[STIX]{x1D6FC}}(z_{j})\cdot w_{j}^{\unicode[STIX]{x1D6FC}}.\end{eqnarray}$$ Let  $\unicode[STIX]{x1D708}_{0}$ be the maximum of the set of all
$\unicode[STIX]{x1D708}_{0}$ be the maximum of the set of all  $\unicode[STIX]{x1D708}\in \mathbb{Z}_{{\geqslant}2}$ such that
$\unicode[STIX]{x1D708}\in \mathbb{Z}_{{\geqslant}2}$ such that  $a_{j,\unicode[STIX]{x1D6FC}}\equiv 0$ holds for any
$a_{j,\unicode[STIX]{x1D6FC}}\equiv 0$ holds for any  $\unicode[STIX]{x1D6FC}$ with
$\unicode[STIX]{x1D6FC}$ with  $|\unicode[STIX]{x1D6FC}|<\unicode[STIX]{x1D708}$ for each
$|\unicode[STIX]{x1D6FC}|<\unicode[STIX]{x1D708}$ for each  $j$. When
$j$. When  $\unicode[STIX]{x1D708}_{0}>n+1$, it follows from
$\unicode[STIX]{x1D708}_{0}>n+1$, it follows from  $\widehat{w}_{j}=w_{j}+O(|w_{j}|^{n+2})$ that
$\widehat{w}_{j}=w_{j}+O(|w_{j}|^{n+2})$ that  $f_{kj,\unicode[STIX]{x1D6FC}}=\widehat{f}_{kj,\unicode[STIX]{x1D6FC}}$, which proves the lemma. When
$f_{kj,\unicode[STIX]{x1D6FC}}=\widehat{f}_{kj,\unicode[STIX]{x1D6FC}}$, which proves the lemma. When  $\unicode[STIX]{x1D708}_{0}=n+1$, we can calculate that
$\unicode[STIX]{x1D708}_{0}=n+1$, we can calculate that
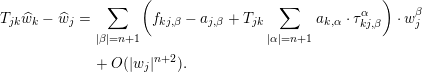 $$\begin{eqnarray}\displaystyle T_{jk}\widehat{w}_{k}-\widehat{w}_{j} & = & \displaystyle \mathop{\sum }_{|\unicode[STIX]{x1D6FD}|=n+1}\biggl(f_{kj,\unicode[STIX]{x1D6FD}}-a_{j,\unicode[STIX]{x1D6FD}}+T_{jk}\mathop{\sum }_{|\unicode[STIX]{x1D6FC}|=n+1}a_{k,\unicode[STIX]{x1D6FC}}\cdot \unicode[STIX]{x1D70F}_{kj,\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D6FC}}\biggr)\cdot w_{j}^{\unicode[STIX]{x1D6FD}}\nonumber\\ \displaystyle & & \displaystyle +\,O(|w_{j}|^{n+2}).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle T_{jk}\widehat{w}_{k}-\widehat{w}_{j} & = & \displaystyle \mathop{\sum }_{|\unicode[STIX]{x1D6FD}|=n+1}\biggl(f_{kj,\unicode[STIX]{x1D6FD}}-a_{j,\unicode[STIX]{x1D6FD}}+T_{jk}\mathop{\sum }_{|\unicode[STIX]{x1D6FC}|=n+1}a_{k,\unicode[STIX]{x1D6FC}}\cdot \unicode[STIX]{x1D70F}_{kj,\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D6FC}}\biggr)\cdot w_{j}^{\unicode[STIX]{x1D6FD}}\nonumber\\ \displaystyle & & \displaystyle +\,O(|w_{j}|^{n+2}).\end{eqnarray}$$By comparing the coefficients, we obtain the equation
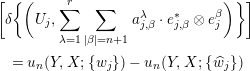 $$\begin{eqnarray}\displaystyle & & \displaystyle \biggl[\unicode[STIX]{x1D6FF}\bigg\{\biggl(U_{j},\mathop{\sum }_{\unicode[STIX]{x1D706}=1}^{r}\mathop{\sum }_{|\unicode[STIX]{x1D6FD}|=n+1}a_{j,\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D706}}\cdot e_{j,\unicode[STIX]{x1D6FD}}^{\ast }\otimes e_{j}^{\unicode[STIX]{x1D6FD}}\biggr)\bigg\}\biggr]\nonumber\\ \displaystyle & & \displaystyle \quad =u_{n}(Y,X;\{w_{j}\})-u_{n}(Y,X;\{\widehat{w}_{j}\})\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \biggl[\unicode[STIX]{x1D6FF}\bigg\{\biggl(U_{j},\mathop{\sum }_{\unicode[STIX]{x1D706}=1}^{r}\mathop{\sum }_{|\unicode[STIX]{x1D6FD}|=n+1}a_{j,\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D706}}\cdot e_{j,\unicode[STIX]{x1D6FD}}^{\ast }\otimes e_{j}^{\unicode[STIX]{x1D6FD}}\biggr)\bigg\}\biggr]\nonumber\\ \displaystyle & & \displaystyle \quad =u_{n}(Y,X;\{w_{j}\})-u_{n}(Y,X;\{\widehat{w}_{j}\})\nonumber\end{eqnarray}$$ in  ${\check{Z}}^{1}(\{U_{j}\},N_{Y/X}\otimes S^{n+1}N_{Y/X}^{\ast })$, which proves the lemma. Finally, we will show the lemma for
${\check{Z}}^{1}(\{U_{j}\},N_{Y/X}\otimes S^{n+1}N_{Y/X}^{\ast })$, which proves the lemma. Finally, we will show the lemma for  $\unicode[STIX]{x1D708}_{0}=\unicode[STIX]{x1D708}<n+1$ by assuming the lemma for
$\unicode[STIX]{x1D708}_{0}=\unicode[STIX]{x1D708}<n+1$ by assuming the lemma for  $\unicode[STIX]{x1D708}_{0}\geqslant \unicode[STIX]{x1D708}+1$. As we may assume that
$\unicode[STIX]{x1D708}_{0}\geqslant \unicode[STIX]{x1D708}+1$. As we may assume that  $2\leqslant \unicode[STIX]{x1D708}\leqslant n$, it holds from the calculation as (2) that
$2\leqslant \unicode[STIX]{x1D708}\leqslant n$, it holds from the calculation as (2) that  $\{(U_{j},\sum _{\unicode[STIX]{x1D706},|\unicode[STIX]{x1D6FD}|=\unicode[STIX]{x1D708}}a_{j,\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D706}}\cdot e_{j,\unicode[STIX]{x1D706}}^{\ast }\otimes e_{j}^{\unicode[STIX]{x1D6FD}})\}$ glue up to define a global section of
$\{(U_{j},\sum _{\unicode[STIX]{x1D706},|\unicode[STIX]{x1D6FD}|=\unicode[STIX]{x1D708}}a_{j,\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D706}}\cdot e_{j,\unicode[STIX]{x1D706}}^{\ast }\otimes e_{j}^{\unicode[STIX]{x1D6FD}})\}$ glue up to define a global section of  $N_{Y/X}\otimes S^{\unicode[STIX]{x1D708}}N_{Y/X}^{\ast }$. Therefore, by Lemma 2.1 and Remark 2.7, it turns out that
$N_{Y/X}\otimes S^{\unicode[STIX]{x1D708}}N_{Y/X}^{\ast }$. Therefore, by Lemma 2.1 and Remark 2.7, it turns out that  $a_{j,\unicode[STIX]{x1D6FC}}^{\unicode[STIX]{x1D706}}$ is a constant function on
$a_{j,\unicode[STIX]{x1D6FC}}^{\unicode[STIX]{x1D706}}$ is a constant function on  $U_{j}$ for each
$U_{j}$ for each  $\unicode[STIX]{x1D6FC}$ with
$\unicode[STIX]{x1D6FC}$ with  $|\unicode[STIX]{x1D6FC}|=\unicode[STIX]{x1D708}$. Define a new system
$|\unicode[STIX]{x1D6FC}|=\unicode[STIX]{x1D708}$. Define a new system  $\{v_{j}\}$ by
$\{v_{j}\}$ by  $v_{j}^{\unicode[STIX]{x1D706}}:=\widehat{w}_{j}^{\unicode[STIX]{x1D706}}-\sum _{|\unicode[STIX]{x1D6FC}|=\unicode[STIX]{x1D708}}a_{j,\unicode[STIX]{x1D6FC}}^{\unicode[STIX]{x1D706}}w_{j}^{\unicode[STIX]{x1D6FC}}$. It is easy to see that
$v_{j}^{\unicode[STIX]{x1D706}}:=\widehat{w}_{j}^{\unicode[STIX]{x1D706}}-\sum _{|\unicode[STIX]{x1D6FC}|=\unicode[STIX]{x1D708}}a_{j,\unicode[STIX]{x1D6FC}}^{\unicode[STIX]{x1D706}}w_{j}^{\unicode[STIX]{x1D6FC}}$. It is easy to see that  $u_{n}(Y,X;\{\widehat{w}_{j}\})=u_{n}(Y,X;\{v_{j}\})$ holds (use
$u_{n}(Y,X;\{\widehat{w}_{j}\})=u_{n}(Y,X;\{v_{j}\})$ holds (use  $T_{jk}w_{k}=w_{j}+O(|w_{j}|^{n+1})$ and the fact that each
$T_{jk}w_{k}=w_{j}+O(|w_{j}|^{n+1})$ and the fact that each  $a_{j,\unicode[STIX]{x1D6FC}}^{\unicode[STIX]{x1D706}}$ is a constant). As
$a_{j,\unicode[STIX]{x1D6FC}}^{\unicode[STIX]{x1D706}}$ is a constant). As  $u_{n}(Y,X;\{w_{j}\})=u_{n}(Y,X;\{v_{j}\})$ holds from the lemma for
$u_{n}(Y,X;\{w_{j}\})=u_{n}(Y,X;\{v_{j}\})$ holds from the lemma for  $\unicode[STIX]{x1D708}_{0}\geqslant \unicode[STIX]{x1D708}+1$, we obtain the equation
$\unicode[STIX]{x1D708}_{0}\geqslant \unicode[STIX]{x1D708}+1$, we obtain the equation  $u_{n}(Y,X;\{\widehat{w}_{j}\})=u_{n}(Y,X;\{w_{j}\})$.◻
$u_{n}(Y,X;\{\widehat{w}_{j}\})=u_{n}(Y,X;\{w_{j}\})$.◻
Proposition 3.7. Let  $\{(U_{j},e_{j})\}$ be a local frame of
$\{(U_{j},e_{j})\}$ be a local frame of  $N_{Y/X}^{\ast }$ as in Section 2.2. Then one and only one of the following holds:
$N_{Y/X}^{\ast }$ as in Section 2.2. Then one and only one of the following holds:
(i) There exists
 $n\geqslant 1$ and a system
$n\geqslant 1$ and a system  $\{w_{j}\}$ of type
$\{w_{j}\}$ of type  $n$ with
$n$ with  $dw_{j}|_{U_{j}}=e_{j}$ and
$dw_{j}|_{U_{j}}=e_{j}$ and  $u_{n}(Y,X;\{w_{j}\})\not =0$. In this case, there is no system
$u_{n}(Y,X;\{w_{j}\})\not =0$. In this case, there is no system  $\{\widehat{w}_{j}\}$ of type
$\{\widehat{w}_{j}\}$ of type  $\unicode[STIX]{x1D708}$ with
$\unicode[STIX]{x1D708}$ with  $d\widehat{w}_{j}|_{U_{j}}=e_{j}$ for any
$d\widehat{w}_{j}|_{U_{j}}=e_{j}$ for any  $\unicode[STIX]{x1D708}>n$.
$\unicode[STIX]{x1D708}>n$.(ii) For each
 $n\geqslant 1$, there exists a system
$n\geqslant 1$, there exists a system  $\{w_{j}\}$ of type
$\{w_{j}\}$ of type  $n$ with
$n$ with  $dw_{j}|_{U_{j}}=e_{j}$ and
$dw_{j}|_{U_{j}}=e_{j}$ and  $u_{n}(Y,X;\{w_{j}\})=0$.
$u_{n}(Y,X;\{w_{j}\})=0$.
Proof. Let  $\{w_{j}\}$ be a system of type
$\{w_{j}\}$ be a system of type  $n$ with
$n$ with  $dw_{j}|_{U_{j}}=e_{j}$ for each
$dw_{j}|_{U_{j}}=e_{j}$ for each  $j$. Then, by Lemmas 3.4 and 3.6, we obtain that
$j$. Then, by Lemmas 3.4 and 3.6, we obtain that  $u_{n}(Y,X;\{w_{j}\})=0$ if and only if there exists a system
$u_{n}(Y,X;\{w_{j}\})=0$ if and only if there exists a system  $\{\widehat{w}_{j}\}$ of type
$\{\widehat{w}_{j}\}$ of type  $n+1$ with
$n+1$ with  $d\widehat{w}_{j}|_{U_{j}}=e_{j}$, which shows the proposition.◻
$d\widehat{w}_{j}|_{U_{j}}=e_{j}$, which shows the proposition.◻
Definition 3.8. We define the type of the pair  $(Y,X)$ as follows:
$(Y,X)$ as follows:  $\text{type}\,(Y,X):=n$ for the case of Proposition 3.7(i), and
$\text{type}\,(Y,X):=n$ for the case of Proposition 3.7(i), and  $\text{type}\,(Y,X):=\infty$ for the case of Proposition 3.7(ii).
$\text{type}\,(Y,X):=\infty$ for the case of Proposition 3.7(ii).
Lemma 3.9.  $\text{type}\,(Y,X)$ does not depend on the choice of
$\text{type}\,(Y,X)$ does not depend on the choice of  $\{e_{j}\}$.
$\{e_{j}\}$.
Proof. Let  $\{(U_{j},e_{j})\}$ and
$\{(U_{j},e_{j})\}$ and  $\{(U_{j},\widehat{e}_{j})\}$ be local frames of
$\{(U_{j},\widehat{e}_{j})\}$ be local frames of  $N_{Y/X}^{\ast }$ with
$N_{Y/X}^{\ast }$ with  $e_{j}=T_{jk}e_{k}$ and
$e_{j}=T_{jk}e_{k}$ and  $\widehat{e}_{j}=\widehat{T}_{jk}\widehat{e}_{k}$ on each
$\widehat{e}_{j}=\widehat{T}_{jk}\widehat{e}_{k}$ on each  $U_{jk}$ (
$U_{jk}$ ( $T_{jk},\widehat{T}_{jk}\in U(r)$). Assume that there exists a system
$T_{jk},\widehat{T}_{jk}\in U(r)$). Assume that there exists a system  $\{w_{j}\}$ of type
$\{w_{j}\}$ of type  $n$ with
$n$ with  $dw_{j}|_{U_{j}}=e_{j}$. By Proposition 3.7, it is sufficient to show the existence of a system
$dw_{j}|_{U_{j}}=e_{j}$. By Proposition 3.7, it is sufficient to show the existence of a system  $\{\widehat{w}_{j}\}$ of type
$\{\widehat{w}_{j}\}$ of type  $n$ with
$n$ with  $d\widehat{w}_{j}|_{U_{j}}=\widehat{e}_{j}$.
$d\widehat{w}_{j}|_{U_{j}}=\widehat{e}_{j}$.
Let
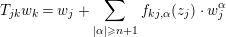 $$\begin{eqnarray}T_{jk}w_{k}=w_{j}+\mathop{\sum }_{|\unicode[STIX]{x1D6FC}|\geqslant n+1}f_{kj,\unicode[STIX]{x1D6FC}}(z_{j})\cdot w_{j}^{\unicode[STIX]{x1D6FC}}\end{eqnarray}$$
$$\begin{eqnarray}T_{jk}w_{k}=w_{j}+\mathop{\sum }_{|\unicode[STIX]{x1D6FC}|\geqslant n+1}f_{kj,\unicode[STIX]{x1D6FC}}(z_{j})\cdot w_{j}^{\unicode[STIX]{x1D6FC}}\end{eqnarray}$$ be the expansion (1) for the system  $\{w_{j}\}$. From Lemma 2.3, we can take
$\{w_{j}\}$. From Lemma 2.3, we can take  $M_{j}\in \text{GL}_{r}(\mathbb{C})$ with
$M_{j}\in \text{GL}_{r}(\mathbb{C})$ with  $\widehat{e}_{j}=M_{j}\cdot e_{j}$. Note that
$\widehat{e}_{j}=M_{j}\cdot e_{j}$. Note that  $M_{j}T_{jk}=\widehat{T}_{jk}M_{k}$ for each
$M_{j}T_{jk}=\widehat{T}_{jk}M_{k}$ for each  $j,k$. Define a new system
$j,k$. Define a new system  $\{\widehat{w}_{j}\}$ by
$\{\widehat{w}_{j}\}$ by  $\widehat{w}_{j}^{\unicode[STIX]{x1D706}}:=\sum _{\unicode[STIX]{x1D707}=1}^{r}(M_{j})_{\unicode[STIX]{x1D707}}^{\unicode[STIX]{x1D706}}\cdot w_{j}^{\unicode[STIX]{x1D707}}$. Then it clearly holds that
$\widehat{w}_{j}^{\unicode[STIX]{x1D706}}:=\sum _{\unicode[STIX]{x1D707}=1}^{r}(M_{j})_{\unicode[STIX]{x1D707}}^{\unicode[STIX]{x1D706}}\cdot w_{j}^{\unicode[STIX]{x1D707}}$. Then it clearly holds that  $d\widehat{w}_{j}=\widehat{e}_{j}$. We can calculate that
$d\widehat{w}_{j}=\widehat{e}_{j}$. We can calculate that
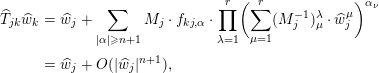 $$\begin{eqnarray}\displaystyle \widehat{T}_{jk}\widehat{w}_{k} & = & \displaystyle \widehat{w}_{j}+\mathop{\sum }_{|\unicode[STIX]{x1D6FC}|\geqslant n+1}M_{j}\cdot f_{kj,\unicode[STIX]{x1D6FC}}\cdot \mathop{\prod }_{\unicode[STIX]{x1D706}=1}^{r}\biggl(\mathop{\sum }_{\unicode[STIX]{x1D707}=1}^{r}(M_{j}^{-1})_{\unicode[STIX]{x1D707}}^{\unicode[STIX]{x1D706}}\cdot \widehat{w}_{j}^{\unicode[STIX]{x1D707}}\biggr)^{\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D708}}}\nonumber\\ \displaystyle & = & \displaystyle \widehat{w}_{j}+O(|\widehat{w}_{j}|^{n+1}),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \widehat{T}_{jk}\widehat{w}_{k} & = & \displaystyle \widehat{w}_{j}+\mathop{\sum }_{|\unicode[STIX]{x1D6FC}|\geqslant n+1}M_{j}\cdot f_{kj,\unicode[STIX]{x1D6FC}}\cdot \mathop{\prod }_{\unicode[STIX]{x1D706}=1}^{r}\biggl(\mathop{\sum }_{\unicode[STIX]{x1D707}=1}^{r}(M_{j}^{-1})_{\unicode[STIX]{x1D707}}^{\unicode[STIX]{x1D706}}\cdot \widehat{w}_{j}^{\unicode[STIX]{x1D707}}\biggr)^{\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D708}}}\nonumber\\ \displaystyle & = & \displaystyle \widehat{w}_{j}+O(|\widehat{w}_{j}|^{n+1}),\nonumber\end{eqnarray}$$which proves the lemma. ◻
4 Proof of Theorem 1.1
4.1 Outline
Let  $\{U_{j}\},\{V_{j}\}$,
$\{U_{j}\},\{V_{j}\}$,  $\{e_{j}\}$,
$\{e_{j}\}$,  $\{T_{jk}\}$, and
$\{T_{jk}\}$, and  $\{w_{j}\}$ be as in Section 2.2. We will prove Theorem 1.1 based on the same idea as in the proof of [Reference UedaU, Theorem 3] and [Reference Koike and OgawaKO, Theorem 1.4]. We will construct a new system
$\{w_{j}\}$ be as in Section 2.2. We will prove Theorem 1.1 based on the same idea as in the proof of [Reference UedaU, Theorem 3] and [Reference Koike and OgawaKO, Theorem 1.4]. We will construct a new system  $\{u_{j}\}$ as the solution of a functional equation
$\{u_{j}\}$ as the solution of a functional equation
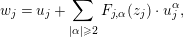 $$\begin{eqnarray}w_{j}=u_{j}+\mathop{\sum }_{|\unicode[STIX]{x1D6FC}|\geqslant 2}F_{j,\unicode[STIX]{x1D6FC}}(z_{j})\cdot u_{j}^{\unicode[STIX]{x1D6FC}},\end{eqnarray}$$
$$\begin{eqnarray}w_{j}=u_{j}+\mathop{\sum }_{|\unicode[STIX]{x1D6FC}|\geqslant 2}F_{j,\unicode[STIX]{x1D6FC}}(z_{j})\cdot u_{j}^{\unicode[STIX]{x1D6FC}},\end{eqnarray}$$where the coefficient functions
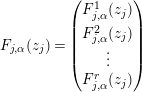 $$\begin{eqnarray}F_{j,\unicode[STIX]{x1D6FC}}(z_{j})=\left(\begin{array}{@{}c@{}}F_{j,\unicode[STIX]{x1D6FC}}^{1}(z_{j})\\ F_{j,\unicode[STIX]{x1D6FC}}^{2}(z_{j})\\ \vdots \\ F_{j,\unicode[STIX]{x1D6FC}}^{r}(z_{j})\end{array}\right)\end{eqnarray}$$
$$\begin{eqnarray}F_{j,\unicode[STIX]{x1D6FC}}(z_{j})=\left(\begin{array}{@{}c@{}}F_{j,\unicode[STIX]{x1D6FC}}^{1}(z_{j})\\ F_{j,\unicode[STIX]{x1D6FC}}^{2}(z_{j})\\ \vdots \\ F_{j,\unicode[STIX]{x1D6FC}}^{r}(z_{j})\end{array}\right)\end{eqnarray}$$ are holomorphic functions which we will construct in Section 4.4 so that  $\{u_{j}\}$ exists and satisfies
$\{u_{j}\}$ exists and satisfies  $T_{jk}u_{k}=u_{j}$ on a neighborhood of
$T_{jk}u_{k}=u_{j}$ on a neighborhood of  $U_{jk}$ for each
$U_{jk}$ for each  $j,k$ (note that it follows from the inverse function theorem that there exists a unique solution
$j,k$ (note that it follows from the inverse function theorem that there exists a unique solution  $u_{j}$ if
$u_{j}$ if  $\sum _{|\unicode[STIX]{x1D6FC}|\geqslant 2}F_{j,\unicode[STIX]{x1D6FC}}(z_{j})\cdot u_{j}^{\unicode[STIX]{x1D6FC}}$ has a positive radius of convergence). After taking such a solution
$\sum _{|\unicode[STIX]{x1D6FC}|\geqslant 2}F_{j,\unicode[STIX]{x1D6FC}}(z_{j})\cdot u_{j}^{\unicode[STIX]{x1D6FC}}$ has a positive radius of convergence). After taking such a solution  $\{u_{j}\}$, we obtain Theorem 1.1(i) by considering a foliation
$\{u_{j}\}$, we obtain Theorem 1.1(i) by considering a foliation  ${\mathcal{F}}$ whose leaves are locally defined by “
${\mathcal{F}}$ whose leaves are locally defined by “ $u_{j}=$ (constant).”
$u_{j}=$ (constant).”
Theorem 1.1(ii) is also shown by considering the same functional equation (3). Under the assumption of Theorem 1.1(ii), we will construct an initial system  $\{w_{j}\}$ so that
$\{w_{j}\}$ so that  $\{w_{j}^{1}=0\}=V_{j}\cap S$ in Section 4.2. Starting from such an initial system, we will see in Section 4.4 that one can choose coefficient functions
$\{w_{j}^{1}=0\}=V_{j}\cap S$ in Section 4.2. Starting from such an initial system, we will see in Section 4.4 that one can choose coefficient functions  $\{F_{j,\unicode[STIX]{x1D6FC}}\}$ so that the following additional property holds for each
$\{F_{j,\unicode[STIX]{x1D6FC}}\}$ so that the following additional property holds for each  $n\geqslant 2$:
$n\geqslant 2$:
- (Property)
 $_{n}$
$_{n}$  $F_{j,\unicode[STIX]{x1D6FC}}^{1}\equiv 0$ holds for any
$F_{j,\unicode[STIX]{x1D6FC}}^{1}\equiv 0$ holds for any  $\unicode[STIX]{x1D6FC}$ with
$\unicode[STIX]{x1D6FC}$ with  $|\unicode[STIX]{x1D6FC}|=n$ and
$|\unicode[STIX]{x1D6FC}|=n$ and  $\unicode[STIX]{x1D6FC}_{1}=0$.
$\unicode[STIX]{x1D6FC}_{1}=0$.
Then it holds that the solution  $\{u_{j}\}$ of the functional equation (3) also satisfies
$\{u_{j}\}$ of the functional equation (3) also satisfies  $\{u_{j}^{1}=0\}=V_{j}\cap S$ for each
$\{u_{j}^{1}=0\}=V_{j}\cap S$ for each  $j$. By considering a foliation
$j$. By considering a foliation  ${\mathcal{G}}_{S}$ whose leaves are locally defined by “
${\mathcal{G}}_{S}$ whose leaves are locally defined by “ $u_{j}^{1}=$ (constant),” we obtain Theorem 1.1(ii).
$u_{j}^{1}=$ (constant),” we obtain Theorem 1.1(ii).
Remark 4.1. It may seem that the foliations  ${\mathcal{F}}$ we will construct in the proof of Theorem 1.1(i) and (ii) are different from each other at first sight. Actually, the solutions
${\mathcal{F}}$ we will construct in the proof of Theorem 1.1(i) and (ii) are different from each other at first sight. Actually, the solutions  $u_{j}$’s we will obtain are different from each other. However, the foliation
$u_{j}$’s we will obtain are different from each other. However, the foliation  ${\mathcal{F}}$ itself does not depend on such differences. It can be shown by the following fact, which is obtained by the same arguments as in Lemma 3.6 and Proposition 3.9: Let
${\mathcal{F}}$ itself does not depend on such differences. It can be shown by the following fact, which is obtained by the same arguments as in Lemma 3.6 and Proposition 3.9: Let  $\{u_{j}\}$ and
$\{u_{j}\}$ and  $\{\widehat{u}_{j}\}$ be systems with
$\{\widehat{u}_{j}\}$ be systems with  $u_{j}=T_{jk}u_{k}$ and
$u_{j}=T_{jk}u_{k}$ and  $\widehat{u}_{j}=\widehat{T}_{jk}\widehat{u}_{k}$ on each
$\widehat{u}_{j}=\widehat{T}_{jk}\widehat{u}_{k}$ on each  $V_{jk}$ (
$V_{jk}$ ( $T_{jk},\widehat{T}_{jk}\in U(r)$). Then there exist
$T_{jk},\widehat{T}_{jk}\in U(r)$). Then there exist  $M_{j}\in \text{GL}_{r}(\mathbb{C})$ and
$M_{j}\in \text{GL}_{r}(\mathbb{C})$ and  $a_{j,\unicode[STIX]{x1D6FC}}\in \mathbb{C}^{r}$ for each
$a_{j,\unicode[STIX]{x1D6FC}}\in \mathbb{C}^{r}$ for each  $j$ and
$j$ and  $\unicode[STIX]{x1D6FC}$ such that
$\unicode[STIX]{x1D6FC}$ such that  $\widehat{u}_{j}=M_{j}\cdot (u_{j}+\sum _{|\unicode[STIX]{x1D6FC}|\geqslant 2}a_{j,\unicode[STIX]{x1D6FC}}\cdot u_{j}^{\unicode[STIX]{x1D6FC}})$ holds on each
$\widehat{u}_{j}=M_{j}\cdot (u_{j}+\sum _{|\unicode[STIX]{x1D6FC}|\geqslant 2}a_{j,\unicode[STIX]{x1D6FC}}\cdot u_{j}^{\unicode[STIX]{x1D6FC}})$ holds on each  $V_{j}$.
$V_{j}$.
4.2 Construction of the initial system  $\{w_{j}\}$
$\{w_{j}\}$
We can use any system  $\{w_{j}\}$ with
$\{w_{j}\}$ with  $dw_{j}|_{U_{j}}=e_{j}$ as an initial system for the proof of Theorem 1.1(i). In what follows, we explain the construction of the initial system
$dw_{j}|_{U_{j}}=e_{j}$ as an initial system for the proof of Theorem 1.1(i). In what follows, we explain the construction of the initial system  $\{w_{j}\}$ under the assumption of (ii).
$\{w_{j}\}$ under the assumption of (ii).
By Remark 2.6 and the complete reducibility of the unitary representation, it follows that the short exact sequence  $0\rightarrow N_{Y/S}\rightarrow N_{Y/X}\rightarrow N_{1}\rightarrow 0$ splits, where
$0\rightarrow N_{Y/S}\rightarrow N_{Y/X}\rightarrow N_{1}\rightarrow 0$ splits, where  $N_{1}:=N_{S/X}|_{Y}$. Let
$N_{1}:=N_{S/X}|_{Y}$. Let  $e_{j}^{1}$ be a local frame of
$e_{j}^{1}$ be a local frame of  $N_{1}^{-1}|_{U_{j}}$ with
$N_{1}^{-1}|_{U_{j}}$ with  $e_{j}^{1}=t_{jk}^{1}e_{k}^{1}$ on
$e_{j}^{1}=t_{jk}^{1}e_{k}^{1}$ on  $U_{jk}$ (
$U_{jk}$ ( $t_{jk}^{1}\in U(1)$), and
$t_{jk}^{1}\in U(1)$), and  $e_{j}^{\prime }=(e_{j}^{2},e_{j}^{3},\ldots ,e_{j}^{r})$ be a local frame of
$e_{j}^{\prime }=(e_{j}^{2},e_{j}^{3},\ldots ,e_{j}^{r})$ be a local frame of  $N_{Y/S}^{\ast }|_{U_{j}}$ with
$N_{Y/S}^{\ast }|_{U_{j}}$ with  $e_{j}^{\prime }=S_{jk}e_{k}^{\prime }$ on
$e_{j}^{\prime }=S_{jk}e_{k}^{\prime }$ on  $U_{jk}$ (
$U_{jk}$ ( $S_{jk}\in U(r-1)$). Take a defining function
$S_{jk}\in U(r-1)$). Take a defining function  $w_{j}^{1}$ of
$w_{j}^{1}$ of  $V_{j}\cap S$ in
$V_{j}\cap S$ in  $V_{j}$ for each
$V_{j}$ for each  $j$. By a simple argument, one can choose
$j$. By a simple argument, one can choose  $\{w_{j}^{1}\}$ so that
$\{w_{j}^{1}\}$ so that  $dw_{j}^{1}=e_{j}^{1}$ holds on each
$dw_{j}^{1}=e_{j}^{1}$ holds on each  $U_{j}$.
$U_{j}$.
Lemma 4.2. Let  $w_{j}^{1}$ be a defining function of
$w_{j}^{1}$ be a defining function of  $V_{j}\cap S$ in
$V_{j}\cap S$ in  $V_{j}$ with
$V_{j}$ with  $dw_{j}^{1}|_{U_{j}}=e_{j}^{1}$ for each
$dw_{j}^{1}|_{U_{j}}=e_{j}^{1}$ for each  $j$, and
$j$, and  $\{(V_{j}\cap S,v_{j})\}=\{(V_{j}\cap S,(v_{j}^{2},v_{j}^{3},\ldots ,v_{j}^{r}))\}$ be a local defining functions system of
$\{(V_{j}\cap S,v_{j})\}=\{(V_{j}\cap S,(v_{j}^{2},v_{j}^{3},\ldots ,v_{j}^{r}))\}$ be a local defining functions system of  $Y\subset V\cap S$ with
$Y\subset V\cap S$ with  $dv_{j}|_{U_{j}}=e_{j}^{\prime }$ for each
$dv_{j}|_{U_{j}}=e_{j}^{\prime }$ for each  $j$. Then there exists a holomorphic function
$j$. Then there exists a holomorphic function  $w_{j}^{\unicode[STIX]{x1D706}}:V_{j}\rightarrow \mathbb{C}$ with
$w_{j}^{\unicode[STIX]{x1D706}}:V_{j}\rightarrow \mathbb{C}$ with  $w_{j}^{\unicode[STIX]{x1D706}}|_{V_{j}\cap S}=v_{j}^{\unicode[STIX]{x1D706}}$ for each
$w_{j}^{\unicode[STIX]{x1D706}}|_{V_{j}\cap S}=v_{j}^{\unicode[STIX]{x1D706}}$ for each  $\unicode[STIX]{x1D706}=2,3,\ldots ,r$ such that
$\unicode[STIX]{x1D706}=2,3,\ldots ,r$ such that  $w_{j}:=(w_{j}^{1},w_{j}^{2},\ldots ,w_{j}^{r})$ satisfies
$w_{j}:=(w_{j}^{1},w_{j}^{2},\ldots ,w_{j}^{r})$ satisfies  $dw_{j}=T_{jk}dw_{k}$ on each
$dw_{j}=T_{jk}dw_{k}$ on each  $U_{jk}$, where
$U_{jk}$, where

Proof. Take a holomorphic function  $w_{j}^{\unicode[STIX]{x1D706}}:V_{j}\rightarrow \mathbb{C}$ with
$w_{j}^{\unicode[STIX]{x1D706}}:V_{j}\rightarrow \mathbb{C}$ with  $w_{j}^{\unicode[STIX]{x1D706}}|_{V_{j}\cap S}=v_{j}^{\unicode[STIX]{x1D706}}$ for each
$w_{j}^{\unicode[STIX]{x1D706}}|_{V_{j}\cap S}=v_{j}^{\unicode[STIX]{x1D706}}$ for each  $\unicode[STIX]{x1D706}=2,3,\ldots ,r$. Then the transition matrix
$\unicode[STIX]{x1D706}=2,3,\ldots ,r$. Then the transition matrix  $D_{jk}:=(\unicode[STIX]{x2202}w_{j}^{\unicode[STIX]{x1D706}}/\unicode[STIX]{x2202}w_{k}^{\unicode[STIX]{x1D707}}|_{U_{jk}})$ of
$D_{jk}:=(\unicode[STIX]{x2202}w_{j}^{\unicode[STIX]{x1D706}}/\unicode[STIX]{x2202}w_{k}^{\unicode[STIX]{x1D707}}|_{U_{jk}})$ of  $\{dw_{j}\}$ can be written in the form of
$\{dw_{j}\}$ can be written in the form of
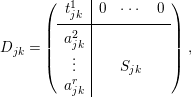
where  $a_{jk}^{\unicode[STIX]{x1D706}}(z_{j})$ is a holomorphic function defined on
$a_{jk}^{\unicode[STIX]{x1D706}}(z_{j})$ is a holomorphic function defined on  $U_{j}$. As
$U_{j}$. As
 $$\begin{eqnarray}\displaystyle e_{j,1}^{\ast }\otimes e_{j}^{1}-e_{k,1}^{\ast }\otimes e_{k}^{1} & = & \displaystyle e_{j,1}^{\ast }\otimes e_{j}^{1}-\mathop{\sum }_{\unicode[STIX]{x1D706}=1}^{r}\mathop{\sum }_{\unicode[STIX]{x1D707}=1}^{r}(D_{kj})_{\unicode[STIX]{x1D706}}^{1}\cdot (D_{kj}^{-1})_{1}^{\unicode[STIX]{x1D707}}\cdot e_{j,\unicode[STIX]{x1D707}}^{\ast }\otimes e_{j}^{\unicode[STIX]{x1D706}}\nonumber\\ \displaystyle & = & \displaystyle -\mathop{\sum }_{\unicode[STIX]{x1D707}=2}^{r}t_{kj}^{1}a_{jk}^{\unicode[STIX]{x1D707}}\cdot e_{j,\unicode[STIX]{x1D707}}^{\ast }\otimes e_{j}^{1},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle e_{j,1}^{\ast }\otimes e_{j}^{1}-e_{k,1}^{\ast }\otimes e_{k}^{1} & = & \displaystyle e_{j,1}^{\ast }\otimes e_{j}^{1}-\mathop{\sum }_{\unicode[STIX]{x1D706}=1}^{r}\mathop{\sum }_{\unicode[STIX]{x1D707}=1}^{r}(D_{kj})_{\unicode[STIX]{x1D706}}^{1}\cdot (D_{kj}^{-1})_{1}^{\unicode[STIX]{x1D707}}\cdot e_{j,\unicode[STIX]{x1D707}}^{\ast }\otimes e_{j}^{\unicode[STIX]{x1D706}}\nonumber\\ \displaystyle & = & \displaystyle -\mathop{\sum }_{\unicode[STIX]{x1D707}=2}^{r}t_{kj}^{1}a_{jk}^{\unicode[STIX]{x1D707}}\cdot e_{j,\unicode[STIX]{x1D707}}^{\ast }\otimes e_{j}^{1},\nonumber\end{eqnarray}$$ it holds that the extension class of the short exact sequence  $0\rightarrow N_{Y/S}\rightarrow N_{Y/X}\rightarrow N_{1}\rightarrow 0$ is equal to
$0\rightarrow N_{Y/S}\rightarrow N_{Y/X}\rightarrow N_{1}\rightarrow 0$ is equal to  $[\{(U_{jk},-\sum _{\unicode[STIX]{x1D707}=2}^{r}t_{kj}^{1}a_{jk}^{\unicode[STIX]{x1D707}}\cdot e_{j,\unicode[STIX]{x1D707}}^{\ast }\otimes e_{j}^{1})\}]$ via the natural isomorphism
$[\{(U_{jk},-\sum _{\unicode[STIX]{x1D707}=2}^{r}t_{kj}^{1}a_{jk}^{\unicode[STIX]{x1D707}}\cdot e_{j,\unicode[STIX]{x1D707}}^{\ast }\otimes e_{j}^{1})\}]$ via the natural isomorphism  $\text{Ext}^{1}(N_{1},N_{Y/S})\cong H^{1}(Y,N_{1}^{-1}\otimes N_{Y/S})$. Thus we can take
$\text{Ext}^{1}(N_{1},N_{Y/S})\cong H^{1}(Y,N_{1}^{-1}\otimes N_{Y/S})$. Thus we can take  $\{(U_{j},(m_{j}^{2}(z_{j}),m_{j}^{3}(z_{j}),\ldots ,m_{j}^{r}(z_{j})))\}$ such that
$\{(U_{j},(m_{j}^{2}(z_{j}),m_{j}^{3}(z_{j}),\ldots ,m_{j}^{r}(z_{j})))\}$ such that
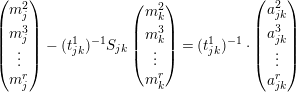 $$\begin{eqnarray}\left(\begin{array}{@{}c@{}}m_{j}^{2}\\ m_{j}^{3}\\ \vdots \\ m_{j}^{r}\end{array}\right)-(t_{jk}^{1})^{-1}S_{jk}\left(\begin{array}{@{}c@{}}m_{k}^{2}\\ m_{k}^{3}\\ \vdots \\ m_{k}^{r}\end{array}\right)=(t_{jk}^{1})^{-1}\cdot \left(\begin{array}{@{}c@{}}a_{jk}^{2}\\ a_{jk}^{3}\\ \vdots \\ a_{jk}^{r}\end{array}\right)\end{eqnarray}$$
$$\begin{eqnarray}\left(\begin{array}{@{}c@{}}m_{j}^{2}\\ m_{j}^{3}\\ \vdots \\ m_{j}^{r}\end{array}\right)-(t_{jk}^{1})^{-1}S_{jk}\left(\begin{array}{@{}c@{}}m_{k}^{2}\\ m_{k}^{3}\\ \vdots \\ m_{k}^{r}\end{array}\right)=(t_{jk}^{1})^{-1}\cdot \left(\begin{array}{@{}c@{}}a_{jk}^{2}\\ a_{jk}^{3}\\ \vdots \\ a_{jk}^{r}\end{array}\right)\end{eqnarray}$$ holds on each  $U_{jk}$, since the short exact sequence splits. Let us consider
$U_{jk}$, since the short exact sequence splits. Let us consider

Then it holds that  $M_{j}^{-1}T_{jk}M_{k}=D_{jk}$. Thus the lemma is shown by considering a new system
$M_{j}^{-1}T_{jk}M_{k}=D_{jk}$. Thus the lemma is shown by considering a new system  $M_{j}w_{j}$.◻
$M_{j}w_{j}$.◻
In what follows, we use the system  $\{w_{j}\}$ as in Lemma 4.2 and use orthonormal frame
$\{w_{j}\}$ as in Lemma 4.2 and use orthonormal frame  $e_{j}:=dw_{j}|_{U_{j}}$ whenever we consider under the assumption of Theorem 1.1(ii).
$e_{j}:=dw_{j}|_{U_{j}}$ whenever we consider under the assumption of Theorem 1.1(ii).
4.3 Preliminary observation for constructing  $\{F_{j,\unicode[STIX]{x1D6FC}}\}\text{}_{\unicode[STIX]{x1D6FC}}$
$\{F_{j,\unicode[STIX]{x1D6FC}}\}\text{}_{\unicode[STIX]{x1D6FC}}$
In this subsection, we give a heuristic explanation of how to construct  $\{F_{j,\unicode[STIX]{x1D6FC}}\}\text{}_{\unicode[STIX]{x1D6FC}}$. For this purpose, we compare the expansions of the function
$\{F_{j,\unicode[STIX]{x1D6FC}}\}\text{}_{\unicode[STIX]{x1D6FC}}$. For this purpose, we compare the expansions of the function  $(T_{jk}w_{k})|_{V_{jk}}$ in two manners by assuming that the solution
$(T_{jk}w_{k})|_{V_{jk}}$ in two manners by assuming that the solution  $u_{j}$ of the functional equation (3) exists and satisfies
$u_{j}$ of the functional equation (3) exists and satisfies  $T_{jk}u_{k}=u_{j}$ on
$T_{jk}u_{k}=u_{j}$ on  $V_{jk}$.
$V_{jk}$.
The first expansion is obtained by using the functional equation (3) on  $V_{k}$ as follows:
$V_{k}$ as follows:
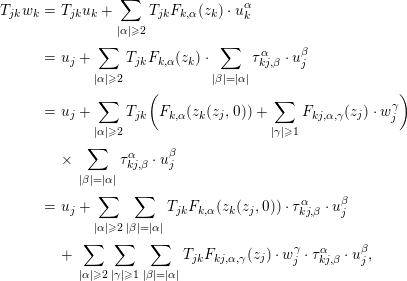 $$\begin{eqnarray}\displaystyle T_{jk}w_{k} & = & \displaystyle T_{jk}u_{k}+\mathop{\sum }_{|\unicode[STIX]{x1D6FC}|\geqslant 2}T_{jk}F_{k,\unicode[STIX]{x1D6FC}}(z_{k})\cdot u_{k}^{\unicode[STIX]{x1D6FC}}\nonumber\\ \displaystyle & = & \displaystyle u_{j}+\mathop{\sum }_{|\unicode[STIX]{x1D6FC}|\geqslant 2}T_{jk}F_{k,\unicode[STIX]{x1D6FC}}(z_{k})\cdot \mathop{\sum }_{|\unicode[STIX]{x1D6FD}|=|\unicode[STIX]{x1D6FC}|}\unicode[STIX]{x1D70F}_{kj,\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D6FC}}\cdot u_{j}^{\unicode[STIX]{x1D6FD}}\nonumber\\ \displaystyle & = & \displaystyle u_{j}+\mathop{\sum }_{|\unicode[STIX]{x1D6FC}|\geqslant 2}T_{jk}\biggl(F_{k,\unicode[STIX]{x1D6FC}}(z_{k}(z_{j},0))+\mathop{\sum }_{|\unicode[STIX]{x1D6FE}|\geqslant 1}F_{kj,\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FE}}(z_{j})\cdot w_{j}^{\unicode[STIX]{x1D6FE}}\biggr)\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\sum }_{|\unicode[STIX]{x1D6FD}|=|\unicode[STIX]{x1D6FC}|}\unicode[STIX]{x1D70F}_{kj,\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D6FC}}\cdot u_{j}^{\unicode[STIX]{x1D6FD}}\nonumber\\ \displaystyle & = & \displaystyle u_{j}+\mathop{\sum }_{|\unicode[STIX]{x1D6FC}|\geqslant 2}\mathop{\sum }_{|\unicode[STIX]{x1D6FD}|=|\unicode[STIX]{x1D6FC}|}T_{jk}F_{k,\unicode[STIX]{x1D6FC}}(z_{k}(z_{j},0))\cdot \unicode[STIX]{x1D70F}_{kj,\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D6FC}}\cdot u_{j}^{\unicode[STIX]{x1D6FD}}\nonumber\\ \displaystyle & & \displaystyle +\,\mathop{\sum }_{|\unicode[STIX]{x1D6FC}|\geqslant 2}\mathop{\sum }_{|\unicode[STIX]{x1D6FE}|\geqslant 1}\mathop{\sum }_{|\unicode[STIX]{x1D6FD}|=|\unicode[STIX]{x1D6FC}|}T_{jk}F_{kj,\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FE}}(z_{j})\cdot w_{j}^{\unicode[STIX]{x1D6FE}}\cdot \unicode[STIX]{x1D70F}_{kj,\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D6FC}}\cdot u_{j}^{\unicode[STIX]{x1D6FD}},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle T_{jk}w_{k} & = & \displaystyle T_{jk}u_{k}+\mathop{\sum }_{|\unicode[STIX]{x1D6FC}|\geqslant 2}T_{jk}F_{k,\unicode[STIX]{x1D6FC}}(z_{k})\cdot u_{k}^{\unicode[STIX]{x1D6FC}}\nonumber\\ \displaystyle & = & \displaystyle u_{j}+\mathop{\sum }_{|\unicode[STIX]{x1D6FC}|\geqslant 2}T_{jk}F_{k,\unicode[STIX]{x1D6FC}}(z_{k})\cdot \mathop{\sum }_{|\unicode[STIX]{x1D6FD}|=|\unicode[STIX]{x1D6FC}|}\unicode[STIX]{x1D70F}_{kj,\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D6FC}}\cdot u_{j}^{\unicode[STIX]{x1D6FD}}\nonumber\\ \displaystyle & = & \displaystyle u_{j}+\mathop{\sum }_{|\unicode[STIX]{x1D6FC}|\geqslant 2}T_{jk}\biggl(F_{k,\unicode[STIX]{x1D6FC}}(z_{k}(z_{j},0))+\mathop{\sum }_{|\unicode[STIX]{x1D6FE}|\geqslant 1}F_{kj,\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FE}}(z_{j})\cdot w_{j}^{\unicode[STIX]{x1D6FE}}\biggr)\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\sum }_{|\unicode[STIX]{x1D6FD}|=|\unicode[STIX]{x1D6FC}|}\unicode[STIX]{x1D70F}_{kj,\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D6FC}}\cdot u_{j}^{\unicode[STIX]{x1D6FD}}\nonumber\\ \displaystyle & = & \displaystyle u_{j}+\mathop{\sum }_{|\unicode[STIX]{x1D6FC}|\geqslant 2}\mathop{\sum }_{|\unicode[STIX]{x1D6FD}|=|\unicode[STIX]{x1D6FC}|}T_{jk}F_{k,\unicode[STIX]{x1D6FC}}(z_{k}(z_{j},0))\cdot \unicode[STIX]{x1D70F}_{kj,\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D6FC}}\cdot u_{j}^{\unicode[STIX]{x1D6FD}}\nonumber\\ \displaystyle & & \displaystyle +\,\mathop{\sum }_{|\unicode[STIX]{x1D6FC}|\geqslant 2}\mathop{\sum }_{|\unicode[STIX]{x1D6FE}|\geqslant 1}\mathop{\sum }_{|\unicode[STIX]{x1D6FD}|=|\unicode[STIX]{x1D6FC}|}T_{jk}F_{kj,\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FE}}(z_{j})\cdot w_{j}^{\unicode[STIX]{x1D6FE}}\cdot \unicode[STIX]{x1D70F}_{kj,\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D6FC}}\cdot u_{j}^{\unicode[STIX]{x1D6FD}},\nonumber\end{eqnarray}$$ where  $F_{kj,\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FE}}$’s are the coefficients of the expansion
$F_{kj,\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FE}}$’s are the coefficients of the expansion
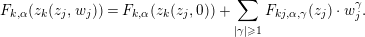 $$\begin{eqnarray}F_{k,\unicode[STIX]{x1D6FC}}(z_{k}(z_{j},w_{j}))=F_{k,\unicode[STIX]{x1D6FC}}(z_{k}(z_{j},0))+\mathop{\sum }_{|\unicode[STIX]{x1D6FE}|\geqslant 1}F_{kj,\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FE}}(z_{j})\cdot w_{j}^{\unicode[STIX]{x1D6FE}}.\end{eqnarray}$$
$$\begin{eqnarray}F_{k,\unicode[STIX]{x1D6FC}}(z_{k}(z_{j},w_{j}))=F_{k,\unicode[STIX]{x1D6FC}}(z_{k}(z_{j},0))+\mathop{\sum }_{|\unicode[STIX]{x1D6FE}|\geqslant 1}F_{kj,\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FE}}(z_{j})\cdot w_{j}^{\unicode[STIX]{x1D6FE}}.\end{eqnarray}$$ on  $V_{jk}$. Denoting by
$V_{jk}$. Denoting by
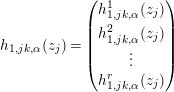 $$\begin{eqnarray}h_{1,jk,\unicode[STIX]{x1D6FC}}(z_{j})=\left(\begin{array}{@{}c@{}}h_{1,jk,\unicode[STIX]{x1D6FC}}^{1}(z_{j})\\ h_{1,jk,\unicode[STIX]{x1D6FC}}^{2}(z_{j})\\ \vdots \\ h_{1,jk,\unicode[STIX]{x1D6FC}}^{r}(z_{j})\end{array}\right)\end{eqnarray}$$
$$\begin{eqnarray}h_{1,jk,\unicode[STIX]{x1D6FC}}(z_{j})=\left(\begin{array}{@{}c@{}}h_{1,jk,\unicode[STIX]{x1D6FC}}^{1}(z_{j})\\ h_{1,jk,\unicode[STIX]{x1D6FC}}^{2}(z_{j})\\ \vdots \\ h_{1,jk,\unicode[STIX]{x1D6FC}}^{r}(z_{j})\end{array}\right)\end{eqnarray}$$ the coefficient of  $u_{j}^{\unicode[STIX]{x1D6FC}}$ in the expansion of the function
$u_{j}^{\unicode[STIX]{x1D6FC}}$ in the expansion of the function
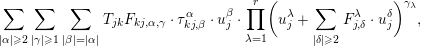 $$\begin{eqnarray}\mathop{\sum }_{|\unicode[STIX]{x1D6FC}|\geqslant 2}\mathop{\sum }_{|\unicode[STIX]{x1D6FE}|\geqslant 1}\mathop{\sum }_{|\unicode[STIX]{x1D6FD}|=|\unicode[STIX]{x1D6FC}|}T_{jk}F_{kj,\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FE}}\cdot \unicode[STIX]{x1D70F}_{kj,\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D6FC}}\cdot u_{j}^{\unicode[STIX]{x1D6FD}}\cdot \mathop{\prod }_{\unicode[STIX]{x1D706}=1}^{r}\biggl(u_{j}^{\unicode[STIX]{x1D706}}+\mathop{\sum }_{|\unicode[STIX]{x1D6FF}|\geqslant 2}F_{j,\unicode[STIX]{x1D6FF}}^{\unicode[STIX]{x1D706}}\cdot u_{j}^{\unicode[STIX]{x1D6FF}}\biggr)^{\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D706}}},\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{|\unicode[STIX]{x1D6FC}|\geqslant 2}\mathop{\sum }_{|\unicode[STIX]{x1D6FE}|\geqslant 1}\mathop{\sum }_{|\unicode[STIX]{x1D6FD}|=|\unicode[STIX]{x1D6FC}|}T_{jk}F_{kj,\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FE}}\cdot \unicode[STIX]{x1D70F}_{kj,\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D6FC}}\cdot u_{j}^{\unicode[STIX]{x1D6FD}}\cdot \mathop{\prod }_{\unicode[STIX]{x1D706}=1}^{r}\biggl(u_{j}^{\unicode[STIX]{x1D706}}+\mathop{\sum }_{|\unicode[STIX]{x1D6FF}|\geqslant 2}F_{j,\unicode[STIX]{x1D6FF}}^{\unicode[STIX]{x1D706}}\cdot u_{j}^{\unicode[STIX]{x1D6FF}}\biggr)^{\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D706}}},\end{eqnarray}$$we obtain
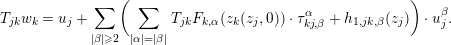 $$\begin{eqnarray}T_{jk}w_{k}=u_{j}+\mathop{\sum }_{|\unicode[STIX]{x1D6FD}|\geqslant 2}\biggl(\mathop{\sum }_{|\unicode[STIX]{x1D6FC}|=|\unicode[STIX]{x1D6FD}|}T_{jk}F_{k,\unicode[STIX]{x1D6FC}}(z_{k}(z_{j},0))\cdot \unicode[STIX]{x1D70F}_{kj,\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D6FC}}+h_{1,jk,\unicode[STIX]{x1D6FD}}(z_{j})\biggr)\cdot u_{j}^{\unicode[STIX]{x1D6FD}}.\end{eqnarray}$$
$$\begin{eqnarray}T_{jk}w_{k}=u_{j}+\mathop{\sum }_{|\unicode[STIX]{x1D6FD}|\geqslant 2}\biggl(\mathop{\sum }_{|\unicode[STIX]{x1D6FC}|=|\unicode[STIX]{x1D6FD}|}T_{jk}F_{k,\unicode[STIX]{x1D6FC}}(z_{k}(z_{j},0))\cdot \unicode[STIX]{x1D70F}_{kj,\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D6FC}}+h_{1,jk,\unicode[STIX]{x1D6FD}}(z_{j})\biggr)\cdot u_{j}^{\unicode[STIX]{x1D6FD}}.\end{eqnarray}$$The second expansion is obtained by using the expansion (1) as follows:
 $$\begin{eqnarray}\displaystyle T_{jk}w_{k} & = & \displaystyle w_{j}+\mathop{\sum }_{|\unicode[STIX]{x1D6FC}|\geqslant 2}f_{kj,\unicode[STIX]{x1D6FC}}(z_{j})\cdot w_{j}^{\unicode[STIX]{x1D6FC}}\nonumber\\ \displaystyle & = & \displaystyle \biggl(u_{j}+\mathop{\sum }_{|\unicode[STIX]{x1D6FC}|\geqslant 2}F_{j,\unicode[STIX]{x1D6FC}}(z_{j})\cdot u_{j}^{\unicode[STIX]{x1D6FC}}\biggr)\nonumber\\ \displaystyle & & \displaystyle +\,\mathop{\sum }_{|\unicode[STIX]{x1D6FC}|\geqslant 2}f_{kj,\unicode[STIX]{x1D6FC}}(z_{j})\cdot \mathop{\prod }_{\unicode[STIX]{x1D706}=1}^{r}\biggl(u_{j}^{\unicode[STIX]{x1D706}}+\mathop{\sum }_{|\unicode[STIX]{x1D6FD}|\geqslant 2}F_{j,\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D706}}(z_{j})\cdot u_{j}^{\unicode[STIX]{x1D6FD}}\biggr)^{\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D706}}}\nonumber\\ \displaystyle & = & \displaystyle u_{j}+\mathop{\sum }_{|\unicode[STIX]{x1D6FC}|\geqslant 2}(F_{j,\unicode[STIX]{x1D6FC}}(z_{j})+h_{2,jk,\unicode[STIX]{x1D6FC}}(z_{j}))\cdot u_{j}^{\unicode[STIX]{x1D6FC}},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle T_{jk}w_{k} & = & \displaystyle w_{j}+\mathop{\sum }_{|\unicode[STIX]{x1D6FC}|\geqslant 2}f_{kj,\unicode[STIX]{x1D6FC}}(z_{j})\cdot w_{j}^{\unicode[STIX]{x1D6FC}}\nonumber\\ \displaystyle & = & \displaystyle \biggl(u_{j}+\mathop{\sum }_{|\unicode[STIX]{x1D6FC}|\geqslant 2}F_{j,\unicode[STIX]{x1D6FC}}(z_{j})\cdot u_{j}^{\unicode[STIX]{x1D6FC}}\biggr)\nonumber\\ \displaystyle & & \displaystyle +\,\mathop{\sum }_{|\unicode[STIX]{x1D6FC}|\geqslant 2}f_{kj,\unicode[STIX]{x1D6FC}}(z_{j})\cdot \mathop{\prod }_{\unicode[STIX]{x1D706}=1}^{r}\biggl(u_{j}^{\unicode[STIX]{x1D706}}+\mathop{\sum }_{|\unicode[STIX]{x1D6FD}|\geqslant 2}F_{j,\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D706}}(z_{j})\cdot u_{j}^{\unicode[STIX]{x1D6FD}}\biggr)^{\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D706}}}\nonumber\\ \displaystyle & = & \displaystyle u_{j}+\mathop{\sum }_{|\unicode[STIX]{x1D6FC}|\geqslant 2}(F_{j,\unicode[STIX]{x1D6FC}}(z_{j})+h_{2,jk,\unicode[STIX]{x1D6FC}}(z_{j}))\cdot u_{j}^{\unicode[STIX]{x1D6FC}},\nonumber\end{eqnarray}$$where we are denoting by
 $$\begin{eqnarray}h_{2,jk,\unicode[STIX]{x1D6FC}}(z_{j})=\left(\begin{array}{@{}c@{}}h_{2,jk,\unicode[STIX]{x1D6FC}}^{1}(z_{j})\\ h_{2,jk,\unicode[STIX]{x1D6FC}}^{2}(z_{j})\\ \vdots \\ h_{2,jk,\unicode[STIX]{x1D6FC}}^{r}(z_{j})\end{array}\right)\end{eqnarray}$$
$$\begin{eqnarray}h_{2,jk,\unicode[STIX]{x1D6FC}}(z_{j})=\left(\begin{array}{@{}c@{}}h_{2,jk,\unicode[STIX]{x1D6FC}}^{1}(z_{j})\\ h_{2,jk,\unicode[STIX]{x1D6FC}}^{2}(z_{j})\\ \vdots \\ h_{2,jk,\unicode[STIX]{x1D6FC}}^{r}(z_{j})\end{array}\right)\end{eqnarray}$$ the coefficient of  $u_{j}^{\unicode[STIX]{x1D6FC}}$ in the expansion of the function
$u_{j}^{\unicode[STIX]{x1D6FC}}$ in the expansion of the function
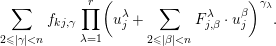 $$\begin{eqnarray}\mathop{\sum }_{2\leqslant |\unicode[STIX]{x1D6FE}|<n}f_{kj,\unicode[STIX]{x1D6FE}}\mathop{\prod }_{\unicode[STIX]{x1D706}=1}^{r}\biggl(u_{j}^{\unicode[STIX]{x1D706}}+\mathop{\sum }_{2\leqslant |\unicode[STIX]{x1D6FD}|<n}F_{j,\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D706}}\cdot u_{j}^{\unicode[STIX]{x1D6FD}}\biggr)^{\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D706}}}.\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{2\leqslant |\unicode[STIX]{x1D6FE}|<n}f_{kj,\unicode[STIX]{x1D6FE}}\mathop{\prod }_{\unicode[STIX]{x1D706}=1}^{r}\biggl(u_{j}^{\unicode[STIX]{x1D706}}+\mathop{\sum }_{2\leqslant |\unicode[STIX]{x1D6FD}|<n}F_{j,\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D706}}\cdot u_{j}^{\unicode[STIX]{x1D6FD}}\biggr)^{\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D706}}}.\end{eqnarray}$$ By comparing these two expansions, it is observed that the coefficient functions  $\{F_{j,\unicode[STIX]{x1D6FD}}\}$ should be chosen so that the equation
$\{F_{j,\unicode[STIX]{x1D6FD}}\}$ should be chosen so that the equation
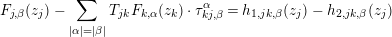 $$\begin{eqnarray}F_{j,\unicode[STIX]{x1D6FD}}(z_{j})-\mathop{\sum }_{|\unicode[STIX]{x1D6FC}|=|\unicode[STIX]{x1D6FD}|}T_{jk}F_{k,\unicode[STIX]{x1D6FC}}(z_{k})\cdot \unicode[STIX]{x1D70F}_{kj,\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D6FC}}=h_{1,jk,\unicode[STIX]{x1D6FD}}(z_{j})-h_{2,jk,\unicode[STIX]{x1D6FD}}(z_{j})\end{eqnarray}$$
$$\begin{eqnarray}F_{j,\unicode[STIX]{x1D6FD}}(z_{j})-\mathop{\sum }_{|\unicode[STIX]{x1D6FC}|=|\unicode[STIX]{x1D6FD}|}T_{jk}F_{k,\unicode[STIX]{x1D6FC}}(z_{k})\cdot \unicode[STIX]{x1D70F}_{kj,\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D6FC}}=h_{1,jk,\unicode[STIX]{x1D6FD}}(z_{j})-h_{2,jk,\unicode[STIX]{x1D6FD}}(z_{j})\end{eqnarray}$$ holds on  $U_{jk}$ for each
$U_{jk}$ for each  $\unicode[STIX]{x1D6FD}$. Note that this equation means that
$\unicode[STIX]{x1D6FD}$. Note that this equation means that
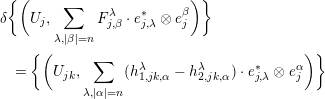 $$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D6FF}\bigg\{\biggl(U_{j},\mathop{\sum }_{\unicode[STIX]{x1D706},|\unicode[STIX]{x1D6FD}|=n}F_{j,\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D706}}\cdot e_{j,\unicode[STIX]{x1D706}}^{\ast }\otimes e_{j}^{\unicode[STIX]{x1D6FD}}\biggr)\bigg\}\nonumber\\ \displaystyle & & \displaystyle \quad =\bigg\{\biggl(U_{jk},\mathop{\sum }_{\unicode[STIX]{x1D706},|\unicode[STIX]{x1D6FC}|=n}(h_{1,jk,\unicode[STIX]{x1D6FC}}^{\unicode[STIX]{x1D706}}-h_{2,jk,\unicode[STIX]{x1D6FC}}^{\unicode[STIX]{x1D706}})\cdot e_{j,\unicode[STIX]{x1D706}}^{\ast }\otimes e_{j}^{\unicode[STIX]{x1D6FC}}\biggr)\bigg\}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D6FF}\bigg\{\biggl(U_{j},\mathop{\sum }_{\unicode[STIX]{x1D706},|\unicode[STIX]{x1D6FD}|=n}F_{j,\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D706}}\cdot e_{j,\unicode[STIX]{x1D706}}^{\ast }\otimes e_{j}^{\unicode[STIX]{x1D6FD}}\biggr)\bigg\}\nonumber\\ \displaystyle & & \displaystyle \quad =\bigg\{\biggl(U_{jk},\mathop{\sum }_{\unicode[STIX]{x1D706},|\unicode[STIX]{x1D6FC}|=n}(h_{1,jk,\unicode[STIX]{x1D6FC}}^{\unicode[STIX]{x1D706}}-h_{2,jk,\unicode[STIX]{x1D6FC}}^{\unicode[STIX]{x1D706}})\cdot e_{j,\unicode[STIX]{x1D706}}^{\ast }\otimes e_{j}^{\unicode[STIX]{x1D6FC}}\biggr)\bigg\}\nonumber\end{eqnarray}$$ holds in  ${\check{Z}}^{1}(\{U_{j}\},N_{Y/X}\otimes S^{n}N_{Y/X}^{\ast })$ for each
${\check{Z}}^{1}(\{U_{j}\},N_{Y/X}\otimes S^{n}N_{Y/X}^{\ast })$ for each  $n\geqslant 2$. Accordingly, we need
$n\geqslant 2$. Accordingly, we need  $[\{(U_{jk},H_{jk,n})\}]=0\in H^{1}(Y,N_{Y/X}\otimes S^{n}N_{Y/X}^{\ast })$ for each
$[\{(U_{jk},H_{jk,n})\}]=0\in H^{1}(Y,N_{Y/X}\otimes S^{n}N_{Y/X}^{\ast })$ for each  $n\geqslant 2$, where
$n\geqslant 2$, where
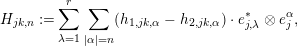 $$\begin{eqnarray}H_{jk,n}:=\mathop{\sum }_{\unicode[STIX]{x1D706}=1}^{r}\mathop{\sum }_{|\unicode[STIX]{x1D6FC}|=n}(h_{1,jk,\unicode[STIX]{x1D6FC}}-h_{2,jk,\unicode[STIX]{x1D6FC}})\cdot e_{j,\unicode[STIX]{x1D706}}^{\ast }\otimes e_{j}^{\unicode[STIX]{x1D6FC}},\end{eqnarray}$$
$$\begin{eqnarray}H_{jk,n}:=\mathop{\sum }_{\unicode[STIX]{x1D706}=1}^{r}\mathop{\sum }_{|\unicode[STIX]{x1D6FC}|=n}(h_{1,jk,\unicode[STIX]{x1D6FC}}-h_{2,jk,\unicode[STIX]{x1D6FC}})\cdot e_{j,\unicode[STIX]{x1D706}}^{\ast }\otimes e_{j}^{\unicode[STIX]{x1D6FC}},\end{eqnarray}$$ which we will actually show in the next subsection by using the assumption  $\text{type}\,(Y,X)=\infty$.
$\text{type}\,(Y,X)=\infty$.
4.4 Inductive construction of  $F_{j,\unicode[STIX]{x1D6FC}}$
$F_{j,\unicode[STIX]{x1D6FC}}$
Based on the observation in the previous subsection, we construct the coefficient functions  $F_{j,\unicode[STIX]{x1D6FC}}$. In the following inductive construction, the following properties of
$F_{j,\unicode[STIX]{x1D6FC}}$. In the following inductive construction, the following properties of  $H_{jk,n}$ are essential:
$H_{jk,n}$ are essential:  $H_{jk,2}=-\sum _{\unicode[STIX]{x1D706}=1}^{r}e_{j,\unicode[STIX]{x1D706}}^{\ast }\otimes f_{kj,2}^{\unicode[STIX]{x1D706}}$ holds and
$H_{jk,2}=-\sum _{\unicode[STIX]{x1D706}=1}^{r}e_{j,\unicode[STIX]{x1D706}}^{\ast }\otimes f_{kj,2}^{\unicode[STIX]{x1D706}}$ holds and  $H_{jk,n}$ depends only on
$H_{jk,n}$ depends only on  $\{F_{j,\unicode[STIX]{x1D6FC}}\}\text{}_{|\unicode[STIX]{x1D6FC}|<n}$ for each
$\{F_{j,\unicode[STIX]{x1D6FC}}\}\text{}_{|\unicode[STIX]{x1D6FC}|<n}$ for each  $n\geqslant 3$. These properties are easily shown by the definition of
$n\geqslant 3$. These properties are easily shown by the definition of  $H_{jk,n}$.
$H_{jk,n}$.
Step  $1$ (The construction of
$1$ (The construction of  $\{F_{j,\unicode[STIX]{x1D6FC}}\}\text{}_{|\unicode[STIX]{x1D6FC}|=2}$)
$\{F_{j,\unicode[STIX]{x1D6FC}}\}\text{}_{|\unicode[STIX]{x1D6FC}|=2}$)
For each  $\unicode[STIX]{x1D6FD}$ with
$\unicode[STIX]{x1D6FD}$ with  $|\unicode[STIX]{x1D6FD}|=2$, we take
$|\unicode[STIX]{x1D6FD}|=2$, we take  $\{(U_{j},F_{j,\unicode[STIX]{x1D6FD}})\}$ as a solution of the equation
$\{(U_{j},F_{j,\unicode[STIX]{x1D6FD}})\}$ as a solution of the equation
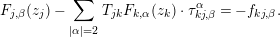 $$\begin{eqnarray}F_{j,\unicode[STIX]{x1D6FD}}(z_{j})-\mathop{\sum }_{|\unicode[STIX]{x1D6FC}|=2}T_{jk}F_{k,\unicode[STIX]{x1D6FC}}(z_{k})\cdot \unicode[STIX]{x1D70F}_{kj,\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D6FC}}=-f_{kj,\unicode[STIX]{x1D6FD}}.\end{eqnarray}$$
$$\begin{eqnarray}F_{j,\unicode[STIX]{x1D6FD}}(z_{j})-\mathop{\sum }_{|\unicode[STIX]{x1D6FC}|=2}T_{jk}F_{k,\unicode[STIX]{x1D6FC}}(z_{k})\cdot \unicode[STIX]{x1D70F}_{kj,\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D6FC}}=-f_{kj,\unicode[STIX]{x1D6FD}}.\end{eqnarray}$$ Note that there actually exists a solution of this equation, since  $u_{1}(Y,X)=0$ holds. Strictly speaking, we choose appropriate solution
$u_{1}(Y,X)=0$ holds. Strictly speaking, we choose appropriate solution  $\{(U_{j},F_{j,\unicode[STIX]{x1D6FC}})\}$ of the above equation by using [Reference UedaU, Lemma 3] (=[Reference Kodaira and SpencerKS, Lemma 2]) or [Reference UedaU, Lemma 4] as we will explain the details in Section 4.5.
$\{(U_{j},F_{j,\unicode[STIX]{x1D6FC}})\}$ of the above equation by using [Reference UedaU, Lemma 3] (=[Reference Kodaira and SpencerKS, Lemma 2]) or [Reference UedaU, Lemma 4] as we will explain the details in Section 4.5.
Claim 4.3. Fix  $\{F_{j,\unicode[STIX]{x1D6FD}}\}\text{}_{|\unicode[STIX]{x1D6FD}|=2}$ as above. Then the following holds:
$\{F_{j,\unicode[STIX]{x1D6FD}}\}\text{}_{|\unicode[STIX]{x1D6FD}|=2}$ as above. Then the following holds:
(a) For any choice of the remaining coefficient functions
 $\{F_{j,\unicode[STIX]{x1D6FC}}\}\text{}_{|\unicode[STIX]{x1D6FC}|>2}$, the solution
$\{F_{j,\unicode[STIX]{x1D6FC}}\}\text{}_{|\unicode[STIX]{x1D6FC}|>2}$, the solution  $\{u_{j}\}$ of the functional equation (3) is a system of type
$\{u_{j}\}$ of the functional equation (3) is a system of type  $2$ if exists.
$2$ if exists.(b) Under the assumption of Theorem 1.1(ii), we can take
 $\{F_{j,\unicode[STIX]{x1D6FD}}\}\text{}_{|\unicode[STIX]{x1D6FD}|=2}$ with
$\{F_{j,\unicode[STIX]{x1D6FD}}\}\text{}_{|\unicode[STIX]{x1D6FD}|=2}$ with  $\text{(Property)}_{2}$.
$\text{(Property)}_{2}$.
Proof. (a) is shown by comparing the expansions of  $(T_{jk}w_{k})|_{V_{jk}}$ in two manners as in the previous section. We skip the details here since the computation is almost the same as (and much easier than) that in the proof of Lemma 4.4 below.
$(T_{jk}w_{k})|_{V_{jk}}$ in two manners as in the previous section. We skip the details here since the computation is almost the same as (and much easier than) that in the proof of Lemma 4.4 below.
Under the assumption of Theorem 1.1(ii),  $f_{kj,\unicode[STIX]{x1D6FC}}^{1}\equiv 0$ holds for each
$f_{kj,\unicode[STIX]{x1D6FC}}^{1}\equiv 0$ holds for each  $\unicode[STIX]{x1D6FC}$ with
$\unicode[STIX]{x1D6FC}$ with  $\unicode[STIX]{x1D6FC}_{1}=0$, since
$\unicode[STIX]{x1D6FC}_{1}=0$, since  $t_{jk}^{1}w_{k}^{1}$ is divisible by
$t_{jk}^{1}w_{k}^{1}$ is divisible by  $w_{j}^{1}$ (recall that we are using an initial system
$w_{j}^{1}$ (recall that we are using an initial system  $\{w_{j}\}$ as in Section 4.2 in this setting). Thus, by considering the decomposition
$\{w_{j}\}$ as in Section 4.2 in this setting). Thus, by considering the decomposition  $S^{m}N_{Y/X}^{\ast }=\bigoplus _{\ell =0}^{m}(N_{1}^{-\ell }\otimes S^{m-\ell }N_{Y/S}^{\ast })$, the defining equation of
$S^{m}N_{Y/X}^{\ast }=\bigoplus _{\ell =0}^{m}(N_{1}^{-\ell }\otimes S^{m-\ell }N_{Y/S}^{\ast })$, the defining equation of  $\{F_{j,\unicode[STIX]{x1D6FC}}^{1}\}\text{}_{|\unicode[STIX]{x1D6FC}|=2,\unicode[STIX]{x1D6FC}_{1}=0}$ can be rewritten by the equation
$\{F_{j,\unicode[STIX]{x1D6FC}}^{1}\}\text{}_{|\unicode[STIX]{x1D6FC}|=2,\unicode[STIX]{x1D6FC}_{1}=0}$ can be rewritten by the equation
 $$\begin{eqnarray}\unicode[STIX]{x1D6FF}\biggl(\bigg\{\biggl(U_{j},\mathop{\sum }_{|\unicode[STIX]{x1D6FC}|=2,\unicode[STIX]{x1D6FC}_{1}=0}F_{j,\unicode[STIX]{x1D6FC}}^{1}\cdot e_{j,1}^{\ast }\otimes e_{j}^{\unicode[STIX]{x1D6FC}}\biggr)\bigg\}\biggr)=0\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FF}\biggl(\bigg\{\biggl(U_{j},\mathop{\sum }_{|\unicode[STIX]{x1D6FC}|=2,\unicode[STIX]{x1D6FC}_{1}=0}F_{j,\unicode[STIX]{x1D6FC}}^{1}\cdot e_{j,1}^{\ast }\otimes e_{j}^{\unicode[STIX]{x1D6FC}}\biggr)\bigg\}\biggr)=0\end{eqnarray}$$ in  ${\check{Z}}^{1}(\{U_{j}\},N_{1}\otimes S^{2}N_{Y/S}^{\ast })$, which proves the assertion (b).◻
${\check{Z}}^{1}(\{U_{j}\},N_{1}\otimes S^{2}N_{Y/S}^{\ast })$, which proves the assertion (b).◻
Step  $(n-1)$ (The construction of
$(n-1)$ (The construction of  $\{F_{j,\unicode[STIX]{x1D6FC}}\}\text{}_{|\unicode[STIX]{x1D6FC}|=n}$)
$\{F_{j,\unicode[STIX]{x1D6FC}}\}\text{}_{|\unicode[STIX]{x1D6FC}|=n}$)
After choosing  $F_{j,\unicode[STIX]{x1D6FC}}$ for each
$F_{j,\unicode[STIX]{x1D6FC}}$ for each  $\unicode[STIX]{x1D6FC}$ with
$\unicode[STIX]{x1D6FC}$ with  $|\unicode[STIX]{x1D6FC}|<n$, we take
$|\unicode[STIX]{x1D6FC}|<n$, we take  $\{(U_{j},F_{j,\unicode[STIX]{x1D6FD}})\}\text{}_{|\unicode[STIX]{x1D6FD}|=n}$ as a solution of the equation
$\{(U_{j},F_{j,\unicode[STIX]{x1D6FD}})\}\text{}_{|\unicode[STIX]{x1D6FD}|=n}$ as a solution of the equation
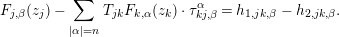 $$\begin{eqnarray}F_{j,\unicode[STIX]{x1D6FD}}(z_{j})-\mathop{\sum }_{|\unicode[STIX]{x1D6FC}|=n}T_{jk}F_{k,\unicode[STIX]{x1D6FC}}(z_{k})\cdot \unicode[STIX]{x1D70F}_{kj,\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D6FC}}=h_{1,jk,\unicode[STIX]{x1D6FD}}-h_{2,jk,\unicode[STIX]{x1D6FD}}.\end{eqnarray}$$
$$\begin{eqnarray}F_{j,\unicode[STIX]{x1D6FD}}(z_{j})-\mathop{\sum }_{|\unicode[STIX]{x1D6FC}|=n}T_{jk}F_{k,\unicode[STIX]{x1D6FC}}(z_{k})\cdot \unicode[STIX]{x1D70F}_{kj,\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D6FC}}=h_{1,jk,\unicode[STIX]{x1D6FD}}-h_{2,jk,\unicode[STIX]{x1D6FD}}.\end{eqnarray}$$ Here we use the fact that  $h_{1,jk,\unicode[STIX]{x1D6FD}}$ and
$h_{1,jk,\unicode[STIX]{x1D6FD}}$ and  $h_{2,jk,\unicode[STIX]{x1D6FD}}$ depend only on
$h_{2,jk,\unicode[STIX]{x1D6FD}}$ depend only on  $\{F_{j,\unicode[STIX]{x1D6FC}}\}\text{}_{|\unicode[STIX]{x1D6FC}|<n}$. The existence of a solution
$\{F_{j,\unicode[STIX]{x1D6FC}}\}\text{}_{|\unicode[STIX]{x1D6FC}|<n}$. The existence of a solution  $\{(U_{j},F_{j,\unicode[STIX]{x1D6FC}})\}$ is assured by Lemma 4.4(a) below. Strictly speaking, we choose appropriate
$\{(U_{j},F_{j,\unicode[STIX]{x1D6FC}})\}$ is assured by Lemma 4.4(a) below. Strictly speaking, we choose appropriate  $\{(U_{j},F_{j,\unicode[STIX]{x1D6FC}})\}$ from the solutions by using [Reference UedaU, Lemma 3] (=[Reference Kodaira and SpencerKS, Lemma 2]) or [Reference UedaU, Lemma 4] as we will explain the details in Section 4.5.
$\{(U_{j},F_{j,\unicode[STIX]{x1D6FC}})\}$ from the solutions by using [Reference UedaU, Lemma 3] (=[Reference Kodaira and SpencerKS, Lemma 2]) or [Reference UedaU, Lemma 4] as we will explain the details in Section 4.5.
Lemma 4.4. Let  $\{F_{j,\unicode[STIX]{x1D6FC}}\}\text{}_{|\unicode[STIX]{x1D6FC}|\leqslant n-1}$ be as in Step
$\{F_{j,\unicode[STIX]{x1D6FC}}\}\text{}_{|\unicode[STIX]{x1D6FC}|\leqslant n-1}$ be as in Step  $(n-2)$. Then the following holds:
$(n-2)$. Then the following holds:
(a)
 $[\{(U_{jk},H_{jk,n})\}]=0\in H^{1}(Y,N_{Y/X}\otimes S^{n}N_{Y/X}^{\ast })$.
$[\{(U_{jk},H_{jk,n})\}]=0\in H^{1}(Y,N_{Y/X}\otimes S^{n}N_{Y/X}^{\ast })$.(b) Let
 $\{F_{j,\unicode[STIX]{x1D6FC}}\}\text{}_{|\unicode[STIX]{x1D6FC}|=n}$ be as above. Then, for any choice of the remaining coefficient functions
$\{F_{j,\unicode[STIX]{x1D6FC}}\}\text{}_{|\unicode[STIX]{x1D6FC}|=n}$ be as above. Then, for any choice of the remaining coefficient functions  $\{F_{j,\unicode[STIX]{x1D6FC}}\}\text{}_{|\unicode[STIX]{x1D6FC}|>n}$, the solution
$\{F_{j,\unicode[STIX]{x1D6FC}}\}\text{}_{|\unicode[STIX]{x1D6FC}|>n}$, the solution  $\{u_{j}\}$ of the functional equation (3) is of type
$\{u_{j}\}$ of the functional equation (3) is of type  $n$ if exists.
$n$ if exists.(c) Under the assumption of Theorem 1.1(ii), we can take
 $\{F_{j,\unicode[STIX]{x1D6FD}}\}\text{}_{|\unicode[STIX]{x1D6FD}|=n}$ with
$\{F_{j,\unicode[STIX]{x1D6FD}}\}\text{}_{|\unicode[STIX]{x1D6FD}|=n}$ with  $\text{(Property)}_{n}$.
$\text{(Property)}_{n}$.
Proof. Fix  $\{F_{j,\unicode[STIX]{x1D6FC}}\}\text{}_{|\unicode[STIX]{x1D6FC}|\geqslant n}$ and consider the solution
$\{F_{j,\unicode[STIX]{x1D6FC}}\}\text{}_{|\unicode[STIX]{x1D6FC}|\geqslant n}$ and consider the solution  $\{u_{j}\}$ of the functional equation (3). By Lemma 4.4(b) for Step
$\{u_{j}\}$ of the functional equation (3). By Lemma 4.4(b) for Step  $(n-2)$, it turns out that
$(n-2)$, it turns out that  $\{u_{j}\}$ is of type
$\{u_{j}\}$ is of type  $n-1$ and thus
$n-1$ and thus
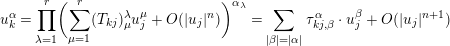 $$\begin{eqnarray}u_{k}^{\unicode[STIX]{x1D6FC}}=\mathop{\prod }_{\unicode[STIX]{x1D706}=1}^{r}\biggl(\mathop{\sum }_{\unicode[STIX]{x1D707}=1}^{r}(T_{kj})_{\unicode[STIX]{x1D707}}^{\unicode[STIX]{x1D706}}u_{j}^{\unicode[STIX]{x1D707}}+O(|u_{j}|^{n})\biggr)^{\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D706}}}=\mathop{\sum }_{|\unicode[STIX]{x1D6FD}|=|\unicode[STIX]{x1D6FC}|}\unicode[STIX]{x1D70F}_{kj,\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D6FC}}\cdot u_{j}^{\unicode[STIX]{x1D6FD}}+O(|u_{j}|^{n+1})\end{eqnarray}$$
$$\begin{eqnarray}u_{k}^{\unicode[STIX]{x1D6FC}}=\mathop{\prod }_{\unicode[STIX]{x1D706}=1}^{r}\biggl(\mathop{\sum }_{\unicode[STIX]{x1D707}=1}^{r}(T_{kj})_{\unicode[STIX]{x1D707}}^{\unicode[STIX]{x1D706}}u_{j}^{\unicode[STIX]{x1D707}}+O(|u_{j}|^{n})\biggr)^{\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D706}}}=\mathop{\sum }_{|\unicode[STIX]{x1D6FD}|=|\unicode[STIX]{x1D6FC}|}\unicode[STIX]{x1D70F}_{kj,\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D6FC}}\cdot u_{j}^{\unicode[STIX]{x1D6FD}}+O(|u_{j}|^{n+1})\end{eqnarray}$$ holds for each  $\unicode[STIX]{x1D6FC}$ with
$\unicode[STIX]{x1D6FC}$ with  $|\unicode[STIX]{x1D6FC}|\geqslant 2$. Consider the expansions
$|\unicode[STIX]{x1D6FC}|\geqslant 2$. Consider the expansions
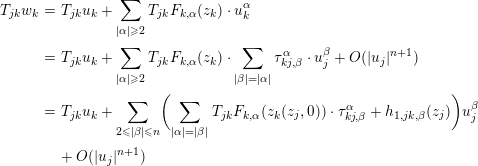 $$\begin{eqnarray}\displaystyle T_{jk}w_{k} & = & \displaystyle T_{jk}u_{k}+\mathop{\sum }_{|\unicode[STIX]{x1D6FC}|\geqslant 2}T_{jk}F_{k,\unicode[STIX]{x1D6FC}}(z_{k})\cdot u_{k}^{\unicode[STIX]{x1D6FC}}\nonumber\\ \displaystyle & = & \displaystyle T_{jk}u_{k}+\mathop{\sum }_{|\unicode[STIX]{x1D6FC}|\geqslant 2}T_{jk}F_{k,\unicode[STIX]{x1D6FC}}(z_{k})\cdot \mathop{\sum }_{|\unicode[STIX]{x1D6FD}|=|\unicode[STIX]{x1D6FC}|}\unicode[STIX]{x1D70F}_{kj,\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D6FC}}\cdot u_{j}^{\unicode[STIX]{x1D6FD}}+O(|u_{j}|^{n+1})\nonumber\\ \displaystyle & = & \displaystyle T_{jk}u_{k}+\mathop{\sum }_{2\leqslant |\unicode[STIX]{x1D6FD}|\leqslant n}\biggl(\mathop{\sum }_{|\unicode[STIX]{x1D6FC}|=|\unicode[STIX]{x1D6FD}|}T_{jk}F_{k,\unicode[STIX]{x1D6FC}}(z_{k}(z_{j},0))\cdot \unicode[STIX]{x1D70F}_{kj,\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D6FC}}+h_{1,jk,\unicode[STIX]{x1D6FD}}(z_{j})\biggr)u_{j}^{\unicode[STIX]{x1D6FD}}\nonumber\\ \displaystyle & & \displaystyle +\,O(|u_{j}|^{n+1})\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle T_{jk}w_{k} & = & \displaystyle T_{jk}u_{k}+\mathop{\sum }_{|\unicode[STIX]{x1D6FC}|\geqslant 2}T_{jk}F_{k,\unicode[STIX]{x1D6FC}}(z_{k})\cdot u_{k}^{\unicode[STIX]{x1D6FC}}\nonumber\\ \displaystyle & = & \displaystyle T_{jk}u_{k}+\mathop{\sum }_{|\unicode[STIX]{x1D6FC}|\geqslant 2}T_{jk}F_{k,\unicode[STIX]{x1D6FC}}(z_{k})\cdot \mathop{\sum }_{|\unicode[STIX]{x1D6FD}|=|\unicode[STIX]{x1D6FC}|}\unicode[STIX]{x1D70F}_{kj,\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D6FC}}\cdot u_{j}^{\unicode[STIX]{x1D6FD}}+O(|u_{j}|^{n+1})\nonumber\\ \displaystyle & = & \displaystyle T_{jk}u_{k}+\mathop{\sum }_{2\leqslant |\unicode[STIX]{x1D6FD}|\leqslant n}\biggl(\mathop{\sum }_{|\unicode[STIX]{x1D6FC}|=|\unicode[STIX]{x1D6FD}|}T_{jk}F_{k,\unicode[STIX]{x1D6FC}}(z_{k}(z_{j},0))\cdot \unicode[STIX]{x1D70F}_{kj,\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D6FC}}+h_{1,jk,\unicode[STIX]{x1D6FD}}(z_{j})\biggr)u_{j}^{\unicode[STIX]{x1D6FD}}\nonumber\\ \displaystyle & & \displaystyle +\,O(|u_{j}|^{n+1})\nonumber\end{eqnarray}$$and
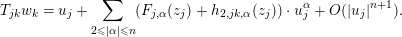 $$\begin{eqnarray}\displaystyle T_{jk}w_{k}=u_{j}+\mathop{\sum }_{2\leqslant |\unicode[STIX]{x1D6FC}|\leqslant n}(F_{j,\unicode[STIX]{x1D6FC}}(z_{j})+h_{2,jk,\unicode[STIX]{x1D6FC}}(z_{j}))\cdot u_{j}^{\unicode[STIX]{x1D6FC}}+O(|u_{j}|^{n+1}). & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle T_{jk}w_{k}=u_{j}+\mathop{\sum }_{2\leqslant |\unicode[STIX]{x1D6FC}|\leqslant n}(F_{j,\unicode[STIX]{x1D6FC}}(z_{j})+h_{2,jk,\unicode[STIX]{x1D6FC}}(z_{j}))\cdot u_{j}^{\unicode[STIX]{x1D6FC}}+O(|u_{j}|^{n+1}). & & \displaystyle \nonumber\end{eqnarray}$$ Note that  $h_{1,jk,\unicode[STIX]{x1D6FD}}$’s and
$h_{1,jk,\unicode[STIX]{x1D6FD}}$’s and  $h_{2,jk,\unicode[STIX]{x1D6FC}}$’s appear in these expansions coincides with those defined in the previous subsection by equation (4). By comparing these, we obtain
$h_{2,jk,\unicode[STIX]{x1D6FC}}$’s appear in these expansions coincides with those defined in the previous subsection by equation (4). By comparing these, we obtain
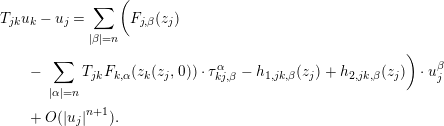 $$\begin{eqnarray}\displaystyle & & \displaystyle T_{jk}u_{k}-u_{j}=\mathop{\sum }_{|\unicode[STIX]{x1D6FD}|=n}\biggl(F_{j,\unicode[STIX]{x1D6FD}}(z_{j})\nonumber\\ \displaystyle & & \displaystyle \qquad -\,\mathop{\sum }_{|\unicode[STIX]{x1D6FC}|=n}T_{jk}F_{k,\unicode[STIX]{x1D6FC}}(z_{k}(z_{j},0))\cdot \unicode[STIX]{x1D70F}_{kj,\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D6FC}}-h_{1,jk,\unicode[STIX]{x1D6FD}}(z_{j})+h_{2,jk,\unicode[STIX]{x1D6FD}}(z_{j})\biggr)\cdot u_{j}^{\unicode[STIX]{x1D6FD}}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,O(|u_{j}|^{n+1}).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle T_{jk}u_{k}-u_{j}=\mathop{\sum }_{|\unicode[STIX]{x1D6FD}|=n}\biggl(F_{j,\unicode[STIX]{x1D6FD}}(z_{j})\nonumber\\ \displaystyle & & \displaystyle \qquad -\,\mathop{\sum }_{|\unicode[STIX]{x1D6FC}|=n}T_{jk}F_{k,\unicode[STIX]{x1D6FC}}(z_{k}(z_{j},0))\cdot \unicode[STIX]{x1D70F}_{kj,\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D6FC}}-h_{1,jk,\unicode[STIX]{x1D6FD}}(z_{j})+h_{2,jk,\unicode[STIX]{x1D6FD}}(z_{j})\biggr)\cdot u_{j}^{\unicode[STIX]{x1D6FD}}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,O(|u_{j}|^{n+1}).\end{eqnarray}$$ By considering this equation (5) in the case where  $F_{j,\unicode[STIX]{x1D6FC}}\equiv 0$ for each
$F_{j,\unicode[STIX]{x1D6FC}}\equiv 0$ for each  $\unicode[STIX]{x1D6FC}$ with
$\unicode[STIX]{x1D6FC}$ with  $|\unicode[STIX]{x1D6FC}|\geqslant n$, we obtain
$|\unicode[STIX]{x1D6FC}|\geqslant n$, we obtain  $u_{n-1}(Y,X;\{u_{j}\})=[\{(U_{jk},-H_{jk,n})\}]$. Thus the assertion (a) follows from the assumption
$u_{n-1}(Y,X;\{u_{j}\})=[\{(U_{jk},-H_{jk,n})\}]$. Thus the assertion (a) follows from the assumption  $u_{n-1}(Y,X)=0$. The assertion (b) also follows directly from equation (5).
$u_{n-1}(Y,X)=0$. The assertion (b) also follows directly from equation (5).
Under the assumption of Theorem 1.1(ii), it follows from the argument as in the proof of Claim 4.3 that the defining equation of  $\{F_{j,\unicode[STIX]{x1D6FC}}^{1}\}\text{}_{|\unicode[STIX]{x1D6FC}|=n,\unicode[STIX]{x1D6FC}_{1}=0}$ can be rewritten by the equation
$\{F_{j,\unicode[STIX]{x1D6FC}}^{1}\}\text{}_{|\unicode[STIX]{x1D6FC}|=n,\unicode[STIX]{x1D6FC}_{1}=0}$ can be rewritten by the equation
 $$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D6FF}\biggl(\bigg\{\biggl(U_{j},\mathop{\sum }_{|\unicode[STIX]{x1D6FC}|=n,\unicode[STIX]{x1D6FC}_{1}=0}F_{j,\unicode[STIX]{x1D6FC}}^{1}\cdot e_{j,1}^{\ast }\otimes e_{j}^{\unicode[STIX]{x1D6FC}}\biggr)\bigg\}\biggr)\nonumber\\ \displaystyle & & \displaystyle \quad =\bigg\{\biggl(U_{jk},\mathop{\sum }_{|\unicode[STIX]{x1D6FC}|=n,\unicode[STIX]{x1D6FC}_{1}=0}(h_{1,jk,\unicode[STIX]{x1D6FC}}^{1}-h_{2,jk,\unicode[STIX]{x1D6FC}}^{1})\cdot e_{j,1}^{\ast }\otimes e_{j}^{\unicode[STIX]{x1D6FC}}\biggr)\bigg\}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D6FF}\biggl(\bigg\{\biggl(U_{j},\mathop{\sum }_{|\unicode[STIX]{x1D6FC}|=n,\unicode[STIX]{x1D6FC}_{1}=0}F_{j,\unicode[STIX]{x1D6FC}}^{1}\cdot e_{j,1}^{\ast }\otimes e_{j}^{\unicode[STIX]{x1D6FC}}\biggr)\bigg\}\biggr)\nonumber\\ \displaystyle & & \displaystyle \quad =\bigg\{\biggl(U_{jk},\mathop{\sum }_{|\unicode[STIX]{x1D6FC}|=n,\unicode[STIX]{x1D6FC}_{1}=0}(h_{1,jk,\unicode[STIX]{x1D6FC}}^{1}-h_{2,jk,\unicode[STIX]{x1D6FC}}^{1})\cdot e_{j,1}^{\ast }\otimes e_{j}^{\unicode[STIX]{x1D6FC}}\biggr)\bigg\}\nonumber\end{eqnarray}$$ in  ${\check{Z}}^{1}(\{U_{j}\},N_{1}\otimes S^{n}N_{Y/S}^{\ast })$. Thus it is sufficient for proving the assertion (c) to show
${\check{Z}}^{1}(\{U_{j}\},N_{1}\otimes S^{n}N_{Y/S}^{\ast })$. Thus it is sufficient for proving the assertion (c) to show  $h_{1,jk,\unicode[STIX]{x1D6FC}}^{1}\equiv 0$ and
$h_{1,jk,\unicode[STIX]{x1D6FC}}^{1}\equiv 0$ and  $h_{2,jk,\unicode[STIX]{x1D6FC}}^{1}\equiv 0$ for each
$h_{2,jk,\unicode[STIX]{x1D6FC}}^{1}\equiv 0$ for each  $\unicode[STIX]{x1D6FC}$ with
$\unicode[STIX]{x1D6FC}$ with  $|\unicode[STIX]{x1D6FC}|=n$ and
$|\unicode[STIX]{x1D6FC}|=n$ and  $\unicode[STIX]{x1D6FC}_{1}=0$, which can be easily checked from Lemma 4.4(c) in Step
$\unicode[STIX]{x1D6FC}_{1}=0$, which can be easily checked from Lemma 4.4(c) in Step  $(\unicode[STIX]{x1D708})$ for each
$(\unicode[STIX]{x1D708})$ for each  $\unicode[STIX]{x1D708}\leqslant n-2$.◻
$\unicode[STIX]{x1D708}\leqslant n-2$.◻
4.5 Norm estimate for  $F_{j,\unicode[STIX]{x1D6FC}}$ in a special setting
$F_{j,\unicode[STIX]{x1D6FC}}$ in a special setting
In this subsection, we estimate the norm of  $F_{j,\unicode[STIX]{x1D6FC}}$ in order to show the convergence of the functional equation (3). Here we treat a special case where
$F_{j,\unicode[STIX]{x1D6FC}}$ in order to show the convergence of the functional equation (3). Here we treat a special case where  $(Y,X)$ is as in Remark 3.5: i.e.
$(Y,X)$ is as in Remark 3.5: i.e.  $N_{Y/X}$ admits a direct decomposition
$N_{Y/X}$ admits a direct decomposition  $N_{Y/X}=N_{1}\oplus N_{2}\oplus \cdots \oplus N_{r}$. Note that, in this case, the defining equation of each
$N_{Y/X}=N_{1}\oplus N_{2}\oplus \cdots \oplus N_{r}$. Note that, in this case, the defining equation of each  $\{F_{j,\unicode[STIX]{x1D6FC}}\}$ is rewritten by the equation
$\{F_{j,\unicode[STIX]{x1D6FC}}\}$ is rewritten by the equation
 $$\begin{eqnarray}\unicode[STIX]{x1D6FF}(\{(U_{j},F_{j,\unicode[STIX]{x1D6FC}}^{\unicode[STIX]{x1D706}})\})=\{(U_{jk},h_{1,jk,\unicode[STIX]{x1D6FC}}^{\unicode[STIX]{x1D706}}-h_{2,jk,\unicode[STIX]{x1D6FC}}^{\unicode[STIX]{x1D706}})\}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FF}(\{(U_{j},F_{j,\unicode[STIX]{x1D6FC}}^{\unicode[STIX]{x1D706}})\})=\{(U_{jk},h_{1,jk,\unicode[STIX]{x1D6FC}}^{\unicode[STIX]{x1D706}}-h_{2,jk,\unicode[STIX]{x1D6FC}}^{\unicode[STIX]{x1D706}})\}\end{eqnarray}$$ in  ${\check{Z}}^{1}(Y,N_{\unicode[STIX]{x1D706}}\otimes N_{\unicode[STIX]{x1D6FC}}^{-\unicode[STIX]{x1D6FC}})$. We additionally assume that
${\check{Z}}^{1}(Y,N_{\unicode[STIX]{x1D706}}\otimes N_{\unicode[STIX]{x1D6FC}}^{-\unicode[STIX]{x1D6FC}})$. We additionally assume that  $N_{Y/X}$ is the holomorphically trivial vector bundle
$N_{Y/X}$ is the holomorphically trivial vector bundle  $\mathbb{I}_{Y}^{(r)}$ of rank
$\mathbb{I}_{Y}^{(r)}$ of rank  $r$ or
$r$ or  $N_{Y/X}\in {\mathcal{S}}^{(r)}(Y):=\bigcup _{A>0}{\mathcal{S}}_{A}^{(r)}(Y)$.
$N_{Y/X}\in {\mathcal{S}}^{(r)}(Y):=\bigcup _{A>0}{\mathcal{S}}_{A}^{(r)}(Y)$.
4.5.1 The case where  $N_{Y/X}\cong \mathbb{I}_{Y}^{(r)}$
$N_{Y/X}\cong \mathbb{I}_{Y}^{(r)}$
Here we consider the case where  $N_{Y/X}\cong \mathbb{I}_{Y}^{(r)}$. Note that, in this case,
$N_{Y/X}\cong \mathbb{I}_{Y}^{(r)}$. Note that, in this case,  $N_{\unicode[STIX]{x1D706}}\otimes N_{\unicode[STIX]{x1D6FC}}^{-\unicode[STIX]{x1D6FC}}\cong \mathbb{I}_{Y}^{(1)}$ holds for any
$N_{\unicode[STIX]{x1D706}}\otimes N_{\unicode[STIX]{x1D6FC}}^{-\unicode[STIX]{x1D6FC}}\cong \mathbb{I}_{Y}^{(1)}$ holds for any  $\unicode[STIX]{x1D706}$ and
$\unicode[STIX]{x1D706}$ and  $\unicode[STIX]{x1D6FC}$. Fix
$\unicode[STIX]{x1D6FC}$. Fix  $U_{j}^{\ast }\Subset U_{j}$ with
$U_{j}^{\ast }\Subset U_{j}$ with  $\bigcup _{j}U_{j}^{\ast }=Y$. Take a constant
$\bigcup _{j}U_{j}^{\ast }=Y$. Take a constant  $K:=K(\mathbb{I}_{Y}^{(1)})$ as in [Reference UedaU, Lemma 3] (=[Reference Kodaira and SpencerKS, Lemma 2]): i.e. for any
$K:=K(\mathbb{I}_{Y}^{(1)})$ as in [Reference UedaU, Lemma 3] (=[Reference Kodaira and SpencerKS, Lemma 2]): i.e. for any  $1$-cocycle
$1$-cocycle  $a=\{(U_{jk},a_{jk})\}\in {\check{Z}}^{1}(\{U_{j}\},{\mathcal{O}}_{Y})$ with
$a=\{(U_{jk},a_{jk})\}\in {\check{Z}}^{1}(\{U_{j}\},{\mathcal{O}}_{Y})$ with  $\Vert a\Vert :=\max _{j,k}\sup _{U_{jk}}|a_{jk}|<\infty$ which is cohomologous to zero, there exists a
$\Vert a\Vert :=\max _{j,k}\sup _{U_{jk}}|a_{jk}|<\infty$ which is cohomologous to zero, there exists a  $0$-cochain
$0$-cochain  $b=\{(U_{j},b_{j})\}\in {\check{C}}^{0}(\{U_{j}\},{\mathcal{O}}_{Y})$ such that
$b=\{(U_{j},b_{j})\}\in {\check{C}}^{0}(\{U_{j}\},{\mathcal{O}}_{Y})$ such that  $a$ is the coboundary of
$a$ is the coboundary of  $b$ and that
$b$ and that  $\Vert b\Vert :=\max _{j}\sup _{U_{j}}|b_{j}|\leqslant K\Vert a\Vert$. Take also a positive number
$\Vert b\Vert :=\max _{j}\sup _{U_{j}}|b_{j}|\leqslant K\Vert a\Vert$. Take also a positive number  $M$ larger than
$M$ larger than  $\max _{j}\max _{\unicode[STIX]{x1D706}}\sup _{V_{j}}|w_{j}^{\unicode[STIX]{x1D706}}|$ and
$\max _{j}\max _{\unicode[STIX]{x1D706}}\sup _{V_{j}}|w_{j}^{\unicode[STIX]{x1D706}}|$ and  $\max _{jk}\max _{\unicode[STIX]{x1D706}}\sup _{V_{jk}}|w_{k}^{\unicode[STIX]{x1D706}}|$, and a sufficiently large positive number
$\max _{jk}\max _{\unicode[STIX]{x1D706}}\sup _{V_{jk}}|w_{k}^{\unicode[STIX]{x1D706}}|$, and a sufficiently large positive number  $R$ so that
$R$ so that  $\{(z_{j},w_{j})\mid z_{j}\in U_{j}\cap U_{k}^{\ast },|w_{j}|<R^{-1}\}\subset V_{k}$ holds for each
$\{(z_{j},w_{j})\mid z_{j}\in U_{j}\cap U_{k}^{\ast },|w_{j}|<R^{-1}\}\subset V_{k}$ holds for each  $j,k$. By using these constants, let us consider the formal series
$j,k$. By using these constants, let us consider the formal series  $A(X)=A(X^{1},X^{2},\ldots ,X^{r})=\sum _{|\unicode[STIX]{x1D6FC}|\geqslant 2}A_{\unicode[STIX]{x1D6FC}}X^{\unicode[STIX]{x1D6FC}}$ defined by
$A(X)=A(X^{1},X^{2},\ldots ,X^{r})=\sum _{|\unicode[STIX]{x1D6FC}|\geqslant 2}A_{\unicode[STIX]{x1D6FC}}X^{\unicode[STIX]{x1D6FC}}$ defined by
 $$\begin{eqnarray}\displaystyle A(X) & = & \displaystyle 2KA(X)\cdot \biggl(-1+\mathop{\prod }_{\unicode[STIX]{x1D706}=1}^{r}\frac{1}{1-R(X^{\unicode[STIX]{x1D706}}+A(X))}\biggr)\nonumber\\ \displaystyle & & \displaystyle +\,2KM\cdot \biggl(-1-R(X^{1}+X^{2}+\cdots +X^{r}+rA(X))\nonumber\\ \displaystyle & & \displaystyle +\mathop{\prod }_{\unicode[STIX]{x1D706}=1}^{r}\frac{1}{1-R(X^{\unicode[STIX]{x1D706}}+A(X))}\biggr).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle A(X) & = & \displaystyle 2KA(X)\cdot \biggl(-1+\mathop{\prod }_{\unicode[STIX]{x1D706}=1}^{r}\frac{1}{1-R(X^{\unicode[STIX]{x1D706}}+A(X))}\biggr)\nonumber\\ \displaystyle & & \displaystyle +\,2KM\cdot \biggl(-1-R(X^{1}+X^{2}+\cdots +X^{r}+rA(X))\nonumber\\ \displaystyle & & \displaystyle +\mathop{\prod }_{\unicode[STIX]{x1D706}=1}^{r}\frac{1}{1-R(X^{\unicode[STIX]{x1D706}}+A(X))}\biggr).\end{eqnarray}$$ Note that, by the inductive argument on  $|\unicode[STIX]{x1D6FC}|$, it is easy to see that each coefficient
$|\unicode[STIX]{x1D6FC}|$, it is easy to see that each coefficient  $A_{\unicode[STIX]{x1D6FC}}$ is determined uniquely and is a positive real number.
$A_{\unicode[STIX]{x1D6FC}}$ is determined uniquely and is a positive real number.
Lemma 4.5. The formal series  $A(X)$ is convergent (i.e.
$A(X)$ is convergent (i.e.  $A(X)$ can be regarded as a holomorphic function defined on a neighborhood of the origin of
$A(X)$ can be regarded as a holomorphic function defined on a neighborhood of the origin of  $\mathbb{C}^{r}$).
$\mathbb{C}^{r}$).
Proof. Let us consider
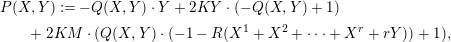 $$\begin{eqnarray}\displaystyle & & \displaystyle P(X,Y):=-Q(X,Y)\cdot Y+2KY\cdot (-Q(X,Y)+1)\nonumber\\ \displaystyle & & \displaystyle \qquad +\,2KM\cdot (Q(X,Y)\cdot (-1-R(X^{1}+X^{2}+\cdots +X^{r}+rY))+1),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle P(X,Y):=-Q(X,Y)\cdot Y+2KY\cdot (-Q(X,Y)+1)\nonumber\\ \displaystyle & & \displaystyle \qquad +\,2KM\cdot (Q(X,Y)\cdot (-1-R(X^{1}+X^{2}+\cdots +X^{r}+rY))+1),\nonumber\end{eqnarray}$$ where  $Q(X,Y):=\prod _{\unicode[STIX]{x1D706}=1}^{r}(1-R(X^{\unicode[STIX]{x1D706}}+Y))\in \mathbb{C}[X,Y]$. As
$Q(X,Y):=\prod _{\unicode[STIX]{x1D706}=1}^{r}(1-R(X^{\unicode[STIX]{x1D706}}+Y))\in \mathbb{C}[X,Y]$. As  $P(0,Y)=-Y+O(Y^{2})$, we can apply the implicit function theorem to obtain a holomorphic function
$P(0,Y)=-Y+O(Y^{2})$, we can apply the implicit function theorem to obtain a holomorphic function  $a(X)$ defined on a neighborhood of the origin of
$a(X)$ defined on a neighborhood of the origin of  $\mathbb{C}^{r}$ with
$\mathbb{C}^{r}$ with  $a(0)=0$ and
$a(0)=0$ and  $P(X,a(X))\equiv 0$. This means that
$P(X,a(X))\equiv 0$. This means that  $a(X)$ satisfies equation (7) and thus we obtain
$a(X)$ satisfies equation (7) and thus we obtain  $a(X)=A(X)$ on a neighborhood of the origin, which proves the lemma.◻
$a(X)=A(X)$ on a neighborhood of the origin, which proves the lemma.◻
In what follows, we will show that one can choose the coefficient functions  $\{F_{j,\unicode[STIX]{x1D6FC}}\}$ as in the previous section so that
$\{F_{j,\unicode[STIX]{x1D6FC}}\}$ as in the previous section so that  $A(X)$ is a dominating series of the function equation (3).
$A(X)$ is a dominating series of the function equation (3).
First, we will show the existence of the solution  $\{(U_{j},F_{j,\unicode[STIX]{x1D6FC}})\}\text{}_{|\unicode[STIX]{x1D6FC}|=2}$ of the equation (6) with
$\{(U_{j},F_{j,\unicode[STIX]{x1D6FC}})\}\text{}_{|\unicode[STIX]{x1D6FC}|=2}$ of the equation (6) with  $\max _{\unicode[STIX]{x1D706}}\Vert \{(U_{j},F_{j,\unicode[STIX]{x1D6FC}}^{\unicode[STIX]{x1D706}})\}\Vert \leqslant A_{\unicode[STIX]{x1D6FC}}$ for each
$\max _{\unicode[STIX]{x1D706}}\Vert \{(U_{j},F_{j,\unicode[STIX]{x1D6FC}}^{\unicode[STIX]{x1D706}})\}\Vert \leqslant A_{\unicode[STIX]{x1D6FC}}$ for each  $\unicode[STIX]{x1D706}=1,2,\ldots ,r$ and
$\unicode[STIX]{x1D706}=1,2,\ldots ,r$ and  $\unicode[STIX]{x1D6FC}$ with
$\unicode[STIX]{x1D6FC}$ with  $|\unicode[STIX]{x1D6FC}|=2$ (
$|\unicode[STIX]{x1D6FC}|=2$ ( $\Vert \{(U_{j},F_{j,\unicode[STIX]{x1D6FC}}^{\unicode[STIX]{x1D706}})\}\Vert :=\max _{j}\sup _{U_{j}}|F_{j,\unicode[STIX]{x1D6FC}}^{\unicode[STIX]{x1D706}}|$). Note that
$\Vert \{(U_{j},F_{j,\unicode[STIX]{x1D6FC}}^{\unicode[STIX]{x1D706}})\}\Vert :=\max _{j}\sup _{U_{j}}|F_{j,\unicode[STIX]{x1D6FC}}^{\unicode[STIX]{x1D706}}|$). Note that  $A_{\unicode[STIX]{x1D6FC}}=2KMR^{2}$ holds for each
$A_{\unicode[STIX]{x1D6FC}}=2KMR^{2}$ holds for each  $\unicode[STIX]{x1D6FC}$ with
$\unicode[STIX]{x1D6FC}$ with  $|\unicode[STIX]{x1D6FC}|=2$. By Cauchy estimate, we obtain the inequality
$|\unicode[STIX]{x1D6FC}|=2$. By Cauchy estimate, we obtain the inequality  $\max _{j}\sup _{U_{j}\cap U_{k}^{\ast }}|f_{kj,\unicode[STIX]{x1D6FC}}^{\unicode[STIX]{x1D706}}|\leqslant MR^{2}$. Combining this inequality and the argument as in [Reference UedaU, p. 599], we obtain
$\max _{j}\sup _{U_{j}\cap U_{k}^{\ast }}|f_{kj,\unicode[STIX]{x1D6FC}}^{\unicode[STIX]{x1D706}}|\leqslant MR^{2}$. Combining this inequality and the argument as in [Reference UedaU, p. 599], we obtain  $\Vert \{(U_{jk},f_{kj,\unicode[STIX]{x1D6FC}}^{\unicode[STIX]{x1D706}})\}\Vert \leqslant 2MR^{2}$ (
$\Vert \{(U_{jk},f_{kj,\unicode[STIX]{x1D6FC}}^{\unicode[STIX]{x1D706}})\}\Vert \leqslant 2MR^{2}$ ( $\Vert \{(U_{j},f_{kj,\unicode[STIX]{x1D6FC}}^{\unicode[STIX]{x1D706}})\}\Vert :=\max _{j,k}\sup _{U_{jk}}|f_{kj,\unicode[STIX]{x1D6FC}}^{\unicode[STIX]{x1D706}}|$). Thus we obtain
$\Vert \{(U_{j},f_{kj,\unicode[STIX]{x1D6FC}}^{\unicode[STIX]{x1D706}})\}\Vert :=\max _{j,k}\sup _{U_{jk}}|f_{kj,\unicode[STIX]{x1D6FC}}^{\unicode[STIX]{x1D706}}|$). Thus we obtain  $\Vert \{(U_{j},F_{j,\unicode[STIX]{x1D6FC}}^{\unicode[STIX]{x1D706}})\}\Vert \leqslant A_{\unicode[STIX]{x1D6FC}}$ from the definition of the constant
$\Vert \{(U_{j},F_{j,\unicode[STIX]{x1D6FC}}^{\unicode[STIX]{x1D706}})\}\Vert \leqslant A_{\unicode[STIX]{x1D6FC}}$ from the definition of the constant  $K$.
$K$.
Next, we will show the existence of the solution  $\{(U_{j},F_{j,\unicode[STIX]{x1D6FC}})\}\text{}_{|\unicode[STIX]{x1D6FC}|=n}$ of equation (6) with
$\{(U_{j},F_{j,\unicode[STIX]{x1D6FC}})\}\text{}_{|\unicode[STIX]{x1D6FC}|=n}$ of equation (6) with  $\max _{\unicode[STIX]{x1D706}}\Vert \{(U_{j},F_{j,\unicode[STIX]{x1D6FC}}^{\unicode[STIX]{x1D706}})\}\Vert \leqslant A_{\unicode[STIX]{x1D6FC}}$ for each
$\max _{\unicode[STIX]{x1D706}}\Vert \{(U_{j},F_{j,\unicode[STIX]{x1D6FC}}^{\unicode[STIX]{x1D706}})\}\Vert \leqslant A_{\unicode[STIX]{x1D6FC}}$ for each  $\unicode[STIX]{x1D706}=1,2,\ldots ,r$ and
$\unicode[STIX]{x1D706}=1,2,\ldots ,r$ and  $\unicode[STIX]{x1D6FC}$ with
$\unicode[STIX]{x1D6FC}$ with  $|\unicode[STIX]{x1D6FC}|=n$ by assuming the assertion for
$|\unicode[STIX]{x1D6FC}|=n$ by assuming the assertion for  $|\unicode[STIX]{x1D6FC}|<n$. Take
$|\unicode[STIX]{x1D6FC}|<n$. Take  $\unicode[STIX]{x1D6FC}$ with
$\unicode[STIX]{x1D6FC}$ with  $|\unicode[STIX]{x1D6FC}|=n$. Then, it follows from the inductive assumption that
$|\unicode[STIX]{x1D6FC}|=n$. Then, it follows from the inductive assumption that  $\max _{j,k}\sup _{U_{j}\cap U_{k}^{\ast }}|h_{1,jk,\unicode[STIX]{x1D6FC}}^{\unicode[STIX]{x1D706}}|$ is bounded by the coefficient of
$\max _{j,k}\sup _{U_{j}\cap U_{k}^{\ast }}|h_{1,jk,\unicode[STIX]{x1D6FC}}^{\unicode[STIX]{x1D706}}|$ is bounded by the coefficient of  $X^{\unicode[STIX]{x1D6FC}}$ in the expansion of
$X^{\unicode[STIX]{x1D6FC}}$ in the expansion of
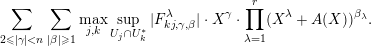 $$\begin{eqnarray}\mathop{\sum }_{2\leqslant |\unicode[STIX]{x1D6FE}|<n}\mathop{\sum }_{|\unicode[STIX]{x1D6FD}|\geqslant 1}\max _{j,k}\sup _{U_{j}\cap U_{k}^{\ast }}|F_{kj,\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D706}}|\cdot X^{\unicode[STIX]{x1D6FE}}\cdot \mathop{\prod }_{\unicode[STIX]{x1D706}=1}^{r}(X^{\unicode[STIX]{x1D706}}+A(X))^{\unicode[STIX]{x1D6FD}_{\unicode[STIX]{x1D706}}}.\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{2\leqslant |\unicode[STIX]{x1D6FE}|<n}\mathop{\sum }_{|\unicode[STIX]{x1D6FD}|\geqslant 1}\max _{j,k}\sup _{U_{j}\cap U_{k}^{\ast }}|F_{kj,\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D706}}|\cdot X^{\unicode[STIX]{x1D6FE}}\cdot \mathop{\prod }_{\unicode[STIX]{x1D706}=1}^{r}(X^{\unicode[STIX]{x1D706}}+A(X))^{\unicode[STIX]{x1D6FD}_{\unicode[STIX]{x1D706}}}.\end{eqnarray}$$ By Cauchy estimate, it is bounded by the coefficient of  $X^{\unicode[STIX]{x1D6FC}}$ in the expansion of
$X^{\unicode[STIX]{x1D6FC}}$ in the expansion of
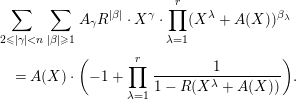 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{2\leqslant |\unicode[STIX]{x1D6FE}|<n}\mathop{\sum }_{|\unicode[STIX]{x1D6FD}|\geqslant 1}A_{\unicode[STIX]{x1D6FE}}R^{|\unicode[STIX]{x1D6FD}|}\cdot X^{\unicode[STIX]{x1D6FE}}\cdot \mathop{\prod }_{\unicode[STIX]{x1D706}=1}^{r}(X^{\unicode[STIX]{x1D706}}+A(X))^{\unicode[STIX]{x1D6FD}_{\unicode[STIX]{x1D706}}}\nonumber\\ \displaystyle & & \displaystyle \quad =A(X)\cdot \biggl(-1+\mathop{\prod }_{\unicode[STIX]{x1D706}=1}^{r}\frac{1}{1-R(X^{\unicode[STIX]{x1D706}}+A(X))}\biggr).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{2\leqslant |\unicode[STIX]{x1D6FE}|<n}\mathop{\sum }_{|\unicode[STIX]{x1D6FD}|\geqslant 1}A_{\unicode[STIX]{x1D6FE}}R^{|\unicode[STIX]{x1D6FD}|}\cdot X^{\unicode[STIX]{x1D6FE}}\cdot \mathop{\prod }_{\unicode[STIX]{x1D706}=1}^{r}(X^{\unicode[STIX]{x1D706}}+A(X))^{\unicode[STIX]{x1D6FD}_{\unicode[STIX]{x1D706}}}\nonumber\\ \displaystyle & & \displaystyle \quad =A(X)\cdot \biggl(-1+\mathop{\prod }_{\unicode[STIX]{x1D706}=1}^{r}\frac{1}{1-R(X^{\unicode[STIX]{x1D706}}+A(X))}\biggr).\nonumber\end{eqnarray}$$ From a similar argument, it can be seen that  $\max _{j,k}\sup _{U_{j}\cap U_{k}^{\ast }}|h_{2,jk,\unicode[STIX]{x1D6FC}}^{\unicode[STIX]{x1D706}}|$ is bounded by the coefficient of
$\max _{j,k}\sup _{U_{j}\cap U_{k}^{\ast }}|h_{2,jk,\unicode[STIX]{x1D6FC}}^{\unicode[STIX]{x1D706}}|$ is bounded by the coefficient of  $X^{\unicode[STIX]{x1D6FC}}$ in the expansion of
$X^{\unicode[STIX]{x1D6FC}}$ in the expansion of
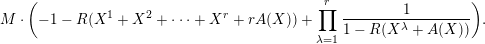 $$\begin{eqnarray}M\cdot \biggl(-1-R(X^{1}+X^{2}+\cdots +X^{r}+rA(X))+\mathop{\prod }_{\unicode[STIX]{x1D706}=1}^{r}\frac{1}{1-R(X^{\unicode[STIX]{x1D706}}+A(X))}\biggr).\end{eqnarray}$$
$$\begin{eqnarray}M\cdot \biggl(-1-R(X^{1}+X^{2}+\cdots +X^{r}+rA(X))+\mathop{\prod }_{\unicode[STIX]{x1D706}=1}^{r}\frac{1}{1-R(X^{\unicode[STIX]{x1D706}}+A(X))}\biggr).\end{eqnarray}$$ Thus, by the argument as in [Reference UedaU, p. 599] and the defining function (7) of  $A(X)$, we obtain the inequality
$A(X)$, we obtain the inequality  $\Vert \{(U_{jk},h_{1,jk,\unicode[STIX]{x1D6FC}}^{\unicode[STIX]{x1D706}}-h_{2,jk,\unicode[STIX]{x1D6FC}}^{\unicode[STIX]{x1D706}})\}\Vert \leqslant K^{-1}A_{\unicode[STIX]{x1D6FC}}$ for each
$\Vert \{(U_{jk},h_{1,jk,\unicode[STIX]{x1D6FC}}^{\unicode[STIX]{x1D706}}-h_{2,jk,\unicode[STIX]{x1D6FC}}^{\unicode[STIX]{x1D706}})\}\Vert \leqslant K^{-1}A_{\unicode[STIX]{x1D6FC}}$ for each  $\unicode[STIX]{x1D706}$. Therefore the assertion follows from the definition of the constant
$\unicode[STIX]{x1D706}$. Therefore the assertion follows from the definition of the constant  $K$.
$K$.
4.5.2 The case where  $N_{Y/X}\in {\mathcal{S}}^{(r)}(Y)$
$N_{Y/X}\in {\mathcal{S}}^{(r)}(Y)$
When  $N_{Y/X}\in {\mathcal{S}}^{(r)}(Y)$, by using [Reference UedaU, Lemma 4] instead of [Reference UedaU, Lemma 3], the same arguments as in Section 4.5.1 can be carried out after replacing the defining function (7) of
$N_{Y/X}\in {\mathcal{S}}^{(r)}(Y)$, by using [Reference UedaU, Lemma 4] instead of [Reference UedaU, Lemma 3], the same arguments as in Section 4.5.1 can be carried out after replacing the defining function (7) of  $A(X)$ with
$A(X)$ with
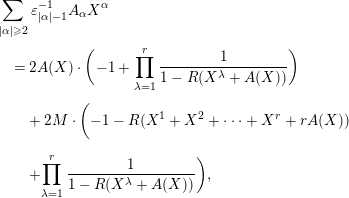 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{|\unicode[STIX]{x1D6FC}|\geqslant 2}\unicode[STIX]{x1D700}_{|\unicode[STIX]{x1D6FC}|-1}^{-1}A_{\unicode[STIX]{x1D6FC}}X^{\unicode[STIX]{x1D6FC}}\nonumber\\ \displaystyle & & \displaystyle \quad =2A(X)\cdot \biggl(-1+\mathop{\prod }_{\unicode[STIX]{x1D706}=1}^{r}\frac{1}{1-R(X^{\unicode[STIX]{x1D706}}+A(X))}\biggr)\nonumber\\ \displaystyle & & \displaystyle \qquad +\,2M\cdot \biggl(-1-R(X^{1}+X^{2}+\cdots +X^{r}+rA(X))\nonumber\\ \displaystyle & & \displaystyle \qquad +\mathop{\prod }_{\unicode[STIX]{x1D706}=1}^{r}\frac{1}{1-R(X^{\unicode[STIX]{x1D706}}+A(X))}\biggr),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{|\unicode[STIX]{x1D6FC}|\geqslant 2}\unicode[STIX]{x1D700}_{|\unicode[STIX]{x1D6FC}|-1}^{-1}A_{\unicode[STIX]{x1D6FC}}X^{\unicode[STIX]{x1D6FC}}\nonumber\\ \displaystyle & & \displaystyle \quad =2A(X)\cdot \biggl(-1+\mathop{\prod }_{\unicode[STIX]{x1D706}=1}^{r}\frac{1}{1-R(X^{\unicode[STIX]{x1D706}}+A(X))}\biggr)\nonumber\\ \displaystyle & & \displaystyle \qquad +\,2M\cdot \biggl(-1-R(X^{1}+X^{2}+\cdots +X^{r}+rA(X))\nonumber\\ \displaystyle & & \displaystyle \qquad +\mathop{\prod }_{\unicode[STIX]{x1D706}=1}^{r}\frac{1}{1-R(X^{\unicode[STIX]{x1D706}}+A(X))}\biggr),\nonumber\end{eqnarray}$$where
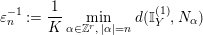 $$\begin{eqnarray}\unicode[STIX]{x1D700}_{n}^{-1}:=\frac{1}{K}\min _{\unicode[STIX]{x1D6FC}\in \mathbb{Z}^{r},\,|\unicode[STIX]{x1D6FC}|=n}d(\mathbb{I}_{Y}^{(1)},N_{\unicode[STIX]{x1D6FC}})\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D700}_{n}^{-1}:=\frac{1}{K}\min _{\unicode[STIX]{x1D6FC}\in \mathbb{Z}^{r},\,|\unicode[STIX]{x1D6FC}|=n}d(\mathbb{I}_{Y}^{(1)},N_{\unicode[STIX]{x1D6FC}})\end{eqnarray}$$ ( $K$ is the constant as in [Reference UedaU, Lemma 4], see also [Reference UedaU, Section 4.6] for the details). Thus, for proving the convergence of the functional equation (3), it is sufficient to see the convergence of the formal series
$K$ is the constant as in [Reference UedaU, Lemma 4], see also [Reference UedaU, Section 4.6] for the details). Thus, for proving the convergence of the functional equation (3), it is sufficient to see the convergence of the formal series  $A(X)$ with the above new defining equation.
$A(X)$ with the above new defining equation.
Consider  $B(Y):=Y+A(Y,Y,\ldots ,Y)=Y+\sum _{n=2}^{\infty }B_{n}Y^{n}$, where
$B(Y):=Y+A(Y,Y,\ldots ,Y)=Y+\sum _{n=2}^{\infty }B_{n}Y^{n}$, where  $B_{n}=\sum _{|\unicode[STIX]{x1D6FC}|=n}A_{\unicode[STIX]{x1D6FC}}$ for each
$B_{n}=\sum _{|\unicode[STIX]{x1D6FC}|=n}A_{\unicode[STIX]{x1D6FC}}$ for each  $n\geqslant 2$. As it can be easily seen that
$n\geqslant 2$. As it can be easily seen that  $A_{\unicode[STIX]{x1D6FC}}\geqslant 0$ holds for each
$A_{\unicode[STIX]{x1D6FC}}\geqslant 0$ holds for each  $\unicode[STIX]{x1D6FC}$, we have
$\unicode[STIX]{x1D6FC}$, we have  $A_{\unicode[STIX]{x1D6FC}}\leqslant B_{|\unicode[STIX]{x1D6FC}|}$. Therefore, for showing the convergence of
$A_{\unicode[STIX]{x1D6FC}}\leqslant B_{|\unicode[STIX]{x1D6FC}|}$. Therefore, for showing the convergence of  $A(X)$, it is sufficient to show that
$A(X)$, it is sufficient to show that  $B(Y)$ has a positive radius of convergence. By considering
$B(Y)$ has a positive radius of convergence. By considering  $X^{1}=X^{2}=\cdots =X^{r}=Y$, we obtain the defining function of
$X^{1}=X^{2}=\cdots =X^{r}=Y$, we obtain the defining function of  $B(Y)$ as follows:
$B(Y)$ as follows:
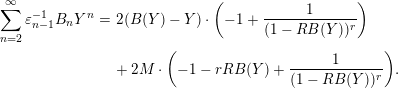 $$\begin{eqnarray}\displaystyle \mathop{\sum }_{n=2}^{\infty }\unicode[STIX]{x1D700}_{n-1}^{-1}B_{n}Y^{n} & = & \displaystyle 2(B(Y)-Y)\cdot \biggl(-1+\frac{1}{(1-RB(Y))^{r}}\biggr)\nonumber\\ \displaystyle & & \displaystyle +\,2M\cdot \biggl(-1-rRB(Y)+\frac{1}{(1-RB(Y))^{r}}\biggr).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathop{\sum }_{n=2}^{\infty }\unicode[STIX]{x1D700}_{n-1}^{-1}B_{n}Y^{n} & = & \displaystyle 2(B(Y)-Y)\cdot \biggl(-1+\frac{1}{(1-RB(Y))^{r}}\biggr)\nonumber\\ \displaystyle & & \displaystyle +\,2M\cdot \biggl(-1-rRB(Y)+\frac{1}{(1-RB(Y))^{r}}\biggr).\nonumber\end{eqnarray}$$ Also consider another formal series  $\widehat{B}(Y)=Y+\sum _{n=2}^{\infty }\widehat{B}_{n}Y^{n}$ defined by
$\widehat{B}(Y)=Y+\sum _{n=2}^{\infty }\widehat{B}_{n}Y^{n}$ defined by
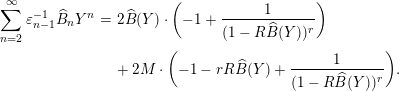 $$\begin{eqnarray}\displaystyle \mathop{\sum }_{n=2}^{\infty }\unicode[STIX]{x1D700}_{n-1}^{-1}\widehat{B}_{n}Y^{n} & = & \displaystyle 2\widehat{B}(Y)\cdot \biggl(-1+\frac{1}{(1-R\widehat{B}(Y))^{r}}\biggr)\nonumber\\ \displaystyle & & \displaystyle +\,2M\cdot \biggl(-1-rR\widehat{B}(Y)+\frac{1}{(1-R\widehat{B}(Y))^{r}}\biggr).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathop{\sum }_{n=2}^{\infty }\unicode[STIX]{x1D700}_{n-1}^{-1}\widehat{B}_{n}Y^{n} & = & \displaystyle 2\widehat{B}(Y)\cdot \biggl(-1+\frac{1}{(1-R\widehat{B}(Y))^{r}}\biggr)\nonumber\\ \displaystyle & & \displaystyle +\,2M\cdot \biggl(-1-rR\widehat{B}(Y)+\frac{1}{(1-R\widehat{B}(Y))^{r}}\biggr).\nonumber\end{eqnarray}$$ As it clearly holds that  $\widehat{B}_{n}\geqslant B_{n}$ for each
$\widehat{B}_{n}\geqslant B_{n}$ for each  $n\geqslant 2$, it is sufficient to show that
$n\geqslant 2$, it is sufficient to show that  $\widehat{B}(Y)$ has a positive radius of convergence. According to Siegel’s argument ([Reference SiegelSi], see also [Reference UedaU, Lemma 5]), it is sufficient to see the following two properties of
$\widehat{B}(Y)$ has a positive radius of convergence. According to Siegel’s argument ([Reference SiegelSi], see also [Reference UedaU, Lemma 5]), it is sufficient to see the following two properties of  $\{\unicode[STIX]{x1D700}_{n}\}$: (a) There exists a positive number
$\{\unicode[STIX]{x1D700}_{n}\}$: (a) There exists a positive number  $A$ such that
$A$ such that  $\unicode[STIX]{x1D700}_{n}<(2n)^{A}$ for any
$\unicode[STIX]{x1D700}_{n}<(2n)^{A}$ for any  $n\geqslant 1$, and (b)
$n\geqslant 1$, and (b)  $\unicode[STIX]{x1D700}_{n-m}^{-1}\leqslant \unicode[STIX]{x1D700}_{n}^{-1}+\unicode[STIX]{x1D700}_{m}^{-1}$ for any
$\unicode[STIX]{x1D700}_{n-m}^{-1}\leqslant \unicode[STIX]{x1D700}_{n}^{-1}+\unicode[STIX]{x1D700}_{m}^{-1}$ for any  $n>m$. The property (a) directly follows from the assumption that
$n>m$. The property (a) directly follows from the assumption that  $N_{Y/X}\in {\mathcal{S}}^{(r)}(Y)$. The property (b) can be shown by
$N_{Y/X}\in {\mathcal{S}}^{(r)}(Y)$. The property (b) can be shown by
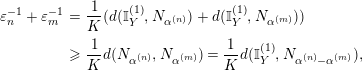 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D700}_{n}^{-1}+\unicode[STIX]{x1D700}_{m}^{-1} & = & \displaystyle \frac{1}{K}(d(\mathbb{I}_{Y}^{(1)},N_{\unicode[STIX]{x1D6FC}^{(n)}})+d(\mathbb{I}_{Y}^{(1)},N_{\unicode[STIX]{x1D6FC}^{(m)}}))\nonumber\\ \displaystyle & {\geqslant} & \displaystyle \frac{1}{K}d(N_{\unicode[STIX]{x1D6FC}^{(n)}},N_{\unicode[STIX]{x1D6FC}^{(m)}})=\frac{1}{K}d(\mathbb{I}_{Y}^{(1)},N_{\unicode[STIX]{x1D6FC}^{(n)}-\unicode[STIX]{x1D6FC}^{(m)}}),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D700}_{n}^{-1}+\unicode[STIX]{x1D700}_{m}^{-1} & = & \displaystyle \frac{1}{K}(d(\mathbb{I}_{Y}^{(1)},N_{\unicode[STIX]{x1D6FC}^{(n)}})+d(\mathbb{I}_{Y}^{(1)},N_{\unicode[STIX]{x1D6FC}^{(m)}}))\nonumber\\ \displaystyle & {\geqslant} & \displaystyle \frac{1}{K}d(N_{\unicode[STIX]{x1D6FC}^{(n)}},N_{\unicode[STIX]{x1D6FC}^{(m)}})=\frac{1}{K}d(\mathbb{I}_{Y}^{(1)},N_{\unicode[STIX]{x1D6FC}^{(n)}-\unicode[STIX]{x1D6FC}^{(m)}}),\nonumber\end{eqnarray}$$ where  $\unicode[STIX]{x1D6FC}^{(n)}\in \mathbb{Z}^{r}$ is an element which attains the minimum in the definition of
$\unicode[STIX]{x1D6FC}^{(n)}\in \mathbb{Z}^{r}$ is an element which attains the minimum in the definition of  $\unicode[STIX]{x1D700}_{n}^{-1}$.
$\unicode[STIX]{x1D700}_{n}^{-1}$.
4.6 End of the proof for the special setting
Assume that  $N_{Y/X}$ is holomorphically trivial or
$N_{Y/X}$ is holomorphically trivial or  $N_{Y/X}\in {\mathcal{S}}^{(r)}(Y)$ holds. Then, by choosing the coefficient functions
$N_{Y/X}\in {\mathcal{S}}^{(r)}(Y)$ holds. Then, by choosing the coefficient functions  $\{F_{j,\unicode[STIX]{x1D6FC}}\}$ as above, we can deduce from the inverse function theorem that there exists a solution
$\{F_{j,\unicode[STIX]{x1D6FC}}\}$ as above, we can deduce from the inverse function theorem that there exists a solution  $\{u_{j}\}$ of the functional equation (3). By shrinking
$\{u_{j}\}$ of the functional equation (3). By shrinking  $V$ if necessary, we may assume that
$V$ if necessary, we may assume that  $u_{j}$ is defined on
$u_{j}$ is defined on  $V_{j}$ for each
$V_{j}$ for each  $j$. From Lemma 4.4(b), it holds that the solutions satisfy
$j$. From Lemma 4.4(b), it holds that the solutions satisfy  $u_{j}=T_{jk}u_{k}$ on each
$u_{j}=T_{jk}u_{k}$ on each  $V_{jk}$. Thus the theorem for this special case follows from the arguments as we already explained in Section 4.1.
$V_{jk}$. Thus the theorem for this special case follows from the arguments as we already explained in Section 4.1.
4.7 Proof for the general setting
When  $N_{Y/X}\in {\mathcal{E}}_{0}^{(r)}(Y)$, consider
$N_{Y/X}\in {\mathcal{E}}_{0}^{(r)}(Y)$, consider  $G:=\text{ker}\,\unicode[STIX]{x1D70C}$, where
$G:=\text{ker}\,\unicode[STIX]{x1D70C}$, where  $\unicode[STIX]{x1D70C}=\unicode[STIX]{x1D70C}_{N_{Y/X}}$ is the unitary representation corresponding to
$\unicode[STIX]{x1D70C}=\unicode[STIX]{x1D70C}_{N_{Y/X}}$ is the unitary representation corresponding to  $N_{Y/X}$. Fix a tubular neighborhood
$N_{Y/X}$. Fix a tubular neighborhood  $V$ of
$V$ of  $Y$ in
$Y$ in  $X$ and regard
$X$ and regard  $G$ as a normal subgroup of
$G$ as a normal subgroup of  $\unicode[STIX]{x1D70B}_{1}(V,\ast )$ by the natural isomorphism
$\unicode[STIX]{x1D70B}_{1}(V,\ast )$ by the natural isomorphism  $\unicode[STIX]{x1D70B}_{1}(Y,\ast )\cong \unicode[STIX]{x1D70B}_{1}(V,\ast )$. From the assumption, there exists a finite normal covering
$\unicode[STIX]{x1D70B}_{1}(Y,\ast )\cong \unicode[STIX]{x1D70B}_{1}(V,\ast )$. From the assumption, there exists a finite normal covering  $\unicode[STIX]{x1D70B}:\widetilde{V}\rightarrow V$ corresponding to
$\unicode[STIX]{x1D70B}:\widetilde{V}\rightarrow V$ corresponding to  $G\subset \unicode[STIX]{x1D70B}_{1}(V,\ast )$. Denote by
$G\subset \unicode[STIX]{x1D70B}_{1}(V,\ast )$. Denote by  $\widetilde{Y}$ the preimage
$\widetilde{Y}$ the preimage  $\unicode[STIX]{x1D70B}^{-1}(Y)$. Then it is clear from the construction that
$\unicode[STIX]{x1D70B}^{-1}(Y)$. Then it is clear from the construction that  $N_{\widetilde{Y}/\widetilde{V}}=(\unicode[STIX]{x1D70B}|_{\widetilde{Y}})^{\ast }N_{Y/X}$ is holomorphically trivial. Let us denote
$N_{\widetilde{Y}/\widetilde{V}}=(\unicode[STIX]{x1D70B}|_{\widetilde{Y}})^{\ast }N_{Y/X}$ is holomorphically trivial. Let us denote  $\unicode[STIX]{x1D70B}^{-1}(V_{j})$ by
$\unicode[STIX]{x1D70B}^{-1}(V_{j})$ by  $\widetilde{V}_{j}$ and
$\widetilde{V}_{j}$ and  $\widetilde{V}_{j}\cap \widetilde{Y}$ by
$\widetilde{V}_{j}\cap \widetilde{Y}$ by  $\widetilde{U}_{j}$. We may assume that
$\widetilde{U}_{j}$. We may assume that  $\widetilde{U}_{j}$ is the union of
$\widetilde{U}_{j}$ is the union of  $d$ copies of
$d$ copies of  $U_{j}$, where
$U_{j}$, where  $d$ is the degree of the map
$d$ is the degree of the map  $\unicode[STIX]{x1D70B}$. Consider the local defining functions system
$\unicode[STIX]{x1D70B}$. Consider the local defining functions system  $\{\widetilde{w}_{j}\}$ defined by
$\{\widetilde{w}_{j}\}$ defined by  $\widetilde{w}_{j}:=(\unicode[STIX]{x1D70B}|_{\widetilde{V}_{j}})^{\ast }w_{j}$.
$\widetilde{w}_{j}:=(\unicode[STIX]{x1D70B}|_{\widetilde{V}_{j}})^{\ast }w_{j}$.
By Lemma 4.6 below,  $(\widetilde{Y},\widetilde{V})$ is of infinite type. Thus, from the result we showed in Section 4.6, we can solve the functional equation (3) with initial system
$(\widetilde{Y},\widetilde{V})$ is of infinite type. Thus, from the result we showed in Section 4.6, we can solve the functional equation (3) with initial system  $\{\widetilde{w}_{j}\}$ on each
$\{\widetilde{w}_{j}\}$ on each  $\widetilde{V}_{j}$ to obtain a local defining functions system
$\widetilde{V}_{j}$ to obtain a local defining functions system  $\{\widetilde{u}_{j}\}$ of
$\{\widetilde{u}_{j}\}$ of  $\widetilde{Y}$ in
$\widetilde{Y}$ in  $\widetilde{V}$ with
$\widetilde{V}$ with  $\widetilde{u}_{j}=T_{jk}\widetilde{u}_{k}$ on each
$\widetilde{u}_{j}=T_{jk}\widetilde{u}_{k}$ on each  $\widetilde{V}_{jk}$. Note that, as
$\widetilde{V}_{jk}$. Note that, as  $\widetilde{w}_{j}=\widetilde{u}_{j}+O(|\widetilde{u}_{j}|^{2})$, it holds that
$\widetilde{w}_{j}=\widetilde{u}_{j}+O(|\widetilde{u}_{j}|^{2})$, it holds that  $d\widetilde{u}_{j}|_{\widetilde{U}_{j}}=(\unicode[STIX]{x1D70B}|_{\widetilde{U}_{j}})^{\ast }e_{j}$.
$d\widetilde{u}_{j}|_{\widetilde{U}_{j}}=(\unicode[STIX]{x1D70B}|_{\widetilde{U}_{j}})^{\ast }e_{j}$.
Define a function  $u_{j}$ on
$u_{j}$ on  $V_{j}$ by
$V_{j}$ by
 $$\begin{eqnarray}(\unicode[STIX]{x1D70B}|_{\widetilde{V}_{j}})^{\ast }u_{j}=\frac{1}{d}\mathop{\sum }_{\unicode[STIX]{x1D708}=1}^{d}i_{\unicode[STIX]{x1D708}}^{\ast }\widetilde{u}_{j},\end{eqnarray}$$
$$\begin{eqnarray}(\unicode[STIX]{x1D70B}|_{\widetilde{V}_{j}})^{\ast }u_{j}=\frac{1}{d}\mathop{\sum }_{\unicode[STIX]{x1D708}=1}^{d}i_{\unicode[STIX]{x1D708}}^{\ast }\widetilde{u}_{j},\end{eqnarray}$$ where  $\{i_{1},i_{2},\ldots ,i_{d}\}$ is the set of deck transformations of
$\{i_{1},i_{2},\ldots ,i_{d}\}$ is the set of deck transformations of  $\unicode[STIX]{x1D70B}$. Clearly it holds that
$\unicode[STIX]{x1D70B}$. Clearly it holds that  $du_{j}|_{U_{j}}=e_{j}$ and
$du_{j}|_{U_{j}}=e_{j}$ and  $\{u_{j}=0\}=U_{j}$ hold, which means that
$\{u_{j}=0\}=U_{j}$ hold, which means that  $\{u_{j}\}$ is a local defining functions system of
$\{u_{j}\}$ is a local defining functions system of  $Y$. It is also easy to see that
$Y$. It is also easy to see that  $u_{j}=T_{jk}u_{k}$ holds on each
$u_{j}=T_{jk}u_{k}$ holds on each  $V_{jk}$, which shows the assertion (i) for the case where
$V_{jk}$, which shows the assertion (i) for the case where  $N_{Y/X}\in {\mathcal{E}}_{0}^{(r)}(Y)$. Under the assumption in Theorem 1.1(ii), it follows from
$N_{Y/X}\in {\mathcal{E}}_{0}^{(r)}(Y)$. Under the assumption in Theorem 1.1(ii), it follows from  $\boldsymbol{(Property)}_{n}$’s that we may assume that
$\boldsymbol{(Property)}_{n}$’s that we may assume that  $\widetilde{u}_{j}^{1}$ is a defining function of
$\widetilde{u}_{j}^{1}$ is a defining function of  $\widetilde{V}_{j}\cap \unicode[STIX]{x1D70B}^{-1}(S)$ in
$\widetilde{V}_{j}\cap \unicode[STIX]{x1D70B}^{-1}(S)$ in  $\widetilde{V}_{j}$ with
$\widetilde{V}_{j}$ with  $d\widetilde{u}_{j}^{1}=\unicode[STIX]{x1D70B}^{\ast }((1+O(|v_{j}|))\cdot dw_{j}^{1})$ on each
$d\widetilde{u}_{j}^{1}=\unicode[STIX]{x1D70B}^{\ast }((1+O(|v_{j}|))\cdot dw_{j}^{1})$ on each  $\widetilde{V}_{j}\cap \unicode[STIX]{x1D70B}^{-1}(S)$. Therefore
$\widetilde{V}_{j}\cap \unicode[STIX]{x1D70B}^{-1}(S)$. Therefore  $u_{j}^{1}$ is a defining function of
$u_{j}^{1}$ is a defining function of  $V_{j}\cap S$ by shrinking
$V_{j}\cap S$ by shrinking  $V$ if necessary, which proves the assertion (ii) for the case where
$V$ if necessary, which proves the assertion (ii) for the case where  $N_{Y/X}\in {\mathcal{E}}_{0}^{(r)}(Y)$.
$N_{Y/X}\in {\mathcal{E}}_{0}^{(r)}(Y)$.
When  $N_{Y/X}\in {\mathcal{E}}_{1}^{(r)}(Y)$, there exists a finite normal covering
$N_{Y/X}\in {\mathcal{E}}_{1}^{(r)}(Y)$, there exists a finite normal covering  $\unicode[STIX]{x1D70B}:\widetilde{Y}\rightarrow Y$ such that
$\unicode[STIX]{x1D70B}:\widetilde{Y}\rightarrow Y$ such that  $(\unicode[STIX]{x1D70B}|_{\widetilde{Y}})^{\ast }N_{Y/X}\in {\mathcal{S}}^{(r)}(\widetilde{Y})$. The theorem for this case is shown by the same argument as above by using this map
$(\unicode[STIX]{x1D70B}|_{\widetilde{Y}})^{\ast }N_{Y/X}\in {\mathcal{S}}^{(r)}(\widetilde{Y})$. The theorem for this case is shown by the same argument as above by using this map  $\unicode[STIX]{x1D70B}$.
$\unicode[STIX]{x1D70B}$.
Lemma 4.6. Let  $\unicode[STIX]{x1D70B},\widetilde{Y},\widetilde{V}$ be as above. Then
$\unicode[STIX]{x1D70B},\widetilde{Y},\widetilde{V}$ be as above. Then  $\text{type}\,(Y,X)=\text{type}\,(\widetilde{Y},\widetilde{V})$ holds.
$\text{type}\,(Y,X)=\text{type}\,(\widetilde{Y},\widetilde{V})$ holds.
Proof. Let
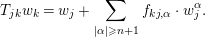 $$\begin{eqnarray}T_{jk}w_{k}=w_{j}+\mathop{\sum }_{|\unicode[STIX]{x1D6FC}|\geqslant n+1}f_{kj,\unicode[STIX]{x1D6FC}}\cdot w_{j}^{\unicode[STIX]{x1D6FC}}.\end{eqnarray}$$
$$\begin{eqnarray}T_{jk}w_{k}=w_{j}+\mathop{\sum }_{|\unicode[STIX]{x1D6FC}|\geqslant n+1}f_{kj,\unicode[STIX]{x1D6FC}}\cdot w_{j}^{\unicode[STIX]{x1D6FC}}.\end{eqnarray}$$ be the expansion (1) for the system  $\{w_{j}\}$. Then, by pulling it back by
$\{w_{j}\}$. Then, by pulling it back by  $\unicode[STIX]{x1D70B}$, we obtain
$\unicode[STIX]{x1D70B}$, we obtain
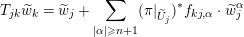 $$\begin{eqnarray}T_{jk}\widetilde{w}_{k}=\widetilde{w}_{j}+\mathop{\sum }_{|\unicode[STIX]{x1D6FC}|\geqslant n+1}(\unicode[STIX]{x1D70B}|_{\widetilde{U}_{j}})^{\ast }f_{kj,\unicode[STIX]{x1D6FC}}\cdot \widetilde{w}_{j}^{\unicode[STIX]{x1D6FC}}\end{eqnarray}$$
$$\begin{eqnarray}T_{jk}\widetilde{w}_{k}=\widetilde{w}_{j}+\mathop{\sum }_{|\unicode[STIX]{x1D6FC}|\geqslant n+1}(\unicode[STIX]{x1D70B}|_{\widetilde{U}_{j}})^{\ast }f_{kj,\unicode[STIX]{x1D6FC}}\cdot \widetilde{w}_{j}^{\unicode[STIX]{x1D6FC}}\end{eqnarray}$$ on each  $\widetilde{V}_{jk}$. Thus,
$\widetilde{V}_{jk}$. Thus,  $\{\widetilde{w}_{j}\}$ is a system of type
$\{\widetilde{w}_{j}\}$ is a system of type  $n$ and
$n$ and
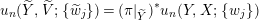 $$\begin{eqnarray}u_{n}(\widetilde{Y},\widetilde{V};\{\widetilde{w}_{j}\})=(\unicode[STIX]{x1D70B}|_{\widetilde{Y}})^{\ast }u_{n}(Y,X;\{w_{j}\})\end{eqnarray}$$
$$\begin{eqnarray}u_{n}(\widetilde{Y},\widetilde{V};\{\widetilde{w}_{j}\})=(\unicode[STIX]{x1D70B}|_{\widetilde{Y}})^{\ast }u_{n}(Y,X;\{w_{j}\})\end{eqnarray}$$ holds. Therefore we obtain the lemma, since the map  $(\unicode[STIX]{x1D70B}|_{\widetilde{Y}})^{\ast }:H^{1}(Y,N_{Y/X}\otimes S^{n}N_{Y/X}^{\ast })\rightarrow H^{1}(Y,N_{\widetilde{Y}/\widetilde{V}}\otimes S^{n}N_{\widetilde{Y}/\widetilde{V}}^{\ast })$ is injective.◻
$(\unicode[STIX]{x1D70B}|_{\widetilde{Y}})^{\ast }:H^{1}(Y,N_{Y/X}\otimes S^{n}N_{Y/X}^{\ast })\rightarrow H^{1}(Y,N_{\widetilde{Y}/\widetilde{V}}\otimes S^{n}N_{\widetilde{Y}/\widetilde{V}}^{\ast })$ is injective.◻
5 Proof of Corollary 1.2
As  $D_{\unicode[STIX]{x1D706}}$’s intersect to each other transversally along
$D_{\unicode[STIX]{x1D706}}$’s intersect to each other transversally along  $C$, it follows that
$C$, it follows that  $N_{C/X}=\bigoplus _{\unicode[STIX]{x1D706}=1}^{n-1}N_{\unicode[STIX]{x1D706}}$ and
$N_{C/X}=\bigoplus _{\unicode[STIX]{x1D706}=1}^{n-1}N_{\unicode[STIX]{x1D706}}$ and  $N_{C/D_{1}}=\bigoplus _{\unicode[STIX]{x1D706}=2}^{n-1}N_{\unicode[STIX]{x1D706}}$, where
$N_{C/D_{1}}=\bigoplus _{\unicode[STIX]{x1D706}=2}^{n-1}N_{\unicode[STIX]{x1D706}}$, where  $N_{\unicode[STIX]{x1D706}}:=N_{D_{\unicode[STIX]{x1D706}}/X}|_{Y}$ for each
$N_{\unicode[STIX]{x1D706}}:=N_{D_{\unicode[STIX]{x1D706}}/X}|_{Y}$ for each  $\unicode[STIX]{x1D706}=1,2,\ldots ,n-1$. Note that each
$\unicode[STIX]{x1D706}=1,2,\ldots ,n-1$. Note that each  $N_{\unicode[STIX]{x1D706}}$ is isomorphic to
$N_{\unicode[STIX]{x1D706}}$ is isomorphic to  $L|_{C}$ and thus it is an element of
$L|_{C}$ and thus it is an element of  ${\mathcal{E}}_{1}^{(1)}(C)$. Thus, as
${\mathcal{E}}_{1}^{(1)}(C)$. Thus, as  $N_{C/X}\cong \oplus ^{r}L|_{C}\in {\mathcal{E}}_{1}^{(r)}(C)$ and
$N_{C/X}\cong \oplus ^{r}L|_{C}\in {\mathcal{E}}_{1}^{(r)}(C)$ and  $H^{1}(C,N_{\unicode[STIX]{x1D706}}\otimes N_{\unicode[STIX]{x1D6FC}}^{-1})\cong H^{1}(C,L|_{C}^{-|\unicode[STIX]{x1D6FC}|+1})=0$ hold, it follows that
$H^{1}(C,N_{\unicode[STIX]{x1D706}}\otimes N_{\unicode[STIX]{x1D6FC}}^{-1})\cong H^{1}(C,L|_{C}^{-|\unicode[STIX]{x1D6FC}|+1})=0$ hold, it follows that  $(X,S:=D_{1},Y:=C)$ satisfies the assumption of Theorem 1.1(ii). Therefore we obtain that the line bundle
$(X,S:=D_{1},Y:=C)$ satisfies the assumption of Theorem 1.1(ii). Therefore we obtain that the line bundle  $L=[D_{1}]$ admits a unitary flat metric
$L=[D_{1}]$ admits a unitary flat metric  $h_{V}$ on a neighborhood
$h_{V}$ on a neighborhood  $V$ of
$V$ of  $C$ (i.e.
$C$ (i.e.  $h_{V}$ is a
$h_{V}$ is a  $C^{\infty }$ Hermitian metric on
$C^{\infty }$ Hermitian metric on  $L|_{V}$ whose Chern curvature is
$L|_{V}$ whose Chern curvature is  $0$).
$0$).
On the other hand,  $L$ admits a singular Hermitian metric
$L$ admits a singular Hermitian metric  $h_{\text{sing}}$ such that
$h_{\text{sing}}$ such that  $h_{\text{sing}}|_{X\setminus C}$ is a
$h_{\text{sing}}|_{X\setminus C}$ is a  $C^{\infty }$ Hermitian metric on
$C^{\infty }$ Hermitian metric on  $L|_{X\setminus C}$,
$L|_{X\setminus C}$,  $h_{\text{sing}}\rightarrow \infty$ holds when a point approaches to
$h_{\text{sing}}\rightarrow \infty$ holds when a point approaches to  $C$, and that Chern curvature current of
$C$, and that Chern curvature current of  $h_{\text{sing}}$ is semipositive. Indeed, the Bergman type singular Hermitian metric
$h_{\text{sing}}$ is semipositive. Indeed, the Bergman type singular Hermitian metric  $h_{\text{sing}}:=(\sum _{\unicode[STIX]{x1D706}=1}^{n-1}h_{\unicode[STIX]{x1D706}}^{-1})^{-1}$ satisfies these properties, where
$h_{\text{sing}}:=(\sum _{\unicode[STIX]{x1D706}=1}^{n-1}h_{\unicode[STIX]{x1D706}}^{-1})^{-1}$ satisfies these properties, where  $h_{\unicode[STIX]{x1D706}}$ is a singular Hermitian metric on
$h_{\unicode[STIX]{x1D706}}$ is a singular Hermitian metric on  $L$ with
$L$ with  $|f_{\unicode[STIX]{x1D706}}|_{h_{\unicode[STIX]{x1D706}}}^{2}\equiv 1$ for a section
$|f_{\unicode[STIX]{x1D706}}|_{h_{\unicode[STIX]{x1D706}}}^{2}\equiv 1$ for a section  $f_{\unicode[STIX]{x1D706}}\in H^{0}(X,L)$ with
$f_{\unicode[STIX]{x1D706}}\in H^{0}(X,L)$ with  $\text{div}(f_{\unicode[STIX]{x1D706}})=D_{\unicode[STIX]{x1D706}}$.
$\text{div}(f_{\unicode[STIX]{x1D706}})=D_{\unicode[STIX]{x1D706}}$.
A  $C^{\infty }$ Hermitian metric
$C^{\infty }$ Hermitian metric  $h$ on
$h$ on  $L$ with semipositive curvature can be constructed by using the regularized minimum construction for these two metrics
$L$ with semipositive curvature can be constructed by using the regularized minimum construction for these two metrics  $h_{V}$ and
$h_{V}$ and  $h_{\text{sing}}$, which is the same construction as we used for proving [Reference KoikeK1, Corollary 3.4].
$h_{\text{sing}}$, which is the same construction as we used for proving [Reference KoikeK1, Corollary 3.4].
In what follows, we explain the detail of the regularized minimum construction. Take a positive constant  $\unicode[STIX]{x1D700}$ and a
$\unicode[STIX]{x1D700}$ and a  $C^{\infty }$ nonnegative function
$C^{\infty }$ nonnegative function  $\unicode[STIX]{x1D703}:\mathbb{R}\rightarrow \mathbb{R}_{{\geqslant}0}$ with support in the interval
$\unicode[STIX]{x1D703}:\mathbb{R}\rightarrow \mathbb{R}_{{\geqslant}0}$ with support in the interval  $[-1,1]$ such that
$[-1,1]$ such that  $\int _{\mathbb{R}}\unicode[STIX]{x1D703}(t)\,dt=1$ and
$\int _{\mathbb{R}}\unicode[STIX]{x1D703}(t)\,dt=1$ and  $\int _{\mathbb{R}}t\unicode[STIX]{x1D703}(t)\,dt=0$ hold. Define a function
$\int _{\mathbb{R}}t\unicode[STIX]{x1D703}(t)\,dt=0$ hold. Define a function  $M:\mathbb{R}^{2}\rightarrow \mathbb{R}$ (“a regularized max function,” see also [Reference DemaillyD1, Section 5.E]) by
$M:\mathbb{R}^{2}\rightarrow \mathbb{R}$ (“a regularized max function,” see also [Reference DemaillyD1, Section 5.E]) by
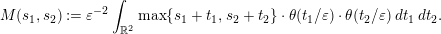 $$\begin{eqnarray}M(s_{1},s_{2}):=\unicode[STIX]{x1D700}^{-2}\int _{\mathbb{R}^{2}}\max \{s_{1}+t_{1},s_{2}+t_{2}\}\cdot \unicode[STIX]{x1D703}(t_{1}/\unicode[STIX]{x1D700})\cdot \unicode[STIX]{x1D703}(t_{2}/\unicode[STIX]{x1D700})\,dt_{1}\,dt_{2}.\end{eqnarray}$$
$$\begin{eqnarray}M(s_{1},s_{2}):=\unicode[STIX]{x1D700}^{-2}\int _{\mathbb{R}^{2}}\max \{s_{1}+t_{1},s_{2}+t_{2}\}\cdot \unicode[STIX]{x1D703}(t_{1}/\unicode[STIX]{x1D700})\cdot \unicode[STIX]{x1D703}(t_{2}/\unicode[STIX]{x1D700})\,dt_{1}\,dt_{2}.\end{eqnarray}$$ Then it is easily checked that this function is nondecreasing in all variables,  $C^{\infty }$ convex on
$C^{\infty }$ convex on  $\mathbb{R}^{2}$, and that
$\mathbb{R}^{2}$, and that  $M(s_{1},s_{2})=\max \{s_{1},s_{2}\}$ holds if
$M(s_{1},s_{2})=\max \{s_{1},s_{2}\}$ holds if  $|s_{1}-s_{2}|>2\unicode[STIX]{x1D700}$. Fix a relatively compact open neighborhood
$|s_{1}-s_{2}|>2\unicode[STIX]{x1D700}$. Fix a relatively compact open neighborhood  $V_{0}$ of
$V_{0}$ of  $C$ in
$C$ in  $V$, and an open covering
$V$, and an open covering  $\{W_{j}\}$ of
$\{W_{j}\}$ of  $X$. By fixing a local trivialization of
$X$. By fixing a local trivialization of  $L$ on each
$L$ on each  $W_{j}$, we can regard the metrics
$W_{j}$, we can regard the metrics  $h_{V}$ and
$h_{V}$ and  $h_{\text{sing}}$ restricted to
$h_{\text{sing}}$ restricted to  $W_{j}\cap V$ and
$W_{j}\cap V$ and  $W_{j}$ as nonnegative functions, say
$W_{j}$ as nonnegative functions, say  $e^{-\unicode[STIX]{x1D711}_{V,j}}$ and
$e^{-\unicode[STIX]{x1D711}_{V,j}}$ and  $e^{-\unicode[STIX]{x1D711}_{\text{sing},j}}$, respectively. Note that
$e^{-\unicode[STIX]{x1D711}_{\text{sing},j}}$, respectively. Note that  $\unicode[STIX]{x1D711}_{V,j}$ is pluriharmonic (and thus it is
$\unicode[STIX]{x1D711}_{V,j}$ is pluriharmonic (and thus it is  $C^{\infty }$ psh) function on
$C^{\infty }$ psh) function on  $W_{j}\cap V$, and that
$W_{j}\cap V$, and that  $\unicode[STIX]{x1D711}_{\text{sing},j}$ is a psh function which is
$\unicode[STIX]{x1D711}_{\text{sing},j}$ is a psh function which is  $C^{\infty }$ on
$C^{\infty }$ on  $W_{j}\setminus C$ and
$W_{j}\setminus C$ and  $\unicode[STIX]{x1D711}_{\text{sing},j}(p)\rightarrow -\infty$ holds as
$\unicode[STIX]{x1D711}_{\text{sing},j}(p)\rightarrow -\infty$ holds as  $p\rightarrow C$. By the compactness of
$p\rightarrow C$. By the compactness of  $\overline{V}\setminus V_{0}$, it holds for sufficiently large number
$\overline{V}\setminus V_{0}$, it holds for sufficiently large number  $N$ that
$N$ that  $\unicode[STIX]{x1D711}_{V,j}(p)+2\unicode[STIX]{x1D700}-N<\unicode[STIX]{x1D711}_{\text{sing},j}(p)$ for all
$\unicode[STIX]{x1D711}_{V,j}(p)+2\unicode[STIX]{x1D700}-N<\unicode[STIX]{x1D711}_{\text{sing},j}(p)$ for all  $j$ and for all
$j$ and for all  $p\in W_{j}\cap (\overline{V}\setminus V_{0})$. For such a number
$p\in W_{j}\cap (\overline{V}\setminus V_{0})$. For such a number  $N$, one can easily see that the function
$N$, one can easily see that the function  $\unicode[STIX]{x1D711}_{j}$ defined by
$\unicode[STIX]{x1D711}_{j}$ defined by
 $$\begin{eqnarray}\unicode[STIX]{x1D711}_{j}(p):=\left\{\begin{array}{@{}ll@{}}M(\unicode[STIX]{x1D711}_{V,j}(p)-N,\unicode[STIX]{x1D711}_{\text{sing},j}(p))\quad & (p\in V)\\ \unicode[STIX]{x1D711}_{\text{sing},j}(p)\quad & (p\in X\setminus \overline{V})\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D711}_{j}(p):=\left\{\begin{array}{@{}ll@{}}M(\unicode[STIX]{x1D711}_{V,j}(p)-N,\unicode[STIX]{x1D711}_{\text{sing},j}(p))\quad & (p\in V)\\ \unicode[STIX]{x1D711}_{\text{sing},j}(p)\quad & (p\in X\setminus \overline{V})\end{array}\right.\end{eqnarray}$$ is a well-defined  $C^{\infty }$ psh function on
$C^{\infty }$ psh function on  $W_{j}$ (here we used the properties of the function
$W_{j}$ (here we used the properties of the function  $M$ we mentioned above). A
$M$ we mentioned above). A  $C^{\infty }$ Hermitian metric
$C^{\infty }$ Hermitian metric  $h$ on
$h$ on  $L$ with semipositive curvature can be defined by
$L$ with semipositive curvature can be defined by  $e^{-\unicode[STIX]{x1D711}_{j}}$ on each
$e^{-\unicode[STIX]{x1D711}_{j}}$ on each  $W_{j}$.
$W_{j}$.
6 Examples
6.1 Deformation spaces of projective manifolds
Let  $B$ be a domain of
$B$ be a domain of  $\mathbb{C}^{r}$ which includes the origin and
$\mathbb{C}^{r}$ which includes the origin and  $\unicode[STIX]{x1D70B}:X\rightarrow B$ be a deformation of projective manifolds: i.e.
$\unicode[STIX]{x1D70B}:X\rightarrow B$ be a deformation of projective manifolds: i.e.  $X$ is a holomorphic manifold of dimension
$X$ is a holomorphic manifold of dimension  $n+r$ and
$n+r$ and  $\unicode[STIX]{x1D70B}$ is a proper holomorphic surjective submersion whose fiber
$\unicode[STIX]{x1D70B}$ is a proper holomorphic surjective submersion whose fiber  $\unicode[STIX]{x1D70B}^{-1}(x)$ is a projective manifold of dimension
$\unicode[STIX]{x1D70B}^{-1}(x)$ is a projective manifold of dimension  $n$ for each
$n$ for each  $x\in X$. Denote by
$x\in X$. Denote by  $Y$ the central fiber
$Y$ the central fiber  $\unicode[STIX]{x1D70B}^{-1}(0)$. Let us assume that
$\unicode[STIX]{x1D70B}^{-1}(0)$. Let us assume that  $Y$ is a smooth fiber for simplicity. In this case,
$Y$ is a smooth fiber for simplicity. In this case,  $N_{Y/X}$ is holomorphically trivial.
$N_{Y/X}$ is holomorphically trivial.
Take a coordinate  $x=(x^{1},x^{2},\ldots ,x^{r})$ of
$x=(x^{1},x^{2},\ldots ,x^{r})$ of  $\mathbb{C}^{r}$. Then, by considering a global defining functions system
$\mathbb{C}^{r}$. Then, by considering a global defining functions system  $w:=\{w^{\unicode[STIX]{x1D706}}:=\unicode[STIX]{x1D70B}^{\ast }x^{\unicode[STIX]{x1D706}}\}$ of
$w:=\{w^{\unicode[STIX]{x1D706}}:=\unicode[STIX]{x1D70B}^{\ast }x^{\unicode[STIX]{x1D706}}\}$ of  $Y$, it is easily seen that the pair
$Y$, it is easily seen that the pair  $(Y,X)$ is of infinite type. In this case, Theorem 1.1(i) is easily checked. Indeed, the foliation
$(Y,X)$ is of infinite type. In this case, Theorem 1.1(i) is easily checked. Indeed, the foliation  ${\mathcal{F}}$ in this case is the one which is induced by the fibration
${\mathcal{F}}$ in this case is the one which is induced by the fibration  $\unicode[STIX]{x1D70B}$. In what follows, we give a simple proof of Theorem 1.1(ii) for this fundamental example.
$\unicode[STIX]{x1D70B}$. In what follows, we give a simple proof of Theorem 1.1(ii) for this fundamental example.
Let  $S\subset X$ be a nonsingular hypersurface such that
$S\subset X$ be a nonsingular hypersurface such that  $Y\subset S$ and
$Y\subset S$ and  $N_{Y/S}$ is unitary flat. Let us consider the line bundle
$N_{Y/S}$ is unitary flat. Let us consider the line bundle  $[S]$. It holds that
$[S]$. It holds that  $[S]|_{Y}=[S]|_{S}|_{Y}=N_{S/X}|_{Y}$. As we have already mentioned in Section 4.2, it follows from Remark 2.6 and the complete reducibility of the unitary representations that
$[S]|_{Y}=[S]|_{S}|_{Y}=N_{S/X}|_{Y}$. As we have already mentioned in Section 4.2, it follows from Remark 2.6 and the complete reducibility of the unitary representations that  $N_{S/X}|_{Y}$ is unitary flat line bundle. Therefore,
$N_{S/X}|_{Y}$ is unitary flat line bundle. Therefore,  $[S]|_{Y}$ is unitary flat and thus it is topologically trivial. As the first Chern class
$[S]|_{Y}$ is unitary flat and thus it is topologically trivial. As the first Chern class  $c_{1}([S]|_{\unicode[STIX]{x1D70B}^{-1}(x)})$ depends continuously on
$c_{1}([S]|_{\unicode[STIX]{x1D70B}^{-1}(x)})$ depends continuously on  $x$, it holds that
$x$, it holds that  $[S]|_{L}$ is also topologically trivial for each leaf
$[S]|_{L}$ is also topologically trivial for each leaf  $L$ of
$L$ of  ${\mathcal{F}}$. Assume that
${\mathcal{F}}$. Assume that  $L\not \subset S$. Then, as the divisor
$L\not \subset S$. Then, as the divisor  $S|_{L}$ is an effective divisor on a projective manifold such that the corresponding line bundle is topologically trivial, it follows that
$S|_{L}$ is an effective divisor on a projective manifold such that the corresponding line bundle is topologically trivial, it follows that  $S\cap L=\emptyset$. Therefore we obtain that
$S\cap L=\emptyset$. Therefore we obtain that  $S=\unicode[STIX]{x1D70B}^{-1}(\overline{S})$ holds, where
$S=\unicode[STIX]{x1D70B}^{-1}(\overline{S})$ holds, where  $\overline{S}:=\unicode[STIX]{x1D70B}(S)$. By shrinking
$\overline{S}:=\unicode[STIX]{x1D70B}(S)$. By shrinking  $B$ and choosing appropriate
$B$ and choosing appropriate  $x$, we may assume that
$x$, we may assume that  $\overline{S}=\{x=(x^{1},x^{2},\ldots ,x^{r})\in B\mid x^{1}=0\}$. Then we can construct the foliation
$\overline{S}=\{x=(x^{1},x^{2},\ldots ,x^{r})\in B\mid x^{1}=0\}$. Then we can construct the foliation  ${\mathcal{G}}_{S}$ as in Theorem 1.1(ii) by considering “
${\mathcal{G}}_{S}$ as in Theorem 1.1(ii) by considering “ $w^{1}=$(constant).”
$w^{1}=$(constant).”
6.2 Projective bundles
Let  $M$ be a compact complex manifold and
$M$ be a compact complex manifold and  $E$ be a holomorphic vector bundle on
$E$ be a holomorphic vector bundle on  $M$ of rank
$M$ of rank  $r+1$. Assume that there exists a subbundle
$r+1$. Assume that there exists a subbundle  $F\subset E$ of rank
$F\subset E$ of rank  $r$ such that
$r$ such that  $F$ is a unitary flat vector bundle and the quotient bundle
$F$ is a unitary flat vector bundle and the quotient bundle  $L:=E/F$ is the holomorphically trivial line bundle. In this subsection, we consider the projective bundle
$L:=E/F$ is the holomorphically trivial line bundle. In this subsection, we consider the projective bundle  $X:=\mathbb{P}(E)$ and the section
$X:=\mathbb{P}(E)$ and the section  $Y\subset X$ of
$Y\subset X$ of  $\unicode[STIX]{x1D70B}:X\rightarrow M$ defined by the natural map
$\unicode[STIX]{x1D70B}:X\rightarrow M$ defined by the natural map  $p:E\rightarrow L$, where we are regarding
$p:E\rightarrow L$, where we are regarding  $\mathbb{P}(E)$ as the relative hyperplane bundle.
$\mathbb{P}(E)$ as the relative hyperplane bundle.
Fix an open covering  $\{U_{j}\}$ of
$\{U_{j}\}$ of  $M$ and take a local frame
$M$ and take a local frame  $(e_{j}^{1},e_{j}^{2},\ldots ,e_{j}^{r})$ of
$(e_{j}^{1},e_{j}^{2},\ldots ,e_{j}^{r})$ of  $F$ with
$F$ with  $e_{j}^{\unicode[STIX]{x1D706}}=\sum _{\unicode[STIX]{x1D707}=1}^{r}(S_{jk}^{-1})_{\unicode[STIX]{x1D707}}^{\unicode[STIX]{x1D706}}\cdot e_{k}^{\unicode[STIX]{x1D707}}$, or equivalently,
$e_{j}^{\unicode[STIX]{x1D706}}=\sum _{\unicode[STIX]{x1D707}=1}^{r}(S_{jk}^{-1})_{\unicode[STIX]{x1D707}}^{\unicode[STIX]{x1D706}}\cdot e_{k}^{\unicode[STIX]{x1D707}}$, or equivalently,  $e_{j,\unicode[STIX]{x1D706}}^{\ast }=\sum _{\unicode[STIX]{x1D707}=1}^{r}(S_{jk})_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D707}}\cdot e_{k,\unicode[STIX]{x1D707}}^{\ast }$ on each
$e_{j,\unicode[STIX]{x1D706}}^{\ast }=\sum _{\unicode[STIX]{x1D707}=1}^{r}(S_{jk})_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D707}}\cdot e_{k,\unicode[STIX]{x1D707}}^{\ast }$ on each  $U_{jk}$ (
$U_{jk}$ ( $S_{jk}\in U(r)$). By extending these appropriately, we obtain a local frame
$S_{jk}\in U(r)$). By extending these appropriately, we obtain a local frame  $e_{j}=(e_{j}^{0},e_{j}^{1},\ldots ,e_{j}^{r})$ of
$e_{j}=(e_{j}^{0},e_{j}^{1},\ldots ,e_{j}^{r})$ of  $E$ with
$E$ with  $e_{j}^{\ast }=\widetilde{S}_{jk}e_{k}^{\ast }$ on each
$e_{j}^{\ast }=\widetilde{S}_{jk}e_{k}^{\ast }$ on each  $U_{jk}$, where
$U_{jk}$, where
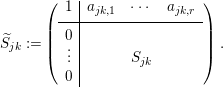
Here the function  $a_{jk,\unicode[STIX]{x1D706}}$ is a holomorphic function defined on
$a_{jk,\unicode[STIX]{x1D706}}$ is a holomorphic function defined on  $U_{jk}$ for each
$U_{jk}$ for each  $\unicode[STIX]{x1D706}$. Fix a neighborhood
$\unicode[STIX]{x1D706}$. Fix a neighborhood  $V_{j}$ of
$V_{j}$ of  $\unicode[STIX]{x1D70B}^{-1}(U_{j})\cap Y$ in
$\unicode[STIX]{x1D70B}^{-1}(U_{j})\cap Y$ in  $\unicode[STIX]{x1D70B}^{-1}(U_{j})$ and a coordinate
$\unicode[STIX]{x1D70B}^{-1}(U_{j})$ and a coordinate  $z_{j}$ of
$z_{j}$ of  $U_{j}$. For each
$U_{j}$. For each  $w_{j}=(w_{j}^{1},w_{j}^{2},\ldots ,w_{j}^{r})\in \mathbb{C}^{r}$, consider the map
$w_{j}=(w_{j}^{1},w_{j}^{2},\ldots ,w_{j}^{r})\in \mathbb{C}^{r}$, consider the map
 $$\begin{eqnarray}(z_{j},w_{j})\mapsto \biggl[e_{j,0}^{\ast }(z_{j})+\mathop{\sum }_{\unicode[STIX]{x1D706}=1}^{r}w_{j}^{\unicode[STIX]{x1D706}}\cdot e_{j,\unicode[STIX]{x1D706}}^{\ast }(z_{j})\biggr]\end{eqnarray}$$
$$\begin{eqnarray}(z_{j},w_{j})\mapsto \biggl[e_{j,0}^{\ast }(z_{j})+\mathop{\sum }_{\unicode[STIX]{x1D706}=1}^{r}w_{j}^{\unicode[STIX]{x1D706}}\cdot e_{j,\unicode[STIX]{x1D706}}^{\ast }(z_{j})\biggr]\end{eqnarray}$$ and regard  $(z_{j},w_{j})$ as a coordinates system of
$(z_{j},w_{j})$ as a coordinates system of  $V_{j}$ by this map. Then we obtain
$V_{j}$ by this map. Then we obtain
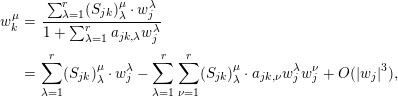 $$\begin{eqnarray}\displaystyle w_{k}^{\unicode[STIX]{x1D707}} & = & \displaystyle \frac{\mathop{\sum }_{\unicode[STIX]{x1D706}=1}^{r}(S_{jk})_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D707}}\cdot w_{j}^{\unicode[STIX]{x1D706}}}{1+\mathop{\sum }_{\unicode[STIX]{x1D706}=1}^{r}a_{jk,\unicode[STIX]{x1D706}}w_{j}^{\unicode[STIX]{x1D706}}}\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{\unicode[STIX]{x1D706}=1}^{r}(S_{jk})_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D707}}\cdot w_{j}^{\unicode[STIX]{x1D706}}-\mathop{\sum }_{\unicode[STIX]{x1D706}=1}^{r}\mathop{\sum }_{\unicode[STIX]{x1D708}=1}^{r}(S_{jk})_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D707}}\cdot a_{jk,\unicode[STIX]{x1D708}}w_{j}^{\unicode[STIX]{x1D706}}w_{j}^{\unicode[STIX]{x1D708}}+O(|w_{j}|^{3}),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle w_{k}^{\unicode[STIX]{x1D707}} & = & \displaystyle \frac{\mathop{\sum }_{\unicode[STIX]{x1D706}=1}^{r}(S_{jk})_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D707}}\cdot w_{j}^{\unicode[STIX]{x1D706}}}{1+\mathop{\sum }_{\unicode[STIX]{x1D706}=1}^{r}a_{jk,\unicode[STIX]{x1D706}}w_{j}^{\unicode[STIX]{x1D706}}}\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{\unicode[STIX]{x1D706}=1}^{r}(S_{jk})_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D707}}\cdot w_{j}^{\unicode[STIX]{x1D706}}-\mathop{\sum }_{\unicode[STIX]{x1D706}=1}^{r}\mathop{\sum }_{\unicode[STIX]{x1D708}=1}^{r}(S_{jk})_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D707}}\cdot a_{jk,\unicode[STIX]{x1D708}}w_{j}^{\unicode[STIX]{x1D706}}w_{j}^{\unicode[STIX]{x1D708}}+O(|w_{j}|^{3}),\nonumber\end{eqnarray}$$and thus
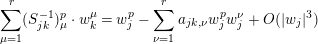 $$\begin{eqnarray}\displaystyle \mathop{\sum }_{\unicode[STIX]{x1D707}=1}^{r}(S_{jk}^{-1})_{\unicode[STIX]{x1D707}}^{p}\cdot w_{k}^{\unicode[STIX]{x1D707}}=w_{j}^{p}-\mathop{\sum }_{\unicode[STIX]{x1D708}=1}^{r}a_{jk,\unicode[STIX]{x1D708}}w_{j}^{p}w_{j}^{\unicode[STIX]{x1D708}}+O(|w_{j}|^{3}) & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathop{\sum }_{\unicode[STIX]{x1D707}=1}^{r}(S_{jk}^{-1})_{\unicode[STIX]{x1D707}}^{p}\cdot w_{k}^{\unicode[STIX]{x1D707}}=w_{j}^{p}-\mathop{\sum }_{\unicode[STIX]{x1D708}=1}^{r}a_{jk,\unicode[STIX]{x1D708}}w_{j}^{p}w_{j}^{\unicode[STIX]{x1D708}}+O(|w_{j}|^{3}) & & \displaystyle \nonumber\end{eqnarray}$$ on each  $V_{jk}$, which can be regarded as the expansion (1) for the local defining functions system
$V_{jk}$, which can be regarded as the expansion (1) for the local defining functions system  $\{w_{j}\}$ with the transition matrix
$\{w_{j}\}$ with the transition matrix  $T_{jk}:=S_{jk}^{-1}$ of
$T_{jk}:=S_{jk}^{-1}$ of  $N_{Y/X}$ (note that
$N_{Y/X}$ (note that  $N_{Y/X}^{\ast }\cong F$).
$N_{Y/X}^{\ast }\cong F$).
Set  $\unicode[STIX]{x1D700}_{j}:=dw_{j}$. Then it follows from the above expansion that the first obstruction class
$\unicode[STIX]{x1D700}_{j}:=dw_{j}$. Then it follows from the above expansion that the first obstruction class  $u_{1}(Y,X;\{w_{j}\})$ is defined by
$u_{1}(Y,X;\{w_{j}\})$ is defined by
 $$\begin{eqnarray}-\mathop{\sum }_{p=1}^{r}\mathop{\sum }_{\unicode[STIX]{x1D708}=1}^{r}a_{jk,\unicode[STIX]{x1D708}}\cdot \unicode[STIX]{x1D700}_{j,p}^{\ast }\otimes \unicode[STIX]{x1D700}_{j}^{p}\cdot \unicode[STIX]{x1D700}_{j}^{\unicode[STIX]{x1D708}}.\end{eqnarray}$$
$$\begin{eqnarray}-\mathop{\sum }_{p=1}^{r}\mathop{\sum }_{\unicode[STIX]{x1D708}=1}^{r}a_{jk,\unicode[STIX]{x1D708}}\cdot \unicode[STIX]{x1D700}_{j,p}^{\ast }\otimes \unicode[STIX]{x1D700}_{j}^{p}\cdot \unicode[STIX]{x1D700}_{j}^{\unicode[STIX]{x1D708}}.\end{eqnarray}$$ On the other hand, it follows from the arguments as in Lemma 4.2 that  $-\sum _{\unicode[STIX]{x1D708}=1}^{r}a_{jk,\unicode[STIX]{x1D708}}\cdot \unicode[STIX]{x1D700}_{j}^{\unicode[STIX]{x1D708}}$ can be regarded as the extension class
$-\sum _{\unicode[STIX]{x1D708}=1}^{r}a_{jk,\unicode[STIX]{x1D708}}\cdot \unicode[STIX]{x1D700}_{j}^{\unicode[STIX]{x1D708}}$ can be regarded as the extension class  $\unicode[STIX]{x1D6FF}(1)\in H^{1}(Y,N_{Y/X}^{\ast })(\cong H^{1}(M,L^{-1}\otimes F))$ of the short exact sequence
$\unicode[STIX]{x1D6FF}(1)\in H^{1}(Y,N_{Y/X}^{\ast })(\cong H^{1}(M,L^{-1}\otimes F))$ of the short exact sequence  $0\rightarrow F\rightarrow E\rightarrow L\rightarrow 0$. Thus we can conclude that
$0\rightarrow F\rightarrow E\rightarrow L\rightarrow 0$. Thus we can conclude that  $u_{1}(Y,X)$ is the image of
$u_{1}(Y,X)$ is the image of  $\text{id}_{N_{Y/X}}\otimes \unicode[STIX]{x1D6FF}(1)\in H^{1}(Y,\text{End}(N_{Y/X})\otimes N_{Y/X}^{\ast })\cong H^{1}(Y,N_{Y/X}\otimes N_{Y/X}^{\ast }\otimes N_{Y/X}^{\ast })$ by the map
$\text{id}_{N_{Y/X}}\otimes \unicode[STIX]{x1D6FF}(1)\in H^{1}(Y,\text{End}(N_{Y/X})\otimes N_{Y/X}^{\ast })\cong H^{1}(Y,N_{Y/X}\otimes N_{Y/X}^{\ast }\otimes N_{Y/X}^{\ast })$ by the map
 $$\begin{eqnarray}H^{1}(Y,N_{Y/X}\otimes N_{Y/X}^{\ast }\otimes N_{Y/X}^{\ast })\rightarrow H^{1}(Y,N_{Y/X}\otimes S^{2}N_{Y/X}^{\ast })\end{eqnarray}$$
$$\begin{eqnarray}H^{1}(Y,N_{Y/X}\otimes N_{Y/X}^{\ast }\otimes N_{Y/X}^{\ast })\rightarrow H^{1}(Y,N_{Y/X}\otimes S^{2}N_{Y/X}^{\ast })\end{eqnarray}$$ induced from the natural map  $N_{Y/X}^{\ast }\otimes N_{Y/X}^{\ast }\rightarrow S^{2}N_{Y/X}^{\ast }$. In what follows, we regard each section of
$N_{Y/X}^{\ast }\otimes N_{Y/X}^{\ast }\rightarrow S^{2}N_{Y/X}^{\ast }$. In what follows, we regard each section of  $S^{2}N_{Y/X}^{\ast }$ as a symmetric section of
$S^{2}N_{Y/X}^{\ast }$ as a symmetric section of  $N_{Y/X}^{\ast }\otimes N_{Y/X}^{\ast }$ and
$N_{Y/X}^{\ast }\otimes N_{Y/X}^{\ast }$ and  $S^{2}N_{Y/X}^{\ast }$ as a unitary flat subbundle of
$S^{2}N_{Y/X}^{\ast }$ as a unitary flat subbundle of  $N_{Y/X}^{\ast }\otimes N_{Y/X}^{\ast }$. Then the natural map
$N_{Y/X}^{\ast }\otimes N_{Y/X}^{\ast }$. Then the natural map  $N_{Y/X}^{\ast }\otimes N_{Y/X}^{\ast }\rightarrow S^{2}N_{Y/X}^{\ast }$ can be regarded as the map
$N_{Y/X}^{\ast }\otimes N_{Y/X}^{\ast }\rightarrow S^{2}N_{Y/X}^{\ast }$ can be regarded as the map  $\unicode[STIX]{x1D700}_{j}^{\unicode[STIX]{x1D707}}\otimes \unicode[STIX]{x1D700}_{j}^{\unicode[STIX]{x1D708}}\mapsto \text{Sym}(\unicode[STIX]{x1D700}_{j}^{\unicode[STIX]{x1D707}}\otimes \unicode[STIX]{x1D700}_{j}^{\unicode[STIX]{x1D708}}):=\frac{1}{2}(\unicode[STIX]{x1D700}_{j}^{\unicode[STIX]{x1D707}}\otimes \unicode[STIX]{x1D700}_{j}^{\unicode[STIX]{x1D708}}+\unicode[STIX]{x1D700}_{j}^{\unicode[STIX]{x1D708}}\otimes \unicode[STIX]{x1D700}_{j}^{\unicode[STIX]{x1D707}})$. By using this, it clearly holds that
$\unicode[STIX]{x1D700}_{j}^{\unicode[STIX]{x1D707}}\otimes \unicode[STIX]{x1D700}_{j}^{\unicode[STIX]{x1D708}}\mapsto \text{Sym}(\unicode[STIX]{x1D700}_{j}^{\unicode[STIX]{x1D707}}\otimes \unicode[STIX]{x1D700}_{j}^{\unicode[STIX]{x1D708}}):=\frac{1}{2}(\unicode[STIX]{x1D700}_{j}^{\unicode[STIX]{x1D707}}\otimes \unicode[STIX]{x1D700}_{j}^{\unicode[STIX]{x1D708}}+\unicode[STIX]{x1D700}_{j}^{\unicode[STIX]{x1D708}}\otimes \unicode[STIX]{x1D700}_{j}^{\unicode[STIX]{x1D707}})$. By using this, it clearly holds that  $u_{1}(Y,X)=0$ if and only if
$u_{1}(Y,X)=0$ if and only if  $s_{\ast }(\unicode[STIX]{x1D6FF}(1))=0\in H^{1}(Y,N_{Y/X}\otimes N_{Y/X}^{\ast }\otimes N_{Y/X}^{\ast })$ holds, where
$s_{\ast }(\unicode[STIX]{x1D6FF}(1))=0\in H^{1}(Y,N_{Y/X}\otimes N_{Y/X}^{\ast }\otimes N_{Y/X}^{\ast })$ holds, where  $s_{\ast }$ is the map induced from
$s_{\ast }$ is the map induced from
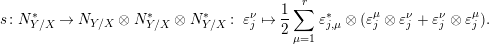 $$\begin{eqnarray}s:N_{Y/X}^{\ast }\rightarrow N_{Y/X}\otimes N_{Y/X}^{\ast }\otimes N_{Y/X}^{\ast }:~\unicode[STIX]{x1D700}_{j}^{\unicode[STIX]{x1D708}}\mapsto \frac{1}{2}\mathop{\sum }_{\unicode[STIX]{x1D707}=1}^{r}\unicode[STIX]{x1D700}_{j,\unicode[STIX]{x1D707}}^{\ast }\otimes (\unicode[STIX]{x1D700}_{j}^{\unicode[STIX]{x1D707}}\otimes \unicode[STIX]{x1D700}_{j}^{\unicode[STIX]{x1D708}}+\unicode[STIX]{x1D700}_{j}^{\unicode[STIX]{x1D708}}\otimes \unicode[STIX]{x1D700}_{j}^{\unicode[STIX]{x1D707}}).\end{eqnarray}$$
$$\begin{eqnarray}s:N_{Y/X}^{\ast }\rightarrow N_{Y/X}\otimes N_{Y/X}^{\ast }\otimes N_{Y/X}^{\ast }:~\unicode[STIX]{x1D700}_{j}^{\unicode[STIX]{x1D708}}\mapsto \frac{1}{2}\mathop{\sum }_{\unicode[STIX]{x1D707}=1}^{r}\unicode[STIX]{x1D700}_{j,\unicode[STIX]{x1D707}}^{\ast }\otimes (\unicode[STIX]{x1D700}_{j}^{\unicode[STIX]{x1D707}}\otimes \unicode[STIX]{x1D700}_{j}^{\unicode[STIX]{x1D708}}+\unicode[STIX]{x1D700}_{j}^{\unicode[STIX]{x1D708}}\otimes \unicode[STIX]{x1D700}_{j}^{\unicode[STIX]{x1D707}}).\end{eqnarray}$$ As we can regard  $N_{Y/X}^{\ast }$ as a unitary flat subbundle (and thus a direct component by the complete reducibility of the unitary representation) of
$N_{Y/X}^{\ast }$ as a unitary flat subbundle (and thus a direct component by the complete reducibility of the unitary representation) of  $N_{Y/X}\otimes N_{Y/X}^{\ast }\otimes N_{Y/X}^{\ast }$ via
$N_{Y/X}\otimes N_{Y/X}^{\ast }\otimes N_{Y/X}^{\ast }$ via  $s$, we can conclude that
$s$, we can conclude that  $u_{1}(Y,X)=0$ holds if and only if
$u_{1}(Y,X)=0$ holds if and only if  $\unicode[STIX]{x1D6FF}(1)=0$ holds, or equivalently,
$\unicode[STIX]{x1D6FF}(1)=0$ holds, or equivalently,  $0\rightarrow F\rightarrow E\rightarrow L\rightarrow 0$ splits.
$0\rightarrow F\rightarrow E\rightarrow L\rightarrow 0$ splits.
Therefore, it holds that the pair  $(Y,X)$ is of type
$(Y,X)$ is of type  $1$ if
$1$ if  $0\rightarrow F\rightarrow E\rightarrow L\rightarrow 0$ does not split. When
$0\rightarrow F\rightarrow E\rightarrow L\rightarrow 0$ does not split. When  $0\rightarrow F\rightarrow E\rightarrow L\rightarrow 0$ splits, it can be easily seen that
$0\rightarrow F\rightarrow E\rightarrow L\rightarrow 0$ splits, it can be easily seen that  $T_{jk}w_{k}=w_{j}$ holds on each
$T_{jk}w_{k}=w_{j}$ holds on each  $V_{jk}$, which shows that the pair
$V_{jk}$, which shows that the pair  $(Y,X)$ is of infinite type in this case.
$(Y,X)$ is of infinite type in this case.
6.3 The blow-up of a del Pezzo manifold at a general point (Proof of Corollary 1.3)
Let  $(V,L)$ be a del Pezzo manifold of degree
$(V,L)$ be a del Pezzo manifold of degree  $1$: i.e.
$1$: i.e.  $V$ is a projective manifold of dimension
$V$ is a projective manifold of dimension  $n$ and
$n$ and  $L$ is an ample line bundle on
$L$ is an ample line bundle on  $V$ with
$V$ with  $K_{V}^{-1}\cong L^{n-1}$ and the self-intersection number
$K_{V}^{-1}\cong L^{n-1}$ and the self-intersection number  $(L^{n})$ is equal to
$(L^{n})$ is equal to  $1$. From [Reference FujitaF, 6.4], it holds that
$1$. From [Reference FujitaF, 6.4], it holds that  $\text{dim}\,H^{0}(V,L)=n$. Take general elements
$\text{dim}\,H^{0}(V,L)=n$. Take general elements  $D_{1},D_{2},\ldots ,D_{n}\in |L|$. By [Reference FujitaF, 4.2] and
$D_{1},D_{2},\ldots ,D_{n}\in |L|$. By [Reference FujitaF, 4.2] and  $(D_{1},D_{2},\ldots ,D_{n})=(L^{n})=1$, it holds that the intersection
$(D_{1},D_{2},\ldots ,D_{n})=(L^{n})=1$, it holds that the intersection  $\bigcap _{\unicode[STIX]{x1D706}=1}^{n}D_{\unicode[STIX]{x1D706}}$ is a point, which we denote by
$\bigcap _{\unicode[STIX]{x1D706}=1}^{n}D_{\unicode[STIX]{x1D706}}$ is a point, which we denote by  $p$. It is clear that
$p$. It is clear that  $D_{\unicode[STIX]{x1D706}}$’s intersect each other transversally at
$D_{\unicode[STIX]{x1D706}}$’s intersect each other transversally at  $p$. From this fact and Bertini’s theorem, we may assume that each
$p$. From this fact and Bertini’s theorem, we may assume that each  $D_{\unicode[STIX]{x1D706}}$ is nonsingular.
$D_{\unicode[STIX]{x1D706}}$ is nonsingular.
Consider a sequence of the subvarieties  $V_{n}:=V,V_{n-1}:=D_{1},V_{n-2}:=D_{1}\cap D_{2},\ldots ,V_{1}:=D_{1}\cap D_{2}\ldots ,\cap D_{n-1}$. Denote by
$V_{n}:=V,V_{n-1}:=D_{1},V_{n-2}:=D_{1}\cap D_{2},\ldots ,V_{1}:=D_{1}\cap D_{2}\ldots ,\cap D_{n-1}$. Denote by  $L_{\unicode[STIX]{x1D706}}$ the restriction
$L_{\unicode[STIX]{x1D706}}$ the restriction  $L|_{V_{\unicode[STIX]{x1D706}}}$ for each
$L|_{V_{\unicode[STIX]{x1D706}}}$ for each  $\unicode[STIX]{x1D706}=1,2,\ldots ,n-1$. Note that it follows from a simple inductive argument that
$\unicode[STIX]{x1D706}=1,2,\ldots ,n-1$. Note that it follows from a simple inductive argument that  $(V_{\unicode[STIX]{x1D706}},L_{\unicode[STIX]{x1D706}})$ is also a del Pezzo manifold of degree
$(V_{\unicode[STIX]{x1D706}},L_{\unicode[STIX]{x1D706}})$ is also a del Pezzo manifold of degree  $1$ for each
$1$ for each  $\unicode[STIX]{x1D706}$. Especially, for
$\unicode[STIX]{x1D706}$. Especially, for  $\unicode[STIX]{x1D706}=1$, it holds that
$\unicode[STIX]{x1D706}=1$, it holds that  $V_{1}$ is an elliptic curve and
$V_{1}$ is an elliptic curve and  $\text{deg}\,L_{1}=1$. Take
$\text{deg}\,L_{1}=1$. Take  $q\in V_{1}$ and denote by
$q\in V_{1}$ and denote by  $\unicode[STIX]{x1D70B}:X\rightarrow V$ the blow-up at
$\unicode[STIX]{x1D70B}:X\rightarrow V$ the blow-up at  $q$. Let us denote by
$q$. Let us denote by  $E$ the exceptional divisor, by
$E$ the exceptional divisor, by  $\widetilde{D}_{\unicode[STIX]{x1D706}}$ the strict transform
$\widetilde{D}_{\unicode[STIX]{x1D706}}$ the strict transform  $(\unicode[STIX]{x1D70B}^{-1})_{\ast }D_{\unicode[STIX]{x1D706}}$, and by
$(\unicode[STIX]{x1D70B}^{-1})_{\ast }D_{\unicode[STIX]{x1D706}}$, and by  $Y$ the strict transform
$Y$ the strict transform  $(\unicode[STIX]{x1D70B}^{-1})_{\ast }V_{1}$. Then it is clear that
$(\unicode[STIX]{x1D70B}^{-1})_{\ast }V_{1}$. Then it is clear that  $\widetilde{D}_{1},\widetilde{D}_{2},\ldots ,\widetilde{D}_{n-1}\in |\widetilde{L}|$, where
$\widetilde{D}_{1},\widetilde{D}_{2},\ldots ,\widetilde{D}_{n-1}\in |\widetilde{L}|$, where  $\widetilde{L}:=\unicode[STIX]{x1D70B}^{\ast }L\otimes {\mathcal{O}}_{X}(-E)$, and that
$\widetilde{L}:=\unicode[STIX]{x1D70B}^{\ast }L\otimes {\mathcal{O}}_{X}(-E)$, and that  $\widetilde{D}_{\unicode[STIX]{x1D706}}$’s intersect each other transversally along
$\widetilde{D}_{\unicode[STIX]{x1D706}}$’s intersect each other transversally along  $Y$. Thus we can apply Corollary 1.2 to this example to obtain Corollary 1.3.
$Y$. Thus we can apply Corollary 1.2 to this example to obtain Corollary 1.3.
6.4 An example of an infinite type pair which does not admit  ${\mathcal{F}}$ as in Theorem 1.1
${\mathcal{F}}$ as in Theorem 1.1
In [Reference UedaU, Section 5.4], Ueda constructed a pair  $(C,S)$ of a surface
$(C,S)$ of a surface  $S$ and a compact curve
$S$ and a compact curve  $C$ of genus
$C$ of genus  $g\geqslant 1$ embedded in
$g\geqslant 1$ embedded in  $S$ with unitary flat normal bundle such that
$S$ with unitary flat normal bundle such that  $(C,S)$ is infinite type, however there does not exist a foliation
$(C,S)$ is infinite type, however there does not exist a foliation  ${\mathcal{F}}$ as in Theorem 1.1. Here we will construct such a pair for the case where the codimension
${\mathcal{F}}$ as in Theorem 1.1. Here we will construct such a pair for the case where the codimension  $r$ is greater than
$r$ is greater than  $1$.
$1$.
Let  $(C,S)$ be as above with
$(C,S)$ be as above with  $g=1$. By shrinking
$g=1$. By shrinking  $S$ to a tubular neighborhood of
$S$ to a tubular neighborhood of  $C$ if necessary, we may assume
$C$ if necessary, we may assume  $\unicode[STIX]{x1D70B}_{1}(C,\ast )\cong \unicode[STIX]{x1D70B}_{1}(S,\ast )$. Denote by
$\unicode[STIX]{x1D70B}_{1}(C,\ast )\cong \unicode[STIX]{x1D70B}_{1}(S,\ast )$. Denote by  $\unicode[STIX]{x1D70C}:=\unicode[STIX]{x1D70C}_{N_{C/S}}$ the unitary representation of
$\unicode[STIX]{x1D70C}:=\unicode[STIX]{x1D70C}_{N_{C/S}}$ the unitary representation of  $\unicode[STIX]{x1D70B}_{1}(C,\ast )$ corresponding to the unitary flat line bundle
$\unicode[STIX]{x1D70B}_{1}(C,\ast )$ corresponding to the unitary flat line bundle  $N_{C/S}$ and by
$N_{C/S}$ and by  $\widetilde{S}\rightarrow S$ the universal covering of
$\widetilde{S}\rightarrow S$ the universal covering of  $S$. Set
$S$. Set  $X:=\widetilde{S}\times \mathbb{C}^{r-1}/\sim$, where
$X:=\widetilde{S}\times \mathbb{C}^{r-1}/\sim$, where  ${\sim}$ is the relation defined by
${\sim}$ is the relation defined by
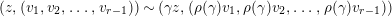 $$\begin{eqnarray}(z,(v_{1},v_{2},\ldots ,v_{r-1}))\sim (\unicode[STIX]{x1D6FE}z,(\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE})v_{1},\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE})v_{2},\ldots ,\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE})v_{r-1}))\end{eqnarray}$$
$$\begin{eqnarray}(z,(v_{1},v_{2},\ldots ,v_{r-1}))\sim (\unicode[STIX]{x1D6FE}z,(\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE})v_{1},\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE})v_{2},\ldots ,\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE})v_{r-1}))\end{eqnarray}$$ for each  $(z,(v_{1},v_{2},\ldots ,v_{r-1}))\in \widetilde{S}\times \mathbb{C}^{r-1}$ and
$(z,(v_{1},v_{2},\ldots ,v_{r-1}))\in \widetilde{S}\times \mathbb{C}^{r-1}$ and  $\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D70B}_{1}(S,\ast )$. We denote by
$\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D70B}_{1}(S,\ast )$. We denote by  $Z$ the submanifold
$Z$ the submanifold  $\widetilde{S}\times \{(0,0,\ldots ,0)\}/\sim$ of
$\widetilde{S}\times \{(0,0,\ldots ,0)\}/\sim$ of  $X$ and by
$X$ and by  $Y$ the submanifold
$Y$ the submanifold  $\widetilde{C}\times \{(0,0,\ldots ,0)\}/\sim$ of
$\widetilde{C}\times \{(0,0,\ldots ,0)\}/\sim$ of  $Z$, where
$Z$, where  $\widetilde{C}\subset \widetilde{S}$ is the universal covering of
$\widetilde{C}\subset \widetilde{S}$ is the universal covering of  $C$. Note that
$C$. Note that  $(Y,Z)$ is naturally isomorphic to
$(Y,Z)$ is naturally isomorphic to  $(C,S)$. As
$(C,S)$. As  $N_{Y/X}\cong N_{C/S}^{\oplus r}$ holds and
$N_{Y/X}\cong N_{C/S}^{\oplus r}$ holds and  $N_{C/S}$ is nontorsion,
$N_{C/S}$ is nontorsion,  $H^{1}(Y,N_{Y/X}\otimes S^{n}N_{Y/X}^{\ast })=0$ holds for each
$H^{1}(Y,N_{Y/X}\otimes S^{n}N_{Y/X}^{\ast })=0$ holds for each  $n\geqslant 2$. Therefore we obtain that
$n\geqslant 2$. Therefore we obtain that  $(Y,X)$ is of infinite type.
$(Y,X)$ is of infinite type.
Assume that there exists a local defining functions system  $\{(V_{j},w_{j})\}$ of
$\{(V_{j},w_{j})\}$ of  $Y$ with
$Y$ with  $w_{j}=T_{jk}w_{k}$ on each
$w_{j}=T_{jk}w_{k}$ on each  $V_{jk}$ (
$V_{jk}$ ( $T_{jk}\in U(r)$), where
$T_{jk}\in U(r)$), where  $\{V_{j}\}$ is as in Section 2.2. Take a local frame
$\{V_{j}\}$ is as in Section 2.2. Take a local frame  $\{e_{j}\}$ of
$\{e_{j}\}$ of  $N_{Y/X}^{\ast }$ such that
$N_{Y/X}^{\ast }$ such that  $e_{j}=t_{jk}e_{k}$ on each
$e_{j}=t_{jk}e_{k}$ on each  $U_{jk}(=Y\cap V_{jk})$, where
$U_{jk}(=Y\cap V_{jk})$, where  $t_{jk}\in U(1)$ is a transition function for some local frames of
$t_{jk}\in U(1)$ is a transition function for some local frames of  $N_{C/S}^{\ast }$. Let
$N_{C/S}^{\ast }$. Let  $A_{j}:U_{j}\rightarrow \text{GL}_{r}(\mathbb{C})$ be a holomorphic function defined by
$A_{j}:U_{j}\rightarrow \text{GL}_{r}(\mathbb{C})$ be a holomorphic function defined by  $e_{j}=A_{j}\cdot dw_{j}|_{U_{j}}$. By considering
$e_{j}=A_{j}\cdot dw_{j}|_{U_{j}}$. By considering  $\{(U_{j},A_{j})\}$ as a global section of the vector bundle
$\{(U_{j},A_{j})\}$ as a global section of the vector bundle  $\text{End}\,(N_{Y/X}^{\ast })$, it follows from Lemma 2.1 that each
$\text{End}\,(N_{Y/X}^{\ast })$, it follows from Lemma 2.1 that each  $A_{j}$ is a constant function (see also [Reference SeshadriSe, Section 1, Proposition 1]). Thus, by replacing
$A_{j}$ is a constant function (see also [Reference SeshadriSe, Section 1, Proposition 1]). Thus, by replacing  $w_{j}$ with
$w_{j}$ with  $A_{j}\cdot w_{j}$, we may assume that
$A_{j}\cdot w_{j}$, we may assume that  $T_{jk}=\text{diag}\,(t_{jk},t_{jk},\ldots ,t_{jk})$. For a fixed index
$T_{jk}=\text{diag}\,(t_{jk},t_{jk},\ldots ,t_{jk})$. For a fixed index  $j_{0}$, it is clear that
$j_{0}$, it is clear that  $w_{j_{0}}^{\unicode[STIX]{x1D706}}|_{V_{j_{0}}\cap Z}\not \equiv 0$ for some
$w_{j_{0}}^{\unicode[STIX]{x1D706}}|_{V_{j_{0}}\cap Z}\not \equiv 0$ for some  $\unicode[STIX]{x1D706}$. Without loss of generality, we may assume
$\unicode[STIX]{x1D706}$. Without loss of generality, we may assume  $\unicode[STIX]{x1D706}=1$. Set
$\unicode[STIX]{x1D706}=1$. Set  $f_{j}:=w_{j}^{1}|_{V_{j}\cap Z}$ for each
$f_{j}:=w_{j}^{1}|_{V_{j}\cap Z}$ for each  $j$. Then, as
$j$. Then, as  $f_{j}=t_{jk}f_{k}$ on each
$f_{j}=t_{jk}f_{k}$ on each  $V_{jk}\cap Z$ and
$V_{jk}\cap Z$ and  $f_{j_{0}}\not \equiv 0$, we obtain that
$f_{j_{0}}\not \equiv 0$, we obtain that  $f_{j}\not \equiv 0$ for any
$f_{j}\not \equiv 0$ for any  $j$ and that the divisors
$j$ and that the divisors  $\text{div}(f_{j})$ glue up to define a divisor
$\text{div}(f_{j})$ glue up to define a divisor  $D$ of
$D$ of  $V\cap Z$ (
$V\cap Z$ ( $V=\cup _{j}V_{j}$). Let
$V=\cup _{j}V_{j}$). Let  $D=aY+\sum _{\unicode[STIX]{x1D708}=1}^{\ell }b_{\unicode[STIX]{x1D708}}W_{\unicode[STIX]{x1D708}}$ be the irreducible decomposition of
$D=aY+\sum _{\unicode[STIX]{x1D708}=1}^{\ell }b_{\unicode[STIX]{x1D708}}W_{\unicode[STIX]{x1D708}}$ be the irreducible decomposition of  $D$ (
$D$ ( $a,b_{\unicode[STIX]{x1D708}}>0$, note that we may assume
$a,b_{\unicode[STIX]{x1D708}}>0$, note that we may assume  $\ell <\infty$ by shrinking
$\ell <\infty$ by shrinking  $V$ if necessary). As the line bundle
$V$ if necessary). As the line bundle  $[D]$ is unitary flat, the intersection number
$[D]$ is unitary flat, the intersection number  $(D,Y)$ can be computed as follows:
$(D,Y)$ can be computed as follows:  $(D,Y)=\text{deg}\,[D]|_{Y}=0$. The self-intersection number
$(D,Y)=\text{deg}\,[D]|_{Y}=0$. The self-intersection number  $(Y,Y)$ is also equal to
$(Y,Y)$ is also equal to  $0$, since
$0$, since  $(Y,Y)=\text{deg}\,N_{Y/Z}=\text{deg}\,N_{C/S}$. Therefore it holds that
$(Y,Y)=\text{deg}\,N_{Y/Z}=\text{deg}\,N_{C/S}$. Therefore it holds that  $(W_{\unicode[STIX]{x1D708}},Y)=0$ for each
$(W_{\unicode[STIX]{x1D708}},Y)=0$ for each  $\unicode[STIX]{x1D708}$, which means that we may assume that
$\unicode[STIX]{x1D708}$, which means that we may assume that  $D=aY$ by shrinking
$D=aY$ by shrinking  $V$ if necessary. Thus it holds that the system
$V$ if necessary. Thus it holds that the system  $\{(V_{j}\cap Z,f_{j})\}$ induces a foliation
$\{(V_{j}\cap Z,f_{j})\}$ induces a foliation  ${\mathcal{F}}$ on a neighborhood of
${\mathcal{F}}$ on a neighborhood of  $C$ in
$C$ in  $S$ as in Theorem 1.1, which contradicts to the property of the pair
$S$ as in Theorem 1.1, which contradicts to the property of the pair  $(C,S)$.
$(C,S)$.
7 Discussion
In this section, we list some remaining problems.
In [Reference UedaU, Section 3], the neighborhood structure of  $Y$ is investigated also for the pair
$Y$ is investigated also for the pair  $(Y,X)$ of finite type for the case where
$(Y,X)$ of finite type for the case where  $r=1$. According to [Reference UedaU, Theorem 1],
$r=1$. According to [Reference UedaU, Theorem 1],  $Y$ admits a fundamental system of strongly pseudoconcave neighborhoods. As an analogy, it seems to be natural to ask the following question for example.
$Y$ admits a fundamental system of strongly pseudoconcave neighborhoods. As an analogy, it seems to be natural to ask the following question for example.
Question 7.1. Let  $X$ be a compact complex manifold and
$X$ be a compact complex manifold and  $Y\subset X$ be a compact complex submanifold with unitary flat normal bundle such that the pair
$Y\subset X$ be a compact complex submanifold with unitary flat normal bundle such that the pair  $(Y,X)$ is of type
$(Y,X)$ is of type  $n<\infty$. What kind of psh functions do there exist on
$n<\infty$. What kind of psh functions do there exist on  $X\setminus Y$?
$X\setminus Y$?
One of the most interesting application of [Reference UedaU, Theorem 1] is the classification of the pairs  $(Y,X)$ of finite type such that
$(Y,X)$ of finite type such that  $X$ is a projective surface and
$X$ is a projective surface and  $Y$ is an elliptic curve [Reference NeemanN, Section 6]. We are also interested in a higher dimensional analogy of this result:
$Y$ is an elliptic curve [Reference NeemanN, Section 6]. We are also interested in a higher dimensional analogy of this result:
Question 7.2. Classify the pairs  $(Y,X)$ of finite type such that
$(Y,X)$ of finite type such that  $X$ is a projective manifold and
$X$ is a projective manifold and  $Y$ is an elliptic curve with unitary flat normal bundle.
$Y$ is an elliptic curve with unitary flat normal bundle.
We are also interested in some concrete examples. In our context, the example of the blow-up of  $\mathbb{P}^{2}$ at nine points is one of the most interesting examples, see [Reference Arnol’dA], [Reference BrunellaB], and [Reference DemaillyD2, Section 1]. The example we treated in Section 6.3 is a natural generalization of this example. From this point of view, it seems to be natural to ask the following:
$\mathbb{P}^{2}$ at nine points is one of the most interesting examples, see [Reference Arnol’dA], [Reference BrunellaB], and [Reference DemaillyD2, Section 1]. The example we treated in Section 6.3 is a natural generalization of this example. From this point of view, it seems to be natural to ask the following:
Question 7.3. (Higher dimensional analogue of [Reference KoikeK3, Question 1.2])
Let  $(V,L),C=V_{1},q,Y,X$ be as in Corollary 1.3 and Section 6.3. Is there a point
$(V,L),C=V_{1},q,Y,X$ be as in Corollary 1.3 and Section 6.3. Is there a point  $q\in C$ such that
$q\in C$ such that  $K_{X}^{-1}$ admits no
$K_{X}^{-1}$ admits no  $C^{\infty }$ Hermitian metric with semipositive curvature, or that
$C^{\infty }$ Hermitian metric with semipositive curvature, or that  $Y$ does not admit a pseudoflat neighborhood system?
$Y$ does not admit a pseudoflat neighborhood system?
In [Reference KoikeK2], we studied the neighborhood structure of a submanifold  $Y$ of
$Y$ of  $X$ with codimension
$X$ with codimension  $r=2$. Under the assumption of the existence of a hypersurface
$r=2$. Under the assumption of the existence of a hypersurface  $S$ of
$S$ of  $X$ with unitary flat normal bundle which includes
$X$ with unitary flat normal bundle which includes  $Y$ as a submanifold, we posed the obstruction classes
$Y$ as a submanifold, we posed the obstruction classes  $u_{n,m}(Y,S,X)\in H^{1}(N_{S/X}|_{Y}^{-n}\otimes N_{Y/S}^{-m})$. Thereafter, we found a mistake in the proof of [Reference KoikeK2, Theorem 1], which is corrected as [Reference Koike and OgawaKO, Theorem 1.4] by using a new obstruction classes
$u_{n,m}(Y,S,X)\in H^{1}(N_{S/X}|_{Y}^{-n}\otimes N_{Y/S}^{-m})$. Thereafter, we found a mistake in the proof of [Reference KoikeK2, Theorem 1], which is corrected as [Reference Koike and OgawaKO, Theorem 1.4] by using a new obstruction classes  $v_{n,m}(Y,S,X)\in H^{1}(N_{S/X}|_{Y}^{-n}\otimes N_{Y/S}^{-m+1})$.
$v_{n,m}(Y,S,X)\in H^{1}(N_{S/X}|_{Y}^{-n}\otimes N_{Y/S}^{-m+1})$.
Question 7.4. What is the relation between  $(u_{n,m}(Y,S,X),v_{n,m}(Y,S,X))$ and
$(u_{n,m}(Y,S,X),v_{n,m}(Y,S,X))$ and  $u_{n}(Y,X)$ we defined in Section 3.1?
$u_{n}(Y,X)$ we defined in Section 3.1?
Acknowledgments
The author would like to give heartful thanks to Prof. Tetsuo Ueda whose comments and suggestions were of inestimable value for my study. He thanks Prof. Kento Fujita who taught him an example of the blow-up of a del Pezzo manifold at a general point. He also thanks Prof. Noboru Ogawa for helpful comments and warm encouragements. He is supported by the Grant-in-Aid for Scientific Research (KAKENHI No. 28-4196) and the Grant-in-Aid for JSPS fellows.