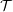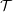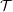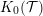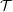Introduction
Degeneration of modules has been intensively studied since at least 1974 (e.g., Gabriel [Reference Gabriel5], Huisgen-Zimmermann, Riedtmann [Reference Riedtmann14], and Zwara [Reference Zwara22, Reference Zwara23]). The concept of degeneration of modules was found to be highly successful in various constructions. Degeneration of modules is defined by the following setting. Let
$k$
be an algebraically closed field, and let
$A$
be a finite-dimensional
$k$
-algebra. Then the
$A$
-module structures on the vector space
$k^{d}$
form an affine algebraic variety
$\operatorname{mod}(A,d)$
on which
$\text{GL}_{d}(k)$
acts by conjugation. Isomorphism classes correspond to orbits under this action, and an
$A$
-module
$M$
degenerates to
$N$
if the point corresponding to
$N$
belongs to the Zariski closure of the
$\text{GL}_{d}(k)$
-orbit of the point corresponding to
$M$
. We write
$M\leqslant _{\text{deg}}N$
in this case. Riedtmann and Zwara showed that
$M\leqslant _{\text{deg}}N$
if and only if there are an
$A$
-module
$Z$
and a short exact sequence 
In collaboration with Jensen and Su [Reference Jensen, Su and Zimmermann8], the second named author started to study an analogous concept for derived categories with a geometrically inspired concept based on orbit closures and then in [Reference Jensen, Su and Zimmermann9], more generally for triangulated categories based on Zwara’s characterization replacing short exact sequences by distinguished triangles. This last relation is denoted by the symbol
${\leqslant}_{\unicode[STIX]{x1D6E5}}$
. Both concepts were highly successfully used in many places (cf. e.g., [Reference Eisele3, Reference Eisele4, Reference Hiramatsu6, Reference Hiramatsu7, Reference Keller, Yang and Zhou10–Reference Krause12, Reference Wang21]). Independently, Yoshino [Reference Yoshino20] gave a scheme theoretic definition for degenerations in the (triangulated) stable category of maximal Cohen–Macaulay modules, and he highlighted that in
$M\leqslant _{\unicode[STIX]{x1D6E5}}N$
, one should assume that the induced endomorphism on
$Z$
should be nilpotent. We denote the relation by
${\leqslant}_{\unicode[STIX]{x1D6E5}+\text{nil}}$
in this case. Yoshino’s scheme theoretic approach was a model for us to give a more general geometric definition for degeneration, which was achieved in [Reference Saorín and Zimmermann16] by introducing a scheme theoretic degeneration
${\leqslant}_{\text{cdeg}}$
.
We then showed that, in case
${\mathcal{T}}$
has split idempotents,
$M\leqslant _{\text{cdeg}}N$
always implies
$M\leqslant _{\unicode[STIX]{x1D6E5}+\text{nil}}N$
, for objects
$M,N\in {\mathcal{T}}$
, the converse being also true when
${\mathcal{T}}$
is the subcategory of compact objects of a compactly generated algebraic triangulated category. Obviously,
$M\leqslant _{\unicode[STIX]{x1D6E5}+\text{nil}}N$
implies
$M\leqslant _{\unicode[STIX]{x1D6E5}}N$
. We further see right from the definition that
$M\leqslant _{\unicode[STIX]{x1D6E5}}N$
implies that
$M$
and
$N$
have the same image in the Grothendieck group of
${\mathcal{T}}$
.
A striking phenomenon is that, unlike in the module case, in triangulated categories
${\mathcal{T}}$
, one may have nonzero objects
$M$
with
$0\leqslant _{\unicode[STIX]{x1D6E5}+\text{nil}}M$
, namely cones of nilpotent endomorphisms of objects of
${\mathcal{T}}$
.
By the above,
$0\leqslant _{\unicode[STIX]{x1D6E5}}N$
implies that
$N$
has a vanishing image in the Grothendieck group of the triangulated category. We then show as our main result that the full triangulated subcategory of
${\mathcal{T}}$
consisting of the objects with image
$0$
in the Grothendieck group of
${\mathcal{T}}$
coincides with the full triangulated subcategory of
${\mathcal{T}}$
generated by objects being degenerations of the zero object of
${\mathcal{T}}$
.
We prove this by showing that both categories actually coincide with the full triangulated subcategory generated by objects of the form
$\bigoplus _{i=1}^{r}(X_{i}\oplus X_{i}[t_{i}])$
for pairwise different odd integers
$t_{i}$
, and objects
$X_{i}$
in some fixed set of generators of
${\mathcal{T}}$
.
Furthermore, we use our result to give examples showing that
$M\leqslant _{\unicode[STIX]{x1D6E5}}N$
does not imply
$M\leqslant _{\unicode[STIX]{x1D6E5}+\text{nil}}N$
and that an object
$M$
with image
$0$
in the Grothendieck group is not necessarily a degeneration of
$0$
, not even in the transitive hull of the relation
${\leqslant}_{\unicode[STIX]{x1D6E5}+\text{nil}}$
.
The paper is organized as follows. In Section 1, we recall the necessary concepts on the various types of degeneration and recall the implications that we proved essentially in our earlier work [Reference Saorín and Zimmermann16, Reference Saorín and Zimmermann17]. In Section 2, we study the image of triangle degenerations of
$0$
in the Grothendieck group, prove our main result, Theorem 7, and give the examples mentioned above.
1 Review on degenerations in triangulated categories
We have different degeneration concepts. The first one, the triangle degeneration, is a triangular category analogue of Zwara’s definition of degeneration in the case of module categories. Zwara says [Reference Zwara22, Reference Zwara23] that for a
$k$
-algebra
$A$
an
$A$
-module
$M$
degenerates to an
$A$
-module
$N$
if and only if there is an
$A$
-module
$Z$
and a short exact sequence 
Yoshino [Reference Yoshino20] highlighted the importance of assuming that the induced endomorphism of
$Z$
should be nilpotent. In the case of a category where Fitting’s lemma holds, we can always assume this fact.
Definition 1. [Reference Jensen, Su and Zimmermann9, Reference Saorín and Zimmermann16] Let
$K$
be a commutative ring and let
${\mathcal{T}}$
be a
$K$
-linear triangulated category. Then for two objects
$M$
and
$N$
in
${\mathcal{T}}$
we get
$M\leqslant _{\unicode[STIX]{x1D6E5}}N$
if and only if there is an object
$Z$
in
${\mathcal{T}}$
and a distinguished triangle
We say that
$M\leqslant _{\unicode[STIX]{x1D6E5}+\text{nil}}N$
if and only if there is such a distinguished triangle with
$v$
is nilpotent.
Note that by [Reference Saorín and Zimmermann17, Proposition 10]
$M\leqslant _{\unicode[STIX]{x1D6E5}+\text{nil}}N$
implies that there is an object
$Z^{\prime }$
and a distinguished triangle
We may write
$M\leqslant _{\unicode[STIX]{x1D6E5},\text{right}}N$
(resp.
$M\leqslant _{\unicode[STIX]{x1D6E5}+\text{nil, right}}N$
) if there is such a distinguished triangle (with
$v^{\prime }$
nilpotent) and, for this paragraph only, write
$M\leqslant _{\unicode[STIX]{x1D6E5},\text{left}}N$
(resp.
$M\leqslant _{\unicode[STIX]{x1D6E5}+\text{nil, left}}N$
) in the situation of Definition 1. Note that
$M\leqslant _{\unicode[STIX]{x1D6E5},\text{left}}N$
(resp.
$M\leqslant _{\unicode[STIX]{x1D6E5}+\text{nil,left}}N$
) in
${\mathcal{T}}$
if and only if
$N\leqslant _{\unicode[STIX]{x1D6E5},\text{right}}M$
(resp.
$N\leqslant _{\unicode[STIX]{x1D6E5}+\text{nil,right}}M$
) in the opposite category
${\mathcal{T}}^{\text{op}}$
. So categorical duality applies and results about
${\leqslant}_{\unicode[STIX]{x1D6E5},\text{left}}$
(resp.
${\leqslant}_{\unicode[STIX]{x1D6E5}+\text{nil, left}}$
) admit categorical dual ones, that we omit to state. Furthermore, if
${\mathcal{T}}$
has split idempotents and Artinian endomorphism rings of objects, or if
${\mathcal{T}}$
is the category of compact objects in a compactly generated algebraic triangulated category, then
$M\leqslant _{\unicode[STIX]{x1D6E5}+\text{nil, right}}N$
if and only if
$M\leqslant _{\unicode[STIX]{x1D6E5}+\text{nil, left}}N$
(see [Reference Saorín and Zimmermann17, Theorem 1]).
A second concept of degeneration, motivated by Yoshino’s work, is given by the following definition.
Definition 2. [Reference Saorín and Zimmermann16] Let
$K$
be a commutative ring and let
${\mathcal{C}}_{K}^{\circ }$
be a
$K$
-linear triangulated category with split idempotents.
A degeneration data for
${\mathcal{C}}_{K}^{\circ }$
is given by
-
∙ a triangulated category
${\mathcal{C}}_{K}$
with split idempotents and a fully faithful embedding
${\mathcal{C}}_{K}^{\circ }\longrightarrow {\mathcal{C}}_{K}$
, -
∙ a triangulated category
${\mathcal{C}}_{V}$
with split idempotents and a full triangulated subcategory
${\mathcal{C}}_{V}^{\circ }$
, -
∙ triangulated functors
$\uparrow _{K}^{V}:{\mathcal{C}}_{K}\longrightarrow {\mathcal{C}}_{V}$
, which we write after the arguments, and
$\unicode[STIX]{x1D6F7}:{\mathcal{C}}_{V}^{\circ }\rightarrow {\mathcal{C}}_{K}$
, so that
$({\mathcal{C}}_{K}^{\circ })\uparrow _{K}^{V}\subseteq {\mathcal{C}}_{V}^{\circ }$
, when we view
${\mathcal{C}}_{K}^{\circ }$
as a full subcategory of
${\mathcal{C}}_{K}$
, -
∙ a natural transformation
$\text{id}_{{\mathcal{C}}_{V}}\stackrel{t}{\longrightarrow }\text{id}_{{\mathcal{C}}_{V}}$
of triangulated functors such that -
∙ for each object
$M$
of
${\mathcal{C}}_{K}^{\circ }$
the morphism is a split monomorphism in
${\mathcal{C}}_{K}$
with cone
$M$
.
is a split monomorphism in 
Remark 3. Our definition of categorical degeneration, given below, is a generalization to general triangulated categories of a definition given by Yoshino [Reference Yoshino20] for the case of stable categories of maximal Cohen–Macaulay modules over a local Gorenstein algebra. In Yoshino’s work (see, e.g., [Reference Yoshino19]) he considers modules over an algebra
$R$
over a field
$K$
and defines degeneration along a suitable discrete valuation
$K$
-algebra
$V$
. Just to emphasize the similarity and facilitate the intuition of the reader, we used in [Reference Saorín and Zimmermann16] subindices
$K$
and
$V$
to denote our categories, but there and in Definition 2 the letters
$K$
and
$V$
play no role.
Definition 4. [Reference Saorín and Zimmermann16] Given two objects
$M$
and
$N$
of
${\mathcal{C}}_{K}^{\circ }$
, we say that
$M$
degenerates to
$N$
in the categorical sense, written
$M\leqslant _{\text{cdeg}}N$
, if there is a degeneration data for
${\mathcal{C}}_{K}^{\circ }$
and an object
$Q$
of
${\mathcal{C}}_{V}^{\circ }$
such that
$$\begin{eqnarray}p(Q)\simeq p(M\uparrow _{K}^{V})\quad \text{in }{\mathcal{C}}_{V}^{\circ }[t^{-1}]\quad \text{and}\quad \unicode[STIX]{x1D6F7}(\operatorname{cone}(t_{Q}))\simeq N,\end{eqnarray}$$
where
${\mathcal{C}}_{V}^{\circ }[t^{-1}]$
is the Gabriel–Zisman localization at the endomorphisms
$t_{X}$
for all objects
$X$
of
${\mathcal{C}}_{V}^{\circ }$
, and where
$p:{\mathcal{C}}_{V}^{\circ }\longrightarrow {\mathcal{C}}_{V}^{\circ }[t^{-1}]$
is the canonical functor. In this case we write
$M\leqslant _{\text{cdeg}}N$
.
We end the section by recalling the connection between these various types of degeneration and with the property of having the same image in the Grothendieck group
$K_{0}({\mathcal{T}})$
.
Theorem 5. Let
${\mathcal{T}}$
be a skeletally small triangulated category with split idempotents and let
$M$
and
$N$
be objects of
${\mathcal{T}}$
. Consider the following assertions:
-
(1)
$M\leqslant _{\text{cdeg}}N$
-
(2)
$M\leqslant _{\unicode[STIX]{x1D6E5}+\text{nil}}N$
-
(3)
$M\leqslant _{\unicode[STIX]{x1D6E5}}N$
-
(4)
$[M]=[N]$
in the Grothendieck group
$K_{0}({\mathcal{T}})$
.
The implications
$(1)\Rightarrow (2)\Rightarrow (3)\Rightarrow (4)$
hold true. When
${\mathcal{T}}$
is the subcategory of compact objects of a compactly generated algebraic triangulated category, the implication
$(2)\Rightarrow (1)$
also holds. When the endomorphism rings of objects in
${\mathcal{T}}$
are all Artinian, the implication
$(3)\Rightarrow (2)$
also holds and
${\leqslant}_{\unicode[STIX]{x1D6E5}}=\leqslant _{\unicode[STIX]{x1D6E5}+\text{nil}}$
is a reflexive and transitive relation in the set of isoclasses of objects of
${\mathcal{T}}$
.
Proof. The implication
$(2)\Rightarrow (3)$
is clear. On the other hand, if assertion 3 holds and we consider the triangle of Definition 1, we then get an equality
$[Z]+[M]=[Z]+[N]$
in
$K_{0}({\mathcal{T}})$
, which implies assertion 4.
On the other hand, the implication
$(1)\Rightarrow (2)$
and, under the extra hypothesis, the implication
$(2)\Rightarrow (1)$
are [Reference Saorín and Zimmermann16, Propositions 8 and 9]. Finally, if the endomorphism ring of each object is Artinian, implication
$(3)\Rightarrow (2)$
and the reflexive and transitive condition of
${\leqslant}_{\unicode[STIX]{x1D6E5}}=\leqslant _{\unicode[STIX]{x1D6E5}+\text{nil}}$
are [Reference Jensen, Su and Zimmermann8, Proposition 2].
We postpone until the next section giving counterexamples to implications
$(3)\Rightarrow (2)$
and
$(4)\Rightarrow (3)$
of Theorem 5.
2 Degeneration of zero and the zero objects in the Grothendieck group
Let
${\mathcal{T}}$
be a skeletally small triangulated category with split idempotents all through this section. By Theorem 5, we know that any object
$N$
that is a degeneration of zero in
${\mathcal{T}}$
has the property that
$[N]=0$
in
$K_{0}({\mathcal{T}})$
. The goal of this section is to compare the subcategories
${\mathcal{T}}_{\unicode[STIX]{x1D6E5}}^{0}$
(resp.
${\mathcal{T}}_{\unicode[STIX]{x1D6E5}+\text{nil}}^{0}$
) and
${\mathcal{T}}^{0}$
of
${\mathcal{T}}$
consisting, respectively, of the objects
$N$
such that
$0\leqslant _{\unicode[STIX]{x1D6E5}}N$
(resp.
$0\leqslant _{\unicode[STIX]{x1D6E5}+\text{nil}}N$
) and the objects
$N$
such that
$[N]=0$
in
$K_{0}({\mathcal{T}})$
.
But, before tackling the problem, let us emphasize the ubiquity of degenerations of
$0$
.
Remark 6. Since
$M\leqslant _{\unicode[STIX]{x1D6E5}}N$
(resp.
$M\leqslant _{\unicode[STIX]{x1D6E5}+\text{nil}}N$
) if and only if there is a distinguished triangle
(resp. with
$v$
nilpotent), we see that this can be written as a homotopy cartesian square. Neeman [Reference Neeman13, Lemmas 1.4.3, 1.4.4] then shows that
$\operatorname{cone}(s)\simeq \operatorname{cone}(v)$
, and so
$0\leqslant _{\unicode[STIX]{x1D6E5}}\operatorname{cone}(s)$
(resp.
$0\leqslant _{\unicode[STIX]{x1D6E5}+\text{nil}}\operatorname{cone}(s)$
). Hence, degenerations of
$0$
are intrinsic in degeneration in triangulated categories.
Recall that, given full subcategories
${\mathcal{U}}$
and
${\mathcal{V}}$
of a triangulated category
${\mathcal{T}}$
, then the subcategory
${\mathcal{U}}\star {\mathcal{V}}$
is the full subcategory of
${\mathcal{T}}$
consisting of the objects
$M$
that fit in a distinguished triangle
$U\longrightarrow M\longrightarrow V\stackrel{}{\longrightarrow }U[1]$
, with
$U\in {\mathcal{U}}$
and
$V\in {\mathcal{V}}$
. It is well known that the operation
$\star$
is associative, in the sense that
$({\mathcal{U}}\star {\mathcal{V}})\star {\mathcal{W}}={\mathcal{U}}\star ({\mathcal{V}}\star {\mathcal{W}})$
, for all subcategories
${\mathcal{U}},{\mathcal{V}},{\mathcal{W}}$
of
${\mathcal{T}}$
(see [Reference Beilinson, Bernstein and Deligne1, Lemme 1.3.10]). If one puts
${\mathcal{U}}^{\star n}=\underbrace{{\mathcal{U}}\star \cdots \star {\mathcal{U}}}_{n\;\text{factors}}$
, for each
$n\geqslant 0$
(with the convention that
${\mathcal{U}}^{\star 0}=0$
), then
${\mathcal{U}}^{\text{ext}}=\bigcup _{n\in \mathbf{N}}{\mathcal{U}}^{\star n}$
is the extension closure of
${\mathcal{U}}$
, that is, the smallest subcategory of
${\mathcal{T}}$
closed under extensions that contains
${\mathcal{U}}$
. The smallest triangulated subcategory of
${\mathcal{T}}$
that contains
${\mathcal{U}}$
, denoted
$\text{tria}_{{\mathcal{T}}}({\mathcal{U}})$
, is
$$\begin{eqnarray}\text{tria}_{{\mathcal{T}}}({\mathcal{U}})=\mathop{\bigcup }_{n\in \mathbb{N}}\mathop{\bigcup }_{(r_{1},\ldots ,r_{n})\in \mathbb{Z}^{n}}{\mathcal{U}}[r_{1}]\star \cdots \star {\mathcal{U}}[r_{n}].\end{eqnarray}$$
In other words, the objects of
$\text{tria}_{{\mathcal{T}}}({\mathcal{U}})$
are precisely those
$M$
admitting a sequence
$$\begin{eqnarray}0=M_{0}\stackrel{f_{1}}{\longrightarrow }M_{1}\stackrel{f_{2}}{\longrightarrow }\cdots \stackrel{f_{n-1}}{\longrightarrow }M_{n-1}\stackrel{f_{n}}{\longrightarrow }M_{n}=M,\end{eqnarray}$$
where
$\text{cone}(f_{k})$
is isomorphic to
$U_{k}[r_{k}]$
, for some
$U_{k}\in {\mathcal{U}}$
and some
$r_{k}\in \mathbb{Z}$
, for all
$k=1,\ldots ,n$
.
In our next main result, we will denote by
$\preccurlyeq _{\unicode[STIX]{x1D6E5}+\text{nil}}$
the smallest transitive relation containing
${\leqslant}_{\unicode[STIX]{x1D6E5}+\text{nil}}$
. Recall that
$\preccurlyeq _{\unicode[STIX]{x1D6E5}+\text{nil}}=\leqslant _{\unicode[STIX]{x1D6E5}+\text{nil}}=\leqslant _{\unicode[STIX]{x1D6E5}}$
whenever all endomorphism rings of objects of
${\mathcal{T}}$
are Artinian (see Theorem 5).
Theorem 7. Let
${\mathcal{S}}$
be a set of objects in the skeletally small triangulated category
${\mathcal{T}}$
having split idempotents such that
${\mathcal{T}}=\text{tria}_{{\mathcal{T}}}({\mathcal{S}})$
, let
$[{\mathcal{S}}]:=\{[S]:S\in {\mathcal{S}}\}$
denote the corresponding set of generators of the group
$K_{0}({\mathcal{T}})$
and let
$\widehat{{\mathcal{S}}}$
be the subcategory of
${\mathcal{T}}$
consisting of the objects
$X$
, which are finite direct sums of shifts of objects in
${\mathcal{S}}$
and are such that
$[X]=0$
in
$K_{0}({\mathcal{T}})$
. Denote by
-
∙
${\mathcal{T}}_{\unicode[STIX]{x1D6E5}}^{0}$
(resp.
${\mathcal{T}}_{\unicode[STIX]{x1D6E5}+\text{nil}}^{0}$
) the full subcategory of
${\mathcal{T}}$
consisting of the objects
$X$
such that
$0\leqslant _{\unicode[STIX]{x1D6E5}}X$
(resp.
$0\leqslant _{\unicode[STIX]{x1D6E5}+\text{nil}}X$
) -
∙ and by
${\mathcal{T}}^{0}$
the (triangulated) subcategory of
${\mathcal{T}}$
consisting of the objects
$M$
such that
$[M]=0$
in the group
$K_{0}({\mathcal{T}})$
.
Then the following assertions hold:
-
(1) An object
$M$
is in
${\mathcal{T}}^{0}$
if, and only if,
$M\leqslant _{\unicode[STIX]{x1D6E5}}X$
(resp.
$M\preccurlyeq _{\unicode[STIX]{x1D6E5}+\text{nil}}X$
), for some
$X\in \widehat{{\mathcal{S}}}$
. When
$[{\mathcal{S}}]$
is a basis of
$K_{0}({\mathcal{T}})$
the objects of
$\widehat{{\mathcal{S}}}$
are precisely the finite direct sums of shifts of objects in
$\bar{{\mathcal{S}}}:=\{S\oplus S[2k+1]:k\in \mathbb{Z};S\in {\mathcal{S}}\}$
. -
(2)
${\mathcal{T}}^{0}=\text{tria}_{{\mathcal{T}}}(S\oplus S[t_{S}]:S\in {\mathcal{S}})$
, for every choice of odd integers
$t_{S}$
. -
(3)
${\mathcal{T}}^{0}$
is the extension closure of
${\mathcal{T}}_{\unicode[STIX]{x1D6E5}}^{0}$
(resp.
${\mathcal{T}}_{\unicode[STIX]{x1D6E5}+\text{nil}}^{0}$
).
Proof. (1) By Theorem 5, the ‘if’ part of this implication is clear. For the ‘only if’ part, we first claim that, for each
$M\in {\mathcal{T}}$
, one has that
$M\preccurlyeq _{\unicode[STIX]{x1D6E5}+\text{nil}}\bigoplus _{S\in {\mathcal{S}}}\bigoplus _{k\in \mathbb{Z}}S[k]^{m_{S,k}}$
, where the
$S$
are in
${\mathcal{S}}$
and the
$m_{k,S}$
are nonnegative integers, all zero but a finite number. Recall that
${\mathcal{T}}=\text{tria}_{{\mathcal{T}}}({\mathcal{S}})$
, and so we have a finite sequence
such that
$C_{k}:=\operatorname{cone}(f_{k})$
is a shift of some object of
${\mathcal{S}}$
, for each
$k=1,\ldots ,n$
. We will settle our claim by induction on
$n>0$
, the case
$n=1$
being clear. Suppose now that
$n>0$
and consider the induced triangle
where
$C_{n}\cong S[k]$
, for some
$S\in {\mathcal{S}}$
and
$k\in \mathbb{Z}$
. Taking the homotopy pushout of
$f_{n}$
and the zero endomorphism
$M_{n-1}\stackrel{0}{\longrightarrow }M_{n-1}$
, we readily see that we have a distinguished triangle
That is, we have
$M\preccurlyeq _{\unicode[STIX]{x1D6E5}+\text{nil}}M_{n-1}\oplus C_{n}\cong M_{n-1}\oplus S[k]$
. The result then follows by induction since
$A_{i}\preccurlyeq _{\unicode[STIX]{x1D6E5}+\text{nil}}B_{i}$
, for
$i=1,2$
, implies that
$A_{1}\oplus A_{2}\preccurlyeq _{\unicode[STIX]{x1D6E5}+\text{nil}}B_{1}\oplus B_{2}$
.
We also claim that
$M\leqslant _{\unicode[STIX]{x1D6E5}}\bigoplus _{S\in {\mathcal{S}}}\bigoplus _{k\in \mathbb{Z}}S[k]^{m_{S,k}}$
, for
$S_{k}$
and
$m_{S,k}$
as in the previous paragraph. Using again the sequence
$(\ast )$
and bearing in mind that each cone
$C_{k}:=\operatorname{cone}(f_{k})$
is a shift of some object in
${\mathcal{S}}$
, we consider the distinguished triangles
for all
$k\in \{1,\ldots ,n-1\}$
. Taking the direct sum of these distinguished triangles, we get a distinguished triangle
and hence
$M\leqslant _{\unicode[STIX]{x1D6E5}}\bigoplus _{k=1}^{n}C_{k}$
, as desired.
The last two paragraphs show that we have
$M\preccurlyeq _{\unicode[STIX]{x1D6E5}+\text{nil}}X$
and
$M\leqslant _{\unicode[STIX]{x1D6E5}}Y$
, for objects
$X,Y$
which are direct sums of shifts of objects of
${\mathcal{S}}$
. When in addition
$M\in {\mathcal{T}}^{0}$
, by Theorem 5, we also have
$[X]=[Y]=0$
in
$K_{0}({\mathcal{T}})$
. Therefore, we have that
$X,Y\in \hat{{\mathcal{S}}}$
. This proves assertion (1), except for the final statement.
To prove that final statement, suppose that
$[{\mathcal{S}}]$
is a basis of
$K_{0}({\mathcal{T}})$
. We claim that in this case each object of
$\hat{{\mathcal{S}}}$
is a direct sum of objects of the form
$S[k]\oplus S[l]=(S\oplus S[l-k])[k]$
, with
$S\in {\mathcal{S}}$
and
$l-k$
odd. This will end the proof. Let then take
$X\in \hat{{\mathcal{S}}}$
and decompose it as
$X=\bigoplus _{S\in {\mathcal{S}}}\bigoplus _{k\in \mathbb{Z}}S[k]^{m_{S,k}}$
. Note that due to the fact that
$[{\mathcal{S}}]$
is a basis of
$K_{0}({\mathcal{T}})$
, the summand
$X_{S}=\bigoplus _{k\in \mathbb{Z}}S[k]^{m_{k,S}}$
also satisfies that
$[X_{S}]=0$
in
$K_{0}({\mathcal{T}})$
, for each
$S\in {\mathcal{S}}$
. So it is not restrictive to assume that
$X=S[k_{1}]^{m_{1}}\oplus S[k_{2}]^{m_{2}}\oplus \cdots \oplus S[k_{r}]^{m_{r}}$
, for some pairwise different integers
$k_{1},\ldots ,k_{r}$
, where, for simplicity, we have put
$m_{k_{i},S}=m_{i}>0$
for
$i=1,\ldots ,r$
. We can reorder the summands in this last direct sum, so that
$k_{i}$
is even, for
$1\leqslant i\leqslant t$
, and
$k_{i}$
is odd, for
$t<i\leqslant n$
. Bearing in mind that
$[S[k]]=(-1)^{k}[S]$
in
$K_{0}({\mathcal{T}})$
, that
$[{\mathcal{S}}]$
is a basis of
$K_{0}({\mathcal{T}})$
and that
$[X]=0$
in this latter abelian group, we conclude that
$\sum _{i=1}^{t}m_{i}=\sum _{i=t+1}^{n}m_{i}$
. We call
$m(X)$
this last integer which is strictly positive when
$X\neq 0$
. An easy induction on
$m(X)$
then settles our claim.
(2) Let
$(t_{S})_{S\in {\mathcal{S}}}$
be a collection of odd integers and put
${\mathcal{D}}:=\operatorname{tria}_{{\mathcal{T}}}(S\oplus S[t_{S}]:S\in {\mathcal{S}})$
. It follows that each object of
${\mathcal{S}}$
is a direct summand of an object of
${\mathcal{D}}$
and since each object
$T$
of
${\mathcal{T}}=\operatorname{tria}_{{\mathcal{T}}}({\mathcal{S}})$
is a finite iterated extension of objects of the form
$S[k]$
, with
$S\in {\mathcal{S}}$
and
$k\in \mathbb{Z}$
, it easily follows that each such
$T$
is a direct summand of an object of
${\mathcal{D}}$
. This means that
${\mathcal{D}}$
is a dense triangulated subcategory of
${\mathcal{T}}$
in the terminology of [Reference Thomason18]. Moreover, we clearly have
${\mathcal{D}}\subseteq {\mathcal{T}}^{0}$
. But [Reference Thomason18, Theorem 2.1] gives an order-preserving bijection between the dense triangulated subcategories of
${\mathcal{T}}$
and the subgroups of
$K_{0}({\mathcal{T}})$
. Since
${\mathcal{T}}^{0}$
corresponds to
$0$
by this bijection we get that
${\mathcal{D}}={\mathcal{T}}^{0}$
, as desired.
(3) Note that assertion (2) implies assertion (3). Indeed, by the comments preceding Theorem 7, assertion (2) says that
${\mathcal{T}}^{0}$
is the extension closure of
$\{(S\oplus S[t_{S}])[n]:S\in {\mathcal{S}}~\text{and}~n\in \mathbb{Z}\}$
, for any choice of odd integers
$t_{S}$
(
$S\in {\mathcal{S}}$
). We may choose
$t_{S}=1$
for each
$S$
, and then we have the split triangle
which shows that
$0\leqslant _{\unicode[STIX]{x1D6E5}+\text{nil}}S\oplus S[1]$
. Since we have inclusions
$$\begin{eqnarray}\{(S\oplus S[1]):S\in {\mathcal{S}}\}\subset {\mathcal{T}}_{\unicode[STIX]{x1D6E5}+\text{nil}}^{0}\subset {\mathcal{T}}_{\unicode[STIX]{x1D6E5}}^{0}\subseteq {\mathcal{T}}^{0}\end{eqnarray}$$
assertion (3) immediately follows.
Example 8. The following are examples of a triangulated category
${\mathcal{T}}$
and a set
${\mathcal{S}}$
of its objects that satisfy the hypotheses of Theorem 7 and, in addition,
$[{\mathcal{S}}]$
is a basis of
$K_{0}({\mathcal{T}})$
. Here,
$K$
is a commutative ring.
-
(1) Call a dg
$K$
-algebra
$A$
homologically nonpositive when
$H^{k}A=0$
, for all
$k>0$
, and call it homologically finite-dimensional when
$H^{\ast }(A)=\bigoplus _{k\in \mathbb{Z}}H^{k}(A)$
is a
$K$
-module of finite length. For instance, any Artin algebra is homologically nonpositive and homologically finite-dimensional over its center, when viewed as dg algebra. Let
$A$
be a homologically nonpositive homologically finite-dimensional dg algebra, and let
${\mathcal{T}}={\mathcal{D}}_{fl}^{b}(A)$
be the subcategory of the derived category
${\mathcal{D}}(A)$
consisting of the dg
$A$
-modules
$M$
such that
$H^{\ast }(M)=\bigoplus _{k\in \mathbb{Z}}H^{k}(M)$
has finite length as a
$K$
-module. When choosing as
${\mathcal{S}}$
a set of representatives, up to isomorphism in
${\mathcal{D}}(A)$
, of the dg
$A$
-modules
$S$
such that
$H^{\ast }(S)=H^{0}(S)$
(i.e., its homology is concentrated in degree zero) and
$H^{0}(S)$
is a simple
$H^{0}(A)$
-module, one has that
${\mathcal{T}}$
and
${\mathcal{S}}$
satisfy the hypotheses of Theorem 7 and
$[{\mathcal{S}}]$
is a basis of
$K_{0}({\mathcal{T}})$
. In particular, taking
$A$
to be an Artin algebra,
${\mathcal{T}}={\mathcal{D}}^{b}(\text{mod}-A)$
and
${\mathcal{S}}$
be a set of representatives, up to isomorphism, of the simple
$A$
-modules (viewed as stalk complexes in degree zero), the hypotheses of Theorem 7 hold and
$[{\mathcal{S}}]$
is a basis of
$K_{0}({\mathcal{T}})$
. -
(2) Suppose that
${\mathcal{A}}$
is an additive category with a set
${\mathcal{S}}^{\prime }$
of objects such that
${\mathcal{A}}=\text{add}({\mathcal{S}}^{\prime })$
and the Grothendieck group
$K_{0}({\mathcal{A}})$
is free with
$\{[S]:S\in {\mathcal{S}}^{\prime }\}$
as a basis. Then the bounded homotopy category
${\mathcal{T}}={\mathcal{K}}^{b}({\mathcal{A}})$
and the set
${\mathcal{S}}={\mathcal{S}}^{\prime }[0]$
of stalk complexes
$S^{\prime }[0]$
, with
$S^{\prime }\in {\mathcal{S}}^{\prime }$
, satisfy the hypotheses of Theorem 7 (see [Reference Rose15, Theorems 1.1 and 1.2]). This includes the case when
${\mathcal{T}}={\mathcal{K}}^{b}(A-\text{proj})$
, where
$A$
is a principal ideal domain or a semiperfect ring, in particular an Artin algebra, by taking as
${\mathcal{S}}^{\prime }$
the set of (isomorphism classes of) indecomposable projective
$A$
-modules
Our next example shows that the implication
$(4)\Rightarrow (3)$
of Theorem 5 is in general not true.
Example 9. Let
$A$
be an Artin algebra and
$S$
be a simple
$A$
-module. For each
$k\in \mathbb{Z}$
the complex
$M=S\oplus S[2k+1]$
has the property that
$[M]=0$
in
$K_{0}(D^{b}(A-\text{mod}))$
. However, it is a
$\unicode[STIX]{x1D6E5}$
-degeneration of zero (i.e.,
$0\leqslant _{\unicode[STIX]{x1D6E5}}M$
) if and only if
$k=0$
or
$k=-1$
.
Indeed, In the final paragraph of the proof of Theorem 7 it is shown that
$0\leqslant _{\unicode[STIX]{x1D6E5}+\text{nil}}S\oplus S[1]$
, which implies by shift that also
$0\leqslant _{\unicode[STIX]{x1D6E5}+\text{nil}}S\oplus S[-1]$
. We then get that
$0\leqslant _{\unicode[STIX]{x1D6E5}}M$
whenever
$k=0,-1$
.
Suppose now that
$k\neq -1,0$
. Note that the homology module
$H^{i}(M)$
is zero, except for
$i=0$
and
$i=-2k-1$
in which case it is equal to
$S$
. If there is a distinguished triangle
in
$D^{b}(A-\text{mod})$
, the associated sequence of homologies gives an exact sequence
which forces
$H^{0}(f)$
and
$H^{1}(f)$
to be isomorphisms since they are a monomorphic and an epimorphic endomorphism, respectively, of finite length modules. Therefore
$S=0$
, and we get a contradiction.
Recall that we denote by
$\preccurlyeq _{\unicode[STIX]{x1D6E5}+\text{nil}}$
the smallest transitive relation on the set of isomorphism classes of objects in
${\mathcal{T}}$
containing
${\leqslant}_{\unicode[STIX]{x1D6E5}+\text{nil}}$
. Our final result shows that the implication
$(3)\Rightarrow (2)$
of Theorem 5 is false, in a strong sense.
Proposition 10. Let
${\mathcal{A}}$
be any skeletally small abelian category for which
${\mathcal{D}}^{b}({\mathcal{A}})$
is well defined, that is, it has
$\operatorname{Hom}$
sets as opposed to proper classes, and let us identify
${\mathcal{A}}$
with the subcategory of
${\mathcal{D}}^{b}({\mathcal{A}})$
consisting of objects
$X$
such that
$H^{i}(X)=0$
, for
$i\neq 0$
. The following assertions hold:
-
(1) If
$Y\leqslant _{\unicode[STIX]{x1D6E5}+\text{nil}}X$
in
${\mathcal{D}}^{b}({\mathcal{A}})$
and
$X\in {\mathcal{A}}$
, then
$Y\in {\mathcal{A}}$
. -
(2) If
$Z$
is an object of
${\mathcal{A}}$
and
$f:Z\longrightarrow Z$
is a monomorphic endomorphism
${\mathcal{A}}$
which is not an isomorphism, then
$X:=\operatorname{Coker}(f)$
satisfies that
$0\leqslant _{\unicode[STIX]{x1D6E5}}X$
in
${\mathcal{T}}:={\mathcal{D}}^{b}({\mathcal{A}})$
(and hence
$[X]=0$
in
$K_{0}({\mathcal{T}})$
), but
$0\not \preccurlyeq _{\unicode[STIX]{x1D6E5}+\text{nil}}X$
.
Proof. (1) Let us consider a distinguished triangle
in
$D^{b}({\mathcal{A}})$
, where
$v$
is a nilpotent endomorphism of
$W$
and
$X\in {\mathcal{A}}$
. The long exact sequence of homologies gives that
is an isomorphism, for
$j\neq 0,1$
, and there is an exact sequence
in
${\mathcal{A}}$
. Proving that
$Y$
has homology concentrated in zero degree reduces to prove that if
$\big(\!\begin{smallmatrix}w\\ g\end{smallmatrix}\!\big):A\longrightarrow A\oplus B$
is an epimorphism in
${\mathcal{A}}$
, for some objects
$A,B\in {\mathcal{A}}$
, where
$w$
is a nilpotent endomorphism of
$A$
, then
$A=B=0$
. This is clear when
$w=0$
. But if
$w\neq 0$
and
$m$
is the nilpotent index of
$w$
(i.e.,
$w^{m}=0\neq w^{m-1}$
), then the composition
is the zero map, which implies that
$w^{m-1}=0$
, thus yielding a contradiction.
(2) We have an induced distinguished triangle
in
${\mathcal{D}}^{b}({\mathcal{A}})$
, thus showing that
$0\leqslant _{\unicode[STIX]{x1D6E5}}X=X[0]$
in the latter triangulated category. Suppose now that
$0\preccurlyeq _{\unicode[STIX]{x1D6E5}+\text{nil}}X$
. Then we have a sequence
$0=X_{0},X_{1},\ldots ,X_{n}=X$
in
$D^{b}({\mathcal{A}})$
such that
${X_{i-1}\leqslant }_{\unicode[STIX]{x1D6E5}+\text{nil}}X_{i}$
and
$X_{i}\neq 0$
for
$i=1,\ldots ,n$
. By assertion 1, we know that all
$X_{i}$
are in
${\mathcal{A}}$
. Replacing
$X$
by
$X_{1}$
if necessary, we get an object
$X\neq 0$
of
${\mathcal{A}}$
such that
$0\leqslant _{\unicode[STIX]{x1D6E5}+\text{nil}}X$
in
${\mathcal{D}}^{b}({\mathcal{A}})$
. We can fix a distinguished triangle
in
${\mathcal{D}}^{b}({\mathcal{A}})$
, where
$u$
is a nilpotent endomorphism of
$Q$
. The long exact sequence of homologies gives then an exact sequence
in
${\mathcal{A}}$
. But it is obvious that a nilpotent endomorphism of an object
$A^{\prime }\in {\mathcal{A}}$
can be a monomorphism or an epimorphism only in case
$A^{\prime }=0$
. We then get
$H^{j}(Q)=0$
for
$j=0,1$
, which in turn implies
$X=0$
and hence a contradiction.
Example 11. Proposition 10 applies to the case when
${\mathcal{A}}=R-\text{mod}$
is the category of finitely generated modules over a Noetherian integral domain
$R$
. Indeed, if
$U(R)$
denotes the group of units of
$R$
, then any element
$x\in R\setminus U(R)$
defines by multiplication a monomorphic endomorphism
$\unicode[STIX]{x1D707}=\unicode[STIX]{x1D707}_{x}:R\longrightarrow R$
in
$R-\text{mod}$
, which is not an isomorphism. Putting
$X:=R/Rx$
, we then get that
$0\leqslant _{\unicode[STIX]{x1D6E5}}X$
but
$0\not \preccurlyeq _{\unicode[STIX]{x1D6E5}+\text{nil}}X$
in
${\mathcal{D}}^{b}(R-\text{mod})$
.
Remark 12. Consider the situation of a triangulated category
${\mathcal{C}}_{K}^{\circ }$
and an object
$M$
of
${\mathcal{C}}_{K}^{\circ }$
with
$0\leqslant _{\text{cdeg}}M$
. It is not hard to see that, with the notations used in Definitions 2 and 4, we get
$M\simeq \unicode[STIX]{x1D6F7}(\operatorname{cone}(t_{Q}))$
with nilpotent endomorphism
$t_{Q}$
for some object
$Q$
in the category
${\mathcal{C}}_{V}^{\circ }$
corresponding to the degeneration data, and
$\unicode[STIX]{x1D6F7}$
the functor
${\mathcal{C}}_{V}^{\circ }\rightarrow {\mathcal{C}}_{K}$
. This, together with Remark 6, pinpoints the difference between degeneration and flat deformations.
