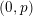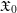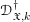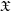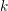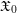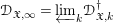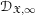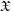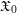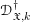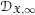1 Introduction
Let ![]() $\mathfrak{o}$ be a complete discrete valuation ring of mixed characteristic
$\mathfrak{o}$ be a complete discrete valuation ring of mixed characteristic ![]() $(0,p)$, with uniformizer
$(0,p)$, with uniformizer ![]() $\unicode[STIX]{x1D71B}$ and fraction field
$\unicode[STIX]{x1D71B}$ and fraction field ![]() $L$. In [Reference Patel, Schmidt and Strauch23], some of us (together with Patel) have introduced sheaves of arithmetic differential operators
$L$. In [Reference Patel, Schmidt and Strauch23], some of us (together with Patel) have introduced sheaves of arithmetic differential operators ![]() $\mathscr{D}_{n,k}^{\dagger }$ on certain semistable formal models
$\mathscr{D}_{n,k}^{\dagger }$ on certain semistable formal models ![]() $\mathfrak{X}_{n}$ of the rigid-analytic projective line over
$\mathfrak{X}_{n}$ of the rigid-analytic projective line over ![]() $L$ (for positive integers
$L$ (for positive integers ![]() $k\geqslant n$). A key result of [Reference Patel, Schmidt and Strauch23] is that
$k\geqslant n$). A key result of [Reference Patel, Schmidt and Strauch23] is that ![]() $\mathfrak{X}_{n}$ is
$\mathfrak{X}_{n}$ is ![]() $\mathscr{D}_{n,k}^{\dagger }$-affine. When
$\mathscr{D}_{n,k}^{\dagger }$-affine. When ![]() $n=0$, the formal model
$n=0$, the formal model ![]() $\mathfrak{X}_{0}$ is formally smooth over
$\mathfrak{X}_{0}$ is formally smooth over ![]() $\text{Spf}(\mathfrak{o})$, and the sheaf
$\text{Spf}(\mathfrak{o})$, and the sheaf ![]() $\mathscr{D}_{0,0}^{\dagger }$ equals Berthelot’s sheaf of arithmetic differential operators, as defined in [Reference Berthelot7], and
$\mathscr{D}_{0,0}^{\dagger }$ equals Berthelot’s sheaf of arithmetic differential operators, as defined in [Reference Berthelot7], and ![]() $\mathscr{D}_{0,0}^{\dagger }$-affinity was known before by a result of one of us [Reference Noot-Huyghe21].
$\mathscr{D}_{0,0}^{\dagger }$-affinity was known before by a result of one of us [Reference Noot-Huyghe21].
In this paper, we generalize the construction of [Reference Patel, Schmidt and Strauch23] and define and study sheaves of arithmetic differential operators on arbitrary admissible formal blow-ups of an arbitrary given smooth formal scheme ![]() $\mathfrak{X}_{0}$ over
$\mathfrak{X}_{0}$ over ![]() $\mathfrak{o}$.
$\mathfrak{o}$.
At the moment, the main application of this generalization is the localization theorem of [Reference Huyghe, Patel, Schmidt and Strauch18]: in this context ![]() $\mathfrak{X}_{0}$ is the smooth model of the flag variety of a connected split reductive group
$\mathfrak{X}_{0}$ is the smooth model of the flag variety of a connected split reductive group ![]() $\mathbb{G}$ over
$\mathbb{G}$ over ![]() $L$, and the main result of [Reference Huyghe, Patel, Schmidt and Strauch18] establishes then an anti-equivalence between the category of admissible locally analytic
$L$, and the main result of [Reference Huyghe, Patel, Schmidt and Strauch18] establishes then an anti-equivalence between the category of admissible locally analytic ![]() $\mathbb{G}(L)$-representations (with trivial character) [Reference Schneider and Teitelbaum24] and the category of so-called coadmissible equivariant arithmetic
$\mathbb{G}(L)$-representations (with trivial character) [Reference Schneider and Teitelbaum24] and the category of so-called coadmissible equivariant arithmetic ![]() $\mathscr{D}$-modules on the system of all formal models of the rigid-analytic flag variety of
$\mathscr{D}$-modules on the system of all formal models of the rigid-analytic flag variety of ![]() $\mathbb{G}$.
$\mathbb{G}$.
In the following, we describe the construction and the main results of this article. Let ![]() $\mathfrak{X}_{0}$ be a smooth formal scheme over
$\mathfrak{X}_{0}$ be a smooth formal scheme over ![]() $\mathfrak{o}$ and let
$\mathfrak{o}$ and let ![]() $\mathscr{D}_{\mathfrak{X}_{0}}^{(m)}$ be Berthelot’s sheaf of arithmetic differential operators of level
$\mathscr{D}_{\mathfrak{X}_{0}}^{(m)}$ be Berthelot’s sheaf of arithmetic differential operators of level ![]() $m$ on
$m$ on ![]() $\mathfrak{X}_{0}$ as defined in [Reference Berthelot7]. For any number
$\mathfrak{X}_{0}$ as defined in [Reference Berthelot7]. For any number ![]() $k\geqslant 0$, we have the subalgebra
$k\geqslant 0$, we have the subalgebra ![]() $\mathscr{D}_{\mathfrak{X}_{0}}^{(k,m)}$ consisting of those differential operators which are generated, locally where we have coordinates
$\mathscr{D}_{\mathfrak{X}_{0}}^{(k,m)}$ consisting of those differential operators which are generated, locally where we have coordinates ![]() $x_{1},\ldots ,x_{M}$ and corresponding derivations
$x_{1},\ldots ,x_{M}$ and corresponding derivations ![]() $\unicode[STIX]{x2202}_{1},\ldots ,\unicode[STIX]{x2202}_{M}$, by operators of the form
$\unicode[STIX]{x2202}_{1},\ldots ,\unicode[STIX]{x2202}_{M}$, by operators of the form
Given an admissible blow-up ![]() $\text{pr}:\mathfrak{X}\rightarrow \mathfrak{X}_{0}$, we let
$\text{pr}:\mathfrak{X}\rightarrow \mathfrak{X}_{0}$, we let ![]() $k_{\mathfrak{X}}$ be the minimal
$k_{\mathfrak{X}}$ be the minimal ![]() $k$ such that
$k$ such that ![]() $\unicode[STIX]{x1D71B}^{k}{\mathcal{O}}_{\mathfrak{X}}\subset {\mathcal{I}}$ for any coherent ideal sheaf
$\unicode[STIX]{x1D71B}^{k}{\mathcal{O}}_{\mathfrak{X}}\subset {\mathcal{I}}$ for any coherent ideal sheaf ![]() ${\mathcal{I}}$ on
${\mathcal{I}}$ on ![]() $\mathfrak{X}_{0}$ whose blow-up is
$\mathfrak{X}_{0}$ whose blow-up is ![]() $\mathfrak{X}$. Our first basic result, see 2.1.15, says that
$\mathfrak{X}$. Our first basic result, see 2.1.15, says that
is naturally a sheaf of rings on ![]() $\mathfrak{X}$ whenever
$\mathfrak{X}$ whenever ![]() $k\geqslant k_{\mathfrak{X}}$. We define
$k\geqslant k_{\mathfrak{X}}$. We define
and call these sheaves arithmetic differential operators of congruence level ![]() $\!$Footnote 1
$\!$Footnote 1 ![]() $k$ on
$k$ on ![]() $\mathfrak{X}$.
$\mathfrak{X}$.
The structure theory of these differential operators goes largely parallel to the classical smooth setting (when ![]() $\mathfrak{X}=\mathfrak{X}_{0}$ and
$\mathfrak{X}=\mathfrak{X}_{0}$ and ![]() $k=0$), as developed by Berthelot [Reference Berthelot7]. In particular, the sheaves
$k=0$), as developed by Berthelot [Reference Berthelot7]. In particular, the sheaves ![]() $\mathscr{D}_{\mathfrak{X}}^{(k,m)},\widehat{\mathscr{D}}_{\mathfrak{X}}^{(k,m)}$ and
$\mathscr{D}_{\mathfrak{X}}^{(k,m)},\widehat{\mathscr{D}}_{\mathfrak{X}}^{(k,m)}$ and ![]() $\mathscr{D}_{\mathfrak{X},k}^{\dagger }$ are sheaves of coherent rings on
$\mathscr{D}_{\mathfrak{X},k}^{\dagger }$ are sheaves of coherent rings on ![]() $\mathfrak{X}$. We then show that Cartan’s theorems A and B hold for the sheaf
$\mathfrak{X}$. We then show that Cartan’s theorems A and B hold for the sheaf ![]() $\mathscr{D}_{\mathfrak{X},k}^{\dagger }$, when restricted to an affine open subscheme
$\mathscr{D}_{\mathfrak{X},k}^{\dagger }$, when restricted to an affine open subscheme ![]() $\mathfrak{U}$ of
$\mathfrak{U}$ of ![]() $\mathfrak{X}$, see 2.2.15. This means that the global sections functor
$\mathfrak{X}$, see 2.2.15. This means that the global sections functor ![]() $\unicode[STIX]{x1D6E4}(\mathfrak{U},-)$ furnishes an equivalence of categories between the coherent modules over
$\unicode[STIX]{x1D6E4}(\mathfrak{U},-)$ furnishes an equivalence of categories between the coherent modules over ![]() $\mathscr{D}_{\mathfrak{U},k}^{\dagger }$ and over
$\mathscr{D}_{\mathfrak{U},k}^{\dagger }$ and over ![]() $\unicode[STIX]{x1D6E4}(\mathfrak{U},\mathscr{D}_{\mathfrak{X},k}^{\dagger })$, respectively. A key result (the “invariance theorem”) shows that in case of a morphism
$\unicode[STIX]{x1D6E4}(\mathfrak{U},\mathscr{D}_{\mathfrak{X},k}^{\dagger })$, respectively. A key result (the “invariance theorem”) shows that in case of a morphism ![]() $\mathfrak{X}^{\prime }\rightarrow \mathfrak{X}$ between admissible blow-ups of
$\mathfrak{X}^{\prime }\rightarrow \mathfrak{X}$ between admissible blow-ups of ![]() $\mathfrak{X}_{0}$, the categories of coherent modules over
$\mathfrak{X}_{0}$, the categories of coherent modules over ![]() $\mathscr{D}_{\mathfrak{X}^{\prime },k}^{\dagger }$ and over
$\mathscr{D}_{\mathfrak{X}^{\prime },k}^{\dagger }$ and over ![]() $\mathscr{D}_{\mathfrak{X},k}^{\dagger }$, respectively, are naturally equivalent, see 2.3.8. As a consequence, we obtain global versions of theorems A and B on the whole blow-up
$\mathscr{D}_{\mathfrak{X},k}^{\dagger }$, respectively, are naturally equivalent, see 2.3.8. As a consequence, we obtain global versions of theorems A and B on the whole blow-up ![]() $\mathfrak{X}$ provided the base
$\mathfrak{X}$ provided the base ![]() $\mathfrak{X}_{0}$ is affine, see 2.3.12.
$\mathfrak{X}_{0}$ is affine, see 2.3.12.
Our next objective is to pass to the projective limit
and to define the category ![]() ${\mathcal{C}}_{\mathfrak{X}}$ of coadmissible
${\mathcal{C}}_{\mathfrak{X}}$ of coadmissible ![]() $\mathscr{D}_{\mathfrak{X},\infty }$-modules. We show that it is a full abelian subcategory of the category of all
$\mathscr{D}_{\mathfrak{X},\infty }$-modules. We show that it is a full abelian subcategory of the category of all ![]() $\mathscr{D}_{\mathfrak{X},\infty }$-modules. Its construction relies on the fact that the ring of local sections
$\mathscr{D}_{\mathfrak{X},\infty }$-modules. Its construction relies on the fact that the ring of local sections ![]() $\unicode[STIX]{x1D6E4}(\mathfrak{V},\mathscr{D}_{\mathfrak{X},\infty })$ over an open affine
$\unicode[STIX]{x1D6E4}(\mathfrak{V},\mathscr{D}_{\mathfrak{X},\infty })$ over an open affine ![]() $\mathfrak{V}$ of
$\mathfrak{V}$ of ![]() $\mathfrak{X}$ is a Fréchet–Stein algebra. Our terminology (as well as the general philosophy behind these constructions) goes back to the fundamental work of Schneider and Teitelbaum who introduced the concept of a Fréchet–Stein algebra and defined and studied the category of coadmissible modules over such a ring, see [Reference Schneider and Teitelbaum24]. In fact, we show that the global sections functor
$\mathfrak{X}$ is a Fréchet–Stein algebra. Our terminology (as well as the general philosophy behind these constructions) goes back to the fundamental work of Schneider and Teitelbaum who introduced the concept of a Fréchet–Stein algebra and defined and studied the category of coadmissible modules over such a ring, see [Reference Schneider and Teitelbaum24]. In fact, we show that the global sections functor ![]() $\unicode[STIX]{x1D6E4}(\mathfrak{V},-)$ induces an equivalence of categories between
$\unicode[STIX]{x1D6E4}(\mathfrak{V},-)$ induces an equivalence of categories between ![]() ${\mathcal{C}}_{\mathfrak{V}}$ and the category of coadmissible
${\mathcal{C}}_{\mathfrak{V}}$ and the category of coadmissible ![]() $\unicode[STIX]{x1D6E4}(\mathfrak{V},\mathscr{D}_{\mathfrak{X},\infty })$-modules, see 3.1.13. Moreover, any coadmissible
$\unicode[STIX]{x1D6E4}(\mathfrak{V},\mathscr{D}_{\mathfrak{X},\infty })$-modules, see 3.1.13. Moreover, any coadmissible ![]() $\mathscr{D}_{\mathfrak{X},\infty }$-module has vanishing higher cohomology on
$\mathscr{D}_{\mathfrak{X},\infty }$-module has vanishing higher cohomology on ![]() $\mathfrak{V}$ (or on preimages of open affines in
$\mathfrak{V}$ (or on preimages of open affines in ![]() $\mathfrak{X}_{0}$). These results should be regarded as Cartan’s theorems A and B in this setting, see 3.1.13 and 3.1.16.
$\mathfrak{X}_{0}$). These results should be regarded as Cartan’s theorems A and B in this setting, see 3.1.13 and 3.1.16.
Finally we consider the Zariski–Riemann space of ![]() $\mathfrak{X}_{0}$, that is, the projective limit
$\mathfrak{X}_{0}$, that is, the projective limit
of all admissible formal blow-ups ![]() $\mathfrak{X}\rightarrow \mathfrak{X}_{0}$, see [Reference Bosch9]. One can then form the inductive limit
$\mathfrak{X}\rightarrow \mathfrak{X}_{0}$, see [Reference Bosch9]. One can then form the inductive limit
where ![]() $\text{sp}_{\mathfrak{X}}:\langle \mathfrak{X}_{0}\rangle \rightarrow \mathfrak{X}$ is the projection map. This is a sheaf of rings on
$\text{sp}_{\mathfrak{X}}:\langle \mathfrak{X}_{0}\rangle \rightarrow \mathfrak{X}$ is the projection map. This is a sheaf of rings on ![]() $\langle \mathfrak{X}_{0}\rangle$. We define the category of coadmissible
$\langle \mathfrak{X}_{0}\rangle$. We define the category of coadmissible ![]() $\mathscr{D}_{\langle \mathfrak{X}_{0}\rangle }$-modules and show that it is an abelian category. We establish analogues of Cartan’s theorems A and B in this setting, see 3.2.6.
$\mathscr{D}_{\langle \mathfrak{X}_{0}\rangle }$-modules and show that it is an abelian category. We establish analogues of Cartan’s theorems A and B in this setting, see 3.2.6.
After we had developed much of the theory presented here (which began with [Reference Patel, Schmidt and Strauch22, Reference Patel, Schmidt and Strauch23]) we became aware of the article [Reference Shiho25] by Shiho, where he introduces sheaves of ![]() $p$-adic differential operators of negative level
$p$-adic differential operators of negative level ![]() $-m$, as they are called there. These are closely related to the sheaves considered here, where the congruence level
$-m$, as they are called there. These are closely related to the sheaves considered here, where the congruence level ![]() $k$ corresponds to Shiho’s level
$k$ corresponds to Shiho’s level ![]() $-m$. We are currently investigating the implications that Shiho’s work has in our context.
$-m$. We are currently investigating the implications that Shiho’s work has in our context.
We also want to mention that Ardakov and Wadsley are developing a theory of ![]() $D$-modules on general smooth rigid-analytic spaces, see [Reference Ardakov1, Reference Ardakov and Wadsley3, Reference Ardakov and Wadsley4]. In their work they consider deformations of crystalline differential operators (as in [Reference Ardakov and Wadsley5]), whereas we take as a starting point certain deformations of Berthelot’s arithmetic differential operators. Though we have not carried this out in the present paper, it is not too difficult to see that the category of coadmissible
$D$-modules on general smooth rigid-analytic spaces, see [Reference Ardakov1, Reference Ardakov and Wadsley3, Reference Ardakov and Wadsley4]. In their work they consider deformations of crystalline differential operators (as in [Reference Ardakov and Wadsley5]), whereas we take as a starting point certain deformations of Berthelot’s arithmetic differential operators. Though we have not carried this out in the present paper, it is not too difficult to see that the category of coadmissible ![]() $\mathscr{D}_{\langle \mathfrak{X}_{0}\rangle }$-modules as defined here, when pulled back to the site of the rigid-analytic space of classical points of
$\mathscr{D}_{\langle \mathfrak{X}_{0}\rangle }$-modules as defined here, when pulled back to the site of the rigid-analytic space of classical points of ![]() $\langle \mathfrak{X}_{0}\rangle$, coincides with the corresponding category studied in [Reference Ardakov1, Reference Ardakov and Wadsley3, Reference Ardakov and Wadsley4].
$\langle \mathfrak{X}_{0}\rangle$, coincides with the corresponding category studied in [Reference Ardakov1, Reference Ardakov and Wadsley3, Reference Ardakov and Wadsley4].
Notations and conventions. We denote by ![]() $\unicode[STIX]{x1D71B}$ a uniformizer of the complete discrete valuation ring
$\unicode[STIX]{x1D71B}$ a uniformizer of the complete discrete valuation ring ![]() $\mathfrak{o}$, and we let
$\mathfrak{o}$, and we let ![]() $|.|_{p}$ be the absolute value on
$|.|_{p}$ be the absolute value on ![]() $L=\text{Frac}(\mathfrak{o})$ which is normalized by
$L=\text{Frac}(\mathfrak{o})$ which is normalized by ![]() $|p|_{p}=p^{-1}$. Throughout this paper,
$|p|_{p}=p^{-1}$. Throughout this paper, ![]() $\mathfrak{S}=\text{Spf}(\mathfrak{o})$. A formal scheme
$\mathfrak{S}=\text{Spf}(\mathfrak{o})$. A formal scheme ![]() $\mathfrak{X}$ over
$\mathfrak{X}$ over ![]() $\mathfrak{S}$ such that
$\mathfrak{S}$ such that ![]() $\unicode[STIX]{x1D71B}{\mathcal{O}}_{\mathfrak{X}}$ is an ideal of definition and which is locally noetherian is called a
$\unicode[STIX]{x1D71B}{\mathcal{O}}_{\mathfrak{X}}$ is an ideal of definition and which is locally noetherian is called a ![]() $\mathfrak{S}$-formal scheme. If the
$\mathfrak{S}$-formal scheme. If the ![]() $\mathfrak{S}$-formal scheme
$\mathfrak{S}$-formal scheme ![]() $\mathfrak{X}$ is smooth over
$\mathfrak{X}$ is smooth over ![]() $\mathfrak{S}$ we denote by
$\mathfrak{S}$ we denote by ![]() $\mathscr{T}_{\mathfrak{X}}$ its relative tangent sheaf. A coherent sheaf of ideals
$\mathscr{T}_{\mathfrak{X}}$ its relative tangent sheaf. A coherent sheaf of ideals ![]() ${\mathcal{I}}\subset {\mathcal{O}}_{\mathfrak{X}}$ is called open if for any open
${\mathcal{I}}\subset {\mathcal{O}}_{\mathfrak{X}}$ is called open if for any open ![]() $\mathfrak{U}\subset \mathfrak{X}$ the restriction of
$\mathfrak{U}\subset \mathfrak{X}$ the restriction of ![]() ${\mathcal{I}}$ to
${\mathcal{I}}$ to ![]() $\mathfrak{U}$ contains
$\mathfrak{U}$ contains ![]() $\unicode[STIX]{x1D71B}^{k}{\mathcal{O}}_{\mathfrak{U}}$ (for some
$\unicode[STIX]{x1D71B}^{k}{\mathcal{O}}_{\mathfrak{U}}$ (for some ![]() $k\in \mathbb{N}$ depending on
$k\in \mathbb{N}$ depending on ![]() $\mathfrak{U}$). A formal scheme which arises from blowing up an open ideal sheaf on
$\mathfrak{U}$). A formal scheme which arises from blowing up an open ideal sheaf on ![]() $\mathfrak{X}$ will be called an admissible blow-up of
$\mathfrak{X}$ will be called an admissible blow-up of ![]() $\mathfrak{X}$. For an integer
$\mathfrak{X}$. For an integer ![]() $i\geqslant 0$ we also denote
$i\geqslant 0$ we also denote ![]() $X_{i}$ the scheme
$X_{i}$ the scheme
where the Cartesian product is taken in the category of locally ringed spaces. Without further mentioning, all occurring modules will be left modules. We let ![]() $\mathbb{N}=\{0,1,2,\ldots \}$ be the set of nonnegative integers.
$\mathbb{N}=\{0,1,2,\ldots \}$ be the set of nonnegative integers.
2 Arithmetic differential operators with congruence level
Let ![]() $\mathfrak{X}_{0}$ be a smooth and separated
$\mathfrak{X}_{0}$ be a smooth and separated ![]() $\mathfrak{S}$-formal scheme, and let
$\mathfrak{S}$-formal scheme, and let
Let us write ![]() ${\mathcal{I}}_{\unicode[STIX]{x1D6E5}}$ for the diagonal ideal of the closed immersion of formal schemes
${\mathcal{I}}_{\unicode[STIX]{x1D6E5}}$ for the diagonal ideal of the closed immersion of formal schemes ![]() $\mathfrak{X}_{0}{\hookrightarrow}\mathfrak{X}_{0}\times \mathfrak{X}_{0}$ and
$\mathfrak{X}_{0}{\hookrightarrow}\mathfrak{X}_{0}\times \mathfrak{X}_{0}$ and ![]() ${\mathcal{I}}_{\unicode[STIX]{x1D6E5},i}$ for the diagonal ideal:
${\mathcal{I}}_{\unicode[STIX]{x1D6E5},i}$ for the diagonal ideal: ![]() $X_{0,i}{\hookrightarrow}X_{0,i}\times X_{0,i}$. We also introduce
$X_{0,i}{\hookrightarrow}X_{0,i}\times X_{0,i}$. We also introduce ![]() $\mathfrak{X}_{0,\mathbb{Q}}$, the generic fiber of
$\mathfrak{X}_{0,\mathbb{Q}}$, the generic fiber of ![]() $\mathfrak{X}_{0}$. It is a rigid-analytic space over
$\mathfrak{X}_{0}$. It is a rigid-analytic space over ![]() $L$. We write
$L$. We write ![]() $\overline{{\mathcal{I}}}_{\unicode[STIX]{x1D6E5}}$ for the diagonal ideal of the closed immersion of analytic spaces
$\overline{{\mathcal{I}}}_{\unicode[STIX]{x1D6E5}}$ for the diagonal ideal of the closed immersion of analytic spaces ![]() $\mathfrak{X}_{0,\mathbb{Q}}{\hookrightarrow}\mathfrak{X}_{0,\mathbb{Q}}\times \mathfrak{X}_{0,\mathbb{Q}}$. We have specialization maps
$\mathfrak{X}_{0,\mathbb{Q}}{\hookrightarrow}\mathfrak{X}_{0,\mathbb{Q}}\times \mathfrak{X}_{0,\mathbb{Q}}$. We have specialization maps ![]() $\mathfrak{X}_{0,\mathbb{Q}}\rightarrow \mathfrak{X}_{0}$ and
$\mathfrak{X}_{0,\mathbb{Q}}\rightarrow \mathfrak{X}_{0}$ and ![]() $\mathfrak{X}_{0,\mathbb{Q}}\times \mathfrak{X}_{0,\mathbb{Q}}\rightarrow \mathfrak{X}_{0}\times \mathfrak{X}_{0}$ which we denote by
$\mathfrak{X}_{0,\mathbb{Q}}\times \mathfrak{X}_{0,\mathbb{Q}}\rightarrow \mathfrak{X}_{0}\times \mathfrak{X}_{0}$ which we denote by ![]() $\text{sp}$. There is a canonical isomorphism
$\text{sp}$. There is a canonical isomorphism ![]() $\text{sp}^{\ast }({\mathcal{I}}_{\unicode[STIX]{x1D6E5}})\simeq \overline{{\mathcal{I}}}_{\unicode[STIX]{x1D6E5}}$. Finally, the relative tangent sheaf
$\text{sp}^{\ast }({\mathcal{I}}_{\unicode[STIX]{x1D6E5}})\simeq \overline{{\mathcal{I}}}_{\unicode[STIX]{x1D6E5}}$. Finally, the relative tangent sheaf ![]() $\mathscr{T}_{\mathfrak{X}_{0}}$ is a locally free
$\mathscr{T}_{\mathfrak{X}_{0}}$ is a locally free ![]() ${\mathcal{O}}_{\mathfrak{X}_{0}}$-module of finite rank equal to the relative dimension
${\mathcal{O}}_{\mathfrak{X}_{0}}$-module of finite rank equal to the relative dimension ![]() $M$ of
$M$ of ![]() $\mathfrak{X}_{0}$ over
$\mathfrak{X}_{0}$ over ![]() $\mathfrak{S}$.
$\mathfrak{S}$.
2.1 The main construction
2.1.1 Definitions over  $\mathfrak{X}_{0}$
$\mathfrak{X}_{0}$
The sheaf of relative differential operators of ![]() $X_{0,i}$ over
$X_{0,i}$ over ![]() $\mathfrak{o}/\unicode[STIX]{x1D71B}^{i+1}$, as introduced in [Reference Grothendieck13, 16.8], will be denoted by
$\mathfrak{o}/\unicode[STIX]{x1D71B}^{i+1}$, as introduced in [Reference Grothendieck13, 16.8], will be denoted by ![]() $\mathscr{D}_{X_{0,i}}$. It naturally acts on the structure sheaf
$\mathscr{D}_{X_{0,i}}$. It naturally acts on the structure sheaf ![]() ${\mathcal{O}}_{X_{0,i}}$. Its subsheaf
${\mathcal{O}}_{X_{0,i}}$. Its subsheaf ![]() $\mathscr{D}_{X_{0,i}}^{n}$ of differential operators of order
$\mathscr{D}_{X_{0,i}}^{n}$ of differential operators of order ![]() ${\leqslant}n$ is defined by
${\leqslant}n$ is defined by
It is a sheaf of locally free ![]() ${\mathcal{O}}_{X_{0,i}}$-modules of finite type and we have
${\mathcal{O}}_{X_{0,i}}$-modules of finite type and we have ![]() $\mathscr{D}_{X_{0,i}}=\mathop{\varinjlim }\nolimits_{n}\mathscr{D}_{X_{0,i}}^{n}$.
$\mathscr{D}_{X_{0,i}}=\mathop{\varinjlim }\nolimits_{n}\mathscr{D}_{X_{0,i}}^{n}$.
For fixed ![]() $n$, the projective limit
$n$, the projective limit ![]() $\mathop{\varprojlim }\nolimits_{i}\mathscr{D}_{X_{0,i}}^{n}$ is a locally free
$\mathop{\varprojlim }\nolimits_{i}\mathscr{D}_{X_{0,i}}^{n}$ is a locally free ![]() ${\mathcal{O}}_{\mathfrak{X}_{0}}$-module of finite type. Taking the inductive limit produces a sheaf of rings
${\mathcal{O}}_{\mathfrak{X}_{0}}$-module of finite type. Taking the inductive limit produces a sheaf of rings
on ![]() $\mathfrak{X}_{0}$. It naturally acts on the structure sheaf
$\mathfrak{X}_{0}$. It naturally acts on the structure sheaf ![]() ${\mathcal{O}}_{\mathfrak{X}_{0}}$ and can be described in local coordinates as follows. Let
${\mathcal{O}}_{\mathfrak{X}_{0}}$ and can be described in local coordinates as follows. Let ![]() $\mathfrak{U}_{0}\subseteq \mathfrak{X}_{0}$ be an open affine endowed with étale coordinates
$\mathfrak{U}_{0}\subseteq \mathfrak{X}_{0}$ be an open affine endowed with étale coordinates ![]() $x_{1},\ldots ,x_{M}$ and corresponding set of derivations
$x_{1},\ldots ,x_{M}$ and corresponding set of derivations ![]() $\unicode[STIX]{x2202}_{1},\ldots ,\unicode[STIX]{x2202}_{M}$. Write
$\unicode[STIX]{x2202}_{1},\ldots ,\unicode[STIX]{x2202}_{M}$. Write ![]() $\unicode[STIX]{x2202}_{l}^{[\unicode[STIX]{x1D708}]}\in \mathscr{D}_{\mathfrak{U}_{0}}$ for the differential operator defined by
$\unicode[STIX]{x2202}_{l}^{[\unicode[STIX]{x1D708}]}\in \mathscr{D}_{\mathfrak{U}_{0}}$ for the differential operator defined by ![]() $\unicode[STIX]{x1D708}!\unicode[STIX]{x2202}_{l}^{[\unicode[STIX]{x1D708}]}=\unicode[STIX]{x2202}_{l}^{\unicode[STIX]{x1D708}}$, and put
$\unicode[STIX]{x1D708}!\unicode[STIX]{x2202}_{l}^{[\unicode[STIX]{x1D708}]}=\unicode[STIX]{x2202}_{l}^{\unicode[STIX]{x1D708}}$, and put ![]() $\text{}\underline{\unicode[STIX]{x1D708}}=(\unicode[STIX]{x1D708}_{1},\ldots ,\unicode[STIX]{x1D708}_{M})\in \mathbb{N}^{M}$,
$\text{}\underline{\unicode[STIX]{x1D708}}=(\unicode[STIX]{x1D708}_{1},\ldots ,\unicode[STIX]{x1D708}_{M})\in \mathbb{N}^{M}$, ![]() $\text{}\underline{\unicode[STIX]{x2202}}^{[\text{}\underline{\unicode[STIX]{x1D708}}]}=\prod _{l=1}^{M}\unicode[STIX]{x2202}_{l}^{[\unicode[STIX]{x1D708}_{l}]}$. One has the following description, involving finite sums,
$\text{}\underline{\unicode[STIX]{x2202}}^{[\text{}\underline{\unicode[STIX]{x1D708}}]}=\prod _{l=1}^{M}\unicode[STIX]{x2202}_{l}^{[\unicode[STIX]{x1D708}_{l}]}$. One has the following description, involving finite sums,
Since ![]() $\mathfrak{X}_{0}$ is a smooth
$\mathfrak{X}_{0}$ is a smooth ![]() $\mathfrak{S}$-formal scheme, one also has the usual sheaves of arithmetic differential operators defined by Berthelot in [Reference Berthelot7]. In particular, for a fixed nonnegative
$\mathfrak{S}$-formal scheme, one also has the usual sheaves of arithmetic differential operators defined by Berthelot in [Reference Berthelot7]. In particular, for a fixed nonnegative ![]() $m$,
$m$, ![]() $\mathscr{D}_{\mathfrak{X}_{0}}^{(m)}$ will denote the sheaf of differential operators over
$\mathscr{D}_{\mathfrak{X}_{0}}^{(m)}$ will denote the sheaf of differential operators over ![]() $\mathfrak{X}_{0}$ of level
$\mathfrak{X}_{0}$ of level ![]() $m$. Taking
$m$. Taking ![]() $\mathfrak{U}_{0}$ to be endowed with local coordinates
$\mathfrak{U}_{0}$ to be endowed with local coordinates ![]() $x_{1},\ldots ,x_{M}$ as before, one introduces the following differential operators
$x_{1},\ldots ,x_{M}$ as before, one introduces the following differential operators
where ![]() $q_{\unicode[STIX]{x1D708}}$ denotes the quotient of the euclidean division of
$q_{\unicode[STIX]{x1D708}}$ denotes the quotient of the euclidean division of ![]() $\unicode[STIX]{x1D708}$ by
$\unicode[STIX]{x1D708}$ by ![]() $p^{m}$. For
$p^{m}$. For ![]() $\text{}\underline{\unicode[STIX]{x1D708}}=(\unicode[STIX]{x1D708}_{1},\ldots ,\unicode[STIX]{x1D708}_{M})\in \mathbb{N}^{M}$, we also define
$\text{}\underline{\unicode[STIX]{x1D708}}=(\unicode[STIX]{x1D708}_{1},\ldots ,\unicode[STIX]{x1D708}_{M})\in \mathbb{N}^{M}$, we also define ![]() $\text{}\underline{\unicode[STIX]{x2202}}^{\langle \text{}\underline{\unicode[STIX]{x1D708}}\rangle }=\prod _{l=1}^{M}\unicode[STIX]{x2202}_{l}^{\langle \unicode[STIX]{x1D708}_{l}\rangle }$. Restricted to
$\text{}\underline{\unicode[STIX]{x2202}}^{\langle \text{}\underline{\unicode[STIX]{x1D708}}\rangle }=\prod _{l=1}^{M}\unicode[STIX]{x2202}_{l}^{\langle \unicode[STIX]{x1D708}_{l}\rangle }$. Restricted to ![]() $\mathfrak{U}_{0}$, the sheaf
$\mathfrak{U}_{0}$, the sheaf ![]() $\mathscr{D}_{\mathfrak{X}_{0}}^{(m)}$ is a sheaf of free
$\mathscr{D}_{\mathfrak{X}_{0}}^{(m)}$ is a sheaf of free ![]() ${\mathcal{O}}_{\mathfrak{U}_{0}}$-modules with basis given by the elements
${\mathcal{O}}_{\mathfrak{U}_{0}}$-modules with basis given by the elements ![]() $\text{}\underline{\unicode[STIX]{x2202}}^{\langle \text{}\underline{\unicode[STIX]{x1D708}}\rangle }$. Berthelot also introduces the following sheaves over
$\text{}\underline{\unicode[STIX]{x2202}}^{\langle \text{}\underline{\unicode[STIX]{x1D708}}\rangle }$. Berthelot also introduces the following sheaves over ![]() $\mathfrak{X}_{0}$
$\mathfrak{X}_{0}$
Let ![]() $k$ be a nonnegative integer, called a congruence level. We define subsheaves
$k$ be a nonnegative integer, called a congruence level. We define subsheaves ![]() $\mathscr{D}_{\mathfrak{X}_{0}}^{(k,m)}$ of subalgebras of the previous sheaves
$\mathscr{D}_{\mathfrak{X}_{0}}^{(k,m)}$ of subalgebras of the previous sheaves ![]() $\mathscr{D}_{\mathfrak{X}_{0}}^{(m)}$ in the following way. Take
$\mathscr{D}_{\mathfrak{X}_{0}}^{(m)}$ in the following way. Take ![]() $\mathfrak{U}_{0}$ endowed with local coordinates
$\mathfrak{U}_{0}$ endowed with local coordinates ![]() $x_{1},\ldots ,x_{M}$ as before. Then the sheaf
$x_{1},\ldots ,x_{M}$ as before. Then the sheaf ![]() $\mathscr{D}_{\mathfrak{X}_{0}}^{(k,m)}$ is free over
$\mathscr{D}_{\mathfrak{X}_{0}}^{(k,m)}$ is free over ![]() $\mathfrak{U}_{0}$ as a sheaf of
$\mathfrak{U}_{0}$ as a sheaf of ![]() ${\mathcal{O}}_{\mathfrak{U}_{0}}$-modules with a basis given by the elements
${\mathcal{O}}_{\mathfrak{U}_{0}}$-modules with a basis given by the elements ![]() $\unicode[STIX]{x1D71B}^{k|\text{}\underline{\unicode[STIX]{x1D708}}|}\text{}\underline{\unicode[STIX]{x2202}}^{\langle \text{}\underline{\unicode[STIX]{x1D708}}\rangle }$. In particular, one has
$\unicode[STIX]{x1D71B}^{k|\text{}\underline{\unicode[STIX]{x1D708}}|}\text{}\underline{\unicode[STIX]{x2202}}^{\langle \text{}\underline{\unicode[STIX]{x1D708}}\rangle }$. In particular, one has
It is easy to check that these sheaves define a subsheaf of ![]() $\mathscr{D}_{\mathfrak{X}_{0}}^{(m)}$ and we call them level
$\mathscr{D}_{\mathfrak{X}_{0}}^{(m)}$ and we call them level ![]() $m$arithmetic differential operators of congruence level
$m$arithmetic differential operators of congruence level ![]() $k$on
$k$on ![]() $\mathfrak{X}_{0}$. We then define as before
$\mathfrak{X}_{0}$. We then define as before
Of course, for ![]() $k=0$ one recovers the sheaves of Berthelot
$k=0$ one recovers the sheaves of Berthelot ![]() $\mathscr{D}_{\mathfrak{X}_{0}}^{(0,m)}=\mathscr{D}_{\mathfrak{X}_{0}}^{(m)}$. Note also, by definition, the sheaf
$\mathscr{D}_{\mathfrak{X}_{0}}^{(0,m)}=\mathscr{D}_{\mathfrak{X}_{0}}^{(m)}$. Note also, by definition, the sheaf ![]() $\mathscr{D}_{\mathfrak{X}_{0},k}^{\dagger }$ is a sheaf of
$\mathscr{D}_{\mathfrak{X}_{0},k}^{\dagger }$ is a sheaf of ![]() $\mathbb{Q}$-algebras.
$\mathbb{Q}$-algebras.
We have the following description over an affine open ![]() $\mathfrak{U}_{0}$ of
$\mathfrak{U}_{0}$ of ![]() $\mathfrak{X}_{0}$ endowed with coordinates
$\mathfrak{X}_{0}$ endowed with coordinates ![]() $x_{1},\ldots ,x_{M}$,
$x_{1},\ldots ,x_{M}$,
where ![]() $|\cdot |$ is any Banach norm on the affinoid algebra
$|\cdot |$ is any Banach norm on the affinoid algebra ![]() ${\mathcal{O}}_{\mathfrak{X}_{0},\mathbb{Q}}(\mathfrak{U}_{0})$.
${\mathcal{O}}_{\mathfrak{X}_{0},\mathbb{Q}}(\mathfrak{U}_{0})$.
2.1.5 Definitions over  $\mathfrak{X}_{0,\mathbb{Q}}$
$\mathfrak{X}_{0,\mathbb{Q}}$
We refer to [Reference Chiarellotto and Le Stum10, 1.1.1] for a basic discussion of the sheaf of algebraic differential operators over a smooth rigid-analytic space such as ![]() $\mathfrak{X}_{0,\mathbb{Q}}$. It is defined in the following way, analogously to the definition given in [Reference Grothendieck13, 16.8] which we have recalled in 2.1.1. As before,
$\mathfrak{X}_{0,\mathbb{Q}}$. It is defined in the following way, analogously to the definition given in [Reference Grothendieck13, 16.8] which we have recalled in 2.1.1. As before, ![]() $\overline{{\mathcal{I}}}_{\unicode[STIX]{x1D6E5}}$ denotes the diagonal ideal of the immersion
$\overline{{\mathcal{I}}}_{\unicode[STIX]{x1D6E5}}$ denotes the diagonal ideal of the immersion ![]() $\mathfrak{X}_{0,\mathbb{Q}}{\hookrightarrow}\mathfrak{X}_{0,\mathbb{Q}}\times \mathfrak{X}_{0,\mathbb{Q}}$. One puts
$\mathfrak{X}_{0,\mathbb{Q}}{\hookrightarrow}\mathfrak{X}_{0,\mathbb{Q}}\times \mathfrak{X}_{0,\mathbb{Q}}$. One puts
which is a sheaf of locally free ![]() ${\mathcal{O}}_{\mathfrak{X}_{0,\mathbb{Q}}}$-modules of finite type and
${\mathcal{O}}_{\mathfrak{X}_{0,\mathbb{Q}}}$-modules of finite type and ![]() $\mathscr{D}_{\mathfrak{X}_{0,\mathbb{Q}}}=\mathop{\varinjlim }\nolimits_{n}\mathscr{D}_{\mathfrak{X}_{0,\mathbb{Q}}}^{n}$. The latter is a sheaf of rings acting naturally on the structure sheaf
$\mathscr{D}_{\mathfrak{X}_{0,\mathbb{Q}}}=\mathop{\varinjlim }\nolimits_{n}\mathscr{D}_{\mathfrak{X}_{0,\mathbb{Q}}}^{n}$. The latter is a sheaf of rings acting naturally on the structure sheaf ![]() ${\mathcal{O}}_{\mathfrak{X}_{0,\mathbb{Q}}}$ of the rigid-analytic space
${\mathcal{O}}_{\mathfrak{X}_{0,\mathbb{Q}}}$ of the rigid-analytic space ![]() $\mathfrak{X}_{0,\mathbb{Q}}$.
$\mathfrak{X}_{0,\mathbb{Q}}$.
Suppose now that
is an admissible blow-up of the formal scheme ![]() $\mathfrak{X}_{0}$ defined by a coherent sheaf of open ideals
$\mathfrak{X}_{0}$ defined by a coherent sheaf of open ideals ![]() ${\mathcal{I}}$ of
${\mathcal{I}}$ of ![]() ${\mathcal{O}}_{\mathfrak{X}_{0}}$ containing
${\mathcal{O}}_{\mathfrak{X}_{0}}$ containing ![]() $\unicode[STIX]{x1D71B}^{k}$. We remark that the ideal
$\unicode[STIX]{x1D71B}^{k}$. We remark that the ideal ![]() ${\mathcal{I}}$ is not determined by the blow-up
${\mathcal{I}}$ is not determined by the blow-up ![]() $\text{pr}:\mathfrak{X}\rightarrow \mathfrak{X}_{0}$, that is, different open ideal sheaves can give rise to isomorphic blow-ups. (For example, the blow-ups defined by
$\text{pr}:\mathfrak{X}\rightarrow \mathfrak{X}_{0}$, that is, different open ideal sheaves can give rise to isomorphic blow-ups. (For example, the blow-ups defined by ![]() ${\mathcal{I}}$ and by
${\mathcal{I}}$ and by ![]() $\unicode[STIX]{x1D71B}^{n}{\mathcal{I}}$ are isomorphic as formal schemes over
$\unicode[STIX]{x1D71B}^{n}{\mathcal{I}}$ are isomorphic as formal schemes over ![]() $\mathfrak{X}_{0}$. The same holds for the ideals
$\mathfrak{X}_{0}$. The same holds for the ideals ![]() ${\mathcal{I}}$ and
${\mathcal{I}}$ and ![]() ${\mathcal{I}}^{r}$.) In the sequel of this article we denote by
${\mathcal{I}}^{r}$.) In the sequel of this article we denote by ![]() $k_{{\mathcal{I}}}$ the minimal
$k_{{\mathcal{I}}}$ the minimal ![]() $k$ such that
$k$ such that ![]() $\unicode[STIX]{x1D71B}^{k}\in {\mathcal{I}}$ and put
$\unicode[STIX]{x1D71B}^{k}\in {\mathcal{I}}$ and put
Let us define now for ![]() $k\geqslant k_{\mathfrak{X}}$ the
$k\geqslant k_{\mathfrak{X}}$ the ![]() ${\mathcal{O}}_{\mathfrak{X}}$-module
${\mathcal{O}}_{\mathfrak{X}}$-module
Note that ![]() $\mathscr{D}_{\mathfrak{X}}^{(k,m)}$ depends not only on the formal scheme
$\mathscr{D}_{\mathfrak{X}}^{(k,m)}$ depends not only on the formal scheme ![]() $\mathfrak{X}$, but also on the blow-up morphism
$\mathfrak{X}$, but also on the blow-up morphism ![]() $\text{pr}$, but we suppress this dependence in the notation. We have the following commutative diagram of ringed spaces, involving the specialization maps
$\text{pr}$, but we suppress this dependence in the notation. We have the following commutative diagram of ringed spaces, involving the specialization maps ![]() $\mathfrak{X}_{0,\mathbb{Q}}\rightarrow \mathfrak{X}_{0}$ and
$\mathfrak{X}_{0,\mathbb{Q}}\rightarrow \mathfrak{X}_{0}$ and ![]() $\mathfrak{X}_{\mathbb{Q}}\rightarrow \mathfrak{X}$, which we denote both by
$\mathfrak{X}_{\mathbb{Q}}\rightarrow \mathfrak{X}$, which we denote both by ![]() $\text{sp}$, and the isomorphism
$\text{sp}$, and the isomorphism ![]() $\tilde{\text{pr}}:\mathfrak{X}_{\mathbb{Q}}\stackrel{\simeq }{\longrightarrow }\mathfrak{X}_{0,\mathbb{Q}}$ induced by the morphism
$\tilde{\text{pr}}:\mathfrak{X}_{\mathbb{Q}}\stackrel{\simeq }{\longrightarrow }\mathfrak{X}_{0,\mathbb{Q}}$ induced by the morphism ![]() $\text{pr}$ on generic fibers:
$\text{pr}$ on generic fibers:

Note that ![]() $\mathscr{D}_{\mathfrak{X}_{\mathbb{Q}}}\simeq \tilde{\text{pr}}^{\ast }\mathscr{D}_{\mathfrak{X}_{0,\mathbb{Q}}}$ for the corresponding sheaves of differential operators on
$\mathscr{D}_{\mathfrak{X}_{\mathbb{Q}}}\simeq \tilde{\text{pr}}^{\ast }\mathscr{D}_{\mathfrak{X}_{0,\mathbb{Q}}}$ for the corresponding sheaves of differential operators on ![]() $\mathfrak{X}_{\mathbb{Q}}$, respectively
$\mathfrak{X}_{\mathbb{Q}}$, respectively ![]() $\mathfrak{X}_{0,\mathbb{Q}}$, as follows from the definition of these sheaves.
$\mathfrak{X}_{0,\mathbb{Q}}$, as follows from the definition of these sheaves.
(i) There is a canonical isomorphism
 $\mathscr{D}_{\mathfrak{X}_{0,\mathbb{Q}}}\simeq \text{sp}^{\ast }\mathscr{D}_{\mathfrak{X}_{0}}$ inducing an injective morphism of sheaves of rings
$\mathscr{D}_{\mathfrak{X}_{0,\mathbb{Q}}}\simeq \text{sp}^{\ast }\mathscr{D}_{\mathfrak{X}_{0}}$ inducing an injective morphism of sheaves of rings  $$\begin{eqnarray}\mathscr{D}_{\mathfrak{X}_{0}}{\hookrightarrow}\text{sp}_{\ast }\mathscr{D}_{\mathfrak{X}_{0,\mathbb{Q}}}.\end{eqnarray}$$
$$\begin{eqnarray}\mathscr{D}_{\mathfrak{X}_{0}}{\hookrightarrow}\text{sp}_{\ast }\mathscr{D}_{\mathfrak{X}_{0,\mathbb{Q}}}.\end{eqnarray}$$(ii) There is a canonical injective map of sheaves of abelian groups
which becomes an isomorphism upon tensoring with $$\begin{eqnarray}\mathscr{D}_{\mathfrak{X}}^{(k,m)}{\hookrightarrow}\text{sp}_{\ast }\mathscr{D}_{\mathfrak{X}_{\mathbb{Q}}},\end{eqnarray}$$
$$\begin{eqnarray}\mathscr{D}_{\mathfrak{X}}^{(k,m)}{\hookrightarrow}\text{sp}_{\ast }\mathscr{D}_{\mathfrak{X}_{\mathbb{Q}}},\end{eqnarray}$$ $\mathbb{Q}$.
$\mathbb{Q}$.
Proof. We have a canonical map ![]() ${\mathcal{O}}_{\mathfrak{X},\mathbb{Q}}\rightarrow \text{sp}_{\ast }{\mathcal{O}}_{\mathfrak{X}_{\mathbb{Q}}}$, that is locally an isomorphism over the formal scheme
${\mathcal{O}}_{\mathfrak{X},\mathbb{Q}}\rightarrow \text{sp}_{\ast }{\mathcal{O}}_{\mathfrak{X}_{\mathbb{Q}}}$, that is locally an isomorphism over the formal scheme ![]() $\mathfrak{X}$ (resp.
$\mathfrak{X}$ (resp. ![]() $\mathfrak{X}_{0}$) and is thus an isomorphism of sheaves. Let us begin by (i). We have a canonical map
$\mathfrak{X}_{0}$) and is thus an isomorphism of sheaves. Let us begin by (i). We have a canonical map ![]() $\mathscr{D}_{\mathfrak{X}_{0,\mathbb{Q}}}\rightarrow \text{sp}^{\ast }\mathscr{D}_{\mathfrak{X}_{0}}$. To check that this is an isomorphism, we can work locally on
$\mathscr{D}_{\mathfrak{X}_{0,\mathbb{Q}}}\rightarrow \text{sp}^{\ast }\mathscr{D}_{\mathfrak{X}_{0}}$. To check that this is an isomorphism, we can work locally on ![]() $\mathfrak{X}_{0}$ and assume that
$\mathfrak{X}_{0}$ and assume that ![]() $\mathfrak{X}_{0}$ is affine, endowed with local coordinates
$\mathfrak{X}_{0}$ is affine, endowed with local coordinates ![]() $x_{1},\ldots ,x_{M}$. Then, using notations 2.1.3 we see that both sheaves are free
$x_{1},\ldots ,x_{M}$. Then, using notations 2.1.3 we see that both sheaves are free ![]() ${\mathcal{O}}_{\mathfrak{X}_{0,\mathbb{Q}}}$-modules with basis
${\mathcal{O}}_{\mathfrak{X}_{0,\mathbb{Q}}}$-modules with basis ![]() $\text{}\underline{\unicode[STIX]{x2202}}^{\text{}\underline{\unicode[STIX]{x1D708}}}$ and
$\text{}\underline{\unicode[STIX]{x2202}}^{\text{}\underline{\unicode[STIX]{x1D708}}}$ and ![]() $\text{}\underline{\unicode[STIX]{x2202}}^{[\text{}\underline{\unicode[STIX]{x1D708}}]}$, respectively. The previous map takes
$\text{}\underline{\unicode[STIX]{x2202}}^{[\text{}\underline{\unicode[STIX]{x1D708}}]}$, respectively. The previous map takes ![]() $\text{}\underline{\unicode[STIX]{x2202}}^{\text{}\underline{\unicode[STIX]{x1D708}}}$ to
$\text{}\underline{\unicode[STIX]{x2202}}^{\text{}\underline{\unicode[STIX]{x1D708}}}$ to ![]() $\text{}\underline{\unicode[STIX]{x2202}}^{[\text{}\underline{\unicode[STIX]{x1D708}}]}\text{}\underline{\unicode[STIX]{x1D708}}!$ and is an isomorphism of sheaves of
$\text{}\underline{\unicode[STIX]{x2202}}^{[\text{}\underline{\unicode[STIX]{x1D708}}]}\text{}\underline{\unicode[STIX]{x1D708}}!$ and is an isomorphism of sheaves of ![]() ${\mathcal{O}}_{\mathfrak{X}_{0,\mathbb{Q}}}$-modules. We obtain the second map of (i) by adjunction and its injectivity follows again using local coordinates. As in [Reference Grothendieck13, 16.8.9], the ring structure on both sheaves makes use of the descriptions 2.1.2, respectively 2.1.6. That the map
${\mathcal{O}}_{\mathfrak{X}_{0,\mathbb{Q}}}$-modules. We obtain the second map of (i) by adjunction and its injectivity follows again using local coordinates. As in [Reference Grothendieck13, 16.8.9], the ring structure on both sheaves makes use of the descriptions 2.1.2, respectively 2.1.6. That the map ![]() $\mathscr{D}_{\mathfrak{X}_{0}}{\hookrightarrow}\text{sp}_{\ast }\mathscr{D}_{\mathfrak{X}_{0,\mathbb{Q}}}$ is compatible with ring structures comes from the fact that
$\mathscr{D}_{\mathfrak{X}_{0}}{\hookrightarrow}\text{sp}_{\ast }\mathscr{D}_{\mathfrak{X}_{0,\mathbb{Q}}}$ is compatible with ring structures comes from the fact that ![]() $\text{sp}^{\ast }({\mathcal{I}}_{\unicode[STIX]{x1D6E5}})\simeq \overline{{\mathcal{I}}}_{\unicode[STIX]{x1D6E5}}$ and
$\text{sp}^{\ast }({\mathcal{I}}_{\unicode[STIX]{x1D6E5}})\simeq \overline{{\mathcal{I}}}_{\unicode[STIX]{x1D6E5}}$ and
Let us prove (ii). From the previous isomorphism, we get an isomorphism
that induces a canonical map ![]() $\text{pr}^{\ast }\mathscr{D}_{\mathfrak{X}_{0}}\rightarrow \text{sp}_{\ast }\mathscr{D}_{\mathfrak{X}_{\mathbb{Q}}}$. Composing with the map
$\text{pr}^{\ast }\mathscr{D}_{\mathfrak{X}_{0}}\rightarrow \text{sp}_{\ast }\mathscr{D}_{\mathfrak{X}_{\mathbb{Q}}}$. Composing with the map ![]() $\mathscr{D}_{\mathfrak{X}_{0}}^{(k,m)}\rightarrow \mathscr{D}_{\mathfrak{X}_{0}}$ we get a map
$\mathscr{D}_{\mathfrak{X}_{0}}^{(k,m)}\rightarrow \mathscr{D}_{\mathfrak{X}_{0}}$ we get a map
It is a local question to prove that this map is injective. Let ![]() $\mathfrak{U}\subset \mathfrak{X}_{0}$ be an open affine formal scheme of
$\mathfrak{U}\subset \mathfrak{X}_{0}$ be an open affine formal scheme of ![]() $\mathfrak{X}_{0}$ such that
$\mathfrak{X}_{0}$ such that ![]() $\mathfrak{U}\subset \text{pr}^{-1}\mathfrak{U}_{0}$, with
$\mathfrak{U}\subset \text{pr}^{-1}\mathfrak{U}_{0}$, with ![]() $\mathfrak{U}_{0}$ endowed with local coordinates
$\mathfrak{U}_{0}$ endowed with local coordinates ![]() $x_{1},\ldots ,x_{M}$. Then these local coordinates give local coordinates always denoted
$x_{1},\ldots ,x_{M}$. Then these local coordinates give local coordinates always denoted ![]() $x_{1},\ldots ,x_{M}$ over the generic fiber
$x_{1},\ldots ,x_{M}$ over the generic fiber ![]() $\mathfrak{U}_{\mathbb{Q}}$ of
$\mathfrak{U}_{\mathbb{Q}}$ of ![]() $\mathfrak{U}$. Using notations 2.1.3, the sheaf
$\mathfrak{U}$. Using notations 2.1.3, the sheaf ![]() $\text{pr}^{\ast }\mathscr{D}_{\mathfrak{U}_{0}}^{(k,m)}$ is a free
$\text{pr}^{\ast }\mathscr{D}_{\mathfrak{U}_{0}}^{(k,m)}$ is a free ![]() ${\mathcal{O}}_{\mathfrak{U}}$-module with basis the operators
${\mathcal{O}}_{\mathfrak{U}}$-module with basis the operators ![]() $\unicode[STIX]{x1D71B}^{k|\text{}\underline{\unicode[STIX]{x1D708}}|}\text{}\underline{\unicode[STIX]{x2202}}^{\langle \text{}\underline{\unicode[STIX]{x1D708}}\rangle }$ whereas the sheaf
$\unicode[STIX]{x1D71B}^{k|\text{}\underline{\unicode[STIX]{x1D708}}|}\text{}\underline{\unicode[STIX]{x2202}}^{\langle \text{}\underline{\unicode[STIX]{x1D708}}\rangle }$ whereas the sheaf ![]() $\text{sp}_{\ast }\mathscr{D}_{\mathfrak{U}_{\mathbb{Q}}}$ is a free
$\text{sp}_{\ast }\mathscr{D}_{\mathfrak{U}_{\mathbb{Q}}}$ is a free ![]() ${\mathcal{O}}_{\mathfrak{U}}\otimes \mathbb{Q}$-module with basis
${\mathcal{O}}_{\mathfrak{U}}\otimes \mathbb{Q}$-module with basis ![]() $\text{}\underline{\unicode[STIX]{x2202}}^{\text{}\underline{\unicode[STIX]{x1D708}}}$. The map we consider takes
$\text{}\underline{\unicode[STIX]{x2202}}^{\text{}\underline{\unicode[STIX]{x1D708}}}$. The map we consider takes ![]() $\unicode[STIX]{x1D71B}^{k|\text{}\underline{\unicode[STIX]{x1D708}}|}\text{}\underline{\unicode[STIX]{x2202}}^{\langle \text{}\underline{\unicode[STIX]{x1D708}}\rangle }$ to
$\unicode[STIX]{x1D71B}^{k|\text{}\underline{\unicode[STIX]{x1D708}}|}\text{}\underline{\unicode[STIX]{x2202}}^{\langle \text{}\underline{\unicode[STIX]{x1D708}}\rangle }$ to ![]() $\unicode[STIX]{x1D71B}^{k|\text{}\underline{\unicode[STIX]{x1D708}}|}q_{\text{}\underline{\unicode[STIX]{x1D708}}}!/\text{}\underline{\unicode[STIX]{x1D708}}!\text{}\underline{\unicode[STIX]{x2202}}^{\text{}\underline{\unicode[STIX]{x1D708}}}$. Since
$\unicode[STIX]{x1D71B}^{k|\text{}\underline{\unicode[STIX]{x1D708}}|}q_{\text{}\underline{\unicode[STIX]{x1D708}}}!/\text{}\underline{\unicode[STIX]{x1D708}}!\text{}\underline{\unicode[STIX]{x2202}}^{\text{}\underline{\unicode[STIX]{x1D708}}}$. Since ![]() $\mathfrak{U}$ is flat over
$\mathfrak{U}$ is flat over ![]() $\mathfrak{o}$, the map
$\mathfrak{o}$, the map ![]() ${\mathcal{O}}_{\mathfrak{U}}\rightarrow {\mathcal{O}}_{\mathfrak{U}}\otimes \mathbb{Q}$ is injective, and this proves that the canonical map
${\mathcal{O}}_{\mathfrak{U}}\rightarrow {\mathcal{O}}_{\mathfrak{U}}\otimes \mathbb{Q}$ is injective, and this proves that the canonical map ![]() $\text{pr}^{\ast }\mathscr{D}_{\mathfrak{X}_{0}}^{(k,m)}\rightarrow \text{sp}_{\ast }\mathscr{D}_{\mathfrak{X}_{\mathbb{Q}}}$ is injective as well. The same argument shows that this map becomes an isomorphism upon tensoring with
$\text{pr}^{\ast }\mathscr{D}_{\mathfrak{X}_{0}}^{(k,m)}\rightarrow \text{sp}_{\ast }\mathscr{D}_{\mathfrak{X}_{\mathbb{Q}}}$ is injective as well. The same argument shows that this map becomes an isomorphism upon tensoring with ![]() $\mathbb{Q}$.◻
$\mathbb{Q}$.◻
Following [Reference Patel, Schmidt and Strauch23], given ![]() $k\geqslant k_{\mathfrak{X}}$, we will construct a
$k\geqslant k_{\mathfrak{X}}$, we will construct a ![]() $p$-adically complete sheaf of arithmetic differential operators
$p$-adically complete sheaf of arithmetic differential operators ![]() $\widehat{\mathscr{D}}_{\mathfrak{X}}^{(k,m)}$ over the (usually nonsmooth) formal scheme
$\widehat{\mathscr{D}}_{\mathfrak{X}}^{(k,m)}$ over the (usually nonsmooth) formal scheme ![]() $\mathfrak{X}$.
$\mathfrak{X}$.
2.1.9 Construction of the ring of differential operators of level  $k$ over
$k$ over  $\mathfrak{X}$
$\mathfrak{X}$
We first observe that the sheaf ![]() $\text{sp}_{\ast }\mathscr{D}_{\mathfrak{X}_{\mathbb{Q}}}$ acts on
$\text{sp}_{\ast }\mathscr{D}_{\mathfrak{X}_{\mathbb{Q}}}$ acts on ![]() $\text{sp}_{\ast }{\mathcal{O}}_{\mathfrak{X}_{\mathbb{Q}}}\simeq {\mathcal{O}}_{\mathfrak{X},\mathbb{Q}}$. By 2.1.8, the sheaf
$\text{sp}_{\ast }{\mathcal{O}}_{\mathfrak{X}_{\mathbb{Q}}}\simeq {\mathcal{O}}_{\mathfrak{X},\mathbb{Q}}$. By 2.1.8, the sheaf ![]() $\mathscr{D}_{\mathfrak{X}}^{(k,m)}$ is a subsheaf of
$\mathscr{D}_{\mathfrak{X}}^{(k,m)}$ is a subsheaf of ![]() $\text{sp}_{\ast }\mathscr{D}_{\mathfrak{X}_{\mathbb{Q}}}$ and
$\text{sp}_{\ast }\mathscr{D}_{\mathfrak{X}_{\mathbb{Q}}}$ and ![]() $\mathscr{D}_{\mathfrak{X},\mathbb{Q}}^{(k,m)}\simeq \text{sp}_{\ast }\mathscr{D}_{\mathfrak{X}_{\mathbb{Q}}}$. We will first check that if
$\mathscr{D}_{\mathfrak{X},\mathbb{Q}}^{(k,m)}\simeq \text{sp}_{\ast }\mathscr{D}_{\mathfrak{X}_{\mathbb{Q}}}$. We will first check that if ![]() $k\geqslant k_{\mathfrak{X}}$, the action of
$k\geqslant k_{\mathfrak{X}}$, the action of ![]() $\text{sp}_{\ast }\mathscr{D}_{\mathfrak{X}_{\mathbb{Q}}}$ on
$\text{sp}_{\ast }\mathscr{D}_{\mathfrak{X}_{\mathbb{Q}}}$ on ![]() ${\mathcal{O}}_{\mathfrak{X},\mathbb{Q}}$ restricts to an action of
${\mathcal{O}}_{\mathfrak{X},\mathbb{Q}}$ restricts to an action of ![]() $\mathscr{D}_{\mathfrak{X}}^{(k,m)}$ on
$\mathscr{D}_{\mathfrak{X}}^{(k,m)}$ on ![]() ${\mathcal{O}}_{\mathfrak{X}}$. This can be checked locally on
${\mathcal{O}}_{\mathfrak{X}}$. This can be checked locally on ![]() $\mathfrak{X}$. For this, we assume that
$\mathfrak{X}$. For this, we assume that ![]() $\mathfrak{X}_{0}=\text{Spf}A$, where
$\mathfrak{X}_{0}=\text{Spf}A$, where ![]() $A$ is a smooth, complete,
$A$ is a smooth, complete, ![]() $\mathfrak{o}$-algebra, endowed with local coordinates
$\mathfrak{o}$-algebra, endowed with local coordinates ![]() $x_{1},\ldots ,x_{M}$. Since
$x_{1},\ldots ,x_{M}$. Since ![]() $\mathfrak{X}_{0}$ is smooth over
$\mathfrak{X}_{0}$ is smooth over ![]() $\text{Spf}\mathfrak{o}$, both rings
$\text{Spf}\mathfrak{o}$, both rings ![]() $A$ and
$A$ and ![]() $A/\unicode[STIX]{x1D71B}A$ are integral domains. We also introduce the differential operators
$A/\unicode[STIX]{x1D71B}A$ are integral domains. We also introduce the differential operators ![]() $\text{}\underline{\unicode[STIX]{x2202}}^{\langle \text{}\underline{\unicode[STIX]{x1D708}}\rangle }$ and
$\text{}\underline{\unicode[STIX]{x2202}}^{\langle \text{}\underline{\unicode[STIX]{x1D708}}\rangle }$ and ![]() $\unicode[STIX]{x1D71B}^{k|\text{}\underline{\unicode[STIX]{x1D708}}|}\text{}\underline{\unicode[STIX]{x2202}}^{\langle \text{}\underline{\unicode[STIX]{x1D708}}\rangle }$ according to 2.1.3, of
$\unicode[STIX]{x1D71B}^{k|\text{}\underline{\unicode[STIX]{x1D708}}|}\text{}\underline{\unicode[STIX]{x2202}}^{\langle \text{}\underline{\unicode[STIX]{x1D708}}\rangle }$ according to 2.1.3, of ![]() $D^{(m)}=\unicode[STIX]{x1D6E4}(\mathfrak{X}_{0},\mathscr{D}_{\mathfrak{X}_{0}}^{(m)})$ and
$D^{(m)}=\unicode[STIX]{x1D6E4}(\mathfrak{X}_{0},\mathscr{D}_{\mathfrak{X}_{0}}^{(m)})$ and ![]() $D^{(k,m)}=\unicode[STIX]{x1D6E4}(\mathfrak{X}_{0},\mathscr{D}_{\mathfrak{X}_{0}}^{(k,m)})$, respectively. We also denote
$D^{(k,m)}=\unicode[STIX]{x1D6E4}(\mathfrak{X}_{0},\mathscr{D}_{\mathfrak{X}_{0}}^{(k,m)})$, respectively. We also denote ![]() $I=\unicode[STIX]{x1D6E4}(\mathfrak{X}_{0},{\mathcal{I}})$ where
$I=\unicode[STIX]{x1D6E4}(\mathfrak{X}_{0},{\mathcal{I}})$ where ![]() $V({\mathcal{I}})$ is the center of the blowing-up
$V({\mathcal{I}})$ is the center of the blowing-up ![]() $\mathfrak{X}$.
$\mathfrak{X}$.
Consider the ![]() $\mathbb{N}$-graded
$\mathbb{N}$-graded ![]() $A$-algebra
$A$-algebra
where the degree ![]() $n$-part
$n$-part ![]() $B_{n}$ equals the
$B_{n}$ equals the ![]() $n$th power
$n$th power ![]() $I^{n}$ of the ideal
$I^{n}$ of the ideal ![]() $I$. In particular,
$I$. In particular, ![]() $I^{0}=A$. This means that
$I^{0}=A$. This means that
the formal completion of ![]() $\text{Proj}(B)$. The algebra
$\text{Proj}(B)$. The algebra ![]() $B$ is integral, as
$B$ is integral, as ![]() $A$ is integral. Let
$A$ is integral. Let ![]() $t\in B_{D}$ be a homogeneous element of degree
$t\in B_{D}$ be a homogeneous element of degree ![]() $D>0$, and let
$D>0$, and let ![]() $C_{t}=B[1/t]_{0}$ be the algebra of degree
$C_{t}=B[1/t]_{0}$ be the algebra of degree ![]() $0$ elements in the homogeneous localization
$0$ elements in the homogeneous localization ![]() $B[1/t]$. Then
$B[1/t]$. Then ![]() $C_{t}$ is nonzero, since
$C_{t}$ is nonzero, since ![]() $B$ is integral. Put
$B$ is integral. Put ![]() $D_{+}(t)=\text{Spf}\;\widehat{C}_{t}$. These open sets form a basis for the Zariski topology of
$D_{+}(t)=\text{Spf}\;\widehat{C}_{t}$. These open sets form a basis for the Zariski topology of ![]() $\mathfrak{X}$.
$\mathfrak{X}$.
Let us observe that the algebra ![]() $B$ is a graded subalgebra of
$B$ is a graded subalgebra of ![]() $A[T]$. Indeed, there is a graded injective ring morphism
$A[T]$. Indeed, there is a graded injective ring morphism
By definition, ![]() $\unicode[STIX]{x1D711}(t)=tT^{D}$. Since localization is flat, we get from this an injective graded morphism
$\unicode[STIX]{x1D711}(t)=tT^{D}$. Since localization is flat, we get from this an injective graded morphism ![]() $B[1/t]\rightarrow A[1/t][T^{\pm 1}]$, where
$B[1/t]\rightarrow A[1/t][T^{\pm 1}]$, where ![]() $A[1/t][T^{\pm 1}]$ is graded by the degree of
$A[1/t][T^{\pm 1}]$ is graded by the degree of ![]() $T$. Because
$T$. Because ![]() $C_{t}=B[1/t]_{0}$ is the subring of degree zero elements in
$C_{t}=B[1/t]_{0}$ is the subring of degree zero elements in ![]() $B[1/t]$, we get an injection
$B[1/t]$, we get an injection
Since ![]() $A\{1/t\}=\unicode[STIX]{x1D6E4}(D(t),{\mathcal{O}}_{\mathfrak{X}_{0}})$, and because
$A\{1/t\}=\unicode[STIX]{x1D6E4}(D(t),{\mathcal{O}}_{\mathfrak{X}_{0}})$, and because ![]() $\mathscr{D}_{\mathfrak{X}_{0}}^{(k,m)}$ acts on the structure sheaf
$\mathscr{D}_{\mathfrak{X}_{0}}^{(k,m)}$ acts on the structure sheaf ![]() ${\mathcal{O}}_{\mathfrak{X}_{0}}$, we get that
${\mathcal{O}}_{\mathfrak{X}_{0}}$, we get that ![]() $A\{1/t\}$ is a
$A\{1/t\}$ is a ![]() $D^{(m)}$-module and thus a
$D^{(m)}$-module and thus a ![]() $D^{(k,m)}$-module. Moreover, as
$D^{(k,m)}$-module. Moreover, as ![]() $A[1/t]$ is integral and noetherian, it embeds into its
$A[1/t]$ is integral and noetherian, it embeds into its ![]() $p$-adic completion
$p$-adic completion ![]() $A\{1/t\}$. This leads us to the following
$A\{1/t\}$. This leads us to the following
(i)
 $A[1/t]$ is a
$A[1/t]$ is a  $D^{(m)}$-submodule of
$D^{(m)}$-submodule of  $A\{1/t\}$,
$A\{1/t\}$,(ii) If
 $k\geqslant k_{\mathfrak{X}}$, then
$k\geqslant k_{\mathfrak{X}}$, then  $C_{t}$ is a
$C_{t}$ is a  $D^{(k,m)}$-submodule of
$D^{(k,m)}$-submodule of  $A[1/t]$.
$A[1/t]$.
Proof. Before giving the proof, we need some notation. Given a fixed nonnegative integer ![]() $m$ and a nonnegative integer
$m$ and a nonnegative integer ![]() $\unicode[STIX]{x1D708}$, one denotes as before by
$\unicode[STIX]{x1D708}$, one denotes as before by ![]() $q$ the quotient of the Euclidean division of
$q$ the quotient of the Euclidean division of ![]() $\unicode[STIX]{x1D708}$ by
$\unicode[STIX]{x1D708}$ by ![]() $p^{m}$. Let
$p^{m}$. Let ![]() $\unicode[STIX]{x1D708}\geqslant \unicode[STIX]{x1D708}^{\prime }$ be two nonnegative integers and
$\unicode[STIX]{x1D708}\geqslant \unicode[STIX]{x1D708}^{\prime }$ be two nonnegative integers and ![]() $\unicode[STIX]{x1D708}^{\prime \prime }:=\unicode[STIX]{x1D708}-\unicode[STIX]{x1D708}^{\prime }$; then for the corresponding numbers
$\unicode[STIX]{x1D708}^{\prime \prime }:=\unicode[STIX]{x1D708}-\unicode[STIX]{x1D708}^{\prime }$; then for the corresponding numbers ![]() $q,q^{\prime }$ and
$q,q^{\prime }$ and ![]() $q^{\prime \prime }$, we define
$q^{\prime \prime }$, we define
which is an integer because ![]() $q\geqslant q^{\prime }+q^{\prime \prime }$. Let us begin with the proof of (i). It is enough to prove that for each
$q\geqslant q^{\prime }+q^{\prime \prime }$. Let us begin with the proof of (i). It is enough to prove that for each ![]() $i\leqslant M$, for each invertible
$i\leqslant M$, for each invertible ![]() $s\in A[1/t]$, for each
$s\in A[1/t]$, for each ![]() $\unicode[STIX]{x1D708}\in \mathbb{N}$,
$\unicode[STIX]{x1D708}\in \mathbb{N}$,
We will prove this by induction on ![]() $\unicode[STIX]{x1D708}$, the case
$\unicode[STIX]{x1D708}$, the case ![]() $\unicode[STIX]{x1D708}=0$ being straightforward. We have
$\unicode[STIX]{x1D708}=0$ being straightforward. We have
see [Reference Berthelot7, (iv) of 2.2.4]. By induction hypothesis the elements ![]() $\unicode[STIX]{x2202}_{i}^{\langle \unicode[STIX]{x1D707}\rangle }(s^{-1})$ lie in
$\unicode[STIX]{x2202}_{i}^{\langle \unicode[STIX]{x1D707}\rangle }(s^{-1})$ lie in ![]() $s^{-(\unicode[STIX]{x1D708}+1)}A$, which proves that
$s^{-(\unicode[STIX]{x1D708}+1)}A$, which proves that ![]() $\unicode[STIX]{x2202}_{i}^{\langle \unicode[STIX]{x1D708}+1\rangle }(s^{-1})\in s^{-(\unicode[STIX]{x1D708}+2)}A$. By applying this to
$\unicode[STIX]{x2202}_{i}^{\langle \unicode[STIX]{x1D708}+1\rangle }(s^{-1})\in s^{-(\unicode[STIX]{x1D708}+2)}A$. By applying this to ![]() $s=t^{-n}$ for
$s=t^{-n}$ for ![]() $n>0$, we see that (i) holds. Let us prove now (ii). We begin the proof with an auxiliary assertion (it is here where we use the assumption
$n>0$, we see that (i) holds. Let us prove now (ii). We begin the proof with an auxiliary assertion (it is here where we use the assumption ![]() $k\geqslant k_{\mathfrak{X}}$).
$k\geqslant k_{\mathfrak{X}}$).
Assertion. Let ![]() $f\in I^{r}$,
$f\in I^{r}$, ![]() $l\in \mathbb{N}$, then
$l\in \mathbb{N}$, then ![]() $\unicode[STIX]{x1D71B}^{kl}\unicode[STIX]{x2202}_{i}^{\langle l\rangle }(f)\in I^{r}$.
$\unicode[STIX]{x1D71B}^{kl}\unicode[STIX]{x2202}_{i}^{\langle l\rangle }(f)\in I^{r}$.
Proof of the assertion. The proof relies on the Leibniz formula [Reference Berthelot7, 2.3.4.1]. We proceed by induction on ![]() $r$. For
$r$. For ![]() $r=0$ the assertion is trivial and for
$r=0$ the assertion is trivial and for ![]() $r=1$, it is true if
$r=1$, it is true if ![]() $l\geqslant 1$ since
$l\geqslant 1$ since ![]() $\unicode[STIX]{x1D71B}^{k}\in I$. For
$\unicode[STIX]{x1D71B}^{k}\in I$. For ![]() $r=1$, it is also true if
$r=1$, it is also true if ![]() $l=0$ since
$l=0$ since ![]() $f\in I$. Let us assume that the result is true for
$f\in I$. Let us assume that the result is true for ![]() $s\leqslant r$. It is enough to prove that
$s\leqslant r$. It is enough to prove that
Denote ![]() $f=hg$, the Leibniz formula of [Reference Berthelot7, 2.3.4.1] states that
$f=hg$, the Leibniz formula of [Reference Berthelot7, 2.3.4.1] states that
By induction hypothesis, for all ![]() $j\leqslant l$,
$j\leqslant l$, ![]() $\unicode[STIX]{x1D71B}^{kj}\unicode[STIX]{x2202}_{i}^{\langle j\rangle }(h)\in I^{r}$ and
$\unicode[STIX]{x1D71B}^{kj}\unicode[STIX]{x2202}_{i}^{\langle j\rangle }(h)\in I^{r}$ and ![]() $\unicode[STIX]{x1D71B}^{k(l-j)}\unicode[STIX]{x2202}_{i}^{\langle l-j\rangle }(g)\in I$, which implies that
$\unicode[STIX]{x1D71B}^{k(l-j)}\unicode[STIX]{x2202}_{i}^{\langle l-j\rangle }(g)\in I$, which implies that ![]() $\unicode[STIX]{x1D71B}^{kl}\unicode[STIX]{x2202}_{i}^{\langle l\rangle }(f)\in I^{r+1}$. This establishes the assertion.
$\unicode[STIX]{x1D71B}^{kl}\unicode[STIX]{x2202}_{i}^{\langle l\rangle }(f)\in I^{r+1}$. This establishes the assertion.
After this preliminary discussion, let ![]() $d>0$. Let us first prove by induction on
$d>0$. Let us first prove by induction on ![]() $\unicode[STIX]{x1D708}$ that for an arbitrary element
$\unicode[STIX]{x1D708}$ that for an arbitrary element ![]() $s\in I^{d}$ which becomes invertible in
$s\in I^{d}$ which becomes invertible in ![]() $A[1/t]$, one has
$A[1/t]$, one has
This is true for ![]() $\unicode[STIX]{x1D708}=0$. Consider then the formula [Reference Berthelot7, (iv) of 2.2.4] with notation 2.1.12
$\unicode[STIX]{x1D708}=0$. Consider then the formula [Reference Berthelot7, (iv) of 2.2.4] with notation 2.1.12
By the induction hypothesis, one knows for any integer ![]() $\unicode[STIX]{x1D707}\leqslant \unicode[STIX]{x1D708}$,
$\unicode[STIX]{x1D707}\leqslant \unicode[STIX]{x1D708}$,
and, by our auxiliary assertion above, one knows
This implies
which proves our claim. Applying this claim to the element ![]() $s=t^{d}\in I^{dD}$ gives for
$s=t^{d}\in I^{dD}$ gives for ![]() $\unicode[STIX]{x1D707}\leqslant p^{m}$
$\unicode[STIX]{x1D707}\leqslant p^{m}$
Then, using again the Leibniz formula, we deduce from this and the auxiliary assertion, for a given homogeneous element ![]() $g\in B$ of degree
$g\in B$ of degree ![]() $dD$, that is,
$dD$, that is, ![]() $\frac{g}{t^{d}}\in C_{t}$, the identity
$\frac{g}{t^{d}}\in C_{t}$, the identity
whose right-hand terms are contained in
This completes the proof of the lemma. ◻
From this we get the
Corollary 2.1.14. ![]() $\widehat{C_{t}}$ is a
$\widehat{C_{t}}$ is a ![]() $D^{(k,m)}$-submodule of
$D^{(k,m)}$-submodule of ![]() $A\{1/t\}_{\mathbb{Q}}$ if
$A\{1/t\}_{\mathbb{Q}}$ if ![]() $k\geqslant k_{\mathfrak{X}}$.
$k\geqslant k_{\mathfrak{X}}$.
Proof. Using previous notations, we see that ![]() $\unicode[STIX]{x1D71B}^{k|\text{}\underline{\unicode[STIX]{x1D708}}|}\unicode[STIX]{x2202}_{i}^{\langle \text{}\underline{\unicode[STIX]{x1D708}}\rangle }$ acts continuously on
$\unicode[STIX]{x1D71B}^{k|\text{}\underline{\unicode[STIX]{x1D708}}|}\unicode[STIX]{x2202}_{i}^{\langle \text{}\underline{\unicode[STIX]{x1D708}}\rangle }$ acts continuously on ![]() $C_{t}$. We can thus extend this action by continuity to get an action on
$C_{t}$. We can thus extend this action by continuity to get an action on ![]() $\widehat{C_{t}}$. By construction this action is induced by the action of
$\widehat{C_{t}}$. By construction this action is induced by the action of ![]() $\unicode[STIX]{x1D6E4}(\mathfrak{X}_{0},\text{sp}_{\ast }\mathscr{D}_{\mathfrak{X}_{0,\mathbb{Q}}})$ on
$\unicode[STIX]{x1D6E4}(\mathfrak{X}_{0},\text{sp}_{\ast }\mathscr{D}_{\mathfrak{X}_{0,\mathbb{Q}}})$ on ![]() $A\{1/t\}_{\mathbb{Q}}$.◻
$A\{1/t\}_{\mathbb{Q}}$.◻
After these local considerations, we come back now to the general situation.
Corollary 2.1.15. Let ![]() $k\geqslant k_{\mathfrak{X}}$. The sheaf
$k\geqslant k_{\mathfrak{X}}$. The sheaf ![]() $\mathscr{D}_{\mathfrak{X}}^{(k,m)}=\text{pr}^{\ast }\mathscr{D}_{\mathfrak{X}_{0}}^{(k,m)}$ is a subsheaf of rings of the sheaf
$\mathscr{D}_{\mathfrak{X}}^{(k,m)}=\text{pr}^{\ast }\mathscr{D}_{\mathfrak{X}_{0}}^{(k,m)}$ is a subsheaf of rings of the sheaf ![]() $\text{sp}_{\ast }\mathscr{D}_{\mathfrak{X}_{\mathbb{Q}}}$. Moreover, it is locally free over
$\text{sp}_{\ast }\mathscr{D}_{\mathfrak{X}_{\mathbb{Q}}}$. Moreover, it is locally free over ![]() ${\mathcal{O}}_{\mathfrak{X}}$.
${\mathcal{O}}_{\mathfrak{X}}$.
Proof. The assertion is local on ![]() $\mathfrak{X}$ and we can assume that
$\mathfrak{X}$ and we can assume that ![]() $\mathfrak{X}_{0}=\text{Spf}\;A$ is affine, endowed with local coordinates
$\mathfrak{X}_{0}=\text{Spf}\;A$ is affine, endowed with local coordinates ![]() $x_{1},\ldots ,x_{M}$. Then, the sheaf
$x_{1},\ldots ,x_{M}$. Then, the sheaf ![]() $\mathscr{D}_{\mathfrak{X}}^{(k,m)}$ is a free
$\mathscr{D}_{\mathfrak{X}}^{(k,m)}$ is a free ![]() ${\mathcal{O}}_{\mathfrak{X}}$-module generated by the operators
${\mathcal{O}}_{\mathfrak{X}}$-module generated by the operators ![]() $\unicode[STIX]{x1D71B}^{k|\text{}\underline{\unicode[STIX]{x1D708}}|}\text{}\underline{\unicode[STIX]{x2202}}^{\langle \text{}\underline{\unicode[STIX]{x1D708}}\rangle }$ (using notations 2.1.3). By the formula of Berthelot [Reference Berthelot7, 2.2.4], one has
$\unicode[STIX]{x1D71B}^{k|\text{}\underline{\unicode[STIX]{x1D708}}|}\text{}\underline{\unicode[STIX]{x2202}}^{\langle \text{}\underline{\unicode[STIX]{x1D708}}\rangle }$ (using notations 2.1.3). By the formula of Berthelot [Reference Berthelot7, 2.2.4], one has
where
To check that ![]() $\mathscr{D}_{\mathfrak{X}}^{(k,m)}$ is a subsheaf of rings of
$\mathscr{D}_{\mathfrak{X}}^{(k,m)}$ is a subsheaf of rings of ![]() $\text{sp}_{\ast }\mathscr{D}_{\mathfrak{X}_{\mathbb{Q}}}$, we thus only have to check, by linearity, that if
$\text{sp}_{\ast }\mathscr{D}_{\mathfrak{X}_{\mathbb{Q}}}$, we thus only have to check, by linearity, that if ![]() $b$ is a section in
$b$ is a section in ![]() ${\mathcal{O}}_{\mathfrak{X}}(\mathfrak{V})$ where
${\mathcal{O}}_{\mathfrak{X}}(\mathfrak{V})$ where ![]() $\mathfrak{V}=\text{Spf}\;\widehat{C_{t}[1/h]}$, see 2.1.14, for some nonzero
$\mathfrak{V}=\text{Spf}\;\widehat{C_{t}[1/h]}$, see 2.1.14, for some nonzero ![]() $t\in A$, and nonzero
$t\in A$, and nonzero ![]() $h\in C_{t}$, and if
$h\in C_{t}$, and if ![]() $\text{}\underline{\unicode[STIX]{x1D708}}\in \mathbb{N}^{M}$, then the element
$\text{}\underline{\unicode[STIX]{x1D708}}\in \mathbb{N}^{M}$, then the element ![]() $\text{}\underline{\unicode[STIX]{x2202}}^{\langle \text{}\underline{\unicode[STIX]{x1D708}}\rangle }\cdot b$ lies in
$\text{}\underline{\unicode[STIX]{x2202}}^{\langle \text{}\underline{\unicode[STIX]{x1D708}}\rangle }\cdot b$ lies in ![]() $\mathscr{D}_{\mathfrak{X}}^{(k,m)}(\mathfrak{V})$. By [Reference Berthelot7, 2.2.4], one has
$\mathscr{D}_{\mathfrak{X}}^{(k,m)}(\mathfrak{V})$. By [Reference Berthelot7, 2.2.4], one has
Since ![]() $\unicode[STIX]{x1D71B}^{k|\text{}\underline{\unicode[STIX]{x1D708}}^{\prime }|}\text{}\underline{\unicode[STIX]{x2202}}^{\langle \text{}\underline{\unicode[STIX]{x1D708}}^{\prime }\rangle }(b)\in {\mathcal{O}}_{\mathfrak{X}}(\mathfrak{V})$ by 2.1.14, this proves that
$\unicode[STIX]{x1D71B}^{k|\text{}\underline{\unicode[STIX]{x1D708}}^{\prime }|}\text{}\underline{\unicode[STIX]{x2202}}^{\langle \text{}\underline{\unicode[STIX]{x1D708}}^{\prime }\rangle }(b)\in {\mathcal{O}}_{\mathfrak{X}}(\mathfrak{V})$ by 2.1.14, this proves that ![]() $\mathscr{D}_{\mathfrak{X}}^{(k,m)}$ is a subring of
$\mathscr{D}_{\mathfrak{X}}^{(k,m)}$ is a subring of ![]() $\mathscr{D}_{\mathfrak{X}_{\mathbb{Q}}}$.◻
$\mathscr{D}_{\mathfrak{X}_{\mathbb{Q}}}$.◻
We finally define the following sheaves of differential operators over ![]() $\mathfrak{X}$ and
$\mathfrak{X}$ and ![]() $X_{i}$
$X_{i}$
We have the following local description over an affine open ![]() $\mathfrak{V}\subseteq \text{pr}^{-1}(\mathfrak{U}_{0})$ where
$\mathfrak{V}\subseteq \text{pr}^{-1}(\mathfrak{U}_{0})$ where ![]() $\mathfrak{U}_{0}$ is an affine open of
$\mathfrak{U}_{0}$ is an affine open of ![]() $\mathfrak{X}_{0}$ endowed with coordinates
$\mathfrak{X}_{0}$ endowed with coordinates ![]() $x_{1},\ldots ,x_{M}$ and derivations
$x_{1},\ldots ,x_{M}$ and derivations ![]() $\unicode[STIX]{x2202}_{1},\ldots ,\unicode[STIX]{x2202}_{M}$:
$\unicode[STIX]{x2202}_{1},\ldots ,\unicode[STIX]{x2202}_{M}$:
where ![]() $|.|$ denotes any Banach norm on
$|.|$ denotes any Banach norm on ![]() ${\mathcal{O}}_{\mathfrak{X},\mathbb{Q}}(\mathfrak{V})$.
${\mathcal{O}}_{\mathfrak{X},\mathbb{Q}}(\mathfrak{V})$.
2.2 First properties
We keep here the hypotheses from the previous section. In particular, ![]() $\mathfrak{X}_{0}$ denotes a smooth formal
$\mathfrak{X}_{0}$ denotes a smooth formal ![]() $\mathfrak{S}$-scheme and
$\mathfrak{S}$-scheme and
denotes an admissible blow-up. For a given natural number ![]() $k\geqslant 0$ we let
$k\geqslant 0$ we let
where ![]() $\mathscr{T}_{\mathfrak{X}_{0}}$ is the relative tangent sheaf of
$\mathscr{T}_{\mathfrak{X}_{0}}$ is the relative tangent sheaf of ![]() $\mathfrak{X}_{0}$ over
$\mathfrak{X}_{0}$ over ![]() $\mathfrak{S}$.
$\mathfrak{S}$.
(i) The sheaf
 $\mathscr{T}_{\mathfrak{X},k}$ is a locally free
$\mathscr{T}_{\mathfrak{X},k}$ is a locally free  ${\mathcal{O}}_{\mathfrak{X}}$-module of rank equal to the relative dimension of
${\mathcal{O}}_{\mathfrak{X}}$-module of rank equal to the relative dimension of  $\mathfrak{X}_{0}$ over
$\mathfrak{X}_{0}$ over  $\mathfrak{S}$.
$\mathfrak{S}$.(ii) Suppose
 $\unicode[STIX]{x1D70B}:\mathfrak{X}^{\prime }\rightarrow \mathfrak{X}$ is a morphism over
$\unicode[STIX]{x1D70B}:\mathfrak{X}^{\prime }\rightarrow \mathfrak{X}$ is a morphism over  $\mathfrak{X}_{0}$ from another admissible blow-up
$\mathfrak{X}_{0}$ from another admissible blow-up  $\text{pr}^{\prime }:\mathfrak{X}^{\prime }\rightarrow \mathfrak{X}_{0}$. Let
$\text{pr}^{\prime }:\mathfrak{X}^{\prime }\rightarrow \mathfrak{X}_{0}$. Let  $k^{\prime },k\geqslant 0$. One has as subsheaves of
$k^{\prime },k\geqslant 0$. One has as subsheaves of  $\mathscr{T}_{\mathfrak{X}^{\prime }}\otimes L$
$\mathscr{T}_{\mathfrak{X}^{\prime }}\otimes L$ $$\begin{eqnarray}\mathscr{T}_{\mathfrak{X}^{\prime },k^{\prime }}=\unicode[STIX]{x1D71B}^{k^{\prime }-k}\text{\{}^{\ast }(\mathscr{T}_{\mathfrak{ X},k}).\end{eqnarray}$$
$$\begin{eqnarray}\mathscr{T}_{\mathfrak{X}^{\prime },k^{\prime }}=\unicode[STIX]{x1D71B}^{k^{\prime }-k}\text{\{}^{\ast }(\mathscr{T}_{\mathfrak{ X},k}).\end{eqnarray}$$
Proof. This follows directly from the definitions. Note that ![]() $(\text{pr}^{\prime })^{\ast }=\unicode[STIX]{x1D70B}^{\ast }\circ \text{pr}^{\ast }$ in (ii).◻
$(\text{pr}^{\prime })^{\ast }=\unicode[STIX]{x1D70B}^{\ast }\circ \text{pr}^{\ast }$ in (ii).◻
Before stating the next proposition, let us recall that ![]() $\text{Sym}^{(m)}(\mathscr{T}_{\mathfrak{X},k})$ denotes the graded level
$\text{Sym}^{(m)}(\mathscr{T}_{\mathfrak{X},k})$ denotes the graded level ![]() $m$ symmetric algebra generated by the sheaf
$m$ symmetric algebra generated by the sheaf ![]() $\mathscr{T}_{\mathfrak{X},k}$ defined in [Reference Huyghe17, Section 1]. This is a graded
$\mathscr{T}_{\mathfrak{X},k}$ defined in [Reference Huyghe17, Section 1]. This is a graded ![]() ${\mathcal{O}}_{\mathfrak{X}}$-algebra
${\mathcal{O}}_{\mathfrak{X}}$-algebra
Over some sufficiently small open affine set ![]() $\mathfrak{U}\subseteq \text{pr}^{-1}(\mathfrak{U}_{0})$ such that
$\mathfrak{U}\subseteq \text{pr}^{-1}(\mathfrak{U}_{0})$ such that ![]() $\mathscr{T}_{\mathfrak{U}_{0}}$ is free with basis
$\mathscr{T}_{\mathfrak{U}_{0}}$ is free with basis ![]() $\unicode[STIX]{x1D709}_{1},\ldots ,\unicode[STIX]{x1D709}_{M}$, one has the description using notation 2.1.3 (i.e.,
$\unicode[STIX]{x1D709}_{1},\ldots ,\unicode[STIX]{x1D709}_{M}$, one has the description using notation 2.1.3 (i.e., ![]() $\unicode[STIX]{x1D708}!\unicode[STIX]{x1D709}_{l}^{\langle \unicode[STIX]{x1D708}\rangle }=q_{\unicode[STIX]{x1D708}}!\unicode[STIX]{x1D709}_{l}^{\unicode[STIX]{x1D708}}$)
$\unicode[STIX]{x1D708}!\unicode[STIX]{x1D709}_{l}^{\langle \unicode[STIX]{x1D708}\rangle }=q_{\unicode[STIX]{x1D708}}!\unicode[STIX]{x1D709}_{l}^{\unicode[STIX]{x1D708}}$)
where the right-hand side is a free ![]() ${\mathcal{O}}_{\mathfrak{X}}(\mathfrak{U})$-module. For the rest of this subsection we fix a number
${\mathcal{O}}_{\mathfrak{X}}(\mathfrak{U})$-module. For the rest of this subsection we fix a number ![]() $k\geqslant k_{\mathfrak{X}}$ (2.1.7).
$k\geqslant k_{\mathfrak{X}}$ (2.1.7).
(i) The sheaves
 $\mathscr{D}_{\mathfrak{X}}^{(k,m)}$ are filtered by the sheaves of differential operators of order
$\mathscr{D}_{\mathfrak{X}}^{(k,m)}$ are filtered by the sheaves of differential operators of order  ${\leqslant}d$, which are
${\leqslant}d$, which are  ${\mathcal{O}}_{\mathfrak{X}}$-coherent modules, and which we denote by
${\mathcal{O}}_{\mathfrak{X}}$-coherent modules, and which we denote by  $\mathscr{D}_{\mathfrak{X},d}^{(k,m)}$. There is a canonical isomorphism of sheaves of graded algebras Moreover, the sheaves
$\mathscr{D}_{\mathfrak{X},d}^{(k,m)}$. There is a canonical isomorphism of sheaves of graded algebras Moreover, the sheaves $$\begin{eqnarray}\text{gr}(\mathscr{D}_{\mathfrak{X}}^{(k,m)})\simeq \text{Sym}^{(m)}(\mathscr{T}_{\mathfrak{ X},k}).\end{eqnarray}$$
$$\begin{eqnarray}\text{gr}(\mathscr{D}_{\mathfrak{X}}^{(k,m)})\simeq \text{Sym}^{(m)}(\mathscr{T}_{\mathfrak{ X},k}).\end{eqnarray}$$ $\mathscr{D}_{X_{i}}^{(k,m)}$ are quasi-coherent
$\mathscr{D}_{X_{i}}^{(k,m)}$ are quasi-coherent  ${\mathcal{O}}_{X_{i}}$-modules.
${\mathcal{O}}_{X_{i}}$-modules.(ii) There is a basis
 $\mathscr{B}$ of the topology of
$\mathscr{B}$ of the topology of  $\mathfrak{X}$ (resp.
$\mathfrak{X}$ (resp.  $X_{i}$), consisting of open affine subsets, such that for any
$X_{i}$), consisting of open affine subsets, such that for any  $\mathfrak{U}\in \mathscr{B}$ (resp.
$\mathfrak{U}\in \mathscr{B}$ (resp.  $U_{i}\in \mathscr{B}$), the ring
$U_{i}\in \mathscr{B}$), the ring  $\mathscr{D}_{\mathfrak{X}}^{(k,m)}(\mathfrak{U})$ (resp.
$\mathscr{D}_{\mathfrak{X}}^{(k,m)}(\mathfrak{U})$ (resp.  $\mathscr{D}_{X_{i}}^{(k,m)}(U_{i})$) is two-sided noetherian.
$\mathscr{D}_{X_{i}}^{(k,m)}(U_{i})$) is two-sided noetherian.(iii) For every formal affine open
 $\mathfrak{U}\subseteq \mathfrak{X}$ (resp. affine open
$\mathfrak{U}\subseteq \mathfrak{X}$ (resp. affine open  $U_{i}\subseteq X_{i}$), the ring
$U_{i}\subseteq X_{i}$), the ring  $\mathscr{D}_{\mathfrak{X}}^{(k,m)}(\mathfrak{U})$ (resp.
$\mathscr{D}_{\mathfrak{X}}^{(k,m)}(\mathfrak{U})$ (resp.  $\mathscr{D}_{X_{i}}^{(k,m)}(U_{i})$) is two-sided noetherian.
$\mathscr{D}_{X_{i}}^{(k,m)}(U_{i})$) is two-sided noetherian.(iv) The sheaves of rings
 $\mathscr{D}_{\mathfrak{X}}^{(k,m)}$ (resp.
$\mathscr{D}_{\mathfrak{X}}^{(k,m)}$ (resp.  $\mathscr{D}_{X_{i}}^{(k,m)}$) are coherent.
$\mathscr{D}_{X_{i}}^{(k,m)}$) are coherent.(v) For every formal affine open
 $\mathfrak{U}\subset \mathfrak{X}$, the ring
$\mathfrak{U}\subset \mathfrak{X}$, the ring  $\widehat{\mathscr{D}}_{\mathfrak{X}}^{(k,m)}(\mathfrak{U})$ is two-sided noetherian.
$\widehat{\mathscr{D}}_{\mathfrak{X}}^{(k,m)}(\mathfrak{U})$ is two-sided noetherian.(vi) The sheaf of rings
 $\widehat{\mathscr{D}}_{\mathfrak{X}}^{(k,m)}$ is coherent.
$\widehat{\mathscr{D}}_{\mathfrak{X}}^{(k,m)}$ is coherent.
Proof. We only do the proof of (i)–(iv) in the case of ![]() $\mathscr{D}_{\mathfrak{X}}^{(k,m)}$, since the same proof works for the sheaf
$\mathscr{D}_{\mathfrak{X}}^{(k,m)}$, since the same proof works for the sheaf ![]() $\mathscr{D}_{X_{i}}^{(k,m)}$. Denote by
$\mathscr{D}_{X_{i}}^{(k,m)}$. Denote by ![]() $\mathscr{D}_{\mathfrak{X}_{0},d}^{(k,m)}$ the sheaf of differential operators of
$\mathscr{D}_{\mathfrak{X}_{0},d}^{(k,m)}$ the sheaf of differential operators of ![]() $\mathscr{D}_{\mathfrak{X}_{0}}^{(k,m)}$ of order
$\mathscr{D}_{\mathfrak{X}_{0}}^{(k,m)}$ of order ![]() ${\leqslant}d$, and
${\leqslant}d$, and ![]() $\mathscr{D}_{\mathfrak{X},d}^{(k,m)}=\text{pr}^{\ast }\mathscr{D}_{\mathfrak{X}_{0},d}^{(k,m)}$. It is straightforward that we have an exact sequence of
$\mathscr{D}_{\mathfrak{X},d}^{(k,m)}=\text{pr}^{\ast }\mathscr{D}_{\mathfrak{X}_{0},d}^{(k,m)}$. It is straightforward that we have an exact sequence of ![]() ${\mathcal{O}}_{\mathfrak{X}_{0}}$-modules on
${\mathcal{O}}_{\mathfrak{X}_{0}}$-modules on ![]() $\mathfrak{X}_{0}$
$\mathfrak{X}_{0}$
Now we apply ![]() $\text{pr}^{\ast }$ and get an exact sequence since
$\text{pr}^{\ast }$ and get an exact sequence since ![]() $\text{Sym}_{d}^{(m)}(\mathscr{T}_{\mathfrak{X}_{0},k})$ is a locally free
$\text{Sym}_{d}^{(m)}(\mathscr{T}_{\mathfrak{X}_{0},k})$ is a locally free ![]() ${\mathcal{O}}_{\mathfrak{X}_{0}}$-module of finite rank. This gives (i). Let
${\mathcal{O}}_{\mathfrak{X}_{0}}$-module of finite rank. This gives (i). Let ![]() $\mathfrak{U}$ be an affine subset of
$\mathfrak{U}$ be an affine subset of ![]() $\text{pr}^{-1}(\mathfrak{U}_{0})$, where
$\text{pr}^{-1}(\mathfrak{U}_{0})$, where ![]() $\mathfrak{U}_{0}\subset \mathfrak{X}_{0}$ has some coordinates
$\mathfrak{U}_{0}\subset \mathfrak{X}_{0}$ has some coordinates ![]() $x_{1},\ldots ,x_{M}$. One has the following description
$x_{1},\ldots ,x_{M}$. One has the following description
Since ![]() $\mathfrak{U}$ is affine and the filtration steps
$\mathfrak{U}$ is affine and the filtration steps ![]() $\mathscr{D}_{\mathfrak{X},d}^{(k,m)}$ are coherent
$\mathscr{D}_{\mathfrak{X},d}^{(k,m)}$ are coherent ![]() ${\mathcal{O}}_{\mathfrak{X}}$-modules for all
${\mathcal{O}}_{\mathfrak{X}}$-modules for all ![]() $d$, the previous exact sequences gives us the following isomorphism
$d$, the previous exact sequences gives us the following isomorphism
Since the latter level ![]() $m$ symmetric algebra is known to be noetherian [Reference Huyghe17, Proposition 1.3.6], this proves (ii). As
$m$ symmetric algebra is known to be noetherian [Reference Huyghe17, Proposition 1.3.6], this proves (ii). As ![]() $\mathscr{B}$ we may take the set of open affine subsets of
$\mathscr{B}$ we may take the set of open affine subsets of ![]() $\mathfrak{X}$ that are contained in some
$\mathfrak{X}$ that are contained in some ![]() $\text{pr}^{-1}(\mathfrak{U}_{0})$, for some open
$\text{pr}^{-1}(\mathfrak{U}_{0})$, for some open ![]() $\mathfrak{U}_{0}\subset \mathfrak{X}_{0}$ endowed with global coordinates. Let now
$\mathfrak{U}_{0}\subset \mathfrak{X}_{0}$ endowed with global coordinates. Let now ![]() $\mathfrak{V},\mathfrak{U}\in \mathscr{B}$ such that
$\mathfrak{V},\mathfrak{U}\in \mathscr{B}$ such that ![]() $\mathfrak{V}\subset \mathfrak{U}$. Since the sheaf
$\mathfrak{V}\subset \mathfrak{U}$. Since the sheaf ![]() $\mathscr{D}_{\mathfrak{X}}^{(k,m)}$ is an inductive limit of coherent
$\mathscr{D}_{\mathfrak{X}}^{(k,m)}$ is an inductive limit of coherent ![]() ${\mathcal{O}}_{\mathfrak{X}}$-modules, one has
${\mathcal{O}}_{\mathfrak{X}}$-modules, one has
In particular, ![]() $\mathscr{D}_{\mathfrak{X}}^{(k,m)}(\mathfrak{V})$ is flat over
$\mathscr{D}_{\mathfrak{X}}^{(k,m)}(\mathfrak{V})$ is flat over ![]() $\mathscr{D}_{\mathfrak{X}}^{(k,m)}(\mathfrak{U})$. This remark and (ii) prove the coherence of the sheaves
$\mathscr{D}_{\mathfrak{X}}^{(k,m)}(\mathfrak{U})$. This remark and (ii) prove the coherence of the sheaves ![]() $\mathscr{D}_{\mathfrak{X}}^{(k,m)}$ exactly as in the proof [Reference Berthelot7, 3.1.3].
$\mathscr{D}_{\mathfrak{X}}^{(k,m)}$ exactly as in the proof [Reference Berthelot7, 3.1.3].
Let us now prove (iii) for ‘left noetherian’ (the proof of the right version is similar). Let ![]() $\mathfrak{U}$ be an affine open of
$\mathfrak{U}$ be an affine open of ![]() $\mathfrak{X}$,
$\mathfrak{X}$, ![]() $\mathscr{D}=\mathscr{D}_{\mathfrak{U}}^{(k,m)}$,
$\mathscr{D}=\mathscr{D}_{\mathfrak{U}}^{(k,m)}$, ![]() $D=\unicode[STIX]{x1D6E4}(\mathfrak{U},\mathscr{D})$,
$D=\unicode[STIX]{x1D6E4}(\mathfrak{U},\mathscr{D})$, ![]() $A=\unicode[STIX]{x1D6E4}(\mathfrak{U},{\mathcal{O}}_{\mathfrak{X}})$ and
$A=\unicode[STIX]{x1D6E4}(\mathfrak{U},{\mathcal{O}}_{\mathfrak{X}})$ and ![]() $\mathfrak{U}=\bigcup \mathfrak{U}_{l}$ a finite cover of
$\mathfrak{U}=\bigcup \mathfrak{U}_{l}$ a finite cover of ![]() $\mathfrak{U}$ by open
$\mathfrak{U}$ by open ![]() $\mathfrak{U}_{l}\in \mathscr{B}$. Since the sheaf
$\mathfrak{U}_{l}\in \mathscr{B}$. Since the sheaf ![]() $\mathscr{D}$ is an inductive limit of coherent
$\mathscr{D}$ is an inductive limit of coherent ![]() ${\mathcal{O}}_{\mathfrak{X}}$-modules, one has
${\mathcal{O}}_{\mathfrak{X}}$-modules, one has
and ![]() $\mathscr{D}$ is a flat
$\mathscr{D}$ is a flat ![]() $D$-module. Moreover, thanks to (ii), we know that
$D$-module. Moreover, thanks to (ii), we know that ![]() $\mathscr{D}_{\mathfrak{X}}(\mathfrak{U}_{l})$ is noetherian for each
$\mathscr{D}_{\mathfrak{X}}(\mathfrak{U}_{l})$ is noetherian for each ![]() $l$. Let
$l$. Let ![]() $(M_{i})$ be an increasing sequence of left ideals of
$(M_{i})$ be an increasing sequence of left ideals of ![]() $D$, and consider
$D$, and consider
which form an increasing sequence of sheaves of ideals of ![]() $\mathscr{D}$ by flatness of
$\mathscr{D}$ by flatness of ![]() $\mathscr{D}$ over
$\mathscr{D}$ over ![]() $D$. The sequence
$D$. The sequence ![]() $\unicode[STIX]{x1D6E4}(\mathfrak{U}_{l},{\mathcal{M}}_{i})$ is thus an increasing sequence of ideals of
$\unicode[STIX]{x1D6E4}(\mathfrak{U}_{l},{\mathcal{M}}_{i})$ is thus an increasing sequence of ideals of ![]() $\unicode[STIX]{x1D6E4}(\mathfrak{U}_{l},\mathscr{D})$, that is stationary since this algebra is noetherian. Since
$\unicode[STIX]{x1D6E4}(\mathfrak{U}_{l},\mathscr{D})$, that is stationary since this algebra is noetherian. Since ![]() $M_{i}$ is an inductive limit of finite type
$M_{i}$ is an inductive limit of finite type ![]() $A$-modules,
$A$-modules, ![]() ${\mathcal{M}}_{i}$ is an inductive limit of coherent
${\mathcal{M}}_{i}$ is an inductive limit of coherent ![]() ${\mathcal{O}}_{\mathfrak{X}}$-modules, thus
${\mathcal{O}}_{\mathfrak{X}}$-modules, thus
Finally we see that ![]() ${\mathcal{M}}_{i|\mathfrak{U}_{l}}$ is stationary for each
${\mathcal{M}}_{i|\mathfrak{U}_{l}}$ is stationary for each ![]() $l$. Since there are finitely many affine open
$l$. Since there are finitely many affine open ![]() $\mathfrak{U}_{l}$, we see that the sequence
$\mathfrak{U}_{l}$, we see that the sequence ![]() $({\mathcal{M}}_{i})$ and thus
$({\mathcal{M}}_{i})$ and thus ![]() $(M_{i})$ are stationary. This proves (iii). Since
$(M_{i})$ are stationary. This proves (iii). Since ![]() $\widehat{\mathscr{D}}_{\mathfrak{X}}^{(k,m)}(\mathfrak{U})$ is the
$\widehat{\mathscr{D}}_{\mathfrak{X}}^{(k,m)}(\mathfrak{U})$ is the ![]() $p$-adic completion of
$p$-adic completion of ![]() $\widehat{\mathscr{D}}_{\mathfrak{X}}^{(k,m)}(\mathfrak{U})$, it is also left and right noetherian [Reference Berthelot7, 3.2.3], which proves (v).
$\widehat{\mathscr{D}}_{\mathfrak{X}}^{(k,m)}(\mathfrak{U})$, it is also left and right noetherian [Reference Berthelot7, 3.2.3], which proves (v).
The coherence of ![]() $\widehat{\mathscr{D}}_{\mathfrak{X}}^{(k,m)}$ follows from (iii), and the fact that
$\widehat{\mathscr{D}}_{\mathfrak{X}}^{(k,m)}$ follows from (iii), and the fact that ![]() $\mathscr{D}_{X_{i}}^{(k,m)}$ is a quasi-coherent
$\mathscr{D}_{X_{i}}^{(k,m)}$ is a quasi-coherent ![]() ${\mathcal{O}}_{X_{i}}$-module, literally as in [Reference Berthelot7, 3.3.3].◻
${\mathcal{O}}_{X_{i}}$-module, literally as in [Reference Berthelot7, 3.3.3].◻
From these considerations, and under our initial condition ![]() $k\geqslant k_{\mathfrak{X}}$, we have the following local versions of Cartan’s Theorem A and B for the restrictions of the sheaves
$k\geqslant k_{\mathfrak{X}}$, we have the following local versions of Cartan’s Theorem A and B for the restrictions of the sheaves ![]() $\mathscr{D}_{X_{i}}^{(k,m)}$ and
$\mathscr{D}_{X_{i}}^{(k,m)}$ and ![]() $\widehat{\mathscr{D}}_{\mathfrak{X}}^{(k,m)}$ to an open affine (formal) subscheme.
$\widehat{\mathscr{D}}_{\mathfrak{X}}^{(k,m)}$ to an open affine (formal) subscheme.
Proposition 2.2.6. (Local theorems A and B for fixed ![]() $m$)
$m$)
(i) Let
 $U_{i}\subset X_{i}$ be an open affine subscheme of
$U_{i}\subset X_{i}$ be an open affine subscheme of  $X_{i}$. The functor
$X_{i}$. The functor  $\unicode[STIX]{x1D6E4}(U_{i},.)$ establishes an equivalence of categories between coherent
$\unicode[STIX]{x1D6E4}(U_{i},.)$ establishes an equivalence of categories between coherent  $\mathscr{D}_{U_{i}}^{(k,m)}$-modules and finite type
$\mathscr{D}_{U_{i}}^{(k,m)}$-modules and finite type  $\unicode[STIX]{x1D6E4}(U_{i},\mathscr{D}_{X_{i}}^{(k,m)})$-modules. In particular, the functor
$\unicode[STIX]{x1D6E4}(U_{i},\mathscr{D}_{X_{i}}^{(k,m)})$-modules. In particular, the functor  $\unicode[STIX]{x1D6E4}(U_{i},.)$ is exact on coherent
$\unicode[STIX]{x1D6E4}(U_{i},.)$ is exact on coherent  $\mathscr{D}_{U_{i}}^{(k,m)}$-modules. Moreover, for any coherent
$\mathscr{D}_{U_{i}}^{(k,m)}$-modules. Moreover, for any coherent  $\mathscr{D}_{U_{i}}^{(k,m)}$-module
$\mathscr{D}_{U_{i}}^{(k,m)}$-module  $\mathscr{M}$ and any
$\mathscr{M}$ and any  $q>0$ one has
$q>0$ one has  $H^{q}(U_{i},\mathscr{M})=0$.
$H^{q}(U_{i},\mathscr{M})=0$.(ii) Let
 $\mathfrak{U}\subset \mathfrak{X}$ be an open affine formal subscheme of
$\mathfrak{U}\subset \mathfrak{X}$ be an open affine formal subscheme of  $\mathfrak{X}$. The functors
$\mathfrak{X}$. The functors  ${\mathcal{M}}\mapsto \unicode[STIX]{x1D6E4}(\mathfrak{U},{\mathcal{M}})$ and
${\mathcal{M}}\mapsto \unicode[STIX]{x1D6E4}(\mathfrak{U},{\mathcal{M}})$ and  $M\mapsto \widehat{\mathscr{D}}_{\mathfrak{U}}^{(k,m)}\otimes M$ are quasi-inverse equivalences of categories between the category of coherent left
$M\mapsto \widehat{\mathscr{D}}_{\mathfrak{U}}^{(k,m)}\otimes M$ are quasi-inverse equivalences of categories between the category of coherent left  $\widehat{\mathscr{D}}_{\mathfrak{U}}^{(k,m)}$-modules and the category of left
$\widehat{\mathscr{D}}_{\mathfrak{U}}^{(k,m)}$-modules and the category of left  $\unicode[STIX]{x1D6E4}(\mathfrak{U},\widehat{\mathscr{D}}_{\mathfrak{U}}^{(k,m)})$-modules of finite type.
$\unicode[STIX]{x1D6E4}(\mathfrak{U},\widehat{\mathscr{D}}_{\mathfrak{U}}^{(k,m)})$-modules of finite type.(iii) Let
 $\mathfrak{U}$ be as in (ii). The functor
$\mathfrak{U}$ be as in (ii). The functor  $\unicode[STIX]{x1D6E4}(\mathfrak{U},.)$ is exact on coherent
$\unicode[STIX]{x1D6E4}(\mathfrak{U},.)$ is exact on coherent  $\widehat{\mathscr{D}}_{\mathfrak{U}}^{(k,m)}$-modules. Moreover, for any coherent
$\widehat{\mathscr{D}}_{\mathfrak{U}}^{(k,m)}$-modules. Moreover, for any coherent  $\widehat{\mathscr{D}}_{\mathfrak{U}}^{(k,m)}$-module
$\widehat{\mathscr{D}}_{\mathfrak{U}}^{(k,m)}$-module  $\mathscr{M}$ and any
$\mathscr{M}$ and any  $q>0$ one has
$q>0$ one has  $H^{q}(\mathfrak{U},\mathscr{M})=0$.
$H^{q}(\mathfrak{U},\mathscr{M})=0$.
Note that (ii) and (iii) of the proposition remains true for the sheaf ![]() $\widehat{\mathscr{D}}_{\mathfrak{U},\mathbb{Q}}^{(k,m)}$ and coherent modules over this sheaf by [Reference Berthelot7, 3.4.6].
$\widehat{\mathscr{D}}_{\mathfrak{U},\mathbb{Q}}^{(k,m)}$ and coherent modules over this sheaf by [Reference Berthelot7, 3.4.6].
Proof. For the convenience of the reader, we start by recalling the following result.
Auxiliary result 2.2.7. (cf. [Reference Berthelot7, Proposition 3.1.3])
Let ![]() $X$ be a scheme,
$X$ be a scheme, ![]() $\mathscr{D}$ be a sheaf of rings over
$\mathscr{D}$ be a sheaf of rings over ![]() $X$ such that, for all affine open
$X$ such that, for all affine open ![]() $U\subset X$,
$U\subset X$, ![]() $\unicode[STIX]{x1D6E4}(U,\mathscr{D})$ is a noetherian ring. We fix an homomorphism
$\unicode[STIX]{x1D6E4}(U,\mathscr{D})$ is a noetherian ring. We fix an homomorphism ![]() ${\mathcal{O}}_{X}\rightarrow \mathscr{D}$ such that the left multiplication by the sections of
${\mathcal{O}}_{X}\rightarrow \mathscr{D}$ such that the left multiplication by the sections of ![]() ${\mathcal{O}}_{X}$ induces a structure of
${\mathcal{O}}_{X}$ induces a structure of ![]() ${\mathcal{O}}_{X}$-coherent ring over
${\mathcal{O}}_{X}$-coherent ring over ![]() $\mathscr{D}$.
$\mathscr{D}$.
(i) The sheaf
 $\mathscr{D}$ is a left coherent sheaf of rings.
$\mathscr{D}$ is a left coherent sheaf of rings.(ii) A left
 $\mathscr{D}$-module
$\mathscr{D}$-module  ${\mathcal{M}}$ is coherent if and only if it is a quasi-coherent
${\mathcal{M}}$ is coherent if and only if it is a quasi-coherent  ${\mathcal{O}}_{X}$-module and, for all affine open
${\mathcal{O}}_{X}$-module and, for all affine open  $U$ of an affine cover of
$U$ of an affine cover of  $X$,
$X$,  $\unicode[STIX]{x1D6E4}(U,{\mathcal{M}})$ is a left
$\unicode[STIX]{x1D6E4}(U,{\mathcal{M}})$ is a left  $\unicode[STIX]{x1D6E4}(U,\mathscr{D})$-module of finite type.
$\unicode[STIX]{x1D6E4}(U,\mathscr{D})$-module of finite type.(iii) Assume that
 $X$ is affine and let
$X$ is affine and let  $D=\unicode[STIX]{x1D6E4}(X,\mathscr{D})$. The functors
$D=\unicode[STIX]{x1D6E4}(X,\mathscr{D})$. The functors  ${\mathcal{M}}\mapsto \unicode[STIX]{x1D6E4}(X,{\mathcal{M}})$ and
${\mathcal{M}}\mapsto \unicode[STIX]{x1D6E4}(X,{\mathcal{M}})$ and  $M\mapsto \mathscr{D}\otimes M$ are quasi-inverse equivalences of categories between the category of coherent left
$M\mapsto \mathscr{D}\otimes M$ are quasi-inverse equivalences of categories between the category of coherent left  $\mathscr{D}$-modules and the category of left
$\mathscr{D}$-modules and the category of left  $D$-modules of finite type. ◻
$D$-modules of finite type. ◻
Consider now the following situation, compare [Reference Berthelot7, 3.3.3]. Let ![]() $\mathfrak{X}^{\prime }$ be an
$\mathfrak{X}^{\prime }$ be an ![]() $\mathfrak{S}$-formal scheme and let
$\mathfrak{S}$-formal scheme and let ![]() $\mathscr{D}$ be a sheaf of rings over
$\mathscr{D}$ be a sheaf of rings over ![]() $\mathfrak{X}^{\prime }$, endowed with a homomorphism
$\mathfrak{X}^{\prime }$, endowed with a homomorphism ![]() ${\mathcal{O}}_{\mathfrak{X}^{\prime }}\rightarrow \mathscr{D}$,
${\mathcal{O}}_{\mathfrak{X}^{\prime }}\rightarrow \mathscr{D}$, ![]() $\mathscr{D}_{i}=\mathscr{D}/p^{i+1}$,
$\mathscr{D}_{i}=\mathscr{D}/p^{i+1}$, ![]() $\widehat{\mathscr{D}}=\mathop{\varprojlim }\nolimits_{i}\mathscr{D}_{i}$. In addition, assume the following conditions (Berthelot’s conditions)
$\widehat{\mathscr{D}}=\mathop{\varprojlim }\nolimits_{i}\mathscr{D}_{i}$. In addition, assume the following conditions (Berthelot’s conditions)
(1) As an
 ${\mathcal{O}}_{\mathfrak{X}^{\prime }}$-module,
${\mathcal{O}}_{\mathfrak{X}^{\prime }}$-module,  $\mathscr{D}$ is the filtered inductive limit of a family of
$\mathscr{D}$ is the filtered inductive limit of a family of  ${\mathcal{O}}_{\mathfrak{X}^{\prime }}$-module
${\mathcal{O}}_{\mathfrak{X}^{\prime }}$-module  $\mathscr{D}_{\unicode[STIX]{x1D706}}$ such that
$\mathscr{D}_{\unicode[STIX]{x1D706}}$ such that  $\mathscr{D}_{\unicode[STIX]{x1D706}}/p^{i}\mathscr{D}_{\unicode[STIX]{x1D706}}$ are
$\mathscr{D}_{\unicode[STIX]{x1D706}}/p^{i}\mathscr{D}_{\unicode[STIX]{x1D706}}$ are  ${\mathcal{O}}_{X_{i}^{\prime }}$-quasi-coherent and
${\mathcal{O}}_{X_{i}^{\prime }}$-quasi-coherent and  $\mathscr{D}_{\unicode[STIX]{x1D706}}\simeq \mathop{\varprojlim }\nolimits_{i}\mathscr{D}_{\unicode[STIX]{x1D706}}/p^{i}\mathscr{D}_{\unicode[STIX]{x1D706}}$.
$\mathscr{D}_{\unicode[STIX]{x1D706}}\simeq \mathop{\varprojlim }\nolimits_{i}\mathscr{D}_{\unicode[STIX]{x1D706}}/p^{i}\mathscr{D}_{\unicode[STIX]{x1D706}}$.(2) For every open set
 $\mathfrak{U}\subset \mathfrak{X}^{\prime }$, the ring
$\mathfrak{U}\subset \mathfrak{X}^{\prime }$, the ring  $\unicode[STIX]{x1D6E4}(\mathfrak{U},\mathscr{D})$ is left noetherian.
$\unicode[STIX]{x1D6E4}(\mathfrak{U},\mathscr{D})$ is left noetherian.
Auxiliary result 2.2.8. With the previous hypotheses, suppose that ![]() $\mathfrak{X}^{\prime }$ is affine, and let
$\mathfrak{X}^{\prime }$ is affine, and let ![]() $\widehat{D}=\unicode[STIX]{x1D6E4}(\mathfrak{X}^{\prime },\widehat{\mathscr{D}})$. Then
$\widehat{D}=\unicode[STIX]{x1D6E4}(\mathfrak{X}^{\prime },\widehat{\mathscr{D}})$. Then ![]() $\widehat{D}$ is left noetherian. If
$\widehat{D}$ is left noetherian. If ![]() $M$ is a
$M$ is a ![]() $\widehat{D}$-module one defines a
$\widehat{D}$-module one defines a ![]() $\widehat{\mathscr{D}}$-module
$\widehat{\mathscr{D}}$-module
For a ![]() $\widehat{\mathscr{D}}$-module
$\widehat{\mathscr{D}}$-module ![]() ${\mathcal{M}}$, the following statements are equivalent
${\mathcal{M}}$, the following statements are equivalent
(i) For all
 $i$, the
$i$, the  $\mathscr{D}_{i}$-module
$\mathscr{D}_{i}$-module  ${\mathcal{M}}/p^{i+1}{\mathcal{M}}$ is coherent and the canonical homomorphism
${\mathcal{M}}/p^{i+1}{\mathcal{M}}$ is coherent and the canonical homomorphism  ${\mathcal{M}}\rightarrow \mathop{\varprojlim }\nolimits_{i}{\mathcal{M}}/p^{i+1}{\mathcal{M}}$ is an isomorphism.
${\mathcal{M}}\rightarrow \mathop{\varprojlim }\nolimits_{i}{\mathcal{M}}/p^{i+1}{\mathcal{M}}$ is an isomorphism.(ii) There exists an isomorphism
 ${\mathcal{M}}\simeq \mathop{\varprojlim }\nolimits_{i}{\mathcal{M}}_{i}$, where
${\mathcal{M}}\simeq \mathop{\varprojlim }\nolimits_{i}{\mathcal{M}}_{i}$, where  $({\mathcal{M}}_{i})$ is a projective system of coherent
$({\mathcal{M}}_{i})$ is a projective system of coherent  $\mathscr{D}_{i}$-modules, such that the transition morphisms factorize via isomorphisms
$\mathscr{D}_{i}$-modules, such that the transition morphisms factorize via isomorphisms  ${\mathcal{M}}_{i}/p^{i}{\mathcal{M}}_{i}\simeq {\mathcal{M}}_{i-1}$.
${\mathcal{M}}_{i}/p^{i}{\mathcal{M}}_{i}\simeq {\mathcal{M}}_{i-1}$.(iii) There exists a finite type
 $\widehat{D}$-module
$\widehat{D}$-module  $M$ and an isomorphism
$M$ and an isomorphism  ${\mathcal{M}}\simeq M^{\unicode[STIX]{x1D6E5}}$.
${\mathcal{M}}\simeq M^{\unicode[STIX]{x1D6E5}}$.(iv)
 ${\mathcal{M}}$ is a coherent
${\mathcal{M}}$ is a coherent  $\widehat{\mathscr{D}}$-module.
$\widehat{\mathscr{D}}$-module.
Proof. The ring ![]() $\widehat{D}$ is noetherian by [Reference Berthelot7, Proposition 3.3.4] and the other results come from [Reference Berthelot7, Proposition 3.3.9].◻
$\widehat{D}$ is noetherian by [Reference Berthelot7, Proposition 3.3.4] and the other results come from [Reference Berthelot7, Proposition 3.3.9].◻
Under the same hypotheses, Berthelot proves in addition the following.
Auxiliary result 2.2.9. (cf. [Reference Berthelot7, Proposition 3.3.10/11])
With the previous hypotheses, suppose that ![]() $\mathfrak{X}^{\prime }$ is affine. The functors
$\mathfrak{X}^{\prime }$ is affine. The functors ![]() $\unicode[STIX]{x1D6E4}(\mathfrak{X}^{\prime },\cdot )$ and
$\unicode[STIX]{x1D6E4}(\mathfrak{X}^{\prime },\cdot )$ and ![]() $M\mapsto M^{\unicode[STIX]{x1D6E5}}$ are equivalences between the category of coherent
$M\mapsto M^{\unicode[STIX]{x1D6E5}}$ are equivalences between the category of coherent ![]() $\widehat{\mathscr{D}}$-modules and the category of finite type
$\widehat{\mathscr{D}}$-modules and the category of finite type ![]() $\widehat{D}$-modules. If
$\widehat{D}$-modules. If ![]() ${\mathcal{M}}$ is a coherent
${\mathcal{M}}$ is a coherent ![]() $\widehat{\mathscr{D}}$-module, then
$\widehat{\mathscr{D}}$-module, then ![]() $\forall q\geqslant 1$,
$\forall q\geqslant 1$, ![]() $H^{q}(\mathfrak{X}^{\prime },{\mathcal{M}})=0$.◻
$H^{q}(\mathfrak{X}^{\prime },{\mathcal{M}})=0$.◻
Now it is clear that part (i) of our Proposition 2.2.6 follows from auxiliary result 2.2.7, since by (iii) of 2.2.2, the rings ![]() $\mathscr{D}_{X_{i}}^{(k,m)}(U_{i})$ are indeed noetherian. Again, from (iii) of 2.2.2, we see that the rings
$\mathscr{D}_{X_{i}}^{(k,m)}(U_{i})$ are indeed noetherian. Again, from (iii) of 2.2.2, we see that the rings ![]() $\mathscr{D}_{\mathfrak{X}}^{(k,m)}(\mathfrak{U})$ are noetherian. Moreover, the sheaf
$\mathscr{D}_{\mathfrak{X}}^{(k,m)}(\mathfrak{U})$ are noetherian. Moreover, the sheaf ![]() $\mathscr{D}_{\mathfrak{X}}^{(k,m)}$ is a filtered inductive limit of the
$\mathscr{D}_{\mathfrak{X}}^{(k,m)}$ is a filtered inductive limit of the ![]() ${\mathcal{O}}_{\mathfrak{X}}$-coherent sheaves
${\mathcal{O}}_{\mathfrak{X}}$-coherent sheaves ![]() $\mathscr{D}_{\mathfrak{X},d}^{(k,m)}$ defined in the proof of 2.2.2. This means that Berthelot’s conditions (1) and (2) are satisfied for
$\mathscr{D}_{\mathfrak{X},d}^{(k,m)}$ defined in the proof of 2.2.2. This means that Berthelot’s conditions (1) and (2) are satisfied for ![]() $\mathfrak{X}^{\prime }=\mathfrak{X}$ and
$\mathfrak{X}^{\prime }=\mathfrak{X}$ and ![]() $\mathscr{D}=\mathscr{D}_{\mathfrak{X}}^{(k,m)}$. Hence, the auxiliary results 2.2.8 and 2.2.9 can be applied in our context, proving (ii) of the proposition. The point (iii) is a direct consequence of (ii). This ends the proof of the Proposition 2.2.6.◻
$\mathscr{D}=\mathscr{D}_{\mathfrak{X}}^{(k,m)}$. Hence, the auxiliary results 2.2.8 and 2.2.9 can be applied in our context, proving (ii) of the proposition. The point (iii) is a direct consequence of (ii). This ends the proof of the Proposition 2.2.6.◻
Proposition 2.2.10. Let ![]() $\mathfrak{U}\subset \mathfrak{X}$ be an open affine formal subscheme of
$\mathfrak{U}\subset \mathfrak{X}$ be an open affine formal subscheme of ![]() $\mathfrak{X}$, and
$\mathfrak{X}$, and ![]() $\mathscr{M}$ a coherent
$\mathscr{M}$ a coherent ![]() $\widehat{\mathscr{D}}_{\mathfrak{U}}^{(k,m)}$-module. Then there are integers
$\widehat{\mathscr{D}}_{\mathfrak{U}}^{(k,m)}$-module. Then there are integers ![]() $a,b\geqslant 0$ and a short exact sequence of coherent
$a,b\geqslant 0$ and a short exact sequence of coherent ![]() $\widehat{\mathscr{D}}_{\mathfrak{U}}^{(k,m)}$-modules:
$\widehat{\mathscr{D}}_{\mathfrak{U}}^{(k,m)}$-modules:
Proof. Denote ![]() $\widehat{D}^{(m)}=\unicode[STIX]{x1D6E4}(\mathfrak{U},\widehat{\mathscr{D}}_{\mathfrak{U}}^{(k,m)})$ which is a noetherian ring by 2.2.2 and
$\widehat{D}^{(m)}=\unicode[STIX]{x1D6E4}(\mathfrak{U},\widehat{\mathscr{D}}_{\mathfrak{U}}^{(k,m)})$ which is a noetherian ring by 2.2.2 and ![]() $M=\unicode[STIX]{x1D6E4}(\mathfrak{U},\mathscr{M})$, which is a finite type
$M=\unicode[STIX]{x1D6E4}(\mathfrak{U},\mathscr{M})$, which is a finite type ![]() $\widehat{D}^{(m)}$-module by the previous Proposition 2.2.6. Since the algebra
$\widehat{D}^{(m)}$-module by the previous Proposition 2.2.6. Since the algebra ![]() $\widehat{D}^{(m)}$ is noetherian, there exists a finite presentation of
$\widehat{D}^{(m)}$ is noetherian, there exists a finite presentation of ![]() $\widehat{D}^{(m)}$-modules
$\widehat{D}^{(m)}$-modules
Tensoring this presentation by ![]() $\widehat{\mathscr{D}}_{\mathfrak{U}}^{(k,m)}$ over the ring
$\widehat{\mathscr{D}}_{\mathfrak{U}}^{(k,m)}$ over the ring ![]() $\widehat{D}^{(m)}$ and observing that
$\widehat{D}^{(m)}$ and observing that
again by 2.2.6, gives the result. ◻
Proposition 2.2.11. We have:
(i) The morphism of sheaves
 $\widehat{\mathscr{D}}_{\mathfrak{X},\mathbb{Q}}^{(k,m)}\rightarrow \widehat{\mathscr{D}}_{\mathfrak{X},\mathbb{Q}}^{(k,m+1)}$ is left and right flat.
$\widehat{\mathscr{D}}_{\mathfrak{X},\mathbb{Q}}^{(k,m)}\rightarrow \widehat{\mathscr{D}}_{\mathfrak{X},\mathbb{Q}}^{(k,m+1)}$ is left and right flat.(ii) The sheaf of rings
 $\mathscr{D}_{\mathfrak{X},k}^{\dagger }$ is coherent.
$\mathscr{D}_{\mathfrak{X},k}^{\dagger }$ is coherent.(iii) For any affine open
 $\mathfrak{U}\subset \mathfrak{X}$,
$\mathfrak{U}\subset \mathfrak{X}$,  $\unicode[STIX]{x1D6E4}(\mathfrak{U},\widehat{\mathscr{D}}_{\mathfrak{X},\mathbb{Q}}^{(k,m+1)})$ is left and right flat over
$\unicode[STIX]{x1D6E4}(\mathfrak{U},\widehat{\mathscr{D}}_{\mathfrak{X},\mathbb{Q}}^{(k,m+1)})$ is left and right flat over  $\unicode[STIX]{x1D6E4}(\mathfrak{U},\widehat{\mathscr{D}}_{\mathfrak{X},\mathbb{Q}}^{(k,m)})$.
$\unicode[STIX]{x1D6E4}(\mathfrak{U},\widehat{\mathscr{D}}_{\mathfrak{X},\mathbb{Q}}^{(k,m)})$.(iv) For any affine open
 $\mathfrak{U}\subset \mathfrak{X}$,
$\mathfrak{U}\subset \mathfrak{X}$,  $\unicode[STIX]{x1D6E4}(\mathfrak{U},\mathscr{D}_{\mathfrak{X},k}^{\dagger })$ is left and right flat over
$\unicode[STIX]{x1D6E4}(\mathfrak{U},\mathscr{D}_{\mathfrak{X},k}^{\dagger })$ is left and right flat over  $\unicode[STIX]{x1D6E4}(\mathfrak{U},\widehat{\mathscr{D}}_{\mathfrak{X},\mathbb{Q}}^{(k,m)})$.
$\unicode[STIX]{x1D6E4}(\mathfrak{U},\widehat{\mathscr{D}}_{\mathfrak{X},\mathbb{Q}}^{(k,m)})$.
Proof. Let us first observe that (ii) follows from the flatness statement of (i) and the last part of 2.2.2 thanks to [Reference Berthelot7, 3.6.1]. For (i), we follow Berthelot’s method described in [Reference Berthelot7, 3.5.3]. For the proof we can restrict ourselves to proving that if ![]() $\mathfrak{U}$ is an affine open of
$\mathfrak{U}$ is an affine open of ![]() $\mathfrak{X}$ contained in the basis of open sets
$\mathfrak{X}$ contained in the basis of open sets ![]() $\mathscr{B}$ from 2.2.2, then the map
$\mathscr{B}$ from 2.2.2, then the map ![]() $\widehat{\mathscr{D}}_{\mathfrak{X},\mathbb{Q}}^{(k,m)}(\mathfrak{U})\rightarrow \widehat{\mathscr{D}}_{\mathfrak{X},\mathbb{Q}}^{(k,m+1)}(\mathfrak{U})$ is left and right flat. In this situation, we have the following explicit description, assuming that
$\widehat{\mathscr{D}}_{\mathfrak{X},\mathbb{Q}}^{(k,m)}(\mathfrak{U})\rightarrow \widehat{\mathscr{D}}_{\mathfrak{X},\mathbb{Q}}^{(k,m+1)}(\mathfrak{U})$ is left and right flat. In this situation, we have the following explicit description, assuming that ![]() $\text{pr}^{\ast }\mathscr{T}_{\mathfrak{X}_{0}}$ is free restricted to
$\text{pr}^{\ast }\mathscr{T}_{\mathfrak{X}_{0}}$ is free restricted to ![]() $\mathfrak{U}$, with basis
$\mathfrak{U}$, with basis ![]() $\unicode[STIX]{x2202}_{1},\ldots ,\unicode[STIX]{x2202}_{M}$ as in 2.1.17,
$\unicode[STIX]{x2202}_{1},\ldots ,\unicode[STIX]{x2202}_{M}$ as in 2.1.17,
where the convergence is in the ![]() $\unicode[STIX]{x1D71B}$-adic topology of
$\unicode[STIX]{x1D71B}$-adic topology of ![]() $B={\mathcal{O}}_{\mathfrak{X}}(\mathfrak{U})$. With this description, we can copy Berthelot’s proof of [Reference Berthelot7, 3.5.3], replacing everywhere the operators
$B={\mathcal{O}}_{\mathfrak{X}}(\mathfrak{U})$. With this description, we can copy Berthelot’s proof of [Reference Berthelot7, 3.5.3], replacing everywhere the operators ![]() $\text{}\underline{\unicode[STIX]{x2202}}^{\langle \text{}\underline{\unicode[STIX]{x1D708}}\rangle }$ by
$\text{}\underline{\unicode[STIX]{x2202}}^{\langle \text{}\underline{\unicode[STIX]{x1D708}}\rangle }$ by ![]() $\unicode[STIX]{x1D71B}^{k|\text{}\underline{\unicode[STIX]{x1D708}}|}\text{}\underline{\unicode[STIX]{x2202}}^{\langle \text{}\underline{\unicode[STIX]{x1D708}}\rangle }$, as follows. First of all, by inserting suitable powers of
$\unicode[STIX]{x1D71B}^{k|\text{}\underline{\unicode[STIX]{x1D708}}|}\text{}\underline{\unicode[STIX]{x2202}}^{\langle \text{}\underline{\unicode[STIX]{x1D708}}\rangle }$, as follows. First of all, by inserting suitable powers of ![]() $\unicode[STIX]{x1D71B}$ into the formula [Reference Berthelot7, (2.2.5.1)] we see that the
$\unicode[STIX]{x1D71B}$ into the formula [Reference Berthelot7, (2.2.5.1)] we see that the ![]() $\mathfrak{o}$-algebra
$\mathfrak{o}$-algebra ![]() $\mathscr{D}_{\mathfrak{X}}^{(k,m)}(\mathfrak{U})$ is generated by
$\mathscr{D}_{\mathfrak{X}}^{(k,m)}(\mathfrak{U})$ is generated by ![]() $B$ and the operators
$B$ and the operators ![]() $\unicode[STIX]{x1D71B}^{kp^{r}}\unicode[STIX]{x2202}_{l}^{[p^{r}]}$ for
$\unicode[STIX]{x1D71B}^{kp^{r}}\unicode[STIX]{x2202}_{l}^{[p^{r}]}$ for ![]() $1\leqslant r\leqslant m$ and
$1\leqslant r\leqslant m$ and ![]() $1\leqslant l\leqslant M$. Now write
$1\leqslant l\leqslant M$. Now write
the latter being the ![]() $\unicode[STIX]{x1D71B}$-adic completion of
$\unicode[STIX]{x1D71B}$-adic completion of ![]() $D^{(k,m)}$ [Reference Berthelot7, 4.3.3.2]. By the above explicit description, the two canonical maps
$D^{(k,m)}$ [Reference Berthelot7, 4.3.3.2]. By the above explicit description, the two canonical maps ![]() $D^{(k,m)}\rightarrow \widehat{D}^{(k,m)}\rightarrow \widehat{D}_{\mathbb{Q}}^{(k,m)}$ are injective and this is also true for the canonical map
$D^{(k,m)}\rightarrow \widehat{D}^{(k,m)}\rightarrow \widehat{D}_{\mathbb{Q}}^{(k,m)}$ are injective and this is also true for the canonical map ![]() $\widehat{D}^{(k,m)}\rightarrow \widehat{D}^{(k,m+1)}$. Indeed, the latter is induced by mapping
$\widehat{D}^{(k,m)}\rightarrow \widehat{D}^{(k,m+1)}$. Indeed, the latter is induced by mapping
and is therefore injective by the above explicit description and the fact that ![]() $\mathfrak{o}$ is torsion-free. Let us consider the subring
$\mathfrak{o}$ is torsion-free. Let us consider the subring ![]() $E$ of
$E$ of ![]() $\widehat{D}_{\mathbb{Q}}^{(k,m)}$ generated by the subsets
$\widehat{D}_{\mathbb{Q}}^{(k,m)}$ generated by the subsets ![]() $\widehat{D}^{(k,m)}$ and
$\widehat{D}^{(k,m)}$ and ![]() $D^{(k,m+1)}$. Since
$D^{(k,m+1)}$. Since ![]() $D_{\mathbb{Q}}^{(k,m+1)}=D_{\mathbb{Q}}^{(k,m)}$, we see that
$D_{\mathbb{Q}}^{(k,m+1)}=D_{\mathbb{Q}}^{(k,m)}$, we see that
As in Berthelot’s proof, we have the following
Auxiliary result 2.2.13. ![]() $E=\widehat{D}^{(k,m)}+D^{(k,m+1)}$.
$E=\widehat{D}^{(k,m)}+D^{(k,m+1)}$.
Proof. Denote by ![]() $E^{\prime }=\widehat{D}^{(k,m)}+D^{(k,m+1)}$. We have to prove that
$E^{\prime }=\widehat{D}^{(k,m)}+D^{(k,m+1)}$. We have to prove that ![]() $E^{\prime }$ is a subalgebra of
$E^{\prime }$ is a subalgebra of ![]() $\widehat{D}^{(k,m+1)}$. It is enough to prove that if
$\widehat{D}^{(k,m+1)}$. It is enough to prove that if ![]() $(P,Q)\in \widehat{D}^{(k,m)}\times D^{(k,m+1)}$, then
$(P,Q)\in \widehat{D}^{(k,m)}\times D^{(k,m+1)}$, then ![]() $P\cdot Q\in E^{\prime }$ and
$P\cdot Q\in E^{\prime }$ and ![]() $Q\cdot P\in E^{\prime }$. Since the proof is the same in both cases, we only treat the product
$Q\cdot P\in E^{\prime }$. Since the proof is the same in both cases, we only treat the product ![]() $P\cdot Q$. As
$P\cdot Q$. As ![]() $Q\in D^{(k,m+1)}$, there exists
$Q\in D^{(k,m+1)}$, there exists ![]() $c>0$ such that
$c>0$ such that ![]() $\unicode[STIX]{x1D71B}^{c}Q\in D^{(k,m)}$. As
$\unicode[STIX]{x1D71B}^{c}Q\in D^{(k,m)}$. As ![]() $P\in \widehat{D}^{(k,m)}$, there exist
$P\in \widehat{D}^{(k,m)}$, there exist ![]() $(P_{1},R_{1})\in D^{(k,m)}\times \widehat{D}^{(k,m)}$ such that
$(P_{1},R_{1})\in D^{(k,m)}\times \widehat{D}^{(k,m)}$ such that ![]() $P=P_{1}+\unicode[STIX]{x1D71B}^{c}R_{1}$, then
$P=P_{1}+\unicode[STIX]{x1D71B}^{c}R_{1}$, then ![]() $PQ=\unicode[STIX]{x1D71B}^{c}R_{1}Q+P_{1}Q\in E^{\prime }$, as
$PQ=\unicode[STIX]{x1D71B}^{c}R_{1}Q+P_{1}Q\in E^{\prime }$, as ![]() $\unicode[STIX]{x1D71B}^{c}R_{1}Q\in \widehat{D}^{(k,m)}$ and
$\unicode[STIX]{x1D71B}^{c}R_{1}Q\in \widehat{D}^{(k,m)}$ and ![]() $P_{1}Q\in D^{(k,m+1)}$.◻
$P_{1}Q\in D^{(k,m+1)}$.◻
Denote by ![]() $\widehat{E}$ the
$\widehat{E}$ the ![]() $\unicode[STIX]{x1D71B}$-adic completion of
$\unicode[STIX]{x1D71B}$-adic completion of ![]() $E$. We can then prove the
$E$. We can then prove the
Auxiliary result 2.2.14. ![]() $\widehat{E}_{\mathbb{Q}}=\widehat{D}_{\mathbb{Q}}^{(k,m+1)}$.
$\widehat{E}_{\mathbb{Q}}=\widehat{D}_{\mathbb{Q}}^{(k,m+1)}$.
Proof. By construction, there are maps
Let us prove that these maps are bijective. If ![]() $R\in D^{(k,m+1)}$ is such that
$R\in D^{(k,m+1)}$ is such that ![]() $\unicode[STIX]{x1D706}_{i}(R)\in \unicode[STIX]{x1D71B}^{i}E$ then there exist
$\unicode[STIX]{x1D706}_{i}(R)\in \unicode[STIX]{x1D71B}^{i}E$ then there exist ![]() $(P,Q)\in \widehat{D}^{(k,m)}\times D^{(k,m+1)}$ such that
$(P,Q)\in \widehat{D}^{(k,m)}\times D^{(k,m+1)}$ such that ![]() $R=\unicode[STIX]{x1D71B}^{i}(P+Q)$, thus
$R=\unicode[STIX]{x1D71B}^{i}(P+Q)$, thus ![]() $\unicode[STIX]{x1D71B}^{i}P=R-\unicode[STIX]{x1D71B}^{i}Q$ has finite order, and
$\unicode[STIX]{x1D71B}^{i}P=R-\unicode[STIX]{x1D71B}^{i}Q$ has finite order, and ![]() $P\in D^{(k,m)}$, that implies that
$P\in D^{(k,m)}$, that implies that ![]() $R\in D^{(k,m+1)}$ and
$R\in D^{(k,m+1)}$ and ![]() $\unicode[STIX]{x1D706}_{i}$ is injective. Pick now
$\unicode[STIX]{x1D706}_{i}$ is injective. Pick now ![]() $R\in E$, and
$R\in E$, and ![]() $(P,Q)\in \widehat{D}^{(k,m)}\times D^{(k,m+1)}$ such that
$(P,Q)\in \widehat{D}^{(k,m)}\times D^{(k,m+1)}$ such that ![]() $R=P+Q$. The operator
$R=P+Q$. The operator ![]() $P$ can be written
$P$ can be written ![]() $P=P_{1}+\unicode[STIX]{x1D71B}^{i}R_{1}$, with
$P=P_{1}+\unicode[STIX]{x1D71B}^{i}R_{1}$, with ![]() $P_{1}\in D^{(k,m)}$ and
$P_{1}\in D^{(k,m)}$ and ![]() $R_{1}\in \widehat{D}^{(k,m)}$, then
$R_{1}\in \widehat{D}^{(k,m)}$, then ![]() $P=P_{1}+R+\unicode[STIX]{x1D71B}^{i}R_{1}$ and
$P=P_{1}+R+\unicode[STIX]{x1D71B}^{i}R_{1}$ and ![]() $\unicode[STIX]{x1D706}_{i}(P_{1}+R\text{ mod }\unicode[STIX]{x1D71B}^{i}D^{(k,m+1)})=P\text{ mod }\unicode[STIX]{x1D71B}^{i}E$, so that
$\unicode[STIX]{x1D706}_{i}(P_{1}+R\text{ mod }\unicode[STIX]{x1D71B}^{i}D^{(k,m+1)})=P\text{ mod }\unicode[STIX]{x1D71B}^{i}E$, so that ![]() $\unicode[STIX]{x1D706}_{i}$ is surjective. We finally see that
$\unicode[STIX]{x1D706}_{i}$ is surjective. We finally see that ![]() $\unicode[STIX]{x1D706}_{i}$ is bijective, which proves the auxiliary result.◻
$\unicode[STIX]{x1D706}_{i}$ is bijective, which proves the auxiliary result.◻
Now, the remaining thing to prove is that ![]() $E$ is noetherian, since this result implies that
$E$ is noetherian, since this result implies that ![]() $\widehat{E}$ is flat over
$\widehat{E}$ is flat over ![]() $E$, thus that
$E$, thus that ![]() $\widehat{D}_{\mathbb{Q}}^{(k,m+1)}$ is flat over
$\widehat{D}_{\mathbb{Q}}^{(k,m+1)}$ is flat over ![]() $\widehat{D}_{\mathbb{Q}}^{(k,m)}$. The proof that
$\widehat{D}_{\mathbb{Q}}^{(k,m)}$. The proof that ![]() $E$ is noetherian proceeds by induction. By our above remark,
$E$ is noetherian proceeds by induction. By our above remark, ![]() $E$ is generated as (left)
$E$ is generated as (left) ![]() $D^{(k,m)}$-module by the elements
$D^{(k,m)}$-module by the elements ![]() $\unicode[STIX]{x1D71B}^{k|\text{}\underline{\unicode[STIX]{x1D708}}|p^{m+1}}(\text{}\underline{\unicode[STIX]{x2202}}^{[p^{m+1}]})^{\text{}\underline{\unicode[STIX]{x1D708}}}$ for
$\unicode[STIX]{x1D71B}^{k|\text{}\underline{\unicode[STIX]{x1D708}}|p^{m+1}}(\text{}\underline{\unicode[STIX]{x2202}}^{[p^{m+1}]})^{\text{}\underline{\unicode[STIX]{x1D708}}}$ for ![]() $\text{}\underline{\unicode[STIX]{x1D708}}\in \mathbb{N}^{M}$. Let
$\text{}\underline{\unicode[STIX]{x1D708}}\in \mathbb{N}^{M}$. Let ![]() $1\leqslant l\leqslant M$. Inserting appropriate powers of
$1\leqslant l\leqslant M$. Inserting appropriate powers of ![]() $\unicode[STIX]{x1D71B}$ into the corresponding formula in Berthelot’s proof one finds
$\unicode[STIX]{x1D71B}$ into the corresponding formula in Berthelot’s proof one finds ![]() $[\unicode[STIX]{x1D71B}^{kp^{m+1}}\unicode[STIX]{x2202}_{l}^{[p^{m+1}]},b]\in D^{(k,m)}$ for any
$[\unicode[STIX]{x1D71B}^{kp^{m+1}}\unicode[STIX]{x2202}_{l}^{[p^{m+1}]},b]\in D^{(k,m)}$ for any ![]() $b\in B$ and so
$b\in B$ and so ![]() $[\unicode[STIX]{x1D71B}^{kp^{m+1}}\unicode[STIX]{x2202}_{l}^{[p^{m+1}]},P]\in \widehat{D}^{(k,m)}$ for any
$[\unicode[STIX]{x1D71B}^{kp^{m+1}}\unicode[STIX]{x2202}_{l}^{[p^{m+1}]},P]\in \widehat{D}^{(k,m)}$ for any ![]() $P\in \widehat{D}^{(k,m)}$. Using the general commutator identity (valid in any associative ring)
$P\in \widehat{D}^{(k,m)}$. Using the general commutator identity (valid in any associative ring) ![]() $[Q^{\unicode[STIX]{x1D708}},P]=[Q^{\unicode[STIX]{x1D708}-1},P]Q+Q^{\unicode[STIX]{x1D708}-1}[Q,P]$ one deduces from this inductively
$[Q^{\unicode[STIX]{x1D708}},P]=[Q^{\unicode[STIX]{x1D708}-1},P]Q+Q^{\unicode[STIX]{x1D708}-1}[Q,P]$ one deduces from this inductively
This is the analogue of the key formula [Reference Berthelot7, (3.5.3.2)]. Now let ![]() $1\leqslant j\leqslant M$ and consider the subring
$1\leqslant j\leqslant M$ and consider the subring ![]() $E_{j}$ of
$E_{j}$ of ![]() $E$ generated by
$E$ generated by ![]() $E_{0}=\widehat{D}^{(k,m)}$ and the operators
$E_{0}=\widehat{D}^{(k,m)}$ and the operators ![]() $\unicode[STIX]{x1D71B}^{kp^{m+1}}\unicode[STIX]{x2202}_{l}^{[p^{m+1}]}$ for
$\unicode[STIX]{x1D71B}^{kp^{m+1}}\unicode[STIX]{x2202}_{l}^{[p^{m+1}]}$ for ![]() $1\leqslant l\leqslant j$. Then
$1\leqslant l\leqslant j$. Then ![]() $E_{0}$ is noetherian by Proposition 2.2.2 and, by our above discussion,
$E_{0}$ is noetherian by Proposition 2.2.2 and, by our above discussion, ![]() $E_{M}=E$. With the key formula at hand, one may now follow Berthelot’s proof word for word to obtain that
$E_{M}=E$. With the key formula at hand, one may now follow Berthelot’s proof word for word to obtain that ![]() $E_{j-1}$ noetherian implies
$E_{j-1}$ noetherian implies ![]() $E_{j}$ noetherian. This proves (i).
$E_{j}$ noetherian. This proves (i).
Let us now prove (iii). Denote ![]() $\widehat{D}_{k,\mathbb{Q}}^{(m)}=\unicode[STIX]{x1D6E4}(\mathfrak{U},\widehat{\mathscr{D}}_{\mathfrak{U},\mathbb{Q}}^{(k,m)})$ and consider
$\widehat{D}_{k,\mathbb{Q}}^{(m)}=\unicode[STIX]{x1D6E4}(\mathfrak{U},\widehat{\mathscr{D}}_{\mathfrak{U},\mathbb{Q}}^{(k,m)})$ and consider ![]() $\unicode[STIX]{x1D6FC}$ an injective map of coherent
$\unicode[STIX]{x1D6FC}$ an injective map of coherent ![]() $\widehat{D}_{k,\mathbb{Q}}^{(m)}$-modules
$\widehat{D}_{k,\mathbb{Q}}^{(m)}$-modules ![]() $\unicode[STIX]{x1D6FC}$ :
$\unicode[STIX]{x1D6FC}$ : ![]() $M{\hookrightarrow}N$. As a consequence of (ii) and (iii) of 2.2.6, we know that the sheaf
$M{\hookrightarrow}N$. As a consequence of (ii) and (iii) of 2.2.6, we know that the sheaf ![]() $\widehat{\mathscr{D}}_{\mathfrak{U},\mathbb{Q}}^{(k,m)}$ is a flat
$\widehat{\mathscr{D}}_{\mathfrak{U},\mathbb{Q}}^{(k,m)}$ is a flat ![]() $\widehat{D}_{k,\mathbb{Q}}^{(m)}$-module. In particular, the map
$\widehat{D}_{k,\mathbb{Q}}^{(m)}$-module. In particular, the map ![]() $\unicode[STIX]{x1D6FC}$ provides an injection of coherent
$\unicode[STIX]{x1D6FC}$ provides an injection of coherent ![]() $\widehat{\mathscr{D}}_{\mathfrak{U},\mathbb{Q}}^{(k,m)}$-modules
$\widehat{\mathscr{D}}_{\mathfrak{U},\mathbb{Q}}^{(k,m)}$-modules
Using the flatness result (i) we also have an injection of coherent ![]() $\widehat{\mathscr{D}}_{\mathfrak{U},\mathbb{Q}}^{(k,m+1)}$-modules
$\widehat{\mathscr{D}}_{\mathfrak{U},\mathbb{Q}}^{(k,m+1)}$-modules
Then we identify (resp. for ![]() $N$)
$N$)
Finally taking global sections of the previous injection and using again 2.2.6, we get an injection of coherent ![]() $\widehat{D}_{k,\mathbb{Q}}^{(m+1)}$-modules
$\widehat{D}_{k,\mathbb{Q}}^{(m+1)}$-modules
that proves (iii). Assertion (iv) follows from the previous one, since, as ![]() $\mathfrak{U}$ is quasi-compact,
$\mathfrak{U}$ is quasi-compact,
and we deduce from (iii) that, for all integer ![]() $m^{\prime }\geqslant m$, the module
$m^{\prime }\geqslant m$, the module ![]() $\unicode[STIX]{x1D6E4}(\mathfrak{U},\widehat{\mathscr{D}}_{\mathfrak{X},\mathbb{Q}}^{(k,m^{\prime })})$ is left and right flat over
$\unicode[STIX]{x1D6E4}(\mathfrak{U},\widehat{\mathscr{D}}_{\mathfrak{X},\mathbb{Q}}^{(k,m^{\prime })})$ is left and right flat over ![]() $\unicode[STIX]{x1D6E4}(\mathfrak{U},\widehat{\mathscr{D}}_{\mathfrak{X},\mathbb{Q}}^{(k,m)})$. We obtain thus (iv) by passing to the inductive limit over
$\unicode[STIX]{x1D6E4}(\mathfrak{U},\widehat{\mathscr{D}}_{\mathfrak{X},\mathbb{Q}}^{(k,m)})$. We obtain thus (iv) by passing to the inductive limit over ![]() $m$. This ends the proof of the Proposition 2.2.11.◻
$m$. This ends the proof of the Proposition 2.2.11.◻
We deduce from this the corresponding version of Proposition 2.2.6 for the sheaf ![]() $\mathscr{D}_{\mathfrak{X},k}^{\dagger }$.
$\mathscr{D}_{\mathfrak{X},k}^{\dagger }$.
Corollary 2.2.15. (Local theorems A and B for varying ![]() $m$) Let
$m$) Let ![]() $\mathfrak{U}\subset \mathfrak{X}$ be an open affine formal subscheme of
$\mathfrak{U}\subset \mathfrak{X}$ be an open affine formal subscheme of ![]() $\mathfrak{X}$. Then:
$\mathfrak{X}$. Then:
(i) The algebra
 $D_{k}^{\dagger }=\unicode[STIX]{x1D6E4}(\mathfrak{U},\mathscr{D}_{\mathfrak{X},k}^{\dagger })$ is coherent.
$D_{k}^{\dagger }=\unicode[STIX]{x1D6E4}(\mathfrak{U},\mathscr{D}_{\mathfrak{X},k}^{\dagger })$ is coherent.(ii) For any open affine subset
 $\mathfrak{U}\subset \mathfrak{X}$, any coherent
$\mathfrak{U}\subset \mathfrak{X}$, any coherent  $\mathscr{D}_{\mathfrak{U},k}^{\dagger }$-module
$\mathscr{D}_{\mathfrak{U},k}^{\dagger }$-module  $\mathscr{M}$, and any
$\mathscr{M}$, and any  $q>0$ one has
$q>0$ one has  $H^{q}(\mathfrak{U},\mathscr{M})=0$.
$H^{q}(\mathfrak{U},\mathscr{M})=0$.(iii) The functor
 $\unicode[STIX]{x1D6E4}(\mathfrak{U},.)$ establishes an equivalence of categories between coherent
$\unicode[STIX]{x1D6E4}(\mathfrak{U},.)$ establishes an equivalence of categories between coherent  $\mathscr{D}_{\mathfrak{U},k}^{\dagger }$-modules and coherent
$\mathscr{D}_{\mathfrak{U},k}^{\dagger }$-modules and coherent  $D_{k}^{\dagger }$-modules. In particular, the functor
$D_{k}^{\dagger }$-modules. In particular, the functor  $\unicode[STIX]{x1D6E4}(\mathfrak{U},.)$ is exact on coherent
$\unicode[STIX]{x1D6E4}(\mathfrak{U},.)$ is exact on coherent  $\mathscr{D}_{\mathfrak{U},k}^{\dagger }$-modules.
$\mathscr{D}_{\mathfrak{U},k}^{\dagger }$-modules.
Proof. Denote ![]() $\widehat{D}_{k,\mathbb{Q}}^{(m)}=\unicode[STIX]{x1D6E4}(\mathfrak{U},\widehat{\mathscr{D}}_{\mathfrak{U},\mathbb{Q}}^{(k,m)})$. Since the scheme
$\widehat{D}_{k,\mathbb{Q}}^{(m)}=\unicode[STIX]{x1D6E4}(\mathfrak{U},\widehat{\mathscr{D}}_{\mathfrak{U},\mathbb{Q}}^{(k,m)})$. Since the scheme ![]() $\mathfrak{U}$ is quasi-compact, the functors
$\mathfrak{U}$ is quasi-compact, the functors ![]() $H^{q}(\mathfrak{U},.)$ commute with inductive limits and we have
$H^{q}(\mathfrak{U},.)$ commute with inductive limits and we have
By (iii) of 2.2.11, the maps ![]() $\widehat{D}_{k,\mathbb{Q}}^{(m)}\rightarrow \widehat{D}_{k,\mathbb{Q}}^{(m+1)}$ are flat, and by 2.2.2 these algebras
$\widehat{D}_{k,\mathbb{Q}}^{(m)}\rightarrow \widehat{D}_{k,\mathbb{Q}}^{(m+1)}$ are flat, and by 2.2.2 these algebras ![]() $\widehat{D}_{k,\mathbb{Q}}^{(m)}$ are noetherian. This shows that the algebra
$\widehat{D}_{k,\mathbb{Q}}^{(m)}$ are noetherian. This shows that the algebra ![]() $D_{k}^{\dagger }$ is coherent [Reference Berthelot7, 3.6.1].
$D_{k}^{\dagger }$ is coherent [Reference Berthelot7, 3.6.1].
Let ![]() $\mathscr{M}$ be a coherent
$\mathscr{M}$ be a coherent ![]() $\mathscr{D}_{\mathfrak{U},k}^{\dagger }$-module. The proof of [Reference Berthelot7, 3.6.2] literally applies in our situation and shows that there is a nonnegative integer
$\mathscr{D}_{\mathfrak{U},k}^{\dagger }$-module. The proof of [Reference Berthelot7, 3.6.2] literally applies in our situation and shows that there is a nonnegative integer ![]() $m_{0}$ and a coherent
$m_{0}$ and a coherent ![]() $\widehat{\mathscr{D}}_{\mathfrak{U},\mathbb{Q}}^{(k,m_{0})}$-module
$\widehat{\mathscr{D}}_{\mathfrak{U},\mathbb{Q}}^{(k,m_{0})}$-module ![]() $\mathscr{N}$ such that
$\mathscr{N}$ such that
Denote ![]() $M=\unicode[STIX]{x1D6E4}(\mathfrak{U},\mathscr{M})$ and for
$M=\unicode[STIX]{x1D6E4}(\mathfrak{U},\mathscr{M})$ and for ![]() $m\geqslant m_{0}$
$m\geqslant m_{0}$
so that ![]() $\mathscr{M}\simeq \mathop{\varinjlim }\nolimits_{m}\mathscr{M}^{(m)}$. Then,
$\mathscr{M}\simeq \mathop{\varinjlim }\nolimits_{m}\mathscr{M}^{(m)}$. Then, ![]() $\forall m\geqslant m_{0}$,
$\forall m\geqslant m_{0}$, ![]() $H^{q}(\mathfrak{U},\mathscr{M}^{(m)})=0$ by 2.2.6, and by passing to the inductive limit we see that
$H^{q}(\mathfrak{U},\mathscr{M}^{(m)})=0$ by 2.2.6, and by passing to the inductive limit we see that ![]() $H^{q}(\mathfrak{U},\mathscr{M})=0$, which proves (ii).
$H^{q}(\mathfrak{U},\mathscr{M})=0$, which proves (ii).
The rest of the proof follows 2.3.7, 2.4.1, 2.4.2 of [Reference Noot-Huyghe21]. For the convenience of the reader, let us summarize the arguments here. From 2.2.10, the ![]() $\widehat{\mathscr{D}}_{\mathfrak{U},\mathbb{Q}}^{(k,m_{0})}$-coherent module
$\widehat{\mathscr{D}}_{\mathfrak{U},\mathbb{Q}}^{(k,m_{0})}$-coherent module ![]() $\mathscr{N}$ admits a resolution
$\mathscr{N}$ admits a resolution
Tensoring this resolution with the sheaf ![]() $\mathscr{D}_{\mathfrak{U},k}^{\dagger }$ gives us a resolution of coherent
$\mathscr{D}_{\mathfrak{U},k}^{\dagger }$ gives us a resolution of coherent ![]() $\mathscr{D}_{\mathfrak{U},k}^{\dagger }$-modules. Since the global section functor is exact on the category of coherent
$\mathscr{D}_{\mathfrak{U},k}^{\dagger }$-modules. Since the global section functor is exact on the category of coherent ![]() $\mathscr{D}_{\mathfrak{U},k}^{\dagger }$-modules because of (ii), we get an exact sequence of coherent
$\mathscr{D}_{\mathfrak{U},k}^{\dagger }$-modules because of (ii), we get an exact sequence of coherent ![]() $D_{k}^{\dagger }$-modules
$D_{k}^{\dagger }$-modules
To see that ![]() $\mathscr{D}_{k}^{\dagger }\otimes _{D_{k}^{\dagger }}M\simeq \mathscr{M}$, we are thus reduced to the case
$\mathscr{D}_{k}^{\dagger }\otimes _{D_{k}^{\dagger }}M\simeq \mathscr{M}$, we are thus reduced to the case ![]() $\mathscr{M}=\mathscr{D}_{\mathfrak{U},k}^{\dagger }$, for which it is obvious. We prove similarly that if
$\mathscr{M}=\mathscr{D}_{\mathfrak{U},k}^{\dagger }$, for which it is obvious. We prove similarly that if ![]() $M$ is a
$M$ is a ![]() $D_{k}^{\dagger }$-coherent module, then
$D_{k}^{\dagger }$-coherent module, then
by reducing to the case where ![]() $M=D_{k}^{\dagger }$. This proves the proposition.◻
$M=D_{k}^{\dagger }$. This proves the proposition.◻
We now give a flatness result when the congruence level ![]() $k$ varies.
$k$ varies.
Proposition 2.2.16. Let ![]() $k,k^{\prime }$ be nonnegative integers such that
$k,k^{\prime }$ be nonnegative integers such that ![]() $k^{\prime }\geqslant k\geqslant k_{\mathfrak{X}}$, then the morphism of sheaves of rings
$k^{\prime }\geqslant k\geqslant k_{\mathfrak{X}}$, then the morphism of sheaves of rings ![]() $\widehat{\mathscr{D}}_{\mathfrak{X},\mathbb{Q}}^{(k^{\prime },m)}{\hookrightarrow}\widehat{\mathscr{D}}_{\mathfrak{X},\mathbb{Q}}^{(k,m)}$ is left and right flat.
$\widehat{\mathscr{D}}_{\mathfrak{X},\mathbb{Q}}^{(k^{\prime },m)}{\hookrightarrow}\widehat{\mathscr{D}}_{\mathfrak{X},\mathbb{Q}}^{(k,m)}$ is left and right flat.
Proof. By induction, it is enough to prove that the morphism ![]() $\widehat{\mathscr{D}}_{\mathfrak{X},\mathbb{Q}}^{(k+1,m)}{\hookrightarrow}\widehat{\mathscr{D}}_{\mathfrak{X},\mathbb{Q}}^{(k,m)}$ is left and right flat. It is also enough to prove the following statement: if
$\widehat{\mathscr{D}}_{\mathfrak{X},\mathbb{Q}}^{(k+1,m)}{\hookrightarrow}\widehat{\mathscr{D}}_{\mathfrak{X},\mathbb{Q}}^{(k,m)}$ is left and right flat. It is also enough to prove the following statement: if ![]() $\mathfrak{U}$ is an affine open of the basis of open sets
$\mathfrak{U}$ is an affine open of the basis of open sets ![]() $\mathscr{B}$ from 2.2.2, then the map
$\mathscr{B}$ from 2.2.2, then the map ![]() $\widehat{\mathscr{D}}_{\mathfrak{X},\mathbb{Q}}^{(k+1,m)}(\mathfrak{U}){\hookrightarrow}\widehat{\mathscr{D}}_{\mathfrak{X},\mathbb{Q}}^{(k,m)}(\mathfrak{U})$ is left and right flat. Denote
$\widehat{\mathscr{D}}_{\mathfrak{X},\mathbb{Q}}^{(k+1,m)}(\mathfrak{U}){\hookrightarrow}\widehat{\mathscr{D}}_{\mathfrak{X},\mathbb{Q}}^{(k,m)}(\mathfrak{U})$ is left and right flat. Denote ![]() $D_{k}=\unicode[STIX]{x1D6E4}(\mathfrak{U},\mathscr{D}_{\mathfrak{X}}^{(k,m)})$ and
$D_{k}=\unicode[STIX]{x1D6E4}(\mathfrak{U},\mathscr{D}_{\mathfrak{X}}^{(k,m)})$ and ![]() $\widehat{D}_{k}=\unicode[STIX]{x1D6E4}(\mathfrak{U},\widehat{\mathscr{D}}_{\mathfrak{X}}^{(k,m)})$ (resp. with
$\widehat{D}_{k}=\unicode[STIX]{x1D6E4}(\mathfrak{U},\widehat{\mathscr{D}}_{\mathfrak{X}}^{(k,m)})$ (resp. with ![]() $k+1$). In our situation, we have the following explicit description (resp. with
$k+1$). In our situation, we have the following explicit description (resp. with ![]() $k+1$), where
$k+1$), where ![]() $B=\unicode[STIX]{x1D6E4}(\mathfrak{U},{\mathcal{O}}_{\mathfrak{X}})$, assuming that
$B=\unicode[STIX]{x1D6E4}(\mathfrak{U},{\mathcal{O}}_{\mathfrak{X}})$, assuming that ![]() $\text{pr}^{\ast }\mathscr{T}_{\mathfrak{X}_{0}}$ is free restricted to
$\text{pr}^{\ast }\mathscr{T}_{\mathfrak{X}_{0}}$ is free restricted to ![]() $\mathfrak{U}$, with basis
$\mathfrak{U}$, with basis ![]() $\unicode[STIX]{x2202}_{1},\ldots ,\unicode[STIX]{x2202}_{M}$ as in 2.1.17,
$\unicode[STIX]{x2202}_{1},\ldots ,\unicode[STIX]{x2202}_{M}$ as in 2.1.17,
Here, convergence is with respect to the ![]() $p$-adic topology on
$p$-adic topology on ![]() $B$. Moreover, we have the inclusion
$B$. Moreover, we have the inclusion ![]() $D_{k}\subset \widehat{D}_{k}$. As in the proof of the Proposition 2.2.11 above, we will use Berthelot’s method [Reference Berthelot7, 3.5.3], and introduce
$D_{k}\subset \widehat{D}_{k}$. As in the proof of the Proposition 2.2.11 above, we will use Berthelot’s method [Reference Berthelot7, 3.5.3], and introduce
Then, since ![]() $D_{k,\mathbb{Q}}=D_{k+1,\mathbb{Q}}$, it is clear that
$D_{k,\mathbb{Q}}=D_{k+1,\mathbb{Q}}$, it is clear that ![]() $E_{\mathbb{Q}}=\widehat{D}_{k+1,\mathbb{Q}}$. Moreover, we have the following
$E_{\mathbb{Q}}=\widehat{D}_{k+1,\mathbb{Q}}$. Moreover, we have the following
Auxiliary result 2.2.17. The ![]() $B$-module
$B$-module ![]() $E$ is a
$E$ is a ![]() $B$-algebra and its
$B$-algebra and its ![]() $p$-adic completion
$p$-adic completion ![]() $\widehat{E}$ is canonically isomorphic to
$\widehat{E}$ is canonically isomorphic to ![]() $\widehat{D}_{k}$.
$\widehat{D}_{k}$.
Proof. Let us first prove that ![]() $E$ is a ring. Any element
$E$ is a ring. Any element ![]() $P$ of
$P$ of ![]() $E$ can be written as
$E$ can be written as
To prove that ![]() $E$ is a ring, it is enough to prove that
$E$ is a ring, it is enough to prove that
Fix ![]() $\text{}\underline{\unicode[STIX]{x1D708}}$, and take
$\text{}\underline{\unicode[STIX]{x1D708}}$, and take ![]() $Q\in \widehat{D}_{k+1}$. We can then write
$Q\in \widehat{D}_{k+1}$. We can then write ![]() $Q=Q_{1}+\unicode[STIX]{x1D71B}^{|\text{}\underline{\unicode[STIX]{x1D708}}|}Q_{2}$, with
$Q=Q_{1}+\unicode[STIX]{x1D71B}^{|\text{}\underline{\unicode[STIX]{x1D708}}|}Q_{2}$, with ![]() $Q_{1}\in D_{k+1}$ and
$Q_{1}\in D_{k+1}$ and ![]() $Q_{2}\in \widehat{D}_{k+1}$. Since
$Q_{2}\in \widehat{D}_{k+1}$. Since ![]() $\unicode[STIX]{x1D71B}^{k|\text{}\underline{\unicode[STIX]{x1D708}}|}\text{}\underline{\unicode[STIX]{x2202}}^{\langle \text{}\underline{\unicode[STIX]{x1D708}}\rangle }\cdot Q_{1}\in D_{k}$, and
$\unicode[STIX]{x1D71B}^{k|\text{}\underline{\unicode[STIX]{x1D708}}|}\text{}\underline{\unicode[STIX]{x2202}}^{\langle \text{}\underline{\unicode[STIX]{x1D708}}\rangle }\cdot Q_{1}\in D_{k}$, and ![]() $Q_{1}\cdot \unicode[STIX]{x1D71B}^{k|\text{}\underline{\unicode[STIX]{x1D708}}|}\text{}\underline{\unicode[STIX]{x2202}}^{\langle \text{}\underline{\unicode[STIX]{x1D708}}\rangle }\in D_{k}$, it remains to prove that
$Q_{1}\cdot \unicode[STIX]{x1D71B}^{k|\text{}\underline{\unicode[STIX]{x1D708}}|}\text{}\underline{\unicode[STIX]{x2202}}^{\langle \text{}\underline{\unicode[STIX]{x1D708}}\rangle }\in D_{k}$, it remains to prove that ![]() $\unicode[STIX]{x1D71B}^{k|\text{}\underline{\unicode[STIX]{x1D708}}|}\text{}\underline{\unicode[STIX]{x2202}}^{\langle \text{}\underline{\unicode[STIX]{x1D708}}\rangle }\cdot \unicode[STIX]{x1D71B}^{|\text{}\underline{\unicode[STIX]{x1D708}}|}Q_{2}\in E$ (resp.
$\unicode[STIX]{x1D71B}^{k|\text{}\underline{\unicode[STIX]{x1D708}}|}\text{}\underline{\unicode[STIX]{x2202}}^{\langle \text{}\underline{\unicode[STIX]{x1D708}}\rangle }\cdot \unicode[STIX]{x1D71B}^{|\text{}\underline{\unicode[STIX]{x1D708}}|}Q_{2}\in E$ (resp. ![]() $\unicode[STIX]{x1D71B}^{|\text{}\underline{\unicode[STIX]{x1D708}}|}Q_{2}\cdot \unicode[STIX]{x1D71B}^{k|\text{}\underline{\unicode[STIX]{x1D708}}|}\text{}\underline{\unicode[STIX]{x2202}}^{\langle \text{}\underline{\unicode[STIX]{x1D708}}\rangle }\in E$). Let us write
$\unicode[STIX]{x1D71B}^{|\text{}\underline{\unicode[STIX]{x1D708}}|}Q_{2}\cdot \unicode[STIX]{x1D71B}^{k|\text{}\underline{\unicode[STIX]{x1D708}}|}\text{}\underline{\unicode[STIX]{x2202}}^{\langle \text{}\underline{\unicode[STIX]{x1D708}}\rangle }\in E$). Let us write
with coefficients ![]() $b_{\text{}\underline{\unicode[STIX]{x1D708}}^{\prime }}\in B$ tending
$b_{\text{}\underline{\unicode[STIX]{x1D708}}^{\prime }}\in B$ tending ![]() $p$-adically to zero in
$p$-adically to zero in ![]() $B$. Besides the coefficients appearing in 2.1.12, we need other modified binomial coefficients [Reference Berthelot7, (1.1.2.2)]
$B$. Besides the coefficients appearing in 2.1.12, we need other modified binomial coefficients [Reference Berthelot7, (1.1.2.2)]
Then, following [Reference Berthelot7, (2.2.4)] we have the following formulas
 $$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D71B}^{k|\text{}\underline{\unicode[STIX]{x1D708}}|}\text{}\underline{\unicode[STIX]{x2202}}^{\langle \text{}\underline{\unicode[STIX]{x1D708}}\rangle }\cdot \unicode[STIX]{x1D71B}^{((k+1)|\text{}\underline{\unicode[STIX]{x1D708}}^{\prime }|+|\text{}\underline{\unicode[STIX]{x1D708}}|)}b_{\text{}\underline{\unicode[STIX]{x1D708}}^{\prime }}\text{}\underline{\unicode[STIX]{x2202}}^{\langle \text{}\underline{\unicode[STIX]{x1D708}}^{\prime }\rangle }\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D71B}^{(k+1)(|\text{}\underline{\unicode[STIX]{x1D708}}|+|\text{}\underline{\unicode[STIX]{x1D708}}^{\prime }|)}\mathop{\sum }_{\text{}\underline{\unicode[STIX]{x1D707}}\leqslant \text{}\underline{\unicode[STIX]{x1D708}}}\left\{\frac{\text{}\underline{\unicode[STIX]{x1D708}}}{\text{}\underline{\unicode[STIX]{x1D707}}}\right\}\left\langle \frac{\text{}\underline{\unicode[STIX]{x1D708}}+\text{}\underline{\unicode[STIX]{x1D708}}^{\prime }-\text{}\underline{\unicode[STIX]{x1D707}}}{\text{}\underline{\unicode[STIX]{x1D708}}^{\prime }}\right\rangle \text{}\underline{\unicode[STIX]{x2202}}^{\langle \text{}\underline{\unicode[STIX]{x1D707}}\rangle }(b_{\text{}\underline{\unicode[STIX]{x1D708}}^{\prime }})\text{}\underline{\unicode[STIX]{x2202}}^{\langle \text{}\underline{\unicode[STIX]{x1D708}}+\text{}\underline{\unicode[STIX]{x1D708}}^{\prime }-\text{}\underline{\unicode[STIX]{x1D707}}\rangle }\in \widehat{D}_{k+1}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D71B}^{k|\text{}\underline{\unicode[STIX]{x1D708}}|}\text{}\underline{\unicode[STIX]{x2202}}^{\langle \text{}\underline{\unicode[STIX]{x1D708}}\rangle }\cdot \unicode[STIX]{x1D71B}^{((k+1)|\text{}\underline{\unicode[STIX]{x1D708}}^{\prime }|+|\text{}\underline{\unicode[STIX]{x1D708}}|)}b_{\text{}\underline{\unicode[STIX]{x1D708}}^{\prime }}\text{}\underline{\unicode[STIX]{x2202}}^{\langle \text{}\underline{\unicode[STIX]{x1D708}}^{\prime }\rangle }\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D71B}^{(k+1)(|\text{}\underline{\unicode[STIX]{x1D708}}|+|\text{}\underline{\unicode[STIX]{x1D708}}^{\prime }|)}\mathop{\sum }_{\text{}\underline{\unicode[STIX]{x1D707}}\leqslant \text{}\underline{\unicode[STIX]{x1D708}}}\left\{\frac{\text{}\underline{\unicode[STIX]{x1D708}}}{\text{}\underline{\unicode[STIX]{x1D707}}}\right\}\left\langle \frac{\text{}\underline{\unicode[STIX]{x1D708}}+\text{}\underline{\unicode[STIX]{x1D708}}^{\prime }-\text{}\underline{\unicode[STIX]{x1D707}}}{\text{}\underline{\unicode[STIX]{x1D708}}^{\prime }}\right\rangle \text{}\underline{\unicode[STIX]{x2202}}^{\langle \text{}\underline{\unicode[STIX]{x1D707}}\rangle }(b_{\text{}\underline{\unicode[STIX]{x1D708}}^{\prime }})\text{}\underline{\unicode[STIX]{x2202}}^{\langle \text{}\underline{\unicode[STIX]{x1D708}}+\text{}\underline{\unicode[STIX]{x1D708}}^{\prime }-\text{}\underline{\unicode[STIX]{x1D707}}\rangle }\in \widehat{D}_{k+1}.\nonumber\end{eqnarray}$$ Passing to the limit in the complete ring ![]() $\widehat{D}_{k+1}$ we see that
$\widehat{D}_{k+1}$ we see that ![]() $\unicode[STIX]{x1D71B}^{k|\text{}\underline{\unicode[STIX]{x1D708}}|}\text{}\underline{\unicode[STIX]{x2202}}^{\langle \text{}\underline{\unicode[STIX]{x1D708}}\rangle }\cdot \unicode[STIX]{x1D71B}^{|\text{}\underline{\unicode[STIX]{x1D708}}|}Q_{2}\in \widehat{D}_{k+1}$. Similarly, we have
$\unicode[STIX]{x1D71B}^{k|\text{}\underline{\unicode[STIX]{x1D708}}|}\text{}\underline{\unicode[STIX]{x2202}}^{\langle \text{}\underline{\unicode[STIX]{x1D708}}\rangle }\cdot \unicode[STIX]{x1D71B}^{|\text{}\underline{\unicode[STIX]{x1D708}}|}Q_{2}\in \widehat{D}_{k+1}$. Similarly, we have
which proves that ![]() $\unicode[STIX]{x1D71B}^{|\text{}\underline{\unicode[STIX]{x1D708}}|}Q_{2}\cdot \unicode[STIX]{x1D71B}^{k|\text{}\underline{\unicode[STIX]{x1D708}}|}\text{}\underline{\unicode[STIX]{x2202}}^{\langle \text{}\underline{\unicode[STIX]{x1D708}}\rangle }\in E$ and that
$\unicode[STIX]{x1D71B}^{|\text{}\underline{\unicode[STIX]{x1D708}}|}Q_{2}\cdot \unicode[STIX]{x1D71B}^{k|\text{}\underline{\unicode[STIX]{x1D708}}|}\text{}\underline{\unicode[STIX]{x2202}}^{\langle \text{}\underline{\unicode[STIX]{x1D708}}\rangle }\in E$ and that ![]() $E$ is a ring.
$E$ is a ring.
Let ![]() $i\geqslant 0$ be an integer and consider now the canonical map
$i\geqslant 0$ be an integer and consider now the canonical map
Let ![]() $P\in E$, and
$P\in E$, and ![]() $Q\in \widehat{D}_{k+1},R\in D_{k}$ such that
$Q\in \widehat{D}_{k+1},R\in D_{k}$ such that ![]() $P=Q+R$. There exist
$P=Q+R$. There exist ![]() $Q_{1}\in D_{k+1}$ and
$Q_{1}\in D_{k+1}$ and ![]() $Q_{2}\in \widehat{D}_{k+1}$ such that
$Q_{2}\in \widehat{D}_{k+1}$ such that ![]() $Q=Q_{1}+\unicode[STIX]{x1D71B}^{i}Q_{2}$. Then
$Q=Q_{1}+\unicode[STIX]{x1D71B}^{i}Q_{2}$. Then
where ![]() $\overline{Q_{1}}$ and
$\overline{Q_{1}}$ and ![]() $\overline{R}$ are the class of
$\overline{R}$ are the class of ![]() $Q_{1}$ and
$Q_{1}$ and ![]() $R$ in the quotient
$R$ in the quotient ![]() $D_{k}/\unicode[STIX]{x1D71B}^{i}D_{k}$. This proves that the map
$D_{k}/\unicode[STIX]{x1D71B}^{i}D_{k}$. This proves that the map ![]() $\unicode[STIX]{x1D706}$ is surjective. Suppose now that
$\unicode[STIX]{x1D706}$ is surjective. Suppose now that ![]() $\unicode[STIX]{x1D706}(\overline{P})=0$ for some
$\unicode[STIX]{x1D706}(\overline{P})=0$ for some ![]() $P\in D_{k}$, then there exist
$P\in D_{k}$, then there exist ![]() $Q\in \widehat{D}_{k+1}$ and
$Q\in \widehat{D}_{k+1}$ and ![]() $R\in D_{k}$ such that
$R\in D_{k}$ such that ![]() $P=\unicode[STIX]{x1D71B}^{i}(Q+R)$. As
$P=\unicode[STIX]{x1D71B}^{i}(Q+R)$. As
we see from the explicit description of ![]() $D_{k+1}$ above that
$D_{k+1}$ above that ![]() $Q\in D_{k+1}$ and finally that
$Q\in D_{k+1}$ and finally that ![]() $P\in \unicode[STIX]{x1D71B}^{i}D_{k}$, which proves that
$P\in \unicode[STIX]{x1D71B}^{i}D_{k}$, which proves that ![]() $\unicode[STIX]{x1D706}$ is injective and thus an isomorphism. This completes the proof of the auxiliary result.◻
$\unicode[STIX]{x1D706}$ is injective and thus an isomorphism. This completes the proof of the auxiliary result.◻
Now, to prove the proposition, it is enough to prove that ![]() $E$ is noetherian. If this is the case, then
$E$ is noetherian. If this is the case, then ![]() $\widehat{E}$ is flat over
$\widehat{E}$ is flat over ![]() $E$, thus
$E$, thus ![]() $\widehat{E}_{\mathbb{Q}}$ is flat over
$\widehat{E}_{\mathbb{Q}}$ is flat over ![]() $E_{\mathbb{Q}}$ and
$E_{\mathbb{Q}}$ and ![]() $\widehat{D}_{k,\mathbb{Q}}$ is flat over
$\widehat{D}_{k,\mathbb{Q}}$ is flat over ![]() $\widehat{D}_{k+1,\mathbb{Q}}$.
$\widehat{D}_{k+1,\mathbb{Q}}$.
Recall [Reference Berthelot7, (2.2.5)] that the ring ![]() $D_{k}$ is generated by the algebra
$D_{k}$ is generated by the algebra ![]() $B$ and the elements
$B$ and the elements ![]() $\unicode[STIX]{x1D71B}^{kp^{a}}\unicode[STIX]{x2202}_{i}^{\langle p^{a}\rangle }=\unicode[STIX]{x1D71B}^{kp^{a}}\unicode[STIX]{x2202}_{i}^{[p^{a}]}$ with
$\unicode[STIX]{x1D71B}^{kp^{a}}\unicode[STIX]{x2202}_{i}^{\langle p^{a}\rangle }=\unicode[STIX]{x1D71B}^{kp^{a}}\unicode[STIX]{x2202}_{i}^{[p^{a}]}$ with ![]() $1\leqslant i\leqslant M$,
$1\leqslant i\leqslant M$, ![]() $1\leqslant a\leqslant m$. Let us define the following algebras: let
$1\leqslant a\leqslant m$. Let us define the following algebras: let ![]() $E_{0}=\widehat{D}_{k+1}$, and for
$E_{0}=\widehat{D}_{k+1}$, and for ![]() $j\geqslant 1$
$j\geqslant 1$![]() $E_{j}$ be the
$E_{j}$ be the ![]() $B$-algebra of
$B$-algebra of ![]() $E$ generated by
$E$ generated by ![]() $\widehat{D}_{k+1}$ and the
$\widehat{D}_{k+1}$ and the ![]() $\unicode[STIX]{x1D71B}^{k\unicode[STIX]{x1D708}_{i}}\unicode[STIX]{x2202}_{i}^{\langle \unicode[STIX]{x1D708}_{i}\rangle }$ with
$\unicode[STIX]{x1D71B}^{k\unicode[STIX]{x1D708}_{i}}\unicode[STIX]{x2202}_{i}^{\langle \unicode[STIX]{x1D708}_{i}\rangle }$ with ![]() $1\leqslant i\leqslant j$ and
$1\leqslant i\leqslant j$ and ![]() $\unicode[STIX]{x1D708}_{i}\in \mathbb{N}$. We also introduce for each
$\unicode[STIX]{x1D708}_{i}\in \mathbb{N}$. We also introduce for each ![]() $j$ and
$j$ and ![]() $s$ an integer satisfying
$s$ an integer satisfying ![]() $1\leqslant s\leqslant m$ the subalgebra
$1\leqslant s\leqslant m$ the subalgebra ![]() $E_{j,s}$ of
$E_{j,s}$ of ![]() $E_{j}$ generated by
$E_{j}$ generated by ![]() $E_{j-1}$ and the
$E_{j-1}$ and the ![]() $\unicode[STIX]{x1D71B}^{kp^{a}}\unicode[STIX]{x2202}_{j}^{[p^{a}]}$ with
$\unicode[STIX]{x1D71B}^{kp^{a}}\unicode[STIX]{x2202}_{j}^{[p^{a}]}$ with ![]() $1\leqslant a\leqslant s$. We define
$1\leqslant a\leqslant s$. We define ![]() $E_{j,0}=E_{j-1}$ for
$E_{j,0}=E_{j-1}$ for ![]() $j\geqslant 1$. By definition, we have
$j\geqslant 1$. By definition, we have ![]() $E_{j,m}=E_{j}$. Now we use the
$E_{j,m}=E_{j}$. Now we use the
Auxiliary result 2.2.18. For each ![]() $j\leqslant M$,
$j\leqslant M$, ![]() $s\leqslant m$, the algebra
$s\leqslant m$, the algebra ![]() $E_{j,s}$ is two-sided noetherian. The algebra
$E_{j,s}$ is two-sided noetherian. The algebra ![]() $E$ is two-sided noetherian.
$E$ is two-sided noetherian.
Proof. We will prove the result by induction on both ![]() $j$ and
$j$ and ![]() $s$. Note that
$s$. Note that ![]() $E_{0}=\widehat{D}_{k+1}$ is noetherian by 2.2.2. By definition,
$E_{0}=\widehat{D}_{k+1}$ is noetherian by 2.2.2. By definition, ![]() $E_{0,0}=E_{0}$ and is thus noetherian.
$E_{0,0}=E_{0}$ and is thus noetherian.
Next, let us prove that if ![]() $E_{j,s-1}$ is noetherian, then
$E_{j,s-1}$ is noetherian, then ![]() $E_{j,s}$ is noetherian if
$E_{j,s}$ is noetherian if ![]() $1\leqslant s\leqslant m$ and
$1\leqslant s\leqslant m$ and ![]() $1\leqslant j\leqslant M$. For this, note that, if
$1\leqslant j\leqslant M$. For this, note that, if ![]() $b\in B$, we have as in [Reference Berthelot7, 3.5.3.2],
$b\in B$, we have as in [Reference Berthelot7, 3.5.3.2],
thus noticing that if ![]() $i<p^{s}$,
$i<p^{s}$, ![]() $\unicode[STIX]{x1D71B}^{ki}\unicode[STIX]{x2202}_{j}^{[i]}\in E_{j,s-1}$, we have
$\unicode[STIX]{x1D71B}^{ki}\unicode[STIX]{x2202}_{j}^{[i]}\in E_{j,s-1}$, we have
Consider the finite type ![]() $\widehat{D}^{(k+1)}$-module
$\widehat{D}^{(k+1)}$-module ![]() $F:=\sum _{i<p^{s}}\widehat{D}^{(k+1)}\unicode[STIX]{x1D71B}^{kp^{i}}\unicode[STIX]{x2202}_{j}^{[i]}$. Then for each finite sum
$F:=\sum _{i<p^{s}}\widehat{D}^{(k+1)}\unicode[STIX]{x1D71B}^{kp^{i}}\unicode[STIX]{x2202}_{j}^{[i]}$. Then for each finite sum ![]() $P=\sum _{\text{}\underline{\unicode[STIX]{x1D708}}}b_{\text{}\underline{\unicode[STIX]{x1D708}}}\unicode[STIX]{x1D71B}^{(k+1)|\text{}\underline{\unicode[STIX]{x1D708}}|}\text{}\underline{\unicode[STIX]{x2202}}^{\langle \text{}\underline{\unicode[STIX]{x1D708}}\rangle }$, we observe that
$P=\sum _{\text{}\underline{\unicode[STIX]{x1D708}}}b_{\text{}\underline{\unicode[STIX]{x1D708}}}\unicode[STIX]{x1D71B}^{(k+1)|\text{}\underline{\unicode[STIX]{x1D708}}|}\text{}\underline{\unicode[STIX]{x2202}}^{\langle \text{}\underline{\unicode[STIX]{x1D708}}\rangle }$, we observe that ![]() $[\unicode[STIX]{x1D71B}^{kp^{s}}\unicode[STIX]{x2202}_{j}^{[p^{s}]},P]\in F$. Since
$[\unicode[STIX]{x1D71B}^{kp^{s}}\unicode[STIX]{x2202}_{j}^{[p^{s}]},P]\in F$. Since ![]() $F$ is a finite type
$F$ is a finite type ![]() $\widehat{D}^{(k+1)}$-module, it is
$\widehat{D}^{(k+1)}$-module, it is ![]() $p$-adically complete, and thus also for each infinite sum
$p$-adically complete, and thus also for each infinite sum ![]() $P\in \widehat{D}^{(k+1)}$, we have
$P\in \widehat{D}^{(k+1)}$, we have ![]() $[\unicode[STIX]{x1D71B}^{kp^{s}}\unicode[STIX]{x2202}_{j}^{[p^{s}]},P]\in F\subset E_{j,s-1}$. Moreover,
$[\unicode[STIX]{x1D71B}^{kp^{s}}\unicode[STIX]{x2202}_{j}^{[p^{s}]},P]\in F\subset E_{j,s-1}$. Moreover, ![]() $[\unicode[STIX]{x1D71B}^{kp^{s}}\unicode[STIX]{x2202}_{j}^{[p^{s}]},\unicode[STIX]{x1D71B}^{kp^{a}}\unicode[STIX]{x2202}_{j}^{[p^{a}]}]=0$ for
$[\unicode[STIX]{x1D71B}^{kp^{s}}\unicode[STIX]{x2202}_{j}^{[p^{s}]},\unicode[STIX]{x1D71B}^{kp^{a}}\unicode[STIX]{x2202}_{j}^{[p^{a}]}]=0$ for ![]() $a\leqslant s-1$. As
$a\leqslant s-1$. As ![]() $E_{j,s-1}$ is an algebra and as we have the formula for
$E_{j,s-1}$ is an algebra and as we have the formula for ![]() $P,Q\in E_{j}$
$P,Q\in E_{j}$
we see that ![]() $\forall P\in E_{j,s-1}$
$\forall P\in E_{j,s-1}$
Then, by induction on ![]() $l$, we deduce that
$l$, we deduce that
Define ![]() $\unicode[STIX]{x1D6E5}:=\unicode[STIX]{x1D71B}^{kp^{s}}\unicode[STIX]{x2202}_{j}^{[p^{s}]}$ for the rest of the proof. We now follow Berthelot’s argument in the proof of [Reference Berthelot7, 3.5.3]. We do the proof for ‘left noetherian’ (the right version is similar). Let
$\unicode[STIX]{x1D6E5}:=\unicode[STIX]{x1D71B}^{kp^{s}}\unicode[STIX]{x2202}_{j}^{[p^{s}]}$ for the rest of the proof. We now follow Berthelot’s argument in the proof of [Reference Berthelot7, 3.5.3]. We do the proof for ‘left noetherian’ (the right version is similar). Let ![]() $I$ be a left ideal of
$I$ be a left ideal of ![]() $E_{j,s}$ and
$E_{j,s}$ and ![]() $J$ be the set of elements
$J$ be the set of elements ![]() $R$ of
$R$ of ![]() $E_{j,s-1}$ such that there exists
$E_{j,s-1}$ such that there exists ![]() $P\in I$ that can be written
$P\in I$ that can be written
with ![]() $R_{i}\in E_{j,s-1}$. If
$R_{i}\in E_{j,s-1}$. If ![]() $R_{1}$ and
$R_{1}$ and ![]() $R_{2}$ are in
$R_{2}$ are in ![]() $J$, write
$J$, write
with ![]() $R_{i}$ and
$R_{i}$ and ![]() $R_{i}^{\prime }$ elements of
$R_{i}^{\prime }$ elements of ![]() $E_{j,s-1}$. Assume
$E_{j,s-1}$. Assume ![]() $l_{1}\geqslant l_{2}$, then, using (2.2.19), we can write
$l_{1}\geqslant l_{2}$, then, using (2.2.19), we can write
with elements ![]() $R_{i}^{\prime \prime }\in E_{j,s-1}$. In particular, we deduce from this that
$R_{i}^{\prime \prime }\in E_{j,s-1}$. In particular, we deduce from this that ![]() $J$ is a left ideal of
$J$ is a left ideal of ![]() $E_{j,s-1}$ generated by a finite set of elements
$E_{j,s-1}$ generated by a finite set of elements ![]() $R_{1},\ldots ,R_{a}$. Moreover,
$R_{1},\ldots ,R_{a}$. Moreover, ![]() $I\bigcap E_{j,s-1}$ is a left ideal of
$I\bigcap E_{j,s-1}$ is a left ideal of ![]() $E_{j,s-1}$ generated by a finite set of elements
$E_{j,s-1}$ generated by a finite set of elements ![]() $Q_{1},\ldots ,Q_{b}$. We see easily then that
$Q_{1},\ldots ,Q_{b}$. We see easily then that ![]() $I$ is generated by the elements
$I$ is generated by the elements ![]() $R_{1},\ldots ,R_{a},Q_{1},\ldots ,Q_{b}$. This proves that
$R_{1},\ldots ,R_{a},Q_{1},\ldots ,Q_{b}$. This proves that ![]() $E_{j,s}$ is noetherian and ends the proof of the auxiliary result.◻
$E_{j,s}$ is noetherian and ends the proof of the auxiliary result.◻
As we have remarked above, the proof of the Proposition 2.2.16 is now complete. ◻
Corollary 2.2.20. Let ![]() $\mathfrak{U}\subset \mathfrak{X}$ be an open affine formal subscheme of
$\mathfrak{U}\subset \mathfrak{X}$ be an open affine formal subscheme of ![]() $\mathfrak{X}$. If
$\mathfrak{X}$. If ![]() $k^{\prime }\geqslant k\geqslant k_{\mathfrak{X}}$, then
$k^{\prime }\geqslant k\geqslant k_{\mathfrak{X}}$, then ![]() $\unicode[STIX]{x1D6E4}(\mathfrak{U},\widehat{\mathscr{D}}_{\mathfrak{X},\mathbb{Q}}^{(k,m)})$ is left and right flat over
$\unicode[STIX]{x1D6E4}(\mathfrak{U},\widehat{\mathscr{D}}_{\mathfrak{X},\mathbb{Q}}^{(k,m)})$ is left and right flat over ![]() $\unicode[STIX]{x1D6E4}(\mathfrak{U},\widehat{\mathscr{D}}_{\mathfrak{X},\mathbb{Q}}^{(k^{\prime },m)})$.
$\unicode[STIX]{x1D6E4}(\mathfrak{U},\widehat{\mathscr{D}}_{\mathfrak{X},\mathbb{Q}}^{(k^{\prime },m)})$.
Proof. Denote ![]() $\widehat{D}_{k,\mathbb{Q}}=\unicode[STIX]{x1D6E4}(\mathfrak{U},\widehat{\mathscr{D}}_{\mathfrak{X},\mathbb{Q}}^{(k,m)})$ and similarly for
$\widehat{D}_{k,\mathbb{Q}}=\unicode[STIX]{x1D6E4}(\mathfrak{U},\widehat{\mathscr{D}}_{\mathfrak{X},\mathbb{Q}}^{(k,m)})$ and similarly for ![]() $k^{\prime }$. Let
$k^{\prime }$. Let ![]() $M{\hookrightarrow}N$ be an injection of finite type
$M{\hookrightarrow}N$ be an injection of finite type ![]() $\widehat{D}_{k^{\prime },\mathbb{Q}}$-modules and put
$\widehat{D}_{k^{\prime },\mathbb{Q}}$-modules and put
Using the equivalence of categories and the exactness in 2.2.6, we have an injection of coherent ![]() $\widehat{\mathscr{D}}_{\mathfrak{U},\mathbb{Q}}^{(k^{\prime },m)}$-modules
$\widehat{\mathscr{D}}_{\mathfrak{U},\mathbb{Q}}^{(k^{\prime },m)}$-modules ![]() $\mathscr{M}{\hookrightarrow}\mathscr{N}$. Using the previous flatness result 2.2.16, we have an injection of coherent
$\mathscr{M}{\hookrightarrow}\mathscr{N}$. Using the previous flatness result 2.2.16, we have an injection of coherent ![]() $\widehat{\mathscr{D}}_{\mathfrak{U},\mathbb{Q}}^{(k,m)}$-modules
$\widehat{\mathscr{D}}_{\mathfrak{U},\mathbb{Q}}^{(k,m)}$-modules
Taking global sections and using again 2.2.6, we observe that
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E4}(\mathfrak{U},\widehat{\mathscr{D}}_{\mathfrak{U},\mathbb{Q}}^{(k,m)}\otimes _{\widehat{\mathscr{D}}_{\mathfrak{ U},\mathbb{Q}}^{(k^{\prime },m)}}\mathscr{M}) & \simeq & \displaystyle \unicode[STIX]{x1D6E4}(\mathfrak{U},\widehat{\mathscr{D}}_{\mathfrak{U},\mathbb{Q}}^{(k,m)}\otimes _{\widehat{D}_{k^{\prime }}}M)\nonumber\\ \displaystyle & \simeq & \displaystyle \unicode[STIX]{x1D6E4}(\mathfrak{U},\widehat{\mathscr{D}}_{\mathfrak{U},\mathbb{Q}}^{(k,m)}\otimes _{\widehat{D}_{k}}\widehat{D}_{k}\otimes _{\widehat{D}_{k^{\prime }}}M)\nonumber\\ \displaystyle & \simeq & \displaystyle \widehat{D}_{k,\mathbb{Q}}\otimes _{\widehat{D}_{k^{\prime },\mathbb{Q}}}M\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E4}(\mathfrak{U},\widehat{\mathscr{D}}_{\mathfrak{U},\mathbb{Q}}^{(k,m)}\otimes _{\widehat{\mathscr{D}}_{\mathfrak{ U},\mathbb{Q}}^{(k^{\prime },m)}}\mathscr{M}) & \simeq & \displaystyle \unicode[STIX]{x1D6E4}(\mathfrak{U},\widehat{\mathscr{D}}_{\mathfrak{U},\mathbb{Q}}^{(k,m)}\otimes _{\widehat{D}_{k^{\prime }}}M)\nonumber\\ \displaystyle & \simeq & \displaystyle \unicode[STIX]{x1D6E4}(\mathfrak{U},\widehat{\mathscr{D}}_{\mathfrak{U},\mathbb{Q}}^{(k,m)}\otimes _{\widehat{D}_{k}}\widehat{D}_{k}\otimes _{\widehat{D}_{k^{\prime }}}M)\nonumber\\ \displaystyle & \simeq & \displaystyle \widehat{D}_{k,\mathbb{Q}}\otimes _{\widehat{D}_{k^{\prime },\mathbb{Q}}}M\nonumber\end{eqnarray}$$ and similarly for ![]() $\mathscr{N}$. Finally, with formula (2.2.21) we arrive at an injection
$\mathscr{N}$. Finally, with formula (2.2.21) we arrive at an injection
which proves the corollary. ◻
We compare now rings with different levels ![]() $k$. Let
$k$. Let ![]() $e=e(L/\mathbb{Q}_{p})$ be the ramification index of the extension
$e=e(L/\mathbb{Q}_{p})$ be the ramification index of the extension ![]() $\mathbb{Q}_{p}\subseteq L$.
$\mathbb{Q}_{p}\subseteq L$.
Proposition 2.2.22. Let ![]() $e^{\prime }\in \mathbb{N}$ such that
$e^{\prime }\in \mathbb{N}$ such that ![]() $e^{\prime }\geqslant \frac{e}{p-1}$.
$e^{\prime }\geqslant \frac{e}{p-1}$.
(i) If
 $k\geqslant k_{\mathfrak{X}}$, and
$k\geqslant k_{\mathfrak{X}}$, and  $k^{\prime }\geqslant k+e^{\prime }$, then we have the following inclusions of sheaves of rings
$k^{\prime }\geqslant k+e^{\prime }$, then we have the following inclusions of sheaves of rings  $$\begin{eqnarray}\mathscr{D}_{\mathfrak{X},k^{\prime }}^{\dagger }{\hookrightarrow}\mathscr{D}_{\mathfrak{ X},k+e^{\prime }}^{\dagger }{\hookrightarrow}\widehat{\mathscr{D}}_{\mathfrak{ X},\mathbb{Q}}^{(k,0)}{\hookrightarrow}\widehat{\mathscr{D}}_{\mathfrak{ X},\mathbb{Q}}^{(k,m)}{\hookrightarrow}\mathscr{D}_{\mathfrak{ X},k}^{\dagger }.\end{eqnarray}$$
$$\begin{eqnarray}\mathscr{D}_{\mathfrak{X},k^{\prime }}^{\dagger }{\hookrightarrow}\mathscr{D}_{\mathfrak{ X},k+e^{\prime }}^{\dagger }{\hookrightarrow}\widehat{\mathscr{D}}_{\mathfrak{ X},\mathbb{Q}}^{(k,0)}{\hookrightarrow}\widehat{\mathscr{D}}_{\mathfrak{ X},\mathbb{Q}}^{(k,m)}{\hookrightarrow}\mathscr{D}_{\mathfrak{ X},k}^{\dagger }.\end{eqnarray}$$(ii) Suppose
 $e\leqslant p-1$. If
$e\leqslant p-1$. If  $k\geqslant k_{\mathfrak{X}}$, and
$k\geqslant k_{\mathfrak{X}}$, and  $k^{\prime }\geqslant k+1$, then we have the following inclusions of sheaves of rings
$k^{\prime }\geqslant k+1$, then we have the following inclusions of sheaves of rings  $$\begin{eqnarray}\mathscr{D}_{\mathfrak{X},k^{\prime }}^{\dagger }{\hookrightarrow}\mathscr{D}_{\mathfrak{ X},k+1}^{\dagger }{\hookrightarrow}\widehat{\mathscr{D}}_{\mathfrak{ X},\mathbb{Q}}^{(k,0)}{\hookrightarrow}\widehat{\mathscr{D}}_{\mathfrak{ X},\mathbb{Q}}^{(k,m)}{\hookrightarrow}\mathscr{D}_{\mathfrak{ X},k}^{\dagger }.\end{eqnarray}$$
$$\begin{eqnarray}\mathscr{D}_{\mathfrak{X},k^{\prime }}^{\dagger }{\hookrightarrow}\mathscr{D}_{\mathfrak{ X},k+1}^{\dagger }{\hookrightarrow}\widehat{\mathscr{D}}_{\mathfrak{ X},\mathbb{Q}}^{(k,0)}{\hookrightarrow}\widehat{\mathscr{D}}_{\mathfrak{ X},\mathbb{Q}}^{(k,m)}{\hookrightarrow}\mathscr{D}_{\mathfrak{ X},k}^{\dagger }.\end{eqnarray}$$
Proof. It is enough to prove (i). The only nontrivial inclusion is
which we may prove locally over some affine open ![]() $\mathfrak{U}\subset \mathfrak{X}$ of the basis of open sets
$\mathfrak{U}\subset \mathfrak{X}$ of the basis of open sets ![]() $\mathscr{B}$ from 2.2.2. We use the following notations
$\mathscr{B}$ from 2.2.2. We use the following notations
As before (2.1.17), we have then the following descriptions, assuming that ![]() $\text{pr}^{\ast }\mathscr{T}_{\mathfrak{X}_{0}}$ is free restricted to
$\text{pr}^{\ast }\mathscr{T}_{\mathfrak{X}_{0}}$ is free restricted to ![]() $\mathfrak{U}$, with basis
$\mathfrak{U}$, with basis ![]() $\unicode[STIX]{x2202}_{1},\ldots ,\unicode[STIX]{x2202}_{M}$,
$\unicode[STIX]{x2202}_{1},\ldots ,\unicode[STIX]{x2202}_{M}$,
 $$\begin{eqnarray}\displaystyle & \displaystyle \widehat{D}_{k}=\left\{\mathop{\sum }_{\text{}\underline{\unicode[STIX]{x1D708}}}\unicode[STIX]{x1D71B}^{k|\text{}\underline{\unicode[STIX]{x1D708}}|}b_{\text{}\underline{\unicode[STIX]{x1D708}}}\text{}\underline{\unicode[STIX]{x2202}}^{\text{}\underline{\unicode[STIX]{x1D708}}}\,|\,b_{\text{}\underline{\unicode[STIX]{x1D708}}}\in B,b_{\text{}\underline{\unicode[STIX]{x1D708}}}\rightarrow 0\right\}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle D_{k}^{\dagger }=\left\{\mathop{\sum }_{\text{}\underline{\unicode[STIX]{x1D708}}}\unicode[STIX]{x1D71B}^{k|\text{}\underline{\unicode[STIX]{x1D708}}|}b_{\text{}\underline{\unicode[STIX]{x1D708}}}\text{}\underline{\unicode[STIX]{x2202}}^{[\text{}\underline{\unicode[STIX]{x1D708}}]}\,|\,b_{\text{}\underline{\unicode[STIX]{x1D708}}}\in B_{\mathbb{Q}}\text{ and }\exists C>0,\unicode[STIX]{x1D702}<1\,|\,\Vert b_{\text{}\underline{\unicode[STIX]{x1D708}}}\Vert <C\unicode[STIX]{x1D702}^{|\text{}\underline{\unicode[STIX]{x1D708}}|}\right\}, & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \widehat{D}_{k}=\left\{\mathop{\sum }_{\text{}\underline{\unicode[STIX]{x1D708}}}\unicode[STIX]{x1D71B}^{k|\text{}\underline{\unicode[STIX]{x1D708}}|}b_{\text{}\underline{\unicode[STIX]{x1D708}}}\text{}\underline{\unicode[STIX]{x2202}}^{\text{}\underline{\unicode[STIX]{x1D708}}}\,|\,b_{\text{}\underline{\unicode[STIX]{x1D708}}}\in B,b_{\text{}\underline{\unicode[STIX]{x1D708}}}\rightarrow 0\right\}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle D_{k}^{\dagger }=\left\{\mathop{\sum }_{\text{}\underline{\unicode[STIX]{x1D708}}}\unicode[STIX]{x1D71B}^{k|\text{}\underline{\unicode[STIX]{x1D708}}|}b_{\text{}\underline{\unicode[STIX]{x1D708}}}\text{}\underline{\unicode[STIX]{x2202}}^{[\text{}\underline{\unicode[STIX]{x1D708}}]}\,|\,b_{\text{}\underline{\unicode[STIX]{x1D708}}}\in B_{\mathbb{Q}}\text{ and }\exists C>0,\unicode[STIX]{x1D702}<1\,|\,\Vert b_{\text{}\underline{\unicode[STIX]{x1D708}}}\Vert <C\unicode[STIX]{x1D702}^{|\text{}\underline{\unicode[STIX]{x1D708}}|}\right\}, & \displaystyle \nonumber\end{eqnarray}$$ where ![]() $\Vert \cdot \Vert$ is any Banach algebra norm on
$\Vert \cdot \Vert$ is any Banach algebra norm on ![]() $B_{\mathbb{Q}}$. For the rest of the proof we endow
$B_{\mathbb{Q}}$. For the rest of the proof we endow ![]() $B_{\mathbb{Q}}$ with the gauge norm
$B_{\mathbb{Q}}$ with the gauge norm ![]() $\Vert \cdot \Vert$ associated with the lattice
$\Vert \cdot \Vert$ associated with the lattice ![]() $B\subset B_{\mathbb{Q}}$. We need the following
$B\subset B_{\mathbb{Q}}$. We need the following
Auxiliary result 2.2.23. Let ![]() $\text{}\underline{\unicode[STIX]{x1D708}}=(\unicode[STIX]{x1D708}_{1},\ldots ,\unicode[STIX]{x1D708}_{M})$, then we have
$\text{}\underline{\unicode[STIX]{x1D708}}=(\unicode[STIX]{x1D708}_{1},\ldots ,\unicode[STIX]{x1D708}_{M})$, then we have
Proof. [Reference Noot-Huyghe20, 1.1.2]. ◻
Let ![]() $P=\sum _{\text{}\underline{\unicode[STIX]{x1D708}}}\unicode[STIX]{x1D71B}^{(k+e^{\prime })|\text{}\underline{\unicode[STIX]{x1D708}}|}b_{\text{}\underline{\unicode[STIX]{x1D708}}}\text{}\underline{\unicode[STIX]{x2202}}^{[\text{}\underline{\unicode[STIX]{x1D708}}]}\in D_{k+e^{\prime }}^{\dagger }$, then there exist
$P=\sum _{\text{}\underline{\unicode[STIX]{x1D708}}}\unicode[STIX]{x1D71B}^{(k+e^{\prime })|\text{}\underline{\unicode[STIX]{x1D708}}|}b_{\text{}\underline{\unicode[STIX]{x1D708}}}\text{}\underline{\unicode[STIX]{x2202}}^{[\text{}\underline{\unicode[STIX]{x1D708}}]}\in D_{k+e^{\prime }}^{\dagger }$, then there exist ![]() $R>0$ and
$R>0$ and ![]() $S>0$ such that
$S>0$ such that
We can write
Then the following inequality holds
Under the conditions of the statement, ![]() $\log _{p}\Vert c_{\text{}\underline{\unicode[STIX]{x1D708}}}\Vert \rightarrow +\infty$ if
$\log _{p}\Vert c_{\text{}\underline{\unicode[STIX]{x1D708}}}\Vert \rightarrow +\infty$ if ![]() $|\text{}\underline{\unicode[STIX]{x1D708}}|\rightarrow +\infty$, which proves that
$|\text{}\underline{\unicode[STIX]{x1D708}}|\rightarrow +\infty$, which proves that ![]() $P\in \widehat{D}_{k,\mathbb{Q}}$. This ends the proof of the Proposition 2.2.22.◻
$P\in \widehat{D}_{k,\mathbb{Q}}$. This ends the proof of the Proposition 2.2.22.◻
We now complete these results by additional flatness results when ![]() $k$ varies.
$k$ varies.
Proposition 2.2.24. Let ![]() $k^{\prime }\geqslant k\geqslant k_{\mathfrak{X}}$.
$k^{\prime }\geqslant k\geqslant k_{\mathfrak{X}}$.
(i) The morphism of sheaves of rings
 $\mathscr{D}_{\mathfrak{X},k^{\prime }}^{\dagger }{\hookrightarrow}\mathscr{D}_{\mathfrak{X},k}^{\dagger }$ is left and right flat.
$\mathscr{D}_{\mathfrak{X},k^{\prime }}^{\dagger }{\hookrightarrow}\mathscr{D}_{\mathfrak{X},k}^{\dagger }$ is left and right flat.(ii) Let
 $\mathfrak{U}\subset \mathfrak{X}$ be an open affine. Then
$\mathfrak{U}\subset \mathfrak{X}$ be an open affine. Then  $\unicode[STIX]{x1D6E4}(\mathfrak{U},\mathscr{D}_{\mathfrak{X},k}^{\dagger })$ is left and right flat over
$\unicode[STIX]{x1D6E4}(\mathfrak{U},\mathscr{D}_{\mathfrak{X},k}^{\dagger })$ is left and right flat over  $\unicode[STIX]{x1D6E4}(\mathfrak{U},\mathscr{D}_{\mathfrak{X},k^{\prime }}^{\dagger })$.
$\unicode[STIX]{x1D6E4}(\mathfrak{U},\mathscr{D}_{\mathfrak{X},k^{\prime }}^{\dagger })$.
Proof. It is enough to prove (ii). Denote ![]() $D_{k}^{\dagger }=\unicode[STIX]{x1D6E4}(\mathfrak{U},\mathscr{D}_{\mathfrak{X},k}^{\dagger })$ (resp. for
$D_{k}^{\dagger }=\unicode[STIX]{x1D6E4}(\mathfrak{U},\mathscr{D}_{\mathfrak{X},k}^{\dagger })$ (resp. for ![]() $k^{\prime }$), and for any integer
$k^{\prime }$), and for any integer ![]() $m\geqslant 0$,
$m\geqslant 0$, ![]() $\widehat{D}_{k,\mathbb{Q}}^{(m)}=\unicode[STIX]{x1D6E4}(\mathfrak{U},\mathscr{D}_{\mathfrak{X},\mathbb{Q}}^{(k,m)})$ (resp. for
$\widehat{D}_{k,\mathbb{Q}}^{(m)}=\unicode[STIX]{x1D6E4}(\mathfrak{U},\mathscr{D}_{\mathfrak{X},\mathbb{Q}}^{(k,m)})$ (resp. for ![]() $k^{\prime }$). Since
$k^{\prime }$). Since ![]() $\mathfrak{U}$ is quasi-compact, we know that
$\mathfrak{U}$ is quasi-compact, we know that
Let ![]() $u$ :
$u$ : ![]() $M{\hookrightarrow}N$ be an injection of coherent
$M{\hookrightarrow}N$ be an injection of coherent ![]() $D_{k^{\prime }}^{\dagger }$-modules, then we have the
$D_{k^{\prime }}^{\dagger }$-modules, then we have the
Auxiliary result 2.2.25. There exist an integer ![]() $m\geqslant 0$ and an injection
$m\geqslant 0$ and an injection ![]() $u^{(m)}$ of coherent
$u^{(m)}$ of coherent ![]() $\widehat{D}_{k^{\prime },\mathbb{Q}}^{(m)}$-modules
$\widehat{D}_{k^{\prime },\mathbb{Q}}^{(m)}$-modules ![]() $u^{(m)}$ :
$u^{(m)}$ : ![]() $M^{(m)}{\hookrightarrow}N^{(m)}$ such that following properties are satisfied.
$M^{(m)}{\hookrightarrow}N^{(m)}$ such that following properties are satisfied.
(i) There are canonical isomorphisms
 $$\begin{eqnarray}\unicode[STIX]{x1D6FC}:D_{k^{\prime }}^{\dagger }\otimes _{\widehat{D}_{k^{\prime },\mathbb{Q}}^{(m)}}M^{(m)}\stackrel{\simeq }{\longrightarrow }M,\qquad \text{and}\qquad \unicode[STIX]{x1D6FD}:D_{k^{\prime }}^{\dagger }\otimes _{\widehat{D}_{k^{\prime },\mathbb{Q}}^{(m)}}N^{(m)}\stackrel{\simeq }{\longrightarrow }N.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FC}:D_{k^{\prime }}^{\dagger }\otimes _{\widehat{D}_{k^{\prime },\mathbb{Q}}^{(m)}}M^{(m)}\stackrel{\simeq }{\longrightarrow }M,\qquad \text{and}\qquad \unicode[STIX]{x1D6FD}:D_{k^{\prime }}^{\dagger }\otimes _{\widehat{D}_{k^{\prime },\mathbb{Q}}^{(m)}}N^{(m)}\stackrel{\simeq }{\longrightarrow }N.\end{eqnarray}$$(ii) There is a commutative diagram of coherent
 $D_{k^{\prime }}^{\dagger }$-modules
$D_{k^{\prime }}^{\dagger }$-modules
Proof. In order to prove the auxiliary result, we first remark that the morphism ![]() $u$ can be extended to any finite presentation of
$u$ can be extended to any finite presentation of ![]() $M$ and
$M$ and ![]() $N$ as
$N$ as ![]() $D_{k^{\prime }}^{\dagger }$-modules. Thus, there exists a diagram of presentations of
$D_{k^{\prime }}^{\dagger }$-modules. Thus, there exists a diagram of presentations of ![]() $D_{k^{\prime }}^{\dagger }$-modules
$D_{k^{\prime }}^{\dagger }$-modules

Furthermore, there exists ![]() $m$ such that the matrices of the maps
$m$ such that the matrices of the maps ![]() $A$ and
$A$ and ![]() $B$ (and of the two vertical arrows completing the square) have coefficients in
$B$ (and of the two vertical arrows completing the square) have coefficients in ![]() $\widehat{D}_{k^{\prime },\mathbb{Q}}^{(m)}$. These then define maps
$\widehat{D}_{k^{\prime },\mathbb{Q}}^{(m)}$. These then define maps
whose cokernel is a coherent ![]() $\widehat{D}_{k^{\prime },\mathbb{Q}}^{(m)}$-module denoted by
$\widehat{D}_{k^{\prime },\mathbb{Q}}^{(m)}$-module denoted by ![]() $M^{(m)}$ (resp.
$M^{(m)}$ (resp. ![]() $N^{(m)}$ is the cokernel of
$N^{(m)}$ is the cokernel of ![]() $B$). We finally get from this the following commutative diagram of exact sequences
$B$). We finally get from this the following commutative diagram of exact sequences

where by definition ![]() $u^{(m)}$ is the induced map by
$u^{(m)}$ is the induced map by ![]() $u$ between
$u$ between ![]() $M^{(m)}$ and
$M^{(m)}$ and ![]() $N^{(m)}$. By construction there are canonical isomorphism
$N^{(m)}$. By construction there are canonical isomorphism
Define now ![]() $K$ to be the kernel of the map
$K$ to be the kernel of the map ![]() $u^{(m)}$ :
$u^{(m)}$ : ![]() $M^{(m)}\rightarrow N^{(m)}$, then as
$M^{(m)}\rightarrow N^{(m)}$, then as ![]() $D_{k^{\prime }}^{\dagger }$ is flat over
$D_{k^{\prime }}^{\dagger }$ is flat over ![]() $\widehat{D}_{k^{\prime },\mathbb{Q}}^{(m)}$ by 2.2.11, we have an exact sequence of
$\widehat{D}_{k^{\prime },\mathbb{Q}}^{(m)}$ by 2.2.11, we have an exact sequence of ![]() $D_{k^{\prime }}^{\dagger }$-modules
$D_{k^{\prime }}^{\dagger }$-modules
showing that
and again, as ![]() $D_{k^{\prime }}^{\dagger }$ is flat over
$D_{k^{\prime }}^{\dagger }$ is flat over ![]() $\widehat{D}_{k^{\prime },\mathbb{Q}}^{(m)}$, that
$\widehat{D}_{k^{\prime },\mathbb{Q}}^{(m)}$, that
Finally, the ![]() $\widehat{D}_{k^{\prime },\mathbb{Q}}^{(m)}$-coherent modules
$\widehat{D}_{k^{\prime },\mathbb{Q}}^{(m)}$-coherent modules ![]() $M^{(m)}/K$ and
$M^{(m)}/K$ and ![]() $N^{(m)}$ satisfy the required properties. This ends the proof of the auxiliary result.◻
$N^{(m)}$ satisfy the required properties. This ends the proof of the auxiliary result.◻
Take ![]() $M^{(m)}$,
$M^{(m)}$, ![]() $N^{(m)}$ and
$N^{(m)}$ and ![]() $u^{(m)}$ :
$u^{(m)}$ : ![]() $M^{(m)}{\hookrightarrow}N^{(m)}$ as given by the auxiliary result. As
$M^{(m)}{\hookrightarrow}N^{(m)}$ as given by the auxiliary result. As ![]() $\widehat{D}_{k,\mathbb{Q}}^{(m)}$ is flat over
$\widehat{D}_{k,\mathbb{Q}}^{(m)}$ is flat over ![]() $\widehat{D}_{k^{\prime },\mathbb{Q}}^{(m)}$ by 2.2.20, we have an injection of coherent
$\widehat{D}_{k^{\prime },\mathbb{Q}}^{(m)}$ by 2.2.20, we have an injection of coherent ![]() $\widehat{D}_{k,\mathbb{Q}}^{(m)}$-modules
$\widehat{D}_{k,\mathbb{Q}}^{(m)}$-modules
We can tensor this map by ![]() $D_{k}^{\dagger }$ which is a flat
$D_{k}^{\dagger }$ which is a flat ![]() $\widehat{D}_{k,\mathbb{Q}}^{(m)}$-module 2.2.11, and use the properties of
$\widehat{D}_{k,\mathbb{Q}}^{(m)}$-module 2.2.11, and use the properties of ![]() $M^{(m)}$ and
$M^{(m)}$ and ![]() $N^{(m)}$ to get an injection
$N^{(m)}$ to get an injection
and this proves the proposition. ◻
We end this part by some global properties of coherent sheaves over ![]() $\mathfrak{X}$ (resp. coherent
$\mathfrak{X}$ (resp. coherent ![]() $D_{k}^{\dagger }$-modules) when the base
$D_{k}^{\dagger }$-modules) when the base ![]() $\mathfrak{X}_{0}$ is affine. In general, the formal scheme
$\mathfrak{X}_{0}$ is affine. In general, the formal scheme ![]() $\mathfrak{X}$ is projective over
$\mathfrak{X}$ is projective over ![]() $\mathfrak{X}_{0}$ and we can consider the Serre twist
$\mathfrak{X}_{0}$ and we can consider the Serre twist ![]() ${\mathcal{O}}_{\mathfrak{X}}(1)$. It is a locally free sheaf of rank
${\mathcal{O}}_{\mathfrak{X}}(1)$. It is a locally free sheaf of rank ![]() $1$ over
$1$ over ![]() $\mathfrak{X}$. If
$\mathfrak{X}$. If ![]() $\mathfrak{U}_{0}$ is an open affine formal subscheme of
$\mathfrak{U}_{0}$ is an open affine formal subscheme of ![]() $\mathfrak{X}_{0}$, and if
$\mathfrak{X}_{0}$, and if ![]() $t\in {\mathcal{I}}(\mathfrak{U}_{0})$, then the restriction of the sheaf
$t\in {\mathcal{I}}(\mathfrak{U}_{0})$, then the restriction of the sheaf ![]() ${\mathcal{O}}_{\mathfrak{X}}(1)$ to the open subset
${\mathcal{O}}_{\mathfrak{X}}(1)$ to the open subset ![]() $D_{+}(t)$ is generated by
$D_{+}(t)$ is generated by ![]() $t$. As usual,
$t$. As usual, ![]() ${\mathcal{I}}$ denotes the ideal sheaf on
${\mathcal{I}}$ denotes the ideal sheaf on ![]() $\mathfrak{X}_{0}$ which gives rise to the blow-up
$\mathfrak{X}_{0}$ which gives rise to the blow-up ![]() $\mathfrak{X}$.
$\mathfrak{X}$.
If ![]() ${\mathcal{M}}$ is a sheaf of
${\mathcal{M}}$ is a sheaf of ![]() ${\mathcal{O}}_{\mathfrak{X}}$-modules over
${\mathcal{O}}_{\mathfrak{X}}$-modules over ![]() $\mathfrak{X}$ and if
$\mathfrak{X}$ and if ![]() $r\in \mathbb{Z}$, then we let
$r\in \mathbb{Z}$, then we let ![]() ${\mathcal{M}}(r)$ denote the twisted sheaf
${\mathcal{M}}(r)$ denote the twisted sheaf
Lemma 2.2.26. Let ![]() $\mathfrak{X}_{0}$ be a noetherian affine formal scheme. For all integers
$\mathfrak{X}_{0}$ be a noetherian affine formal scheme. For all integers ![]() $r$, there is an isomorphism
$r$, there is an isomorphism ![]() ${\mathcal{O}}_{\mathfrak{X},\mathbb{Q}}(-r)\simeq {\mathcal{O}}_{\mathfrak{X},\mathbb{Q}}(-1)$.
${\mathcal{O}}_{\mathfrak{X},\mathbb{Q}}(-r)\simeq {\mathcal{O}}_{\mathfrak{X},\mathbb{Q}}(-1)$.
Proof. We can assume as in 2.1.9, that ![]() $\mathfrak{X}_{0}=\text{Spf}(A)$, and that the ideal
$\mathfrak{X}_{0}=\text{Spf}(A)$, and that the ideal ![]() ${\mathcal{I}}$ is generated by the elements
${\mathcal{I}}$ is generated by the elements ![]() $(\unicode[STIX]{x1D71B}^{k_{\mathfrak{X}}},f_{1},\ldots ,f_{r})$. The formal scheme
$(\unicode[STIX]{x1D71B}^{k_{\mathfrak{X}}},f_{1},\ldots ,f_{r})$. The formal scheme ![]() $\mathfrak{X}$ is then covered by the open formal subschemes
$\mathfrak{X}$ is then covered by the open formal subschemes
and
where ![]() $u_{i}$ is a generator of
$u_{i}$ is a generator of ![]() ${\mathcal{O}}_{\mathfrak{X}}(1)_{|D_{+}(f_{i})}$. By definition, we have a section
${\mathcal{O}}_{\mathfrak{X}}(1)_{|D_{+}(f_{i})}$. By definition, we have a section
Moreover, the following equations hold
 $$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x1D71B}^{k_{\mathfrak{X}}}}{u_{0}}=\frac{f_{i}}{u_{i}}\in {\mathcal{O}}_{\mathfrak{X}}(-1)(D_{+}(f_{i})), & \displaystyle \nonumber\\ \displaystyle & \displaystyle \frac{\unicode[STIX]{x1D71B}^{k_{\mathfrak{X}}}}{u_{i}}=\frac{\unicode[STIX]{x1D71B}^{k_{\mathfrak{X}}}}{f_{i}}\cdot \frac{\unicode[STIX]{x1D71B}^{k_{\mathfrak{X}}}}{u_{0}}\in {\mathcal{O}}_{\mathfrak{X}}(D_{+}(f_{i}))\cdot \frac{\unicode[STIX]{x1D71B}^{k_{\mathfrak{X}}}}{u_{0}}. & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x1D71B}^{k_{\mathfrak{X}}}}{u_{0}}=\frac{f_{i}}{u_{i}}\in {\mathcal{O}}_{\mathfrak{X}}(-1)(D_{+}(f_{i})), & \displaystyle \nonumber\\ \displaystyle & \displaystyle \frac{\unicode[STIX]{x1D71B}^{k_{\mathfrak{X}}}}{u_{i}}=\frac{\unicode[STIX]{x1D71B}^{k_{\mathfrak{X}}}}{f_{i}}\cdot \frac{\unicode[STIX]{x1D71B}^{k_{\mathfrak{X}}}}{u_{0}}\in {\mathcal{O}}_{\mathfrak{X}}(D_{+}(f_{i}))\cdot \frac{\unicode[STIX]{x1D71B}^{k_{\mathfrak{X}}}}{u_{0}}. & \displaystyle \nonumber\end{eqnarray}$$ This proves that ![]() ${\mathcal{O}}_{\mathfrak{X},\mathbb{Q}}(-1)$ is free with basis
${\mathcal{O}}_{\mathfrak{X},\mathbb{Q}}(-1)$ is free with basis ![]() $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D71B}^{k_{\mathfrak{X}}}/u_{0}$. If
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D71B}^{k_{\mathfrak{X}}}/u_{0}$. If ![]() $r\geqslant 0$,
$r\geqslant 0$, ![]() ${\mathcal{O}}_{\mathfrak{X},\mathbb{Q}}(-r)\simeq {\mathcal{O}}_{\mathfrak{X},\mathbb{Q}}(-1)^{\otimes r}$ is thus a free
${\mathcal{O}}_{\mathfrak{X},\mathbb{Q}}(-r)\simeq {\mathcal{O}}_{\mathfrak{X},\mathbb{Q}}(-1)^{\otimes r}$ is thus a free ![]() ${\mathcal{O}}_{\mathfrak{X},\mathbb{Q}}$-module of rank one as well. Since
${\mathcal{O}}_{\mathfrak{X},\mathbb{Q}}$-module of rank one as well. Since ![]() ${\mathcal{O}}_{\mathfrak{X},\mathbb{Q}}(r)$ is the dual of
${\mathcal{O}}_{\mathfrak{X},\mathbb{Q}}(r)$ is the dual of ![]() ${\mathcal{O}}_{\mathfrak{X},\mathbb{Q}}(-r)$, it is then also a free
${\mathcal{O}}_{\mathfrak{X},\mathbb{Q}}(-r)$, it is then also a free ![]() ${\mathcal{O}}_{\mathfrak{X},\mathbb{Q}}$-module of rank one.◻
${\mathcal{O}}_{\mathfrak{X},\mathbb{Q}}$-module of rank one.◻
We assume from now on until the rest of this subsection 2.2 that the formal scheme ![]() $\mathfrak{X}_{0}$ is affine. Let
$\mathfrak{X}_{0}$ is affine. Let ![]() $k\geqslant k_{\mathfrak{X}}$. To simplify the notation, we write
$k\geqslant k_{\mathfrak{X}}$. To simplify the notation, we write ![]() $\mathscr{D}:=\mathscr{D}_{\mathfrak{X}}^{(k,m)}$ and we denote by
$\mathscr{D}:=\mathscr{D}_{\mathfrak{X}}^{(k,m)}$ and we denote by ![]() $\widehat{\mathscr{D}}$ the
$\widehat{\mathscr{D}}$ the ![]() $p$-adic completion of this sheaf. We also let
$p$-adic completion of this sheaf. We also let ![]() $\mathscr{D}^{\dagger }=\mathop{\varinjlim }\nolimits_{m}\widehat{\mathscr{D}}_{\mathfrak{X},\mathbb{Q}}^{(k,m)}$.
$\mathscr{D}^{\dagger }=\mathop{\varinjlim }\nolimits_{m}\widehat{\mathscr{D}}_{\mathfrak{X},\mathbb{Q}}^{(k,m)}$.
Let us first consider the reduction ![]() $\mathscr{D}_{i}=\widehat{\mathscr{D}}/\unicode[STIX]{x1D71B}^{i+1}\widehat{\mathscr{D}}$. This is a coherent sheaf thanks to 2.2.7 and a quasi-coherent sheaf of
$\mathscr{D}_{i}=\widehat{\mathscr{D}}/\unicode[STIX]{x1D71B}^{i+1}\widehat{\mathscr{D}}$. This is a coherent sheaf thanks to 2.2.7 and a quasi-coherent sheaf of ![]() ${\mathcal{O}}_{X_{i}}$-modules. Let
${\mathcal{O}}_{X_{i}}$-modules. Let ![]() ${\mathcal{M}}$ be a coherent
${\mathcal{M}}$ be a coherent ![]() $\mathscr{D}_{i}$-module.
$\mathscr{D}_{i}$-module.
Lemma 2.2.27. There exist ![]() $a,r\in \mathbb{N}$ such that there is a surjection of coherent
$a,r\in \mathbb{N}$ such that there is a surjection of coherent ![]() $\mathscr{D}_{i}$-modules
$\mathscr{D}_{i}$-modules
Proof. As the sheaf ![]() ${\mathcal{M}}$ is quasi-coherent over the noetherian scheme
${\mathcal{M}}$ is quasi-coherent over the noetherian scheme ![]() $X_{i}$, it is an inductive limit of its
$X_{i}$, it is an inductive limit of its ![]() ${\mathcal{O}}_{X_{i}}$-coherent subsheaves. Moreover,
${\mathcal{O}}_{X_{i}}$-coherent subsheaves. Moreover, ![]() $\mathscr{D}_{i}$ is an inductive limit of the coherent sheaves
$\mathscr{D}_{i}$ is an inductive limit of the coherent sheaves ![]() $\mathscr{D}_{i,n}$ of differential operators of order less than
$\mathscr{D}_{i,n}$ of differential operators of order less than ![]() $n$. We can thus write
$n$. We can thus write
where ![]() ${\mathcal{M}}^{(n)}$ is a coherent
${\mathcal{M}}^{(n)}$ is a coherent ![]() ${\mathcal{O}}_{X_{i}}$-module. Take an open affine subscheme
${\mathcal{O}}_{X_{i}}$-module. Take an open affine subscheme ![]() $U\subset X_{i}$. Then
$U\subset X_{i}$. Then ![]() $\mathscr{D}_{i}(U)$ is noetherian and
$\mathscr{D}_{i}(U)$ is noetherian and ![]() ${\mathcal{M}}(U)$ is a
${\mathcal{M}}(U)$ is a ![]() $\mathscr{D}_{i}(U)$-module of finite type. Hence, there exists
$\mathscr{D}_{i}(U)$-module of finite type. Hence, there exists ![]() $N>0$ such that
$N>0$ such that
Since
we see that ![]() $\mathscr{D}_{i}(U)\cdot {\mathcal{M}}^{(N)}(U)={\mathcal{M}}(U)$ and using (iii) of 2.2.7, we find a surjection
$\mathscr{D}_{i}(U)\cdot {\mathcal{M}}^{(N)}(U)={\mathcal{M}}(U)$ and using (iii) of 2.2.7, we find a surjection ![]() $\mathscr{D}_{U}\otimes {\mathcal{M}}_{|U}^{(N)}{\twoheadrightarrow}{\mathcal{M}}_{|U}$. As
$\mathscr{D}_{U}\otimes {\mathcal{M}}_{|U}^{(N)}{\twoheadrightarrow}{\mathcal{M}}_{|U}$. As ![]() $X_{i}$ is quasi-compact,
$X_{i}$ is quasi-compact, ![]() $X_{i}$ can be covered by a finite number of affine open subsets. There exists therefore
$X_{i}$ can be covered by a finite number of affine open subsets. There exists therefore ![]() $N^{\prime }$ and a surjection
$N^{\prime }$ and a surjection ![]() $\mathscr{D}_{i}\otimes {\mathcal{M}}^{(N^{\prime })}{\twoheadrightarrow}{\mathcal{M}}$. As
$\mathscr{D}_{i}\otimes {\mathcal{M}}^{(N^{\prime })}{\twoheadrightarrow}{\mathcal{M}}$. As ![]() ${\mathcal{M}}^{(N^{\prime })}$ is a coherent
${\mathcal{M}}^{(N^{\prime })}$ is a coherent ![]() ${\mathcal{O}}_{X_{i}}$-module, there exist
${\mathcal{O}}_{X_{i}}$-module, there exist ![]() $r\in \mathbb{N}$,
$r\in \mathbb{N}$, ![]() $a\in \mathbb{N}$ and a surjection
$a\in \mathbb{N}$ and a surjection ![]() $({\mathcal{O}}_{X_{i}}(-a))^{r}{\twoheadrightarrow}{\mathcal{M}}^{(N^{\prime })}$ and this proves the lemma.◻
$({\mathcal{O}}_{X_{i}}(-a))^{r}{\twoheadrightarrow}{\mathcal{M}}^{(N^{\prime })}$ and this proves the lemma.◻
(i) There exists
 $a\geqslant 0$ such that
$a\geqslant 0$ such that  $$\begin{eqnarray}\forall b\geqslant a,\qquad \forall l>0,\qquad H^{l}(X_{i},\mathscr{D}_{i}(b))=0.\end{eqnarray}$$
$$\begin{eqnarray}\forall b\geqslant a,\qquad \forall l>0,\qquad H^{l}(X_{i},\mathscr{D}_{i}(b))=0.\end{eqnarray}$$(ii) Let
 ${\mathcal{M}}$ be a coherent
${\mathcal{M}}$ be a coherent  $\mathscr{D}_{i}$-module, then there exists
$\mathscr{D}_{i}$-module, then there exists  $a\geqslant 0$ such that
$a\geqslant 0$ such that  $$\begin{eqnarray}\forall b\geqslant a,\qquad \forall l>0,\qquad H^{l}(X_{i},{\mathcal{M}}(b))=0.\end{eqnarray}$$
$$\begin{eqnarray}\forall b\geqslant a,\qquad \forall l>0,\qquad H^{l}(X_{i},{\mathcal{M}}(b))=0.\end{eqnarray}$$
Proof. We have ![]() $R\unicode[STIX]{x1D6E4}(X_{i},\mathscr{D}_{i}(b))=R\unicode[STIX]{x1D6E4}(X_{0,i},\cdot )\circ R\text{pr}_{\ast }\mathscr{D}_{i}(b)$. As
$R\unicode[STIX]{x1D6E4}(X_{i},\mathscr{D}_{i}(b))=R\unicode[STIX]{x1D6E4}(X_{0,i},\cdot )\circ R\text{pr}_{\ast }\mathscr{D}_{i}(b)$. As ![]() $X_{0,i}$ is affine, it is enough to prove that
$X_{0,i}$ is affine, it is enough to prove that ![]() $R^{l}\text{pr}_{\ast }\mathscr{D}_{i}(b)=0$ for
$R^{l}\text{pr}_{\ast }\mathscr{D}_{i}(b)=0$ for ![]() $l\geqslant 1$ and for
$l\geqslant 1$ and for ![]() $b\geqslant a$. Take
$b\geqslant a$. Take ![]() $\mathfrak{U}_{0}\subset \mathfrak{X}_{0}$ affine, endowed with coordinates
$\mathfrak{U}_{0}\subset \mathfrak{X}_{0}$ affine, endowed with coordinates ![]() $x_{1},\ldots ,x_{M}$ and let
$x_{1},\ldots ,x_{M}$ and let ![]() $\mathfrak{U}=\text{pr}^{-1}(\mathfrak{U}_{0})$ and
$\mathfrak{U}=\text{pr}^{-1}(\mathfrak{U}_{0})$ and ![]() $U=\mathfrak{U}\times \text{Spec}(\mathfrak{o}/\unicode[STIX]{x1D71B}^{i+1}\mathfrak{o})$. Denote by
$U=\mathfrak{U}\times \text{Spec}(\mathfrak{o}/\unicode[STIX]{x1D71B}^{i+1}\mathfrak{o})$. Denote by ![]() ${\mathcal{O}}_{\mathfrak{U}}(1)$ the restriction to
${\mathcal{O}}_{\mathfrak{U}}(1)$ the restriction to ![]() $\mathfrak{U}$ of the Serre twist over
$\mathfrak{U}$ of the Serre twist over ![]() $\mathfrak{X}$. Then
$\mathfrak{X}$. Then ![]() $\mathscr{D}_{i|U}$ is a free
$\mathscr{D}_{i|U}$ is a free ![]() ${\mathcal{O}}_{U}$-module, so that there exists
${\mathcal{O}}_{U}$-module, so that there exists ![]() $c$ such that
$c$ such that
By taking the maximum ![]() $a$ of the constants
$a$ of the constants ![]() $c$ for each affine open
$c$ for each affine open ![]() $\mathfrak{U}_{0}$ of a finite cover of
$\mathfrak{U}_{0}$ of a finite cover of ![]() $\mathfrak{X}_{0}$ by such affine subschemes
$\mathfrak{X}_{0}$ by such affine subschemes ![]() $\mathfrak{U}_{0}$, we get that
$\mathfrak{U}_{0}$, we get that ![]() $R^{l}\text{pr}_{\ast }\mathscr{D}_{i}(b)=0$ for
$R^{l}\text{pr}_{\ast }\mathscr{D}_{i}(b)=0$ for ![]() $l>0$ and
$l>0$ and ![]() $b\geqslant a$ and this proves part (i) of the lemma. For the second assertion, we will prove the following statement by decreasing induction on
$b\geqslant a$ and this proves part (i) of the lemma. For the second assertion, we will prove the following statement by decreasing induction on ![]() $K$:
$K$:
For all coherent ![]() $\mathscr{D}_{i}$-modules
$\mathscr{D}_{i}$-modules ![]() ${\mathcal{N}}$, there exists
${\mathcal{N}}$, there exists ![]() $a\geqslant 0$, such that
$a\geqslant 0$, such that
If ![]() $K\geqslant M+1$, the result is clear, since
$K\geqslant M+1$, the result is clear, since ![]() ${\mathcal{N}}$ is a quasi-coherent sheaf on a scheme of dimension
${\mathcal{N}}$ is a quasi-coherent sheaf on a scheme of dimension ![]() $M$. Suppose now that the result is true for a given
$M$. Suppose now that the result is true for a given ![]() $K\geqslant 2$, and consider a coherent
$K\geqslant 2$, and consider a coherent ![]() $\mathscr{D}_{i}$-module
$\mathscr{D}_{i}$-module ![]() ${\mathcal{N}}$. By the previous lemma, there exist
${\mathcal{N}}$. By the previous lemma, there exist ![]() $a$ and
$a$ and ![]() $r$ and a exact sequence of coherent
$r$ and a exact sequence of coherent ![]() $\mathscr{D}_{i}$-modules
$\mathscr{D}_{i}$-modules
Tensoring this sequence by ![]() ${\mathcal{O}}_{X_{i}}(c_{1}+c_{2})$ where
${\mathcal{O}}_{X_{i}}(c_{1}+c_{2})$ where ![]() $c_{1}$,
$c_{1}$, ![]() $c_{2}$ are nonnegative integers and looking at the cohomology long exact sequence, we get exact sequences for all
$c_{2}$ are nonnegative integers and looking at the cohomology long exact sequence, we get exact sequences for all ![]() $L$
$L$
By the induction hypothesis, there exists ![]() $c_{1}$ such that
$c_{1}$ such that ![]() $\forall L\geqslant K,\forall d\geqslant c_{1},H^{L}(X_{i},{\mathcal{M}}(d))=0$, and by (i), there exists
$\forall L\geqslant K,\forall d\geqslant c_{1},H^{L}(X_{i},{\mathcal{M}}(d))=0$, and by (i), there exists ![]() $c_{2}$ such that
$c_{2}$ such that ![]() $\forall L\geqslant 1,\forall d\geqslant c_{2},H^{L}(X_{i},\mathscr{D}_{i}(d))=0$. Finally, if
$\forall L\geqslant 1,\forall d\geqslant c_{2},H^{L}(X_{i},\mathscr{D}_{i}(d))=0$. Finally, if ![]() $d\geqslant a+c_{1}+c_{2}$, for every
$d\geqslant a+c_{1}+c_{2}$, for every ![]() $L\geqslant K-1\geqslant 1$, we get that
$L\geqslant K-1\geqslant 1$, we get that ![]() $H^{L}(X_{i},{\mathcal{N}}(d))=0$. This proves (ii) by induction as claimed.◻
$H^{L}(X_{i},{\mathcal{N}}(d))=0$. This proves (ii) by induction as claimed.◻
(i) For any coherent
 $\widehat{\mathscr{D}}$-module
$\widehat{\mathscr{D}}$-module  ${\mathcal{M}}$, there exist
${\mathcal{M}}$, there exist  $a,r\in \mathbb{N}$ and a surjection of coherent
$a,r\in \mathbb{N}$ and a surjection of coherent  $\widehat{\mathscr{D}}$-modules
$\widehat{\mathscr{D}}$-modules  $$\begin{eqnarray}(\widehat{\mathscr{D}}(-a))^{r}{\twoheadrightarrow}{\mathcal{M}}.\end{eqnarray}$$
$$\begin{eqnarray}(\widehat{\mathscr{D}}(-a))^{r}{\twoheadrightarrow}{\mathcal{M}}.\end{eqnarray}$$(ii) For any coherent
 $\widehat{\mathscr{D}}_{\mathbb{Q}}$-module
$\widehat{\mathscr{D}}_{\mathbb{Q}}$-module  ${\mathcal{M}}$, there exist
${\mathcal{M}}$, there exist  $r\in \mathbb{N}$ and a surjection of coherent
$r\in \mathbb{N}$ and a surjection of coherent  $\widehat{\mathscr{D}}_{\mathbb{Q}}$-modules
$\widehat{\mathscr{D}}_{\mathbb{Q}}$-modules  $$\begin{eqnarray}(\widehat{\mathscr{D}}_{\mathbb{Q}})^{r}{\twoheadrightarrow}{\mathcal{M}}.\end{eqnarray}$$
$$\begin{eqnarray}(\widehat{\mathscr{D}}_{\mathbb{Q}})^{r}{\twoheadrightarrow}{\mathcal{M}}.\end{eqnarray}$$(iii) For any coherent
 $\mathscr{D}^{\dagger }$-module
$\mathscr{D}^{\dagger }$-module  ${\mathcal{M}}$, there exist
${\mathcal{M}}$, there exist  $r\in \mathbb{N}$ and a surjection of coherent
$r\in \mathbb{N}$ and a surjection of coherent  $\mathscr{D}^{\dagger }$-modules
$\mathscr{D}^{\dagger }$-modules  $$\begin{eqnarray}(\mathscr{D}^{\dagger })^{r}{\twoheadrightarrow}{\mathcal{M}}.\end{eqnarray}$$
$$\begin{eqnarray}(\mathscr{D}^{\dagger })^{r}{\twoheadrightarrow}{\mathcal{M}}.\end{eqnarray}$$
Proof. Let ![]() ${\mathcal{M}}$ be a coherent
${\mathcal{M}}$ be a coherent ![]() $\widehat{\mathscr{D}}$-module. For part (i), we need to show that there exists a nonnegative integer
$\widehat{\mathscr{D}}$-module. For part (i), we need to show that there exists a nonnegative integer ![]() $a$ such that the twist
$a$ such that the twist ![]() ${\mathcal{M}}(a)$ is generated by a finite number of global sections. Let
${\mathcal{M}}(a)$ is generated by a finite number of global sections. Let ![]() ${\mathcal{M}}_{t}$ be the torsion part of
${\mathcal{M}}_{t}$ be the torsion part of ![]() ${\mathcal{M}}$, which is a coherent submodule of
${\mathcal{M}}$, which is a coherent submodule of ![]() ${\mathcal{M}}$, since
${\mathcal{M}}$, since ![]() $\widehat{\mathscr{D}}(\mathfrak{U})$ is noetherian for every affine open
$\widehat{\mathscr{D}}(\mathfrak{U})$ is noetherian for every affine open ![]() $\mathfrak{U}$. Over an affine open
$\mathfrak{U}$. Over an affine open ![]() $\mathfrak{U}$ of
$\mathfrak{U}$ of ![]() $\mathfrak{X}$, the module
$\mathfrak{X}$, the module ![]() ${\mathcal{M}}_{t}(\mathfrak{U})$ is a finite type module over
${\mathcal{M}}_{t}(\mathfrak{U})$ is a finite type module over ![]() $\widehat{\mathscr{D}}(\mathfrak{U})$ and there exists a constant
$\widehat{\mathscr{D}}(\mathfrak{U})$ and there exists a constant ![]() $c$ such that
$c$ such that ![]() $\unicode[STIX]{x1D71B}^{c}{\mathcal{M}}_{t}(\mathfrak{U})=0$. Since
$\unicode[STIX]{x1D71B}^{c}{\mathcal{M}}_{t}(\mathfrak{U})=0$. Since ![]() $\mathfrak{X}$ can be covered by a finite number of open affine formal subschemes, there exists
$\mathfrak{X}$ can be covered by a finite number of open affine formal subschemes, there exists ![]() $L$ such that
$L$ such that ![]() $\unicode[STIX]{x1D71B}^{L}{\mathcal{M}}_{t}=0$. Then for
$\unicode[STIX]{x1D71B}^{L}{\mathcal{M}}_{t}=0$. Then for ![]() $i\geqslant L$, and denoting
$i\geqslant L$, and denoting ![]() ${\mathcal{G}}_{0}={\mathcal{M}}/(\unicode[STIX]{x1D71B}{\mathcal{M}}+{\mathcal{M}}_{t})$ we have exact sequences
${\mathcal{G}}_{0}={\mathcal{M}}/(\unicode[STIX]{x1D71B}{\mathcal{M}}+{\mathcal{M}}_{t})$ we have exact sequences
Since ![]() ${\mathcal{G}}_{0}$ is a coherent
${\mathcal{G}}_{0}$ is a coherent ![]() $\mathscr{D}_{0}$-module, there exists
$\mathscr{D}_{0}$-module, there exists ![]() $a_{1}\geqslant 0$ so that
$a_{1}\geqslant 0$ so that ![]() $H^{1}(X_{0},{\mathcal{G}}_{0}(b))=0$ for every
$H^{1}(X_{0},{\mathcal{G}}_{0}(b))=0$ for every ![]() $b\geqslant a_{1}$. As a consequence, if
$b\geqslant a_{1}$. As a consequence, if ![]() $b\geqslant a_{1}$, for all
$b\geqslant a_{1}$, for all ![]() $i\geqslant L$ we have surjections
$i\geqslant L$ we have surjections
Since ![]() ${\mathcal{M}}/\unicode[STIX]{x1D71B}^{L}{\mathcal{M}}$ is a coherent
${\mathcal{M}}/\unicode[STIX]{x1D71B}^{L}{\mathcal{M}}$ is a coherent ![]() $\mathscr{D}_{L-1}$-module, there exists
$\mathscr{D}_{L-1}$-module, there exists ![]() $a\geqslant a_{1}$ and a surjection
$a\geqslant a_{1}$ and a surjection ![]() $s$ :
$s$ : ![]() $\mathscr{D}_{L-1}^{r}{\twoheadrightarrow}{\mathcal{M}}/\unicode[STIX]{x1D71B}^{L}{\mathcal{M}}(a)$ defined by global sections
$\mathscr{D}_{L-1}^{r}{\twoheadrightarrow}{\mathcal{M}}/\unicode[STIX]{x1D71B}^{L}{\mathcal{M}}(a)$ defined by global sections ![]() $e_{1},\ldots ,e_{r}\in \unicode[STIX]{x1D6E4}(X_{L-1},{\mathcal{M}}/\unicode[STIX]{x1D71B}^{L}{\mathcal{M}}(a))$. Finally we see by induction on
$e_{1},\ldots ,e_{r}\in \unicode[STIX]{x1D6E4}(X_{L-1},{\mathcal{M}}/\unicode[STIX]{x1D71B}^{L}{\mathcal{M}}(a))$. Finally we see by induction on ![]() $i$ that these sections
$i$ that these sections ![]() $e_{1},\ldots ,e_{r}$ can be lifted to global sections of
$e_{1},\ldots ,e_{r}$ can be lifted to global sections of ![]() $\unicode[STIX]{x1D6E4}(\mathfrak{X},{\mathcal{M}}/\unicode[STIX]{x1D71B}^{i}{\mathcal{M}}(a))$ for every
$\unicode[STIX]{x1D6E4}(\mathfrak{X},{\mathcal{M}}/\unicode[STIX]{x1D71B}^{i}{\mathcal{M}}(a))$ for every ![]() $i$, and thus to global sections of
$i$, and thus to global sections of ![]() $\unicode[STIX]{x1D6E4}(\mathfrak{X},{\mathcal{M}}(a))$. These sections define a map
$\unicode[STIX]{x1D6E4}(\mathfrak{X},{\mathcal{M}}(a))$. These sections define a map ![]() $\widehat{\mathscr{D}}^{r}\rightarrow {\mathcal{M}}(a)$ that is surjective since it is surjective mod
$\widehat{\mathscr{D}}^{r}\rightarrow {\mathcal{M}}(a)$ that is surjective since it is surjective mod ![]() $\unicode[STIX]{x1D71B}$. This proves the part (i).
$\unicode[STIX]{x1D71B}$. This proves the part (i).
Assertion (ii) follows from (i) and Lemma 2.2.26. For (iii), we remark that, if ![]() ${\mathcal{M}}$ is a coherent
${\mathcal{M}}$ is a coherent ![]() $\mathscr{D}^{\dagger }$-module, there exists a coherent
$\mathscr{D}^{\dagger }$-module, there exists a coherent ![]() $\widehat{\mathscr{D}}$-module
$\widehat{\mathscr{D}}$-module ![]() ${\mathcal{N}}$ such that
${\mathcal{N}}$ such that
We can then apply (ii) to ![]() ${\mathcal{N}}$ and this proves (iii).◻
${\mathcal{N}}$ and this proves (iii).◻
2.3 An invariance theorem for admissible blow-ups
We keep here the hypotheses from the previous section. In particular, ![]() $\mathfrak{X}_{0}$ denotes a smooth formal
$\mathfrak{X}_{0}$ denotes a smooth formal ![]() $\mathfrak{S}$-scheme and
$\mathfrak{S}$-scheme and
denotes an admissible blow-up. Let ![]() $\text{pr}^{\prime }:\mathfrak{X}^{\prime }\rightarrow \mathfrak{X}_{0}$ be another admissible formal blow-up and let
$\text{pr}^{\prime }:\mathfrak{X}^{\prime }\rightarrow \mathfrak{X}_{0}$ be another admissible formal blow-up and let ![]() $\unicode[STIX]{x1D70B}:\mathfrak{X}^{\prime }\rightarrow \mathfrak{X}$ be a morphism over
$\unicode[STIX]{x1D70B}:\mathfrak{X}^{\prime }\rightarrow \mathfrak{X}$ be a morphism over ![]() $\mathfrak{X}_{0}$, inducing an isomorphism between the associated rigid-analytic spaces
$\mathfrak{X}_{0}$, inducing an isomorphism between the associated rigid-analytic spaces ![]() $\mathfrak{X}_{\mathbb{Q}}$ and
$\mathfrak{X}_{\mathbb{Q}}$ and ![]() $\mathfrak{X}_{\mathbb{Q}}^{\prime }$ (which are both canonically isomorphic to the rigid-analytic space
$\mathfrak{X}_{\mathbb{Q}}^{\prime }$ (which are both canonically isomorphic to the rigid-analytic space ![]() $\mathfrak{X}_{0,\mathbb{Q}}$ associated to
$\mathfrak{X}_{0,\mathbb{Q}}$ associated to ![]() $\mathfrak{X}_{0}$). Then we have the following invariance property. This does not make use of the smoothness assumption for
$\mathfrak{X}_{0}$). Then we have the following invariance property. This does not make use of the smoothness assumption for ![]() $\mathfrak{X}_{0}$.
$\mathfrak{X}_{0}$.
Proposition 2.3.1. The functors ![]() $\unicode[STIX]{x1D70B}_{\ast }$ (resp.
$\unicode[STIX]{x1D70B}_{\ast }$ (resp. ![]() $\unicode[STIX]{x1D70B}^{\ast }$) are exact on the category of coherent
$\unicode[STIX]{x1D70B}^{\ast }$) are exact on the category of coherent ![]() ${\mathcal{O}}_{\mathfrak{X}^{\prime },\mathbb{Q}}$-modules (resp. coherent
${\mathcal{O}}_{\mathfrak{X}^{\prime },\mathbb{Q}}$-modules (resp. coherent ![]() ${\mathcal{O}}_{\mathfrak{X},\mathbb{Q}}$-modules) and induce an equivalence of categories between coherent
${\mathcal{O}}_{\mathfrak{X},\mathbb{Q}}$-modules) and induce an equivalence of categories between coherent ![]() ${\mathcal{O}}_{\mathfrak{X}^{\prime },\mathbb{Q}}$-modules and coherent
${\mathcal{O}}_{\mathfrak{X}^{\prime },\mathbb{Q}}$-modules and coherent ![]() ${\mathcal{O}}_{\mathfrak{X},\mathbb{Q}}$-modules.
${\mathcal{O}}_{\mathfrak{X},\mathbb{Q}}$-modules.
Proof. Let ![]() $\text{sp}$ (resp.
$\text{sp}$ (resp. ![]() $\text{sp}^{\prime }$) be the specialization map
$\text{sp}^{\prime }$) be the specialization map ![]() $\mathfrak{X}_{\mathbb{Q}}\rightarrow \mathfrak{X}$ (resp.
$\mathfrak{X}_{\mathbb{Q}}\rightarrow \mathfrak{X}$ (resp. ![]() $\mathfrak{X}_{\mathbb{Q}}^{\prime }\rightarrow \mathfrak{X}^{\prime }$). Then by Tate’s acyclicity theorem one knows that
$\mathfrak{X}_{\mathbb{Q}}^{\prime }\rightarrow \mathfrak{X}^{\prime }$). Then by Tate’s acyclicity theorem one knows that ![]() $\text{sp}_{\ast }$ is exact over the category of coherent
$\text{sp}_{\ast }$ is exact over the category of coherent ![]() ${\mathcal{O}}_{\mathfrak{X}_{\mathbb{Q}}}$-modules. Moreover, via specialization, the category of coherent
${\mathcal{O}}_{\mathfrak{X}_{\mathbb{Q}}}$-modules. Moreover, via specialization, the category of coherent ![]() ${\mathcal{O}}_{\mathfrak{X}_{\mathbb{Q}}}$-modules over the rigid space
${\mathcal{O}}_{\mathfrak{X}_{\mathbb{Q}}}$-modules over the rigid space ![]() $\mathfrak{X}_{\mathbb{Q}}$ is equivalent to the category of coherent
$\mathfrak{X}_{\mathbb{Q}}$ is equivalent to the category of coherent ![]() ${\mathcal{O}}_{\mathfrak{X},\mathbb{Q}}$-modules over the formal scheme
${\mathcal{O}}_{\mathfrak{X},\mathbb{Q}}$-modules over the formal scheme ![]() $\mathfrak{X}$ [Reference Berthelot7, discussion after (4.1.3.1)] and similarly for
$\mathfrak{X}$ [Reference Berthelot7, discussion after (4.1.3.1)] and similarly for ![]() $\mathfrak{X}^{\prime }$. Let
$\mathfrak{X}^{\prime }$. Let ![]() $\tilde{\unicode[STIX]{x1D70B}}$ be the induced map by
$\tilde{\unicode[STIX]{x1D70B}}$ be the induced map by ![]() $\unicode[STIX]{x1D70B}$ between the analytic spaces
$\unicode[STIX]{x1D70B}$ between the analytic spaces ![]() $\mathfrak{X}_{\mathbb{Q}}^{\prime }$ and
$\mathfrak{X}_{\mathbb{Q}}^{\prime }$ and ![]() $\mathfrak{X}_{\mathbb{Q}}$, which is an isomorphism by assumption. One has the following commutative diagram
$\mathfrak{X}_{\mathbb{Q}}$, which is an isomorphism by assumption. One has the following commutative diagram

from which we can deduce the following
Lemma 2.3.2. With the previous notations, there is an isomorphism
Proof. Let us first note that ![]() $R\tilde{\unicode[STIX]{x1D70B}}_{\ast }{\mathcal{O}}_{{\mathfrak{X}^{\prime }}_{\mathbb{Q}}}\simeq {\mathcal{O}}_{\mathfrak{X}_{\mathbb{Q}}}$ because
$R\tilde{\unicode[STIX]{x1D70B}}_{\ast }{\mathcal{O}}_{{\mathfrak{X}^{\prime }}_{\mathbb{Q}}}\simeq {\mathcal{O}}_{\mathfrak{X}_{\mathbb{Q}}}$ because ![]() $\tilde{\unicode[STIX]{x1D70B}}$ is an isomorphism of analytic spaces. Since
$\tilde{\unicode[STIX]{x1D70B}}$ is an isomorphism of analytic spaces. Since ![]() $R\text{sp}_{\ast }^{\prime }{\mathcal{O}}_{{\mathfrak{X}^{\prime }}_{\mathbb{Q}}}={\mathcal{O}}_{\mathfrak{X}^{\prime },\mathbb{Q}}$ (and the same with
$R\text{sp}_{\ast }^{\prime }{\mathcal{O}}_{{\mathfrak{X}^{\prime }}_{\mathbb{Q}}}={\mathcal{O}}_{\mathfrak{X}^{\prime },\mathbb{Q}}$ (and the same with ![]() $\mathfrak{X}$), we can compute using the previous diagram
$\mathfrak{X}$), we can compute using the previous diagram ![]() $R\unicode[STIX]{x1D70B}_{\ast }{\mathcal{O}}_{\mathfrak{X}^{\prime },\mathbb{Q}}\simeq R\text{sp}_{\ast }R\tilde{\unicode[STIX]{x1D70B}}_{\ast }{\mathcal{O}}_{{\mathfrak{X}^{\prime }}_{\mathbb{Q}}}\simeq {\mathcal{O}}_{\mathfrak{X},\mathbb{Q}}$. This proves the lemma.◻
$R\unicode[STIX]{x1D70B}_{\ast }{\mathcal{O}}_{\mathfrak{X}^{\prime },\mathbb{Q}}\simeq R\text{sp}_{\ast }R\tilde{\unicode[STIX]{x1D70B}}_{\ast }{\mathcal{O}}_{{\mathfrak{X}^{\prime }}_{\mathbb{Q}}}\simeq {\mathcal{O}}_{\mathfrak{X},\mathbb{Q}}$. This proves the lemma.◻
Let us now prove the proposition. Let ![]() ${\mathcal{F}}$ be a coherent
${\mathcal{F}}$ be a coherent ![]() ${\mathcal{O}}_{\mathfrak{X}^{\prime },\mathbb{Q}}$-module, then by [Reference Berthelot7, 4.1.3] there exists a coherent
${\mathcal{O}}_{\mathfrak{X}^{\prime },\mathbb{Q}}$-module, then by [Reference Berthelot7, 4.1.3] there exists a coherent ![]() ${\mathcal{O}}_{{\mathfrak{X}^{\prime }}_{\mathbb{Q}}}$-module
${\mathcal{O}}_{{\mathfrak{X}^{\prime }}_{\mathbb{Q}}}$-module ![]() $\tilde{{\mathcal{F}}}$ such that
$\tilde{{\mathcal{F}}}$ such that ![]() ${\mathcal{F}}=\text{sp}_{\ast }^{\prime }\tilde{{\mathcal{F}}}$. Considering again the previous diagram, we compute
${\mathcal{F}}=\text{sp}_{\ast }^{\prime }\tilde{{\mathcal{F}}}$. Considering again the previous diagram, we compute
As ![]() $\tilde{\unicode[STIX]{x1D70B}}$ is an isomorphism,
$\tilde{\unicode[STIX]{x1D70B}}$ is an isomorphism, ![]() $R^{i}\tilde{\unicode[STIX]{x1D70B}}_{\ast }\tilde{{\mathcal{F}}}=0$ if
$R^{i}\tilde{\unicode[STIX]{x1D70B}}_{\ast }\tilde{{\mathcal{F}}}=0$ if ![]() $i\geqslant 1$ and
$i\geqslant 1$ and ![]() $\tilde{\unicode[STIX]{x1D70B}}_{\ast }\tilde{{\mathcal{F}}}$ is a coherent
$\tilde{\unicode[STIX]{x1D70B}}_{\ast }\tilde{{\mathcal{F}}}$ is a coherent ![]() ${\mathcal{O}}_{\mathfrak{X}_{\mathbb{Q}}}$-module. Finally,
${\mathcal{O}}_{\mathfrak{X}_{\mathbb{Q}}}$-module. Finally, ![]() $R\text{sp}_{\ast }$ is reduced to
$R\text{sp}_{\ast }$ is reduced to ![]() $\text{sp}_{\ast }$ and the spectral sequence of the composite functors degenerates, giving us that
$\text{sp}_{\ast }$ and the spectral sequence of the composite functors degenerates, giving us that ![]() $R^{i}\unicode[STIX]{x1D70B}_{\ast }{\mathcal{F}}=0$ if
$R^{i}\unicode[STIX]{x1D70B}_{\ast }{\mathcal{F}}=0$ if ![]() $i\geqslant 1$ and
$i\geqslant 1$ and ![]() $\unicode[STIX]{x1D70B}_{\ast }{\mathcal{F}}$ is a coherent
$\unicode[STIX]{x1D70B}_{\ast }{\mathcal{F}}$ is a coherent ![]() ${\mathcal{O}}_{\mathfrak{X},\mathbb{Q}}$-module. It is moreover clear that
${\mathcal{O}}_{\mathfrak{X},\mathbb{Q}}$-module. It is moreover clear that ![]() $\unicode[STIX]{x1D70B}^{\ast }$ preserves coherence. Consider the map of coherent
$\unicode[STIX]{x1D70B}^{\ast }$ preserves coherence. Consider the map of coherent ![]() ${\mathcal{O}}_{\mathfrak{X}^{\prime },\mathbb{Q}}$-modules
${\mathcal{O}}_{\mathfrak{X}^{\prime },\mathbb{Q}}$-modules ![]() $\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D70B}_{\ast }{\mathcal{F}}\rightarrow {\mathcal{F}}$. To prove that this is an isomorphism is local on
$\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D70B}_{\ast }{\mathcal{F}}\rightarrow {\mathcal{F}}$. To prove that this is an isomorphism is local on ![]() $\mathfrak{X}$, which we can assume to be affine. In this case, it is enough to prove the statement for
$\mathfrak{X}$, which we can assume to be affine. In this case, it is enough to prove the statement for ![]() ${\mathcal{F}}={\mathcal{O}}_{\mathfrak{X}^{\prime },\mathbb{Q}}$, since
${\mathcal{F}}={\mathcal{O}}_{\mathfrak{X}^{\prime },\mathbb{Q}}$, since ![]() $\unicode[STIX]{x1D70B}_{\ast }$ is exact. But
$\unicode[STIX]{x1D70B}_{\ast }$ is exact. But ![]() $\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D70B}_{\ast }{\mathcal{O}}_{\mathfrak{X}^{\prime },\mathbb{Q}}\simeq \unicode[STIX]{x1D70B}^{\ast }{\mathcal{O}}_{\mathfrak{X},\mathbb{Q}}$ because of the lemma and thus
$\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D70B}_{\ast }{\mathcal{O}}_{\mathfrak{X}^{\prime },\mathbb{Q}}\simeq \unicode[STIX]{x1D70B}^{\ast }{\mathcal{O}}_{\mathfrak{X},\mathbb{Q}}$ because of the lemma and thus ![]() $\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D70B}_{\ast }{\mathcal{O}}_{\mathfrak{X}^{\prime },\mathbb{Q}}\simeq {\mathcal{O}}_{\mathfrak{X}^{\prime },\mathbb{Q}}$.
$\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D70B}_{\ast }{\mathcal{O}}_{\mathfrak{X}^{\prime },\mathbb{Q}}\simeq {\mathcal{O}}_{\mathfrak{X}^{\prime },\mathbb{Q}}$.
Let ![]() ${\mathcal{E}}$ be a coherent
${\mathcal{E}}$ be a coherent ![]() ${\mathcal{O}}_{\mathfrak{X},\mathbb{Q}}$-module and consider the canonical map
${\mathcal{O}}_{\mathfrak{X},\mathbb{Q}}$-module and consider the canonical map ![]() ${\mathcal{E}}\rightarrow \unicode[STIX]{x1D70B}_{\ast }\unicode[STIX]{x1D70B}^{\ast }{\mathcal{E}}$. Again, since
${\mathcal{E}}\rightarrow \unicode[STIX]{x1D70B}_{\ast }\unicode[STIX]{x1D70B}^{\ast }{\mathcal{E}}$. Again, since ![]() $\unicode[STIX]{x1D70B}_{\ast }$ is exact, we are reduced to the case where
$\unicode[STIX]{x1D70B}_{\ast }$ is exact, we are reduced to the case where ![]() $\mathfrak{X}$ is affine and
$\mathfrak{X}$ is affine and ![]() ${\mathcal{E}}={\mathcal{O}}_{\mathfrak{X},\mathbb{Q}}$ to prove that this map is an isomorphism. In this case, the isomorphism follows again from the lemma.
${\mathcal{E}}={\mathcal{O}}_{\mathfrak{X},\mathbb{Q}}$ to prove that this map is an isomorphism. In this case, the isomorphism follows again from the lemma.
Since ![]() $\unicode[STIX]{x1D70B}_{\ast }$ and
$\unicode[STIX]{x1D70B}_{\ast }$ and ![]() $\unicode[STIX]{x1D70B}^{\ast }$ are quasi-inverse to each other, and
$\unicode[STIX]{x1D70B}^{\ast }$ are quasi-inverse to each other, and ![]() $\unicode[STIX]{x1D70B}_{\ast }$ is an exact functor,
$\unicode[STIX]{x1D70B}_{\ast }$ is an exact functor, ![]() $\unicode[STIX]{x1D70B}^{\ast }$ is exact as well. This finishes the proof of the proposition.◻
$\unicode[STIX]{x1D70B}^{\ast }$ is exact as well. This finishes the proof of the proposition.◻
In the sequel of this article, we will give a version of the invariance property 2.3.1 for ![]() $\mathscr{D}$-modules. Recall that we have the sheaves of differential operators
$\mathscr{D}$-modules. Recall that we have the sheaves of differential operators ![]() $\mathscr{D}_{\mathfrak{X},k}^{\dagger },\widehat{\mathscr{D}}_{\mathfrak{X},\mathbb{Q}}^{(k,m)}$ etc. for
$\mathscr{D}_{\mathfrak{X},k}^{\dagger },\widehat{\mathscr{D}}_{\mathfrak{X},\mathbb{Q}}^{(k,m)}$ etc. for ![]() $k\geqslant k_{\mathfrak{X}}$, see previous subsection, at our disposal (similarly for
$k\geqslant k_{\mathfrak{X}}$, see previous subsection, at our disposal (similarly for ![]() $\mathfrak{X}^{\prime }$). In the following we fix a congruence level
$\mathfrak{X}^{\prime }$). In the following we fix a congruence level ![]() $k\geqslant \text{max}\{k_{\mathfrak{X}},k_{\mathfrak{X}^{\prime }}\}$.
$k\geqslant \text{max}\{k_{\mathfrak{X}},k_{\mathfrak{X}^{\prime }}\}$.
For a ![]() $\mathscr{D}_{\mathfrak{X}^{\prime },k}^{\dagger }$-module
$\mathscr{D}_{\mathfrak{X}^{\prime },k}^{\dagger }$-module ![]() $\mathscr{M}$, we let, as usual,
$\mathscr{M}$, we let, as usual, ![]() $\unicode[STIX]{x1D70B}_{\ast }\mathscr{M}$ denote the push-forward of
$\unicode[STIX]{x1D70B}_{\ast }\mathscr{M}$ denote the push-forward of ![]() $\mathscr{M}$ in the sense of abelian sheaves (and analogously in the case of
$\mathscr{M}$ in the sense of abelian sheaves (and analogously in the case of ![]() $\widehat{\mathscr{D}}_{\mathfrak{X}^{\prime },\mathbb{Q}}^{(k,m)}$-modules). Conversely, there is a functor
$\widehat{\mathscr{D}}_{\mathfrak{X}^{\prime },\mathbb{Q}}^{(k,m)}$-modules). Conversely, there is a functor ![]() $\unicode[STIX]{x1D70B}^{!}$ in the other direction constructed as usual using the formalism of inverse images of
$\unicode[STIX]{x1D70B}^{!}$ in the other direction constructed as usual using the formalism of inverse images of ![]() $\mathscr{D}$-modules: first of all, by definition of the sheaves
$\mathscr{D}$-modules: first of all, by definition of the sheaves ![]() $\mathscr{D}_{X_{i}^{\prime }}^{(k,m)}$ and
$\mathscr{D}_{X_{i}^{\prime }}^{(k,m)}$ and ![]() $\mathscr{D}_{X_{i}}^{(k,m)}$, see (2.1.16), and the fact that
$\mathscr{D}_{X_{i}}^{(k,m)}$, see (2.1.16), and the fact that ![]() $(\text{pr}^{\prime })^{\ast }=\unicode[STIX]{x1D70B}^{\ast }\circ \text{pr}^{\ast }$ we have
$(\text{pr}^{\prime })^{\ast }=\unicode[STIX]{x1D70B}^{\ast }\circ \text{pr}^{\ast }$ we have
and the sheaf ![]() $\mathscr{D}_{X_{i}^{\prime }}^{(k,m)}$ can be uniquely endowed with a structure of right
$\mathscr{D}_{X_{i}^{\prime }}^{(k,m)}$ can be uniquely endowed with a structure of right ![]() $\unicode[STIX]{x1D70B}^{-1}\mathscr{D}_{X_{i}}^{(k,m)}$-module. Passing to the
$\unicode[STIX]{x1D70B}^{-1}\mathscr{D}_{X_{i}}^{(k,m)}$-module. Passing to the ![]() $p$-adic completion, we see that the sheaf
$p$-adic completion, we see that the sheaf ![]() $\widehat{\mathscr{D}}_{\mathfrak{X}^{\prime }}^{(k,m)}$ is a sheaf of right
$\widehat{\mathscr{D}}_{\mathfrak{X}^{\prime }}^{(k,m)}$ is a sheaf of right ![]() $\unicode[STIX]{x1D70B}^{-1}\widehat{\mathscr{D}}_{\mathfrak{X}}^{(k,m)}$-modules. Then, passing to the inductive limit over
$\unicode[STIX]{x1D70B}^{-1}\widehat{\mathscr{D}}_{\mathfrak{X}}^{(k,m)}$-modules. Then, passing to the inductive limit over ![]() $m$ implies that
$m$ implies that ![]() $\mathscr{D}_{\mathfrak{X}^{\prime },k}^{\dagger }$ is a right
$\mathscr{D}_{\mathfrak{X}^{\prime },k}^{\dagger }$ is a right ![]() $\unicode[STIX]{x1D70B}^{-1}\mathscr{D}_{\mathfrak{X},k}^{\dagger }$-module. For a
$\unicode[STIX]{x1D70B}^{-1}\mathscr{D}_{\mathfrak{X},k}^{\dagger }$-module. For a ![]() $\mathscr{D}_{\mathfrak{X},k}^{\dagger }$-module
$\mathscr{D}_{\mathfrak{X},k}^{\dagger }$-module ![]() $\mathscr{M}$, we then define
$\mathscr{M}$, we then define
and we make the analogous definition in the case of ![]() $\widehat{\mathscr{D}}_{\mathfrak{X},\mathbb{Q}}^{(k,m)}$-modules.Footnote 2
$\widehat{\mathscr{D}}_{\mathfrak{X},\mathbb{Q}}^{(k,m)}$-modules.Footnote 2
Before stating the next theorem, we need the following lemmas. Denote by ![]() ${\mathcal{A}}$ the abelian category of projective systems
${\mathcal{A}}$ the abelian category of projective systems ![]() $K_{\bullet }=(K_{i})_{i\in \mathbb{N}}=(K_{0}\leftarrow K_{1}\leftarrow \cdots \,)$ of
$K_{\bullet }=(K_{i})_{i\in \mathbb{N}}=(K_{0}\leftarrow K_{1}\leftarrow \cdots \,)$ of ![]() ${\mathcal{O}}_{\mathfrak{X}}$-modules
${\mathcal{O}}_{\mathfrak{X}}$-modules ![]() $K_{i}$, where
$K_{i}$, where ![]() $K_{i}$ is annihilated by multiplication by
$K_{i}$ is annihilated by multiplication by ![]() $\unicode[STIX]{x1D71B}^{i+1}$ for every
$\unicode[STIX]{x1D71B}^{i+1}$ for every ![]() $i\geqslant 0$. Put
$i\geqslant 0$. Put ![]() ${\mathcal{P}}^{b}=D^{b}({\mathcal{A}})$. Note that for a complex
${\mathcal{P}}^{b}=D^{b}({\mathcal{A}})$. Note that for a complex ![]() $(K^{n})_{n\in \mathbb{Z}}$ in
$(K^{n})_{n\in \mathbb{Z}}$ in ![]() ${\mathcal{P}}^{b}$, where each
${\mathcal{P}}^{b}$, where each ![]() $K^{n}=(K_{i}^{n})_{i\in \mathbb{N}}$, there exists
$K^{n}=(K_{i}^{n})_{i\in \mathbb{N}}$, there exists ![]() $J>0$ so that
$J>0$ so that ![]() ${\mathcal{H}}^{n}(K^{\bullet })=0$ if
${\mathcal{H}}^{n}(K^{\bullet })=0$ if ![]() $|n|>J$ (
$|n|>J$ (![]() $n\in \mathbb{Z}$). The functor
$n\in \mathbb{Z}$). The functor ![]() $\varprojlim :{\mathcal{A}}\rightarrow \text{Mod}({\mathcal{O}}_{\mathfrak{X}})$ extends to a derived functor
$\varprojlim :{\mathcal{A}}\rightarrow \text{Mod}({\mathcal{O}}_{\mathfrak{X}})$ extends to a derived functor ![]() $R\varprojlim$ from the derived category
$R\varprojlim$ from the derived category ![]() ${\mathcal{P}}^{b}$ to the bounded derived category
${\mathcal{P}}^{b}$ to the bounded derived category ![]() $D^{b}({\mathcal{O}}_{\mathfrak{X}}):=D^{b}(\text{Mod}({\mathcal{O}}_{\mathfrak{X}}))$ because
$D^{b}({\mathcal{O}}_{\mathfrak{X}}):=D^{b}(\text{Mod}({\mathcal{O}}_{\mathfrak{X}}))$ because ![]() $R\varprojlim$ has cohomological dimension
$R\varprojlim$ has cohomological dimension ![]() $1$, see [Reference Hartshorne14, 4.1].
$1$, see [Reference Hartshorne14, 4.1].
Lemma 2.3.4. Let ![]() $N\in \mathbb{N}$, and let
$N\in \mathbb{N}$, and let ![]() $K_{\bullet }$ be an object of
$K_{\bullet }$ be an object of ![]() ${\mathcal{A}}$ such that
${\mathcal{A}}$ such that ![]() $\unicode[STIX]{x1D71B}^{N}K_{\bullet }=0$, then the complex
$\unicode[STIX]{x1D71B}^{N}K_{\bullet }=0$, then the complex ![]() $\mathbb{Q}\otimes _{\mathbb{Z}}R\varprojlim K_{\bullet }$ is quasi-isomorphic to 0 in
$\mathbb{Q}\otimes _{\mathbb{Z}}R\varprojlim K_{\bullet }$ is quasi-isomorphic to 0 in ![]() $D^{b}({\mathcal{O}}_{\mathfrak{X},\mathbb{Q}})$.
$D^{b}({\mathcal{O}}_{\mathfrak{X},\mathbb{Q}})$.
Proof. In the following we consider ![]() $K_{\bullet }$ as an object in
$K_{\bullet }$ as an object in ![]() ${\mathcal{P}}^{b}$ concentrated in degree zero. By hypothesis, the map
${\mathcal{P}}^{b}$ concentrated in degree zero. By hypothesis, the map ![]() $\unicode[STIX]{x1D71B}^{N}\,\cdot :K_{\bullet }\rightarrow K_{\bullet }$ factorizes through the zero complex
$\unicode[STIX]{x1D71B}^{N}\,\cdot :K_{\bullet }\rightarrow K_{\bullet }$ factorizes through the zero complex
After applying ![]() $R^{k}\varprojlim ={\mathcal{H}}^{k}\circ R\varprojlim$, for
$R^{k}\varprojlim ={\mathcal{H}}^{k}\circ R\varprojlim$, for ![]() $k\in \mathbb{Z}$, we find that multiplication with
$k\in \mathbb{Z}$, we find that multiplication with ![]() $\unicode[STIX]{x1D71B}^{N}$ factorizes
$\unicode[STIX]{x1D71B}^{N}$ factorizes
meaning that for every ![]() $k\in \mathbb{Z}$,
$k\in \mathbb{Z}$, ![]() $\unicode[STIX]{x1D71B}^{N}R^{k}\varprojlim K_{\bullet }=0$ and thus
$\unicode[STIX]{x1D71B}^{N}R^{k}\varprojlim K_{\bullet }=0$ and thus
This proves the lemma, as ![]() $\mathbb{Q}$ is flat over
$\mathbb{Q}$ is flat over ![]() $\mathbb{Z}$ and as this module is the
$\mathbb{Z}$ and as this module is the ![]() $k$th cohomology sheaf of the complex
$k$th cohomology sheaf of the complex
◻
Lemma 2.3.5. Let ![]() $N\in \mathbb{N}$, and let
$N\in \mathbb{N}$, and let ![]() ${\mathcal{E}}^{\bullet }$,
${\mathcal{E}}^{\bullet }$, ![]() ${\mathcal{F}}^{\bullet }$ two objects of
${\mathcal{F}}^{\bullet }$ two objects of ![]() ${\mathcal{P}}^{b}$, and
${\mathcal{P}}^{b}$, and ![]() $h:{\mathcal{E}}^{\bullet }\rightarrow {\mathcal{F}}^{\bullet }$ a morphism in
$h:{\mathcal{E}}^{\bullet }\rightarrow {\mathcal{F}}^{\bullet }$ a morphism in ![]() ${\mathcal{P}}^{b}$ so that the mapping cone
${\mathcal{P}}^{b}$ so that the mapping cone ![]() ${\mathcal{C}}^{\bullet }$ of
${\mathcal{C}}^{\bullet }$ of ![]() $h$ (defined up to a quasi-isomorphism) satisfies
$h$ (defined up to a quasi-isomorphism) satisfies
Then the map ![]() $h$ induces a quasi-isomorphism
$h$ induces a quasi-isomorphism
Proof. First note that since ![]() ${\mathcal{E}}^{\bullet }$ and
${\mathcal{E}}^{\bullet }$ and ![]() ${\mathcal{F}}^{\bullet }$ have bounded cohomology, this is also the case of
${\mathcal{F}}^{\bullet }$ have bounded cohomology, this is also the case of ![]() ${\mathcal{C}}^{\bullet }$, so that the condition of the lemma involves only a finite number of
${\mathcal{C}}^{\bullet }$, so that the condition of the lemma involves only a finite number of ![]() $j\in \mathbb{Z}$. More precisely, there exists
$j\in \mathbb{Z}$. More precisely, there exists ![]() $J\in \mathbb{N}$, such that the sheaves
$J\in \mathbb{N}$, such that the sheaves ![]() ${\mathcal{H}}^{j}({\mathcal{C}}^{\bullet })$ are zero for all
${\mathcal{H}}^{j}({\mathcal{C}}^{\bullet })$ are zero for all ![]() $j$ satisfying the condition
$j$ satisfying the condition ![]() $|j|>J$. Using the cohomological truncations functors
$|j|>J$. Using the cohomological truncations functors ![]() $\unicode[STIX]{x1D70E}_{{\geqslant}n}$ as defined in [Reference Hartshorne15, I, 7], and denoting
$\unicode[STIX]{x1D70E}_{{\geqslant}n}$ as defined in [Reference Hartshorne15, I, 7], and denoting ![]() $\unicode[STIX]{x1D70E}_{{>}n}$ of [Reference Hartshorne15, I, 7] by
$\unicode[STIX]{x1D70E}_{{>}n}$ of [Reference Hartshorne15, I, 7] by ![]() $\unicode[STIX]{x1D70E}_{{\geqslant}n+1}$, we have for each
$\unicode[STIX]{x1D70E}_{{\geqslant}n+1}$, we have for each ![]() $n$ a triangle in
$n$ a triangle in ![]() ${\mathcal{P}}^{b}$ [Reference Hartshorne15, I, 7.2]
${\mathcal{P}}^{b}$ [Reference Hartshorne15, I, 7.2]
We will prove by decreasing induction on ![]() $n$ that
$n$ that ![]() $\mathbb{Q}\otimes R\varprojlim \unicode[STIX]{x1D70E}_{{\geqslant}n}({\mathcal{C}}^{\bullet })$ is quasi-isomorphic to
$\mathbb{Q}\otimes R\varprojlim \unicode[STIX]{x1D70E}_{{\geqslant}n}({\mathcal{C}}^{\bullet })$ is quasi-isomorphic to ![]() $0$. This is true if
$0$. This is true if ![]() $n=J+1$. Assume that this is true for
$n=J+1$. Assume that this is true for ![]() $n+1$, then after applying
$n+1$, then after applying ![]() $\mathbb{Q}\otimes R\varprojlim$ to the previous triangle, we get a triangle
$\mathbb{Q}\otimes R\varprojlim$ to the previous triangle, we get a triangle
As by hypothesis ![]() $\unicode[STIX]{x1D71B}^{N}{\mathcal{H}}^{n}({\mathcal{C}}^{\bullet })=0$, we see by applying the previous Lemma 2.3.4 to the projective system
$\unicode[STIX]{x1D71B}^{N}{\mathcal{H}}^{n}({\mathcal{C}}^{\bullet })=0$, we see by applying the previous Lemma 2.3.4 to the projective system ![]() ${\mathcal{H}}^{n}({\mathcal{C}}^{\bullet })$ that
${\mathcal{H}}^{n}({\mathcal{C}}^{\bullet })$ that ![]() $\mathbb{Q}\otimes R\varprojlim {\mathcal{H}}^{n}({\mathcal{C}}^{\bullet })$ is quasi-isomorphic to
$\mathbb{Q}\otimes R\varprojlim {\mathcal{H}}^{n}({\mathcal{C}}^{\bullet })$ is quasi-isomorphic to ![]() $0$. Therefore, we have a quasi-isomorphism
$0$. Therefore, we have a quasi-isomorphism
and the complex ![]() $\mathbb{Q}\otimes R\varprojlim \unicode[STIX]{x1D70E}_{{\geqslant}n}({\mathcal{C}}^{\bullet })$ is hence quasi-isomorphic to
$\mathbb{Q}\otimes R\varprojlim \unicode[STIX]{x1D70E}_{{\geqslant}n}({\mathcal{C}}^{\bullet })$ is hence quasi-isomorphic to ![]() $0$. Thus, we conclude that for all
$0$. Thus, we conclude that for all ![]() $n$,
$n$, ![]() $\mathbb{Q}\otimes R\varprojlim \unicode[STIX]{x1D70E}_{{\geqslant}n}({\mathcal{C}}^{\bullet })$ is quasi-isomorphic to
$\mathbb{Q}\otimes R\varprojlim \unicode[STIX]{x1D70E}_{{\geqslant}n}({\mathcal{C}}^{\bullet })$ is quasi-isomorphic to ![]() $0$. Since
$0$. Since ![]() ${\mathcal{C}}^{\bullet }$ has bounded cohomology, it is quasi-isomorphic to
${\mathcal{C}}^{\bullet }$ has bounded cohomology, it is quasi-isomorphic to ![]() $\unicode[STIX]{x1D70E}_{{\geqslant}n}({\mathcal{C}}^{\bullet })$ for
$\unicode[STIX]{x1D70E}_{{\geqslant}n}({\mathcal{C}}^{\bullet })$ for ![]() $n$ small enough and this finally proves that
$n$ small enough and this finally proves that ![]() $\mathbb{Q}\otimes R\varprojlim {\mathcal{C}}^{\bullet }$ is quasi-isomorphic to
$\mathbb{Q}\otimes R\varprojlim {\mathcal{C}}^{\bullet }$ is quasi-isomorphic to ![]() $0$. Now we consider the triangle in
$0$. Now we consider the triangle in ![]() ${\mathcal{P}}^{b}$
${\mathcal{P}}^{b}$
and apply ![]() $\mathbb{Q}\otimes R\varprojlim$. In this way we obtain a triangle
$\mathbb{Q}\otimes R\varprojlim$. In this way we obtain a triangle
and since ![]() $\mathbb{Q}\otimes R\varprojlim {\mathcal{C}}^{\bullet }$ is quasi-isomorphic to
$\mathbb{Q}\otimes R\varprojlim {\mathcal{C}}^{\bullet }$ is quasi-isomorphic to ![]() $0$, we see that the first map of the latter triangle is a quasi-isomorphism as claimed.◻
$0$, we see that the first map of the latter triangle is a quasi-isomorphism as claimed.◻
As before, we denote the associated rigid-analytic space of ![]() $\mathfrak{X}$ by
$\mathfrak{X}$ by ![]() $\mathfrak{X}_{\mathbb{Q}}$. From 2.3.1 and Lemma 2.3.2
$\mathfrak{X}_{\mathbb{Q}}$. From 2.3.1 and Lemma 2.3.2 ![]() $R^{j}\unicode[STIX]{x1D70B}_{\ast }{\mathcal{O}}_{\mathfrak{X}^{\prime },\mathbb{Q}}=0$ for
$R^{j}\unicode[STIX]{x1D70B}_{\ast }{\mathcal{O}}_{\mathfrak{X}^{\prime },\mathbb{Q}}=0$ for ![]() $j>0$ and
$j>0$ and ![]() $\unicode[STIX]{x1D70B}_{\ast }{\mathcal{O}}_{\mathfrak{X}^{\prime },\mathbb{Q}}={\mathcal{O}}_{\mathfrak{X},\mathbb{Q}}$. As the map
$\unicode[STIX]{x1D70B}_{\ast }{\mathcal{O}}_{\mathfrak{X}^{\prime },\mathbb{Q}}={\mathcal{O}}_{\mathfrak{X},\mathbb{Q}}$. As the map ![]() $\unicode[STIX]{x1D70B}$ is proper, the sheaves
$\unicode[STIX]{x1D70B}$ is proper, the sheaves ![]() $R^{j}\unicode[STIX]{x1D70B}_{\ast }{\mathcal{O}}_{\mathfrak{X}^{\prime }}$ are coherent
$R^{j}\unicode[STIX]{x1D70B}_{\ast }{\mathcal{O}}_{\mathfrak{X}^{\prime }}$ are coherent ![]() ${\mathcal{O}}_{\mathfrak{X}}$-modules and there is
${\mathcal{O}}_{\mathfrak{X}}$-modules and there is ![]() $N\geqslant 0$ such that
$N\geqslant 0$ such that ![]() $\unicode[STIX]{x1D71B}^{N}R^{j}\unicode[STIX]{x1D70B}_{\ast }{\mathcal{O}}_{\mathfrak{X}^{\prime }}=0$ for all
$\unicode[STIX]{x1D71B}^{N}R^{j}\unicode[STIX]{x1D70B}_{\ast }{\mathcal{O}}_{\mathfrak{X}^{\prime }}=0$ for all ![]() $j>0$ and such that the kernel and cokernel of the natural map
$j>0$ and such that the kernel and cokernel of the natural map ![]() ${\mathcal{O}}_{\mathfrak{X}}\rightarrow \unicode[STIX]{x1D70B}_{\ast }{\mathcal{O}}_{\mathfrak{X}^{\prime }}$ are killed by
${\mathcal{O}}_{\mathfrak{X}}\rightarrow \unicode[STIX]{x1D70B}_{\ast }{\mathcal{O}}_{\mathfrak{X}^{\prime }}$ are killed by ![]() $\unicode[STIX]{x1D71B}^{N}$ as well. For any
$\unicode[STIX]{x1D71B}^{N}$ as well. For any ![]() $i\geqslant 0$, let as usual
$i\geqslant 0$, let as usual ![]() $X_{i}$ be the reduction of
$X_{i}$ be the reduction of ![]() $\mathfrak{X}$ mod
$\mathfrak{X}$ mod ![]() $\unicode[STIX]{x1D71B}^{i+1}$ and similarly for
$\unicode[STIX]{x1D71B}^{i+1}$ and similarly for ![]() $\mathfrak{X}^{\prime }$ and denote by
$\mathfrak{X}^{\prime }$ and denote by ![]() $\unicode[STIX]{x1D70B}_{i}:X_{i}^{\prime }\rightarrow X_{i}$ the morphism induced by
$\unicode[STIX]{x1D70B}_{i}:X_{i}^{\prime }\rightarrow X_{i}$ the morphism induced by ![]() $\unicode[STIX]{x1D70B}$. We will need the following
$\unicode[STIX]{x1D70B}$. We will need the following
Auxiliary result 2.3.6. Let ![]() $i\geqslant 0$.
$i\geqslant 0$.
(i) Kernel and cokernel of the canonical map
 ${\mathcal{O}}_{X_{i}}\rightarrow \unicode[STIX]{x1D70B}_{i\ast }{\mathcal{O}}_{X_{i}^{\prime }}$ are annihilated by
${\mathcal{O}}_{X_{i}}\rightarrow \unicode[STIX]{x1D70B}_{i\ast }{\mathcal{O}}_{X_{i}^{\prime }}$ are annihilated by  $\unicode[STIX]{x1D71B}^{2N}$.
$\unicode[STIX]{x1D71B}^{2N}$.(ii) For all
 $j\geqslant 1$, one has
$j\geqslant 1$, one has  $\unicode[STIX]{x1D71B}^{2N}R^{j}\unicode[STIX]{x1D70B}_{i\ast }{\mathcal{O}}_{X_{i}^{\prime }}=0$.
$\unicode[STIX]{x1D71B}^{2N}R^{j}\unicode[STIX]{x1D70B}_{i\ast }{\mathcal{O}}_{X_{i}^{\prime }}=0$.
Proof. As the formal scheme ![]() $\mathfrak{X}^{\prime }$ is flat, there are exact sequences
$\mathfrak{X}^{\prime }$ is flat, there are exact sequences
Applying ![]() $R^{j}\unicode[STIX]{x1D70B}_{\ast }$, we get exact sequences for any
$R^{j}\unicode[STIX]{x1D70B}_{\ast }$, we get exact sequences for any ![]() $i$ and
$i$ and ![]() $j\geqslant 1$,
$j\geqslant 1$,
that prove that ![]() $\unicode[STIX]{x1D71B}^{2N}R^{j}\unicode[STIX]{x1D70B}_{i\ast }{\mathcal{O}}_{X_{i}^{\prime }}=0$. Moreover, we can consider the following commutative diagram of exact sequences
$\unicode[STIX]{x1D71B}^{2N}R^{j}\unicode[STIX]{x1D70B}_{i\ast }{\mathcal{O}}_{X_{i}^{\prime }}=0$. Moreover, we can consider the following commutative diagram of exact sequences

By the snake lemma the kernel of the canonical map ![]() ${\mathcal{O}}_{X_{i}}\rightarrow \unicode[STIX]{x1D70B}_{i\ast }{\mathcal{O}}_{X_{i}^{\prime }}$ is killed by
${\mathcal{O}}_{X_{i}}\rightarrow \unicode[STIX]{x1D70B}_{i\ast }{\mathcal{O}}_{X_{i}^{\prime }}$ is killed by ![]() $\unicode[STIX]{x1D71B}^{2N}$. By chasing the diagram we also see that the cokernel of this map is also killed by
$\unicode[STIX]{x1D71B}^{2N}$. By chasing the diagram we also see that the cokernel of this map is also killed by ![]() $\unicode[STIX]{x1D71B}^{2N}$ for all
$\unicode[STIX]{x1D71B}^{2N}$ for all ![]() $i$. This proves the auxiliary result.◻
$i$. This proves the auxiliary result.◻
Lemma 2.3.7. Let ![]() $\unicode[STIX]{x1D70B}:\mathfrak{X}^{\prime }\rightarrow \mathfrak{X}$ be a morphism over
$\unicode[STIX]{x1D70B}:\mathfrak{X}^{\prime }\rightarrow \mathfrak{X}$ be a morphism over ![]() $\mathfrak{X}_{0}$ between admissible formal blow-ups of the smooth formal scheme
$\mathfrak{X}_{0}$ between admissible formal blow-ups of the smooth formal scheme ![]() $\mathfrak{X}_{0}$. Let
$\mathfrak{X}_{0}$. Let ![]() $k\geqslant \max \{k_{\mathfrak{X}},k_{\mathfrak{X}^{\prime }}\}$.
$k\geqslant \max \{k_{\mathfrak{X}},k_{\mathfrak{X}^{\prime }}\}$.
(i) Then we have:
 $R^{j}\unicode[STIX]{x1D70B}_{\ast }\mathscr{D}_{\mathfrak{X}^{\prime },k}^{\dagger }=0$ for
$R^{j}\unicode[STIX]{x1D70B}_{\ast }\mathscr{D}_{\mathfrak{X}^{\prime },k}^{\dagger }=0$ for  $j>0$. Moreover,
$j>0$. Moreover,  $\unicode[STIX]{x1D70B}_{\ast }\mathscr{D}_{\mathfrak{X}^{\prime },k}^{\dagger }=\mathscr{D}_{\mathfrak{X},k}^{\dagger }$.
$\unicode[STIX]{x1D70B}_{\ast }\mathscr{D}_{\mathfrak{X}^{\prime },k}^{\dagger }=\mathscr{D}_{\mathfrak{X},k}^{\dagger }$.(ii) There is a canonical isomorphism
 $\mathscr{D}_{\mathfrak{X}^{\prime },k}^{\dagger }\simeq \unicode[STIX]{x1D70B}^{!}\mathscr{D}_{\mathfrak{X},k}^{\dagger }$.
$\mathscr{D}_{\mathfrak{X}^{\prime },k}^{\dagger }\simeq \unicode[STIX]{x1D70B}^{!}\mathscr{D}_{\mathfrak{X},k}^{\dagger }$.
Proof. Since ![]() $R^{j}\unicode[STIX]{x1D70B}_{\ast }$ commutes with inductive limits, it suffices to prove the claim for
$R^{j}\unicode[STIX]{x1D70B}_{\ast }$ commutes with inductive limits, it suffices to prove the claim for ![]() $\widehat{\mathscr{D}}_{\mathfrak{X}^{\prime },\mathbb{Q}}^{(k,m)}$. Abbreviate
$\widehat{\mathscr{D}}_{\mathfrak{X}^{\prime },\mathbb{Q}}^{(k,m)}$. Abbreviate ![]() $\widehat{\mathscr{D}}_{\mathfrak{X}^{\prime }}=\widehat{\mathscr{D}}_{\mathfrak{X}^{\prime }}^{(k,m)}$ (and similarly for
$\widehat{\mathscr{D}}_{\mathfrak{X}^{\prime }}=\widehat{\mathscr{D}}_{\mathfrak{X}^{\prime }}^{(k,m)}$ (and similarly for ![]() $\mathfrak{X}$), and
$\mathfrak{X}$), and ![]() $\mathscr{D}_{X_{i}^{\prime }}=\widehat{\mathscr{D}}_{\mathfrak{X}^{\prime },k}^{(m)}/\unicode[STIX]{x1D71B}^{i+1}\widehat{\mathscr{D}}_{\mathfrak{X}^{\prime },k}^{(m)}$ (and similarly for
$\mathscr{D}_{X_{i}^{\prime }}=\widehat{\mathscr{D}}_{\mathfrak{X}^{\prime },k}^{(m)}/\unicode[STIX]{x1D71B}^{i+1}\widehat{\mathscr{D}}_{\mathfrak{X}^{\prime },k}^{(m)}$ (and similarly for ![]() $X_{i}$). We need to compute
$X_{i}$). We need to compute ![]() $R\unicode[STIX]{x1D70B}_{\ast }\widehat{\mathscr{D}}_{\mathfrak{X}^{\prime }}$. Note that by [26, Tag 0BKS]
$R\unicode[STIX]{x1D70B}_{\ast }\widehat{\mathscr{D}}_{\mathfrak{X}^{\prime }}$. Note that by [26, Tag 0BKS] ![]() $R\mathop{\varprojlim }\nolimits_{i}\mathscr{D}_{X_{i}^{\prime }}\simeq \mathop{\varprojlim }\nolimits_{i}\mathscr{D}_{X_{i}^{\prime }}$, so that
$R\mathop{\varprojlim }\nolimits_{i}\mathscr{D}_{X_{i}^{\prime }}\simeq \mathop{\varprojlim }\nolimits_{i}\mathscr{D}_{X_{i}^{\prime }}$, so that
by [26, Lemma 20.32.2]. As the sheaf ![]() $\mathscr{D}_{X_{i}}$ is a flat
$\mathscr{D}_{X_{i}}$ is a flat ![]() ${\mathcal{O}}_{X_{i}}$-module, the projection formula gives a canonical isomorphism
${\mathcal{O}}_{X_{i}}$-module, the projection formula gives a canonical isomorphism
so that the canonical map ![]() ${\mathcal{O}}_{X_{i}}\rightarrow R\unicode[STIX]{x1D70B}_{i\ast }{\mathcal{O}}_{X_{i}^{\prime }}$ induces a map of projective systems of complexes
${\mathcal{O}}_{X_{i}}\rightarrow R\unicode[STIX]{x1D70B}_{i\ast }{\mathcal{O}}_{X_{i}^{\prime }}$ induces a map of projective systems of complexes ![]() $h:(\mathscr{D}_{X_{i}})_{i}\rightarrow (R\unicode[STIX]{x1D70B}_{i\ast }\mathscr{D}_{X_{i}^{\prime }})_{i}$. We consider these projective systems as objects of
$h:(\mathscr{D}_{X_{i}})_{i}\rightarrow (R\unicode[STIX]{x1D70B}_{i\ast }\mathscr{D}_{X_{i}^{\prime }})_{i}$. We consider these projective systems as objects of ![]() ${\mathcal{P}}^{b}$. By applying
${\mathcal{P}}^{b}$. By applying ![]() $R\mathop{\varprojlim }\nolimits_{i}$ to
$R\mathop{\varprojlim }\nolimits_{i}$ to ![]() $h$, we get the canonical map
$h$, we get the canonical map ![]() $\widehat{h}:\widehat{\mathscr{D}}_{\mathfrak{X}}\rightarrow R\unicode[STIX]{x1D70B}_{\ast }\widehat{\mathscr{D}}_{\mathfrak{X}^{\prime }}$. Moreover, we have
$\widehat{h}:\widehat{\mathscr{D}}_{\mathfrak{X}}\rightarrow R\unicode[STIX]{x1D70B}_{\ast }\widehat{\mathscr{D}}_{\mathfrak{X}^{\prime }}$. Moreover, we have
By flat base change from ![]() ${\mathcal{O}}_{X_{i}}$ to
${\mathcal{O}}_{X_{i}}$ to ![]() $\mathscr{D}_{X_{i}}$, the previous auxiliary result 2.3.6(i) implies that the kernel and the cokernel of the map
$\mathscr{D}_{X_{i}}$, the previous auxiliary result 2.3.6(i) implies that the kernel and the cokernel of the map ![]() $(\mathscr{D}_{X_{i}})_{i}\rightarrow (\unicode[STIX]{x1D70B}_{i\ast }\mathscr{D}_{X_{i}^{\prime }})_{i}$ of projective systems are annihilated by
$(\mathscr{D}_{X_{i}})_{i}\rightarrow (\unicode[STIX]{x1D70B}_{i\ast }\mathscr{D}_{X_{i}^{\prime }})_{i}$ of projective systems are annihilated by ![]() $\unicode[STIX]{x1D71B}^{2N}$. Similarly, by 2.3.6(ii) the projective systems
$\unicode[STIX]{x1D71B}^{2N}$. Similarly, by 2.3.6(ii) the projective systems ![]() $(R^{j}\unicode[STIX]{x1D70B}_{i\ast }\mathscr{D}_{X_{i}^{\prime }})_{i}$ for
$(R^{j}\unicode[STIX]{x1D70B}_{i\ast }\mathscr{D}_{X_{i}^{\prime }})_{i}$ for ![]() $j\geqslant 1$ are annihilated by
$j\geqslant 1$ are annihilated by ![]() $\unicode[STIX]{x1D71B}^{2N}$. Let
$\unicode[STIX]{x1D71B}^{2N}$. Let ![]() ${\mathcal{C}}^{\bullet }$ be the cone of
${\mathcal{C}}^{\bullet }$ be the cone of ![]() $h$, then, as the functor
$h$, then, as the functor ![]() ${\mathcal{H}}^{0}$ is a cohomological functor [Reference Hartshorne15, definition, p. 27] we have the following exact cohomology sequence of projective systems of sheaves
${\mathcal{H}}^{0}$ is a cohomological functor [Reference Hartshorne15, definition, p. 27] we have the following exact cohomology sequence of projective systems of sheaves
and ![]() $\forall j\geqslant 1$
$\forall j\geqslant 1$
We thus see that the cohomology of ![]() ${\mathcal{C}}^{\bullet }$ is annihilated by
${\mathcal{C}}^{\bullet }$ is annihilated by ![]() $\unicode[STIX]{x1D71B}^{2N}$, so that we can apply Lemma 2.3.5 and obtain a quasi-isomorphism
$\unicode[STIX]{x1D71B}^{2N}$, so that we can apply Lemma 2.3.5 and obtain a quasi-isomorphism ![]() $\widehat{h}\otimes \mathbb{Q}:\widehat{\mathscr{D}}_{\mathfrak{X},\mathbb{Q}}\stackrel{\simeq }{\longrightarrow }R\unicode[STIX]{x1D70B}_{\ast }\widehat{\mathscr{D}}_{\mathfrak{X}^{\prime },\mathbb{Q}}$. By passing to the cohomology sheaves (and to the inductive limit over all
$\widehat{h}\otimes \mathbb{Q}:\widehat{\mathscr{D}}_{\mathfrak{X},\mathbb{Q}}\stackrel{\simeq }{\longrightarrow }R\unicode[STIX]{x1D70B}_{\ast }\widehat{\mathscr{D}}_{\mathfrak{X}^{\prime },\mathbb{Q}}$. By passing to the cohomology sheaves (and to the inductive limit over all ![]() $m$), this proves (i). The part (ii) follows from the definition of the functor
$m$), this proves (i). The part (ii) follows from the definition of the functor ![]() $\unicode[STIX]{x1D70B}^{!}$, see 2.3.3.◻
$\unicode[STIX]{x1D70B}^{!}$, see 2.3.3.◻
We can now state the
Theorem 2.3.8. Let ![]() $\unicode[STIX]{x1D70B}:\mathfrak{X}^{\prime }\rightarrow \mathfrak{X}$ be a morphism over
$\unicode[STIX]{x1D70B}:\mathfrak{X}^{\prime }\rightarrow \mathfrak{X}$ be a morphism over ![]() $\mathfrak{X}_{0}$ between admissible formal blow-ups of the smooth formal scheme
$\mathfrak{X}_{0}$ between admissible formal blow-ups of the smooth formal scheme ![]() $\mathfrak{X}_{0}$. Let
$\mathfrak{X}_{0}$. Let ![]() $k\geqslant \max \{k_{\mathfrak{X}},k_{\mathfrak{X}^{\prime }}\}$.
$k\geqslant \max \{k_{\mathfrak{X}},k_{\mathfrak{X}^{\prime }}\}$.
(i) If
 $\mathscr{M}$ is a coherent
$\mathscr{M}$ is a coherent  $\mathscr{D}_{\mathfrak{X}^{\prime },k}^{\dagger }$-module, then
$\mathscr{D}_{\mathfrak{X}^{\prime },k}^{\dagger }$-module, then  $R^{j}\unicode[STIX]{x1D70B}_{\ast }\mathscr{M}=0$ for
$R^{j}\unicode[STIX]{x1D70B}_{\ast }\mathscr{M}=0$ for  $j>0$. Moreover,
$j>0$. Moreover,  $\unicode[STIX]{x1D70B}_{\ast }\mathscr{D}_{\mathfrak{X}^{\prime },k}^{\dagger }=\mathscr{D}_{\mathfrak{X},k}^{\dagger }$, so that
$\unicode[STIX]{x1D70B}_{\ast }\mathscr{D}_{\mathfrak{X}^{\prime },k}^{\dagger }=\mathscr{D}_{\mathfrak{X},k}^{\dagger }$, so that  $\unicode[STIX]{x1D70B}_{\ast }$ induces an exact functor between coherent modules over
$\unicode[STIX]{x1D70B}_{\ast }$ induces an exact functor between coherent modules over  $\mathscr{D}_{\mathfrak{X}^{\prime },k}^{\dagger }$ and
$\mathscr{D}_{\mathfrak{X}^{\prime },k}^{\dagger }$ and  $\mathscr{D}_{\mathfrak{X},k}^{\dagger }$, respectively.
$\mathscr{D}_{\mathfrak{X},k}^{\dagger }$, respectively.(ii) The formation
 $\unicode[STIX]{x1D70B}^{!}$ is an exact functor from the category of coherent
$\unicode[STIX]{x1D70B}^{!}$ is an exact functor from the category of coherent  $\mathscr{D}_{\mathfrak{X},k}^{\dagger }$-modules to the category of coherent
$\mathscr{D}_{\mathfrak{X},k}^{\dagger }$-modules to the category of coherent  $\mathscr{D}_{\mathfrak{X}^{\prime },k}^{\dagger }$-modules, and
$\mathscr{D}_{\mathfrak{X}^{\prime },k}^{\dagger }$-modules, and  $\unicode[STIX]{x1D70B}^{!}$ and
$\unicode[STIX]{x1D70B}^{!}$ and  $\unicode[STIX]{x1D70B}_{\ast }$ are quasi-inverse equivalences between these categories.
$\unicode[STIX]{x1D70B}_{\ast }$ are quasi-inverse equivalences between these categories.
The same statement holds for coherent modules over ![]() $\widehat{\mathscr{D}}_{\mathfrak{X},\mathbb{Q}}^{(k,m)}$ and
$\widehat{\mathscr{D}}_{\mathfrak{X},\mathbb{Q}}^{(k,m)}$ and ![]() $\widehat{\mathscr{D}}_{\mathfrak{X}^{\prime },\mathbb{Q}}^{(k,m)}$, respectively.
$\widehat{\mathscr{D}}_{\mathfrak{X}^{\prime },\mathbb{Q}}^{(k,m)}$, respectively.
Proof. The first assertion of part (i) is true for ![]() $\mathscr{D}_{\mathfrak{X}^{\prime },k}^{\dagger }$ by the previous Lemma 2.3.7. Now there is a basis of the topology of
$\mathscr{D}_{\mathfrak{X}^{\prime },k}^{\dagger }$ by the previous Lemma 2.3.7. Now there is a basis of the topology of ![]() $\mathfrak{X}$ consisting of affine opens
$\mathfrak{X}$ consisting of affine opens ![]() $\mathfrak{V}$ such that
$\mathfrak{V}$ such that ![]() $\text{pr}(\mathfrak{V})$ is contained in some affine open of
$\text{pr}(\mathfrak{V})$ is contained in some affine open of ![]() $\mathfrak{X}_{0}$. For this reason, if some statement is local on
$\mathfrak{X}_{0}$. For this reason, if some statement is local on ![]() $\mathfrak{X}$, then we can assume that
$\mathfrak{X}$, then we can assume that ![]() $\mathfrak{X}_{0}$ is affine. To prove (i) of the theorem for coherent
$\mathfrak{X}_{0}$ is affine. To prove (i) of the theorem for coherent ![]() $\mathscr{D}_{\mathfrak{X}^{\prime },k}^{\dagger }$-modules, we can thus assume (and we do assume) that
$\mathscr{D}_{\mathfrak{X}^{\prime },k}^{\dagger }$-modules, we can thus assume (and we do assume) that ![]() $\mathfrak{X}_{0}$ is affine. Then
$\mathfrak{X}_{0}$ is affine. Then ![]() $\mathfrak{X}$ and
$\mathfrak{X}$ and ![]() $\mathfrak{X}^{\prime }$ are admissible blow-ups of a smooth affine formal scheme
$\mathfrak{X}^{\prime }$ are admissible blow-ups of a smooth affine formal scheme ![]() $\mathfrak{X}_{0}$ and we still call
$\mathfrak{X}_{0}$ and we still call ![]() $\unicode[STIX]{x1D70B}$ the map
$\unicode[STIX]{x1D70B}$ the map ![]() $\mathfrak{X}^{\prime }\rightarrow \mathfrak{X}$. We consider now the following assertion depending on
$\mathfrak{X}^{\prime }\rightarrow \mathfrak{X}$. We consider now the following assertion depending on ![]() $j$:
$j$:
We will prove this assertion for any ![]() $j\geqslant 1$ by decreasing induction on
$j\geqslant 1$ by decreasing induction on ![]() $j$. The statement for
$j$. The statement for ![]() $j=1$ establishes then the first assertion of part (i) in general. Since
$j=1$ establishes then the first assertion of part (i) in general. Since ![]() $\mathfrak{X}^{\prime }$ has dimension
$\mathfrak{X}^{\prime }$ has dimension ![]() ${\leqslant}M+1$, the assertion is true for
${\leqslant}M+1$, the assertion is true for ![]() $j=M+2$. Assume that the assertion is true for
$j=M+2$. Assume that the assertion is true for ![]() $j+1$ and take a coherent
$j+1$ and take a coherent ![]() $\mathscr{D}_{\mathfrak{X}^{\prime },k}^{\dagger }$-module
$\mathscr{D}_{\mathfrak{X}^{\prime },k}^{\dagger }$-module ![]() $\mathscr{M}$. Since
$\mathscr{M}$. Since ![]() $\mathfrak{X}_{0}$ is affine, we can apply 2.2.29 to find a nonnegative integer
$\mathfrak{X}_{0}$ is affine, we can apply 2.2.29 to find a nonnegative integer ![]() $r$ and an exact sequence of coherent
$r$ and an exact sequence of coherent ![]() $\mathscr{D}_{\mathfrak{X}^{\prime },k}^{\dagger }$-modules
$\mathscr{D}_{\mathfrak{X}^{\prime },k}^{\dagger }$-modules
Since ![]() $j\geqslant 1$ and since
$j\geqslant 1$ and since ![]() $R^{j}\unicode[STIX]{x1D70B}_{\ast }\mathscr{D}_{\mathfrak{X}^{\prime },k}^{\dagger }=0$ by Lemma 2.3.7, the long exact sequence for
$R^{j}\unicode[STIX]{x1D70B}_{\ast }\mathscr{D}_{\mathfrak{X}^{\prime },k}^{\dagger }=0$ by Lemma 2.3.7, the long exact sequence for ![]() $\unicode[STIX]{x1D70B}_{\ast }$ gives us an isomorphism
$\unicode[STIX]{x1D70B}_{\ast }$ gives us an isomorphism
But the right-hand side is zero by the induction hypothesis applied to ![]() $\mathscr{N}$. This establishes the assertion for
$\mathscr{N}$. This establishes the assertion for ![]() $j$ and completes the induction step. This ends the proof of the first assertion of part (i).
$j$ and completes the induction step. This ends the proof of the first assertion of part (i).
What remains to prove for part (i) is that ![]() $\unicode[STIX]{x1D70B}_{\ast }{\mathcal{M}}$ is coherent over
$\unicode[STIX]{x1D70B}_{\ast }{\mathcal{M}}$ is coherent over ![]() $\mathscr{D}_{\mathfrak{X},k}^{\dagger }$ if
$\mathscr{D}_{\mathfrak{X},k}^{\dagger }$ if ![]() ${\mathcal{M}}$ is coherent over
${\mathcal{M}}$ is coherent over ![]() $\mathscr{D}_{\mathfrak{X}^{\prime },k}^{\dagger }$. To show this, we continue to assume that
$\mathscr{D}_{\mathfrak{X}^{\prime },k}^{\dagger }$. To show this, we continue to assume that ![]() $\mathfrak{X}_{0}$ is affine. By 2.2.29, there is a finite presentation
$\mathfrak{X}_{0}$ is affine. By 2.2.29, there is a finite presentation
Applying ![]() $\unicode[STIX]{x1D70B}_{\ast }$ and using that
$\unicode[STIX]{x1D70B}_{\ast }$ and using that ![]() $\unicode[STIX]{x1D70B}_{\ast }$ is exact, we obtain a finite presentation for
$\unicode[STIX]{x1D70B}_{\ast }$ is exact, we obtain a finite presentation for ![]() $\unicode[STIX]{x1D70B}_{\ast }{\mathcal{M}}$, which implies that the latter is coherent.
$\unicode[STIX]{x1D70B}_{\ast }{\mathcal{M}}$, which implies that the latter is coherent.
Let us prove part (ii) in the case of coherent ![]() $\mathscr{D}_{\mathfrak{X},k}^{\dagger }$-modules, the case of coherent
$\mathscr{D}_{\mathfrak{X},k}^{\dagger }$-modules, the case of coherent ![]() $\widehat{\mathscr{D}}_{\mathfrak{X},\mathbb{Q}}^{(k,m)}$-modules can be treated analogously. By definition of the functor
$\widehat{\mathscr{D}}_{\mathfrak{X},\mathbb{Q}}^{(k,m)}$-modules can be treated analogously. By definition of the functor ![]() $\unicode[STIX]{x1D70B}^{!}$, see 2.3.3, we have
$\unicode[STIX]{x1D70B}^{!}$, see 2.3.3, we have ![]() $\unicode[STIX]{x1D70B}^{!}\mathscr{D}_{\mathfrak{X},k}^{\dagger }=\mathscr{D}_{\mathfrak{X}^{\prime },k}^{\dagger }$. To prove that
$\unicode[STIX]{x1D70B}^{!}\mathscr{D}_{\mathfrak{X},k}^{\dagger }=\mathscr{D}_{\mathfrak{X}^{\prime },k}^{\dagger }$. To prove that ![]() $\unicode[STIX]{x1D70B}^{!}$ preserves coherence is local on
$\unicode[STIX]{x1D70B}^{!}$ preserves coherence is local on ![]() $\mathfrak{X}$, so that we can (and will) again assume that
$\mathfrak{X}$, so that we can (and will) again assume that ![]() $\mathfrak{X}_{0}$ is affine. Let
$\mathfrak{X}_{0}$ is affine. Let ![]() $\mathscr{M}$ be a coherent
$\mathscr{M}$ be a coherent ![]() $\mathscr{D}_{\mathfrak{X},k}^{\dagger }$-module. We can apply Proposition 2.2.29 to
$\mathscr{D}_{\mathfrak{X},k}^{\dagger }$-module. We can apply Proposition 2.2.29 to ![]() $\mathfrak{X}$ and obtain a finite presentation
$\mathfrak{X}$ and obtain a finite presentation
Since the tensor product is right exact, we get a finite presentation of ![]() $\unicode[STIX]{x1D70B}^{!}\mathscr{M}$
$\unicode[STIX]{x1D70B}^{!}\mathscr{M}$
which implies that ![]() $\unicode[STIX]{x1D70B}^{!}\mathscr{M}$ is a coherent
$\unicode[STIX]{x1D70B}^{!}\mathscr{M}$ is a coherent ![]() $\mathscr{D}_{\mathfrak{X}^{\prime },k}^{\dagger }$-module. In particular, the functor
$\mathscr{D}_{\mathfrak{X}^{\prime },k}^{\dagger }$-module. In particular, the functor ![]() $\unicode[STIX]{x1D70B}^{!}$ preserves coherence. The map
$\unicode[STIX]{x1D70B}^{!}$ preserves coherence. The map ![]() $\unicode[STIX]{x1D70B}^{-1}\mathscr{M}\rightarrow \unicode[STIX]{x1D70B}^{!}\mathscr{M}$ sending
$\unicode[STIX]{x1D70B}^{-1}\mathscr{M}\rightarrow \unicode[STIX]{x1D70B}^{!}\mathscr{M}$ sending ![]() $x$ to
$x$ to ![]() $1\otimes x$ induces a morphism
$1\otimes x$ induces a morphism
which is natural in ![]() $\mathscr{M}$. Whether
$\mathscr{M}$. Whether ![]() $can_{\mathscr{M}}$ is an isomorphism can be decided locally on
$can_{\mathscr{M}}$ is an isomorphism can be decided locally on ![]() $\mathfrak{X}$, and we can again assume that
$\mathfrak{X}$, and we can again assume that ![]() $\mathfrak{X}_{0}$ is affine.
$\mathfrak{X}_{0}$ is affine. ![]() $\mathfrak{X}$ and
$\mathfrak{X}$ and ![]() $\mathfrak{X}^{\prime }$ are admissible blow-ups of
$\mathfrak{X}^{\prime }$ are admissible blow-ups of ![]() $\mathfrak{X}_{0}$, and by 2.2.29 there is a finite presentation
$\mathfrak{X}_{0}$, and by 2.2.29 there is a finite presentation
and so ![]() $\unicode[STIX]{x1D70B}^{!}\mathscr{M}$ admits a finite presentation
$\unicode[STIX]{x1D70B}^{!}\mathscr{M}$ admits a finite presentation
We apply ![]() $\unicode[STIX]{x1D70B}_{\ast }$ to this latter sequence and use that
$\unicode[STIX]{x1D70B}_{\ast }$ to this latter sequence and use that ![]() $\unicode[STIX]{x1D70B}_{\ast }$ is exact (by (i)), together with 2.3.7 to obtain the finite presentation
$\unicode[STIX]{x1D70B}_{\ast }$ is exact (by (i)), together with 2.3.7 to obtain the finite presentation
The natural transformation ![]() $can$ induces a morphism from 2.3.9 to 2.3.10, and because
$can$ induces a morphism from 2.3.9 to 2.3.10, and because ![]() $can_{\mathscr{D}_{\mathfrak{X},k}^{\dagger }}$ is an isomorphism, so is
$can_{\mathscr{D}_{\mathfrak{X},k}^{\dagger }}$ is an isomorphism, so is ![]() $can_{\mathscr{M}}$.
$can_{\mathscr{M}}$.
In the reverse direction, let ![]() $\mathscr{M}^{\prime }$ be a coherent
$\mathscr{M}^{\prime }$ be a coherent ![]() $\mathscr{D}_{\mathfrak{X}^{\prime },k}^{\dagger }$-module. There is a map
$\mathscr{D}_{\mathfrak{X}^{\prime },k}^{\dagger }$-module. There is a map
sending ![]() $P\otimes x$ to
$P\otimes x$ to ![]() $Px$, which is natural in
$Px$, which is natural in ![]() $\mathscr{M}^{\prime }$. Whether this map is bijective can be decided locally on
$\mathscr{M}^{\prime }$. Whether this map is bijective can be decided locally on ![]() $\mathfrak{X}$ and we may assume that
$\mathfrak{X}$ and we may assume that ![]() $\mathfrak{X}_{0}$ is affine, and
$\mathfrak{X}_{0}$ is affine, and ![]() $\mathfrak{X}^{\prime }$ and
$\mathfrak{X}^{\prime }$ and ![]() $\mathfrak{X}$ are admissible blow-ups of
$\mathfrak{X}$ are admissible blow-ups of ![]() $\mathfrak{X}_{0}$. Since
$\mathfrak{X}_{0}$. Since ![]() $\unicode[STIX]{x1D70B}_{\ast }$ is exact, and using 2.2.29 over
$\unicode[STIX]{x1D70B}_{\ast }$ is exact, and using 2.2.29 over ![]() $\mathfrak{X}^{\prime }$, we are reduced to the case where
$\mathfrak{X}^{\prime }$, we are reduced to the case where ![]() $\mathscr{M}^{\prime }=\mathscr{D}_{\mathfrak{X}^{\prime },k}^{\dagger }$. In this case
$\mathscr{M}^{\prime }=\mathscr{D}_{\mathfrak{X}^{\prime },k}^{\dagger }$. In this case ![]() $\unicode[STIX]{x1D70B}^{!}\unicode[STIX]{x1D70B}_{\ast }\mathscr{D}_{\mathfrak{X}^{\prime },k}^{\dagger }\simeq \mathscr{D}_{\mathfrak{X}^{\prime },k}^{\dagger }$ by (i). From all of this, we can conclude that
$\unicode[STIX]{x1D70B}^{!}\unicode[STIX]{x1D70B}_{\ast }\mathscr{D}_{\mathfrak{X}^{\prime },k}^{\dagger }\simeq \mathscr{D}_{\mathfrak{X}^{\prime },k}^{\dagger }$ by (i). From all of this, we can conclude that ![]() $\unicode[STIX]{x1D70B}^{!}$ and
$\unicode[STIX]{x1D70B}^{!}$ and ![]() $\unicode[STIX]{x1D70B}_{\ast }$ are quasi-inverse functors. As
$\unicode[STIX]{x1D70B}_{\ast }$ are quasi-inverse functors. As ![]() $\unicode[STIX]{x1D70B}_{\ast }$ is exact on coherent
$\unicode[STIX]{x1D70B}_{\ast }$ is exact on coherent ![]() $\mathscr{D}_{\mathfrak{X}^{\prime },k}^{\dagger }$-modules,
$\mathscr{D}_{\mathfrak{X}^{\prime },k}^{\dagger }$-modules, ![]() $\unicode[STIX]{x1D70B}^{!}$ is exact on coherent
$\unicode[STIX]{x1D70B}^{!}$ is exact on coherent ![]() $\mathscr{D}_{\mathfrak{X},k}^{\dagger }$-modules.◻
$\mathscr{D}_{\mathfrak{X},k}^{\dagger }$-modules.◻
Corollary 2.3.11. In the situation of the preceding theorem, one has
As an application of the invariance theorem we can extend the local theorems A and B 2.2.6 and 2.2.15 to global statements, provided that the base ![]() $\mathfrak{X}_{0}$ is affine.Footnote 3.
$\mathfrak{X}_{0}$ is affine.Footnote 3.
Theorem 2.3.12. (Global theorems A and B over an affine base) Let ![]() $\mathfrak{X}_{0}$ be affine.
$\mathfrak{X}_{0}$ be affine.
(i) For any coherent
 $\widehat{\mathscr{D}}_{\mathfrak{X},\mathbb{Q}}^{(k,m)}$-module
$\widehat{\mathscr{D}}_{\mathfrak{X},\mathbb{Q}}^{(k,m)}$-module  $\mathscr{M}$ and for all
$\mathscr{M}$ and for all  $q>0$ one has
$q>0$ one has  $H^{q}(\mathfrak{X},\mathscr{M})=0$.
$H^{q}(\mathfrak{X},\mathscr{M})=0$.(ii) The functor
 $\unicode[STIX]{x1D6E4}(\mathfrak{X},-)$ is an equivalence between the category of coherent
$\unicode[STIX]{x1D6E4}(\mathfrak{X},-)$ is an equivalence between the category of coherent  $\widehat{\mathscr{D}}_{\mathfrak{X},\mathbb{Q}}^{(k,m)}$-modules and the category of coherent
$\widehat{\mathscr{D}}_{\mathfrak{X},\mathbb{Q}}^{(k,m)}$-modules and the category of coherent  $\unicode[STIX]{x1D6E4}(\mathfrak{X},\widehat{\mathscr{D}}_{\mathfrak{X},\mathbb{Q}}^{(k,m)})$-modules.
$\unicode[STIX]{x1D6E4}(\mathfrak{X},\widehat{\mathscr{D}}_{\mathfrak{X},\mathbb{Q}}^{(k,m)})$-modules.
The same statement holds for coherent modules over ![]() $\mathscr{D}_{\mathfrak{X},k}^{\dagger }$ and
$\mathscr{D}_{\mathfrak{X},k}^{\dagger }$ and ![]() $\unicode[STIX]{x1D6E4}(\mathfrak{X},\mathscr{D}_{\mathfrak{X},k}^{\dagger })$.
$\unicode[STIX]{x1D6E4}(\mathfrak{X},\mathscr{D}_{\mathfrak{X},k}^{\dagger })$.
Proof. Denote by ![]() $\unicode[STIX]{x1D70B}:\mathfrak{X}\rightarrow \mathfrak{X}_{0}$ the blow-up morphism. The functor
$\unicode[STIX]{x1D70B}:\mathfrak{X}\rightarrow \mathfrak{X}_{0}$ the blow-up morphism. The functor ![]() $\unicode[STIX]{x1D6E4}(\mathfrak{X},.)$ equals the composite of the two functors
$\unicode[STIX]{x1D6E4}(\mathfrak{X},.)$ equals the composite of the two functors ![]() $\unicode[STIX]{x1D70B}_{\ast }$ and
$\unicode[STIX]{x1D70B}_{\ast }$ and ![]() $\unicode[STIX]{x1D6E4}(\mathfrak{X}_{0},-)$. Hence the theorem follows from 2.3.8 and its corollary 2.3.11 and 2.2.15.◻
$\unicode[STIX]{x1D6E4}(\mathfrak{X}_{0},-)$. Hence the theorem follows from 2.3.8 and its corollary 2.3.11 and 2.2.15.◻
3 Coadmissible  $\mathscr{D}$-modules on
$\mathscr{D}$-modules on  $\mathfrak{X}$ and the Zariski–Riemann space
$\mathfrak{X}$ and the Zariski–Riemann space
We continue to denote throughout this section by ![]() $\mathfrak{X}_{0}$ a smooth formal
$\mathfrak{X}_{0}$ a smooth formal ![]() $\mathfrak{S}$-scheme, and we consider an admissible formal blow-up
$\mathfrak{S}$-scheme, and we consider an admissible formal blow-up
The purpose of the first subsection is to study projective systems ![]() $(\mathscr{M}_{k})_{k\geqslant k_{\mathfrak{X}}}$ of coherent modules
$(\mathscr{M}_{k})_{k\geqslant k_{\mathfrak{X}}}$ of coherent modules ![]() $\mathscr{M}_{k}$ over
$\mathscr{M}_{k}$ over ![]() $\mathscr{D}_{\mathfrak{X},k}^{\dagger }$, and to pass to their associated projective limits. In the second subsection we will then let
$\mathscr{D}_{\mathfrak{X},k}^{\dagger }$, and to pass to their associated projective limits. In the second subsection we will then let ![]() $\mathfrak{X}$ vary in the system of all admissible formal blow-ups of
$\mathfrak{X}$ vary in the system of all admissible formal blow-ups of ![]() $\mathfrak{X}_{0}$.
$\mathfrak{X}_{0}$.
3.1 Coadmissible  $\mathscr{D}$-modules on
$\mathscr{D}$-modules on  $\mathfrak{X}$
$\mathfrak{X}$
We make the general convention that ![]() $k$ always denotes an integer which is at least as large as
$k$ always denotes an integer which is at least as large as ![]() $k_{\mathfrak{X}}$.
$k_{\mathfrak{X}}$.
3.1.1 Fréchet–Stein algebras
Let ![]() $B$ be a noetherian
$B$ be a noetherian ![]() $K$-Banach algebra. We recall that any finitely generated
$K$-Banach algebra. We recall that any finitely generated ![]() $B$-module has a canonical structure as
$B$-module has a canonical structure as ![]() $B$-Banach module and any
$B$-Banach module and any ![]() $B$-linear map between two such modules is continuous. The topology can be defined as the quotient topology with respect to any chosen finite presentation of the module [Reference Schneider and Teitelbaum24, Proposition 2.1].
$B$-linear map between two such modules is continuous. The topology can be defined as the quotient topology with respect to any chosen finite presentation of the module [Reference Schneider and Teitelbaum24, Proposition 2.1].
We recall from [Reference Schneider and Teitelbaum24, Section 3] that a ![]() $K$-Fréchet algebra
$K$-Fréchet algebra ![]() $A$ is called Fréchet–Stein if there is a projective system
$A$ is called Fréchet–Stein if there is a projective system ![]() $(A_{k},A_{k+1}\rightarrow A_{k})_{k\in \mathbb{N}}$ of (left) noetherian
$(A_{k},A_{k+1}\rightarrow A_{k})_{k\in \mathbb{N}}$ of (left) noetherian ![]() $K$-Banach algebras
$K$-Banach algebras ![]() $A_{k}$ with (right) flat transition maps
$A_{k}$ with (right) flat transition maps ![]() $A_{k+1}\rightarrow A_{k}$, and an isomorphism of topological
$A_{k+1}\rightarrow A_{k}$, and an isomorphism of topological ![]() $K$-algebras
$K$-algebras ![]() $A\simeq \mathop{\varprojlim }\nolimits_{k}A_{k}$ such that each of the induced maps
$A\simeq \mathop{\varprojlim }\nolimits_{k}A_{k}$ such that each of the induced maps ![]() $A\rightarrow A_{k}$ has dense image. For the following definition we fix such an isomorphism. We denote by
$A\rightarrow A_{k}$ has dense image. For the following definition we fix such an isomorphism. We denote by ![]() ${\mathcal{C}}_{A}$ the full abelian subcategory of the category of all (left)
${\mathcal{C}}_{A}$ the full abelian subcategory of the category of all (left) ![]() $A$-modules consisting of the coadmissible
$A$-modules consisting of the coadmissible ![]() $A$-modules, as introduced in [Reference Schneider and Teitelbaum24]. For an
$A$-modules, as introduced in [Reference Schneider and Teitelbaum24]. For an ![]() $A$-module
$A$-module ![]() $M$ to be coadmissible means that there is a projective system
$M$ to be coadmissible means that there is a projective system ![]() $(M_{k},M_{k+1}\rightarrow M_{k})_{k\in \mathbb{N}}$, where each
$(M_{k},M_{k+1}\rightarrow M_{k})_{k\in \mathbb{N}}$, where each ![]() $M_{k}$ is a finitely generated
$M_{k}$ is a finitely generated ![]() $A_{k}$-module, such that
$A_{k}$-module, such that
(i) the transition map
 $M_{k+1}\rightarrow M_{k}$ is a homomorphism of
$M_{k+1}\rightarrow M_{k}$ is a homomorphism of  $A_{k+1}$-modules, and the induced map
$A_{k+1}$-modules, and the induced map  $A_{k}\otimes _{A_{k+1}}M_{k+1}\rightarrow M_{k}$ is an isomorphism of
$A_{k}\otimes _{A_{k+1}}M_{k+1}\rightarrow M_{k}$ is an isomorphism of  $A_{k}$-modules, and
$A_{k}$-modules, and(ii)
 $M$ is isomorphic to
$M$ is isomorphic to  $\mathop{\varprojlim }\nolimits_{k}M_{k}$ as an
$\mathop{\varprojlim }\nolimits_{k}M_{k}$ as an  $A$-module.
$A$-module.
(The projective limit is considered as an ![]() $A$-module via the fixed isomorphismFootnote 4
$A$-module via the fixed isomorphismFootnote 4 ![]() $A\simeq \mathop{\varprojlim }\nolimits_{k}A_{k}$.) We sometimes call
$A\simeq \mathop{\varprojlim }\nolimits_{k}A_{k}$.) We sometimes call ![]() $(M_{k})$ an
$(M_{k})$ an ![]() $(A_{k})$-sequence for
$(A_{k})$-sequence for ![]() $M$. For
$M$. For ![]() $M=\mathop{\varprojlim }\nolimits_{k}M_{k}\in {\mathcal{C}}_{A}$ we have that the image of
$M=\mathop{\varprojlim }\nolimits_{k}M_{k}\in {\mathcal{C}}_{A}$ we have that the image of ![]() $M\rightarrow M_{k}$ is dense with respect to the canonical topology for any
$M\rightarrow M_{k}$ is dense with respect to the canonical topology for any ![]() $k$, and
$k$, and ![]() $\varprojlim _{k}^{(1)}M_{k}=0$, see [Reference Schneider and Teitelbaum24, first theorem in Section 3].
$\varprojlim _{k}^{(1)}M_{k}=0$, see [Reference Schneider and Teitelbaum24, first theorem in Section 3].
3.1.2 The sheaf  $\mathscr{D}_{\mathfrak{X},\infty }$
$\mathscr{D}_{\mathfrak{X},\infty }$
We denote by
the projective limit of the system of sheaves ![]() $\mathscr{D}_{\mathfrak{X},k}^{\dagger }$. Then
$\mathscr{D}_{\mathfrak{X},k}^{\dagger }$. Then ![]() $\mathscr{D}_{\mathfrak{X},\infty }$ is again a sheaf of rings and for every open subset
$\mathscr{D}_{\mathfrak{X},\infty }$ is again a sheaf of rings and for every open subset ![]() $\mathfrak{V}\subset \mathfrak{X}$ we have
$\mathfrak{V}\subset \mathfrak{X}$ we have ![]() $\mathscr{D}_{\mathfrak{X},\infty }(\mathfrak{V})=\mathop{\varprojlim }\nolimits_{k}\mathscr{D}_{\mathfrak{X},k}^{\dagger }(\mathfrak{V})$.
$\mathscr{D}_{\mathfrak{X},\infty }(\mathfrak{V})=\mathop{\varprojlim }\nolimits_{k}\mathscr{D}_{\mathfrak{X},k}^{\dagger }(\mathfrak{V})$.
(i) The canonical morphism of sheaves
 $\widehat{\mathscr{D}}_{\mathfrak{X},\mathbb{Q}}^{(k,0)}\rightarrow \mathscr{D}_{\mathfrak{X},k}^{\dagger }$ induces an isomorphism
$\widehat{\mathscr{D}}_{\mathfrak{X},\mathbb{Q}}^{(k,0)}\rightarrow \mathscr{D}_{\mathfrak{X},k}^{\dagger }$ induces an isomorphism  $$\begin{eqnarray}\mathop{\varprojlim }\nolimits_{k}\widehat{\mathscr{D}}_{\mathfrak{X},\mathbb{Q}}^{(k,0)}\stackrel{\simeq }{\longrightarrow }\mathop{\varprojlim }\nolimits_{k}\mathscr{D}_{\mathfrak{X},k}^{\dagger }=\mathscr{D}_{\mathfrak{ X},\infty }.\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\varprojlim }\nolimits_{k}\widehat{\mathscr{D}}_{\mathfrak{X},\mathbb{Q}}^{(k,0)}\stackrel{\simeq }{\longrightarrow }\mathop{\varprojlim }\nolimits_{k}\mathscr{D}_{\mathfrak{X},k}^{\dagger }=\mathscr{D}_{\mathfrak{ X},\infty }.\end{eqnarray}$$(ii) For every affine open subset
 $\mathfrak{V}\subset \mathfrak{X}$ the isomorphism induced from (i) gives
$\mathfrak{V}\subset \mathfrak{X}$ the isomorphism induced from (i) gives $$\begin{eqnarray}\mathscr{D}_{\mathfrak{X},\infty }(\mathfrak{V})=\mathop{\varprojlim }\nolimits_{k}\widehat{\mathscr{D}}_{\mathfrak{X},\mathbb{Q}}^{(k,0)}(\mathfrak{V})\end{eqnarray}$$
$$\begin{eqnarray}\mathscr{D}_{\mathfrak{X},\infty }(\mathfrak{V})=\mathop{\varprojlim }\nolimits_{k}\widehat{\mathscr{D}}_{\mathfrak{X},\mathbb{Q}}^{(k,0)}(\mathfrak{V})\end{eqnarray}$$ $\mathscr{D}_{\mathfrak{X},\infty }(\mathfrak{V})$ the structure of a Fréchet–Stein algebra.
$\mathscr{D}_{\mathfrak{X},\infty }(\mathfrak{V})$ the structure of a Fréchet–Stein algebra.(iii) Let
 $\mathfrak{U}\subset \mathfrak{X}_{0}$ be an open affine subset which can be equipped with a system of étale coordinates
$\mathfrak{U}\subset \mathfrak{X}_{0}$ be an open affine subset which can be equipped with a system of étale coordinates  $x_{1},\ldots ,x_{M}$ and
$x_{1},\ldots ,x_{M}$ and  $\unicode[STIX]{x2202}_{1},\ldots ,\unicode[STIX]{x2202}_{M}$ the corresponding derivations. Then, for any affine open
$\unicode[STIX]{x2202}_{1},\ldots ,\unicode[STIX]{x2202}_{M}$ the corresponding derivations. Then, for any affine open  $\mathfrak{V}\subset \text{pr}^{-1}(\mathfrak{U})$ we have (3.1.5)where
$\mathfrak{V}\subset \text{pr}^{-1}(\mathfrak{U})$ we have (3.1.5)where $$\begin{eqnarray}\mathscr{D}_{\mathfrak{X},\infty }(\mathfrak{V})=\left\{\left.\mathop{\sum }_{\text{}\underline{\unicode[STIX]{x1D708}}}a_{\text{}\underline{\unicode[STIX]{x1D708}}}\text{}\underline{\unicode[STIX]{x2202}}^{\text{}\underline{\unicode[STIX]{x1D708}}}\,\right|\,a_{\text{}\underline{\unicode[STIX]{x1D708}}}\in {\mathcal{O}}_{\mathfrak{X},\mathbb{Q}}(\mathfrak{V}),\forall R>0:\lim _{|\text{}\underline{\unicode[STIX]{x1D708}}|\rightarrow \infty }\Vert a_{\text{}\underline{\unicode[STIX]{x1D708}}}\Vert R^{|\text{}\underline{\unicode[STIX]{x1D708}}|}=0\right\},\end{eqnarray}$$
$$\begin{eqnarray}\mathscr{D}_{\mathfrak{X},\infty }(\mathfrak{V})=\left\{\left.\mathop{\sum }_{\text{}\underline{\unicode[STIX]{x1D708}}}a_{\text{}\underline{\unicode[STIX]{x1D708}}}\text{}\underline{\unicode[STIX]{x2202}}^{\text{}\underline{\unicode[STIX]{x1D708}}}\,\right|\,a_{\text{}\underline{\unicode[STIX]{x1D708}}}\in {\mathcal{O}}_{\mathfrak{X},\mathbb{Q}}(\mathfrak{V}),\forall R>0:\lim _{|\text{}\underline{\unicode[STIX]{x1D708}}|\rightarrow \infty }\Vert a_{\text{}\underline{\unicode[STIX]{x1D708}}}\Vert R^{|\text{}\underline{\unicode[STIX]{x1D708}}|}=0\right\},\end{eqnarray}$$ $\Vert \cdot \Vert$ is any submultiplicative Banach space norm on
$\Vert \cdot \Vert$ is any submultiplicative Banach space norm on  ${\mathcal{O}}_{\mathfrak{X},\mathbb{Q}}(\mathfrak{V})$.
${\mathcal{O}}_{\mathfrak{X},\mathbb{Q}}(\mathfrak{V})$.(iv) Let
 $\mathfrak{X}^{\prime }\rightarrow \mathfrak{X}_{0}$ be another admissible formal blow-up, and let
$\mathfrak{X}^{\prime }\rightarrow \mathfrak{X}_{0}$ be another admissible formal blow-up, and let  $\unicode[STIX]{x1D70B}:\mathfrak{X}^{\prime }\rightarrow \mathfrak{X}$ be a morphism over
$\unicode[STIX]{x1D70B}:\mathfrak{X}^{\prime }\rightarrow \mathfrak{X}$ be a morphism over  $\mathfrak{X}_{0}$. Then the canonical isomorphisms
$\mathfrak{X}_{0}$. Then the canonical isomorphisms  $\unicode[STIX]{x1D70B}_{\ast }\mathscr{D}_{\mathfrak{X}^{\prime },k}^{\dagger }=\mathscr{D}_{\mathfrak{X},k}^{\dagger }$, for
$\unicode[STIX]{x1D70B}_{\ast }\mathscr{D}_{\mathfrak{X}^{\prime },k}^{\dagger }=\mathscr{D}_{\mathfrak{X},k}^{\dagger }$, for  $k\geqslant \max \{k_{\mathfrak{X}^{\prime }},k_{\mathfrak{X}}\}$, see 2.3.8, give rise to a canonical isomorphism (3.1.6)
$k\geqslant \max \{k_{\mathfrak{X}^{\prime }},k_{\mathfrak{X}}\}$, see 2.3.8, give rise to a canonical isomorphism (3.1.6) $$\begin{eqnarray}\unicode[STIX]{x1D70B}_{\ast }\mathscr{D}_{\mathfrak{X}^{\prime },\infty }=\mathscr{D}_{\mathfrak{X},\infty }.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70B}_{\ast }\mathscr{D}_{\mathfrak{X}^{\prime },\infty }=\mathscr{D}_{\mathfrak{X},\infty }.\end{eqnarray}$$
Proof. Take an affine open ![]() $\mathfrak{V}\subset \mathfrak{X}$. We deduce from the Proposition 2.2.22 that the projective systems of
$\mathfrak{V}\subset \mathfrak{X}$. We deduce from the Proposition 2.2.22 that the projective systems of ![]() $K$-algebras
$K$-algebras ![]() $\mathscr{D}_{\mathfrak{X},k}^{\dagger }(\mathfrak{V})$ and
$\mathscr{D}_{\mathfrak{X},k}^{\dagger }(\mathfrak{V})$ and ![]() $\widehat{\mathscr{D}}_{\mathfrak{X},\mathbb{Q}}^{(k,0)}(\mathfrak{V})$ are equivalent. This proves (i). For (ii), note that the transition map
$\widehat{\mathscr{D}}_{\mathfrak{X},\mathbb{Q}}^{(k,0)}(\mathfrak{V})$ are equivalent. This proves (i). For (ii), note that the transition map ![]() $\widehat{\mathscr{D}}_{\mathfrak{X},\mathbb{Q}}^{(k+1,0)}(\mathfrak{V})\rightarrow \widehat{\mathscr{D}}_{\mathfrak{X},\mathbb{Q}}^{(k,0)}(\mathfrak{V})$ is a flat homomorphism between noetherian Banach algebras, according to Propositions 2.2.16 and 2.2.2. Moreover, each ring
$\widehat{\mathscr{D}}_{\mathfrak{X},\mathbb{Q}}^{(k+1,0)}(\mathfrak{V})\rightarrow \widehat{\mathscr{D}}_{\mathfrak{X},\mathbb{Q}}^{(k,0)}(\mathfrak{V})$ is a flat homomorphism between noetherian Banach algebras, according to Propositions 2.2.16 and 2.2.2. Moreover, each ring ![]() $\widehat{\mathscr{D}}_{\mathfrak{X},\mathbb{Q}}^{(k,0)}(\mathfrak{V})$ contains the local sections over
$\widehat{\mathscr{D}}_{\mathfrak{X},\mathbb{Q}}^{(k,0)}(\mathfrak{V})$ contains the local sections over ![]() $\mathfrak{V}$ of the ring of algebraic (finite order) differential operators
$\mathfrak{V}$ of the ring of algebraic (finite order) differential operators ![]() $\mathscr{D}_{\mathfrak{X},\mathbb{Q}}=\text{pr}^{\ast }\mathscr{D}_{\mathfrak{X}_{0},\mathbb{Q}}$. Hence, each induced map
$\mathscr{D}_{\mathfrak{X},\mathbb{Q}}=\text{pr}^{\ast }\mathscr{D}_{\mathfrak{X}_{0},\mathbb{Q}}$. Hence, each induced map ![]() $\mathscr{D}_{\mathfrak{X},\infty }(\mathfrak{V})\rightarrow \widehat{\mathscr{D}}_{\mathfrak{X},\mathbb{Q}}^{(k,0)}(\mathfrak{V})$ has dense image, as required. To prove (iii), we assume additionally
$\mathscr{D}_{\mathfrak{X},\infty }(\mathfrak{V})\rightarrow \widehat{\mathscr{D}}_{\mathfrak{X},\mathbb{Q}}^{(k,0)}(\mathfrak{V})$ has dense image, as required. To prove (iii), we assume additionally ![]() $\mathfrak{V}\subset \text{pr}^{-1}\mathfrak{U}$. By part (i), is then enough to show
$\mathfrak{V}\subset \text{pr}^{-1}\mathfrak{U}$. By part (i), is then enough to show
Denote by ![]() $E$ the right-hand side of the preceding equality. Recall that
$E$ the right-hand side of the preceding equality. Recall that
Let ![]() $P=\sum _{\text{}\underline{\unicode[STIX]{x1D708}}}a_{\text{}\underline{\unicode[STIX]{x1D708}}}\text{}\underline{\unicode[STIX]{x2202}}^{\text{}\underline{\unicode[STIX]{x1D708}}}\,\in E$. Since all Banach algebra norms over
$P=\sum _{\text{}\underline{\unicode[STIX]{x1D708}}}a_{\text{}\underline{\unicode[STIX]{x1D708}}}\text{}\underline{\unicode[STIX]{x2202}}^{\text{}\underline{\unicode[STIX]{x1D708}}}\,\in E$. Since all Banach algebra norms over ![]() ${\mathcal{O}}_{\mathfrak{X},\mathbb{Q}}(\mathfrak{V})$ are equivalent, we can use the
${\mathcal{O}}_{\mathfrak{X},\mathbb{Q}}(\mathfrak{V})$ are equivalent, we can use the ![]() $p$-adic norm
$p$-adic norm ![]() $|\cdot |_{p}$ of
$|\cdot |_{p}$ of ![]() ${\mathcal{O}}_{\mathfrak{X},\mathbb{Q}}(\mathfrak{V})$ relatively to the lattice
${\mathcal{O}}_{\mathfrak{X},\mathbb{Q}}(\mathfrak{V})$ relatively to the lattice ![]() ${\mathcal{O}}_{\mathfrak{X}}(\mathfrak{V})$. Fix
${\mathcal{O}}_{\mathfrak{X}}(\mathfrak{V})$. Fix ![]() $k\in \mathbb{N}$ and define
$k\in \mathbb{N}$ and define
then, using the ramification index ![]() $e$ of the extension
$e$ of the extension ![]() $L/\mathbb{Q}_{p}$, we get that
$L/\mathbb{Q}_{p}$, we get that
Thus ![]() $P=\sum _{\text{}\underline{\unicode[STIX]{x1D708}}}\unicode[STIX]{x1D71B}^{k|\text{}\underline{\unicode[STIX]{x1D708}}|}b_{\text{}\underline{\unicode[STIX]{x1D708}}}\text{}\underline{\unicode[STIX]{x2202}}^{\text{}\underline{\unicode[STIX]{x1D708}}}\in \widehat{\mathscr{D}}_{\mathfrak{X},\mathbb{Q}}^{(k,0)}(\mathfrak{V})$. Conversely, let
$P=\sum _{\text{}\underline{\unicode[STIX]{x1D708}}}\unicode[STIX]{x1D71B}^{k|\text{}\underline{\unicode[STIX]{x1D708}}|}b_{\text{}\underline{\unicode[STIX]{x1D708}}}\text{}\underline{\unicode[STIX]{x2202}}^{\text{}\underline{\unicode[STIX]{x1D708}}}\in \widehat{\mathscr{D}}_{\mathfrak{X},\mathbb{Q}}^{(k,0)}(\mathfrak{V})$. Conversely, let ![]() $P=\sum _{\text{}\underline{\unicode[STIX]{x1D708}}}a_{\text{}\underline{\unicode[STIX]{x1D708}}}\text{}\underline{\unicode[STIX]{x2202}}^{\text{}\underline{\unicode[STIX]{x1D708}}}\,\in \mathop{\varprojlim }\nolimits_{k}\widehat{\mathscr{D}}_{\mathfrak{X},\mathbb{Q}}^{(k,0)}(\mathfrak{V})$ and
$P=\sum _{\text{}\underline{\unicode[STIX]{x1D708}}}a_{\text{}\underline{\unicode[STIX]{x1D708}}}\text{}\underline{\unicode[STIX]{x2202}}^{\text{}\underline{\unicode[STIX]{x1D708}}}\,\in \mathop{\varprojlim }\nolimits_{k}\widehat{\mathscr{D}}_{\mathfrak{X},\mathbb{Q}}^{(k,0)}(\mathfrak{V})$ and ![]() $R>0$. Choose
$R>0$. Choose ![]() $k>0$ such that
$k>0$ such that
Since ![]() $P=\sum _{\text{}\underline{\unicode[STIX]{x1D708}}}\unicode[STIX]{x1D71B}^{k|\text{}\underline{\unicode[STIX]{x1D708}}|}b_{\text{}\underline{\unicode[STIX]{x1D708}}}\text{}\underline{\unicode[STIX]{x2202}}^{\text{}\underline{\unicode[STIX]{x1D708}}}\,\in \widehat{\mathscr{D}}_{\mathfrak{X},\mathbb{Q}}^{(k,0)}(\mathfrak{V})$,
$P=\sum _{\text{}\underline{\unicode[STIX]{x1D708}}}\unicode[STIX]{x1D71B}^{k|\text{}\underline{\unicode[STIX]{x1D708}}|}b_{\text{}\underline{\unicode[STIX]{x1D708}}}\text{}\underline{\unicode[STIX]{x2202}}^{\text{}\underline{\unicode[STIX]{x1D708}}}\,\in \widehat{\mathscr{D}}_{\mathfrak{X},\mathbb{Q}}^{(k,0)}(\mathfrak{V})$, ![]() $|b_{\text{}\underline{\unicode[STIX]{x1D708}}}|_{p}\rightarrow 0$, thus
$|b_{\text{}\underline{\unicode[STIX]{x1D708}}}|_{p}\rightarrow 0$, thus
proving that ![]() $P\in E$, as required for (iii).
$P\in E$, as required for (iii).
Let us prove (iv). Let ![]() $\mathfrak{V}\subset \mathfrak{X}$, then from part (i) of Proposition 2.3.8, we know that
$\mathfrak{V}\subset \mathfrak{X}$, then from part (i) of Proposition 2.3.8, we know that ![]() $\mathscr{D}_{\mathfrak{X},k}^{\dagger }(\mathfrak{V})=\mathscr{D}_{\mathfrak{X}^{\prime },k}^{\dagger }(\unicode[STIX]{x1D70B}^{-1}(\mathfrak{V}))$. We deduce from this the equations
$\mathscr{D}_{\mathfrak{X},k}^{\dagger }(\mathfrak{V})=\mathscr{D}_{\mathfrak{X}^{\prime },k}^{\dagger }(\unicode[STIX]{x1D70B}^{-1}(\mathfrak{V}))$. We deduce from this the equations
Let us remark that the sheaf ![]() $\mathscr{D}_{\mathfrak{X},\infty }$ does only depend on the formal scheme
$\mathscr{D}_{\mathfrak{X},\infty }$ does only depend on the formal scheme ![]() $\mathfrak{X}$ and not on the blow-up morphism
$\mathfrak{X}$ and not on the blow-up morphism ![]() $\text{pr}$. Indeed, suppose that
$\text{pr}$. Indeed, suppose that ![]() $\mathfrak{X}$ is realized as the blow-up of two smooth formal schemes
$\mathfrak{X}$ is realized as the blow-up of two smooth formal schemes ![]() $\mathfrak{X}_{0}$ and
$\mathfrak{X}_{0}$ and ![]() $\mathfrak{X}_{0}^{\prime }$. We may assume that
$\mathfrak{X}_{0}^{\prime }$. We may assume that ![]() $\mathfrak{X}_{0}$ and
$\mathfrak{X}_{0}$ and ![]() $\mathfrak{X}_{0}^{\prime }$ are affine and endowed with coordinates. To any given
$\mathfrak{X}_{0}^{\prime }$ are affine and endowed with coordinates. To any given ![]() $k$, there exists
$k$, there exists ![]() $k^{\prime }\geqslant k$ such that
$k^{\prime }\geqslant k$ such that ![]() $\unicode[STIX]{x1D71B}^{k^{\prime }}\text{\{}^{\ast }\mathscr{T}_{\mathfrak{X}_{0}^{\prime }}$ is contained in
$\unicode[STIX]{x1D71B}^{k^{\prime }}\text{\{}^{\ast }\mathscr{T}_{\mathfrak{X}_{0}^{\prime }}$ is contained in ![]() $\unicode[STIX]{x1D71B}^{k}\text{pr}^{\ast }\mathscr{T}_{\mathfrak{X}_{0}}$, inside the tangent sheaf
$\unicode[STIX]{x1D71B}^{k}\text{pr}^{\ast }\mathscr{T}_{\mathfrak{X}_{0}}$, inside the tangent sheaf ![]() $\mathscr{T}_{\mathfrak{X}_{\mathbb{Q}}}$ of the generic fiber
$\mathscr{T}_{\mathfrak{X}_{\mathbb{Q}}}$ of the generic fiber ![]() $\mathfrak{X}_{\mathbb{Q}}$. The two projective systems
$\mathfrak{X}_{\mathbb{Q}}$. The two projective systems ![]() $(\widehat{\mathscr{D}}_{\mathfrak{X},\mathbb{Q}}^{(k,0)})_{k\geqslant k_{\mathfrak{X}}}$ (relative to the blow-up morphisms
$(\widehat{\mathscr{D}}_{\mathfrak{X},\mathbb{Q}}^{(k,0)})_{k\geqslant k_{\mathfrak{X}}}$ (relative to the blow-up morphisms ![]() $\text{pr}$ and
$\text{pr}$ and ![]() $\text{\{}$) are therefore cofinal and their projective limits are therefore isomorphic.
$\text{\{}$) are therefore cofinal and their projective limits are therefore isomorphic.
For every affine open subset ![]() $\mathfrak{V}\subset \mathfrak{X}$ we have, according to the preceding proposition, the abelian category of coadmissible
$\mathfrak{V}\subset \mathfrak{X}$ we have, according to the preceding proposition, the abelian category of coadmissible ![]() $\mathscr{D}_{\mathfrak{X},\infty }(\mathfrak{V})$-modules
$\mathscr{D}_{\mathfrak{X},\infty }(\mathfrak{V})$-modules ![]() ${\mathcal{C}}_{\mathscr{D}_{\mathfrak{X},\infty }(\mathfrak{V})}$. We give an alternative description of these modules using the projective system of algebras
${\mathcal{C}}_{\mathscr{D}_{\mathfrak{X},\infty }(\mathfrak{V})}$. We give an alternative description of these modules using the projective system of algebras ![]() $\mathscr{D}_{\mathfrak{X},k}^{\dagger }(\mathfrak{V})$.
$\mathscr{D}_{\mathfrak{X},k}^{\dagger }(\mathfrak{V})$.
Proposition 3.1.7. Let ![]() $\mathfrak{V}\subset \mathfrak{X}$ be an affine open. A
$\mathfrak{V}\subset \mathfrak{X}$ be an affine open. A ![]() $\mathscr{D}_{\mathfrak{X},\infty }(\mathfrak{V})$-module
$\mathscr{D}_{\mathfrak{X},\infty }(\mathfrak{V})$-module ![]() $M$ is coadmissible if and only if there is a projective system
$M$ is coadmissible if and only if there is a projective system ![]() $(M_{k},M_{k+1}\rightarrow M_{k})$, where each
$(M_{k},M_{k+1}\rightarrow M_{k})$, where each ![]() $M_{k}$ is a finitely presented
$M_{k}$ is a finitely presented ![]() $\mathscr{D}_{\mathfrak{X},k}^{\dagger }(\mathfrak{V})$-module, such that
$\mathscr{D}_{\mathfrak{X},k}^{\dagger }(\mathfrak{V})$-module, such that
(i) the transition map
 $M_{k+1}\rightarrow M_{k}$ is
$M_{k+1}\rightarrow M_{k}$ is  $\mathscr{D}_{\mathfrak{X},k+1}^{\dagger }(\mathfrak{V})$-linear and induces an isomorphism of
$\mathscr{D}_{\mathfrak{X},k+1}^{\dagger }(\mathfrak{V})$-linear and induces an isomorphism of $$\begin{eqnarray}\mathscr{D}_{\mathfrak{X},k}^{\dagger }(\mathfrak{V})\otimes _{\mathscr{ D}_{\mathfrak{X},k+1}^{\dagger }(\mathfrak{V})}M_{k+1}\simeq M_{k}\end{eqnarray}$$
$$\begin{eqnarray}\mathscr{D}_{\mathfrak{X},k}^{\dagger }(\mathfrak{V})\otimes _{\mathscr{ D}_{\mathfrak{X},k+1}^{\dagger }(\mathfrak{V})}M_{k+1}\simeq M_{k}\end{eqnarray}$$ $\mathscr{D}_{\mathfrak{X},k}^{\dagger }(\mathfrak{V})$-modules, and
$\mathscr{D}_{\mathfrak{X},k}^{\dagger }(\mathfrak{V})$-modules, and(ii)
 $M$ is isomorphic to
$M$ is isomorphic to  $\mathop{\varprojlim }\nolimits_{k}M_{k}$ as an
$\mathop{\varprojlim }\nolimits_{k}M_{k}$ as an  $\mathscr{D}_{\mathfrak{X},\infty }(\mathfrak{V})$-module.
$\mathscr{D}_{\mathfrak{X},\infty }(\mathfrak{V})$-module.
Proof. This follows from the discussion given in the proof of [Reference Emerton11, Proposition 1.2.9] and we explain the main points. We write ![]() $A_{k}=\widehat{\mathscr{D}}_{\mathfrak{X},\mathbb{Q}}^{(k,0)}(\mathfrak{V})$ and
$A_{k}=\widehat{\mathscr{D}}_{\mathfrak{X},\mathbb{Q}}^{(k,0)}(\mathfrak{V})$ and ![]() $B_{k}=\mathscr{D}_{\mathfrak{X},k}^{\dagger }(\mathfrak{V})$. We have strictly increasing functions
$B_{k}=\mathscr{D}_{\mathfrak{X},k}^{\dagger }(\mathfrak{V})$. We have strictly increasing functions ![]() $\unicode[STIX]{x1D719}$ and
$\unicode[STIX]{x1D719}$ and ![]() $\unicode[STIX]{x1D713}$ mapping
$\unicode[STIX]{x1D713}$ mapping ![]() $\mathbb{N}$ to itself such that the map
$\mathbb{N}$ to itself such that the map ![]() $A\rightarrow A_{k}$ (resp.
$A\rightarrow A_{k}$ (resp. ![]() $A\rightarrow B_{k}$) factors through the map
$A\rightarrow B_{k}$) factors through the map ![]() $A\rightarrow B_{\unicode[STIX]{x1D719}(k)}$ (resp.
$A\rightarrow B_{\unicode[STIX]{x1D719}(k)}$ (resp. ![]() $A\rightarrow A_{\unicode[STIX]{x1D713}(k)}$). Indeed, we may take
$A\rightarrow A_{\unicode[STIX]{x1D713}(k)}$). Indeed, we may take ![]() $\unicode[STIX]{x1D719}(k)=k+e^{\prime }$ and
$\unicode[STIX]{x1D719}(k)=k+e^{\prime }$ and ![]() $\unicode[STIX]{x1D713}(k)=k$ with
$\unicode[STIX]{x1D713}(k)=k$ with ![]() $e^{\prime }\geqslant \frac{e}{p-1}$ a fixed number, according to the Proposition 2.2.22. In particular, the systems of
$e^{\prime }\geqslant \frac{e}{p-1}$ a fixed number, according to the Proposition 2.2.22. In particular, the systems of ![]() $K$-algebras
$K$-algebras ![]() $A_{k}$ and
$A_{k}$ and ![]() $B_{k}$ are equivalent. Now suppose
$B_{k}$ are equivalent. Now suppose ![]() $N$ is coadmissible with system of Banach modules
$N$ is coadmissible with system of Banach modules ![]() $N_{k}$. For
$N_{k}$. For ![]() $k\geqslant 1$ define the finitely presented
$k\geqslant 1$ define the finitely presented ![]() $B_{k}$-module
$B_{k}$-module
Since ![]() $\unicode[STIX]{x1D713}(k+1)\geqslant \unicode[STIX]{x1D713}(k)$, the map
$\unicode[STIX]{x1D713}(k+1)\geqslant \unicode[STIX]{x1D713}(k)$, the map ![]() $N_{\unicode[STIX]{x1D713}(k+1)}\rightarrow N_{\unicode[STIX]{x1D713}(k)}$ induces a map
$N_{\unicode[STIX]{x1D713}(k+1)}\rightarrow N_{\unicode[STIX]{x1D713}(k)}$ induces a map ![]() $M_{k+1}\rightarrow M_{k}$ and then a map
$M_{k+1}\rightarrow M_{k}$ and then a map ![]() $B_{k}\otimes _{B_{k+1}}M_{k+1}\rightarrow M_{k}$. This map is bijective as follows from the diagram presented in the proof of [Reference Emerton11, Proposition 1.2.9]. Moreover, the projection map
$B_{k}\otimes _{B_{k+1}}M_{k+1}\rightarrow M_{k}$. This map is bijective as follows from the diagram presented in the proof of [Reference Emerton11, Proposition 1.2.9]. Moreover, the projection map ![]() $M\rightarrow N_{\unicode[STIX]{x1D713}(k)}$ induces a
$M\rightarrow N_{\unicode[STIX]{x1D713}(k)}$ induces a ![]() $A$-linear map
$A$-linear map
compatible with ![]() $M_{k+1}\rightarrow M_{k}$. This gives an
$M_{k+1}\rightarrow M_{k}$. This gives an ![]() $A$-linear map
$A$-linear map ![]() $M\rightarrow \mathop{\varprojlim }\nolimits_{k}M_{k}$ and it remains to see that it is bijective. We have the natural map
$M\rightarrow \mathop{\varprojlim }\nolimits_{k}M_{k}$ and it remains to see that it is bijective. We have the natural map ![]() $N_{\unicode[STIX]{x1D713}(k)}\rightarrow M_{k}$. On the other hand,
$N_{\unicode[STIX]{x1D713}(k)}\rightarrow M_{k}$. On the other hand, ![]() $\unicode[STIX]{x1D713}(\unicode[STIX]{x1D719}(k))\geqslant k$ such that there is a map
$\unicode[STIX]{x1D713}(\unicode[STIX]{x1D719}(k))\geqslant k$ such that there is a map
using the map ![]() $B_{\unicode[STIX]{x1D719}(k)}\rightarrow A_{k}$. Hence the systems
$B_{\unicode[STIX]{x1D719}(k)}\rightarrow A_{k}$. Hence the systems ![]() $(M_{k})$ and
$(M_{k})$ and ![]() $(N_{k})$ are equivalent and
$(N_{k})$ are equivalent and
This shows that the system ![]() $(M_{k})$ is as required for
$(M_{k})$ is as required for ![]() $M$. Conversely, starting with a module
$M$. Conversely, starting with a module ![]() $M$ and such a system
$M$ and such a system ![]() $(M_{k})$ the coadmissibility of
$(M_{k})$ the coadmissibility of ![]() $M$ follows with the same argument.◻
$M$ follows with the same argument.◻
Definition 3.1.8. A ![]() $\mathscr{D}_{\mathfrak{X},\infty }$-module
$\mathscr{D}_{\mathfrak{X},\infty }$-module ![]() $\mathscr{M}$ is called coadmissible if there is a projective system
$\mathscr{M}$ is called coadmissible if there is a projective system
where ![]() $\mathscr{M}_{k}$ is a coherent
$\mathscr{M}_{k}$ is a coherent ![]() $\widehat{\mathscr{D}}_{\mathfrak{X},\mathbb{Q}}^{(k,0)}$-module, such that
$\widehat{\mathscr{D}}_{\mathfrak{X},\mathbb{Q}}^{(k,0)}$-module, such that
(i) the transition map
 $\mathscr{M}_{k+1}\rightarrow \mathscr{M}_{k}$ is
$\mathscr{M}_{k+1}\rightarrow \mathscr{M}_{k}$ is  $\widehat{\mathscr{D}}_{\mathfrak{X},\mathbb{Q}}^{(k+1,0)}$-linear and the induced map (3.1.9)is an isomorphism as
$\widehat{\mathscr{D}}_{\mathfrak{X},\mathbb{Q}}^{(k+1,0)}$-linear and the induced map (3.1.9)is an isomorphism as $$\begin{eqnarray}\widehat{\mathscr{D}}_{\mathfrak{X},\mathbb{Q}}^{(k,0)}\otimes _{\widehat{\mathscr{ D}}_{\mathfrak{X},\mathbb{Q}}^{(k+1,0)}}\mathscr{M}_{k+1}\longrightarrow \mathscr{M}_{k}\end{eqnarray}$$
$$\begin{eqnarray}\widehat{\mathscr{D}}_{\mathfrak{X},\mathbb{Q}}^{(k,0)}\otimes _{\widehat{\mathscr{ D}}_{\mathfrak{X},\mathbb{Q}}^{(k+1,0)}}\mathscr{M}_{k+1}\longrightarrow \mathscr{M}_{k}\end{eqnarray}$$ $\widehat{\mathscr{D}}_{\mathfrak{X},\mathbb{Q}}^{(k,0)}$-modules, and
$\widehat{\mathscr{D}}_{\mathfrak{X},\mathbb{Q}}^{(k,0)}$-modules, and(ii)
 $\mathscr{M}$ is isomorphic to
$\mathscr{M}$ is isomorphic to  $\mathop{\varprojlim }\nolimits_{k}\mathscr{M}_{k}$ as
$\mathop{\varprojlim }\nolimits_{k}\mathscr{M}_{k}$ as  $\mathscr{D}_{\mathfrak{X},\infty }$-module.
$\mathscr{D}_{\mathfrak{X},\infty }$-module.
We denote by
the full subcategory of coadmissible ![]() $\mathscr{D}_{\mathfrak{X},\infty }$-modules in the category of all
$\mathscr{D}_{\mathfrak{X},\infty }$-modules in the category of all ![]() $\mathscr{D}_{\mathfrak{X},\infty }$-modules.
$\mathscr{D}_{\mathfrak{X},\infty }$-modules.
Proposition 3.1.10. A ![]() $\mathscr{D}_{\mathfrak{X},\infty }$-module
$\mathscr{D}_{\mathfrak{X},\infty }$-module ![]() $\mathscr{M}$ is coadmissible if and only if there is a projective system
$\mathscr{M}$ is coadmissible if and only if there is a projective system ![]() $(\mathscr{M}_{k},\mathscr{M}_{k+1}\rightarrow \mathscr{M}_{k})_{k\geqslant k_{\mathfrak{X}}}$, where
$(\mathscr{M}_{k},\mathscr{M}_{k+1}\rightarrow \mathscr{M}_{k})_{k\geqslant k_{\mathfrak{X}}}$, where ![]() $\mathscr{M}_{k}$ is a coherent
$\mathscr{M}_{k}$ is a coherent ![]() $\mathscr{D}_{\mathfrak{X},k}^{\dagger }$-module, such that
$\mathscr{D}_{\mathfrak{X},k}^{\dagger }$-module, such that
(i) the transition map
 $\mathscr{M}_{k+1}\rightarrow \mathscr{M}_{k}$ is
$\mathscr{M}_{k+1}\rightarrow \mathscr{M}_{k}$ is  $\mathscr{D}_{\mathfrak{X},k+1}^{\dagger }$-linear and the induced morphism of sheaves (3.1.11)is an isomorphism of
$\mathscr{D}_{\mathfrak{X},k+1}^{\dagger }$-linear and the induced morphism of sheaves (3.1.11)is an isomorphism of $$\begin{eqnarray}\mathscr{D}_{\mathfrak{X},k}^{\dagger }\otimes _{\mathscr{ D}_{\mathfrak{X},k+1}^{\dagger }}\mathscr{M}_{k+1}\longrightarrow \mathscr{M}_{k}\end{eqnarray}$$
$$\begin{eqnarray}\mathscr{D}_{\mathfrak{X},k}^{\dagger }\otimes _{\mathscr{ D}_{\mathfrak{X},k+1}^{\dagger }}\mathscr{M}_{k+1}\longrightarrow \mathscr{M}_{k}\end{eqnarray}$$ $\mathscr{D}_{\mathfrak{X},k}^{\dagger }$-modules, and
$\mathscr{D}_{\mathfrak{X},k}^{\dagger }$-modules, and(ii)
 $\mathscr{M}$ is isomorphic to
$\mathscr{M}$ is isomorphic to  $\mathop{\varprojlim }\nolimits_{k}\mathscr{M}_{k}$ as
$\mathop{\varprojlim }\nolimits_{k}\mathscr{M}_{k}$ as  $\mathscr{D}_{\mathfrak{X},\infty }$-module.
$\mathscr{D}_{\mathfrak{X},\infty }$-module.
Proof. This follows literally as for the modules of local sections, see Proposition 3.1.7, taking into account that Proposition 2.2.22 holds on the level of sheaves. ◻
The following statement is a version of the invariance Theorem 2.3.8 for coadmissible modules.
Proposition 3.1.12. Let ![]() $\mathfrak{X}^{\prime }\rightarrow \mathfrak{X}_{0}$ be another admissible formal blow-up, and let
$\mathfrak{X}^{\prime }\rightarrow \mathfrak{X}_{0}$ be another admissible formal blow-up, and let ![]() $\unicode[STIX]{x1D70B}:\mathfrak{X}^{\prime }\rightarrow \mathfrak{X}$ be a morphism over
$\unicode[STIX]{x1D70B}:\mathfrak{X}^{\prime }\rightarrow \mathfrak{X}$ be a morphism over ![]() $\mathfrak{X}_{0}$. Then, for every coadmissible
$\mathfrak{X}_{0}$. Then, for every coadmissible ![]() $\mathscr{D}_{\mathfrak{X}^{\prime },\infty }$-module
$\mathscr{D}_{\mathfrak{X}^{\prime },\infty }$-module ![]() $\mathscr{M}$ the sheaf
$\mathscr{M}$ the sheaf ![]() $\unicode[STIX]{x1D70B}_{\ast }\mathscr{M}$ is a coadmissible
$\unicode[STIX]{x1D70B}_{\ast }\mathscr{M}$ is a coadmissible ![]() $\mathscr{D}_{\mathfrak{X},\infty }$-module via the isomorphism
$\mathscr{D}_{\mathfrak{X},\infty }$-module via the isomorphism ![]() $\unicode[STIX]{x1D70B}_{\ast }\mathscr{D}_{\mathfrak{X}^{\prime },\infty }=\mathscr{D}_{\mathfrak{X},\infty }$. Moreover, one has an equivalence of categories
$\unicode[STIX]{x1D70B}_{\ast }\mathscr{D}_{\mathfrak{X}^{\prime },\infty }=\mathscr{D}_{\mathfrak{X},\infty }$. Moreover, one has an equivalence of categories
Proof. Write ![]() $\mathscr{M}=\mathop{\varprojlim }\nolimits_{k}\mathscr{M}_{k}$ with coherent
$\mathscr{M}=\mathop{\varprojlim }\nolimits_{k}\mathscr{M}_{k}$ with coherent ![]() $\mathscr{D}_{\mathfrak{X}^{\prime },k}^{\dagger }$-modules
$\mathscr{D}_{\mathfrak{X}^{\prime },k}^{\dagger }$-modules ![]() $\mathscr{M}_{k}$. By 2.3.8 we know that each sheaf
$\mathscr{M}_{k}$. By 2.3.8 we know that each sheaf ![]() $\unicode[STIX]{x1D70B}_{\ast }(\mathscr{M}_{k})$ is a coherent
$\unicode[STIX]{x1D70B}_{\ast }(\mathscr{M}_{k})$ is a coherent ![]() $\mathscr{D}_{\mathfrak{X},k}^{\dagger }$-module. Moreover,
$\mathscr{D}_{\mathfrak{X},k}^{\dagger }$-module. Moreover, ![]() $\unicode[STIX]{x1D70B}_{\ast }(\mathscr{M})=\mathop{\varprojlim }\nolimits_{k}\unicode[STIX]{x1D70B}_{\ast }(\mathscr{M}_{k})$, and
$\unicode[STIX]{x1D70B}_{\ast }(\mathscr{M})=\mathop{\varprojlim }\nolimits_{k}\unicode[STIX]{x1D70B}_{\ast }(\mathscr{M}_{k})$, and
Note here that the exact functor ![]() $\unicode[STIX]{x1D70B}_{\ast }$, see 2.3.8, indeed commutes with the tensor product: this may be checked over an open affine
$\unicode[STIX]{x1D70B}_{\ast }$, see 2.3.8, indeed commutes with the tensor product: this may be checked over an open affine ![]() $\mathfrak{V}\subseteq \mathfrak{X}^{\prime }$ where we may take a finite presentation of the restriction of the module
$\mathfrak{V}\subseteq \mathfrak{X}^{\prime }$ where we may take a finite presentation of the restriction of the module ![]() $\mathscr{M}_{k+1}$ to
$\mathscr{M}_{k+1}$ to ![]() $\mathfrak{V}$ as
$\mathfrak{V}$ as ![]() $\mathscr{D}_{\mathfrak{V},k+1}^{\dagger }$-module to reduce to the case of the sheaf
$\mathscr{D}_{\mathfrak{V},k+1}^{\dagger }$-module to reduce to the case of the sheaf ![]() $\mathscr{D}_{\mathfrak{V},k+1}^{\dagger }$, as in the proof of the preceding theorem. This shows
$\mathscr{D}_{\mathfrak{V},k+1}^{\dagger }$, as in the proof of the preceding theorem. This shows ![]() $\unicode[STIX]{x1D70B}_{\ast }\mathscr{M}\in {\mathcal{C}}_{\mathfrak{X}}$. Conversely, suppose
$\unicode[STIX]{x1D70B}_{\ast }\mathscr{M}\in {\mathcal{C}}_{\mathfrak{X}}$. Conversely, suppose ![]() $\mathscr{N}=\mathop{\varprojlim }\nolimits_{k}\mathscr{N}_{k}\in {\mathcal{C}}_{\mathfrak{X}}$ with coherent
$\mathscr{N}=\mathop{\varprojlim }\nolimits_{k}\mathscr{N}_{k}\in {\mathcal{C}}_{\mathfrak{X}}$ with coherent ![]() $\mathscr{D}_{\mathfrak{X},k}^{\dagger }$-modules
$\mathscr{D}_{\mathfrak{X},k}^{\dagger }$-modules ![]() $\mathscr{N}_{k}$. Then
$\mathscr{N}_{k}$. Then ![]() $\unicode[STIX]{x1D70B}^{!}{\mathcal{N}}:=\mathop{\varprojlim }\nolimits_{k}\unicode[STIX]{x1D70B}^{!}\mathscr{N}_{k}$ lies in
$\unicode[STIX]{x1D70B}^{!}{\mathcal{N}}:=\mathop{\varprojlim }\nolimits_{k}\unicode[STIX]{x1D70B}^{!}\mathscr{N}_{k}$ lies in ![]() ${\mathcal{C}}_{\mathfrak{X}^{\prime }}$, since the projective system of coherent
${\mathcal{C}}_{\mathfrak{X}^{\prime }}$, since the projective system of coherent ![]() $\mathscr{D}_{\mathfrak{X}^{\prime },k}^{\dagger }$-modules
$\mathscr{D}_{\mathfrak{X}^{\prime },k}^{\dagger }$-modules ![]() $\unicode[STIX]{x1D70B}^{!}\mathscr{N}_{k}$ satisfies
$\unicode[STIX]{x1D70B}^{!}\mathscr{N}_{k}$ satisfies
 $$\begin{eqnarray}\displaystyle \mathscr{D}_{\mathfrak{X}^{\prime },k}^{\dagger }\otimes _{\mathscr{D}_{\mathfrak{ X}^{\prime },k+1}^{\dagger }}\unicode[STIX]{x1D70B}^{!}\mathscr{N}_{k+1} & \simeq & \displaystyle \mathscr{D}_{\mathfrak{X}^{\prime },k}^{\dagger }\otimes _{\mathscr{D}_{\mathfrak{ X}^{\prime },k+1}^{\dagger }}\Big(\mathscr{D}_{\mathfrak{X}^{\prime },k+1}^{\dagger }\otimes _{\unicode[STIX]{x1D70B}^{-1}\mathscr{D}_{\mathfrak{X},k+1}^{\dagger }}\unicode[STIX]{x1D70B}^{-1}\mathscr{N}_{k+1}\Big)\nonumber\\ \displaystyle & \simeq & \displaystyle \mathscr{D}_{\mathfrak{X}^{\prime },k}^{\dagger }\otimes _{\unicode[STIX]{x1D70B}^{-1}\mathscr{D}_{\mathfrak{X},k}^{\dagger }}\Big(\unicode[STIX]{x1D70B}^{-1}\mathscr{D}_{\mathfrak{X},k}^{\dagger }\otimes _{\unicode[STIX]{x1D70B}^{-1}\mathscr{D}_{\mathfrak{X},k+1}^{\dagger }}\unicode[STIX]{x1D70B}^{-1}\mathscr{N}_{k+1}\Big)\nonumber\\ \displaystyle & \simeq & \displaystyle \unicode[STIX]{x1D70B}^{!}\Big(\mathscr{D}_{\mathfrak{X},k}^{\dagger }\otimes _{\mathscr{D}_{\mathfrak{X},k+1}^{\dagger }}\mathscr{N}_{k+1}\Big)\nonumber\\ \displaystyle & \simeq & \displaystyle \unicode[STIX]{x1D70B}^{!}\mathscr{N}_{k}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathscr{D}_{\mathfrak{X}^{\prime },k}^{\dagger }\otimes _{\mathscr{D}_{\mathfrak{ X}^{\prime },k+1}^{\dagger }}\unicode[STIX]{x1D70B}^{!}\mathscr{N}_{k+1} & \simeq & \displaystyle \mathscr{D}_{\mathfrak{X}^{\prime },k}^{\dagger }\otimes _{\mathscr{D}_{\mathfrak{ X}^{\prime },k+1}^{\dagger }}\Big(\mathscr{D}_{\mathfrak{X}^{\prime },k+1}^{\dagger }\otimes _{\unicode[STIX]{x1D70B}^{-1}\mathscr{D}_{\mathfrak{X},k+1}^{\dagger }}\unicode[STIX]{x1D70B}^{-1}\mathscr{N}_{k+1}\Big)\nonumber\\ \displaystyle & \simeq & \displaystyle \mathscr{D}_{\mathfrak{X}^{\prime },k}^{\dagger }\otimes _{\unicode[STIX]{x1D70B}^{-1}\mathscr{D}_{\mathfrak{X},k}^{\dagger }}\Big(\unicode[STIX]{x1D70B}^{-1}\mathscr{D}_{\mathfrak{X},k}^{\dagger }\otimes _{\unicode[STIX]{x1D70B}^{-1}\mathscr{D}_{\mathfrak{X},k+1}^{\dagger }}\unicode[STIX]{x1D70B}^{-1}\mathscr{N}_{k+1}\Big)\nonumber\\ \displaystyle & \simeq & \displaystyle \unicode[STIX]{x1D70B}^{!}\Big(\mathscr{D}_{\mathfrak{X},k}^{\dagger }\otimes _{\mathscr{D}_{\mathfrak{X},k+1}^{\dagger }}\mathscr{N}_{k+1}\Big)\nonumber\\ \displaystyle & \simeq & \displaystyle \unicode[STIX]{x1D70B}^{!}\mathscr{N}_{k}.\nonumber\end{eqnarray}$$ It follows from 2.3.8 that the functor ![]() ${\mathcal{N}}\mapsto \unicode[STIX]{x1D70B}^{!}{\mathcal{N}}$ is a quasi-inverse to the functor
${\mathcal{N}}\mapsto \unicode[STIX]{x1D70B}^{!}{\mathcal{N}}$ is a quasi-inverse to the functor ![]() $\unicode[STIX]{x1D70B}_{\ast }:{\mathcal{C}}_{\mathfrak{X}^{\prime }}\rightarrow {\mathcal{C}}_{\mathfrak{X}}$. These functors are therefore mutually inverse equivalences of categories.◻
$\unicode[STIX]{x1D70B}_{\ast }:{\mathcal{C}}_{\mathfrak{X}^{\prime }}\rightarrow {\mathcal{C}}_{\mathfrak{X}}$. These functors are therefore mutually inverse equivalences of categories.◻
Theorem 3.1.13. (Theorem A for coadmissible modules on ![]() $\mathfrak{X}$) Let
$\mathfrak{X}$) Let ![]() $\mathfrak{V}\subset \mathfrak{X}$ be an affine open subset. Then the global sections functor
$\mathfrak{V}\subset \mathfrak{X}$ be an affine open subset. Then the global sections functor ![]() $\unicode[STIX]{x1D6E4}(\mathfrak{V},-)$ induces an equivalence of categories
$\unicode[STIX]{x1D6E4}(\mathfrak{V},-)$ induces an equivalence of categories
Proof. This is an application of Proposition 2.2.15. Abbreviate ![]() $D_{k}^{\dagger }=\unicode[STIX]{x1D6E4}(\mathfrak{V},\mathscr{D}_{\mathfrak{V},k}^{\dagger })$. Let
$D_{k}^{\dagger }=\unicode[STIX]{x1D6E4}(\mathfrak{V},\mathscr{D}_{\mathfrak{V},k}^{\dagger })$. Let ![]() $\mathscr{M}\in {\mathcal{C}}_{\mathfrak{V}}$ with coherent
$\mathscr{M}\in {\mathcal{C}}_{\mathfrak{V}}$ with coherent ![]() $\mathscr{D}_{\mathfrak{X},k}^{\dagger }$-modules
$\mathscr{D}_{\mathfrak{X},k}^{\dagger }$-modules ![]() $\mathscr{M}_{k}$. Then
$\mathscr{M}_{k}$. Then ![]() $M_{k}=\unicode[STIX]{x1D6E4}(\mathfrak{V},\mathscr{M}_{k})$ is a coherent
$M_{k}=\unicode[STIX]{x1D6E4}(\mathfrak{V},\mathscr{M}_{k})$ is a coherent ![]() $D_{k}^{\dagger }$-module and
$D_{k}^{\dagger }$-module and ![]() $M=\unicode[STIX]{x1D6E4}(\mathfrak{V},\mathscr{M})=\mathop{\varprojlim }\nolimits_{k}M_{k}$. Taking global sections in the isomorphism
$M=\unicode[STIX]{x1D6E4}(\mathfrak{V},\mathscr{M})=\mathop{\varprojlim }\nolimits_{k}M_{k}$. Taking global sections in the isomorphism
shows that the canonical map
is an isomorphism, too. Indeed, this is clear in the case ![]() $\mathscr{M}_{k+1}=\mathscr{D}_{\mathfrak{V},k+1}^{\dagger }$ and the general case follows from taking a finite presentation of
$\mathscr{M}_{k+1}=\mathscr{D}_{\mathfrak{V},k+1}^{\dagger }$ and the general case follows from taking a finite presentation of ![]() $\mathscr{M}_{k+1}$ as
$\mathscr{M}_{k+1}$ as ![]() $\mathscr{D}_{\mathfrak{V},k+1}^{\dagger }$-module. We conclude with Proposition 3.1.7 that
$\mathscr{D}_{\mathfrak{V},k+1}^{\dagger }$-module. We conclude with Proposition 3.1.7 that ![]() $M\in {\mathcal{C}}_{\mathscr{D}_{\mathfrak{X},\infty }(\mathfrak{V})}$. Conversely, given
$M\in {\mathcal{C}}_{\mathscr{D}_{\mathfrak{X},\infty }(\mathfrak{V})}$. Conversely, given ![]() $M\in {\mathcal{C}}_{\mathscr{D}_{\mathfrak{X},\infty }(\mathfrak{V})}$ with coherent
$M\in {\mathcal{C}}_{\mathscr{D}_{\mathfrak{X},\infty }(\mathfrak{V})}$ with coherent ![]() $D_{k}^{\dagger }$-modules
$D_{k}^{\dagger }$-modules ![]() $M_{k}$ the
$M_{k}$ the ![]() $\mathscr{D}_{\mathfrak{V},k}^{\dagger }$-module
$\mathscr{D}_{\mathfrak{V},k}^{\dagger }$-module ![]() $\mathscr{M}_{k}=\mathscr{D}_{\mathfrak{V},k}^{\dagger }\otimes _{D_{k}^{\dagger }}M_{k}$ is coherent and these modules satisfy 3.1.14. Indeed, that the canonical map 3.1.14 is an isomorphism can be checked on global sections and follows then from the compatibility with the tensor product. This shows that
$\mathscr{M}_{k}=\mathscr{D}_{\mathfrak{V},k}^{\dagger }\otimes _{D_{k}^{\dagger }}M_{k}$ is coherent and these modules satisfy 3.1.14. Indeed, that the canonical map 3.1.14 is an isomorphism can be checked on global sections and follows then from the compatibility with the tensor product. This shows that ![]() $\mathscr{M}=\mathop{\varprojlim }\nolimits_{k}\mathscr{M}_{k}$ lies in
$\mathscr{M}=\mathop{\varprojlim }\nolimits_{k}\mathscr{M}_{k}$ lies in ![]() ${\mathcal{C}}_{\mathfrak{V}}$. This provides a quasi-inverse to
${\mathcal{C}}_{\mathfrak{V}}$. This provides a quasi-inverse to ![]() $\unicode[STIX]{x1D6E4}(\mathfrak{V},-)$.◻
$\unicode[STIX]{x1D6E4}(\mathfrak{V},-)$.◻
Lemma 3.1.15. Let ![]() $\mathscr{M}\in {\mathcal{C}}_{\mathfrak{X}}$ with a projective system
$\mathscr{M}\in {\mathcal{C}}_{\mathfrak{X}}$ with a projective system ![]() $(\mathscr{M}_{k})$ of coherent
$(\mathscr{M}_{k})$ of coherent ![]() $\widehat{\mathscr{D}}_{\mathfrak{X},\mathbb{Q}}^{(k,0)}$-modules, as in 3.1.8. Let
$\widehat{\mathscr{D}}_{\mathfrak{X},\mathbb{Q}}^{(k,0)}$-modules, as in 3.1.8. Let ![]() $\mathfrak{V}\subset \mathfrak{X}$ be an open subset, which is affine or of the form
$\mathfrak{V}\subset \mathfrak{X}$ be an open subset, which is affine or of the form ![]() $\text{pr}^{-1}(\mathfrak{U})$ for an affine open
$\text{pr}^{-1}(\mathfrak{U})$ for an affine open ![]() $\mathfrak{U}\subset \mathfrak{X}_{0}$. Then the projective system
$\mathfrak{U}\subset \mathfrak{X}_{0}$. Then the projective system ![]() $(\mathscr{M}_{k}(\mathfrak{V}))_{k\geqslant k_{\mathfrak{X}}}$ has the following properties:
$(\mathscr{M}_{k}(\mathfrak{V}))_{k\geqslant k_{\mathfrak{X}}}$ has the following properties:
(i) For
 $k^{\prime }\geqslant k$ the transition map
$k^{\prime }\geqslant k$ the transition map  $\mathscr{M}_{k^{\prime }}(\mathfrak{V})\rightarrow \mathscr{M}_{k}(\mathfrak{V})$ is uniformly continuous.
$\mathscr{M}_{k^{\prime }}(\mathfrak{V})\rightarrow \mathscr{M}_{k}(\mathfrak{V})$ is uniformly continuous.(ii) For all
 $k\geqslant k_{\mathfrak{X}}$ there exists
$k\geqslant k_{\mathfrak{X}}$ there exists  $k^{\prime }\geqslant k$ such that for all
$k^{\prime }\geqslant k$ such that for all  $k^{\prime \prime }\geqslant k^{\prime }$ the image of
$k^{\prime \prime }\geqslant k^{\prime }$ the image of  $\mathscr{M}_{k^{\prime \prime }}(\mathfrak{V})\rightarrow \mathscr{M}_{k}(\mathfrak{U})$ is dense in
$\mathscr{M}_{k^{\prime \prime }}(\mathfrak{V})\rightarrow \mathscr{M}_{k}(\mathfrak{U})$ is dense in  $\text{im}(\mathscr{M}_{k^{\prime }}(\mathfrak{V})\rightarrow \mathscr{M}_{k}(\mathfrak{V}))$.
$\text{im}(\mathscr{M}_{k^{\prime }}(\mathfrak{V})\rightarrow \mathscr{M}_{k}(\mathfrak{V}))$.(iii)
 $\varprojlim _{k}^{(1)}\mathscr{M}_{k}(\mathfrak{V})=0$.
$\varprojlim _{k}^{(1)}\mathscr{M}_{k}(\mathfrak{V})=0$.
Proof. (a) To begin with, we assume here that ![]() $\mathfrak{V}$ is open affine in
$\mathfrak{V}$ is open affine in ![]() $\mathfrak{X}$. Since a continuous map between normed spaces is uniformly continuous, (i) is clear. Abbreviate
$\mathfrak{X}$. Since a continuous map between normed spaces is uniformly continuous, (i) is clear. Abbreviate ![]() $D_{k}=\unicode[STIX]{x1D6E4}(\mathfrak{V},\widehat{\mathscr{D}}_{\mathfrak{X},\mathbb{Q}}^{(k,0)})$ and
$D_{k}=\unicode[STIX]{x1D6E4}(\mathfrak{V},\widehat{\mathscr{D}}_{\mathfrak{X},\mathbb{Q}}^{(k,0)})$ and ![]() $M_{k}=\unicode[STIX]{x1D6E4}(\mathfrak{V},\mathscr{M}_{k})$. By the above theorem
$M_{k}=\unicode[STIX]{x1D6E4}(\mathfrak{V},\mathscr{M}_{k})$. By the above theorem ![]() $M\in {\mathcal{C}}_{\mathscr{D}_{\mathfrak{X},\infty }(\mathfrak{V})}$ and, by the general properties of Fréchet–Stein algebras which we have recalled above, it remains to see that the modules
$M\in {\mathcal{C}}_{\mathscr{D}_{\mathfrak{X},\infty }(\mathfrak{V})}$ and, by the general properties of Fréchet–Stein algebras which we have recalled above, it remains to see that the modules ![]() $M_{k}=\mathscr{M}_{k}(\mathfrak{V})$ form a
$M_{k}=\mathscr{M}_{k}(\mathfrak{V})$ form a ![]() $(D_{k})$-sequence for
$(D_{k})$-sequence for ![]() $M$. This is an application of Proposition 2.2.6: First,
$M$. This is an application of Proposition 2.2.6: First, ![]() $M_{k}$ is a coherent
$M_{k}$ is a coherent ![]() $D_{k}$-module. Applying
$D_{k}$-module. Applying ![]() $\unicode[STIX]{x1D6E4}(\mathfrak{V},-)$ to the isomorphism
$\unicode[STIX]{x1D6E4}(\mathfrak{V},-)$ to the isomorphism
shows that the canonical map
is an isomorphism. Indeed, this is clear in the case where the restriction of ![]() $\mathscr{M}_{k+1}$ to
$\mathscr{M}_{k+1}$ to ![]() $\mathfrak{V}$ equals
$\mathfrak{V}$ equals ![]() $\widehat{\mathscr{D}}_{\mathfrak{V},\mathbb{Q}}^{(k,0)}$ and the general case follows from taking a finite presentation of it as
$\widehat{\mathscr{D}}_{\mathfrak{V},\mathbb{Q}}^{(k,0)}$ and the general case follows from taking a finite presentation of it as ![]() $\widehat{\mathscr{D}}_{\mathfrak{V},\mathbb{Q}}^{(k,0)}$-module.
$\widehat{\mathscr{D}}_{\mathfrak{V},\mathbb{Q}}^{(k,0)}$-module.
(b) Now let ![]() $\mathfrak{V}=\text{pr}^{-1}(\mathfrak{U})$ be the preimage of an open affine subset
$\mathfrak{V}=\text{pr}^{-1}(\mathfrak{U})$ be the preimage of an open affine subset ![]() $\mathfrak{U}\subset \mathfrak{X}_{0}$. We consider the projective system
$\mathfrak{U}\subset \mathfrak{X}_{0}$. We consider the projective system ![]() $(\text{pr}_{\ast }\mathscr{M}_{k})_{k}$ of coherent
$(\text{pr}_{\ast }\mathscr{M}_{k})_{k}$ of coherent ![]() $\widehat{\mathscr{D}}_{\mathfrak{X}_{0},\mathbb{Q}}^{(k,0)}$-modules. By 3.1.12, this is a projective system for the sheaf
$\widehat{\mathscr{D}}_{\mathfrak{X}_{0},\mathbb{Q}}^{(k,0)}$-modules. By 3.1.12, this is a projective system for the sheaf ![]() $\text{pr}_{\ast }\mathscr{M}\in {\mathcal{C}}_{\mathfrak{X}_{0}}$. As we have seen in part (a), statements (i)–(iii) hold for the open affine subset
$\text{pr}_{\ast }\mathscr{M}\in {\mathcal{C}}_{\mathfrak{X}_{0}}$. As we have seen in part (a), statements (i)–(iii) hold for the open affine subset ![]() $\mathfrak{U}$ of
$\mathfrak{U}$ of ![]() $\mathfrak{X}_{0}$ and the projective system
$\mathfrak{X}_{0}$ and the projective system ![]() $(\text{pr}_{\ast }\mathscr{M}_{k})_{k}$, and they thus hold also for
$(\text{pr}_{\ast }\mathscr{M}_{k})_{k}$, and they thus hold also for ![]() $\mathfrak{V}=\text{pr}^{-1}(\mathfrak{U})$ and the projective system
$\mathfrak{V}=\text{pr}^{-1}(\mathfrak{U})$ and the projective system ![]() $(\mathscr{M}_{k})_{k}$.◻
$(\mathscr{M}_{k})_{k}$.◻
Theorem 3.1.16. (Theorem B for coadmissible modules on ![]() $\mathfrak{X}$) Let
$\mathfrak{X}$) Let ![]() $\text{pr}:\mathfrak{X}\rightarrow \mathfrak{X}_{0}$ be an admissible blow-up. Suppose
$\text{pr}:\mathfrak{X}\rightarrow \mathfrak{X}_{0}$ be an admissible blow-up. Suppose ![]() $\mathscr{M}=\mathop{\varprojlim }\nolimits_{k}\mathscr{M}_{k}$ is a coadmissible
$\mathscr{M}=\mathop{\varprojlim }\nolimits_{k}\mathscr{M}_{k}$ is a coadmissible ![]() $\mathscr{D}_{\mathfrak{X},\infty }$-module with coherent
$\mathscr{D}_{\mathfrak{X},\infty }$-module with coherent ![]() $\widehat{\mathscr{D}}_{\mathfrak{X},\mathbb{Q}}^{(k,0)}$-modules
$\widehat{\mathscr{D}}_{\mathfrak{X},\mathbb{Q}}^{(k,0)}$-modules ![]() $\mathscr{M}_{k}$. Then
$\mathscr{M}_{k}$. Then ![]() $R\mathop{\varprojlim }\nolimits_{k}\mathscr{M}_{k}=\mathscr{M}$. Moreover, given any open subset
$R\mathop{\varprojlim }\nolimits_{k}\mathscr{M}_{k}=\mathscr{M}$. Moreover, given any open subset ![]() $\mathfrak{V}\subset \mathfrak{X}$ which is affine or the preimage
$\mathfrak{V}\subset \mathfrak{X}$ which is affine or the preimage ![]() $\text{pr}^{-1}(\mathfrak{U})$ of an open affine
$\text{pr}^{-1}(\mathfrak{U})$ of an open affine ![]() $\mathfrak{U}\subset \mathfrak{X}_{0}$, we have
$\mathfrak{U}\subset \mathfrak{X}_{0}$, we have ![]() $H^{q}(\mathfrak{V},\mathscr{M})=0$ for all
$H^{q}(\mathfrak{V},\mathscr{M})=0$ for all ![]() $q>0$. In particular, if
$q>0$. In particular, if ![]() $\mathfrak{X}_{0}$ is affine, then
$\mathfrak{X}_{0}$ is affine, then ![]() $H^{q}(\mathfrak{X},\mathscr{M})=0$ for all
$H^{q}(\mathfrak{X},\mathscr{M})=0$ for all ![]() $q>0$.
$q>0$.
Proof. Our aim is to apply [26, Tag 0BKS]. To this end, we let ![]() ${\mathcal{B}}$ be the set of open subsets
${\mathcal{B}}$ be the set of open subsets ![]() $\mathfrak{V}\subset \mathfrak{X}$ which are affine or of the form
$\mathfrak{V}\subset \mathfrak{X}$ which are affine or of the form ![]() $\text{pr}^{-1}(\mathfrak{U})$ for some open affine
$\text{pr}^{-1}(\mathfrak{U})$ for some open affine ![]() $\mathfrak{U}\subset \mathfrak{X}_{0}$. We are going to show that the three hypotheses of [26, Tag 0BKS] are fulfilled, namely
$\mathfrak{U}\subset \mathfrak{X}_{0}$. We are going to show that the three hypotheses of [26, Tag 0BKS] are fulfilled, namely
(i) Every open subset of
 $\mathfrak{X}$ has a covering whose members are elements of
$\mathfrak{X}$ has a covering whose members are elements of  ${\mathcal{B}}$.
${\mathcal{B}}$.(ii) For every
 $\mathfrak{V}\in {\mathcal{B}}$, all
$\mathfrak{V}\in {\mathcal{B}}$, all  $k\geqslant 0$, and all
$k\geqslant 0$, and all  $q>0$ one has
$q>0$ one has  $H^{q}(\mathfrak{V},\mathscr{M}_{k})=0$.
$H^{q}(\mathfrak{V},\mathscr{M}_{k})=0$.(iii) For every
 $\mathfrak{V}\in {\mathcal{B}}$ one has
$\mathfrak{V}\in {\mathcal{B}}$ one has  $\varprojlim _{k}^{(1)}\mathscr{M}_{k}(\mathfrak{V})=0$.
$\varprojlim _{k}^{(1)}\mathscr{M}_{k}(\mathfrak{V})=0$.
Proof of these conditions.
(i) This is true because
 ${\mathcal{B}}$ is a basis of the topology of
${\mathcal{B}}$ is a basis of the topology of  $\mathfrak{X}$.
$\mathfrak{X}$.(ii) This is true by 2.2.6 (iii) for
 $\mathfrak{V}$ open affine, and by 2.3.12 when
$\mathfrak{V}$ open affine, and by 2.3.12 when  $\mathfrak{V}$ is the preimage of an open affine subset in
$\mathfrak{V}$ is the preimage of an open affine subset in  $\mathfrak{X}_{0}$.
$\mathfrak{X}_{0}$.(iii) This is true by 3.1.15. ◻
This shows that the conclusions of [26, Tag 0BKS] hold, namely that ![]() $R\mathop{\varprojlim }\nolimits_{k}\mathscr{M}_{k}=\mathscr{M}$, and that
$R\mathop{\varprojlim }\nolimits_{k}\mathscr{M}_{k}=\mathscr{M}$, and that ![]() $H^{q}(\mathfrak{V},\mathscr{M})=0$ for all
$H^{q}(\mathfrak{V},\mathscr{M})=0$ for all ![]() $q>0$ and every
$q>0$ and every ![]() $\mathfrak{V}\in {\mathcal{B}}$. In particular,
$\mathfrak{V}\in {\mathcal{B}}$. In particular, ![]() $H^{q}(\mathfrak{X},\mathscr{M})=0$ for all
$H^{q}(\mathfrak{X},\mathscr{M})=0$ for all ![]() $q>0$, if
$q>0$, if ![]() $\mathfrak{X}_{0}$ is affine.◻
$\mathfrak{X}_{0}$ is affine.◻
Theorem 3.1.17. The category ![]() ${\mathcal{C}}_{\mathfrak{X}}$ of coadmissible
${\mathcal{C}}_{\mathfrak{X}}$ of coadmissible ![]() $\mathscr{D}_{\mathfrak{X},\infty }$-modules is abelian.
$\mathscr{D}_{\mathfrak{X},\infty }$-modules is abelian.
Proof. The argument is similar to [Reference Schneider and Teitelbaum24, 3.5], adapted to our situation.
(a) For the purpose of this proof denote by ![]() ${\mathcal{C}}oh$ the category of projective systems
${\mathcal{C}}oh$ the category of projective systems ![]() $(\mathscr{M}_{k},\mathscr{M}_{k+1}\rightarrow \mathscr{M}_{k})_{k\geqslant 0}$, where
$(\mathscr{M}_{k},\mathscr{M}_{k+1}\rightarrow \mathscr{M}_{k})_{k\geqslant 0}$, where ![]() $\mathscr{M}_{k}$ is a coherent
$\mathscr{M}_{k}$ is a coherent ![]() $\widehat{\mathscr{D}}_{\mathfrak{X},\mathbb{Q}}^{(k,0)}$-module, such that for every
$\widehat{\mathscr{D}}_{\mathfrak{X},\mathbb{Q}}^{(k,0)}$-module, such that for every ![]() $k\geqslant 0$ the canonical
$k\geqslant 0$ the canonical ![]() $\widehat{\mathscr{D}}_{\mathfrak{X},\mathbb{Q}}^{(k,0)}$-linear homomorphism
$\widehat{\mathscr{D}}_{\mathfrak{X},\mathbb{Q}}^{(k,0)}$-linear homomorphism ![]() $\widehat{\mathscr{D}}_{\mathfrak{X},\mathbb{Q}}^{(k,0)}\otimes _{\widehat{\mathscr{D}}_{\mathfrak{X},\mathbb{Q}}^{(k+1,0)}}\mathscr{M}_{k+1}\rightarrow \mathscr{M}_{k}$ is an isomorphism. Morphisms in
$\widehat{\mathscr{D}}_{\mathfrak{X},\mathbb{Q}}^{(k,0)}\otimes _{\widehat{\mathscr{D}}_{\mathfrak{X},\mathbb{Q}}^{(k+1,0)}}\mathscr{M}_{k+1}\rightarrow \mathscr{M}_{k}$ is an isomorphism. Morphisms in ![]() ${\mathcal{C}}oh$ are morphisms of projective systems. By the flatness result of 2.2.16 the category
${\mathcal{C}}oh$ are morphisms of projective systems. By the flatness result of 2.2.16 the category ![]() ${\mathcal{C}}oh$ is abelian, where (co)kernels and (co)images in
${\mathcal{C}}oh$ is abelian, where (co)kernels and (co)images in ![]() ${\mathcal{C}}oh$ coincide with the corresponding notions in the category of all projective systems
${\mathcal{C}}oh$ coincide with the corresponding notions in the category of all projective systems ![]() $(\mathscr{M}_{k},\mathscr{M}_{k+1}\rightarrow \mathscr{M}_{k})_{k\geqslant 0}$.
$(\mathscr{M}_{k},\mathscr{M}_{k+1}\rightarrow \mathscr{M}_{k})_{k\geqslant 0}$.
(b) Consider the functor ![]() ${\mathcal{C}}oh\rightarrow {\mathcal{C}}_{\mathfrak{X}}$,
${\mathcal{C}}oh\rightarrow {\mathcal{C}}_{\mathfrak{X}}$, ![]() $(\mathscr{M}_{k})_{k}\mapsto \mathop{\varprojlim }\nolimits_{k}\mathscr{M}_{k}$, which is essentially surjective. In order to show that it is also fully faithful, we prove the following statement: if
$(\mathscr{M}_{k})_{k}\mapsto \mathop{\varprojlim }\nolimits_{k}\mathscr{M}_{k}$, which is essentially surjective. In order to show that it is also fully faithful, we prove the following statement: if ![]() $\mathscr{M}=\mathop{\varprojlim }\nolimits_{k}\mathscr{M}_{k}$ is a coadmissible
$\mathscr{M}=\mathop{\varprojlim }\nolimits_{k}\mathscr{M}_{k}$ is a coadmissible ![]() $\mathscr{D}_{\mathfrak{X},\infty }$-module, then the canonical map
$\mathscr{D}_{\mathfrak{X},\infty }$-module, then the canonical map ![]() $\widehat{\mathscr{D}}_{\mathfrak{X},\mathbb{Q}}^{(k,0)}\otimes _{\mathscr{D}_{\mathfrak{X},\infty }}\mathscr{M}\rightarrow \mathscr{M}_{k}$ is an isomorphism for any
$\widehat{\mathscr{D}}_{\mathfrak{X},\mathbb{Q}}^{(k,0)}\otimes _{\mathscr{D}_{\mathfrak{X},\infty }}\mathscr{M}\rightarrow \mathscr{M}_{k}$ is an isomorphism for any ![]() $k$. If
$k$. If ![]() $\mathfrak{V}\subseteq \mathfrak{X}$ is open affine, then
$\mathfrak{V}\subseteq \mathfrak{X}$ is open affine, then
is bijective, according to 3.1.13 and [Reference Schneider and Teitelbaum24, Corollary 3.1] for the Fréchet–Stein algebra ![]() $\mathscr{D}_{\mathfrak{X},\infty }(\mathfrak{V})$. This shows that the morphism of presheaves
$\mathscr{D}_{\mathfrak{X},\infty }(\mathfrak{V})$. This shows that the morphism of presheaves
where ![]() $\mathfrak{U}$ runs through all open subsets in
$\mathfrak{U}$ runs through all open subsets in ![]() $\mathfrak{X}$, sheafifies to give the desired isomorphism
$\mathfrak{X}$, sheafifies to give the desired isomorphism ![]() $\widehat{\mathscr{D}}_{\mathfrak{X},\mathbb{Q}}^{(k,0)}\otimes _{\mathscr{D}_{\mathfrak{X},\infty }}\mathscr{M}\stackrel{\simeq }{\longrightarrow }\mathscr{M}_{k}$. The functor
$\widehat{\mathscr{D}}_{\mathfrak{X},\mathbb{Q}}^{(k,0)}\otimes _{\mathscr{D}_{\mathfrak{X},\infty }}\mathscr{M}\stackrel{\simeq }{\longrightarrow }\mathscr{M}_{k}$. The functor ![]() $\mathop{\varprojlim }\nolimits_{k}:{\mathcal{C}}oh\rightarrow {\mathcal{C}}_{\mathfrak{X}}$, being essentially surjective and fully faithful, is therefore an equivalence of categories.
$\mathop{\varprojlim }\nolimits_{k}:{\mathcal{C}}oh\rightarrow {\mathcal{C}}_{\mathfrak{X}}$, being essentially surjective and fully faithful, is therefore an equivalence of categories.
(c) It is clear that direct sums of coadmissible modules are coadmissible, and the category ![]() ${\mathcal{C}}_{\mathfrak{X}}$ is hence an additive category. Moreover, any morphism between coadmissible modules comes from a morphism in the abelian category
${\mathcal{C}}_{\mathfrak{X}}$ is hence an additive category. Moreover, any morphism between coadmissible modules comes from a morphism in the abelian category ![]() ${\mathcal{C}}oh$ which has a (co)kernel and a (co)image. Since the functor
${\mathcal{C}}oh$ which has a (co)kernel and a (co)image. Since the functor ![]() $\mathop{\varprojlim }\nolimits_{k}:{\mathcal{C}}oh\rightarrow \text{Mod}(\mathscr{D}_{\mathfrak{X},\infty })$ is exact, by 3.1.16, it commutes with the formation of (co)kernels and (co)images. Thus, the category
$\mathop{\varprojlim }\nolimits_{k}:{\mathcal{C}}oh\rightarrow \text{Mod}(\mathscr{D}_{\mathfrak{X},\infty })$ is exact, by 3.1.16, it commutes with the formation of (co)kernels and (co)images. Thus, the category ![]() ${\mathcal{C}}_{\mathfrak{X}}$ is abelian.◻
${\mathcal{C}}_{\mathfrak{X}}$ is abelian.◻
3.2 Coadmissible  $\mathscr{D}$-modules on the Zariski–Riemann space
$\mathscr{D}$-modules on the Zariski–Riemann space  $\langle \mathfrak{X}_{0}\rangle$
$\langle \mathfrak{X}_{0}\rangle$
We finally explain how to pass from the previous construction and results to the projective limit in ![]() $\mathfrak{X}$, that is to say, to the Zariski–Riemann space of
$\mathfrak{X}$, that is to say, to the Zariski–Riemann space of ![]() $\mathfrak{X}_{0}$.
$\mathfrak{X}_{0}$.
3.2.1 The Zariski–Riemann space  $\langle \mathfrak{X}_{0}\rangle$
$\langle \mathfrak{X}_{0}\rangle$
Let ![]() ${\mathcal{F}}_{\mathfrak{X}_{0}}$ be the set of all admissible formal blow-ups
${\mathcal{F}}_{\mathfrak{X}_{0}}$ be the set of all admissible formal blow-ups ![]() $\mathfrak{X}\rightarrow \mathfrak{X}_{0}$.Footnote 5 This set is partially ordered by setting
$\mathfrak{X}\rightarrow \mathfrak{X}_{0}$.Footnote 5 This set is partially ordered by setting ![]() $\mathfrak{X}^{\prime }\succcurlyeq \mathfrak{X}$ if the blow-up morphism
$\mathfrak{X}^{\prime }\succcurlyeq \mathfrak{X}$ if the blow-up morphism ![]() $\mathfrak{X}^{\prime }\rightarrow \mathfrak{X}_{0}$ factors as
$\mathfrak{X}^{\prime }\rightarrow \mathfrak{X}_{0}$ factors as ![]() $\mathfrak{X}^{\prime }\stackrel{\unicode[STIX]{x1D70B}}{\longrightarrow }\mathfrak{X}\rightarrow \mathfrak{X}_{0}$, where
$\mathfrak{X}^{\prime }\stackrel{\unicode[STIX]{x1D70B}}{\longrightarrow }\mathfrak{X}\rightarrow \mathfrak{X}_{0}$, where ![]() $\mathfrak{X}\rightarrow \mathfrak{X}_{0}$ is the blow-up morphism. The morphism
$\mathfrak{X}\rightarrow \mathfrak{X}_{0}$ is the blow-up morphism. The morphism ![]() $\unicode[STIX]{x1D70B}:\mathfrak{X}^{\prime }\rightarrow \mathfrak{X}$ is then uniquely determined by the universal property of blowing-up, and is itself a blow-up morphism [Reference Liu19, Chapter 8, 1.24], and we will denote it henceforth by
$\unicode[STIX]{x1D70B}:\mathfrak{X}^{\prime }\rightarrow \mathfrak{X}$ is then uniquely determined by the universal property of blowing-up, and is itself a blow-up morphism [Reference Liu19, Chapter 8, 1.24], and we will denote it henceforth by ![]() $\unicode[STIX]{x1D70B}_{\mathfrak{X}^{\prime },\mathfrak{X}}$. By [Reference Bosch9, Remark 10 in Section 8.2] the set
$\unicode[STIX]{x1D70B}_{\mathfrak{X}^{\prime },\mathfrak{X}}$. By [Reference Bosch9, Remark 10 in Section 8.2] the set ![]() ${\mathcal{F}}_{\mathfrak{X}_{0}}$ is directed in the sense that any two elements have a common upper bound, and we can consider the topological space equal to the projective limit Footnote 6
${\mathcal{F}}_{\mathfrak{X}_{0}}$ is directed in the sense that any two elements have a common upper bound, and we can consider the topological space equal to the projective limit Footnote 6
This is the Zariski–Riemann space associated with ![]() $\mathfrak{X}_{0}$. For its basic properties we refer to [Reference Bosch9, 9.3].
$\mathfrak{X}_{0}$. For its basic properties we refer to [Reference Bosch9, 9.3].
3.2.2 Sheaves on the space  $\langle \mathfrak{X}_{0}\rangle$
$\langle \mathfrak{X}_{0}\rangle$
For ![]() $\mathfrak{X}\in {\mathcal{F}}_{\mathfrak{X}_{0}}$ we denote the canonical projection map
$\mathfrak{X}\in {\mathcal{F}}_{\mathfrak{X}_{0}}$ we denote the canonical projection map ![]() $\langle \mathfrak{X}_{0}\rangle \rightarrow \mathfrak{X}$ by
$\langle \mathfrak{X}_{0}\rangle \rightarrow \mathfrak{X}$ by ![]() $\text{sp}_{\mathfrak{X}}$. If
$\text{sp}_{\mathfrak{X}}$. If ![]() $\mathfrak{X}^{\prime }\succcurlyeq \mathfrak{X}$ in
$\mathfrak{X}^{\prime }\succcurlyeq \mathfrak{X}$ in ![]() ${\mathcal{F}}_{\mathfrak{X}_{0}}$, we have
${\mathcal{F}}_{\mathfrak{X}_{0}}$, we have ![]() $\text{sp}_{\mathfrak{X}}=\unicode[STIX]{x1D70B}_{\mathfrak{X}^{\prime },\mathfrak{X}}\circ \text{sp}_{\mathfrak{X}^{\prime }}$. The isomorphism
$\text{sp}_{\mathfrak{X}}=\unicode[STIX]{x1D70B}_{\mathfrak{X}^{\prime },\mathfrak{X}}\circ \text{sp}_{\mathfrak{X}^{\prime }}$. The isomorphism ![]() $(\unicode[STIX]{x1D70B}_{\mathfrak{X}^{\prime },\mathfrak{X}})_{\ast }\mathscr{D}_{\mathfrak{X}^{\prime },\infty }=\mathscr{D}_{\mathfrak{X},\infty }$ from 3.1.6, together with the adjunction map
$(\unicode[STIX]{x1D70B}_{\mathfrak{X}^{\prime },\mathfrak{X}})_{\ast }\mathscr{D}_{\mathfrak{X}^{\prime },\infty }=\mathscr{D}_{\mathfrak{X},\infty }$ from 3.1.6, together with the adjunction map ![]() $\unicode[STIX]{x1D70B}_{\mathfrak{X}^{\prime },\mathfrak{X}}^{-1}\circ (\unicode[STIX]{x1D70B}_{\mathfrak{X}^{\prime },\mathfrak{X}})_{\ast }\rightarrow \text{id}$ gives rise to a canonical map
$\unicode[STIX]{x1D70B}_{\mathfrak{X}^{\prime },\mathfrak{X}}^{-1}\circ (\unicode[STIX]{x1D70B}_{\mathfrak{X}^{\prime },\mathfrak{X}})_{\ast }\rightarrow \text{id}$ gives rise to a canonical map
These morphisms of sheaves satisfy
whenever ![]() $\mathfrak{X}^{\prime \prime }\succcurlyeq \mathfrak{X}^{\prime }\succcurlyeq \mathfrak{X}$. We then obtain an inductive system
$\mathfrak{X}^{\prime \prime }\succcurlyeq \mathfrak{X}^{\prime }\succcurlyeq \mathfrak{X}$. We then obtain an inductive system ![]() $(\text{sp}_{\mathfrak{X}}^{-1}\mathscr{D}_{\mathfrak{X},\infty })_{\mathfrak{X}\in {\mathcal{F}}_{\mathfrak{X}_{0}}}$ of sheaves of rings on
$(\text{sp}_{\mathfrak{X}}^{-1}\mathscr{D}_{\mathfrak{X},\infty })_{\mathfrak{X}\in {\mathcal{F}}_{\mathfrak{X}_{0}}}$ of sheaves of rings on ![]() $\langle \mathfrak{X}_{0}\rangle$, and we put
$\langle \mathfrak{X}_{0}\rangle$, and we put
Definition 3.2.4. A ![]() $\mathscr{D}_{\langle \mathfrak{X}_{0}\rangle }$-module
$\mathscr{D}_{\langle \mathfrak{X}_{0}\rangle }$-module ![]() $\mathscr{M}$ is called coadmissible if there is a family
$\mathscr{M}$ is called coadmissible if there is a family ![]() $(\mathscr{M}_{\mathfrak{X}},\unicode[STIX]{x1D713}_{\mathfrak{X},\mathfrak{X}^{\prime }}^{\mathscr{M}})$ of coadmissible
$(\mathscr{M}_{\mathfrak{X}},\unicode[STIX]{x1D713}_{\mathfrak{X},\mathfrak{X}^{\prime }}^{\mathscr{M}})$ of coadmissible ![]() $\mathscr{D}_{\mathfrak{X},\infty }$-modules
$\mathscr{D}_{\mathfrak{X},\infty }$-modules ![]() $\mathscr{M}_{\mathfrak{X}}$, for all
$\mathscr{M}_{\mathfrak{X}}$, for all ![]() $\mathfrak{X}\in {\mathcal{F}}_{\mathfrak{X}_{0}}$, together with an isomorphism
$\mathfrak{X}\in {\mathcal{F}}_{\mathfrak{X}_{0}}$, together with an isomorphism
of ![]() $\mathscr{D}_{\mathfrak{X},\infty }$-modules, whenever we have
$\mathscr{D}_{\mathfrak{X},\infty }$-modules, whenever we have ![]() $\mathfrak{X}^{\prime }\succcurlyeq \mathfrak{X}$ in
$\mathfrak{X}^{\prime }\succcurlyeq \mathfrak{X}$ in ![]() ${\mathcal{F}}_{\mathfrak{X}_{0}}$. This system of modules and isomorphisms is required to satisfy the following conditions:
${\mathcal{F}}_{\mathfrak{X}_{0}}$. This system of modules and isomorphisms is required to satisfy the following conditions:
(i) Whenever
 $\mathfrak{X}^{\prime \prime }\succcurlyeq \mathfrak{X}^{\prime }\succcurlyeq \mathfrak{X}$ in
$\mathfrak{X}^{\prime \prime }\succcurlyeq \mathfrak{X}^{\prime }\succcurlyeq \mathfrak{X}$ in  ${\mathcal{F}}_{\mathfrak{X}_{0}}$ the following transitivity condition holds:
${\mathcal{F}}_{\mathfrak{X}_{0}}$ the following transitivity condition holds:  $$\begin{eqnarray}\unicode[STIX]{x1D713}_{\mathfrak{X}^{\prime },\mathfrak{X}}^{\mathscr{M}}\circ (\unicode[STIX]{x1D70B}_{\mathfrak{ X}^{\prime },\mathfrak{X}})_{\ast }(\unicode[STIX]{x1D713}_{\mathfrak{X}^{\prime \prime },\mathfrak{X}^{\prime }}^{\mathscr{ M}})=\unicode[STIX]{x1D713}_{\mathfrak{ X}^{\prime \prime },\mathfrak{X}}^{\mathscr{M}}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D713}_{\mathfrak{X}^{\prime },\mathfrak{X}}^{\mathscr{M}}\circ (\unicode[STIX]{x1D70B}_{\mathfrak{ X}^{\prime },\mathfrak{X}})_{\ast }(\unicode[STIX]{x1D713}_{\mathfrak{X}^{\prime \prime },\mathfrak{X}^{\prime }}^{\mathscr{ M}})=\unicode[STIX]{x1D713}_{\mathfrak{ X}^{\prime \prime },\mathfrak{X}}^{\mathscr{M}}.\end{eqnarray}$$(ii)
 $\mathscr{M}$ is isomorphic to the inductive limit
$\mathscr{M}$ is isomorphic to the inductive limit  $\mathop{\varinjlim }\nolimits_{\mathfrak{X}}\text{sp}_{\mathfrak{X}}^{-1}\mathscr{M}_{\mathfrak{X}}$ as
$\mathop{\varinjlim }\nolimits_{\mathfrak{X}}\text{sp}_{\mathfrak{X}}^{-1}\mathscr{M}_{\mathfrak{X}}$ as  $\mathscr{D}_{\langle \mathfrak{X}_{0}\rangle }$-module.
$\mathscr{D}_{\langle \mathfrak{X}_{0}\rangle }$-module.
Note that the transition morphism ![]() $\text{sp}_{\mathfrak{X}}^{-1}\mathscr{M}_{\mathfrak{X}}\rightarrow \text{sp}_{\mathfrak{X}^{\prime }}^{-1}\mathscr{M}_{\mathfrak{X}^{\prime }}$ in the inductive limit in (ii) is defined by applying the functor
$\text{sp}_{\mathfrak{X}}^{-1}\mathscr{M}_{\mathfrak{X}}\rightarrow \text{sp}_{\mathfrak{X}^{\prime }}^{-1}\mathscr{M}_{\mathfrak{X}^{\prime }}$ in the inductive limit in (ii) is defined by applying the functor ![]() $\text{sp}_{\mathfrak{X}^{\prime }}^{-1}$ to the morphism
$\text{sp}_{\mathfrak{X}^{\prime }}^{-1}$ to the morphism
The latter is obtained from ![]() $(\unicode[STIX]{x1D713}_{\mathfrak{X}^{\prime },\mathfrak{X}}^{\mathscr{M}})^{-1}:\mathscr{M}_{\mathfrak{X}}\stackrel{\simeq }{\longrightarrow }(\unicode[STIX]{x1D70B}_{\mathfrak{X}^{\prime },\mathfrak{X}})_{\ast }\mathscr{M}_{\mathfrak{X}^{\prime }}$ and the adjunction map
$(\unicode[STIX]{x1D713}_{\mathfrak{X}^{\prime },\mathfrak{X}}^{\mathscr{M}})^{-1}:\mathscr{M}_{\mathfrak{X}}\stackrel{\simeq }{\longrightarrow }(\unicode[STIX]{x1D70B}_{\mathfrak{X}^{\prime },\mathfrak{X}})_{\ast }\mathscr{M}_{\mathfrak{X}^{\prime }}$ and the adjunction map ![]() $\unicode[STIX]{x1D70B}_{\mathfrak{X}^{\prime },\mathfrak{X}}^{-1}\circ (\unicode[STIX]{x1D70B}_{\mathfrak{X}^{\prime },\mathfrak{X}})_{\ast }\rightarrow \text{id}$.
$\unicode[STIX]{x1D70B}_{\mathfrak{X}^{\prime },\mathfrak{X}}^{-1}\circ (\unicode[STIX]{x1D70B}_{\mathfrak{X}^{\prime },\mathfrak{X}})_{\ast }\rightarrow \text{id}$.
We denote by
the full subcategory of coadmissible ![]() $\mathscr{D}_{\langle \mathfrak{X}_{0}\rangle }$-modules in the category of all
$\mathscr{D}_{\langle \mathfrak{X}_{0}\rangle }$-modules in the category of all ![]() $\mathscr{D}_{\langle \mathfrak{X}_{0}\rangle }$-modules.
$\mathscr{D}_{\langle \mathfrak{X}_{0}\rangle }$-modules.
Proposition 3.2.5. Let ![]() $\mathfrak{X}\in {\mathcal{F}}_{\mathfrak{X}_{0}}$. One has an equivalence of categories
$\mathfrak{X}\in {\mathcal{F}}_{\mathfrak{X}_{0}}$. One has an equivalence of categories
Moreover, the category ![]() ${\mathcal{C}}_{\langle \mathfrak{X}_{0}\rangle }$ is abelian.
${\mathcal{C}}_{\langle \mathfrak{X}_{0}\rangle }$ is abelian.
Proof. Let ![]() $\mathscr{M}=\mathop{\varinjlim }\nolimits_{\mathfrak{X}}\text{sp}_{\mathfrak{X}}^{-1}\mathscr{M}_{\mathfrak{X}}$ and let
$\mathscr{M}=\mathop{\varinjlim }\nolimits_{\mathfrak{X}}\text{sp}_{\mathfrak{X}}^{-1}\mathscr{M}_{\mathfrak{X}}$ and let ![]() $\mathfrak{X}^{\prime }\succcurlyeq \mathfrak{X}$. There is a canonical isomorphism
$\mathfrak{X}^{\prime }\succcurlyeq \mathfrak{X}$. There is a canonical isomorphism
Indeed, let ![]() $\mathfrak{U}\subseteq \mathfrak{X}$ be an open and let
$\mathfrak{U}\subseteq \mathfrak{X}$ be an open and let ![]() $\mathfrak{V}=\unicode[STIX]{x1D70B}_{\mathfrak{X}^{\prime },\mathfrak{X}}^{-1}(\mathfrak{U})$. Then
$\mathfrak{V}=\unicode[STIX]{x1D70B}_{\mathfrak{X}^{\prime },\mathfrak{X}}^{-1}(\mathfrak{U})$. Then
using that ![]() $\text{sp}_{\mathfrak{X}^{\prime }}(\text{sp}_{\mathfrak{X}}^{-1}(\mathfrak{U}))=\mathfrak{V}$. But
$\text{sp}_{\mathfrak{X}^{\prime }}(\text{sp}_{\mathfrak{X}}^{-1}(\mathfrak{U}))=\mathfrak{V}$. But ![]() $\mathscr{M}_{\mathfrak{X}^{\prime }}(\mathfrak{V})\simeq \mathscr{M}_{\mathfrak{X}}(\mathfrak{U})$ via the map
$\mathscr{M}_{\mathfrak{X}^{\prime }}(\mathfrak{V})\simeq \mathscr{M}_{\mathfrak{X}}(\mathfrak{U})$ via the map ![]() $\unicode[STIX]{x1D713}_{\mathfrak{X}^{\prime },\mathfrak{X}}^{\mathscr{M}}$. In particular, we get an isomorphism
$\unicode[STIX]{x1D713}_{\mathfrak{X}^{\prime },\mathfrak{X}}^{\mathscr{M}}$. In particular, we get an isomorphism
This shows that the functor ![]() $(\text{sp}_{\mathfrak{X}})_{\ast }$ appearing in the proposition is well defined. In the other direction, let
$(\text{sp}_{\mathfrak{X}})_{\ast }$ appearing in the proposition is well defined. In the other direction, let ![]() $\mathscr{M}\in {\mathcal{C}}_{\mathfrak{X}}$ and define for
$\mathscr{M}\in {\mathcal{C}}_{\mathfrak{X}}$ and define for ![]() $\mathfrak{X}^{\prime }\succcurlyeq \mathfrak{X}$ the module
$\mathfrak{X}^{\prime }\succcurlyeq \mathfrak{X}$ the module ![]() $\mathscr{M}_{\mathfrak{X}^{\prime }}$ as
$\mathscr{M}_{\mathfrak{X}^{\prime }}$ as ![]() $\mathscr{M}_{\mathfrak{X}^{\prime }}:=(\unicode[STIX]{x1D70B}_{\mathfrak{X}^{\prime },\mathfrak{X}})^{!}\mathscr{M}_{\mathfrak{X}}$, see 3.1.12. Note that
$\mathscr{M}_{\mathfrak{X}^{\prime }}:=(\unicode[STIX]{x1D70B}_{\mathfrak{X}^{\prime },\mathfrak{X}})^{!}\mathscr{M}_{\mathfrak{X}}$, see 3.1.12. Note that ![]() $(\unicode[STIX]{x1D70B}_{\mathfrak{X}^{\prime },\mathfrak{X}})_{\ast }(\mathscr{M}_{\mathfrak{X}^{\prime }})\simeq \mathscr{M}_{\mathfrak{X}}$. The family
$(\unicode[STIX]{x1D70B}_{\mathfrak{X}^{\prime },\mathfrak{X}})_{\ast }(\mathscr{M}_{\mathfrak{X}^{\prime }})\simeq \mathscr{M}_{\mathfrak{X}}$. The family ![]() $(\mathscr{M}_{\mathfrak{X}^{\prime }})$ then satisfies the conditions (i) and (ii) in the above definition and its inductive limit
$(\mathscr{M}_{\mathfrak{X}^{\prime }})$ then satisfies the conditions (i) and (ii) in the above definition and its inductive limit ![]() $\mathscr{M}$ lies therefore in
$\mathscr{M}$ lies therefore in ![]() ${\mathcal{C}}_{\langle \mathfrak{X}_{0}\rangle }$. This gives a quasi-inverse to the functor
${\mathcal{C}}_{\langle \mathfrak{X}_{0}\rangle }$. This gives a quasi-inverse to the functor ![]() $(\text{sp}_{\mathfrak{X}})_{\ast }$ and shows that we have an equivalence of categories
$(\text{sp}_{\mathfrak{X}})_{\ast }$ and shows that we have an equivalence of categories ![]() ${\mathcal{C}}_{\langle \mathfrak{X}_{0}\rangle }\stackrel{\simeq }{\rightarrow }{\mathcal{C}}_{\mathfrak{X}},$ as claimed. We now show that the latter quasi-inverse functor is in fact an exact functor. To this end, let
${\mathcal{C}}_{\langle \mathfrak{X}_{0}\rangle }\stackrel{\simeq }{\rightarrow }{\mathcal{C}}_{\mathfrak{X}},$ as claimed. We now show that the latter quasi-inverse functor is in fact an exact functor. To this end, let
be an exact sequence in ![]() ${\mathcal{C}}_{\mathfrak{X}}$. The exactness of the sequence
${\mathcal{C}}_{\mathfrak{X}}$. The exactness of the sequence
can be verified after restricting the sheaves to an open subset of the form ![]() $\text{sp}_{\mathfrak{X}^{\prime }}^{-1}(\mathfrak{U})$ for some open
$\text{sp}_{\mathfrak{X}^{\prime }}^{-1}(\mathfrak{U})$ for some open ![]() $\mathfrak{U}\subset \mathfrak{X}^{\prime }$ where
$\mathfrak{U}\subset \mathfrak{X}^{\prime }$ where ![]() $\mathfrak{X}^{\prime }\succcurlyeq \mathfrak{X}$. Taking local sections in the above sequence yields the sequence
$\mathfrak{X}^{\prime }\succcurlyeq \mathfrak{X}$. Taking local sections in the above sequence yields the sequence
This sequence is exact, by the exactness of filtered direct limits and the exactness of the functors ![]() $\unicode[STIX]{x1D70B}_{\mathfrak{X}^{\prime \prime },\mathfrak{X}^{\prime }}^{!}$, see 3.1.12. Since the category
$\unicode[STIX]{x1D70B}_{\mathfrak{X}^{\prime \prime },\mathfrak{X}^{\prime }}^{!}$, see 3.1.12. Since the category ![]() ${\mathcal{C}}_{\langle \mathfrak{X}_{0}\rangle }$ is now seen to be equivalent to the abelian category
${\mathcal{C}}_{\langle \mathfrak{X}_{0}\rangle }$ is now seen to be equivalent to the abelian category ![]() ${\mathcal{C}}_{\mathfrak{X}}$ via an exact functor, it is abelian, too.◻
${\mathcal{C}}_{\mathfrak{X}}$ via an exact functor, it is abelian, too.◻
Theorem 3.2.6. (Theorems A and B for coadmissible ![]() $\mathscr{D}_{\langle \mathfrak{X}_{0}\rangle }$-modules) Suppose
$\mathscr{D}_{\langle \mathfrak{X}_{0}\rangle }$-modules) Suppose ![]() $\mathfrak{X}_{0}$ is affine.
$\mathfrak{X}_{0}$ is affine.
(i) One has an equivalence of categories
 $$\begin{eqnarray}\unicode[STIX]{x1D6E4}(\langle \mathfrak{X}_{0}\rangle ,-):{\mathcal{C}}_{\langle \mathfrak{X}_{0}\rangle }\stackrel{\simeq }{\longrightarrow }{\mathcal{C}}_{\mathscr{D}_{\mathfrak{X}_{0},\infty }(\mathfrak{X}_{0})}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E4}(\langle \mathfrak{X}_{0}\rangle ,-):{\mathcal{C}}_{\langle \mathfrak{X}_{0}\rangle }\stackrel{\simeq }{\longrightarrow }{\mathcal{C}}_{\mathscr{D}_{\mathfrak{X}_{0},\infty }(\mathfrak{X}_{0})}.\end{eqnarray}$$(ii) For every
 $\mathscr{M}\in {\mathcal{C}}_{\langle \mathfrak{X}_{0}\rangle }$ and every
$\mathscr{M}\in {\mathcal{C}}_{\langle \mathfrak{X}_{0}\rangle }$ and every  $q>0$ one has
$q>0$ one has  $$\begin{eqnarray}H^{q}(\langle \mathfrak{X}_{0}\rangle ,\mathscr{M})=0.\end{eqnarray}$$
$$\begin{eqnarray}H^{q}(\langle \mathfrak{X}_{0}\rangle ,\mathscr{M})=0.\end{eqnarray}$$
Proof. Part (i) follows from the preceding proposition together with Theorem 3.1.13. By [Reference Fujiwara and Kato12, 0.3.1.19] the canonical map
is an isomorphism. Thus, part (ii) follows from 3.1.16. ◻
3.3 Examples
The first example is given by the structure sheaf of the Zariski–Riemann space tensored with ![]() $\mathbb{Q}$. Let us denote
$\mathbb{Q}$. Let us denote
Proposition 3.3.1. The sheaf ![]() ${\mathcal{O}}_{\langle \mathfrak{X}_{0}\rangle ,\mathbb{Q}}$ is a coadmissible
${\mathcal{O}}_{\langle \mathfrak{X}_{0}\rangle ,\mathbb{Q}}$ is a coadmissible ![]() $\mathscr{D}_{\langle \mathfrak{X}_{0}\rangle }$-module.
$\mathscr{D}_{\langle \mathfrak{X}_{0}\rangle }$-module.
Proof. If ![]() $\mathfrak{X},\mathfrak{X}^{\prime }\in {\mathcal{F}}_{\mathfrak{X}_{0}}$ and
$\mathfrak{X},\mathfrak{X}^{\prime }\in {\mathcal{F}}_{\mathfrak{X}_{0}}$ and ![]() $\unicode[STIX]{x1D70B}$ :
$\unicode[STIX]{x1D70B}$ : ![]() $\mathfrak{X}^{\prime }\rightarrow \mathfrak{X}$ is a morphism over
$\mathfrak{X}^{\prime }\rightarrow \mathfrak{X}$ is a morphism over ![]() $\mathfrak{X}_{0}$, then
$\mathfrak{X}_{0}$, then ![]() $\unicode[STIX]{x1D70B}_{\ast }{\mathcal{O}}_{\mathfrak{X}^{\prime },\mathbb{Q}}={\mathcal{O}}_{\mathfrak{X},\mathbb{Q}}$ by 2.3.1. By 3.2.5 we have an equivalence of categories
$\unicode[STIX]{x1D70B}_{\ast }{\mathcal{O}}_{\mathfrak{X}^{\prime },\mathbb{Q}}={\mathcal{O}}_{\mathfrak{X},\mathbb{Q}}$ by 2.3.1. By 3.2.5 we have an equivalence of categories ![]() ${\mathcal{C}}_{\langle \mathfrak{X}_{0}\rangle }\rightarrow {\mathcal{C}}_{\mathfrak{X}_{0}}$ with an explicit quasi-inverse. From these considerations we see that the claim will follow from the fact that
${\mathcal{C}}_{\langle \mathfrak{X}_{0}\rangle }\rightarrow {\mathcal{C}}_{\mathfrak{X}_{0}}$ with an explicit quasi-inverse. From these considerations we see that the claim will follow from the fact that ![]() ${\mathcal{O}}_{\mathfrak{X}_{0},\mathbb{Q}}\in {\mathcal{C}}_{\mathfrak{X}_{0}}$.
${\mathcal{O}}_{\mathfrak{X}_{0},\mathbb{Q}}\in {\mathcal{C}}_{\mathfrak{X}_{0}}$.
For any integer ![]() $k$, the sheaf
$k$, the sheaf ![]() ${\mathcal{O}}_{\mathfrak{X}_{0},\mathbb{Q}}$ is a
${\mathcal{O}}_{\mathfrak{X}_{0},\mathbb{Q}}$ is a ![]() $\mathscr{D}_{\mathfrak{X}_{0},k}^{\dagger }$-module. Let
$\mathscr{D}_{\mathfrak{X}_{0},k}^{\dagger }$-module. Let ![]() $\mathfrak{U}_{0}\subset \mathfrak{X}_{0}$ an affine open of
$\mathfrak{U}_{0}\subset \mathfrak{X}_{0}$ an affine open of ![]() $\mathfrak{X}_{0}$ with coordinates
$\mathfrak{X}_{0}$ with coordinates ![]() $x_{1},\ldots ,x_{M}$, and corresponding derivations
$x_{1},\ldots ,x_{M}$, and corresponding derivations ![]() $\unicode[STIX]{x2202}_{1},\ldots ,\unicode[STIX]{x2202}_{M}$. Following 2.1.17, we write
$\unicode[STIX]{x2202}_{1},\ldots ,\unicode[STIX]{x2202}_{M}$. Following 2.1.17, we write
We have the following lemma, using the notation ![]() $\text{}\underline{0}=(0,\ldots ,0)$.
$\text{}\underline{0}=(0,\ldots ,0)$.
Lemma 3.3.2. Let ![]() $P\in D_{k}^{\dagger }$, there exist
$P\in D_{k}^{\dagger }$, there exist ![]() $P_{1},\ldots ,P_{M}\in D_{k}^{\dagger }$ and
$P_{1},\ldots ,P_{M}\in D_{k}^{\dagger }$ and ![]() $a_{\text{}\underline{0}}\in {\mathcal{O}}_{\mathfrak{X}_{0},\mathbb{Q}}(\mathfrak{U}_{0})$ such that
$a_{\text{}\underline{0}}\in {\mathcal{O}}_{\mathfrak{X}_{0},\mathbb{Q}}(\mathfrak{U}_{0})$ such that
Proof. The proof of this lemma is essentially the proof of the Spencer lemma by Berthelot [Reference Berthelot6, 3.2.1] for the case ![]() $k=0$, meaning for the sheaf of arithmetic differential operators. Let us denote
$k=0$, meaning for the sheaf of arithmetic differential operators. Let us denote ![]() $\text{}\underline{1}=(1,0,\ldots ,0)\in \mathbb{N}^{M}$ and by
$\text{}\underline{1}=(1,0,\ldots ,0)\in \mathbb{N}^{M}$ and by ![]() $OP_{1}$ the set of operators in
$OP_{1}$ the set of operators in ![]() $D_{k}^{\dagger }$ such that
$D_{k}^{\dagger }$ such that ![]() $a_{\text{}\underline{\unicode[STIX]{x1D708}}}=0$ if
$a_{\text{}\underline{\unicode[STIX]{x1D708}}}=0$ if ![]() $\unicode[STIX]{x1D708}_{1}\neq 0$. Let
$\unicode[STIX]{x1D708}_{1}\neq 0$. Let ![]() $P=\sum _{\text{}\underline{\unicode[STIX]{x1D708}}}\unicode[STIX]{x1D71B}^{k|\text{}\underline{\unicode[STIX]{x1D708}}|}a_{\text{}\underline{\unicode[STIX]{x1D708}}}\text{}\underline{\unicode[STIX]{x2202}}^{[\text{}\underline{\unicode[STIX]{x1D708}}]}\in D_{k}^{\dagger }$, and consider
$P=\sum _{\text{}\underline{\unicode[STIX]{x1D708}}}\unicode[STIX]{x1D71B}^{k|\text{}\underline{\unicode[STIX]{x1D708}}|}a_{\text{}\underline{\unicode[STIX]{x1D708}}}\text{}\underline{\unicode[STIX]{x2202}}^{[\text{}\underline{\unicode[STIX]{x1D708}}]}\in D_{k}^{\dagger }$, and consider
then, as ![]() $|1/\unicode[STIX]{x1D708}_{1}|_{p}=O(|\unicode[STIX]{x1D708}_{1}|_{p})=O(|\text{}\underline{\unicode[STIX]{x1D708}}|_{p})$ when
$|1/\unicode[STIX]{x1D708}_{1}|_{p}=O(|\unicode[STIX]{x1D708}_{1}|_{p})=O(|\text{}\underline{\unicode[STIX]{x1D708}}|_{p})$ when ![]() $|\text{}\underline{\unicode[STIX]{x1D708}}|_{p}\rightarrow +\infty$, this operator
$|\text{}\underline{\unicode[STIX]{x1D708}}|_{p}\rightarrow +\infty$, this operator ![]() $P_{1}$ belongs to
$P_{1}$ belongs to ![]() $D_{k}^{\dagger }$ (here
$D_{k}^{\dagger }$ (here ![]() $|.|_{p}$ is the usual
$|.|_{p}$ is the usual ![]() $p$-adic norm over the field
$p$-adic norm over the field ![]() $\mathbb{Q}$). Moreover, since we have the identity
$\mathbb{Q}$). Moreover, since we have the identity
we get that ![]() $P=P_{1}\unicode[STIX]{x2202}_{1}+Q_{1}$ where
$P=P_{1}\unicode[STIX]{x2202}_{1}+Q_{1}$ where ![]() $Q_{1}\in OP_{1}$. We can now apply the same procedure to
$Q_{1}\in OP_{1}$. We can now apply the same procedure to ![]() $Q_{1}$ relatively to
$Q_{1}$ relatively to ![]() $\unicode[STIX]{x2202}_{2}$. Doing this, we see that there exist
$\unicode[STIX]{x2202}_{2}$. Doing this, we see that there exist ![]() $P_{2}\in D_{k}^{\dagger }$ and
$P_{2}\in D_{k}^{\dagger }$ and ![]() $Q_{2}$ with no terms containing neither
$Q_{2}$ with no terms containing neither ![]() $\unicode[STIX]{x2202}_{1}$, nor
$\unicode[STIX]{x2202}_{1}$, nor ![]() $\unicode[STIX]{x2202}_{2}$, such that
$\unicode[STIX]{x2202}_{2}$, such that ![]() $P=P_{1}\unicode[STIX]{x2202}_{1}+P_{2}\unicode[STIX]{x2202}_{2}+Q_{2}$. We finally find the lemma iterating
$P=P_{1}\unicode[STIX]{x2202}_{1}+P_{2}\unicode[STIX]{x2202}_{2}+Q_{2}$. We finally find the lemma iterating ![]() $M$ times. Note that the
$M$ times. Note that the ![]() $a_{\text{}\underline{0}}$ term given by the lemma is necessarily the same as the initial
$a_{\text{}\underline{0}}$ term given by the lemma is necessarily the same as the initial ![]() $a_{\text{}\underline{0}}$ term of
$a_{\text{}\underline{0}}$ term of ![]() $P$.◻
$P$.◻
This allows us to prove the
Lemma 3.3.3. There is a presentation

Proof. Let ![]() $\mathfrak{V}_{0}\subset \mathfrak{U}_{0}$ be affine, and denote by
$\mathfrak{V}_{0}\subset \mathfrak{U}_{0}$ be affine, and denote by ![]() $D_{k}^{\dagger }=\unicode[STIX]{x1D6E4}(\mathfrak{V}_{0},\mathscr{D}_{\mathfrak{X}_{0},k}^{\dagger })$, we have to prove that we have a presentation, with the same maps as in the statement
$D_{k}^{\dagger }=\unicode[STIX]{x1D6E4}(\mathfrak{V}_{0},\mathscr{D}_{\mathfrak{X}_{0},k}^{\dagger })$, we have to prove that we have a presentation, with the same maps as in the statement
Let ![]() $P\in D_{k}^{\dagger }$,
$P\in D_{k}^{\dagger }$, ![]() $P=\sum _{\text{}\underline{\unicode[STIX]{x1D708}}}\unicode[STIX]{x1D71B}^{k|\text{}\underline{\unicode[STIX]{x1D708}}|}a_{\text{}\underline{\unicode[STIX]{x1D708}}}\text{}\underline{\unicode[STIX]{x2202}}^{[\text{}\underline{\unicode[STIX]{x1D708}}]}$, such that
$P=\sum _{\text{}\underline{\unicode[STIX]{x1D708}}}\unicode[STIX]{x1D71B}^{k|\text{}\underline{\unicode[STIX]{x1D708}}|}a_{\text{}\underline{\unicode[STIX]{x1D708}}}\text{}\underline{\unicode[STIX]{x2202}}^{[\text{}\underline{\unicode[STIX]{x1D708}}]}$, such that ![]() $P(1)=a_{\text{}\underline{0}}=0$. By the previous lemma, there exist
$P(1)=a_{\text{}\underline{0}}=0$. By the previous lemma, there exist ![]() $P_{1},\ldots ,P_{M}$ such that
$P_{1},\ldots ,P_{M}$ such that ![]() $P=\sum _{i=1}^{M}P_{i}\unicode[STIX]{x2202}_{i}$ so that
$P=\sum _{i=1}^{M}P_{i}\unicode[STIX]{x2202}_{i}$ so that ![]() $P\in \text{im}(\unicode[STIX]{x1D713})$.◻
$P\in \text{im}(\unicode[STIX]{x1D713})$.◻
Let us come back now to the proof of the proposition. Using this presentation, we see that ![]() ${\mathcal{O}}_{\mathfrak{X}_{0},\mathbb{Q}}$ is a coherent
${\mathcal{O}}_{\mathfrak{X}_{0},\mathbb{Q}}$ is a coherent ![]() $\mathscr{D}_{\mathfrak{X}_{0},k}^{\dagger }$-module, and that we have canonical compatibility relations
$\mathscr{D}_{\mathfrak{X}_{0},k}^{\dagger }$-module, and that we have canonical compatibility relations
Finally the ![]() $\mathscr{D}_{\mathfrak{X}_{0},\infty }$-module
$\mathscr{D}_{\mathfrak{X}_{0},\infty }$-module ![]() ${\mathcal{O}}_{\mathfrak{X}_{0},\mathbb{Q}}$ is isomorphic to the constant projective system of coherent
${\mathcal{O}}_{\mathfrak{X}_{0},\mathbb{Q}}$ is isomorphic to the constant projective system of coherent ![]() $\mathscr{D}_{\mathfrak{X}_{0},k}^{\dagger }$-modules
$\mathscr{D}_{\mathfrak{X}_{0},k}^{\dagger }$-modules ![]() $({\mathcal{O}}_{\mathfrak{X}_{0},\mathbb{Q}})$ and is an element of
$({\mathcal{O}}_{\mathfrak{X}_{0},\mathbb{Q}})$ and is an element of ![]() ${\mathcal{C}}_{\mathfrak{X}_{0}}$. As explained at the beginning of the proof, this implies that
${\mathcal{C}}_{\mathfrak{X}_{0}}$. As explained at the beginning of the proof, this implies that ![]() ${\mathcal{O}}_{\langle \mathfrak{X}_{0}\rangle ,\mathbb{Q}}\in {\mathcal{C}}_{\langle \mathfrak{X}_{0}\rangle }$. This ends the proof of the proposition.◻
${\mathcal{O}}_{\langle \mathfrak{X}_{0}\rangle ,\mathbb{Q}}\in {\mathcal{C}}_{\langle \mathfrak{X}_{0}\rangle }$. This ends the proof of the proposition.◻
For the second example, we consider a Cartier divisor ![]() $\mathfrak{Z}$, which is assumed to be smooth over
$\mathfrak{Z}$, which is assumed to be smooth over ![]() $\mathfrak{o}$, of the formal scheme
$\mathfrak{o}$, of the formal scheme ![]() $\mathfrak{X}_{0}$. As above, we denote by
$\mathfrak{X}_{0}$. As above, we denote by ![]() $\mathfrak{X}_{0,\mathbb{Q}}$ and
$\mathfrak{X}_{0,\mathbb{Q}}$ and ![]() $\mathfrak{Z}_{\mathbb{Q}}$ the rigid-analytic spaces associated with
$\mathfrak{Z}_{\mathbb{Q}}$ the rigid-analytic spaces associated with ![]() $\mathfrak{X}_{0}$ and
$\mathfrak{X}_{0}$ and ![]() $\mathfrak{Z}$, respectively. Let
$\mathfrak{Z}$, respectively. Let ![]() $U=\mathfrak{X}_{0,\mathbb{Q}}\backslash \mathfrak{Z}_{\mathbb{Q}}$ be the open complement, and
$U=\mathfrak{X}_{0,\mathbb{Q}}\backslash \mathfrak{Z}_{\mathbb{Q}}$ be the open complement, and ![]() $j:U\rightarrow \mathfrak{X}_{0,\mathbb{Q}}$ the inclusion of rigid spaces. We have the specialization map
$j:U\rightarrow \mathfrak{X}_{0,\mathbb{Q}}$ the inclusion of rigid spaces. We have the specialization map ![]() $\text{sp}:\mathfrak{X}_{0,\mathbb{Q}}\rightarrow \mathfrak{X}_{0}$.
$\text{sp}:\mathfrak{X}_{0,\mathbb{Q}}\rightarrow \mathfrak{X}_{0}$.
Proposition 3.3.4. The sheaf ![]() $\text{sp}_{\ast }j_{\ast }{\mathcal{O}}_{U}$ is a coadmissible
$\text{sp}_{\ast }j_{\ast }{\mathcal{O}}_{U}$ is a coadmissible ![]() $\mathscr{D}_{\mathfrak{X}_{0},\infty }$-module.
$\mathscr{D}_{\mathfrak{X}_{0},\infty }$-module.
Proof. We freely use the notation and terminology of [Reference Berthelot6, 4.0.1]. Let us consider
and ![]() ${\mathcal{V}}_{s}(V_{k})$ the set of strict neighborhoods of
${\mathcal{V}}_{s}(V_{k})$ the set of strict neighborhoods of ![]() $V_{k}$. Note that
$V_{k}$. Note that ![]() $V_{k}$ is well defined since
$V_{k}$ is well defined since ![]() $\mathfrak{Z}$ is a Cartier divisor of
$\mathfrak{Z}$ is a Cartier divisor of ![]() $\mathfrak{X}_{0}$. If
$\mathfrak{X}_{0}$. If ![]() $\mathfrak{V}=\text{Spf}A$ is an open affine subset of
$\mathfrak{V}=\text{Spf}A$ is an open affine subset of ![]() $\mathfrak{X}_{0}$, such that
$\mathfrak{X}_{0}$, such that ![]() $\mathfrak{Z}\bigcap \mathfrak{V}=V(t_{1})$, then
$\mathfrak{Z}\bigcap \mathfrak{V}=V(t_{1})$, then
Note that
We introduce also
where ![]() $j_{W}$ :
$j_{W}$ : ![]() $W\rightarrow \mathfrak{X}_{0,\mathbb{Q}}$ is the inclusion in
$W\rightarrow \mathfrak{X}_{0,\mathbb{Q}}$ is the inclusion in ![]() $\mathfrak{X}_{0,\mathbb{Q}}$ of a strict neighborhood
$\mathfrak{X}_{0,\mathbb{Q}}$ of a strict neighborhood ![]() $W$ of
$W$ of ![]() $V_{k}$. We have an inclusion
$V_{k}$. We have an inclusion ![]() $V_{k}\subset V_{k+1}$ and
$V_{k}\subset V_{k+1}$ and ![]() $V_{k+1}$ is a strict neighborhood of
$V_{k+1}$ is a strict neighborhood of ![]() $V_{k}$, so that
$V_{k}$, so that ![]() ${\mathcal{V}}_{s}(V_{k+1})\subset {\mathcal{V}}_{s}(V_{k})$. As a consequence, for any
${\mathcal{V}}_{s}(V_{k+1})\subset {\mathcal{V}}_{s}(V_{k})$. As a consequence, for any ![]() $k$, there is a canonical morphism
$k$, there is a canonical morphism ![]() ${\mathcal{E}}_{k+1}^{\dagger }\rightarrow {\mathcal{E}}_{k}^{\dagger }$. Moreover, since
${\mathcal{E}}_{k+1}^{\dagger }\rightarrow {\mathcal{E}}_{k}^{\dagger }$. Moreover, since ![]() $\text{sp}_{\ast }$ commutes with projective limits, we have
$\text{sp}_{\ast }$ commutes with projective limits, we have
The proposition will follow from the
(i) The sheaf
 ${\mathcal{E}}_{k}^{\dagger }$ is a coherent
${\mathcal{E}}_{k}^{\dagger }$ is a coherent  $\mathscr{D}_{\mathfrak{X}_{0},k}^{\dagger }$-module.
$\mathscr{D}_{\mathfrak{X}_{0},k}^{\dagger }$-module.(ii) The canonical map
 ${\mathcal{E}}_{k+1}^{\dagger }\rightarrow {\mathcal{E}}_{k}^{\dagger }$ induces a canonical isomorphism of coherent
${\mathcal{E}}_{k+1}^{\dagger }\rightarrow {\mathcal{E}}_{k}^{\dagger }$ induces a canonical isomorphism of coherent  $\mathscr{D}_{\mathfrak{X}_{0},k}^{\dagger }$-modules,
$\mathscr{D}_{\mathfrak{X}_{0},k}^{\dagger }$-modules,  $$\begin{eqnarray}\mathscr{D}_{\mathfrak{X}_{0},k}^{\dagger }\otimes _{\mathscr{ D}_{\mathfrak{X}_{0},k+1}^{\dagger }}{\mathcal{E}}_{k+1}^{\dagger }\simeq {\mathcal{E}}_{k}^{\dagger }.\end{eqnarray}$$
$$\begin{eqnarray}\mathscr{D}_{\mathfrak{X}_{0},k}^{\dagger }\otimes _{\mathscr{ D}_{\mathfrak{X}_{0},k+1}^{\dagger }}{\mathcal{E}}_{k+1}^{\dagger }\simeq {\mathcal{E}}_{k}^{\dagger }.\end{eqnarray}$$
Proof. Let ![]() $W$ be admissible open in
$W$ be admissible open in ![]() $\mathfrak{X}_{L}$. Then
$\mathfrak{X}_{L}$. Then ![]() $W$ is the generic fiber of some Zariski open
$W$ is the generic fiber of some Zariski open ![]() $\mathfrak{W}^{\prime }$ of
$\mathfrak{W}^{\prime }$ of ![]() $\mathfrak{X}^{\prime }$ where
$\mathfrak{X}^{\prime }$ where ![]() $\text{pr}:\mathfrak{X}^{\prime }\rightarrow \mathfrak{X}_{0}$ is an admissible blow-up of
$\text{pr}:\mathfrak{X}^{\prime }\rightarrow \mathfrak{X}_{0}$ is an admissible blow-up of ![]() $\mathfrak{X}_{0}$. Denote by
$\mathfrak{X}_{0}$. Denote by ![]() $j^{\prime }$ the inclusion :
$j^{\prime }$ the inclusion : ![]() $\mathfrak{W}^{\prime }{\hookrightarrow}\mathfrak{X}^{\prime }$. Then
$\mathfrak{W}^{\prime }{\hookrightarrow}\mathfrak{X}^{\prime }$. Then ![]() $j_{\ast }^{\prime }{\mathcal{O}}_{\mathfrak{W}^{\prime },\mathbb{Q}}$ is a
$j_{\ast }^{\prime }{\mathcal{O}}_{\mathfrak{W}^{\prime },\mathbb{Q}}$ is a ![]() $\mathscr{D}_{\mathfrak{X}^{\prime },k^{\prime }}^{\dagger }$-module, for
$\mathscr{D}_{\mathfrak{X}^{\prime },k^{\prime }}^{\dagger }$-module, for ![]() $k^{\prime }\geqslant k_{\mathfrak{X}^{\prime }}$, so that the sheaf
$k^{\prime }\geqslant k_{\mathfrak{X}^{\prime }}$, so that the sheaf ![]() $\text{sp}_{\ast }j_{W\ast }{\mathcal{O}}_{W}=\text{pr}_{\ast }j_{\ast }^{\prime }{\mathcal{O}}_{\mathfrak{W}^{\prime },\mathbb{Q}}$ has an action of
$\text{sp}_{\ast }j_{W\ast }{\mathcal{O}}_{W}=\text{pr}_{\ast }j_{\ast }^{\prime }{\mathcal{O}}_{\mathfrak{W}^{\prime },\mathbb{Q}}$ has an action of ![]() $\mathscr{D}_{\mathfrak{X}_{0},k^{\prime }}^{\dagger }$ as
$\mathscr{D}_{\mathfrak{X}_{0},k^{\prime }}^{\dagger }$ as ![]() $\mathscr{D}_{\mathfrak{X}_{0},k^{\prime }}^{\dagger }=\text{pr}_{\ast }\mathscr{D}_{\mathfrak{X}^{\prime },k^{\prime }}^{\dagger }$ by 2.3.8. In particular, the sheaf
$\mathscr{D}_{\mathfrak{X}_{0},k^{\prime }}^{\dagger }=\text{pr}_{\ast }\mathscr{D}_{\mathfrak{X}^{\prime },k^{\prime }}^{\dagger }$ by 2.3.8. In particular, the sheaf ![]() $\text{sp}_{\ast }j_{W\ast }{\mathcal{O}}_{W}$ is a
$\text{sp}_{\ast }j_{W\ast }{\mathcal{O}}_{W}$ is a ![]() $\mathscr{D}_{\mathfrak{X}_{0},\infty }$-module for any admissible open
$\mathscr{D}_{\mathfrak{X}_{0},\infty }$-module for any admissible open ![]() $W$. As a consequence, the sheaf
$W$. As a consequence, the sheaf ![]() ${\mathcal{E}}_{k}^{\dagger }$ has a structure of
${\mathcal{E}}_{k}^{\dagger }$ has a structure of ![]() $\mathscr{D}_{\mathfrak{X}_{0},\infty }$-module as well. Let us check locally that this structure extends to a structure of
$\mathscr{D}_{\mathfrak{X}_{0},\infty }$-module as well. Let us check locally that this structure extends to a structure of ![]() $\mathscr{D}_{\mathfrak{X}_{0},k}^{\dagger }$-module. Let
$\mathscr{D}_{\mathfrak{X}_{0},k}^{\dagger }$-module. Let ![]() $\mathfrak{V}=\text{Spf}A\subset \mathfrak{X}_{0}$ be affine open in
$\mathfrak{V}=\text{Spf}A\subset \mathfrak{X}_{0}$ be affine open in ![]() $\mathfrak{X}_{0}$ such that
$\mathfrak{X}_{0}$ such that ![]() $\mathfrak{Z}\bigcap \mathfrak{V}=V(t_{1})$ where
$\mathfrak{Z}\bigcap \mathfrak{V}=V(t_{1})$ where ![]() $t_{1}$ is a local coordinate on
$t_{1}$ is a local coordinate on ![]() $\mathfrak{V}$. Then we have the following description, where
$\mathfrak{V}$. Then we have the following description, where ![]() $A_{L}=A\otimes L$ is an affinoid algebra,
$A_{L}=A\otimes L$ is an affinoid algebra,
Denote by ![]() $\unicode[STIX]{x2202}_{1}$ the derivation corresponding to the coordinate
$\unicode[STIX]{x2202}_{1}$ the derivation corresponding to the coordinate ![]() $t_{1}$, and
$t_{1}$, and ![]() $\unicode[STIX]{x2202}_{2},\ldots ,\unicode[STIX]{x2202}_{M}$ the other derivations. Let us denote
$\unicode[STIX]{x2202}_{2},\ldots ,\unicode[STIX]{x2202}_{M}$ the other derivations. Let us denote ![]() $D_{k}^{\dagger }=\mathscr{D}_{\mathfrak{X}_{0},k}^{\dagger }(\mathfrak{V})$, then we have the following description using 2.1.17
$D_{k}^{\dagger }=\mathscr{D}_{\mathfrak{X}_{0},k}^{\dagger }(\mathfrak{V})$, then we have the following description using 2.1.17
To prove the lemma it is thus enough to check the
Lemma 3.3.6. There is a presentation

Proof. Again, we follow the proof by Berthelot [Reference Berthelot6, 4.4.2] of the analogous statement for arithmetic differential operators. It is clear that ![]() $\text{im}(\unicode[STIX]{x1D713})\subset \ker (\unicode[STIX]{x1D711})$. Observe that
$\text{im}(\unicode[STIX]{x1D713})\subset \ker (\unicode[STIX]{x1D711})$. Observe that
Let ![]() $h=\sum a_{\unicode[STIX]{x1D708}}\unicode[STIX]{x1D71B}^{k\unicode[STIX]{x1D708}}t_{1}^{-\unicode[STIX]{x1D708}-1}\in {\mathcal{E}}_{k}^{\dagger }(\mathfrak{V})$, then
$h=\sum a_{\unicode[STIX]{x1D708}}\unicode[STIX]{x1D71B}^{k\unicode[STIX]{x1D708}}t_{1}^{-\unicode[STIX]{x1D708}-1}\in {\mathcal{E}}_{k}^{\dagger }(\mathfrak{V})$, then ![]() $P=\sum _{\unicode[STIX]{x1D708}}(-1)^{\unicode[STIX]{x1D708}}\unicode[STIX]{x1D71B}^{k\unicode[STIX]{x1D708}}a_{\unicode[STIX]{x1D708}}\unicode[STIX]{x2202}_{1}^{[\unicode[STIX]{x1D708}]}$ belongs to
$P=\sum _{\unicode[STIX]{x1D708}}(-1)^{\unicode[STIX]{x1D708}}\unicode[STIX]{x1D71B}^{k\unicode[STIX]{x1D708}}a_{\unicode[STIX]{x1D708}}\unicode[STIX]{x2202}_{1}^{[\unicode[STIX]{x1D708}]}$ belongs to ![]() $D_{k}^{\dagger }$ and
$D_{k}^{\dagger }$ and ![]() $P(1/t_{1})=h$, so that
$P(1/t_{1})=h$, so that ![]() $\unicode[STIX]{x1D711}$ is surjective. Let now
$\unicode[STIX]{x1D711}$ is surjective. Let now ![]() $P\in \ker (\unicode[STIX]{x1D711})$, then, applying repeatedly Lemma 3.3.2, we see that modulo
$P\in \ker (\unicode[STIX]{x1D711})$, then, applying repeatedly Lemma 3.3.2, we see that modulo ![]() $\text{im}(\unicode[STIX]{x1D713})$,
$\text{im}(\unicode[STIX]{x1D713})$, ![]() $P$ can be written
$P$ can be written ![]() $P=\sum _{\unicode[STIX]{x1D708}}\unicode[STIX]{x1D71B}^{k\unicode[STIX]{x1D708}}a_{\unicode[STIX]{x1D708}}\unicode[STIX]{x2202}_{1}^{[\unicode[STIX]{x1D708}]}$, with coefficients
$P=\sum _{\unicode[STIX]{x1D708}}\unicode[STIX]{x1D71B}^{k\unicode[STIX]{x1D708}}a_{\unicode[STIX]{x1D708}}\unicode[STIX]{x2202}_{1}^{[\unicode[STIX]{x1D708}]}$, with coefficients ![]() $a_{\unicode[STIX]{x1D708}}\in A_{L}$ such that
$a_{\unicode[STIX]{x1D708}}\in A_{L}$ such that ![]() $\sum _{\unicode[STIX]{x1D708}}\unicode[STIX]{x1D71B}^{k\unicode[STIX]{x1D708}}(-1)^{\unicode[STIX]{x1D708}}a_{\unicode[STIX]{x1D708}}(t_{1})^{-\unicode[STIX]{x1D708}-1}=0\in {\mathcal{E}}_{k}^{\dagger }(\mathfrak{V})$. Moreover, there exist
$\sum _{\unicode[STIX]{x1D708}}\unicode[STIX]{x1D71B}^{k\unicode[STIX]{x1D708}}(-1)^{\unicode[STIX]{x1D708}}a_{\unicode[STIX]{x1D708}}(t_{1})^{-\unicode[STIX]{x1D708}-1}=0\in {\mathcal{E}}_{k}^{\dagger }(\mathfrak{V})$. Moreover, there exist ![]() $C>0,\unicode[STIX]{x1D702}<1$ such that
$C>0,\unicode[STIX]{x1D702}<1$ such that ![]() $|a_{\unicode[STIX]{x1D708}}|<C\unicode[STIX]{x1D702}^{\unicode[STIX]{x1D708}}$ where
$|a_{\unicode[STIX]{x1D708}}|<C\unicode[STIX]{x1D702}^{\unicode[STIX]{x1D708}}$ where ![]() $|\cdot |$ is a Banach norm on
$|\cdot |$ is a Banach norm on ![]() $A_{L}$. Denote
$A_{L}$. Denote
Let us now state the following
Auxiliary result 3.3.7. There exist ![]() $C^{\prime }>0,\unicode[STIX]{x1D702}^{\prime }<1$ such that
$C^{\prime }>0,\unicode[STIX]{x1D702}^{\prime }<1$ such that ![]() $|b_{j}|<C^{\prime }|\unicode[STIX]{x1D71B}|^{kj}{\unicode[STIX]{x1D702}^{\prime }}^{j}$.
$|b_{j}|<C^{\prime }|\unicode[STIX]{x1D71B}|^{kj}{\unicode[STIX]{x1D702}^{\prime }}^{j}$.
Proof. Berthelot proved this lemma for ![]() $k=0$ in [Reference Berthelot6, 4.2.1]. Let us check that the proof can be adapted to any
$k=0$ in [Reference Berthelot6, 4.2.1]. Let us check that the proof can be adapted to any ![]() $k$. Since
$k$. Since ![]() $\mathfrak{V}$ is smooth, the affinoid algebra
$\mathfrak{V}$ is smooth, the affinoid algebra ![]() $A_{L}$ is reduced, so that the spectral seminorm is a norm and defines the Banach topology on
$A_{L}$ is reduced, so that the spectral seminorm is a norm and defines the Banach topology on ![]() $A_{L}$. All Banach norms being equivalent, we can use this norm to prove the statement, which we keep on denoting by
$A_{L}$. All Banach norms being equivalent, we can use this norm to prove the statement, which we keep on denoting by ![]() $|\cdot |$. Let
$|\cdot |$. Let ![]() $\mathfrak{V}_{\mathbb{Q}}=\text{Spf}A_{L}$ be the generic fiber of
$\mathfrak{V}_{\mathbb{Q}}=\text{Spf}A_{L}$ be the generic fiber of ![]() $\mathfrak{V}$, seen as rigid-analytic space. Let
$\mathfrak{V}$, seen as rigid-analytic space. Let ![]() $\unicode[STIX]{x1D702}^{\prime }>\unicode[STIX]{x1D702}$, such that
$\unicode[STIX]{x1D702}^{\prime }>\unicode[STIX]{x1D702}$, such that ![]() $\unicode[STIX]{x1D702}^{\prime }<1$ and some power
$\unicode[STIX]{x1D702}^{\prime }<1$ and some power ![]() $(\unicode[STIX]{x1D702}^{\prime })^{n}$ lies in the valuation group of
$(\unicode[STIX]{x1D702}^{\prime })^{n}$ lies in the valuation group of ![]() $L$ for some positive integer
$L$ for some positive integer ![]() $n$. We consider the following admissible cover of
$n$. We consider the following admissible cover of ![]() $\mathfrak{V}_{\mathbb{Q}}$ by open
$\mathfrak{V}_{\mathbb{Q}}$ by open ![]() $V_{1}$ and
$V_{1}$ and ![]() $V_{2}$ defined by
$V_{2}$ defined by
It is enough to bound the spectral norm of the ![]() $b_{j}$ on each of this affinoid open. As
$b_{j}$ on each of this affinoid open. As ![]() $A_{L}$ is reduced,
$A_{L}$ is reduced, ![]() $\unicode[STIX]{x1D6E4}(V_{1},{\mathcal{O}}_{\mathfrak{X}_{L}})$, resp.
$\unicode[STIX]{x1D6E4}(V_{1},{\mathcal{O}}_{\mathfrak{X}_{L}})$, resp. ![]() $\unicode[STIX]{x1D6E4}(V_{2},{\mathcal{O}}_{\mathfrak{X}_{L}})$, is reduced as well by Corollary 10 of [Reference Bosch, Güntzer and Remmert8, 7.3.2], so that the spectral norm induced a norm on these two affinoid open sets. If
$\unicode[STIX]{x1D6E4}(V_{2},{\mathcal{O}}_{\mathfrak{X}_{L}})$, is reduced as well by Corollary 10 of [Reference Bosch, Güntzer and Remmert8, 7.3.2], so that the spectral norm induced a norm on these two affinoid open sets. If ![]() $x\in V_{1}$, then
$x\in V_{1}$, then
Consider
which is the Banach algebra of analytic functions on the affinoid ![]() $\{x\in \mathfrak{V}_{\mathbb{Q}}\,|\,|\unicode[STIX]{x1D71B}|^{k}\leqslant |t_{1}(x)|\leqslant 1\}$. Obviously,
$\{x\in \mathfrak{V}_{\mathbb{Q}}\,|\,|\unicode[STIX]{x1D71B}|^{k}\leqslant |t_{1}(x)|\leqslant 1\}$. Obviously, ![]() ${\mathcal{E}}_{k}^{\dagger }(\mathfrak{V})\subset B$. If
${\mathcal{E}}_{k}^{\dagger }(\mathfrak{V})\subset B$. If ![]() $x\in V_{2}$, then
$x\in V_{2}$, then
so that the series ![]() $\sum _{\unicode[STIX]{x1D708}}\unicode[STIX]{x1D71B}^{k\unicode[STIX]{x1D708}}(-1)^{\unicode[STIX]{x1D708}}a_{\unicode[STIX]{x1D708}}(t_{1})^{-\unicode[STIX]{x1D708}-1}$ converges to some element
$\sum _{\unicode[STIX]{x1D708}}\unicode[STIX]{x1D71B}^{k\unicode[STIX]{x1D708}}(-1)^{\unicode[STIX]{x1D708}}a_{\unicode[STIX]{x1D708}}(t_{1})^{-\unicode[STIX]{x1D708}-1}$ converges to some element ![]() $b\in \unicode[STIX]{x1D6E4}(V_{2},{\mathcal{O}}_{\mathfrak{X}_{L}})$. Moreover, the image of this element
$b\in \unicode[STIX]{x1D6E4}(V_{2},{\mathcal{O}}_{\mathfrak{X}_{L}})$. Moreover, the image of this element ![]() $b$ in
$b$ in ![]() $B$ is zero. The support of
$B$ is zero. The support of ![]() $b$ is a closed affinoid subset of
$b$ is a closed affinoid subset of ![]() $V_{2}$, and at each point
$V_{2}$, and at each point ![]() $x$ of this support,
$x$ of this support, ![]() $|t_{1}(x)|<|\unicode[STIX]{x1D71B}^{k}|$. By the maximum principle, increasing
$|t_{1}(x)|<|\unicode[STIX]{x1D71B}^{k}|$. By the maximum principle, increasing ![]() $\unicode[STIX]{x1D702}^{\prime }$ if necessary, provided that
$\unicode[STIX]{x1D702}^{\prime }$ if necessary, provided that ![]() $\unicode[STIX]{x1D702}^{\prime }<1$, we can assume that the support is contained in
$\unicode[STIX]{x1D702}^{\prime }<1$, we can assume that the support is contained in ![]() $\{x\,|\,|t_{1}(x)|\leqslant \,|\unicode[STIX]{x1D71B}|^{k}(2\unicode[STIX]{x1D702}^{\prime }-1)\}$, so that
$\{x\,|\,|t_{1}(x)|\leqslant \,|\unicode[STIX]{x1D71B}|^{k}(2\unicode[STIX]{x1D702}^{\prime }-1)\}$, so that ![]() $h=0$ restricted to
$h=0$ restricted to ![]() $V_{2}$. Then we have the following upper bound for
$V_{2}$. Then we have the following upper bound for ![]() $x\in V_{2}$
$x\in V_{2}$
 $$\begin{eqnarray}|b_{j}(x)|=\left|\mathop{\sum }_{\unicode[STIX]{x1D708}\geqslant j+1}\unicode[STIX]{x1D71B}^{k\unicode[STIX]{x1D708}}a_{\unicode[STIX]{x1D708}}(t_{1}(x))^{j-\unicode[STIX]{x1D708}}\right|\leqslant C|\unicode[STIX]{x1D71B}|^{kj}{\unicode[STIX]{x1D702}^{\prime }}^{j}.\end{eqnarray}$$
$$\begin{eqnarray}|b_{j}(x)|=\left|\mathop{\sum }_{\unicode[STIX]{x1D708}\geqslant j+1}\unicode[STIX]{x1D71B}^{k\unicode[STIX]{x1D708}}a_{\unicode[STIX]{x1D708}}(t_{1}(x))^{j-\unicode[STIX]{x1D708}}\right|\leqslant C|\unicode[STIX]{x1D71B}|^{kj}{\unicode[STIX]{x1D702}^{\prime }}^{j}.\end{eqnarray}$$◻
Let us come back to the proof of 3.3.6. We need to check that ![]() $P=\sum _{\unicode[STIX]{x1D708}}\unicode[STIX]{x1D71B}^{k\unicode[STIX]{x1D708}}a_{\unicode[STIX]{x1D708}}\unicode[STIX]{x2202}_{1}^{[\unicode[STIX]{x1D708}]}$, such that
$P=\sum _{\unicode[STIX]{x1D708}}\unicode[STIX]{x1D71B}^{k\unicode[STIX]{x1D708}}a_{\unicode[STIX]{x1D708}}\unicode[STIX]{x2202}_{1}^{[\unicode[STIX]{x1D708}]}$, such that ![]() $\sum _{\unicode[STIX]{x1D708}}\unicode[STIX]{x1D71B}^{k\unicode[STIX]{x1D708}}(-1)^{\unicode[STIX]{x1D708}}a_{\unicode[STIX]{x1D708}}(t_{1})^{-\unicode[STIX]{x1D708}-1}=0\in {\mathcal{E}}_{k}^{\dagger }(\mathfrak{V})$, belongs to
$\sum _{\unicode[STIX]{x1D708}}\unicode[STIX]{x1D71B}^{k\unicode[STIX]{x1D708}}(-1)^{\unicode[STIX]{x1D708}}a_{\unicode[STIX]{x1D708}}(t_{1})^{-\unicode[STIX]{x1D708}-1}=0\in {\mathcal{E}}_{k}^{\dagger }(\mathfrak{V})$, belongs to ![]() $\text{im}(\unicode[STIX]{x1D713})$. Let us define
$\text{im}(\unicode[STIX]{x1D713})$. Let us define
and
that belongs to ![]() $D_{k}^{\dagger }$ thanks to 3.3.7. Berthelot checked at the end of the proof of [Reference Berthelot6, 4.2.1], that
$D_{k}^{\dagger }$ thanks to 3.3.7. Berthelot checked at the end of the proof of [Reference Berthelot6, 4.2.1], that ![]() $P=Qt_{1}$. But since this is true in
$P=Qt_{1}$. But since this is true in ![]() $D_{0}^{\dagger }$, this is also true in
$D_{0}^{\dagger }$, this is also true in ![]() $D_{k}^{\dagger }$ and
$D_{k}^{\dagger }$ and ![]() $P=Qt_{1}$. By hypothesis,
$P=Qt_{1}$. By hypothesis, ![]() $b_{0}=0$, and by Lemma 3.3.2, this implies that there exists
$b_{0}=0$, and by Lemma 3.3.2, this implies that there exists ![]() $Q_{1}\in D_{k}^{\dagger }$ such that
$Q_{1}\in D_{k}^{\dagger }$ such that ![]() $Q=Q_{1}\unicode[STIX]{x2202}_{1}$. We finally conclude that
$Q=Q_{1}\unicode[STIX]{x2202}_{1}$. We finally conclude that ![]() $P=Q_{1}\unicode[STIX]{x2202}_{1}t_{1}$ and that
$P=Q_{1}\unicode[STIX]{x2202}_{1}t_{1}$ and that ![]() $P\in \text{im}(\unicode[STIX]{x1D713})$.
$P\in \text{im}(\unicode[STIX]{x1D713})$.
This presentation proves (i) and (ii) of 3.3.5 and completes the proof of 3.3.4. ◻
We remark that results similar to 3.3.4 have recently been obtained independently and in slightly greater generality by Ardakov–Bode–Wadsley in their setting [Reference Ardakov, Bode and Wadsley2].
Acknowledgments
T.S. would like to acknowledge support of the Heisenberg programme of Deutsche Forschungsgemeinschaft (SCHM 3062/1-1) during 2014–2015 when starting to work on this project. M.S. is grateful for the hospitality and support of the following institutions where work on this project has been accomplished: Institut de Recherche Mathématique Avancée (IRMA) of the University of Strasbourg, Centre Henri Lebesgue, Institut de Recherche Mathématique de Rennes (IRMAR).