Introduction
Basic copper hydroxychloride salts are of much interest to a wide variety of researchers; in fields ranging from the development and use of fungicides (e.g. for the treatment of peronospora in vineyards) to those investigating frustrated magnetism. The description of the synthesis of a whole range of compositions, most notably by Feitknecht and co-workers, (Feitknecht, Reference Feitknecht1949; Oswald and Feitknecht, Reference Oswald and Feitknecht1964) are continued and extended today − at an industrial scale for some particular compositions. Erdös et al. (Reference Erdös, Denzler and Altorfer1981) have described in detail a series of (partly) hydrated basic copper hydroxychlorides that form at moderate temperatures through the corrosion of copper held at increasing temperatures in NH3-containing and oxygenated aqueous solutions of CaCl2. One of these, described as 4Cu(OH)2⋅CaCl2⋅3.5H2O, was estimated as tetragonal with at least a P42 symmetry and lattice of a = 9.392 and c = 15.077 Å, and was compared by Erdös et al. to the calumetite of Williams (Reference Williams1963). It was also observed to dehydrate via a complex sequence of further hydroxychloride phases. Another phase is described as rehydrating in a hexagonal lattice with composition 3Cu(OH)2⋅CaCl2⋅H2O, with a = 6.66 Å and c = 5.81 Å. This latter phase has been isolated synthetically and described, from natural samples, as centennialite, a relative of the kapellasite family (Crichton and Müller, Reference Crichton and Müller2017). The synthesis of single crystals has been further elaborated (Sun et al., Reference Sun, Huang, Pan and Mi2016), which has also afforded more detailed structural analysis at 213 K, to a noncentrosymmetric P3m1 with disordered Ca positions (Yoshida et al., Reference Yoshida, Noguchi, Matsushita, Ishii, Ihara, Oda, Okabe, Yamashita, Nakazawa, Takata, Kida, Narumi and Hagiwara2017). Centennialite, thus proposed, has a chemistry and lattice essentially as described by Erdös et al. and is, as are the kapellasites in general, a trigonal phase that exhibits the same 2-dimensional Kagome pattern of planar 4-coordinated Cu sites separated by M 2+ polyhedra much desired by investigators of frustrated magnetism, but more particularly in this case due to the significant mismatch between the ionic radii of the divalent cations, which limits site intermixing.
As part of their same study, Crichton and Müller also synthesised a composition that was identical to the initial phase of Erdös et al., with a composition of CaCu4(OH)8Cl2⋅3.5H2O and demonstrated that a centennialite could be obtained from it by heating, which reflected the measurements made previously upon their synthetic counterparts (Erdös et al., Reference Erdös, Denzler and Altorfer1981). The solution of that structure led to a proposition for a calumetite model that matched a variety of data from various sources, including those newly collected from Williams (Reference Williams1963) actual samples. Similar phases were also isolated by Lubej et al. (Reference Lubej, Koloini and Pohar2004) during optimisation of the synthetic processes involved in the production of Cuprablau-Z. Crichton and Müller's structural description led them to further propose a topological relationship between their proposed calumetite structure and the kapellasite-like centennialite. In doing so they generated a structural motif, which reduces to the tetragonal lattice shared by Erdös et al.'s observed intermediate hemihydrate. The structural similarity between these phases prompted Erdös et al. to promote topotaxy and pseudomorphosis in the sequence of phases observed. Williams’ calumetite has since been redefined with the formula to include essential Ca, as CaCu4(OH)8Cl2⋅3.5H2O (Miyawaki et al., Reference Miyawaki, Hatert, Pasero and Mills2019). This is in line with the expectations from the synthetic compound of Erdös et al., and the models refined against Williams’ samples by Crichton and Müller. This consequently discredited ‘vondechenite' (Schlüter et al., Reference Schlüter, Malcherek, Pohl and Schäfer2019) as identical to the pre-existing calumetite. The single-crystal results obtained by those authors were coincident to the structure presented in Crichton and Müller's table 6 and identical to the composition of the material produced by Erdös et al. (Reference Erdös, Denzler and Altorfer1981).
In an investigation of the wider utility of the same synthetic protocol used for the synthesis of the Ca-essential compounds (Tables 1–2), we have successfully produced synthetic equivalents to various kapellasites: Zn, a = 6.31468(10) Å and c = 5.72310(19) Å (cf. a = 6.300(1) Å and c = 5.733(1) Å, kapellasite; Krause et al., Reference Krause, Bernhardt, Braithwaite, Kolitsch and Pritchard2006); Mg, a = 6.27815(23) Å and c = 5.7595(5) Å (cf. a = 6.2733(4) Å and c = 5.7472(5) Å, haydeeite; Malcherek and Schlüter, Reference Malcherek and Schlüter2007); Mn, a = 6.42533(17) Å and c = 5.71048(11) Å (cf. a = 6.4168(4) Å and c = 5.7099(4) Å, misakiite; Nishio-Hamane et al., Reference Nishio-Hamane, Momma, Ohnishi, Shimobayashi, Miyawaki, Tomita, Okuma, Kampf and Minakawa2017), centennialite, calumetite (and both together), Crichton and Müller (Reference Crichton and Müller2017); clinoatacamite-like: Cd, with a = 6.3889(10) Å, b = 7.05329(11) Å, c = 9.3378(11) Å and β = 99.034(15)° (e.g. McQueen et al., Reference McQueen, Han, Freedman, Stephens, Lee and Nocera2011); Ni, with a = 6.1746(6) Å, b = 6.8821(5) Å, c = 9.0308(7) Å and β = 99.46(8)° and rhombohedral forms: Co, with a = 6.8476(4) Å and c = 14.1382(22) Å (cf. a = 6.8436(6) Å and c = 14.0637(10) Å, leverettite; Kampf et al., Reference Kampf, Sciberras, Williams, Dini and Molina Doloso2013); Zn, a = 6.85427(10) Å and c = 14.1387(5) Å (cf. a = 6.834(1) Å and c = 14.075(2) Å herbertsmithite; Braithwaite et al., Reference Braithwaite, Mereiter, Parr and Clark2004); Mg, with a = 6.8397(6) and c = 13.952(3) Å (cf. a = 6.8345(2) Å and c = 14.0022(7) Å, tondiite; Malcherek et al., Reference Malcherek, Bindi, Dini, Ghiara, Molina Donoso, Nestola, Rossi and Schlüter2014). In addition, attempted reactions with Ba, Li, Na and K failed and produced tenorite (+/- witherite, possibly through reaction with entrained (NH4)2CO3). Similarly, the use of mercury(II) chloride yielded calomel, Hg2Cl2, instead of any obvious discrete Cu precipitate. No atacamites or botallackites were produced. Interestingly, the M2+ = Sr run produced another calumetite-like phase which has not been described previously from Nature or synthesis. It has demonstrably the same structure as the Ca-essential phase and it is the fuller description of this phase that forms this manuscript. A centennialite equivalent has not yet been identified, but, given the increased discordance between the ionic radii of Cu2+ and Sr2+, it too should go beyond the magnetic properties presented by the kapellasites, by excluding the potential for site intermixing (e.g. Iida et al., Reference Iida, Yoshida, Nakao, Jeschke, Iqbal, Nakajima, Ohira–Kawamura, Munakata, Inamura, Murai, Ishikado, Kumai, Okada, Oda, Kakurai and Matsuda2020, Yoshida et al., Reference Yoshida, Noguchi, Matsushita, Ishii, Ihara, Oda, Okabe, Yamashita, Nakazawa, Takata, Kida, Narumi and Hagiwara2017). The failure of the Ba (Hg is rather different) and Cd compositions may indicate limits, for example based on ionic radii, to formation of calumetite-like phases; leaving Pb (we recall that murdochite that shares very similar topological features; e.g. Dubler et al., Reference Dubler, Vedani and Oswald1983) and some select lanthanoids as the remaining contenders.
Table 1: Results of the synthesis of atacamite and kapellasite-like compounds using compressed air as oxidant.

* Reaction conditions: Cu (μm-sized powder for organic synthesis or turnings; 1 g), metal chloride (0.5 M solution; 200 ml) with aqueous ammonia solution added (33 mass-%), reaction temperature corresponds to oil-bath temperature, 500 ml washing bottle; Drechsel insert (Por. 1); compressed air.
** Reaction conditions identical to those described before, but without addition of ammonia solution.
Table 2. Results of the synthesis of atacamite and kapellasite-like compounds using oxygen as oxidant.

* Reaction conditions: Cu (μm-sized powder for organic synthesis or turnings; 1 g), metal chloride (0.5 M solution; 200 ml) reaction temperature corresponds to oil-bath temperature, 500 ml washing bottle; Drechsel insert; oxygen.
** Addition of aqueous ammonia solution (33 mass-%) as indicated.
*** Elemental analysis gives: 13.6 (calculated 13.8) wt.% Sr, 42.5 (40.0) Cu, 27.3 (29.0) O, 10.6 (11.2) Cl, 2.41 (2.38) H. This reduces to a charge-constrained stoichiometry Sr0.91Cu4.15(O1.00H1.008)8.00Cl2.29⋅3.50H2O.
**** For elemental analysis data see text.
Synthesis
Copper powder (1 g; 0.0157 mol; μm-sized powder for organic synthesis) was transferred into a washing bottle (500 ml), then solutions of strontium chloride hexahydrate (53.32 g; 0.2 mol) in demineralised water (200 ml) and aqueous ammonia (for detailed reaction conditions see Table 2) were added.
The reaction mixture was heated with stirring, then oxygen was passed through with the help of a standard Drechsel insert. Efficient mixing was assured by vigorous bubble-stirring as well as magnetic agitation. The colour of the reaction mixture changed gradually from colourless to blue-grey, RHS 119C, accompanied by the formation of a thick slurry, while the suspended copper particles disappeared gradually. After a reaction time of 4 h, additional aqueous ammonia (10 ml; 33 mass-% of NH3) was added. Gas-bubbling and heating was continued for a period of 2 h.
After cooling to ambient temperature, the blue-grey product was collected on a Büchner funnel, rinsed with water (3 × 10 ml), EtOH abs. (2 × 10 ml) and Et2O (2 × 10 ml), and dried over silica gel. The yield was 1.95 g (20% based on Cu) of a blue-grey powder. The infrared (IR) spectra, collected on a Specac Golden Gate ATR device, identified the following bands (vs = very strong): ν = 3609, 3425, 3303, 3146 (vs), 1613, 1299, 1190, 900 (vs), 723 cm–1.
Chemistry
Quantitative chemical analyses of all elements present were performed by Mikroanalytisches Labor Pascher, Remagen, Germany. The data calculated for SrCu4(OH)8Cl2⋅3.5H2O (611.7 g/mol) were (wt.%): H 2.47, O 30.06, Cl 11.59, Sr 14.32 and Cu 41.55. Measured data were: H 2.39 (2.41), O 30.37 (30.37), Cl 11.4 (11.5), Sr 14.4 (14.4) and Cu 41.2 (41.4), where values in parentheses refer to the result of independent double determinations (Table 2; batch CuSrOx 60/1). Estimations (provided by the same laboratory) of the absolute experimental errors of the various analytical processes involved are: H 0.1 mass% (by IR spectroscopy on water following combustion in oxygen flow); Cl– 0.2 mass% (by ion chromatography, following dissolution in H2O/HNO3); O 1 mass% (by hot wire detection of CO, following burning in carbon and chromatographic gas separation), and Cu and Sr, 1 and 0.2 mass%, respectively (both by inductively coupled plasma atomic emission spectroscopy following dissolution in hydrochloric acid).
Data collection and refinement
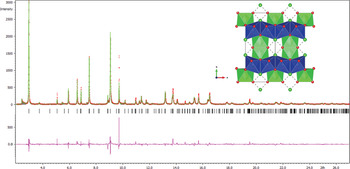
The recovered sample was placed into a 0.9 mm glass capillary and mounted on a sample spinner at ID31, ESRF, where ADX data were collected at λ = 0.3999(1) Å (Fitch, Reference Fitch2004). Given the evident similarity of 1 with calumetite and Erdös et al.'s phase, the model was refined with initial coordinates given by Crichton and Müller (Reference Crichton and Müller2017), in Cmcm. The resulting refinement, in Jana2006 (Petříček et al., Reference Petříček, Dušek and Plantinus2014), given in Tables 3,4 and Fig. 1, reproduces the expected calumetite-like model, which has been compared previously (Crichton and Müller, Reference Crichton and Müller2017; Schlüter et al., Reference Schlüter, Malcherek, Pohl and Schäfer2019) to the rhenate of Jarek et al. (Reference Jarek, Holynska, Slepokura and Lis2007). Structural elements also share similar structural features with centennialite; e.g. Cu–Sr–Cu angles ~60° (here, 58.23(9)°). The characteristic array of Cu–OH planar polyhedra, with average length of 1.965 Å, form the equatorial bonds in the highly Jahn–Teller distorted octahedra (distortion at 0.2291, quadratic elongation at 1.1224), capped by the weak apical Cu–Cl of 3.190(5) Å (Table 5). The Sr[2OH, 2OH, 4H2O] square antiprisms are more regular (distortion of 0.049) with the four weaker 2.760(9) Å bonds to the water molecule at Ow and 2+2 to the bridging oxygens between the four surrounding Cu polyhedra, at 2× 2.434(7) and 2× 2.567(14) Å. While the Cu–Cl bond is weaker than in comparable atacamites, the pyramidal Ow–(H2)⋅⋅⋅Cl distance is remarkably strong and regular. Each Ow is coordinated in a tetrahedral arrangement to two Sr (2.760(8) Å) and two Cl (2.908(9) Å), with a low distortion of 0.02 and elongation of 1.006, and these form an infinite edge-sharing mackinawite-like sheet. Such a bonding environment, and the H-bonding scheme that will decorate it, is anticipated to provide considerable strength to this water-rich ‘layer’. This model was subsequently imported to Endeavour (Putz et al., Reference Putz, Schoen and Jansen1999) for attempted location of H sites. This progressed in two stages; 16H were added to a fully charged and occupied fixed structure, which, in 80% of tests located potential water positions on a 16h position at, on average, (0.282, 0.043, 0.060) and is analogous to the part-occupied water position in centennialite, being coordinated by the Sr polyhedron. They also mirror those of CaCl(ReO4)⋅4H2O (Jarek et al., Reference Jarek, Holynska, Slepokura and Lis2007), where they provide a water-rich layer that caps the Ca polyhedron. An additional cycle with a further 16H failed to adequately locate the OH groups, with 90% of the tests offering 8f and 8g positions that are likely to be over-symmetrical averages. These incomplete potential proton locations were then excluded from the model illustrated in Fig. 1, though we allowed the Ow occupancy to vary. This refines to occupancy = 0.900(13) (on 8e, Z = 2) and is equivalent to 3.60(21) H2O and coincident with our independent analyses.

Fig. 1. Rietveld refinement of data from ID31 using Jana2006 against the model produced for 1 shown inset, using Vesta (Momma and Izumi, Reference Momma and Izzumi2011). Excluded regions correspond to lattice doubled (hk0) positions.
Table 3. Crystal data, data collection and structure refinement details.

Table 4. Atom positions, occupancies and temperature factors.

Table 5. Selected bond and interatomic distances (Å).

The resulting average structure is entirely consistent with that expected from a comparison with calumetite. However, and as discussed in Crichton and Müller (Reference Crichton and Müller2017), there are a significant number of additional reflections that indicate hkl-dependent peak shape, specifically (hk0) reflections of a notionally doubled pseudotetragonal (a = √2a1) lattice, with significant peak asymmetry, that can typically arise from stacking defects.
Modelling structural disorder
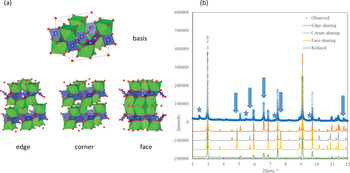
Using the refined model as an illustration, it is straightforward to describe the same average structure in DIFFaX+ (Leoni et al., Reference Leoni, Gualtieri and Roveri2004) using one basis and a transition vector (TV) between the basis and its adjacent layer. In this case, in order to test easily accessible site- and the layer-ordering schemes, we only require that the basis represent the lower half of the average structure expanded to a √2 × √2 cell (+ lattice repeat; Fig. 2) and have changed the stacking direction to z. As a first step, we can simply investigate the effect of different stacking sequences of the basis to identify if the extra-average peaks and peak-shapes are reproduced by repeating an average structure basis at different locations above the previous, corresponding to edge-sharing, corner-sharing, or face-sharing adjacent Sr-polyhedra (Fig. 2).

Fig. 2. (a) The basis is produced by halving the average structure over a doubled lattice. Adjacent layers may be combined with different TVs that give rise to edge-, corner- and face-sharing SrOH–H2O polyhedral. Calculation of end-members and comparing these with the observed diffraction data (b) highlights the gross similarity of these models, their characteristic differences both between each other and with the observed (arrows) and their inability to fit those peaks characteristic of disordered layer structures (starred) when their probabilities are refined.
The corner-sharing construction reduces, with symmetry search over a 2 × 2 × 12 sample, to the basis, which may be Erdös et al.'s hemihydrate. The edge-sharing construction reduces to the average Cmcm, shared with calumetite and the face-sharing to an I-centred tetragonal structure of the same size, which bears more than a passing resemblance to the Ba2Cu3O4Cl2-type structure, well known to the superconductor community (e.g. Pitschke et al., Reference Pitschke, Krabbes and Mattern1995). A comparison of these calculated ordered structures highlights their similarities and the location of characteristic peaks in the structures produced. In refining the different TVs that give rise to these stacking sequences, it is possible to introduce some degree of stacking disorder. While the result of this succeeds in reproducing a pattern equivalent to that produced by the average Rietveld refinement, it is no better. Inspection of the resulting probabilities indicates why: >99% of TVs produced are edge-sharing. A slightly defective stacking sequence of otherwise identical layers is not an efficient way of mirroring the defects in our observation. Another, perhaps additional, mechanism is required that allows for interlayer disorder without disrupting the intralayer stacking sequence significantly from average; i.e. edge-sharing. This is done, here, by ordering the ½-occupied Sr sites.
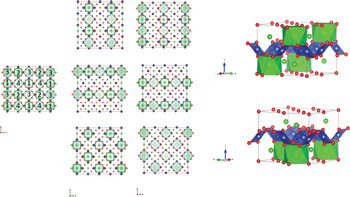
Site ordering can occur in several (but limited) ways in the basis; the following illustrate six options for a revised series of layers, which retain layer chemistry but where the half the available Sr sites are fully occupied: in vertical (1, 3; 2, 4) distributions, in horizontal (1, 4; 3, 2), and diagonal bottom- (1, 2) and one top-occupied (3, 4) (Fig. 3). For the sake of simplicity, each layer has been chosen to have the same origin and any inherent symmetry has been removed. Other layers are of course possible by changing the total Sr per layer and other arithmetic constructions can be combined with layer rotation and full symmetrical descriptions to provide similar model solutions that are more elegant. This would reduce these 6 layers to two; in P4mm, a ≈ a1, c = ½ b1 Å and Pmma, a ≈ √2a1, b ≈ a, c = ½ b1 Å, Fig. 3).

Fig. 3. Ordering over a 2a1, 2a1 lattice provides 6 bases that can be combined following the refinement of their populating probabilities to provide a model for site disorder (or Sr ordering within layers, for all other atoms are effectively constant), over the modelling of the diffraction intensities. These 6 layers reduce to two, which, if used, would provide for a more elegant model construction, in Pnma and P4mm.
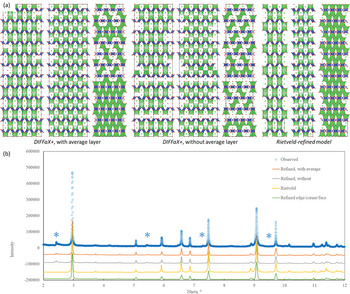
In this case, instead of varying the probabilities of an edge- face- or corner-sharing TV between otherwise identical layers, the TVs are identical (edge-sharing) and it is to a different occupancy pattern within layers that we affix the probabilities. That is, we effectively refine their population rather than how they commute. The sum will lead to a different Sr site order pattern, which will be determined only by minimising the difference between the diffraction patterns produced and that observed. The result is the following, shown in Fig. 4. Which is only a marginal improvement over the edge-sharing average above, but where, more importantly, it has reproduced intensities at lattice-doubled (110, 210, 320, etc) positions, including the generation of some asymmetry. A 2×2×12 layer snap-shot of part of the structure that produces this diffraction pattern looks like Fig. 4.

Fig. 4. (a) The refined structures of 1 following refinement of probability of Sr ordering schemes occurring in face-sharing arrangement, including the possibility of disordered layers (leftmost three, viewed along equivalent a, c, <110>), without (central three; available as crystallographic information files, deposited with the Principal Editor of Mineralogical Magazine and available as Supplementary material) and the Rietveld refined average structure (rightmost). These models are compared with the observed in part (b), showing from top, observed, with ordered model, with disordered allowed, without disordered layers in grey, followed by the Rietveld calculated pattern and, in green, the result of refining stacking sequences (edge-, corner- and face-sharing) average layers. The former pair and the latter pair produce equivalent fits with the former the only models that reproduce relevant intensities at the asterisked locations. The structure is therefore best modelled by stacking sequences of ordered layers in an edge-sharing arrangement, where the presence of some defective disordered layers does not degrade the fit quality.
Similar constructions were also refined but without the inclusion of an average layer (all bases have ordered Sr). These result in an equivalent fit. Quite clearly elements of order are retained, where nearly no defects are visible in two of these images, viewed-off axis (Fig. 4a), left and centre of each group). However, any thoughts that there is no in-plane disorder is dispelled with an on-axis display (rightmost of each group). The disordering is in fact almost complete with no repeated sequence of identical layers along the stacking direction (equivalent to the y direction in the Cmcm lattice). Refinement of probabilities of layer occurrence against diffraction data has, though, produced a hierarchical structure with local preferences (still limited only by diffraction) that creates local structures; the most common probabilities (>55%) give rise to a layer combination that sees sites 1,3|TV|1,4 and its opposite 2,4|TV|2,3 occupied, at 50% likelihood, 1,4|TV|1,4 and 2,3|TV|2,3; at 25% both 3,4|TV|1,2 and 1,2|TV|3,4 are equally probable. The latter pair, when isolated, reduce to a Pmma lattice; the former, to orthometric C2/c lattices at √2a1 × b1, and the intermediate set to P21/c, the same size as the average, indeed the lattice that Crichton and Müller alluded to earlier. It is notable that none produce occupations that reproduce the average in a two layer sequence. At the next hierarchical level, the two highest probability layers will combine with the next pair; i.e. 1,3|TV|1,4|TV|1,4 and 2,4|TV|2,3|TV|2,3 to account for some 75% of all short-range structures starting from layers 1 and 2 and give the diagonal climb to the Sr occupation evident in the figures. That these two subunits form with equal probability, is testament to the pseudotetragonal lattice of the average. From the 12-layer structure produced, we can also demonstrate the validity of the overall average structure as a fair representative of this by rebinning the fractional positions by z’ =12z-int(12z) and reducing c’ to c/12. Such an operation reproduces the basis, itself derived directly from one half of the average structure. Evidently, as the diffraction pattern fits equivalently to, or even better than, the average Rietveld refinement, they are, at least, equivalent descriptions.
So what is the correct structure? These shown are only one potential model, many are possible from the recursively integrated intensities that are refined against the observed data. However, it is clear that the average crystallographic data is a fair representation of the average summation over the stacking direction. It appears the case that any disorder is highly directional and is caused by site ordering within layers as the principle source, here modelled only over Sr sites; and we recall that low-temperature refinements of centennialite also indicate disorder over Ca sites (Yoshida et al., Reference Yoshida, Noguchi, Matsushita, Ishii, Ihara, Oda, Okabe, Yamashita, Nakazawa, Takata, Kida, Narumi and Hagiwara2017). As alluded to earlier, the potential for steric issues abound in the anticipated H-bonding structure of the average, with (O)H atoms occupying the 8f and 8g sites, or split to nearby 16h positions, leading to short ½ occupied H–H distances. Ordering of these may also drive the inherent structural disorder. Whatever the mechanism, by this demonstration we are not required to alter the overall bulk chemistry significantly by introducing extra triply- or fully-vacant Sr layers, nor is there recourse to add any additional TV, or any Sr sites from those that control the construction of the average structure. When refined, it also appears that patterns are repeated that ensure that local features (and stoichiometry) are preserved and that ordering is very near complete in two axial directions.
Where the combination of local patterns differ from average, they may be separated and investigated to see if they are energetically favourable. These may be polytypes, polymorphs or other topological cousins with related chemistries, such as the hemihydrate of Erdös et al. (Reference Erdös, Denzler and Altorfer1981).
Comparing calumetite to a centennialite, a ‘centennialite-(Sr)', should it exist, might be anticipated to have a similar lattice of a ≈ 6.67 Å and a longer c-axis of c ≈ 6.08 Å (given the proportionally longer Sr–Ow bonds), increasing the canting of Cu planes from the Sr–Cu–Sr plane. It seems likely then, from our survey and these considerations, that centennialites are limited to Ca and, possibly, Sr. From the proposed ‘centennialite-(Sr)' lattice, and by using equivalent atomic positions, a first-order approximation of the J interactions can be nonetheless be calculated and synthesis targeted.
Conclusion
The Sr-equivalent of calumetite has been synthesised and its structure described, a description enabled by the investigation using DIFFaX+ satisfies other features of the diffraction pattern of this phase and, in all probability, these can be transferred to the Ca analogue, calumetite. From elements of the structure contained herein, a first estimate of the structure of the ‘Sr-centennialite' can be made.
Acknowledgements
Data presented here were collected at beamline ID31 during beamtime allocated to in-house research, we thank Prof. A. N. Fitch of the ESRF for making this available. Prof. P. Leverett and Dr. A. S. Askenov are thanked for their helpful and constructive reviews of the original manuscript.
Supplementary material
To view supplementary material for this article, please visit https://doi.org/10.1180/mgm.2021.66