Introduction
The kagomé net of corner-connected triangles is a common structural component of many different minerals. It been the subject of intensive study in recent years because of its unusual magnetic properties including magnetic frustration, as typified by Fe3+ jarosite-group minerals (Pati and Rao, Reference Pati and Rao2008). The kagomé net was first named by the Japanese physicist Itiro Syôzi (Reference Syôzi1951), based on its resemblance to the woven patterns of bamboo baskets, where the interlacing laths form triangular and hexagonal holes. The net is well represented in art and architecture as trihexagonal tiling, one of the semi-regular tilings by regular polygons (Fig. 1a). It is a combination of triangular and hexagonal tiling such that around each vertex, two hexagons and two triangles alternate, giving the Schläfli symbol 6.3.6.3 (O'Keeffe and Hyde, Reference O'Keeffe and Hyde1980). The tiling and its central six-pointed star (hexagram) have been used as decorative motifs since antiquity. When metal atoms at the nodes of the net have octahedral coordination with corner sharing connectivity between the octahedra it is referred to as a kagomé network (Pati and Rao, Reference Pati and Rao2008). The anion arrangement was first described in the tungsten bronze Rb0.27WO3 (Magneli, Reference Magneli1952) and has become known as hexagonal tungsten bronze (HTB). This net, with symbol 3.4.6.4 is another semi-regular tiling found in ornament (Fig. 1b).

Fig. 1. (a) Trihexagonal tiling. Nodes (blue circles) correspond to a kagomé net. (b) Tiling in which the nodes correspond to the equatorial anions of a hexagonal tungsten bronze network of corner-connected octahedra, centred by kagomé net cations.
Kagomé nets are ubiquitous in mineral structures. In perovskite-group minerals and ReO3-related minerals like bernalite, Fe(OH)3 (Birch et al., Reference Birch, Pring, Reller and Schmalle1992), the {111} planes of anions form kagomé nets, while natural metallic alloys like auricupride, AuCu3, and the sulfate mineral sulphohalite, Na6FCl(SO4)2 have the antiperovskite structure with {111} kagomé nets of metal atoms (Krivovichev, Reference Krivovichev2008). In the atacamite family of minerals, typified by herbertsmithite, Cu3Zn(OH)6Cl2, the Cu2+ cations occupy the nodes of a three dimensional (3D) kagomé network of edge-shared Cu(OH,Cl)6 octahedra. This family of minerals has been studied in detail as candidates for quantum spin liquids (Malcherek et al., Reference Malcherek, Welch and Williams2018). Spinel-group and pyrochlore-group minerals also have 3D kagomé networks, with the nodes forming a corner-connected tetrahedral framework, while alunite-supergroup minerals have two-dimensional kagomé networks. Minerals containing ordered intergrowths of kagomé networks are also known. They include phyllotungstite and pittongite, with intergrowths of HTB and pyrochlore layers (Grey et al., Reference Grey, Birch, Bougerol and Mills2006) and perhamite-group minerals with intergrowth of HTB and zeolite (Mills et al., Reference Mills, Sejkora, Kampf, Grey, Bastow, Ball, Adams, Raudsepp and Cooper2012). We present here a consideration of kagomé HTB networks in minerals from the perspective of tilting of the octahedra.
The HTB structure
The HTB compounds have the general formula AyBX3, y ≤ ⅓, where A is a large univalent cation such as K, Rb and Cs; B is most commonly W (W6+/W5+) or Fe (Fe3+/Fe2+); and X is O or F. The aristotype HTB structure has space group P6/mmm with the atoms located at the following Wyckoff sites (italics are used for atom sites and non-italics for atoms in the chemical formulae): A site = 1b (0,0,½); B = 3f (½,0,0); Xa = 3g (½,0,½); and Xe = 6l (x,2x,0) with x = 1/(3+√3) = 0.211 (Whittle et al., Reference Whittle, Schmid and Howard2015). Xa and Xe are apical and equatorial anions.
The kagomé net of B cations has octahedral coordination by X anions and the octahedra share corners to form triangular groupings of octahedra around large hexagonal cavities as shown in Fig. 2a. Normal to the plane of the Figure the layers of octahedra share corners. The cell parameters are related to the octahedral bond length d by the following expressions: a = √2(1+√3)d and c = 2d. Using the Gagné and Hawthorne (Reference Gagné and Hawthorne2015) bond-valence parameters for undistorted W6+O6 octahedra, d is 1.909 Å, giving a = 7.376 Å and c = 3.818 Å in WO3. In M xWO3, a portion of the W is pentavalent and the parameters will be larger. e.g. for x = ⅓, the cell parameters based on undistorted octahedra are a = 7.426 Å and c = 3.844 Å.
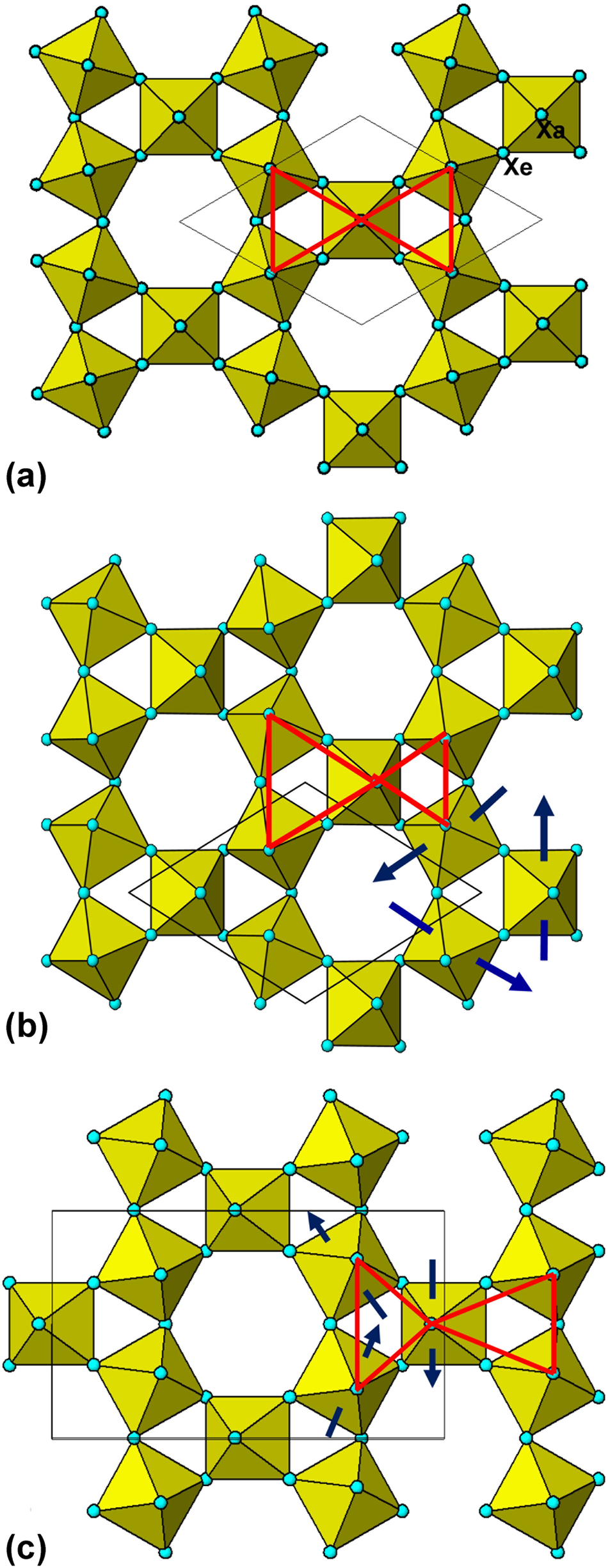
Fig. 2. (a) HTB layer of corner-connected octahedra. (b) P63/mmc-type tilting of octahedra. (c) Cmcm-type tilting of octahedra.
The HTB structure was first solved by Magneli (Reference Magneli1953), for Rb0.27WO3 in space group P63/mcm with cell parameters a = 7.39 Å and c = 7.54 Å. The doubled c axis is due to small displacements of the W atoms which reverse their direction from one layer to the next (second-order Jahn–Teller effect for the d 0 W6+ cation, Kunz and Brown, Reference Kunz and Brown1995). No ordered tilting of the octahedra is possible in P63/mcm as it would be inconsistent with the c glide. Pye and Dickens (Reference Pye and Dickens1979) conducted a structural study on K0.26WO3, using neutron diffraction which is more sensitive to the oxygen atoms and observed reflections, h0l, l = 2n + 1 that violate the c glide. They refined the structure in P6322 and found that the planes of oxygen atoms that are coplanar with W in P63/mcm are ‘puckered’ in P6322. As described by Whittle et al. (Reference Whittle, Schmid and Howard2015) this puckering corresponds to ordered octahedral tilting about 2-fold axes as shown in Fig. 2b. This tilting scheme is a type of ‘breathing’ movement of the octahedra, whereby the apical anions, Xa, of triangular groups of corner-linked octahedra move inwards and the apices of the surrounding triangular groups move outwards. The HTB aristotype structure combined with this tilt system has space group P63/mmc, but it is lowered to P6322 when the W displacements are included.
For the octahedral connectivity to be maintained as the octahedra are tilted there has to be a shrinkage in the unit-cell dimensions. The decrease in the cell parameters as a function of tilt angle, Φ, for the HTB P63/mmc structure, with doubled c axis relative to the aristotype, is a = √2(1+√3cosΦ)d, c = 4dcosΦ. For HTB structures previously refined in P63/mcm (Magneli, Reference Magneli1953; Labbé, Reference Labbé, Goreaud, Raveau and Monier1978) the reported unit-cell parameters are generally smaller than calculated for the aristotype structure and these equations can be used to estimate the tilting angle. For AxWO3, A = K, Rb and Cs, tilting angles of the order of 5° are calculated. For the compound Cs0.29WO3, Prinz et al. (Reference Prinz1992) conducted a single-crystal X-ray diffraction (XRD) refinement in P6322 and noted that the displacement of O2 (≡ Xa) corresponds to a tilting angle of 6.7(4)° whereas the displacement of O1(≡ Xe) corresponds to a tilt angle of 4.6(8)°, indicating that the octahedra do not tilt as perfectly rigid bodies.
Campbell et al. (Reference Campbell, Howard, Averett, Whittle, Schmid, Yost and Stokes2018) applied group theoretical analysis to determine all possible octahedral tilting modes for HTB structures, with the octahedra considered as rigid units. They found ten subgroups of the aristotype P6/mmm structure where tilting maintained the integrity of the octahedral corner linkages for very small tilt angles. Whittle et al. (Reference Whittle, Schmid and Howard2018) noted that only three of the subgroups have each of the octahedra tilting through the same angle and are most likely to occur. These have space groups P63/mmc (Fig. 2b), Cmcm (with b = √3a) and P6/mmm with doubled a, b and c parameters. Whittle et al. (Reference Whittle, Schmid and Howard2015) noted that there have been no reports in the literature of structures with the third tilt system.
Examples of compounds with Cmcm-type tilting are the fluorides, β-BF3, B = Al and Ga (Le Bail et al., Reference Le Bail, Jacoboni, Leblanc, De Pape, Duroy and Fourquet1988) and (H2O)0.33FeF3 (LeBlanc et al., Reference Leblanc, Ferey, Chevallier, Calage and De Pape1983). The tilting scheme in these compounds is shown in Fig. 2c. It involves different combinations of 2-fold rotation axes to that shown in Fig. 2b. The octahedral tilting results in the equilateral triangles of apical anions in adjacent triangular groupings of octahedra in the aristotype being converted to pairs of compressed and elongated isosceles triangles. The mean tilt angle increases from 7.2° in β-AlF3 to 12.9° in β-GaF3 to 14.5° in (H2O)0.33FeF3. The increase in tilt angle follows the order of increasing electronegativity of B, with Al < Ga < Fe. This is consistent with the octahedral tilting being driven by B ns–X 2p σ-bonding covalency in these HTB compounds, as proposed for the A-cation-absent perovskite TeO3 by Mizoguchi et al. (Reference Mizoguchi, Woodward, Byeon and Parise2004). In the HTB structures the triangular groupings of octahedra (Fig. 2a) have strongly bent B–X–B linkages (~150°) that are more conducive to covalent σ-bonding than the 180° B–X–B linkages in perovskite. The HTB oxides, ANbW2O9, A = K and Rb, also have the octahedral tilt system shown in Fig. 2c, with a lowering of space group symmetry to Cmc21 to take account of polar displacements of the B-site cations (McNulty et al., Reference McNulty, Gibbs, Lightfoot and Morrison2019).
Thus far, we have considered only HTB structures in which the HTB layers are corner-connected along [001] to form 3D frameworks as shown in Fig. 3a. Le Bail and co-workers (Le Bail et al., Reference Le Bail, Jacoboni, Leblanc, De Pape, Duroy and Fourquet1988; Le Bail et al., Reference Le Bail, Gao, Fourquet and Jacobini1990; Le Bail, Reference Le Bail2009; Courbion et al., Reference Courbion, Jacoboni and De Pape1976) have characterised the structures of a number of hydrous alkali aluminium fluorides which have in common a separation of the HTB layers with alkali cations and water molecules between the layers, so that the composition of the layer is B(Xe)4/2(Xa)2 = BX4. The example of K3Al3F12⋅H2O (Le Bail Reference Le Bail2009) is shown in Fig. 3b. Inspection of the structure reported by Le Bail (Reference Le Bail2009) shows that the octahedral tilt system is the Immm system of Campbell et al. (Reference Campbell, Howard, Averett, Whittle, Schmid, Yost and Stokes2018) in which one third of the octahedra are untilted.

Fig. 3. (a) Corner-connection of HTB layers in CsxWO3. (b) Separate HTB layers in K3Al3F12.H2O.
Despite the great variety of synthetic HTB structures with various octahedral tilt systems, there have been only a few natural examples reported. Only one mineral with corner-connected HTB layers as in Fig. 3a has been published. It is wumuite, KAl0.33W2.67O9, with space group P6/mmm and unit-cell parameters a = 7.2952(5) and c = 3.7711(3) Å (Li and Xue, Reference Li and Xue2018). A second mineral, tewite, K1.5(Te1.25W0.25)W5O19, with space group Pban and unit-cell parameters a = 7.2585((4), b = 25.810(1) and c = 3.8177(2) Å has a modified HTB structure (Li et al., Reference Li, Xue and Xiong2019). In tewite, 10 Å wide slabs of HTB parallel to (010) are interconnected via corner sharing with strongly distorted TeO6 octahedra. The octahedra in the HTB slabs are not tilted. The mineral meymacite, WO3.nH2O, is usually reported as being amorphous but a recent transmission electron microscopy and Raman microscopy study of iron-bearing meymacite by Tarassov and Tarassova (Reference Tarassov and Tarassova2018) showed that it comprises nano-scale domains with the same kind of HTB derivative structure as in the synthetic phase WO3⋅⅓H2O (Gerand et al., Reference Gerand, Nowogrocki and Figlarz1981). In this structure, with space group Fmm2 and cell parameters a = 7.359(3), b = 12.513(6) and c = 7.704(5) Å, successive HTB layers along [001] are shifted by a/2, so that only two-thirds of the octahedra in adjacent layers are corner-connected. The other one third of octahedra have their apices (O═W–H2O) above and below the hexagonal rings in adjacent layers.
In contrast to the limited number of natural HTB compounds with corner-connected layer structures, there are several extended families of minerals for which the structures are built from HTB layers where the apical anions are not shared between layers as in Fig. 3a but are capped by polyhedra. The type and size of the capping polyhedron is linked to the magnitude of octahedral tilting as will be described in the following sections.
Capped HTB structures
As shown in Fig. 2b, the P63/mmc-scheme of tilting of the HTB octahedra alternately expands and contracts the equilateral triangles of apical anions. The shortening of the distance between the anions in the smaller triangle as a function of the tilting angle is given by the equation below for undistorted octahedra.
Where e is the octahedral edge distance. With no tilting the Xa–Xa separation is e/2(1+√3) = 0.5ahex, which is of the order of 3.72 Å for HTB compounds discussed above. We consider different cases of octahedral tilting so that the Xa–Xa distance decreases to match the polyhedral edge-distance of various polyhedra, leading to different HTB derivative structures.
Pyrochlore minerals and HTB-pyrochlore intgergrowths
Pyrochlore was the name originally given to a mineral of composition (Na,Ca)2Nb2O6(OH,F), but is now the name of a mineral group with general composition (for stoichiometric minerals) A2B2X6Y (Atencio et al., Reference Atencio, Andrade, Christy, Gieré and Kartashov2010). The aristotype has cubic symmetry, Fd ![]() $\bar{3}$m, with a ≈ 10.4 Å and atoms at the Wyckoff sites: A site = 16d (½,½,½); B = 16c (0,0,0); X = 48f (x,⅛,⅛); Y = 8b (⅜,⅜,⅜) where x = 0.3125 for undistorted BX6 octahedra and x = 0.375 for undistorted AX6Y2 cubes (Subramanian et al., Reference Subramanian, Aravamudan and Subba Rao1983). The much stronger bonding of the B cations to X forces the value of x to be close to 0.3125, leading to strong distortion of the A cation-centred polyhedra. This is an inherent source of strain in pyrochlore structures.
$\bar{3}$m, with a ≈ 10.4 Å and atoms at the Wyckoff sites: A site = 16d (½,½,½); B = 16c (0,0,0); X = 48f (x,⅛,⅛); Y = 8b (⅜,⅜,⅜) where x = 0.3125 for undistorted BX6 octahedra and x = 0.375 for undistorted AX6Y2 cubes (Subramanian et al., Reference Subramanian, Aravamudan and Subba Rao1983). The much stronger bonding of the B cations to X forces the value of x to be close to 0.3125, leading to strong distortion of the A cation-centred polyhedra. This is an inherent source of strain in pyrochlore structures.
The pyrochlore structure is usually described as an anion-deficient fluorite derivative structure with face-centred cubic (fcc) stacking of alternating A3B and B3A metal atom layers parallel to the {111}fluorite planes (Subramanian et al., Reference Subramanian, Aravamudan and Subba Rao1983; Fuentes et al., Reference Fuentes, Montemayor, Maczka, Lang, Ewing and Amador2018; Trump et al., Reference Trump, Koohpayeh, Livi, Wen, Arpoino, Ramasse, Brydson, Feygenson, Takeda, Takigawa, Kimura, Nakatsuji, Broholm and McQueen2018). Both the A and B atoms form 3D kagomé arrays of anion-centred corner-connected tetrahedra, YA4 and □B4 (□ = vacancy) (Pannetier and Lucas, Reference Pannetier and Lucas1970) as shown in Fig. 4. The composition of the net of YA4 tetrahedra is A2Y and that of the □B4 net with octahedral coordination of the B atoms by X is B2X6, leading to a representation of the pyrochlore formula that emphasises the independence of the two sublattices, B2X6.A2Y. Defect pyrochlore minerals have vacancies at the A and Y sites and incorporation of H2O giving A2–mB2X6Y1–n⋅pH2O (Hogarth, Reference Hogarth1977) although minor loss of X can also occur under extreme alteration (Lumpkin and Ewing Reference Lumpkin and Ewing1995).

Fig. 4. Corner connected A4 tetrahedra (blue) and B4 tetrahedra (yellow) in pyrochlore
The pyrochlore B2X6 framework can be derived formally from BX4 HTB layers by increasing the octahedral tilt angle until Xa–Xa decreases to match the BX6 octahedral edge distance. With Xa–Xa = e, equation 1 is used to calculate the tilt angle, giving 15.8° for undistorted octahedra. At this tilt angle the same type of BX6 octahedron that forms the HTB layer can exactly cap the smaller triangles of apical anions, Xa, as shown in Fig. 5. Adding successive HTB layers with capping of the smaller triangles on both sides of the layers leads directly to the B2X6 octahedral framework in pyrochlore. Formally it is given by 3BX4 + B(cap) = B4X12 (no reaction mechanism implied).

Fig. 5. Capping of small triangles of Xa anions by octahedra in pyrochlore {111} HTB layer.
Since the establishment of a nomenclature scheme for the pyrochlore supergroup of minerals (Atencio et al., Reference Atencio, Andrade, Christy, Gieré and Kartashov2010; Christy and Atencio, Reference Christy and Atencio2013) there have been numerous publications on new minerals of the supergroup with high quality single-crystal refinements of the structures. We have calculated the octahedral tilt angles from the published structural data, after first converting the cubic Fd ![]() $\bar{3}$m cells and coordinates to R
$\bar{3}$m cells and coordinates to R ![]() $\bar{3}$m hexagonal cells for ease of calculation of the tilt angles. In the hexagonal cell the tilt angle can be calculated separately from the vertical displacement of the equatorial anions, Xe, and from the horizontal displacement of the apical anions, Xa. The results are given in Table 1. The minerals hydrokenoralstonite with Al in the B site (Atencio et al., Reference Atencio, Andrade, Bastos Neto and Pereira2017) and hydrokenoelsmoreite-3C with W 6+ in the B site, (Mills et al., Reference Mills, Christy, Rumsey and Spratt2016) both have measured tilt angles that agree with the value of 15.8° calculated from equation 1. These two minerals have almost perfect octahedra with X–B–X angles of 90° and all X–X edges equal. The other minerals listed in Table 1 have tilt angles that deviate from the ideal value, with the deviation increasing from pyrochlore-group minerals (B = Nb) to microlites (B = Ta) to roméite-group minerals (B = Sb). For all these minerals the cubic cell x coordinate for the anion is higher than the ideal value of 0.3125 that corresponds to a perfect octahedron. With increasing x above this value the geometry is described as a flattened trigonal prism (Subramanian et al., Reference Subramanian, Aravamudan and Subba Rao1983). It is this distortion that results in different experimental tilt angles being calculated from the Xe and Xa anions, although the average stays close to the calculated value of 15.8° from equation 1.
$\bar{3}$m hexagonal cells for ease of calculation of the tilt angles. In the hexagonal cell the tilt angle can be calculated separately from the vertical displacement of the equatorial anions, Xe, and from the horizontal displacement of the apical anions, Xa. The results are given in Table 1. The minerals hydrokenoralstonite with Al in the B site (Atencio et al., Reference Atencio, Andrade, Bastos Neto and Pereira2017) and hydrokenoelsmoreite-3C with W 6+ in the B site, (Mills et al., Reference Mills, Christy, Rumsey and Spratt2016) both have measured tilt angles that agree with the value of 15.8° calculated from equation 1. These two minerals have almost perfect octahedra with X–B–X angles of 90° and all X–X edges equal. The other minerals listed in Table 1 have tilt angles that deviate from the ideal value, with the deviation increasing from pyrochlore-group minerals (B = Nb) to microlites (B = Ta) to roméite-group minerals (B = Sb). For all these minerals the cubic cell x coordinate for the anion is higher than the ideal value of 0.3125 that corresponds to a perfect octahedron. With increasing x above this value the geometry is described as a flattened trigonal prism (Subramanian et al., Reference Subramanian, Aravamudan and Subba Rao1983). It is this distortion that results in different experimental tilt angles being calculated from the Xe and Xa anions, although the average stays close to the calculated value of 15.8° from equation 1.
Table 1. Structural data for pyrochlore-group minerals and compounds.
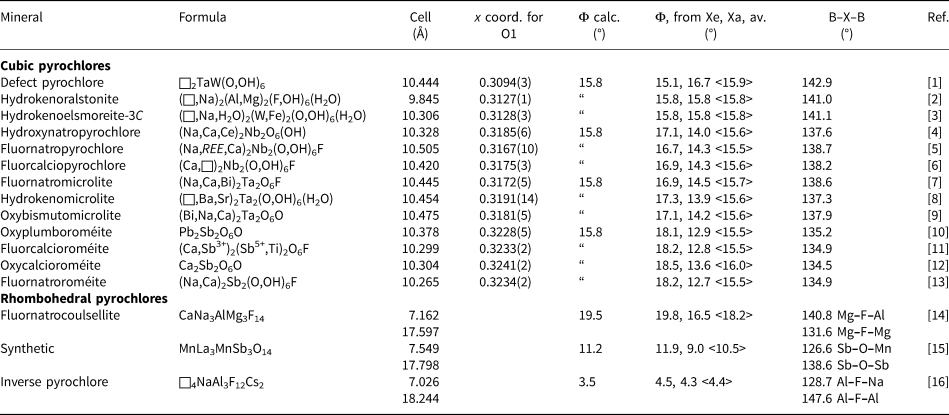
References: [1] Groult et al. (Reference Groult, Pannetier and Raveau1982); [2] Atencio et al. (Reference Atencio, Andrade, Bastos Neto and Pereira2017); [3] Mills et al. (Reference Mills, Christy, Rumsey and Spratt2016); [4] Ivanyuk et al. (Reference Ivanyuk, Yakovenchuk, Panikorovskii, Konoplyova, Pakhomovsky, Bazai, Bocharov and Krivovichev2019); [5] Yin et al. (Reference Yin, Li, Yang, Ge, Xu and Wang2015); [6] Bonazzi et al. (Reference Bonazzi, Bindi, Zoppi, Capitani and Olmi2006); [7] Witzke et al. (Reference Witzke, Steins, Doering, Schuckmann, Wegner and Pollmann2011); [8] Andrade et al. (Reference Andrade, Atencio, Chukanov and Ellena2013); [9] Kasatkin et al. (Reference Kasatkin, Britvin, Peretyazhko, Chukanov, Škoda and Agakhanov2020); [10] Halenius and Bosi (Reference Hålenius and Bosi2013); [11] Atencio et al. (Reference Atencio, Ciriotti and Andrade2013); [12] Biagioni et al. (Reference Biagioni, Orlandi, Nestola and Bianchin2013); [13] Matsubara et al. (Reference Matsubara, Kato, Shimizu, Sekiuchi and Suzuki1996); [14] Mumme et al. (Reference Mumme, Grey, Birch, Pring, Bougerol and Wilson2010); [15] Fu and Ijdo (Reference Fu and Ijdo2014); and [16] Courbion et al. (Reference Courbion, Jacoboni and De Pape1976).
As seen from Table 1, within each pyrochlore group the trigonal antiprism distortion does not appear to depend significantly on the A cation, with similar distortions for A cations varying from Pb2+ and Bi3+ to Ca2+, Na+ and H2O (defect keno pyrochlores). There is however, a clear inverse correlation between the magnitude of the distortion and the B–X–B angle. The distortion is greatest for B = Sb which has the smallest B–X–B angles. Sb is the most electronegative of the B elements in Table 1, which suggests that the distortion occurs to increase the B ns–X 2p covalent σ-bonding strength, as we noted earlier for the HTB compounds.
The cubic pyrochlores in Table 1 all have a single B cation, so the tilt angle calculated from equation 1 is the same for all. In contrast, rhombohedral pyrochlores, with 1:3 ordering of the A and B cations, AA’3BB’3X14, have widely different tilt angles, depending on the relative sizes of the B and B’ cations. In fluornatrocoulsellite, CaNa3AlMg3F14 (Mumme et al., Reference Mumme, Grey, Birch, Pring, Bougerol and Wilson2010) the HTB cation, Mg2+, is considerably larger than the capping cation Al3+, and so larger tilt angles are required for the triangles of apical anions of the HTB layer to fit to the base of the capping octahedra. With Xa–Xa and e in equation 1 calculated for undistorted AlF6 and MgF6 octahedra from bond-valence sum (BVS) parameters for fluorides (Brese and O'Keeffe, Reference Brese and O'Keeffe1991) the calculated tilt angle is 19.5°. This compares with a mean value of 18.2° obtained from the refined crystal structure. The MgF6 octahedra are relatively distorted with F–Mg–F angles in the range 84.1 to 91.4 and F–F edge distances of 2.63 to 2.91 Å. The tilted HTB layers in fluornatrocoulsellite are shown in Fig. 6a.

Fig. 6. [100] projections of the structures of rhombohedral pyrochlores (a) fluornatrocoulsellite, octahedral tilt angle = 19.5°; (b) Cs2NaAl3F12, tilt angle = 3.5°. Tilts shown by red arrows.
In contrast to fluornatrocoulsellite, the 1:3 ordered rhombohedral pyrochlore Mn2+La3Mn2+Sb3O14 (Fu and Ijdo, Reference Fu and Ijdo2014) has a smaller HTB cation, Sb5+, than the capping cation, Mn2+. In this case smaller octahedral tilts are required to match Xa–Xa to the base of the capping octahedron. For undistorted octahedra, application of equation 1 gives a tilt angle of 11.2°, compared to 10.5° measured from the refined structure. The MnO6 polyhedron is a flattened trigonal antiprism with angles of 79.9 and 100.1°.
An extreme example of B cation size difference in 1:3 ordered rhombohedral pyrochlores is the defect pyrochlore of composition □4NaAl3F12Cs2 (Courbion et al., Reference Courbion, Jacoboni and De Pape1976). This is an example of the so-called inverse pyrochlores, where the very large Cs+ cation occupies the 8b site normally occupied by the Y anion. The B cations in the HTB layers are Al3+ and the capping cations are Na+. Application of equation 1 shows that a tilting angle of only 3.5° is required to match the capping NaF6 to the HTB anions. The pyrochlore framework is shown in Fig. 6b. The Cs+ cations have 15 anion neighbours with distances in the range 3.03 to 3.55 Å, giving a nearly ideal BVS of 1.10.
When the Cs is replaced by Rb or K the P63/mmc-type octahedral tilting system is unable to provide suitably sized cavities for the smaller cations. Instead, a different system of tilting occurs which involves puckering of the kagomé nets of Al3+ cations to meet the bonding requirements of K+/Rb+ (Le Bail et al., Reference Le Bail, Gao, Fourquet and Jacobini1990). The tilting system belongs to the Immm space-group type reported by Campbell et al. (Reference Campbell, Howard, Averett, Whittle, Schmid, Yost and Stokes2018). As shown in Fig. 7a the Immm-type tilting involves only two-thirds of the octahedra, which form [010] chains in K2NaAl3F12; the other octahedra are untilted. The tilting changes the pairs of equilateral triangles of Xa anions to isosceles triangles. As a result of the tilting the untilted octahedra are displaced above and below the plane of the tilted octahedra as shown in Fig. 7b. In K2NaAl3F12 the displacements along c* are ± 0.5 Å. The planar kagomé net of cations becomes strongly corrugated as a result. Such tilting cannot occur in corner-connected HTB structures without the breaking of interlayer corner connections, but in pyrochlore-type structures it can occur, albeit with strong distortion of the capping BX6 polyhedra as shown in Fig. 7b for the NaF6 polyhedron in K2NaAl3F12..
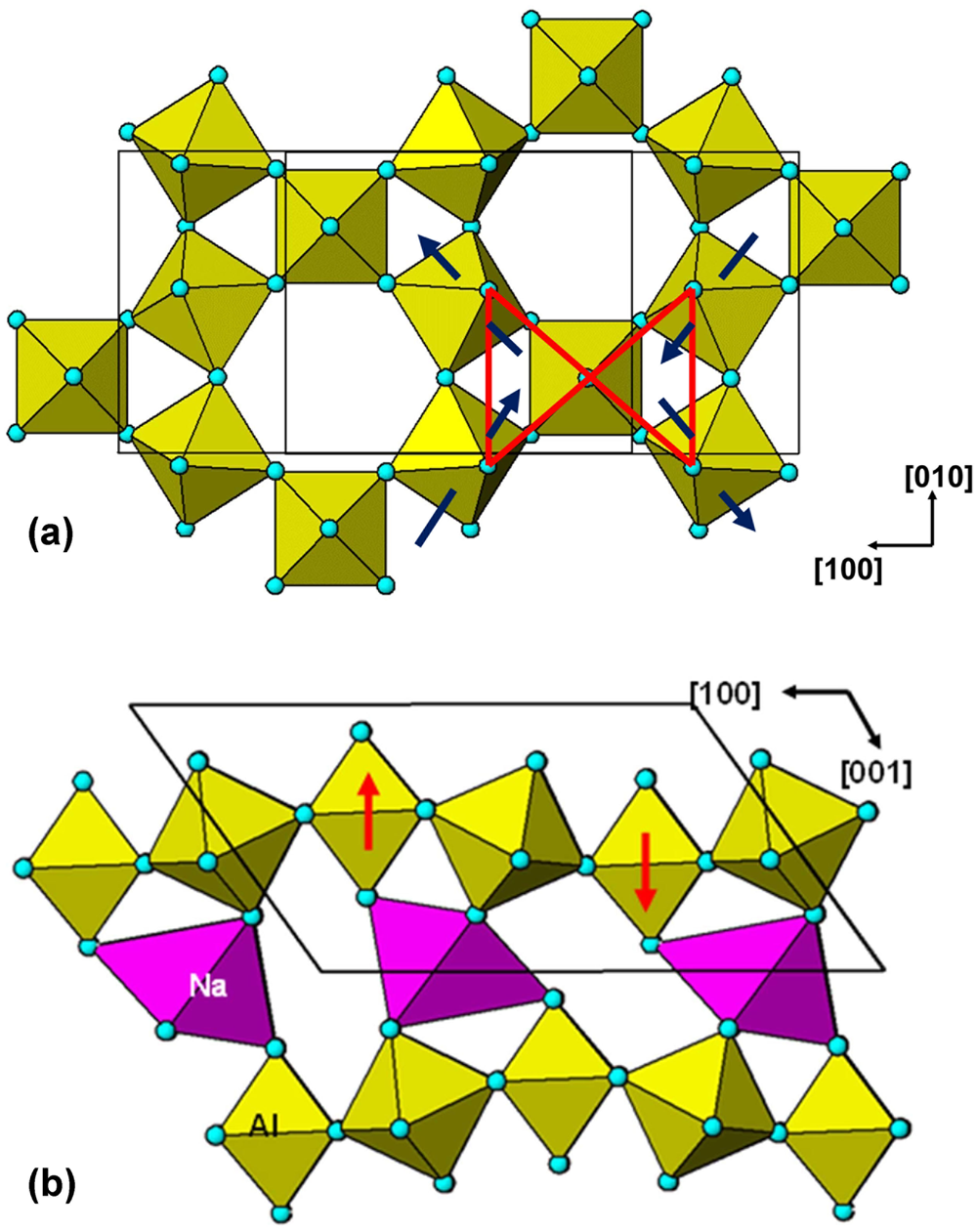
Fig. 7. (a) Immm-type tilting of octahedra in K2NaAl3F12 as viewed along c*. (b) [010] projection of K2NaAl3F12 structure, showing large displacement of untilted octahedra along c* (red arrows).
The 1:3 ordered rhombohedral pyrochlores have quite different in-plane B–X–B and out-of-plane B’–X–B angles with the difference between them reversing when B’ changes from being smaller than B to greater than B. For the antimony compound, the Sb–O–Sb angle of 138.6° is higher than the Sb–O–Sb angle in the four different roméite-group cubic pyrochlores in Table 1, which are in the narrow range 134.5 to 135.2°, suggesting that the bonding requirements for the A and A’ cations are important in this case.
The crystal structure results for the mineral hydrokenoelsmoreite-3C (Mills et al., Reference Mills, Christy, Rumsey and Spratt2016) require further consideration. In the refined structure the WO6 octahedra are undistorted and the W is undisplaced from the ideal 16c site. This is in contrast to W in HTB compounds, AxWO3, where crystal structure studies show the W to be displaced from the centre of the octahedron by ~0.10 to 0.15 Å, consistent with a second-order Jahn Teller distortion for the d 0 cation (Pye and Dickens, Reference Pye and Dickens1979; Labbé et al., Reference Labbé, Goreaud, Raveau and Monier1978; Prinz, Reference Prinz1992). In addition W has a relatively high electronegativity, comparable with that for Sb according to the Pauling scale, and a similar B–X–B angle might be expected. A possible answer to this dilemma is that displacements of W and O do occur but they are short-range ordered and are manifested only indirectly by elevated atomic displacement parameters. The U eq values are 0.023 Å2 for W and 0.021 Å2 for O in hydrokenoelsmoreite whereas they are much smaller at 0.007 Å2 for Al and 0.011 Å2 for OH in the related defect pyrochlore hydrokenoralstonite (Atencio et al., Reference Atencio, Andrade, Bastos Neto and Pereira2017). The U eq values for hydrokenoelsmoreite correspond to root-mean-square displacements of ~0.15 Å. This is the same magnitude as the W displacements in HTB compounds and the anion displacements in the Sb pyrochlores.
The absence of long-range ordering of W displacements in hydrokenoelsmoreite is a specific example of the more general phenomenon of geometric frustration in the pyrochlore structure (McQueen et al., Reference McQueen, West, Muegge, Huang, Noble, Zandbergen and Cava2008; Trump et al., Reference Trump, Koohpayeh, Livi, Wen, Arpoino, Ramasse, Brydson, Feygenson, Takeda, Takigawa, Kimura, Nakatsuji, Broholm and McQueen2018). As shown in Fig. 4, the B cation kagomé network comprises a 3D array of corner-connected tetrahedra. Displacement of B involves ‘breathing’ or rotation of the B4 tetrahedra and the inherent geometric frustration means that the displacements point in different directions, thus cancelling out in statistical displacements when modelled in Fd ![]() $\bar{3}$m. McQueen et al. (Reference McQueen, West, Muegge, Huang, Noble, Zandbergen and Cava2008) compared neutron powder XRD refinements of CaYNb2O7 and other pyrochlores in space group Fd
$\bar{3}$m. McQueen et al. (Reference McQueen, West, Muegge, Huang, Noble, Zandbergen and Cava2008) compared neutron powder XRD refinements of CaYNb2O7 and other pyrochlores in space group Fd ![]() $\bar{3}$m, with and without displacement of Nb along <111>. Without displacement the isotropic displacement parameter for Nb in CaYNb2O7 was 0.019(1) Å2. Refinement of the Nb (x,x,x) coordinate resulted in a displacement of 0.145 Å from the ideal position with a lowering of U eq to 0.013(1) Å2 and an improved fit to the data. A consequence of the distortion of the Nb kagomé network is that the Nb–O–Nb angle is changed from 132.4° in the ideal Fd
$\bar{3}$m, with and without displacement of Nb along <111>. Without displacement the isotropic displacement parameter for Nb in CaYNb2O7 was 0.019(1) Å2. Refinement of the Nb (x,x,x) coordinate resulted in a displacement of 0.145 Å from the ideal position with a lowering of U eq to 0.013(1) Å2 and an improved fit to the data. A consequence of the distortion of the Nb kagomé network is that the Nb–O–Nb angle is changed from 132.4° in the ideal Fd ![]() $\bar{3}$m structure to values of 125, 132.4 and 139.2° in the displaced-Nb structure. Similar results could be expected from local displacements of the B cations in hydrokenoelsmoreite and other minerals.
$\bar{3}$m structure to values of 125, 132.4 and 139.2° in the displaced-Nb structure. Similar results could be expected from local displacements of the B cations in hydrokenoelsmoreite and other minerals.
Given that the pyrochlore structure can be derived from the HTB structure by capping of the apical anions, the possibility exists for intergrowth of the two structure types. In nature this is confirmed for the minerals phyllotungstite (Walenta, Reference Walenta1984; Grey et al., Reference Grey, Mumme and MacRae2013) and pittongite (Birch et al., Reference Birch, Grey, Mills, Bougerol, Pring and Ansermet2007; Grey et al., Reference Grey, Birch, Bougerol and Mills2006). Phyllotungstite, (□,Pb,Cs)10(W,Fe)14(O,OH)42(H2O)4 is orthorhombic (pseudohexagonal), Cmcm with a = 7.298, b = 12.640 (= √3a) and c = 19.582 Å. The structure is shown in projection along [110] in Fig. 8. It comprises 6 Å wide blocks of pyrochlore intergrown along [001] with two HTB layers of width 3.8 Å, giving a c axis periodicity of 2 × (6 + 3.8) = 19.6 Å. An alternative description is in terms of ordered unit-cell twinning of the pyrochlore structure, where the twin planes lie between two HTB layers. The tilting of the octahedra in the HTB layers is required to match that of the octahedra in the pyrochlore blocks, and so ideally it has a magnitude of 15.8° (from equation 1). This is higher than for any reported HTB structures.
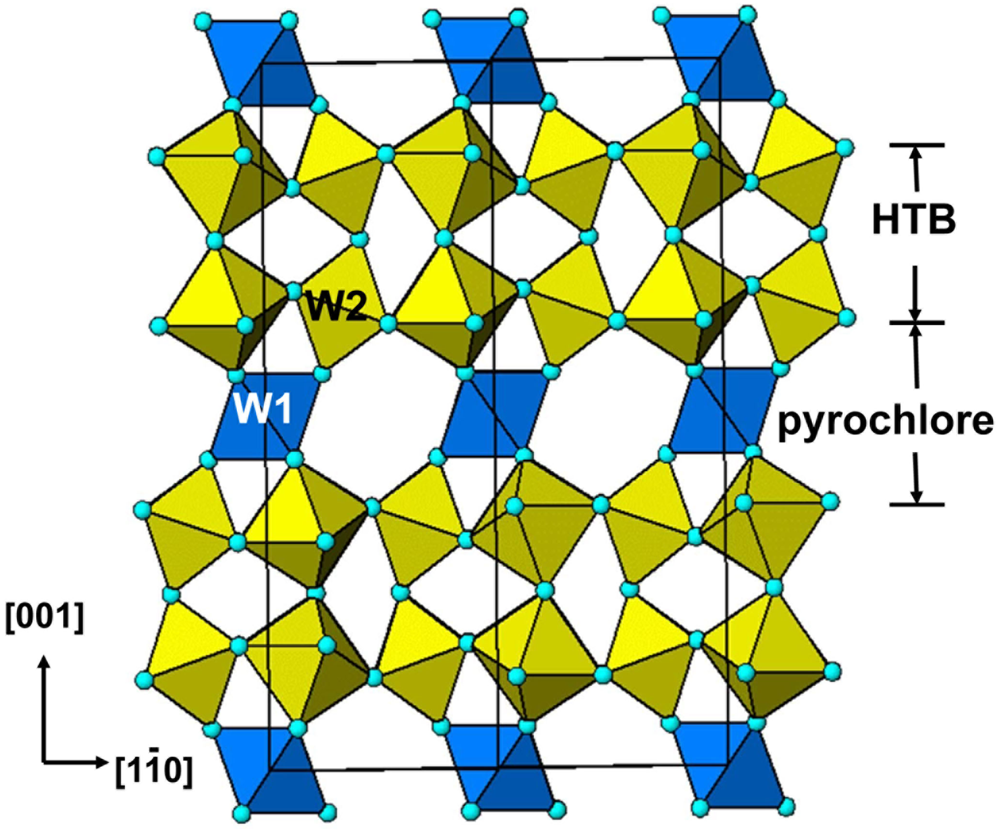
Fig. 8. [110] projection of the phyllotungstite structure.
In pittongite, (□,Na,H2O)32(W,Fe)36(O,OH)108(H2O)12 there are both 6 Å and 12 Å wide pyrochlore blocks intergrown with double HTB layers, giving a c axis periodicity of 2× (6 + 3.8 + 12 + 3.8) = 51.2 Å (actual c = 50.49 Å). Again, the structure can be described as unit-cell twinning of pyrochlore blocks. In this case the pyochlore blocks are of two different widths. At the twin planes, pairs of HTB layers are corner-connected. In the system Bi2O3–Fe2O3–Nb2O5, synthetic intergrowth phases have been structurally characterised that correspond to 12 Å-wide pyrochlore block intergrown with HTB (c = 2 × (12 + 3.9) = 31.8 Å) and to a rhombohedral form of the pittongite sequence with c = 3 × (6 + 3.9 + 12 + 3.9) = 77.4 Å, demonstrating that long-range ordering of quite complex intergrowth sequences of the two structure types is possible (Grey et al., Reference Grey, Mumme, Vanderah, Roth and Bougerol2007).
An intriguing example of a pyrochlore intergrowth structure has been reported by Crosnier et al. (Reference Crosnier, Pagnoux, Guyomard, Verbaere, Piffard and Tournoux1991) for the compound Cs8Nb10O23(Si3O9)2, with space group P63/mmc, a = 7.342 Å and c = 22.166 Å. In this compound HTB layers of corner-connected NbO6 octahedra are capped on both sides by NbO6, giving pyrochlore blocks of composition Nb5O18. The pyrochlore blocks are interconnected along [001] via corner sharing of the capping octahedra with cyclic Si3O9 clusters. Crosnier et al. (Reference Crosnier, Pagnoux, Guyomard, Verbaere, Piffard and Tournoux1991) describe the structure as an intergrowth of pyrochlore-type and benitoite-type (BaTiSi3O9)-type structures. The capping octahedra are common to both the benitoite blocks (with Nb replacing Ti) and the pyrochlore blocks. The intergrowth framework is then [Nb3O12Nb2/2O6/2] + [Nb2/2Si3O3O6/2], where 2/2 and 6/2 indicate sharing between the two blocks. The Cs+ cations occupy large cavities located between the hexagonal rings of the HTB layers and the Si3O9 rings.
Zirconolite minerals
Zirconolite was the name given to a monoclinic mineral of composition CaZrTi2O7, and it is now the group name for three different mineral polytypes with the same ideal formula and with substitutions of mainly rare earth elements (REE) for Ca and Nb, and Ta and Fe for Ti (Bayliss et al., Reference Bayliss, Mazzi, Munno and White1989). Like pyrochlore, the zirconolite structure can be described as an ordered anion-deficient fluorite derivative structure, with a fcc array of cations. However, while pyrochlore has an alternation of <111> fluorite cation layers of composition AB3 and B3A, the alternating layers of small and large cations in zirconolite have the compositions B3B’ and A2A’2. Ti4+ cations occupy both the kagomé net sites (B) and sites in the hexagonal rings within the net (B’, displaced from the centre of the ring). The large cation layers contain parallel chains of edge-shared distorted cubes (A) and mono-capped trigonal antiprisms (A’).
In the aristotype mineral, zirconolite-2M, with space group C2/c and cell parameters a ≈ 12.4 Å, b ≈ 7.3 Å, c ≈ 11.4 Å and β ≈ 100.5° (Gatehouse et al., Reference Gatehouse, Grey, Hill and Rossell1981) the chains of large cations are oriented parallel to [110] and [1![]() $\bar{1}$0] in successive A2A’2 layers. Zirconolite-3T, with trigonal space group P3121 and cell parameters a ≈ 7.3 Å and c ≈ 17.0 Å (Grey et al., Reference Grey, Mumme, Ness, Roth and Smith2003; Zubkova et al., Reference Zubkova, Chukanov, Pekov, Ternes, Schüller and Pushcharovsky2018), has the chains of large cations oriented parallel to [100], [010] and [110] in successive layers, so making angles of 120° with each other. Orthorhombic zirconolite-3O, with space group Cmca, a ≈ 7.3 Å, b ≈ 14.1 Å and c ≈ 10.2 Å, differs significantly from the other polytypes in that the kagomé net of small cations is not planar, but has a sawtooth shape with large (>1 Å) displacements of the cations out of the plane of the net (Chukanov et al., Reference Chukanov, Zubkova, Pekov, Vigasina, Polekhovsky, Ternes, Schüller, Britvin and Pushcharovsky2019). The corner-connected octahedra do not have the HTB layer topology of trans-corner connection. There is periodic shearing along an octahedral edge so that there is a mixture of trans- and cis-corner sharing of the octahedra. The same type of sawtooth HTB layers occur in the walentaite-group minerals (Grey et al., Reference Grey, Hochleitner, Rewitzer, Riboldi-Tunnicliffe, Kampf, MacRae, Mumme, Kaliwoda, Friis and Martin2020).
$\bar{1}$0] in successive A2A’2 layers. Zirconolite-3T, with trigonal space group P3121 and cell parameters a ≈ 7.3 Å and c ≈ 17.0 Å (Grey et al., Reference Grey, Mumme, Ness, Roth and Smith2003; Zubkova et al., Reference Zubkova, Chukanov, Pekov, Ternes, Schüller and Pushcharovsky2018), has the chains of large cations oriented parallel to [100], [010] and [110] in successive layers, so making angles of 120° with each other. Orthorhombic zirconolite-3O, with space group Cmca, a ≈ 7.3 Å, b ≈ 14.1 Å and c ≈ 10.2 Å, differs significantly from the other polytypes in that the kagomé net of small cations is not planar, but has a sawtooth shape with large (>1 Å) displacements of the cations out of the plane of the net (Chukanov et al., Reference Chukanov, Zubkova, Pekov, Vigasina, Polekhovsky, Ternes, Schüller, Britvin and Pushcharovsky2019). The corner-connected octahedra do not have the HTB layer topology of trans-corner connection. There is periodic shearing along an octahedral edge so that there is a mixture of trans- and cis-corner sharing of the octahedra. The same type of sawtooth HTB layers occur in the walentaite-group minerals (Grey et al., Reference Grey, Hochleitner, Rewitzer, Riboldi-Tunnicliffe, Kampf, MacRae, Mumme, Kaliwoda, Friis and Martin2020).
From the perspective of HTB layer octahedral tilting, the zirconolite 2M and 3T polytypes have the P63/mmc type of tilt system (symmetrical ‘breathing’, Fig. 2b) with capping of the smaller triangles of Xa anions by A'X7 mono-capped trigonal antiprisms as shown in Fig. 9. Unlike the pyrochlores where the capping polyhedron links to the small triangles of anions in the HTB layers both above and below, the A'X7 polyhedron in zirconolites has only one flat triangular face and so has only one-sided capping. Alternate A'X7 polyhedra along the chains cap the layers alternately above and below the polyhedra.
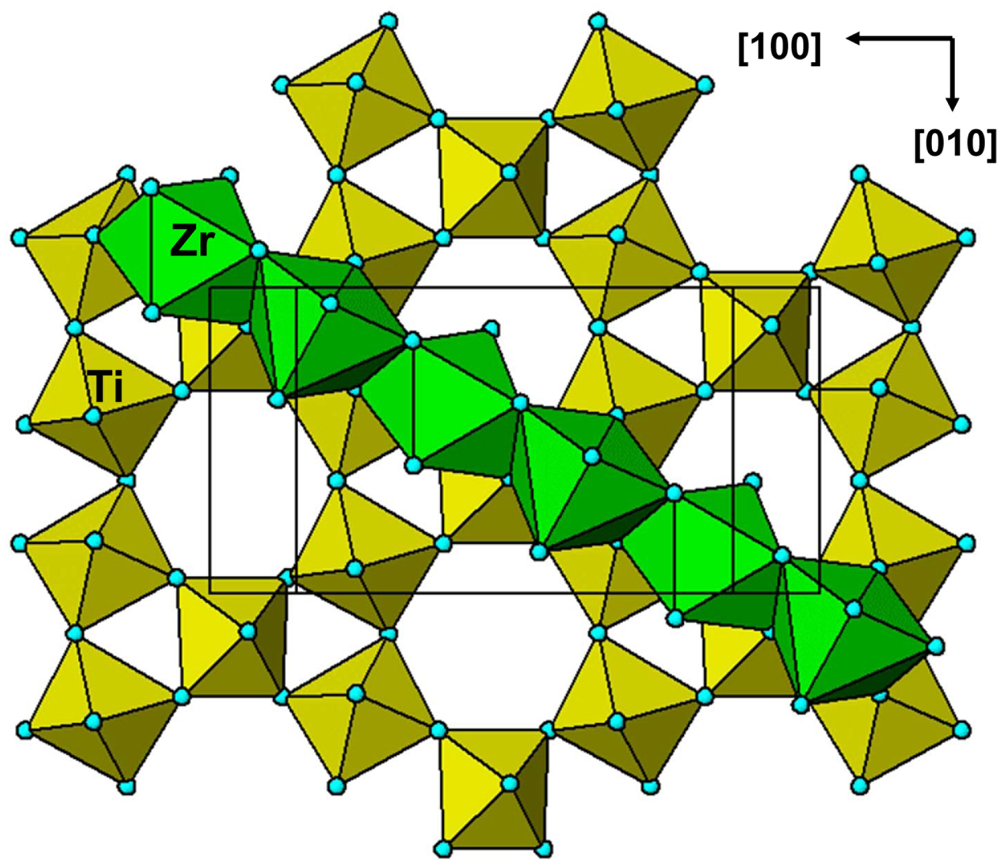
Fig. 9. Capping of HTB layer with ZrO7 in zirconolite-2M. Alternate ZrO7 polyhedra have their capping triangular faces pointing to the HTB layer below and the HTB layer above (not shown).
For zirconolite-2M the triangular base of the ZrO7 polyhedron has O–O = 2.97 Å, and the O–O edge of an undistorted TiO6 octahedron from BVS calculations is 2.77 Å. Substituting these values in equation 1 gives an octahedral tilt angle of 12.8°. This is considerably smaller than for cubic pyrochlore, reflecting the larger size of the capping cation relative to the B cation. The tilt angle measured from the crystal structure is 10.5° based on the movement of the apical anions and 17° based on the displacement of the equatorial anions. The disparity between the two values reflects the large angular distortions of the TiO6 polyhedra, with O–Ti–O angles in the range 78.4 to 98.4° and O–O distances from 2.48 to 2.97 Å. The shortest O–O distances correspond to edges that are shared with trigonal bipyramidal TiO5 polyhedra in the hexagonal rings. The in-plane Ti–O–Ti and out-of-plane Ti–O–Zr angles have almost the same ranges, 133.1 to 138.3 and 131.9 to 136.7°, respectively. This contrasts with the rhombohedral pyrochlore, Mn2La3Sb3O14, which has a similar tilt angle but has quite different in-plane Sb–O–Sb and out-of-plane Sb–O–Mn angles of 128.7 and 147.6, respectively, (Table 1). The geometry of the octahedral tilting in the zirconolite-3T polytype (Grey et al., Reference Grey, Mumme, Ness, Roth and Smith2003) is almost identical to that reported above for the 2M polytype.
Alunite-supergroup minerals and related compounds
Alunite-supergroup minerals have the general formula AB3(TX4)2X’6 with wide ranges of large A cations, small B cations and with tetrahedral groups being mainly SO4, PO4, AsO4 and X’ = O, OH, F and H2O (Bayliss et al., Reference Bayliss, Kolitsch, Nickel and Pring2010). Jarosite minerals, AFe3+3(SO4)2(OH)6 are the most well-known of the alunite-supergroup minerals due to their role in acid mine drainage and metallurgical processes, their identification on Mars and their magnetic properties (Majzlan et al., Reference Majzlan, Glasnak, Fisher, White, Johnson, Woodfield and Boerio-Goates2010; Mills et al., Reference Mills, Nestola, Kahlenberg, Christy, Hejny and Redhammer2013).).
The minerals have rhombohedral symmetry, R ![]() $\bar{3}$m, with a ≈ 7 Å, c ≈ 17 Å and with atoms at the following Wyckoff sites: A site = 3a: 0,0,0; B site = 9d: ½, 0, ½; T site = 6c: 0,0,z; z ≈ 0.3; X1 = 6c: z ≈ 0.4; X2 = 18h: x,–x, z: x ≈ 0.22, z≈ –0.05; and X3 = 18h: x ≈ ⅛, z ≈ 0.13.
$\bar{3}$m, with a ≈ 7 Å, c ≈ 17 Å and with atoms at the following Wyckoff sites: A site = 3a: 0,0,0; B site = 9d: ½, 0, ½; T site = 6c: 0,0,z; z ≈ 0.3; X1 = 6c: z ≈ 0.4; X2 = 18h: x,–x, z: x ≈ 0.22, z≈ –0.05; and X3 = 18h: x ≈ ⅛, z ≈ 0.13.
The structure can be described as based on HTB layers with strongly tilted octahedra giving small and large triangular groupings of apical anions as shown in Fig. 2b. The small triangles are capped by TX4 tetrahedra and the large triangles are capped by AX6 flattened trigonal antiprisms. The complete coordination for A comprises two interpenetrating trigonal antiprisms; A co-ordinates to 6 Xe anions (site X3) in the form of an elongated prism and to 6 Xa anions (site X2) forming a flattened prism. Goreaud and Raveau (Reference Goreaud and Raveau1980) have previously described the relationship of the alunite structure to that of pyrochlore with BX6 sandwiched between opposing small triangles in the HTB layers in pyrochlore and AX6 (the flattened trigonal prism) sandwiched between opposing large triangles in alunite (Fig. 10). In Table 2, are listed the results of octahedral tilting calculations for alunite supergroup members that cover a wide range of size differentials between the B cation and the capping T and A cations.

Fig. 10. Capping of large HTB triangles with AX6 flattened trigonal antiprism in jarosite, compared with capping of small HTB triangles with BX6 octahedron in pyrochlore (after Goreaud and Raveau, Reference Goreaud and Raveau1980).
Table 2. Structural data for alunite-supergroup minerals.

References: [1] Mills et al. (Reference Mills, Nestola, Kahlenberg, Christy, Hejny and Redhammer2013); [2] Majzlan et al. (Reference Majzlan, Stevens, Boerio-Goates, Woodfield, Navrotsky, Burns, Crawford and Amos2004); [3] Najorka et al. (Reference Najorka, Lewis, Spratt and Sephton2016); [4] Dzikowski et al. (Reference Dzikowski, Groat and Jambor2006); [5] Kato (Reference Kato1987); [6] Blount (Reference Blount1974); [7] U. Kolitsch (pers. comm.); [8] Cooper and Hawthorne (Reference Cooper and Hawthorne2012); and [9] Mills et al. (Reference Mills, Kartashov, Kampf and Raudsepp2010).
The jarosite minerals have the largest size disparity between B and T (B = Fe3+, T = S) and the largest calculated tilt angle of 22°. They also appear to be the least strained of the alunite minerals. The deviation of the O–Fe–O angles from 90° is of the order of only 1° and the octahedral tilt angles measured from the displacements of the Xa and Xe anions vary by ~2°. The changing of the A cation size has no significant effect on the tilting but there is a correlation between the A–Xe distance in the elongated trigonal prism and the cell parameter c. A linear correlation between the average ionic radius of the A cation and the c axis length has been reported for alunite-supergroup minerals by Sato et al. (Reference Sato, Nakai, Miyawaki and Matsubara2009). Because the TX4 tetrahedra only cap the HTB layer on one side they cannot influence the interlayer spacing in the same way that the BX6 double-capping octahedra can in pyrochlore structures. Instead the interlayer spacing in alunite-supergroup minerals is responsive to change in size of the A cation.
The plumbogummite group of minerals, gorceixite, goyazite and crandallite have a smaller Al3+ cation at the B site and a larger P5+ as a capping cation and the calculated tilt angle is correspondingly lowered to 18.5°. These minerals are more strained than the jarosites. The departure of the O–Al–O angles from 90° increases with decreasing A cation size from ± 2° for gorceixite to ± 3° for crandallite. In the latter mineral, the Ca cation is displaced from the 2a site to the more general 18f site (x,0,0, x = 0.044; Blount Reference Blount1974) to meet its bonding and valence requirements. The strain is also manifested in a larger disparity (3 to 4°) between the octahedral tilt angles measured from the Xa and Xe displacements. At the smaller tilting angle relative to the jarosites, the large triangle of Xa anions is not as expanded as in jarosites and the A–Xa and A–Xe distances are closer to one another, with the ratio (A–Xa)/(A–Xe) even reversing from greater than 1 to less than 1 in the case of gorceixite.
The dussertite-group minerals have As5+ as the capping cation, larger than P5+ in the plumbogummite-group minerals and the tilting angle is correspondingly smaller at 16.0°. The AlO6 polyhedra are even more distorted trigonal antiprisms than for the plumbogummite minerals, with O–Al–O angles in the range 85.0 to 95.0 for arsenoflorencite-(La) and greater discrepancies between the measured tilting angles. In the examples in Table 2, the A cations change from large monovalent cations in jarosites to smaller divalent cations in plumbogummites to even smaller trivalent and divalent cations in the dussertite-group minerals, with the added complication of Pb2+ having a lone pair electron configuration and a displacement from the 2a site to an 18f site as for crandallite. The observed increasing distortion of the Al-centred trigonal antiprisms must be a direct consequence of the A cation bonding and valence requirements having a more dominant role in establishing the equilibrium atomic arrangement.
The compound NH4(V5+O2)3(Se4+O3)2 (Vaughey et al., Reference Vaughey, Harrison, Dussack and Jacobson1994) is closely related to alunite-supergroup minerals, as is evident when its formula is written as NH4V3(SeO3)2O6. In this compound, HTB layers of VO6 octahedra are capped by SeO3 trigonal pyramids. The compound has hexagonal symmetry, space group P63, with a = 7.137 Å and c = 11.462 Å. In contrast to alunite minerals, where the tetrahedral apices point to the centres of hexagonal rings in adjacent HTB layers, the selenite compound has two independent SeO3 groups with the pyramids on one side of each HTB layer pointing towards the hexagonal ring in the adjacent layer and the SeO3 on the opposite side of each HTB layer pointing towards the larger triangle of Xa anions in the adjacent layer. This arrangement has a 2-layer hexagonal repeat compared to the 3-layer rhombohedral repeat for alunite minerals. The base of the SeO3 pyramids and the average edge distance for the AlO6 octahedra are almost identical so the tilting angle is almost the same as in pyrochlore structures, 15.5 Å. The polar compounds A2(WO3)3SeO3 (A = NH4, Rb and Cs; Harrison et al., Reference Harrison, Dussack, Vogt and Jacobson1995) and A2(MoO3)3SeO3 (A = Rb and Tl; Chang et al., Reference Chang, Kim and Halasyamani2010) are also related closely to the alunite structure. In these compounds, with space group P63 and similar cell dimensions to the above compound, the SeO3 trigonal pyramids cap the smaller triangles of the HTB layers on only one side of the layers. The compound Cs3Sb3Ge2O13 (Pagnoux et al., Reference Pagnoux, Verbaere, Piffard and Tournoux1993), space group P63/mmc, a = 7.31 Å and c = 16.73 Å, has an alunite-related structure based on HTB layers of SbO6 octahedra, capped with GeO4 tetrahedra. In this structure the GeO4 tetrahedra in adjacent layers share their apical anion giving Ge2O7 groups that link the HTB layer together. The base of the GeO4 tetrahedron is somewhat larger than the SbO6 edge length and the calculated octahedral tilting angle is 14.2°, smaller than for the selenites.
The alunite-type structure is amenable to intergrowth with other structure types. In the perhamite-group minerals, perhamite and krasnoite (Mills et al., Reference Mills, Mumme, Grey and Bordet2006, Reference Mills, Sejkora, Kampf, Grey, Bastow, Ball, Adams, Raudsepp and Cooper2012) pairs of alunite-type layers are intergrown with zeolitic groupings of cyclic Si3O9 linked into 4-member rings by corner sharing with AlO4 tetrahedra. The latter corner-connect to the apical anions of the PO4 tetrahedra of the alunite layers as shown in Fig. 11. The minerals are trigonal, P ![]() $\bar{3}$m1, with a ≈ 7.0 Å and c ≈ 20.2 Å. Perhamite has the composition Ca3Al8Si3P4O24(OH)14⋅8H2O. The intergrowth can be written as 2[Al3X12P2XX½] + [Al2X2/2Si3X9], where X = O or OH. Ca2+ cations and H2O are located within 8-sided [100] channels located between the two intergrowth components as shown in Mills et al. (Reference Mills, Mumme, Grey and Bordet2006). The alunite-type layers have the composition of plumbogummite-group minerals and the calculated octahedral tilting is 18.5° (Table 2). The mineral iangreyite, Ca2Al7(PO4)2(PO3OH)2(OH,F)15⋅8H2O with space group P321, a ≈ 7.00 Å and c ≈ 16.7 Å, has a closely related intergrowth structure, in which the zeolitic Al2X2/2Si3X9 groups are replaced by AlX5 trigonal bipyramids that share their apices with the PO4 tetrahedra of the alunite-type layers (Mills et al., Reference Mills, Kampf, Sejkora, Adams, Birch and Plásil2011).
$\bar{3}$m1, with a ≈ 7.0 Å and c ≈ 20.2 Å. Perhamite has the composition Ca3Al8Si3P4O24(OH)14⋅8H2O. The intergrowth can be written as 2[Al3X12P2XX½] + [Al2X2/2Si3X9], where X = O or OH. Ca2+ cations and H2O are located within 8-sided [100] channels located between the two intergrowth components as shown in Mills et al. (Reference Mills, Mumme, Grey and Bordet2006). The alunite-type layers have the composition of plumbogummite-group minerals and the calculated octahedral tilting is 18.5° (Table 2). The mineral iangreyite, Ca2Al7(PO4)2(PO3OH)2(OH,F)15⋅8H2O with space group P321, a ≈ 7.00 Å and c ≈ 16.7 Å, has a closely related intergrowth structure, in which the zeolitic Al2X2/2Si3X9 groups are replaced by AlX5 trigonal bipyramids that share their apices with the PO4 tetrahedra of the alunite-type layers (Mills et al., Reference Mills, Kampf, Sejkora, Adams, Birch and Plásil2011).

Fig. 11. Intergrowth of crandallite-type layers and zeolitic clusters in perhamite.
Weberite minerals and related compounds
Weberite is the name originally given to a fluoride mineral found in southern Greenland, with composition Na2MgAlF7 (Bøgvard, Reference Bøgvard1938). Its crystal structure was determined approximately by Byström (Reference Byström1944) and refined by Giuseppetti and Tadini (Reference Giuseppetti and Tadini1978) in space group Imma, with a = 7.060 Å, b = 10.000 Å and c = 7.303 Å. Like pyrochlore and zirconolite, weberite can be described as an ordered anion-deficient fluorite structure with general formula A2B2X7 in which alternate (111)fluorite planes of composition AB3 and A3B form a fcc array (Cai and Nino, Reference Cai and Nino2009; Grey et al., Reference Grey, Mumme, Ness, Roth and Smith2003). The A3 and B3 arrays are both kagomé nets, parallel to (011) of the aristotype weberite cell with octahedral coordination of the small B cations to form a HTB network and 8-coordination of the large A cations. The weberite and pyrochlore structures differ in the location of the capping B cation in the A3B layers. In pyrochlore the capping cation connects to eclipsed triangular arrays of Xa anions in the HTB layers on either side of the capping cation, whereas in weberite the capping cation coordinates to only two Xa anions on either side and completes its six-fold coordination with two unshared anions. As a result, the weberite small-cation framework has the composition B2X7 whereas the pyrochlore small-cation framework composition is B2X6.
The octahedra in the HTB layers of weberite undergo a different tilting scheme to that in pyrochlore. The octahedral tilting in weberite corresponds to the Cmcm space group type tilting reported by Campbell et al. (Reference Campbell, Howard, Averett, Whittle, Schmid, Yost and Stokes2018) and shown in Fig. 2c. In contrast to P63/mmc tilting, where the triangular groupings of Xa anions all move in towards a central point or all move out, the Cmcm tilting results in pairs of Xe anions in one triangle moving inwards and the third anion moving out, with the reverse occurring in the adjacent triangle, thus producing pairs of compressed and elongated isosceles triangles. The pair of Xa anions that moves in as a result of tilting provides the base for connection of the capping cation in weberite. The HTB layer and its capping octahedra are shown in Fig. 12.

Fig. 12. Capping of HTB layer in weberite (polytype 3T).
There are three different ways that a second HTB layer can join to two Xa anions of the capping octahedra in Fig. 13. One of the connections results in the unshared anions being in a trans configuration, shown in Fig. 13a while the other two connections have the unshared anions in a cis configuration, shown in Fig. 13b. The different sequences of capping configurations lead to several different weberite polytypes, distinguished by symmetry and the number of HTB layers. The aristotype mineral is weberite 2O (2-layer orthorhombic) and it has the unshared anions of the capping octahedra in trans configuration. Other weberite polytypes include 2M, 4M, 5M, 6M, 7M, 3T, 6T and 8O (Cai and Nino, Reference Cai and Nino2009). In all polytypes except the arisotype 2O, the unit cells have a hexagonal (a ≈ 7.3 Å) or orthohexagonal base and a repeat normal to the base of n × 6 Å, where 6 Å is the interlayer separation for the (001) HTB layers.

Fig. 13. Connectivity of capping octahedron to adjacent HTB layers in weberite. (a) trans-configuration; (b) cis-configuration.
The weberite 2M polytpe with space group C2/c and cell parameters a ≈ 12.3 Å, b ≈ 7.3 Å, c ≈ 12.8 Å and β ≈ 109.3° has the capping octahedra in cis configuration whereas the 4M polytype with doubled c axis has an alternation of cis and trans configurations. Similarly the 3T polytype, with space group P3121, a ≈ 7.3 Å and c ≈ 18 Å has each of the three capping octahedra in cis configuration while the 6T polytype with space group P31 and doubled c axis has an alternation of cis and trans octahedra.
Doped Ca2Ta2O7 compounds have been structurally characterised as 5M, 6M and 7M polytypes (Grey et al., Reference Grey, Roth, Mumme, Bendersky and Minor1999, Reference Grey, Roth, Mumme, Planes, Bendersky, Li and Chenavas2001, Grey and Roth, Reference Grey and Roth2000). These compounds differ from other weberite polytypes in having periodic pseudo-unit-cell twinning of the cation layers (“pseudo” because B is reflected into A across the twin plane). The twin planes are on B3A layers and correspond to elements of hexagonal stacking of the layers. For example, the 6M polytype has a stacking sequence hccccchcccch. In the h-stacked layers the kagomé net is corrugated, with cations displaced along [001] by ± 0.15 Å. The 5-layer cubic-stacked blocks correspond to weberite type. The 5M polytype exists in two structural forms, which have the same unit cell and space group, C2, and the same layer stacking sequence of hccchccccch, but Nb-doped 5M Ca2Ta2O7 has weberite blocks between the h-stacked layers and Sm-doped 5M Ca2Ta2O7 has weberite in the 5-layer-wide fcc block and pyrochlore in the 3-layer-wide block. The interface capping layer and adjacent HTB layers in this structure is shown in Fig. 14. The octahedral tilting changes from P63/mmc-type in the pyrochlore blocks to Cmcm-type in the weberite blocks, so that the capping octahedra shown in Fig. 14 share 3 anions with octahedra in the pyrochlore CaTa3 layer on one side and only two anions with octahedra in the weberite CaTa3 layer on the opposite side.

Fig. 14. Interface layer of capping octahedra between pyrochlore-type and weberite-type layers in (Ca,Sm)2Ta2O7-5M.
Octahedral tilting by sin–1(√2/√3); transformation of HTB corner sharing to edge sharing
Substitution of Φ = sin–1(√2/√3) = 54.73° (half the tetrahedral angle) into equation 1 gives Xa–Xa = 0. i.e. the three Xa anions meet at a point. This octahedral tilting angle results in the triangles of corner-shared octahedra in the HTB layer being converted to triangles of edge-shared octahedra, with loss of four anions per triangle. Formally, for a trivalent metal hydrated HTB layer the transformation can be written as a dehydration: M3+3(OH)9(H2O)3 → M3+3O(OH)7 + 4H2O. The hexagonal kagomé net is maintained but it has shrunk from (1 + √3)e to 2e where e is the octahedral edge.
In Fig. 15 is shown the case where the triangles of Xa anions are capped by octahedra as in pyrochlore. Tilting of the octahedra and displacement of the capping cations to the adjacent triangles as shown in the Figure converts the pyrochlore network, M4X12, to the spinel network of edge-shared octahedra, M4X8 with loss of 4X. The octahedral framework in spinel has the same 3D kagomé net of corner-connected B4 tetrahedra as in pyrochlore. Another family of minerals with the same topology is the paratacamite group, of which an example is herbertsmithite, Cu3Zn(OH)6Cl2 (Malcherek et al., Reference Malcherek, Welch and Williams2018). In herbertsmithite Cu2+ cations form the kagomé net and Zn2+ are the capping cations.

Fig. 15. (a) Tilting of octahedra in HTB layer by 54.7°, with displacement of capping octahedron and loss of apical anions to give (b) spinel-type structure.
Acknowledgments
The author thanks Dr. Chris Howard for advice on different octahedral tilt systems in hexagonal tungsten bronze compounds, Dr. Patrick Woodward for advice on the driving forces for octahedral tilting in perovskites and two reviewers for helpful comments.



















