Introduction
Ionic radii have been used widely to study and evaluate the crystal structure of compounds. Although ionic radius is a powerful tool for describing such structures, other factors should also be considered when discussing structural stability. Cation–cation repulsion comes into play when evaluating anisotropic lattice distortions in structures with edge-shared polyhedra, which cannot be predicted by ionic radii consideration alone. For instance, understanding the stability of the garnet structure requires studying the repulsion between cations across shared edges of polyhedra (Nakatsuka et al., Reference Nakatsuka, Yoshiasa and Takeno1995, Tokuda et al., Reference Tokuda, Yoshiasa, Mashimo, Iishi and Nakatsuka2018). In the structural study of the Y3Al3–xGaxO12 (0 ≤ x ≤ 5) garnet solid solution, which shows a large deviation from Vegard's law, the preference of Ga3+ for the tetrahedral site brings about a decrease in the cation–cation repulsive force across the polyhedral shared edges with increasing Ga3+ content. The anomalous cation distribution in Y3Al3–xGaxO12 garnet is a consequence of the strong covalency of the Ga–O bond and the need for decreased cation–cation repulsion (Nakatsuka et al. Reference Nakatsuka, Yoshiasa and Yamanaka1999).
In the ABO4 zircon-type structure, a chain of alternating edge-sharing BO4 tetrahedra and AO8 triangular dodecahedra along the c axis is the principal structural unit. Similar chains of edge-sharing polyhedra exist in garnet-type structures. Fukunaga and Yamaoka (Reference Fukunaga and Yamaoka1979) investigated the pressure-induced phase transition in ABX 4 type compounds and proposed the classification diagram of ABX 4 type compounds with two parameters t = (r A + r B)/r O and k = r A/r B, where r is the ionic radius of the respective element. In recent years, Errandonea and Manjón (Reference Errandonea and Manjón2008) reviewed studies on pressure-induced phase transitions of ABX 4 compounds to understand the effect of pressure on their structure and physical properties on the basis of ionic radii. According to these studies, zircon ZrSiO4 is transformed to scheelite-type ZrSiO4 (reidite) by applying pressure. As well as the garnet structure, an investigation of the zircon–reidite transition from the viewpoint of cation–cation repulsion between shared edges of polyhedra will elucidate new aspects of the pressure-induced phase transition of ABX 4 compounds.
Recently, the high-pressure phase ZrSiO4 (reidite) was discovered in an upper-Eocene impact ejecta layer in marine sediments on the upper continental slope of New Jersey, USA and on Barbados (Glass and Liu, Reference Glass and Liu2001). Shock experiments showed that the phase transition from zircon to reidite started at a pressure of ~30 GPa and finished at ~53 GPa, at a temperature of ~600 K (Mashimo et al., Reference Mashimo, Nagayama and Sawaoka1983; Kusaba et al., Reference Kusaba, Syono, Kikuchi and Fukuoka1985). The zircon–reidite transition and dissociation boundary were determined for pressures between 8.3–9.7 GPa and temperatures between 1100–1900 K by Ono et al. (Reference Ono, Funakoshi, Nakajima, Tange and Katsura2004) and Tange and Takahashi (Reference Tange and Takahashi2004), respectively. Akaogi et al. (Reference Akaogi, Hashimoto and Kojitani2018) suggested that zircon transforms to reidite and dissociates into two phases (SiO2 stishovite and cotunnite-type ZrO2) at 330 km and 610 km depths, respectively, along the normal mantle geotherm. Reidite was first synthesised by Reid and Ringwood (Reference Reid and Ringwood1969). Then Liu (Reference Liu1979) revealed that reidite undergoes dissociation into an assemblage of SiO2 stishovite and cotunnite-type ZrO2 by using the static pressure range of 10–30 GPa at ~1000°C with a diamond-anvil cell. Kusaba et al. (Reference Kusaba, Yagi, Kikuchi and Syono1986) reported that a zircon (space group I41/amd) from a recovered shock-compression sample converted to an isomorphic scheelite-type structure (space group I41/a), as shown in Fig. 1. Very limited reidite data are available, and structural investigations are reported only for powder X-ray diffraction.
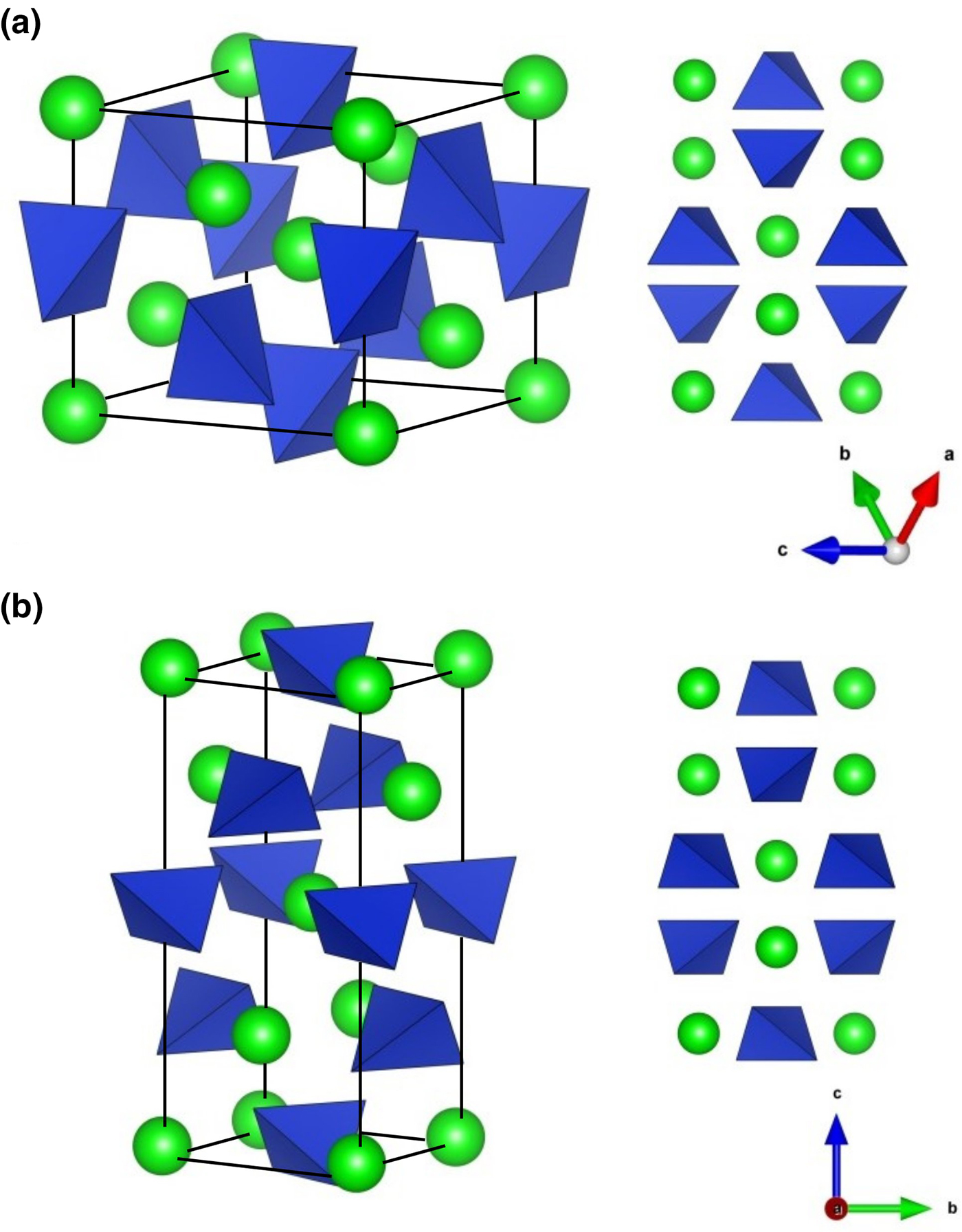
Fig. 1. Crystal structure of (a) zircon (Kolesov et al., Reference Kolesov, Geiger and Armbruster2001) and (b) reidite. Circles and tetrahedra represent Zr4+ and SiO4, respectively (drawn using VESTA; Momma and Izumi, Reference Momma and Izumi2008).
Zircon (ZrSiO4) has been used to determine the ages of tectonic events using host minerals for radioactive elements such as U or Th. Thus, radiation damaged (metamictised) zircons are often found in crustal igneous, metamorphic and sedimentary rocks. Metamictisation is defined as the amorphous state of a substance that has lost its periodic structure (Brøgger, Reference Brøgger1893). Metamictisation is a radiation-induced, periodic-to-aperiodic phase transition caused by α-particles from the U or Th decay series (Hamberg, Reference Hamberg1914). Damage by α-decay has two components that occur simultaneously. The first is that an α-particle (4.5–5.0 MeV) from a radionuclide displaces several hundred atoms, creating isolated Frenkel defect pairs at the end of its flight. The second is that an α-recoil atom (0.07–0.09 MeV) also generates Frenkel defect pairs and produces several thousand atomic displacements by releasing its energy to elastic scatterings. Anomalous distortion of lattice parameters has been reported for zircon from Sri Lanka. Murakami et al. (Reference Murakami, Chakoumakos, Ewing, Lumpkin and Weber1991) suggested that point defects in the early stages of damage accumulation (< 3.0 × 1015 α-decays/mg) undergo self-annealing in natural zircon under ambient conditions.
We first report single-crystal data of synthetic scheelite-type ZrSiO4 (reidite) and discuss its structural features compared with those in a previous report on synthetic zircon. Moreover, we report the structural refinement of a radiation-damaged natural zircon we obtained recently from Okueyama, Japan. This natural zircon is younger than that studied by Ríos et al. (Reference Ríos, Malcherek, Salje and Domeneghetti2000) from Sri Lanka and shows no anomalous lattice distortion. Therefore, a structural comparison between the Sri Lankan and Okueyama zircons provides important information on the effect of radiation damage and its thermal recovery. In this study, we consider the zircon–reidite phase transition and the effect of radiation damage on zircon from the viewpoint of cation–cation repulsion between shared edges of polyhedra.
Experimental methods
Specimen preparation and characterisation
Zircon was synthesised from an equimolar mixture of reagent-grade ZrO2 (>99%, Wako Co.) and SiO2 (>99%, Kanto Kagaku Co.) by heating at 1773 K for 314 hr with nine times intermittent mixing. Reidite was synthesised from synthesised zircon using a Kawai-type double-staged multianvil apparatus at Gakushuin University. The starting material was put into a cylindrical Pt capsule heater in a 5 wt.% Cr2O3-doped MgO octahedron, and was kept at 15 GPa and 1773 K for 3 h. After quenching under pressure, the sample was recovered to ambient conditions. The synthesised sample was confirmed as single-phase reidite by microfocus X-ray diffraction and powder X-ray diffraction.
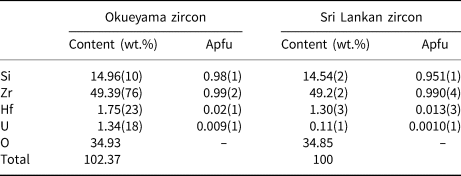
Natural zircon crystals were obtained from granite in Okueyama, Miyazaki Prefecture, Japan, and are light yellow under sunlight and fluorescent yellow under ultraviolet light. The Okueyama granite is part of the Miocene pluton of the Outer Zone of Southwest Japan, and has been aged radiometrically at 14 Ma (Shibata, Reference Shibata1978). The compositions of the samples were determined with a JEOL scanning electron microscope (SEM JSM-7001F) and an Oxford energy dispersive X-ray analyser (EDS INCA SYSTEM). The composition of the Okueyama zircons is shown in Table 1. Wollastonite CaSiO3, and pure metals of Zr, Hf and U were used as standard materials. The average content (ten spot analyses) totals ~102 wt.%. The Okueyama zircon contains 1.75(23) wt.% Hf and 1.34(18) wt.% U at the A site and no impurities at the B site. According to this result, the averaged chemical formula of the Okueyama zircon is (Zr0.97Hf0.02U0.01)Σ1.00Si0.98O4, with a somewhat low B-site total of 0.98(1) Si per formula unit. Lower B-site and excess A-site cations in the Okueyama zircon are also observed in Sri Lankan zircons (Murakami et al., Reference Murakami, Chakoumakos, Ewing, Lumpkin and Weber1991).
Table 1. Averaged chemical composition of Okueyama and Sri Lankan zircons (Ríos et al., Reference Ríos, Malcherek, Salje and Domeneghetti2000)*.
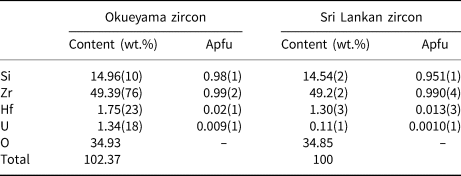
* Apfu – atoms per formula unit on the basis of O = 4.00 apfu.
Single-crystal X-ray diffraction
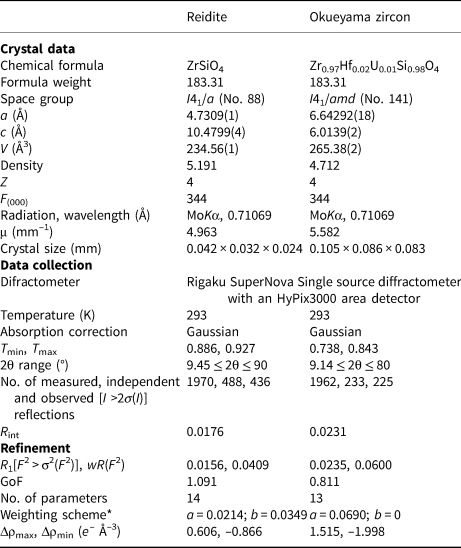
Single-crystal X-ray diffraction for the synthetic reidite and natural Okueyama zircon was performed using a SuperNova, Single source at offset/far, HyPix3000 diffractometer. Monochromated MoKα radiation obtained by an X-ray generator (50 kV and 0.8 mA) was focused by a mirror. Details of the data collection are listed in Table 2.
Table 2. Crystal structure and single-crystal X-ray diffraction data for reidite and Okueyama zircon.
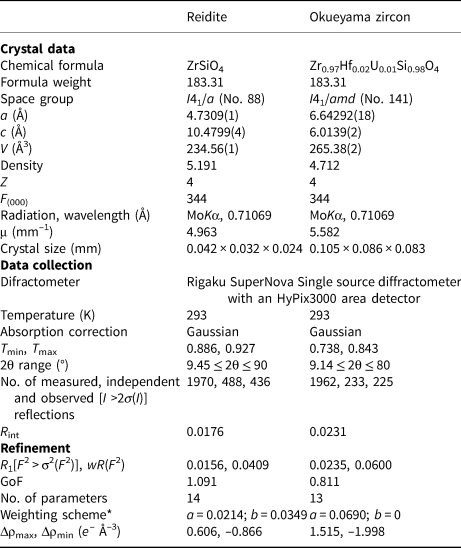
*w = 1/[σ2(FO2) + (aP)2 + bP]; P = (Max(FO2, 0) + 2FC2)/3
Refinement
The structure was obtained with the ShelXT solution program using intrinsic phasing and refined with the ShelXL refinement package using least-squares minimisation (Sheldrick, Reference Sheldrick2015). During the least-square refinements a correction for isotropic extinction was applied. After several refinement cycles the displacement parameters were converted from an isotropic to an anisotropic model. The refined coordination and atomic displacement parameters are listed in Table 3. The final R1 factors of reidite and zircon were 0.0156 and 0.0235, respectively.
Table 3. Atom coordinates and refined anisotropic displacement parameters (Å2) for reidite, Okueyama zircon and previous reports.*

* RD = radiation damaged, NRD = non-radiation damaged.
Results and discussion
Pressure-induced phase transition from zircon to reidite
Generally, pressure-induced phase transitions occur with increasing cation coordination number. However, an increase of cation coordination number is not sufficient to explain high-pressure transformation in ABO4 compounds. Monazite-type arsenates and vanadates, for example, are known to transform to a scheelite-type structure under high pressure with no change of cation coordination number (Stubican and Roy, Reference Stubican and Roy1959). As for the zircon–reidite phase transition, the cation coordination number does not change. The density of reidite increases ~10% from that of low-pressure-phase zircon. This compression was explained by Kusaba et al. (Reference Kusaba, Yagi, Kikuchi and Syono1986). The [110] direction in the zircon structure is converted by simple shearing to the [001] direction in the scheelite structure, during which the intersecting angle between [100] and [010] increases from 90° to ~115°, which causes the increase in ZrSiO4 density. This mechanism accounts for structural transformation without long-range atomic diffusion. Hence, the c axis of the scheelite structure in reidite corresponds to the [110] direction of the zircon structure, as shown in Fig 1. The respective vectors az, bz and cz can be represented by a linear combination with the vectors ar, br and cr in zircon:
 $$\eqalign{& {\bi a}_z = \cos 53.4^\circ {\bi a}_r + \cos 67.6^\circ {\bi b}_r + \cos 45^\circ {\bi c}_r \cr & {\bi b}_z = \cos 126.7^\circ {\bi a}_r + \cos 112.4^\circ {\bi b}_r + \cos 45^\circ {\bi c}_r \cr & {\bi c}_z = \cos 57.4^\circ {\bi a}_r + \cos 147.4^\circ {\bi b}_r + \cos 90^\circ {\bi c}_r} $$
$$\eqalign{& {\bi a}_z = \cos 53.4^\circ {\bi a}_r + \cos 67.6^\circ {\bi b}_r + \cos 45^\circ {\bi c}_r \cr & {\bi b}_z = \cos 126.7^\circ {\bi a}_r + \cos 112.4^\circ {\bi b}_r + \cos 45^\circ {\bi c}_r \cr & {\bi c}_z = \cos 57.4^\circ {\bi a}_r + \cos 147.4^\circ {\bi b}_r + \cos 90^\circ {\bi c}_r} $$where a z, b z and c z correspond to reidite axes and a r, b r and c r to zircon axes. In the discussion of the zircon and reidite structures, attention should be given to the above correspondence of axes.
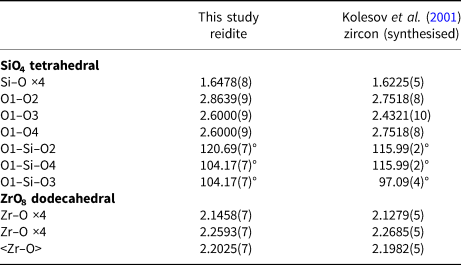
The configuration of SiO4 tetrahedra is important in understanding the phase transition from zircon to reidite. A comparison of SiO4 configurations between zircon and reidite is shown in Fig. 2. The zircon–reidite phase transition can be understood by twisting and translations of SiO4 tetrahedra. From the view of the a r axis in reidite (Fig. 2a), there is no tetrahedral displacement along the b r axis. The SiO4 translations are along the a r and c r axes. The large expansion (~12%) along the c r axis is caused, however, by the large contraction (~17%) along the a r axis observed from the view of the b r axis.
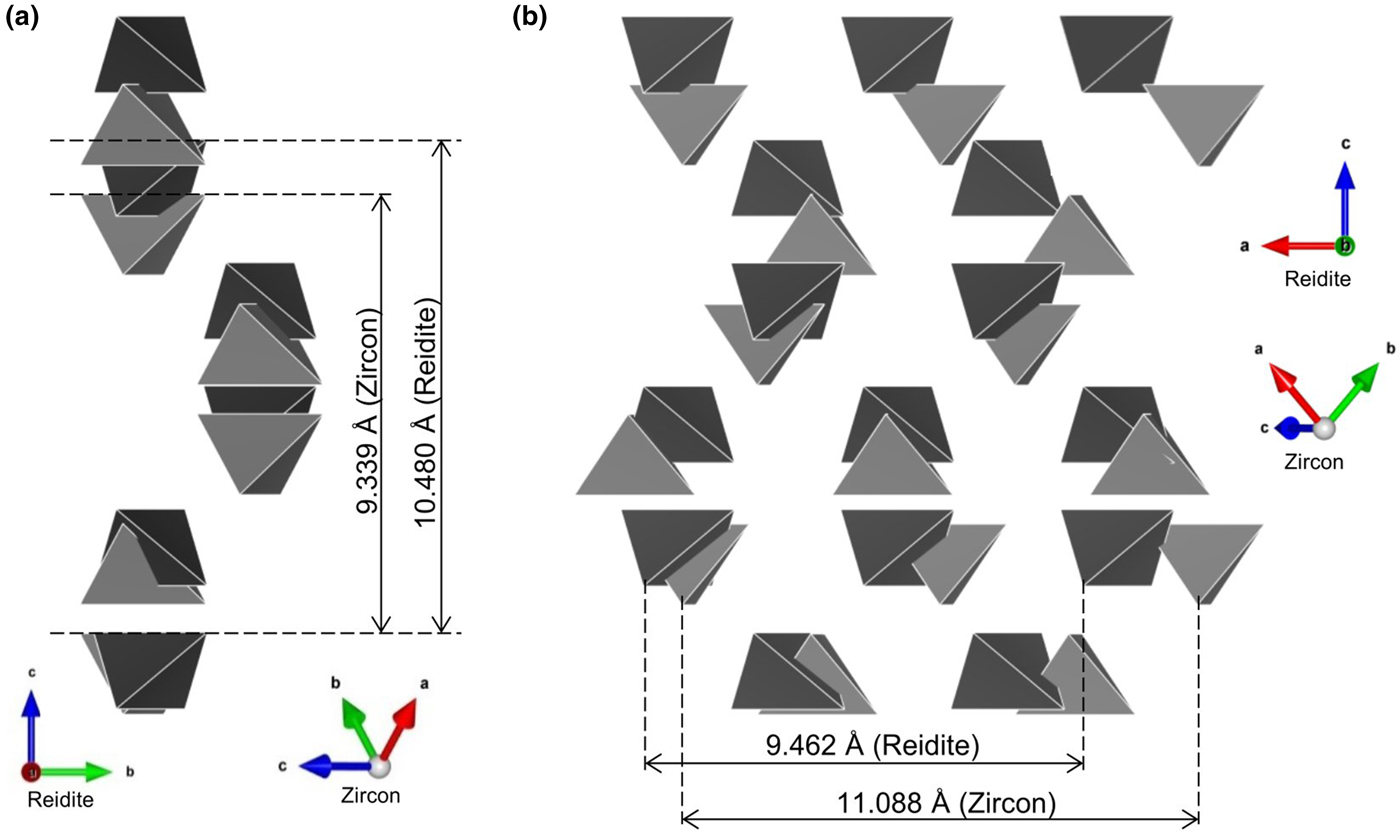
Fig. 2. Comparison of SiO4 configurations between zircon (Kolesov, et al., Reference Kolesov, Geiger and Armbruster2001) and reidite projected on (100)reidite (a) and (010)reidite (b). The grey and black tetrahedra correspond to the SiO4 of zircon and reidite, respectively.
The twisting and translations of SiO4 tetrahedra in the zircon structure cause the shared edge between SiO4 tetrahedra and ZrO8 dodecahedra to disappear, as shown in Fig. 3. The disappearance of the SiO4–ZrO8 shared edge yields structural stability according to Pauling's third rule (Pauling, Reference Pauling1929, Reference Pauling1960). Although the density of reidite is higher than that of zircon, the volume of the SiO4 tetrahedron of reidite is larger than that of zircon. The O–O atomic distances of SiO4 also change in the phase transition. In the zircon structure, there are four larger O–O distances and two shorter O–O distances corresponding to the SiO4–ZrO8 shared edge. However, there are four shorter O–O distances and two longer ones in the reidite structure (Table 4). Such changes in O–O distance are caused by twisting of the SiO4 tetrahedra. The SiO4 twisting is represented by the rotation of O1–O2 and O3–O4 bonds perpendicular to the a r axis, as shown in Fig. 3. The O1–O3 and O2–O4 distances in reidite expand as the SiO4–ZrO8 shared edge disappears. Although the mean-square displacement (MSD) of the Si atom in pure zircon is nearly isotropic despite the SiO4–ZrO8 shared edge, the MSD of the Si atom in reidite is anisotropic (U 11 < U 33). The thermal vibration ellipsoid of reidite Si is elongated only towards the longer O1–O2 and O3–O4 bonds in the tetrahedron. Because of the SiO4 twisting, the 41 axis in zircon, which is the c z axis, disappears, and the new 41 axis is generated as a primary axis along [110]z, which corresponds to the c r axis.
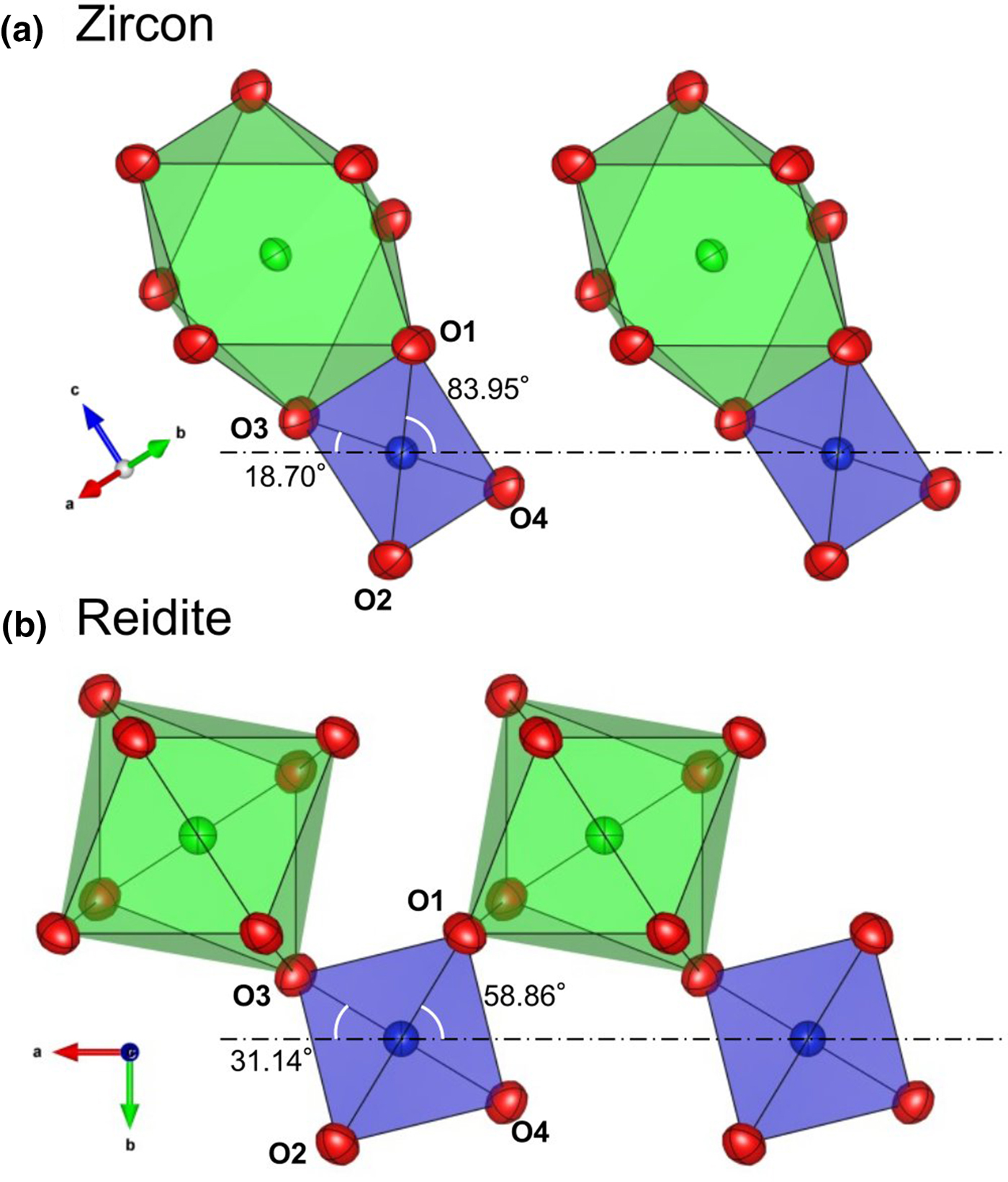
Fig. 3. Twisting of SiO4 in (a) zircon (Kolesov, et al., Reference Kolesov, Geiger and Armbruster2001) and (b) reidite. Dot-dash lines are the compressed directions of SiO4 tetrahedra parallel to the a r axis. Twisting of SiO4 is represented by angles formed by dot-dash lines and O1–O2 and O3–O4 bonds. The O1–O3 and O2–O4 bonds correspond to the SiO4–ZrO8 shared edge in the zircon structure.
Table 4. Comparison of bond distances (Å) and angles (°) for reidite and zircon.

Although the SiO4–ZrO8 shared edges disappear, the ZrO8–ZrO8 shared edges remain through the phase transition. The ZrO8–ZrO8 shared-edge length in reidite is longer than that in zircon despite the closer Zr–Zr distance. As far as Zr4+–Zr4+ repulsion between ZrO8–ZrO8, this cation–cation repulsion contributes a structural destabilisation energetically. We can deduce that the structural stability brought by the disappearance of SiO4–ZrO8 shared edges overcomes the instability from enhanced Zr4+–Zr4+ repulsions. If this hypothesis is correct, we can conclude that the Si4+–Zr4+ repulsion is stronger than the Zr4+–Zr4+ repulsion.
Radiation-damaged natural zircon
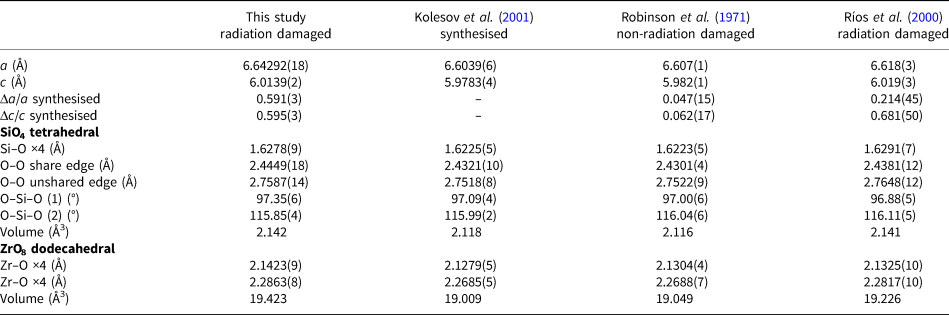
To compare with previous studies of natural zircon (Robinson et al., Reference Robinson, Gibbs and Ribbe1971 and Ríos et al., Reference Ríos, Malcherek, Salje and Domeneghetti2000) and synthetic zircon (Kolesov et al., Reference Kolesov, Geiger and Armbruster2001), their structural information is listed in Table 5. Robinson et al. (Reference Robinson, Gibbs and Ribbe1971) investigated natural non-radiation-damaged zircon from a syenite in Kragerø, Norway, that contained only ~1 wt.% Hf. Ríos et al. (Reference Ríos, Malcherek, Salje and Domeneghetti2000) used radiation-damaged zircon from Sri Lanka (age 570 ± 20 Ma), whose composition was Zr0.99Hf0.01Si0.95O4 (1.3 wt.% Hf and <0.01 wt.% U). The lattice parameters of natural zircon are greater than those of synthetic zircon. On the basis of the lattice parameters of synthetic zircon, the ratios Δa/a and Δc/c of the non-radiation-damaged zircon are 0.047(15)% and 0.062(17)%, respectively, while those of the Okueyama zircon are 0.591(3)% and 0.595(3)%, respectively. The lattice expansion of the radiation-damaged zircon is obviously greater than that of the non-radiation damaged one.
Table 5. Comparison of structural parameters for radiation-damaged and non-radiation-damaged zircons.

When a zircon is subjected to a stress, the unit cell of the zircon structure elongates along the a z axis rather than along the c z axis (Hazen and Finger, Reference Hazen and Finger1979). However, the expansion in the Sri Lankan radiation-damaged zircon is greater along the c axis (Δc/c = 0.681(50)%) than the a axis (Δa/a = 0.214(45)%), where Δa/a and Δc/c represent the difference in lattice parameter between analysed sample and standard (Kolesov et al., Reference Kolesov, Geiger and Armbruster2001) divided with the lattice parameter of the standard. In studies of 239Pu-doped zircon and neutron-irradiated zircon, the net lattice expansion by radiation damage is almost equal, within 5.0 ×1018 α-decays/mg (Weber et al., Reference Weber, Ewing, Catlow, Díaz de la Rubia, Hobbs, Kinoshita, Matzke, Motta, Nastasi, Salje, Vance and Zinkle1998). Murakami et al. (Reference Murakami, Chakoumakos, Ewing, Lumpkin and Weber1991) suggested that point defects in the early stages of damage accumulation (<3.0 ×1015 α-decays/mg) undergo self-annealing in natural zircon under ambient conditions. We expect that the relaxation of the expansion along the a z axis is energetically more favourable than that along the c z axis. The Sri Lankan zircon underwent defect annealing over a long geological time period. The Okueyama zircon is younger and, moreover, the Okueyama granite consists of a single magma chamber, which solidified as a zoned pluton (Takahashi, Reference Takahashi1986). Accordingly, we conclude that Okueyama zircons did not undergo thermal recovery of the lattice expansion.
The differences between the Sri Lankan and Okueyama zircons appear in the SiO4 tetrahedron. The Si–O bond distances in radiation-damaged zircons are significantly longer than in non-radiation-damaged zircons. The increase in Si–O bond distances of radiation-damaged zircon comes from a disordered static displacement of atoms due to the α-decay event. Note that the Si vacancy also contributes to the expansion of the Si–O bond length in radiation-damaged zircon. The O–O shared-edge lengths of radiation-damaged zircon are longer than that of non-radiation-damaged zircon. In non-radiation-damaged zircon, effects of Si+4–Zr+4 repulsions are shielded by the shorter O–O shared-edge length. There are two kinds of O–Si–O bond angle in the zircon structure, as shown in Fig. 4: (1) the O–Si–O angle is with the shared edge between SiO4 and ZrO8; and (2) the O–Si–O angle is with the unshared edge. The O–Si–O (1) angle of the Sri Lankan zircon is smaller than that of the Okueyama zircon, which yields a shorter O–O shared-edge length (Table 5). As for the ZrO8 dodecahedron, the Zr–O bond distance, which links to Si–O bonds in the Sri Lankan zircon, is also shorter than that of the Okueyama zircon. The O–Zr–O (1) angle is with the shared edge between SiO4 and ZrO8. The O–Zr–O angle of the Sri Lankan zircon is smaller than that of the Okueyama zircon. The shorter Zr–O bond distances and O–O shared-edge lengths mean that the cation–cation repulsion between SiO4 and ZrO8 is suppressed more in zircon studied by Ríos et al. (Reference Ríos, Malcherek, Salje and Domeneghetti2000) than in the Okueyama zircon. Old Sri Lankan zircons are more structurally relaxed than the young Okueyama zircons. The relaxation of the expansion along the a axis may result from the suppression of the cation–cation repulsion between SiO4 and ZrO8.
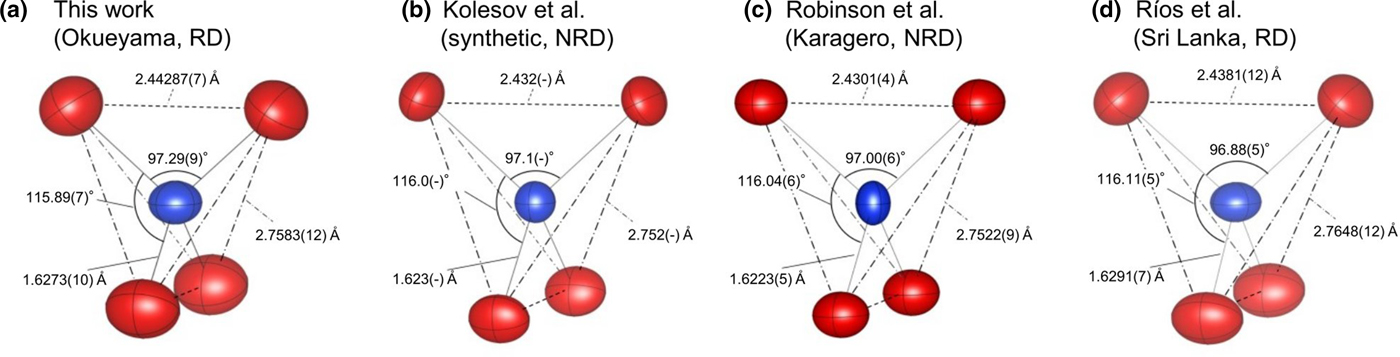
Fig. 4. SiO4 tetrahedron in the Okueyama zircon. Dotted and dot-dash lines correspond to the O–O shared edge and unshared edge, respectively. Thermal motions of atoms are drawn as ellipsoids of 99% probability. Note: RD = radiation damaged, NRD = non-radiation damaged.
This can be evaluated by comparing the amplitude of the anisotropic temperature factor as an index of repulsion between cations, as observed in garnet-type (pyrope) and rutile-type (stishovite) structures, where the amplitude decreases in parallel to the direction of repulsion between cations. However, in contrast, it is observed in this work that the amplitude increases in the vertical direction. We observed larger MSD parameters in the Okueyama zircon than in the non-radiation-damaged zircons. In radiation-damaged zircon, the larger MSD of the atoms contains the contribution of disordered static displacements of atoms due to the α-decay event. Although Zr and Si thermal ellipsoids in non-radiation-damaged zircon are almost spherical (U 11 ≈ U 33), the thermal ellipsoids in radiation-damaged zircon are obviously flattened (U 11 > U 33). The parameters U 11 and U 33 of Zr and Si are the MSD along the a z and c z axes, respectively. In particular, U 11 > U 33 implies Si4+–Zr4+ repulsion between SiO4 and ZrO8. Although the MSD parameters of all atoms in the Sri Lankan zircon show the same tendency as in the Okueyama zircon, those values are smaller than those for the Okueyama zircon. From this result, we expect the Si4+–Zr4+ repulsion in SiO4–ZrO8 to be weakened by thermal recovery over geological time. The static displacement of Si and Zr from the 8d site due to radiation damage contributes to the flattening of vibration ellipsoids perpendicular to the SiO4–ZrO4 shared edge.
Conclusion
As far as we know, this is the first report on structural data of reidite from single-crystal X-ray diffraction. The mechanism of the zircon–reidite transition can be understood as the twisting and translation of SiO4 tetrahedra, which accounts for the structural transformation without long-range atomic diffusion. The shared edge between the SiO4 tetrahedron and ZrO8 dodecahedron disappears in the transition from the zircon to reidite structure. The disappearance of the SiO4–ZrO8 shared edge yields structural stability according to Pauling's third rule.
We discussed the structural refinement of radiation-damaged Okueyama zircons by comparison with a previous study of synthetic and natural non-radiation-damaged and radiation-damaged zircons. Lattice expansions for the Okueyama zircon are different from those of the radiation-damaged Sri Lankan zircon, which is older. The Sri Lankan zircon underwent defect annealing over a longer geological time period. We conclude that Okueyama zircons did not undergo thermal recovery of the lattice expansion. This thermal relaxation appears especially at atomic distances in the SiO4 tetrahedron. The Okueyama zircon shows a longer Si–O bond and O–O shared-edge lengths. These structural features imply that the Si4+–Zr4+ repulsion in SiO4–ZrO8 are weakened by thermal recovery over geological time.
These structural changes in zircon, induced by pressure or thermal recovery from radiation damage, can be understood by considering the cation–cation repulsion in the SiO4–ZrO8 shared edge. Our study suggests that the cation–cation repulsion in a shared edge should not be ignored and provides fruitful insight into structural stability in edge-sharing compounds.
Supplementary material
To view supplementary material for this article, please visit https://doi.org/10.1180/mgm.2019.27
Acknowledgements
Mark Kurban, M.Sc., from Edanz Group (www.edanzediting.com/ac) edited a draft of this manuscript.