Introduction
In our 2015 paper (Cassingham et al., Reference Cassingham, Corkhill, Backhouse, Hand, Ryan, Vienna and Hyatt2015) an analysis of UK Magnox – ThORP blend glass dissolution kinetics was presented as a function of composition, temperature, pH and solution chemistry according to the Transition State Theory (Eyring, Reference Eyring1935). The modified version of this kinetic rate equation for glass (Grambow, Reference Grambow1985), is given by:
$$r_i = \vec kv_ia_{H^ +} ^\eta \exp \left( {\displaystyle{{ - E_a} \over {RT}}} \right)\left[ {1 - {\left( {\displaystyle{Q \over {K_g}}} \right)}^{\rm \sigma}} \right]$$where r i (in g m–2 d–1), is the dissolution rate of element i, 
$\vec k$ (in g m–2 d–1) the forward rate constant, v i the stoichiometric coefficient for element i, E a the activation energy, RT the product of the gas constant and the absolute temperature, 
$a_{H^ +} $ the hydrogen ion activity, η the power-law coefficient, Q (unitless) the activity product of the rate-limiting reaction, K g the pseudo-equilibrium constant for the rate-controlling phase and σ the overall reaction order. Under conditions of the single-pass flow-through method considered in this paper, calculation of the dissolution rate using equation 1 assumes that the saturation state of the system, given by Q/K g is equal to zero (Q ≈ 0), so that equation 1 becomes:
$$r_i\; = \vec kv_ia_{H^ +} ^\eta \exp \left( {\displaystyle{{ - E_a} \over {RT}}} \right)$$Taking logs gives:
$$\log R_i = \log \vec k + \eta {\rm pH} - \displaystyle{{E_a} \over {2.303RT}}$$where R i = r i/v i is the normalized release rate for element i.
Following further analysis of the data in Cassingham et al. (Reference Cassingham, Corkhill, Backhouse, Hand, Ryan, Vienna and Hyatt2015), it became apparent that the forward rate constant, activation energy, E a and the pH power law coefficient, η, were, erroneously calculated sequentially, rather than simultaneously. The fact that the solution conditions under which the data were collected were far from equilibrium, implying congruent dissolution, should have led to pH and temperature independent values for η. As can be seen in Tables 4–6 of our original article, these parameters are not independent. It also became apparent that there were minor errors on the tabulated dissolution rate data. Herein we present the corrected data and analysis, as performed by simultaneous non-linear regression of the dissolution rate data, according to McGrail et al. (Reference McGrail, Ebert, Bakel and Peeler1997).
Kinetic data for Magnox – ThORP blend nuclear waste glass simulants
Table 1 presents the normalized dissolution rates of MT25 (Magnox-ThORP glass with a 25 wt.% waste loading) and MT30 (Magnox-ThORP glass with a 30 wt.% waste loading) as a function of pH and temperature. The differences between each composition (ΔR i) are also highlighted. Table 1 is a corrected version of table 3 in Cassingham et al. (Reference Cassingham, Corkhill, Backhouse, Hand, Ryan, Vienna and Hyatt2015). We have also taken the opportunity to report some additional 90°C data, which were used to improve the multivariate data fitting.
Table 1. Normalized dissolution rate (in g m–2 d–1) of Si (R Si), B (R B) and Na (R Na) and for MT25 and MT30 blend simulated waste glass as a function of pH (pH measured at temperature [pH(T)] and pH calculated at room temperature [pH(23°C)] are both stated) and temperature, including the magnitude of the difference in normalized dissolution rate (ΔR i) between the two compositions.
In Cassingham et al. (Reference Cassingham, Corkhill, Backhouse, Hand, Ryan, Vienna and Hyatt2015) the values of the activation energies and the η values were obtained by separate linear regressions, while holding either pH or temperature constant. In fact, it has been shown that a multivariate analysis should be used to avoid erroneously indicating that E a depends on pH or η on temperature (McGrail et al., Reference McGrail, Ebert, Bakel and Peeler1997). In addition, the intrinsic rate constant, 
$\vec k$, was reported as the intercept of the pH power law coefficient regression. Table 2 gives the corrected values for all three terms as calculated by simultaneous linear regression over pH and 1/(2.303RT) using equation 3 for MT25 and MT30. By performing this analysis, the values obtained for η and E a for each species considered (B, Na and Si) are not significantly different, within the margins of error (Table 2), demonstrating that the MT25 and MT30 glass compositions undergo congruent dissolution.
Table 2. Calculated η values, activation energies and forward rate terms together with the correlation coefficient of the fit, and estimated error terms for MT25 and MT30 waste simulant glasses.
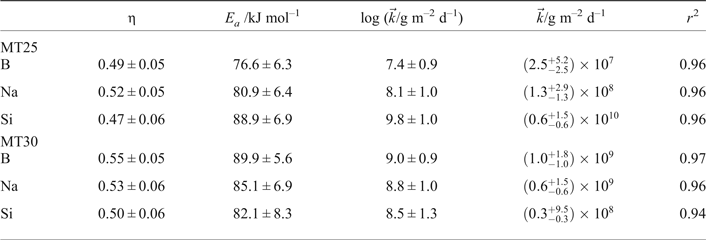
As the regression is conducted on log R i a value of 
$\log \vec k$, is obtained, hence this is reported along with the estimated errors in 
$\log \vec k$ in Table 2. For completeness, values of 
$\vec k$ and 
$\Delta \vec k$ (the estimated error in 
$\vec k$) are also reported in Table 2. As the estimated error, 
$\Delta ( {\log \vec k})$, in 
$\log \vec k$ is typically of the order of 10%, when standard propagation of error manipulation is undertaken, the value of 
$\Delta \vec k$ lies between two and three times the value of 
$\vec k$, implying that 
$\vec k$ may become negative which is physically impossible; accordingly the maximum negative error has been taken as being equal to 
$\vec k$. Estimating the error in 
$\vec k$ by evaluating 
$10^{[ {\log \vec k + \Delta ( {\log \vec k} )} ]}$ and 
$10^{[ {\log \vec k - \Delta ( {\log \vec k})}]}$ yields similar or slightly smaller negative errors and notably larger positive errors to those reported in Table 2. Overall the size of the 
$\Delta \vec k$ values indicate that the calculated 
$\vec k$ values have limited meaning.
Acknowledgements
The authors wish to thank Jim Neeway and Joe Ryan (PNNL) for helpful discussions in the re-analysis of the data. This work was funded in full by EPSRC under grant EP/F055412/1: Decommissioning Immobilisation And Management of Nuclear Wastes for Disposal (DIAMOND). CLC is grateful to EPSRC for the award of an ECR Fellowship (EP/N017374/1) and AJF would like to acknowledge the EPSRC Next Generation Nuclear Centre for Doctoral Training Centre for the provision of a studentship under grant EP/L015390/1. NCH is grateful to the Royal Academy of Engineering and the Nuclear Decommissioning Authority for funding.
