In a recent paper Zaffiro et al. (Reference Zaffiro, Angel and Alvaro2019) compiled from the literature an internally consistent dataset to constrain the volume and cell parameter variation with P and T of the mineral rutile, TiO2. The dataset consists of 111 data, made up of 17 direct measurements of elastic moduli, 12 direct measurements of dimensional changes with temperature by interferometry and 82 determinations of unit-cell parameters by diffraction. Some of these data were determined at elevated or low T at room pressure, and some at elevated P at room temperature. There are no available data at simultaneous non-ambient T and P. Assumptions must therefore be made about either the type of EoS and/or some of the values of its parameters in order to obtain a P–V–T EoS for rutile.
Zaffiro et al. (Reference Zaffiro, Angel and Alvaro2019) explored whether a thermal-pressure EoS could be used to fit the data of rutile. A Birch–Murnaghan EoS was used to describe the compressional behaviour of rutile at room temperature in combination with a Mie–Grüneisen–Debye (MGD) EoS to describe the thermal pressure. The MGD EoS is based on the quasi-harmonic approximation (Anderson, Reference Anderson1995), in which the thermal pressure is derived from a simplified phonon density of states (the Debye model) characterised by the Debye temperature θD:
It is assumed that q is a constant parameter. Therefore θD is only dependent on the volume V through the thermal Grüneisen parameter γ:
The parameters V 0, θD0 and γ0 are the values at room conditions. The increase in thermal pressure due to an increase in temperature above room temperature T 0 is then:
in which  $D\left({{{{\rm \theta }_D} \over T}} \right)$ represents the Debye function, R is the gas constant and n is the number of atoms in the formula unit corresponding to the molar volume V.
$D\left({{{{\rm \theta }_D} \over T}} \right)$ represents the Debye function, R is the gas constant and n is the number of atoms in the formula unit corresponding to the molar volume V.
The analysis of rutile by Zaffiro et al. (Reference Zaffiro, Angel and Alvaro2019) further assumed that the value of the parameter q was 0, which corresponds to the value of γ being independent of volume and thus the same for all P and T. This is consistent with the limited experimental data for rutile (see discussion on p. 343 of Zaffiro et al., Reference Zaffiro, Angel and Alvaro2019). With q = 0 the high-temperature measurements of the adiabatic bulk modulus (Isaak et al., Reference Isaak, Carnes, Anderson, Cynn and Hake1998) cannot be fit (Fig. 1) when the value of the pressure derivative of the bulk modulus  $K^{\prime}_0$ is ~7 a value derived from the available high-pressure data. Therefore Zaffiro et al. (Reference Zaffiro, Angel and Alvaro2019) concluded that a MGD EoS cannot fit the data of rutile. However, the bulk modulus in the MGD EoS at high temperatures also depends on the value of q (e.g. Anderson, Reference Anderson1995; Jackson, Reference Jackson1998; Kroll et al., Reference Kroll, Kirfel, Heinemann and Barbier2012; Angel et al., Reference Angel, Miozzi and Alvaro2019a), in addition to
$K^{\prime}_0$ is ~7 a value derived from the available high-pressure data. Therefore Zaffiro et al. (Reference Zaffiro, Angel and Alvaro2019) concluded that a MGD EoS cannot fit the data of rutile. However, the bulk modulus in the MGD EoS at high temperatures also depends on the value of q (e.g. Anderson, Reference Anderson1995; Jackson, Reference Jackson1998; Kroll et al., Reference Kroll, Kirfel, Heinemann and Barbier2012; Angel et al., Reference Angel, Miozzi and Alvaro2019a), in addition to  $K^{\prime}_0\;$and K 0. This can be seen clearly if the total pressure is written out in full, using a 3rd-order Birch–Murnaghan EoS (Birch, Reference Birch1947) for the isothermal compression:
$K^{\prime}_0\;$and K 0. This can be seen clearly if the total pressure is written out in full, using a 3rd-order Birch–Murnaghan EoS (Birch, Reference Birch1947) for the isothermal compression:
Fig. 1. (a) The volume variation of rutile with temperature is well-reproduced by all of the EoS. (b) The adiabatic Reuss bulk modulus data is well-fitted by both the previously published isothermal EoS (Zaffiro et al., Reference Zaffiro, Angel and Alvaro2019), and an MGD thermal-pressure EoS with q = 1.5. It is not fitted by an MGD EoS with  $K_{TR0}^{\prime} \sim 7.2$ and q = 0. The data sources are listed in table 1 of Zaffiro et al. (Reference Zaffiro, Angel and Alvaro2019).
$K_{TR0}^{\prime} \sim 7.2$ and q = 0. The data sources are listed in table 1 of Zaffiro et al. (Reference Zaffiro, Angel and Alvaro2019).
The bulk modulus at any P and T is  $K_T ={-}V\left({{{\partial P} \over {\partial V}}} \right)_T$. Equation 4 shows that the derivative (∂P/∂V)T depends on not only the first term, P(T 0, V), but also on the values of γ(V) and θD(V) in
$K_T ={-}V\left({{{\partial P} \over {\partial V}}} \right)_T$. Equation 4 shows that the derivative (∂P/∂V)T depends on not only the first term, P(T 0, V), but also on the values of γ(V) and θD(V) in  $\Delta P_{th}\lpar {T\comma \;V} \rpar $, which in turn depend on the value of q (Equations 1 and 2; Jackson, Reference Jackson1998; Kroll et al., Reference Kroll, Kirfel, Heinemann and Barbier2012). An increase in the value of q leads to a decrease in the bulk modulus at high temperatures and ambient pressure (Fig. 1).
$\Delta P_{th}\lpar {T\comma \;V} \rpar $, which in turn depend on the value of q (Equations 1 and 2; Jackson, Reference Jackson1998; Kroll et al., Reference Kroll, Kirfel, Heinemann and Barbier2012). An increase in the value of q leads to a decrease in the bulk modulus at high temperatures and ambient pressure (Fig. 1).
We have therefore re-fitted the self-consistent dataset of rutile with a MGD EoS including refinement of the parameter q using EosFit7c (Angel et al., Reference Angel, Gonzalez-Platas and Alvaro2014) and the same methods as Zaffiro et al. (Reference Zaffiro, Angel and Alvaro2019). Because the parameters θD0, γ0 and q appear in the expression for the thermal pressure (Equations 3, 4) their values are correlated with one another and the value chosen for the molar volume, V 0, at ambient conditions (e.g. Jackson, Reference Jackson1998; Kroll et al., Reference Kroll, Kirfel, Heinemann and Barbier2012). This correlation makes no significant difference to the properties of rutile (e.g. bulk modulus and thermal expansion) predicted by the MGD EoS, but it means that the parameter values are only valid when used with the chosen value of V 0. We therefore rescaled the experimental data for volumes (Zaffiro et al., Reference Zaffiro, Angel and Alvaro2019) to a common V 0 = 18.82 cm3/mol (Holland and Powell, Reference Holland and Powell2011), and then refined its value to allow for the various small inconsistencies in ‘room’ conditions between experimental datasets. We also removed the over-weighting of the room-pressure determination of the bulk modulus (Isaak et al., Reference Isaak, Carnes, Anderson, Cynn and Hake1998) which is necessary to stabilise refinement of the parameters of the isothermal-type EoS (Zaffiro et al., Reference Zaffiro, Angel and Alvaro2019).
The simultaneous refinement of all EoS parameters for the MGD EoS is stable and the refined parameter values are listed in Table 1. In particular, the refined value of γ0 = 1.40(2) agrees with the values estimated from experiments (Isaak et al., Reference Isaak, Carnes, Anderson, Cynn and Hake1998). With q = 1.5(7), γ is predicted to increase slightly with increasing temperature at room pressure, for example γ = 1.44 at 1100 K. Figure 1a shows that the volume variation of rutile with temperature is equally-well described by the MGD EoS with q = 0 or q = 1.5, as well as the isothermal type of EoS (Zaffiro et al., Reference Zaffiro, Angel and Alvaro2019). Figure 1b shows that the high-temperature bulk modulus data of rutile is reproduced with q = 1.5 and a value of  $K^{\prime}_0$ = 7.2(5) that is consistent with the high-pressure data. Therefore, the conclusion drawn by Zaffiro et al. (Reference Zaffiro, Angel and Alvaro2019) that the MGD EoS cannot fit the published data of rutile is incorrect, as it was based on the incorrect assumption that q = 0. Although rutile does exhibit anisotropic thermal pressure (fig. 3 in Zaffiro et al., Reference Zaffiro, Angel and Alvaro2019), the conclusion that this prevents a MGD EoS from fitting the data is also incorrect. This is not unreasonable because the unit-cell strains along the isochors are small, ~0.5% per 1000 K of temperature increase (fig. 3b in Zaffiro et al., Reference Zaffiro, Angel and Alvaro2019). Therefore the phonon mode wavenumbers will change along the isochor by an amount
$K^{\prime}_0$ = 7.2(5) that is consistent with the high-pressure data. Therefore, the conclusion drawn by Zaffiro et al. (Reference Zaffiro, Angel and Alvaro2019) that the MGD EoS cannot fit the published data of rutile is incorrect, as it was based on the incorrect assumption that q = 0. Although rutile does exhibit anisotropic thermal pressure (fig. 3 in Zaffiro et al., Reference Zaffiro, Angel and Alvaro2019), the conclusion that this prevents a MGD EoS from fitting the data is also incorrect. This is not unreasonable because the unit-cell strains along the isochors are small, ~0.5% per 1000 K of temperature increase (fig. 3b in Zaffiro et al., Reference Zaffiro, Angel and Alvaro2019). Therefore the phonon mode wavenumbers will change along the isochor by an amount  ${\sim} \mathop \sum \limits_i 0.005{\rm \omega }_{i0}{\rm \gamma }_i$ per 1000 K where ωi0 is the frequency at room conditions and the
${\sim} \mathop \sum \limits_i 0.005{\rm \omega }_{i0}{\rm \gamma }_i$ per 1000 K where ωi0 is the frequency at room conditions and the  ${\rm \gamma }_i$ are the components of the Grüneisen tensor for each phonon mode (Angel et al., Reference Angel, Murri, Mihailova and Alvaro2019b). Using the values of the
${\rm \gamma }_i$ are the components of the Grüneisen tensor for each phonon mode (Angel et al., Reference Angel, Murri, Mihailova and Alvaro2019b). Using the values of the  ${\rm \gamma }_i$ for rutile (Musiyachenko, unpublished data) the wavenumber shifts would not exceed 11 cm−1 per 1000 K along the isochor. For 10 of the 15 phonon modes of rutile, the calculated shifts are less than 1% of the phonon mode wavenumbers at room conditions, and therefore they might be expected to have a minimal effect on the thermodynamics.
${\rm \gamma }_i$ for rutile (Musiyachenko, unpublished data) the wavenumber shifts would not exceed 11 cm−1 per 1000 K along the isochor. For 10 of the 15 phonon modes of rutile, the calculated shifts are less than 1% of the phonon mode wavenumbers at room conditions, and therefore they might be expected to have a minimal effect on the thermodynamics.
Table 1. EoS parameters for rutile.
As noted above, the values of the parameters θD0 and γ0 are correlated with the value of V 0 in the least-squares procedure and, as a consequence, they are also sensitive to the weighting schemes applied to the experimental data, especially those close to room conditions. Extensive analysis shows that the variation in individual parameter values is less than 1 estimated standard deviation of the values. Nonetheless it is possible to reduce this correlation. Kroll et al. (Reference Kroll, Schmid-Beurmann, Sell, Buescher, Dohr and Kirfel2019) noted that the values of both θD and  ${{{\rm \gamma }\lpar V \rpar } \over V}$ vary very weakly with T and P and proposed a modification of the MGD in which they are kept constant. Because the first condition corresponds to a value of q = 0 (Eqn. 1) and the second to a value of q = 1 (Eqn. 2) we name this the ‘q-compromise’ thermal-pressure model. The removal of the parameter q greatly reduces the correlation between the remaining parameters whose values change very little compared to the full refinement of the MGD EoS (Table 1), and results in a marginally better quality of fit to the data (
${{{\rm \gamma }\lpar V \rpar } \over V}$ vary very weakly with T and P and proposed a modification of the MGD in which they are kept constant. Because the first condition corresponds to a value of q = 0 (Eqn. 1) and the second to a value of q = 1 (Eqn. 2) we name this the ‘q-compromise’ thermal-pressure model. The removal of the parameter q greatly reduces the correlation between the remaining parameters whose values change very little compared to the full refinement of the MGD EoS (Table 1), and results in a marginally better quality of fit to the data ( ${\rm \chi }_w^2 $) with one less parameter.
${\rm \chi }_w^2 $) with one less parameter.
At metamorphic conditions the volumes, bulk moduli and thermal expansion coefficients predicted by both versions of the MGD EoS (Table 1) and isothermal EoS are indistinguishable within the uncertainties derived from the least-squares fits of the parameters. As a consequence there are only small differences in the isomekes (Rosenfeld and Chase, Reference Rosenfeld and Chase1961) of rutile with garnets; those with the MGD EoS of rutile maintain positive slopes to higher temperatures than those of the isothermal EoS (fig. 5 in Zaffiro et al., Reference Zaffiro, Angel and Alvaro2019) before developing dP/dT < 0 with further temperature increase. The conclusion that rutile inclusions trapped in garnets during metamorphism should, from the EoS, exhibit negative pressures is still valid and independent of the type of EoS chosen to model the P–V–T behaviour of rutile.
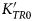 $K_{TR0}^{\prime} $ = 7.2(5), θD = 399(20) K, γ0= 1.40(2) and q = 1.5(7). This EoS predicts volumes, bulk moduli and volume thermal expansion coefficients for rutile at metamorphic conditions that are statistically indistinguishable from those predicted by the ‘isothermal’ type of EoS reported previously.
$K_{TR0}^{\prime} $ = 7.2(5), θD = 399(20) K, γ0= 1.40(2) and q = 1.5(7). This EoS predicts volumes, bulk moduli and volume thermal expansion coefficients for rutile at metamorphic conditions that are statistically indistinguishable from those predicted by the ‘isothermal’ type of EoS reported previously.
 $K_{TR0}^{\prime} \sim 7.2$ and q = 0. The data sources are listed in table 1 of Zaffiro et al. (2019).
$K_{TR0}^{\prime} \sim 7.2$ and q = 0. The data sources are listed in table 1 of Zaffiro et al. (2019).
In a recent paper Zaffiro et al. (Reference Zaffiro, Angel and Alvaro2019) compiled from the literature an internally consistent dataset to constrain the volume and cell parameter variation with P and T of the mineral rutile, TiO2. The dataset consists of 111 data, made up of 17 direct measurements of elastic moduli, 12 direct measurements of dimensional changes with temperature by interferometry and 82 determinations of unit-cell parameters by diffraction. Some of these data were determined at elevated or low T at room pressure, and some at elevated P at room temperature. There are no available data at simultaneous non-ambient T and P. Assumptions must therefore be made about either the type of EoS and/or some of the values of its parameters in order to obtain a P–V–T EoS for rutile.
Zaffiro et al. (Reference Zaffiro, Angel and Alvaro2019) explored whether a thermal-pressure EoS could be used to fit the data of rutile. A Birch–Murnaghan EoS was used to describe the compressional behaviour of rutile at room temperature in combination with a Mie–Grüneisen–Debye (MGD) EoS to describe the thermal pressure. The MGD EoS is based on the quasi-harmonic approximation (Anderson, Reference Anderson1995), in which the thermal pressure is derived from a simplified phonon density of states (the Debye model) characterised by the Debye temperature θD:
It is assumed that q is a constant parameter. Therefore θD is only dependent on the volume V through the thermal Grüneisen parameter γ:
The parameters V 0, θD0 and γ0 are the values at room conditions. The increase in thermal pressure due to an increase in temperature above room temperature T 0 is then:
in which $D\left({{{{\rm \theta }_D} \over T}} \right)$ represents the Debye function, R is the gas constant and n is the number of atoms in the formula unit corresponding to the molar volume V.
$D\left({{{{\rm \theta }_D} \over T}} \right)$ represents the Debye function, R is the gas constant and n is the number of atoms in the formula unit corresponding to the molar volume V.
The analysis of rutile by Zaffiro et al. (Reference Zaffiro, Angel and Alvaro2019) further assumed that the value of the parameter q was 0, which corresponds to the value of γ being independent of volume and thus the same for all P and T. This is consistent with the limited experimental data for rutile (see discussion on p. 343 of Zaffiro et al., Reference Zaffiro, Angel and Alvaro2019). With q = 0 the high-temperature measurements of the adiabatic bulk modulus (Isaak et al., Reference Isaak, Carnes, Anderson, Cynn and Hake1998) cannot be fit (Fig. 1) when the value of the pressure derivative of the bulk modulus $K^{\prime}_0$ is ~7 a value derived from the available high-pressure data. Therefore Zaffiro et al. (Reference Zaffiro, Angel and Alvaro2019) concluded that a MGD EoS cannot fit the data of rutile. However, the bulk modulus in the MGD EoS at high temperatures also depends on the value of q (e.g. Anderson, Reference Anderson1995; Jackson, Reference Jackson1998; Kroll et al., Reference Kroll, Kirfel, Heinemann and Barbier2012; Angel et al., Reference Angel, Miozzi and Alvaro2019a), in addition to
$K^{\prime}_0$ is ~7 a value derived from the available high-pressure data. Therefore Zaffiro et al. (Reference Zaffiro, Angel and Alvaro2019) concluded that a MGD EoS cannot fit the data of rutile. However, the bulk modulus in the MGD EoS at high temperatures also depends on the value of q (e.g. Anderson, Reference Anderson1995; Jackson, Reference Jackson1998; Kroll et al., Reference Kroll, Kirfel, Heinemann and Barbier2012; Angel et al., Reference Angel, Miozzi and Alvaro2019a), in addition to  $K^{\prime}_0\;$and K 0. This can be seen clearly if the total pressure is written out in full, using a 3rd-order Birch–Murnaghan EoS (Birch, Reference Birch1947) for the isothermal compression:
$K^{\prime}_0\;$and K 0. This can be seen clearly if the total pressure is written out in full, using a 3rd-order Birch–Murnaghan EoS (Birch, Reference Birch1947) for the isothermal compression:
Fig. 1. (a) The volume variation of rutile with temperature is well-reproduced by all of the EoS. (b) The adiabatic Reuss bulk modulus data is well-fitted by both the previously published isothermal EoS (Zaffiro et al., Reference Zaffiro, Angel and Alvaro2019), and an MGD thermal-pressure EoS with q = 1.5. It is not fitted by an MGD EoS with $K_{TR0}^{\prime} \sim 7.2$ and q = 0. The data sources are listed in table 1 of Zaffiro et al. (Reference Zaffiro, Angel and Alvaro2019).
$K_{TR0}^{\prime} \sim 7.2$ and q = 0. The data sources are listed in table 1 of Zaffiro et al. (Reference Zaffiro, Angel and Alvaro2019).
The bulk modulus at any P and T is $K_T ={-}V\left({{{\partial P} \over {\partial V}}} \right)_T$. Equation 4 shows that the derivative (∂P/∂V)T depends on not only the first term, P(T 0, V), but also on the values of γ(V) and θD(V) in
$K_T ={-}V\left({{{\partial P} \over {\partial V}}} \right)_T$. Equation 4 shows that the derivative (∂P/∂V)T depends on not only the first term, P(T 0, V), but also on the values of γ(V) and θD(V) in  $\Delta P_{th}\lpar {T\comma \;V} \rpar $, which in turn depend on the value of q (Equations 1 and 2; Jackson, Reference Jackson1998; Kroll et al., Reference Kroll, Kirfel, Heinemann and Barbier2012). An increase in the value of q leads to a decrease in the bulk modulus at high temperatures and ambient pressure (Fig. 1).
$\Delta P_{th}\lpar {T\comma \;V} \rpar $, which in turn depend on the value of q (Equations 1 and 2; Jackson, Reference Jackson1998; Kroll et al., Reference Kroll, Kirfel, Heinemann and Barbier2012). An increase in the value of q leads to a decrease in the bulk modulus at high temperatures and ambient pressure (Fig. 1).
We have therefore re-fitted the self-consistent dataset of rutile with a MGD EoS including refinement of the parameter q using EosFit7c (Angel et al., Reference Angel, Gonzalez-Platas and Alvaro2014) and the same methods as Zaffiro et al. (Reference Zaffiro, Angel and Alvaro2019). Because the parameters θD0, γ0 and q appear in the expression for the thermal pressure (Equations 3, 4) their values are correlated with one another and the value chosen for the molar volume, V 0, at ambient conditions (e.g. Jackson, Reference Jackson1998; Kroll et al., Reference Kroll, Kirfel, Heinemann and Barbier2012). This correlation makes no significant difference to the properties of rutile (e.g. bulk modulus and thermal expansion) predicted by the MGD EoS, but it means that the parameter values are only valid when used with the chosen value of V 0. We therefore rescaled the experimental data for volumes (Zaffiro et al., Reference Zaffiro, Angel and Alvaro2019) to a common V 0 = 18.82 cm3/mol (Holland and Powell, Reference Holland and Powell2011), and then refined its value to allow for the various small inconsistencies in ‘room’ conditions between experimental datasets. We also removed the over-weighting of the room-pressure determination of the bulk modulus (Isaak et al., Reference Isaak, Carnes, Anderson, Cynn and Hake1998) which is necessary to stabilise refinement of the parameters of the isothermal-type EoS (Zaffiro et al., Reference Zaffiro, Angel and Alvaro2019).
The simultaneous refinement of all EoS parameters for the MGD EoS is stable and the refined parameter values are listed in Table 1. In particular, the refined value of γ0 = 1.40(2) agrees with the values estimated from experiments (Isaak et al., Reference Isaak, Carnes, Anderson, Cynn and Hake1998). With q = 1.5(7), γ is predicted to increase slightly with increasing temperature at room pressure, for example γ = 1.44 at 1100 K. Figure 1a shows that the volume variation of rutile with temperature is equally-well described by the MGD EoS with q = 0 or q = 1.5, as well as the isothermal type of EoS (Zaffiro et al., Reference Zaffiro, Angel and Alvaro2019). Figure 1b shows that the high-temperature bulk modulus data of rutile is reproduced with q = 1.5 and a value of $K^{\prime}_0$ = 7.2(5) that is consistent with the high-pressure data. Therefore, the conclusion drawn by Zaffiro et al. (Reference Zaffiro, Angel and Alvaro2019) that the MGD EoS cannot fit the published data of rutile is incorrect, as it was based on the incorrect assumption that q = 0. Although rutile does exhibit anisotropic thermal pressure (fig. 3 in Zaffiro et al., Reference Zaffiro, Angel and Alvaro2019), the conclusion that this prevents a MGD EoS from fitting the data is also incorrect. This is not unreasonable because the unit-cell strains along the isochors are small, ~0.5% per 1000 K of temperature increase (fig. 3b in Zaffiro et al., Reference Zaffiro, Angel and Alvaro2019). Therefore the phonon mode wavenumbers will change along the isochor by an amount
$K^{\prime}_0$ = 7.2(5) that is consistent with the high-pressure data. Therefore, the conclusion drawn by Zaffiro et al. (Reference Zaffiro, Angel and Alvaro2019) that the MGD EoS cannot fit the published data of rutile is incorrect, as it was based on the incorrect assumption that q = 0. Although rutile does exhibit anisotropic thermal pressure (fig. 3 in Zaffiro et al., Reference Zaffiro, Angel and Alvaro2019), the conclusion that this prevents a MGD EoS from fitting the data is also incorrect. This is not unreasonable because the unit-cell strains along the isochors are small, ~0.5% per 1000 K of temperature increase (fig. 3b in Zaffiro et al., Reference Zaffiro, Angel and Alvaro2019). Therefore the phonon mode wavenumbers will change along the isochor by an amount  ${\sim} \mathop \sum \limits_i 0.005{\rm \omega }_{i0}{\rm \gamma }_i$ per 1000 K where ωi0 is the frequency at room conditions and the
${\sim} \mathop \sum \limits_i 0.005{\rm \omega }_{i0}{\rm \gamma }_i$ per 1000 K where ωi0 is the frequency at room conditions and the  ${\rm \gamma }_i$ are the components of the Grüneisen tensor for each phonon mode (Angel et al., Reference Angel, Murri, Mihailova and Alvaro2019b). Using the values of the
${\rm \gamma }_i$ are the components of the Grüneisen tensor for each phonon mode (Angel et al., Reference Angel, Murri, Mihailova and Alvaro2019b). Using the values of the  ${\rm \gamma }_i$ for rutile (Musiyachenko, unpublished data) the wavenumber shifts would not exceed 11 cm−1 per 1000 K along the isochor. For 10 of the 15 phonon modes of rutile, the calculated shifts are less than 1% of the phonon mode wavenumbers at room conditions, and therefore they might be expected to have a minimal effect on the thermodynamics.
${\rm \gamma }_i$ for rutile (Musiyachenko, unpublished data) the wavenumber shifts would not exceed 11 cm−1 per 1000 K along the isochor. For 10 of the 15 phonon modes of rutile, the calculated shifts are less than 1% of the phonon mode wavenumbers at room conditions, and therefore they might be expected to have a minimal effect on the thermodynamics.
Table 1. EoS parameters for rutile.
All EoS use a Birch–Murnaghan 3rd-order EoS for the compressional part at ambient temperature. For a full definition of the thermal part of the EoSs, see Angel et al. (Reference Angel, Alvaro and Nestola2018). These parameters are available in the supplementary materials (see below) and at www.rossangel.net as .eos files that can be used in the EosFit suite of programs.
As noted above, the values of the parameters θD0 and γ0 are correlated with the value of V 0 in the least-squares procedure and, as a consequence, they are also sensitive to the weighting schemes applied to the experimental data, especially those close to room conditions. Extensive analysis shows that the variation in individual parameter values is less than 1 estimated standard deviation of the values. Nonetheless it is possible to reduce this correlation. Kroll et al. (Reference Kroll, Schmid-Beurmann, Sell, Buescher, Dohr and Kirfel2019) noted that the values of both θD and ${{{\rm \gamma }\lpar V \rpar } \over V}$ vary very weakly with T and P and proposed a modification of the MGD in which they are kept constant. Because the first condition corresponds to a value of q = 0 (Eqn. 1) and the second to a value of q = 1 (Eqn. 2) we name this the ‘q-compromise’ thermal-pressure model. The removal of the parameter q greatly reduces the correlation between the remaining parameters whose values change very little compared to the full refinement of the MGD EoS (Table 1), and results in a marginally better quality of fit to the data (
${{{\rm \gamma }\lpar V \rpar } \over V}$ vary very weakly with T and P and proposed a modification of the MGD in which they are kept constant. Because the first condition corresponds to a value of q = 0 (Eqn. 1) and the second to a value of q = 1 (Eqn. 2) we name this the ‘q-compromise’ thermal-pressure model. The removal of the parameter q greatly reduces the correlation between the remaining parameters whose values change very little compared to the full refinement of the MGD EoS (Table 1), and results in a marginally better quality of fit to the data ( ${\rm \chi }_w^2 $) with one less parameter.
${\rm \chi }_w^2 $) with one less parameter.
At metamorphic conditions the volumes, bulk moduli and thermal expansion coefficients predicted by both versions of the MGD EoS (Table 1) and isothermal EoS are indistinguishable within the uncertainties derived from the least-squares fits of the parameters. As a consequence there are only small differences in the isomekes (Rosenfeld and Chase, Reference Rosenfeld and Chase1961) of rutile with garnets; those with the MGD EoS of rutile maintain positive slopes to higher temperatures than those of the isothermal EoS (fig. 5 in Zaffiro et al., Reference Zaffiro, Angel and Alvaro2019) before developing dP/dT < 0 with further temperature increase. The conclusion that rutile inclusions trapped in garnets during metamorphism should, from the EoS, exhibit negative pressures is still valid and independent of the type of EoS chosen to model the P–V–T behaviour of rutile.
Acknowledgements
This work was supported by ERC starting grant 714936 ‘True Depths’ to Matteo Alvaro. We thank our colleagues in Pavia, Mara Murri, Mattia Mazzucchelli and Kira Musiyachenko for discussions.
Supplementary material
To view supplementary material for this article, please visit https://doi.org/10.1180/mgm.2020.14