Let En+1, for some integer n ≥ 0, be the (n + 1)-dimensional Euclidean space, and denote by Sn the standard n–sphere in En+1, 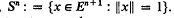. It is convenient to introduce the (–1)-dimensional sphere 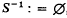, where 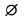denotes the empty set. By an i-dimensional subsphere T of Sn, i = 0 n, we understand the intersection of Sn with some (i+1)-dimensional subspace of En+1. The affine hull of T always contains, with this definition, the origin of En+1. is the unique (–1)-dimensional subsphere of Sn. 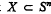By the spherical hull, sph X, of a set , we understand the intersection of all subspheres of Sn containing X. Further we set dim X: = dim sph X. The interior, the boundary and the complement of an arbitrary set 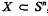, with respect to Sn, shall be denoted by int X, bd X and cpl X. Finally we define the relative interior rel int X to be the interior of 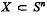with respect to the usual topology sphZ . For 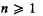each (n–1)-dimensional subsphere of Sn defines two closed hemispheres of Sn, whose common boundary it is. The two hemispheres of the sphere Sº are denned to be the two one-pointed subsets of Sº. A subset 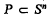is called a closed (spherical) polytope, if it is the intersection of finitely many closed hemispheres, and, if, in addition, it does not contain a subsphere of Sn. 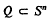is called an i-dimensional, relatively open polytope, 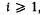, or shortly an i-open polytope, if there exists a closed polytope 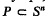such that dim P = i and Q = rel int P. 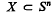is called a closed polyhedron, if it is a finite union of closed polytopes P1 …, Pr. The empty set 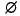is the only (–1)-dimensional closed polyhedron of Sn. We denote by 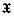the set of all closed polyhedra of Sn. 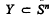is called an i-open polyhedron, for some 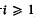, if there are finitely many i-open polytopes Q1 …, Qr in Sn such that 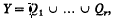, and dim 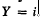. By we denote the set of all i-open polyhedra. Clearly 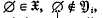for all 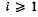, and each i-dimensional subsphere of Sn, 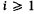, belongs to 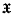and to 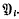, For each i-dimensional subsphere T of Sn, set . A map 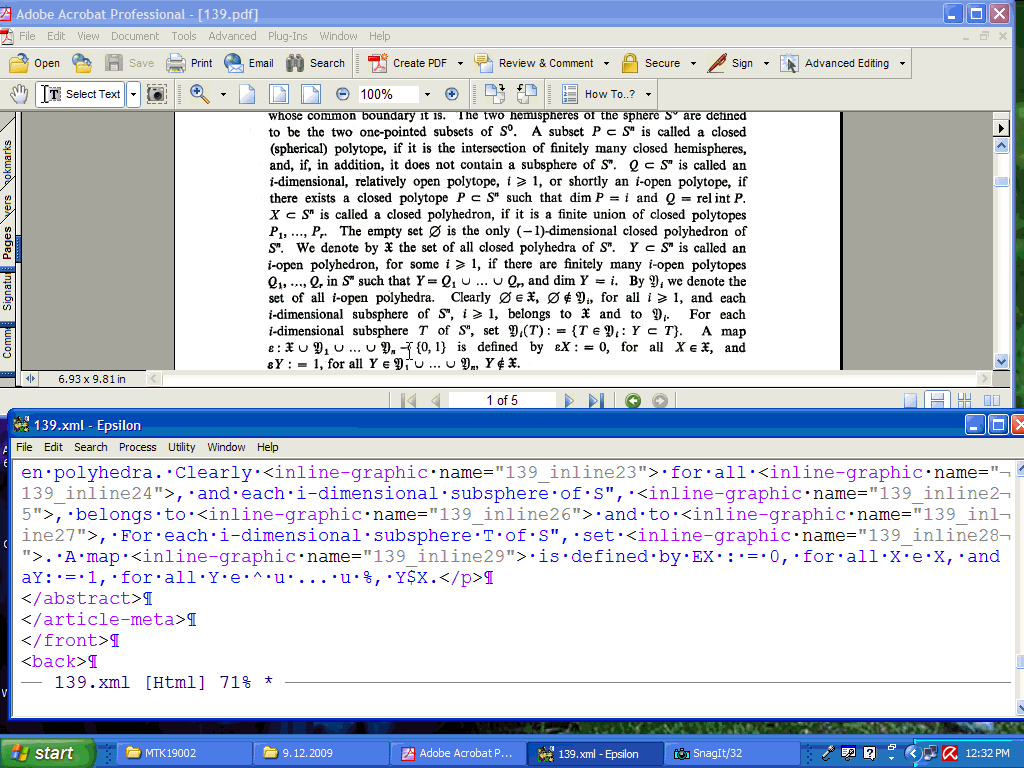is defined by 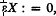, for all 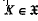, and, for all .

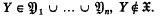In 1944 and 1945 H. Hadwiger [1, 2] proved the following theorems.

Theorem A. Let En be covered by n + 1 closed sets. Then there is one of the sets, within which all distances are realized.

Theorem B. Let En be covered by 4n−3 closed sets that are all mutually congruent. Then all distances are realized within each set.

Here a distance d is realized within a set S, if there are points x, y in S at distance d apart.

Introduction. Gale diagrams, and similar techniques, have been used in several recent investigations into the combinatorial properties of convex polytopes. Here we describe other applications, namely to problems concerning sections and projections of polytopes of a given combinatorial type. For example, in §4 we shall show that every n–dimensional convex polytope with at most n + 2 vertices possesses the universal shadow boundary (usb) property: If is a subcomplex of the boundary complex ℬ (P) of P, and set is homeomorphic to an (n – 2)-sphere, then there exists a polytope P', combinatorially isomorphic to P, such that the complex corresponding to is a shadow boundary of P'. We shall also show that this is the best possible result in that polytopes with n + 3 or more vertices do not, in general, have the usb property. A second application of the method, to be described in §5, is to the construction of non-realisable complexes.

Prime number theory is concerned with the distribution of primes in sequences of natural numbers, such as arithmetic progressions or polynomial sequences. An extensive range of such questions is embraced by

Hypothesis H (Schinzel, see [10]. Let f1, …, fgbe distinct irreducible polynomials in Z[x] (with positive leading coefficients) and suppose that f1 …fghas no fixed prime divisors. Then there exist infinitely many integers n such that each fi (n) (i = 1, …, g) is prime.

Introduction. This paper is concerned with an interpretation of some experiments on certain axisymmetric inertial oscillations of a rotating fluid in a thick spherical shell. These oscillations are the counterparts to the ones reported by Aldridge and Toomre† (1969) for a full sphere of rotating fluid. A description of the arrangements for both experiments is presented in A & T; some of the measured eigen-frequencies for spherical shells of rotating fluid given by Aldridge (1967) are presented here for comparison with values calculated from a variational principle.

In this note I settle a question which arose out of my first paper under the above title (cf. [1]), where I considered the classgroup C(Z(Γ)) of the integral groupring Z(Γ) of a finite Abelian group Γ. This classgroup maps onto the classgroup C() of the maximal order of the rational groupring Q(Γ), and C() is the product of the ideal classgroups of the algebraic number fields which occur as components of Q(Γ) and is thus in a sense known. One is then interested in the kernel D(Z(Γ)) of C(Z(Γ)) → C() and in its order k(Γ). In [1] I proved that, for Γ a p-group, k(Γ) is a power of p. I also computed k(Γ) for small exponents. My computation used crucially the fact that, for the groups Γ considered, the groups of units of algebraic integers which occurred were finite, i.e. that the only number fields which turned up were Q and Q(n) with n4 = 1 or n6 = 1. The numerical results obtained led me to the question whether in fact k(Γ) tends to infinity with the order of Γ.

A tournament is a relational structure on the non-empty set T such that for x, y ∈ T exactly one of the three relations

holds. Here x → y expresses the fact that {x, y} ∈ → and we sometimes write this in the alternative form y ← x. Extending the notation to subsets of T we write A → B or B ← A if a → b holds for all pairs a, b with a ∈ A and b ∈ B. is a subtournament of , and is an extension of , if T′ ⊂ T and →′ is the restriction of → to T′; we will usually write 〈′, → 〉 instead of 〈 ′, → ′〉. In particular, if |T − T′| = k, we call a k-poinf extension of .

It is shown that the equations governing the motion of a set of circular vortex rings, separated by distances large compared with their dimensions, can be written in canonical form.

Viscoelastic and viscoinelastic flows through straight ducts of different cross-sectional shapes have engaged the attention of a number of workers. These results may be found in all standard texts on the subject. The viscoelastic flows present a more complex analysis than the viscous flows, and for this reason a viscoelastic solution can rarely be obtained in an explicit and usable form. In this note, we obtain a simple formula relating the drag per unit length of the duct, the pressure gradient, the cross-sectional area, and the rate of flux across the section for a duct of arbitrary cross-section without explicitly solving for the physical components of velocity. This result may be of interest to workers experimenting with the non-Newtonian fluids. The recent work of Nigam and Arunachalam [1], which gives a similar result for the drag in viscous flows, can be deduced very easily from the present analysis.

Heilbronn [5] proved that for any ε > 0 there exists C(ε) such that for any real θ and N ≥ 1 there is an integer x satisfying

where ‖α‖ denotes the difference between α and the nearest integer, taken positively. The result is uniform in θ and so analogous to Dirichlet's inequality for the fractional parts of nθ. The result has been generalized to simultaneous approximations by Danicic [1] and Ming-chit Liu [6]. Here we shall extend the result to any finite number of simultaneous approximations when x2 is replaced by a k-th power.

A uniqueness theorem is obtained for a theory of linear thermoelasticity which allows for“second sound”. Propagation of acceleration waves in an isotropic material is also discussed.

Abstract. Bose-Chaudhuri-Hocquenghem and Justesen codes are used to pack equa spheres in n–dimensional Euclidean space with density Δ satisfying

for all sufficiently large n of the form m 2m, where m is a power of 4. These appear to be the densest packings yet constructed in high dimensional space.

Introduction. Let F be a subset of a group G (written additively) and let κ be a positive integer. Following [1] we shall write

and

We shall be concerned with two boundary value problems for the Falkner-Skan Equation

when –β is a small positive number. Our interest is in solutions of (1) which exhibit “reversed flow”; that is, solutions f such that f′(x) < 0 for small positive values of x. The boundary conditions which we wish to consider are

and

In a conversation with Professor R. G. Stoneham, he mentioned the estimate which he had found for a new type of exponential sum, namely

where p is a prime, g a primitive root mod p, pp × b, and l ≤ X ≤ p − 2. I found a proof and sent it to him. In correspondence with him and Professor D. A. Burgess,‡ I learnt that the estimate arose in Stoneham's work on normal numbers, in which they had been interested for some time. A proof of (1) will appear as a lemma in a paper by Stoneham [1] which has been submitted for publication. In fact, each of them has found several proofs of (1), and in particular, Burgess had found quite a simple one which is practically the same as my proof. However, my presentation led to an interesting generalization.

By a plane tree or rooted plane tree is meant a realization of a tree or rooted tree by points and arcs in the plane. By an isomorphism between two plane trees or rooted plane trees is meant an isomorphism in the usual sense for such trees which preserves the clockwise cyclic order of the edges about each node. In [2] Harary, Prins, and Tutte demonstrate how Polya's Theorem may be used to obtain formal expressions for the enumerating functions for unrooted, rooted, and other species of plane trees. In the process they obtain the explicit formula

for the number of nonisomorphic planted plane trees with n ≥ 1 edges. (A planted tree is a rooted tree with root at a node of degree one.)

Let a−N,…, aN be any complex numbers and let

If y1,y2,…,yM are any real numbers such that

one form of the large sieve inequality (see [1], Chapter 2 and the Appendix) asserts that

where yM+1 ≡ y1 (mod 1).

Integral geometry is the study of measures of sets of geometric figures. Commonly a measure of this sort is an integral of a density or differential form; the density is determined by the type of figure, but is independent of the particular set of such figures to which the measure is assigned. As one of the simplest examples, the area of a plane convex point set K is the integral over K of the density dx dy for points with Cartesian co-ordinates x, y. But when we assign a Hausdorff linear measure to the set of boundary points of K, we obtain a measure of quite another sort. This is representable as a Stieltjes integral of arc length density; here the density depends on the choice of K. The examples suggest examining measures for other sets of figures, where each such set is made up of all those figures from a certain class which support, in some sense, a convex body. Further, the examples lead us to expect that measures of this kind will appear as integrals of densities which may depend on the choices of . Here we treat a question of the type just described: to determine a measure for sets of q–flats which support a convex body.

In an earlier paper [10], I presented a base for the kernel, and in particular for the null space of I - λo K ((p.39). I remarked then that the base did not quite correspond to the arrangement given by Zaanen (cf. [13; p. 280], [14; pp. 339, 342]). The purpose of the present paper is to present an alternative base which does correspond to Zaanen's arrangement.

Let 2 = p1 < p2 < … be the sequence of consecutive prime numbers. Put dn = pn+l − pn. Turán and I proved [1] that the inequalities dn+1 > dn and dn+1 < dn both have infinitely many solutions. It is not known if dn = dn+l has infinitely many solutions. The answer is undoubtedly affirmative but the proof will probably be very difficult [2]. It was a great surprise and disappointment to us that we could not prove that dn+2 > dn+1 > dn has infinitely many solutions. We could not even prove that (− 1)n (dn+l − dn) changes sign infinitely often. It seems certain that the answer to both of these questions is affirmative and perhaps a simple proof can be found.