Given a sequence a(l), a(2), a(3), … of complex numbers such that a(n) ≤ 0(nc) for some c > 0, we define, for Im(z) > 0,

where q(λ) = exp (2πiz/λ), λ > 0 and a is a real number. Throughout this paper, for complex numbers x, w with x ≠ 0, xw = exp (w log x) and the principal branch is taken for the logarithm. Then it is easily verified that the infinite product converges absolutely and uniformly in every compact subset of the upper half plane H. Hence f(z) is holomorphic in H. The aim of this paper is to determine holomorphic functions in H defined by (1) which satisfy the special transformation formula

for some real number k under certain assumptions.

A recent paper [1] indicates that the beginnings of dynamic stall, near an aerofoil's leading edge, for instance, can be regarded as the finite-time nonlinear breakdown of a boundary layer subjected to an angle of attack above the critical value for the existence of a steady solution. The present theoretical study shows that the same non-linear breakdown can occur even in the below-critical regime. This happens particularly when reversed flow is present since short wavelength disturbances are then unstable and accumulate, for certain confined initial conditions, to force the finite-time collapse. A number of marginal cases with forward or reversed, subsonic or supersonic, oncoming motion are also noted and shed extra light on the instability and subsequent breakdown.

Let Φ : L → ℤ be a positive definite even unimodular quadratic form, L ≅ ℤn; we put f(x) = Φ(x)/2 and call (L, f) a lattice, for short. Let min f be the minimum of the numbers f(x) ≠ 0. Fixing n (a multiple of 8), one is interested in the largest possible minimum. It follows from the theory of modular forms (cf. Sloane [6]) that

Attempts to extend known two-dimensional results (Ursell, 1947) to the fully three-dimensional case can lead to unpredictable results. We show how the use of a variational approximation for a finite plane vertical barrier leads to apparently different results when different formulations are used. The reason for this is not so much that the method is wrong, but rather that several different limits are taken in the process, which are hard to control. We suggest an alternative matching scheme, based on Ayad and Leppington (1977), which holds for the case ka → ∞, l/a → ∞, kl → ∞, where / is the length of the barrier, a its depth and k the wavelength of the incident wave. The method is applied to a channel with impeding side walls, as a model of French's (1977) wave-energy device.

In this paper the authors formulate a boundary-initial value problem for a linear elastic porous body saturated with an inviscid fluid and establish a continuous dependence theorem (Theorem 2) and two uniqueness theorems (Theorems 3, 4) for a particular class of such continua. Theorems 2, 3 are proved without hypotheses on the sign of the constants and, if the domain is unbounded, under mild assumptions on the spatial asymptotic behaviour of the field variables. Theorem 4 holds for body-forces not equal to zero and, if the domain is unbounded, without restrictions upon the behaviour of the unknown fields at infinity, but under suitable conditions on the sign of the constants.

Let an be a non-increasing real sequence such that 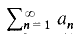converges; then clearly an ↓ 0. We shall ignore the trivial case where an = 0 for all large n, and so we assume that an > 0 for all n, from now onwards. In [1] J. B. Wilker introduced certain new sequences associated with the rate of convergence of 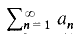, and obtained various relations between them, in order to investigate packing problems in convex geometry. Let us define

We write P, Q and T respectively for the inferior limits of pn, qn and tn, and P1, Q1 and T1 for the corresponding superior limits. Further, we put

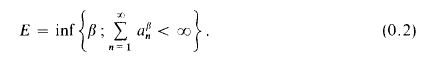
It is immediately clear from these definitions and our assumptions about an that

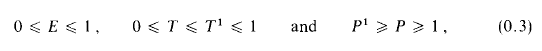
the latter since nan → 0 by Olivier's theorem [2, p. 124].

We consider the second order linear differential equation

where p and q are real-valued and p(t) > 0 for all t ≥ T. Our interest here is the oscillatory nature of solutions of (1.1). More particularly we consider the following questions, (I), (II) and (III).

We define s-dimensional Hausdorff outer measure on subsets of ℝn by

Here | | denotes the diameter of a set. The Souslin sets, which include the Borel sets, are Hs-measurable for any s ≥ 0.

In this note we present a simple way of obtaining the universal field of fractions of certain free rings as a subfield of an ultrapower of a (by no means unique) skew field. This method of embedding was discovered by Amitsur in [1]; our presentation uses Cohn's specialization lemma and the embedding is constructed in terms of full matrices over the rings in question (Theorem 3.2). In particular, if k is an infinite commutative field, the universal field of fractions of a free k-algebra can be realized as a subfield of an ultrapower of any skew extension of k, with centre k, which is infinite dimensional over k. Thus many problems concerning the universal field of fractions of a free k-algebra can be settled by studying skew extensions of k of relatively simple structure. More precisely and more generally, let E be a skew field with centre k and denote by R the free E-ring on X over k. Write U for the universal field of fractions of R and assume that U embeds in an ultrapower of a skew field D. Then by Łos' theorem, U inherits the first-order properties of D which can be expressed by universal sentences.

In [4] we initiated a study of K-Lusin sets. We characterized the K-Lusin sets in a Hausdorff space X as the sets that can be obtained as the image of some paracompact Čech complete space G, under a continuous injective map that maps discrete families in G to discretely σ-decomposable families in X [4, Theorem 2, p. 195]. Unfortunately, we cannot substantiate a second characterization of K-Lusin sets in completely regular spaces, given in the second part of Theorem 14 of [4].

Let l be a prime and let v ≥ 1 be an integer (when l = 2 we assume v ≥ 2). Any ring, A, with unit, possesses mod lv algebraic K-groups [B] denoted by Ki(A; Z/v) (i ≥ 0). For i ≥ 2, Ki(A; Z/lv) = [Pi(lv), BGLA +], the group of based homotopy classes of maps from the Moore space , to BGLA+, the classifying space of algebraic K-theory [G–Q ; W].

This paper is concerned with the solution of the following interesting geometrical problem. For what set of n points on the sphere is the sum of all Euclidean distances between points maximal, and what is the maximum?

Our starting point is the following surprising “invariance principle” due to K. B. Stolarsky: The sum of the distances between points plus the quadratic average of a discrepancy type quantity is constant. Thus the sum of distances is maximized by a well distributed set of points. We now introduce some notation to make the statement more precise.

Let K be a number field and E/K an elliptic curve. As is well known [3, 4,[ if K has class number 1, then there exists a global minimal Weierstrass equation for E. Our main goal in this paper is to prove the following converse to this statement.

In July 1982, I was asked by Prof. Jorgen Hoffmann-Jorgensen to construct an uncountable compact set K in the line which was symmetric about 0 and had the property that, for all n, the set of sums of n-tuples from K has measure 0. There are two equivalent conditions: the set of such sums should never contain an interval, or K* ≠ ℝ, where K* is the subgroup of (ℝ, +) generated by K. I did so, and the set I constructed had entropy dimension 0 (and thus also Hausdorff dimension 0). Hoffmann-Jorgensen showed that every set of entropy dimension 0 would exhibit the same behaviour. However, I did not believe that the essence of the example lay in its dimension, and I here modify my construction so that the set K has dimension 1 (and thus also entropy dimension 1), while K* ≠ ℝ, as before. By contrast, the Cantor ternary set has dimension log3(2), but the set of differences is the interval [ –1, 1], so that it does generate ℝ. It follows that the property under consideration is arithmetical rather than dimensional.

It is proved here that, if G is a positive definite integral ternary quadratic lattice of discriminant d and c is a squarefree integer which is primitively represented by the genus of G, then G primitively represents all sufficiently large integers of the type ct2, with g.c.d. (t, 2d) = 1, which are primitively represented by the spinor genus of G.

It has been shown in [1, 2] that it is sometimes possible to justify the uncoupled and quasi-static approximations which are commonly invoked to simplify the solution of initial and boundary value problems in the linear theory of thermoelasticity. The justification involves showing, among other things, that the temperature predicted by the coupled dynamic theory is approximated by a solution of the classical heat equation.

A study is made of Stokes flows in which a line rotlet or stokeslet is in the presence of a circular cylinder in a viscous fluid. In contrast to the Stokes Paradox for flow past an isolated cylinder, it is shown that if either type of singularity, with suitably chosen strength and location, is present, there can exist a flow which is uniform at infinity. A similar phenomenon can occur when two equal cylinders rotate with equal and opposite angular velocities, and the flow pattern is then such that there is a closed streamline enclosing both cylinders.

For x, y ≥ 1, let Ψ(x, y) denote the number of positive integers less than or equal to x and free of prime factors greater than y. The behaviour of the function Ψ(x, y) has been the object of numerous articles (see e.g. Norton's memoir [5] and the bibliography there). It turns out that a good approximation to ψ(x, y)/x is given by ρ(log x/log y), where the function ρ(t) is defined for t ≥ 0 as the continuous solution of the equations

In 1942 Piccard [10] gave an example of a set of real numbers whose sum set has zero Lebesgue measure but whose difference set contains an interval. About thirty years later various authors (Connolly, Jackson, Williamson and Woodall) in a series of papers constructed F σ sets E in ℝ such that E – E contains an interval while the K-fold sum set

has zero Lebesgue measure for progressively larger values of k.

It is shown that every compact convex set in with mean width equal to that of a line segment of length 2 and with Steiner point at the origin is contained in the unit ball. As a consequence, the diameter with respect to the Hausdorff metric of the space of all such sets is 1. There also results a sharp bound for the Hausdorff distance between any two compact convex sets.