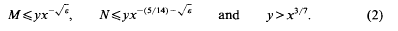In this short paper, we shall give a new estimate for the exponential sum S(H, M, N), where
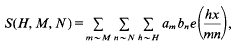
e( ξ,) = exp (2πiξ;) for a real number ξ, am and bn are complex numbers with |am| ≤ 1 and |bn| ≤ l, H, M, N ≤1, 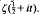 , x is a large number, ε is a sufficiently small positive number, and Y ≤ x(½)−ε (h ∼ H means 1≤h/H < 2 and so on). In making application of the Rosser-Iwaniec linear sieve of Iwaniec [6] to find almost primes in short intervals of the type (x − y, x], Halberstam, Heath-Brown and Richert [4] first considered an estimate for S(H, M, N) to the effect that
, x is a large number, ε is a sufficiently small positive number, and Y ≤ x(½)−ε (h ∼ H means 1≤h/H < 2 and so on). In making application of the Rosser-Iwaniec linear sieve of Iwaniec [6] to find almost primes in short intervals of the type (x − y, x], Halberstam, Heath-Brown and Richert [4] first considered an estimate for S(H, M, N) to the effect that

with MN as large as possible. Later, better estimates were given in Iwaniec and Laborde [7], and Fouvry and Iwaniec [3]. Of course, the most interesting case would be finding P2 numbers in a short interval (x − y, x]. The related estimate of [7] implies that (1) holds provided that