In this paper we shall be concerned with the following problem. Let k1 ≤ k2 ≤…≤ ks be natural numbers, λ1,…, λs be nonzero real numbers, not all of the same sign. Is it then true that the values taken by
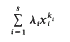
at integer points (x1,…, xs) ∈ ℤk are dense on the real line, provided at least one of the ratios λi/λj, is irrational? We shall refer to this, for brevity, as the inequality problem for k1,…, ks. Optimistically one may conjecture that the inequality problem is true whenever
